Dear Editor,
Following an emotionally intensive and fearful traumatic event, some individuals develop anxiety disorders such as post-traumatic stress disorder (PTSD) [1]. Cognitive therapy is used as an effective therapy to suppress fearful and/or traumatic memories; however, it fails in almost half of the anxious patients, resulting in the return of fearful memories [2]. Therefore, intensive research has been conducted to identify genetic, neural, biochemical, behavioral, or computational markers that predict vulnerability to developing PTSD, and/or the response to cognitive therapy [3].
In laboratory settings, Pavlovian fear conditioning and fear extinction represent models of PTSD and cognitive therapy [4]. During fear conditioning, an association between a neutral conditioned stimulus (CS+) and a strong and aversive unconditioned stimulus (US, e.g. electrical shock) occurs. Later on, presentation of the non-aversive CS+ alone is sufficient to elicit a strong conditioned response. During fear extinction, the conditioned fear responses are attenuated by repeated presentation of the CS+ alone. Although extinction can suppress the fear memory via different mechanisms, the original fear might recover following extinction [5–7].
Studies in PTSD patients, fear-conditioned human subjects and in experimental animals have identified markers that predict individual differences in terms of the strength of fear memory and/or the recovery of fear [3]. For instance, a higher level of PTSD symptoms before treatment predicts failure of cognitive therapy and recovery of symptoms [8]. A poor response to cognitive therapy in PTSD patients is associated with increases in amygdala activation [9] and decreases in medial prefrontal cortex and hippocampus activation [10]. However, it remains unclear whether such findings reflect predisposing risk factors that predict vulnerability to developing PTSD and resistance to cognitive therapy, or they represent pathological changes induced by the traumatic experience. Furthermore, fear conditioning studies in human subjects show that the degree of recruitment of the amygdala is correlated with the conditioned response during fear learning, memory retrieval, and extinction learning [11]. In mice, brain-derived neurotrophic factor levels in the medial prefrontal cortex predict successful extinction [12]. Fear reactivity predicts the strength of fear memory in rats [13]. Therefore, fear conditioning studies also provide markers that can predict the strength of fear memory and/or recovery of fear. To date, very few studies have attempted to implement computational approaches to identify mathematically-derived predictors of fear memory and recovery. Compared with the above behavioral, biochemical, or imaging approaches, such a mathematical approach would be simpler, less invasive, more cost-effective, and easily validated in experimental animals and human subjects. It has been noted that the quality of learning, as well as response severity, might be among the major determinants of the strength of fear memory and/or recovery of fear [3]. In support of this hypothesis, a study using mathematical analyses of human fear conditioning datasets found that the quality of extinction learning predicts the spontaneous recovery of fear in individual human subjects [14].
In the current study, we show that individual differences in the rate of fear learning (referred to as S) calculated from prediction error-based (Rescorla-Wagner [15]) or Hebb-based [16, 17] learning models, as well as the maximum unconditioned response during fear conditioning (Rmax), determine the quality of fear learning. A mathematically-derived value (S*Rmax) was found to correlate with the strength of fear memory, extinction rate, and spontaneous recovery of fear. Furthermore, we established a new computational model to simulate fear learning (the Integrative model). The new model improved the simulation of fear learning curves, reduced variations, and slightly improved the correlations between the S(Integrative)*Rmax value and fear memory, extinction, and recovery. We tested/validated our mathematical approach as well as our de novo Integrative model by using fear conditioning datasets from mice and human subjects (see Fig. 1A for the study design and Supplementary material 1 for the methods and technical details).
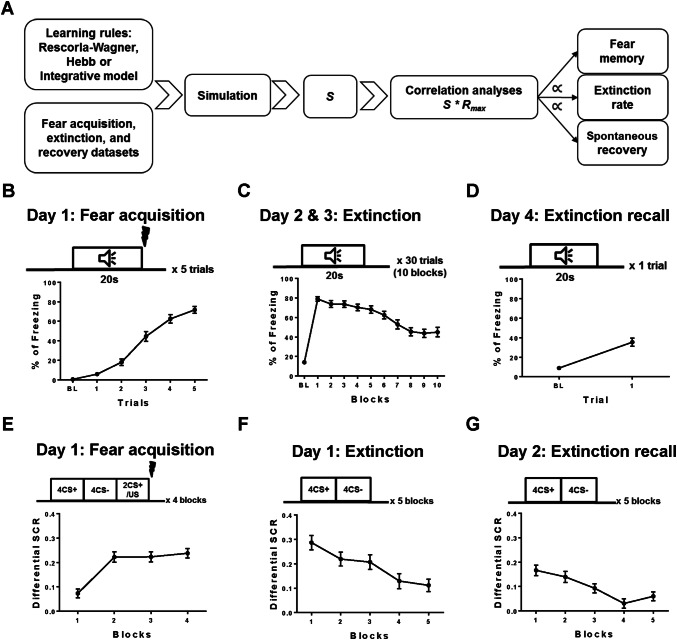
Fig. 1.
A Schematic of the design and logical flow of the current study. B–D Datasets of fear acquisition (B), extinction (C), and recovery (D) in mice. Behavioral readouts are presented as percentage of freezing (% of freezing). E–G Datasets of fear acquisition (E), extinction (F), and recovery (G) in human subjects. Data are presented as the differential skin conductance response (SCR). Mean ± SEM.
We first generated experimental datasets of fear acquisition and recovery in mice (n = 32 throughout the study). The mice were given five trials of tone–shock pairings. The freezing behavior increased steadily and significantly over the five trials, indicating successful fear learning (ANOVA repeated measure, F(31, 155) = 3.05, P < 0.0001, Fig. 1B). During extinction learning (days 2 and 3), the freezing behavior gradually declined over the 10 blocks of training, suggesting successful extinction of fear (F(31, 310) = 14.0, P < 0.0001; Fig. 1C). To evaluate the recovery of fear, an extinction recall test was conducted on day 4 (Fig. 1D). Following the presentation of a single CS+, some mice exhibited low freezing behavior; others exhibited high percentages of freezing (Fig. 1D; see Supplementary material 2 for detailed behavioral readouts of individual mice), suggesting variations in the recovery of conditioned fear following extinction. To extend our mathematical approach to human subjects, we obtained human fear conditioning (Fig. 1E), extinction (Fig. 1F) and extinction recall (Fig. 1G) datasets that were generated from a cohort of controls (n = 106), published by another group of researchers [18]. The same sets of data have also been published in an analytical study of individual differences in extinction learning [14]. We refer the readers to these two studies for detailed methods (see also Supplementary material 1). The data are presented in Fig. 1E–G here as received from the source (see Supplementary material 2 for the differential skin conductance response [SCR] of individuals during each phase).
Next, we applied Rescorla-Wagner (equation 1), Hebb (equation 2), and the Integrative model (equation 3) learning rules, ran simulations of fear learning curves until they reached/approached the asymptotic learning level, corrected them to the minimum error relative to the experimental data (equation 4), and generated representative curves for all the mice (see Supplementary material 1 for explanations of the models/equations).
| 1 |
| 2 |
| 3 |
| 4 |
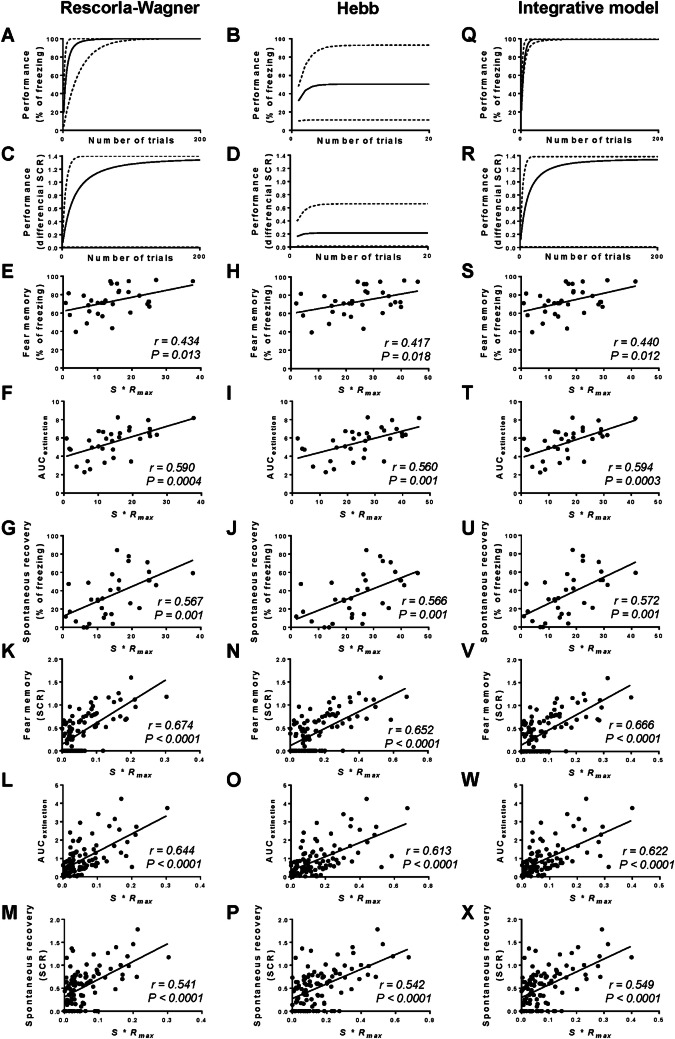
With the Rescorla-Wagner model, the mice learned the task very rapidly as revealed by the rapid increase in the percentage of freezing during early trials (Fig. 2A, solid line). The mouse curve approached the asymptotic learning level (~99.99%, percentage of freezing) after ~140 trials (Fig. 2A). With the Hebb learning rule, the mice also learned the task much faster (Fig. 2B, solid line). However, unlike the Rescorla-Wager simulation curve, the Hebb-derived curve approached the asymptotic level after only ~18 trials. Furthermore, the asymptotic level of the Hebb curve was lower (~50.50%; Fig. 2B). In datasets from human subjects, we used the same criteria and derived the learning curves based on the Rescorla-Wagner (Fig. 2C) and Hebb (Fig. 2D) learning models. With the Rescorla-Wagner model, participants learned the task and approached the asymptotic learning level (differential SCR: ~1.33) after ~173 trials (Fig. 2C, solid line). With the Hebb learning rule, they approached the asymptotic level (~0.21) after only ~12 trials (Fig. 2D, solid line; see Supplementary material 3 for all simulation data).
Fig. 2.
A–D, Q, and R Simulation curves of fear learning in mice (A, B, Q) and human subjects (C, D, R). Solid lines, average learning curves of individuals; dashed lines, highest (upper) and lowest (lower) learning curves (range). Simulation readouts are presented as the percentage of freezing (% of freezing) for mice, and as differential skin conductance response (SCR) for human subjects. E–P and S–X Correlations between S*Rmax and fear memory, extinction rate (AUCextinction), and recovery of fear in mice (E–J and S–U) and human subjects (K–P and V–X).
Importantly, regardless of the model used, the pattern of the learning curves of individual mice and human subjects differed in terms of speed of learning and maximum responses reached (Fig. 2A–D, dotted lines indicate minimum and maximum learning curves). Therefore, we concluded that S and Rmax might be among the key determinants shaping the dynamics of fear learning, and hence might provide a certain predictive power to identify individuals with stronger fear memory, slower extinction rate, and/or greater fear recovery.
Based on the above rationale, we calculated S from the simulation curves based on equations 1, 2, and 3 and obtained the value of Rmax from the fear conditioning data (Supplementary material 4). We defined the maximum unconditioned response during fear conditioning (Rmax) as the mean of two maximum emotional responses exhibited by individuals in response to presentations of the aversive US during learning in mice (percentage of freezing) and human subjects (SCR). The area under the curve of the extinction curve (AUCextinction) was used as an indicator of the extinction rate (a high AUC indicates slow extinction; Supplementary material 2). The conditioned response to the presentation of the first CS+ during extinction learning was used as a measure of fear memory in mice and human subjects. The conditioned response to the presentation of the first CS+ during the extinction recall test was used as a measure of the spontaneous recovery in mice and human subjects.
We checked the predictive power of S and Rmax by conducting a series of correlation analyses. In the mouse datasets, S(Rescorla-Wagner)*Rmax correlated with the strength of fear memory (Pearson’s test, r = 0.434, P = 0.013; Fig. 2E), extinction rate (r = 0.590, P = 0.0004; Fig. 2F), and strength of fear recovery (r = 0.567, P = 0.001; Fig. 2G). Similarly, S(Hebb)*Rmax correlated with the strength of fear memory (r = 0.417, P = 0.018; Fig. 2H), extinction rate (r = 0.560, P = 0.001; Fig. 2I), and fear recovery (r = 0.566, P = 0.001; Fig. 2J). In the human datasets, we conducted similar correlation analyses. Strikingly, S(Rescorla-Wagner)*Rmax positively correlated with the strength of fear memory (r = 0.674, P < 0.0001; Fig. 2K), extinction rate (r = 0.644, P < 0.0001; Fig. 2L), and fear recovery (r = 0.541, P < 0.0001; Fig. 2M). S(Hebb)*Rmax also correlated with the strength of fear memory (r = 0.652, P < 0.0001; Fig. 2N), extinction rate (r = 0.613, P < 0.0001; Fig. 2O), and fear recovery (r = 0.542, P < 0.0001; Fig. 2P).
Finally, we noted that the Rescorla-Wagner simulation curve required a large number of trials to reach the maximum behavioral readout and/or the asymptotic level of learning. Meanwhile, the Hebb simulation curve reached the asymptotic level too rapidly, and this level was far below the maximum experimental behavioral readout. Thus, we established a new learning model (the Integrative model), in which we integrated both teaching styles. In this model, we hypothesize that during early trials (when the shock is not expected), prediction error learning quickly teaches the circuitry, driving the behavioral readout close to maximum levels. Once the learning gain declines and the shock is anticipated (no discrepancy, no prediction error learning), the Hebb principle of synapse potentiation takes over the circuitry-teaching process (when cells fire together, the circuitry further wires together), leading to a rapid attainment of the target asymptotic level of memory and/or behavioral readout (see equation 3 and Supplementary material 1).
With the Integrative model, the mice learned the task rapidly and the simulation curve approached the asymptotic learning level after ~90 trials (Fig. 2Q, solid line). The dynamics of the Integrative model curve showed a significantly faster learning rate than that generated by the Rescorla-Wagner model and reached a significantly higher asymptotic level than that generated by the Hebb model (Fig. 2A, B, Q, solid lines). Interestingly, the individual variations were also reduced as indicated by the smaller range in the simulation data generated by the Integrative model than that generated by the other two models (Fig. 2 A, B, Q, dotted lines). We applied the same criteria to the human datasets and found similar patterns as the curve approached the asymptotic learning level after ~155 trials (Fig. 2R, solid line; see Supplementary material 3 for simulation data). Furthermore, we checked whether the S*Rmax value derived from our model using the criteria described above (S(Integrative)*Rmax, Supplementary material 4) retained similar predictive power. In mice, S(Integrative)*Rmax correlated with the strength of fear memory (r = 0.440, P = 0.012; Fig. 2S), extinction rate (r = 0.594, P = 0.0003; Fig. 2T), and strength of fear recovery (r = 0.572, P = 0.001; Fig. 2U). In the human datasets, S(Integrative)*Rmax positively correlated with the strength of fear memory (r = 0.666, P < 0.0001; Fig. 2V), extinction rate (r = 0.622, P < 0.0001; Fig. 2W), and fear recovery (r = 0.549, P < 0.0001; Fig. 2X). Thus, by using two well-established learning models and a de novo learning model that we established (the Integrative model) we identified two key determinants of the dynamics of fear learning. The mathematically-derived value of these determinants (S*Rmax) can, to a certain extent, predict the strength of fear memories, efficacy of extinction, and recovery of fear in mice and human subjects.
Theoretical studies suggest that associative fear learning follows either prediction error [15] or Hebbian [16] learning theories. The prediction error model views associative learning as a discrepancy between the predicted outcome of the conditioning trial and the actual unexpected outcome of the trial. The unexpected US during early trials is, therefore, more effective in supporting learning than the expected US during later trials [15, 19]. Studies have provided compelling evidence for the involvement of this model in dictating the neuronal circuitry during fear learning [19–21]. On the other hand, the Hebb learning model depends on potentiation of the CS+ synaptic inputs on postsynaptic cells in the lateral amygdala. The potentiation of the weak CS+ inputs is facilitated by postsynaptic depolarization induced by the co-occurring strong US inputs [16]. Studies also provide evidence for the involvement of this model in dictating the neuronal circuitry during fear learning [22, 23]. Thus, it remains debatable which learning model the associative fear learning might follow. Recently, it has been hypothesized that the circuitry and neurotransmitters mediating conditioned fear might be more complex than previously thought, and hence the brain might use both learning models during fear memory encoding [20, 22, 23].
Our results support the latter hypothesis. The simulation studies showed that both learning models successfully generated a fast learning phase during early trials, followed by a slow learning phase and finally reaching an asymptotic level of learning (Fig. 2A–D). Furthermore, S(Rescorla-Wagner)*Rmax and S(Hebb)*Rmax had similarly significant correlations with the strength of fear memory and fear recovery. Thus, both models are equally reliable in reflecting learning curve dynamics as well as in predicting the heterogeneity in the quality of fear learning, retention, and recovery among individuals. However, the Hebb-based simulation curves reached the asymptotic learning levels earlier than the Rescorla-Wagner-based curves. Moreover, the Rescorla-Wagner-based curves approached asymptotic learning levels close to those obtained by real experimental data (100 for mice and 1.4 for human subjects); meanwhile, the Hebb-based curves did not. Thus, there are differences between the models in terms of simulating fear learning processes. Such differences might stem from the different compositions of their equations. For instance, unlike the Rescorla-Wagner equation, the Hebb equation does not include a value for the asymptotic learning level (λ). As mentioned above, it is also possible that both teaching styles are involved in fear memory encoding; however, each style dictates the circuitry at a different phase during the encoding processes (i.e. early versus later trials). We established the Integrative model based on this hypothesis. Interestingly, this model resulted in improving dynamics of the simulation curves, reducing variations among individuals, and showing slightly better correlations between S(Integrative)*Rmax and certain behavioral readouts.
In conclusion, we introduce a mathematical approach to derive a value (S*Rmax) that predicts the strength of fear memory, extinction efficacy, and spontaneous recovery of fear. Our data support the view that individual differences in learning quality and/or response severity might predict vulnerability and resilience in certain psychiatric disorders such as PTSD [3, 14].
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
This work was supported by grants from the National Natural Science Foundation of China (31970942 and 81573408), a Fudan University-Shanghai Institute of Materia Medica Chinese Academy of Science joint grant (FU-SIMM20174015), a Shanghai Municipal Science and Technology Major Project (2018SHZDZX01) and ZJLab, and a Natural Science Foundation of Shanghai grant (16ZR1403200). We sincerely thank Dr. Catherine Hartley (Sakler Institute for Developmental Psychology, Weill Cornell Medical College, NY) and Dr. Elizabeth Phelps (Department of Psychology, New York University, NY) for the courteous gesture of providing us with the human datasets and instructing us on the calculation of differential SCR.
Conflict of interest
The authors declare no conflicts of interest related to this work.
Footnotes
Yan Gao and Wei Li have contributed equally to this work.
References
- 1.Kessler RC, Chiu WT, Demler O, Merikangas KR, Walters EE. Prevalence, severity, and comorbidity of 12-month DSM-IV disorders in the National Comorbidity Survey Replication. Arch Gen Psychiatry. 2005;62:617–627. doi: 10.1001/archpsyc.62.6.617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Foa EB. Psychosocial therapy for posttraumatic stress disorder. J Clin Psychiatry. 2006;67(Suppl 2):40–45. [PubMed] [Google Scholar]
- 3.Yehuda R, LeDoux J. Response variation following trauma: a translational neuroscience approach to understanding PTSD. Neuron. 2007;56:19–32. doi: 10.1016/j.neuron.2007.09.006. [DOI] [PubMed] [Google Scholar]
- 4.LeDoux J. The Emotional Brain: The Mysterious Underpinnings of Emotional Life. Simon & Schuster, 1996.
- 5.Myers KM, Davis M. Behavioral and neural analysis of extinction. Neuron. 2002;36:567–584. doi: 10.1016/S0896-6273(02)01064-4. [DOI] [PubMed] [Google Scholar]
- 6.Han SL, Xu TL. Unraveling the mechanisms of memory extinction. Neurosci Bull. 2018;34:385–388. doi: 10.1007/s12264-017-0198-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guo YC, Yuan T, Guo BY. The secret of fear memory attenuation: facing fears. Neurosci Bull. 2019;35:775–777. doi: 10.1007/s12264-019-00380-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Blanchard EB, Hickling EJ, Malta LS, Jaccard J, Devineni T, Veazey CH, et al. Prediction of response to psychological treatment among motor vehicle accident survivors with PTSD. Behav Therapy. 2003;34:351–363. doi: 10.1016/S0005-7894(03)80005-9. [DOI] [Google Scholar]
- 9.Bryant RA, Felmingham K, Kemp A, Das P, Hughes G, Peduto A, et al. Amygdala and ventral anterior cingulate activation predicts treatment response to cognitive behaviour therapy for post-traumatic stress disorder. Psychol Med. 2008;38:555–561. doi: 10.1017/S0033291707002231. [DOI] [PubMed] [Google Scholar]
- 10.Rauch SL, Shin LM, Phelps EA. Neurocircuitry models of posttraumatic stress disorder and extinction: human neuroimaging research[mdash]past, present, and future. Biol Psychiatry. 2006;60:376–382. doi: 10.1016/j.biopsych.2006.06.004. [DOI] [PubMed] [Google Scholar]
- 11.Phelps EA, Delgado MR, Nearing KI, LeDoux JE. Extinction learning in humans: role of the amygdala and vmPFC. Neuron. 2004;43:897–905. doi: 10.1016/j.neuron.2004.08.042. [DOI] [PubMed] [Google Scholar]
- 12.Peters J, Dieppa-Perea LM, Melendez LM, Quirk GJ. Induction of fear extinction with hippocampal-infralimbic BDNF. Science. 2010;328:1288–1290. doi: 10.1126/science.1186909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bush DE, Sotres-Bayon F, LeDoux JE. Individual differences in fear: isolating fear reactivity and fear recovery phenotypes. J Trauma Stress. 2007;20:413–422. doi: 10.1002/jts.20261. [DOI] [PubMed] [Google Scholar]
- 14.Gershman SJ, Hartley CA. Individual differences in learning predict the return of fear. Learn Behav. 2015;43:243–250. doi: 10.3758/s13420-015-0176-z. [DOI] [PubMed] [Google Scholar]
- 15.Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical Conditioning II: Current Research and Theory. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
- 16.Hebb DO. The Organization of Behavior. New York: Wiley & Sons; 1949. [Google Scholar]
- 17.Cooper RP, Cook R, Dickinson A, Heyes CM. Associative (not Hebbian) learning and the mirror neuron system. Neurosci Lett. 2013;540:28–36. doi: 10.1016/j.neulet.2012.10.002. [DOI] [PubMed] [Google Scholar]
- 18.Hartley CA, McKenna MC, Salman R, Holmes A, Casey BJ, Phelps EA, et al. Serotonin transporter polyadenylation polymorphism modulates the retention of fear extinction memory. Proc Natl Acad Sci U S A. 2012;109:5493–5498. doi: 10.1073/pnas.1202044109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.McNally GP, Johansen JP, Blair HT. Placing prediction into the fear circuit. Trends Neurosci. 2011;34:283–292. doi: 10.1016/j.tins.2011.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Johansen JP, Tarpley JW, LeDoux JE, Blair HT. Neural substrates for expectation-modulated fear learning in the amygdala and periaqueductal gray. Nat Neurosci. 2010;13:979–986. doi: 10.1038/nn.2594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yu K, Ahrens S, Zhang X, Schiff H, Ramakrishnan C, Fenno L, et al. The central amygdala controls learning in the lateral amygdala. Nat Neurosci. 2017;20:1680–1685. doi: 10.1038/s41593-017-0009-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Johansen JP, Diaz-Mataix L, Hamanaka H, Ozawa T, Ycu E, Koivumaa J, et al. Hebbian and neuromodulatory mechanisms interact to trigger associative memory formation. Proc Natl Acad Sci U S A. 2014;111:E5584–5592. doi: 10.1073/pnas.1421304111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Johansen JP, Hamanaka H, Monfils MH, Behnia R, Deisseroth K, Blair HT, et al. Optical activation of lateral amygdala pyramidal cells instructs associative fear learning. Proc Natl Acad Sci U S A. 2010;107:12692–12697. doi: 10.1073/pnas.1002418107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.