ProtExA: A tool for post-processing proteomics data providing differential expression metrics, co-expression networks and functional analytics

Abstract

ProTExA is a web-tool that provides a post-processing workflow for the analysis of protein and gene expression datasets. Using network-based bioinformatics approaches, ProTExA facilitates differential expression analysis and co-expression network analysis as well as pathway and post-pathway analysis. Specifically, for a given set of protein-gene expression data across samples, ProTExA: (1) performs statistical analysis and filtering to highlight the differentially expressed proteins-genes, (2) performs enrichment analysis to identify top-scored pathways, (3) generates pathway-to-pathway and pathway-to-gene networks (4) generates protein and gene co-expression networks using a variety of methodologies, and (5) applies clustering methodologies to identify sub-networks of co-expressed proteins-genes. The proposed web-tool is a simple yet informative tool, towards understanding and exploitation of protein and gene expression datasets, especially for those that do not have the expertise and local resources to replicate specific analyses in the context of collaborative and scientific data exchanging.

1. Introduction background & summary

In spite the fact that advancements in Mass Spectrometry (MS) have led to powerful technologies that allow for large-scale identification and characterization of proteins, the lack of end-user solutions for protein expression data analysis and visualization, remains an open issue. Current state-of-the-art tools for biomarker and pathway discovery have been mostly focused on the analysis of genomic and transcriptomic datasets, as opposed to proteomics software workflows [1]. Such tools although they provide significant information about the quality and biological variability of proteins-genes and their expressions across different samples, they are limited to the processing and statistical visualisation of raw data, as well as to the identification-quantification of proteins [2], [3], [4]. Existing pipelines for protein and gene expression data analysis [5], can be found in separate tools which in effect make almost impossible for someone without having a least of software development skills, to construct an overall analysis framework that leads to biomarker and pathway identification [6], [7]. Expanding on this type of research and development, our contribution here draws from recently introduced Systems Bioinformatics approaches that enable the possibility for understanding the cellular and molecular mechanisms as well as discovering a series of biomarkers related to specific diseases [5]. Recently, the scientific community has put significant effort towards the generation of inferred networks that can be exported from omics raw-data as well as to the discovery of candidate pathways behind a disease. Entropic approaches have shown to be effective in several experiments, indicating a challenging and promising direction in systems biology [8], [9].

In this line of thought, we propose ProTExA, a web-tool that extends the results differential expression analysis of proteins and genes, to the construction of protein-to-protein and gene-to-gene co-expression networks and to identification of significant pathways related to a specific experiment under study. ProTExA allows for: (1) rapidly performing extensive differential statistical analysis and filtering, (2) creating co-expression networks using a series of different mathematical models, (3) applying network clustering methodologies to identify sub-networks of co-expressed proteins-genes, (4) performing enrichment analysis to identify top-scored pathways related to specific diseases and (5) exporting pathway-to-pathway and pathway-to-gene networks that derive from enrichment analysis. The characterization and identification of protein and gene co-expression network topologies as well as the creation of diverse combinations of molecular and pathway networks generated by ProTExA, in a common framework of analysis, can pave the way for a deeper understanding of proteomic and transcriptomic expression datasets, towards the realization of the precision medicine vision.

2. Software description & methods

2.1. General design and implementation

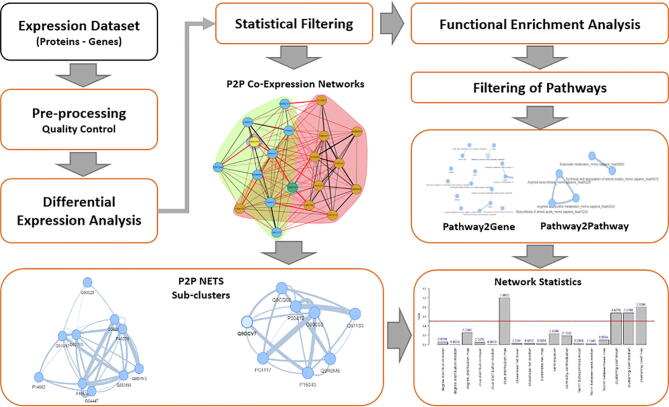
ProTExA comes with a frontend web interface that consists of the mainframe and a help page, written in HTML, PHP and JavaScript language environments. The mainframe provides six individual steps designed to guide the user until the end of the workflow process. The backend of ProTExA has been written in R environment, where several functionalities have been parallelised to achieve fast performance. Evaluation, testing and understanding of ProTExA functionalities can be easily performed by means of three available example datasets provided on the web site. The overall workflow of ProTExA combines three major pillars of analysis that are globally used in bioinformatics pipelines for omics data analysis, able to provide significant information about the functional nature and connectivity of protein-gene expressions and the involved biological pathways. These include: (i) statistical differential analysis of protein- and gene-expression datasets, in order to identify lists of top-scored proteins-genes related to the specific biological condition under study, (ii) enrichment analysis to identify related pathways and their functional connectivity, (iii) creation and clustering of protein-to-protein (P2P) and gene-to-gene (G2G) co-expression networks based on pure mathematical models. The employed network-based methodologies mainly draw from the graph theory, while important R packages employed for this work, include: (1) the igraph R package [10], for network manipulation, (2) the LIMMA R package [11] that has been widely used for analysing data from gene expression experiments, (2) the parmigene [12] for the construction of statistically inferred networks, and (3) the EnrichR package [13] for the enrichment analysis. The proposed tool is available online at the Bioinformatics Group web servers (http://bioinformatics.cing.ac.cy), located at the Cyprus Institute of Neurology and Genetics (CING). The overall ProTExA workflow provides six flexible wizard-based steps to the user, while individual processing stages are depicted in Fig. 1.

Fig. 1.

Schematic workflow of the ProTExA web-tool.

ProTExA allows the analysis of either protein or gene expression datasets and further provides: lists of statistically significant differentiated proteins and genes, co-expression networks, and pathways related to specific biological experiment. The tool is available online at the Bioinformatics Group web servers (http://bioinformatics.cing.ac.cy), located at the Cyprus Institute of Neurology and Genetics (CING).

Specifically, the pre-processing stage depicted in Fig. 1, involves the selection of appropriate imputation schemes, while automated scripts inform and prompt the user on how to proceed with the pre-processing of the input dataset. The differential expression analysis that follows, allows the user to decide among a series of normalisation schemes and transformation of the dataset. Statistical filtering options provide a series of available statistical parameters that allow the user to design his own filter for his dataset. These indicatively include adjustments based on p-value and fold-change parameters, sorting types, and maximum number top-scored items to keep. In analogous manner, pathway enrichment and filtering stages involve a multi-parametric framework of analysis that allow the user to discover top-scored pathways and visualise them in a network-based form. Finally, the creation and clustering of co-expression networks can be performed by means of several diverse methodologies that allow the user to evaluate co-expressions either at protein or at gene level. In the following, we provide analytical description of the main pillars and the associated pipelines as well as additional arguments that support the significance of this tool and its potential contribution to the scientific community.

2.2. Input data types and format specifications

ProTExA currently accepts a very simple and generic file format that includes either protein or gene expression information as well as the sample names and related conditions (classes), accordingly. The underlying format can be easily constructed by a non-experienced user. Current version of ProTExA supports only label-free protein expression datasets as well as gene expression datasets obtained from microarray gene expression datasets. The proposed web-framework supports protein expression datasets for 12 different types of species, as shown in Table 1. The data files used to support this type of service were obtained from the UniProt global repository (www.uniprot.org). A specific algorithm was developed to transform the data according to the needs for this web-tool, where all the available proteins (per species) were mapped to their corresponding genes. Updates to this repository are performed in a monthly basis.

Table 1.

List of supported organisms and related repositories.

#	Organism	Description	Repository
1	HUMAN	Homo sapiens	UniProt
2	MOUSE	Mus musculus	UniProt
3	RAT	Rattus norvegicus	UniProt
4	ARATH	Arabidopsis thaliana	UniProt
5	CAEEL	Caenorhabditis elegans	UniProt
6	CHICK	Gallus gallus	UniProt
7	DANRE	Danio rerio	UniProt
8	DICDI	Dictyostelium discoideum	UniProt
9	DROME	Drosophila melanogaster	UniProt
10	ECOLI	Escherichia coli (strain K12)	UniProt
11	SCHPO	Schizosaccharomyces pombe (strain 972/ATCC 24843)	UniProt
12	YEAST	Saccharomyces cerevisiae (strain ATCC 204508/S288c)	UniProt

2.3. Data pre-processing methods (imputation)

Depending on the way in which expression sets under study have been obtained, in several cases, additional pre-processing stages (usually defined as imputation process) may be required, prior performing any statistical analysis. To handle this requirement, additional methods for data imputation, were rooted in ProTExA web-tool in order to be performed to where is required. All schemes treat duplicated rows in the same way, by keeping one row that contains the mean value of all the duplicated rows per sample. In addition entries that include protein-gene names separated by semi-colon, the script keeps only the first name. These read as follows:

The default pre-processing scheme: This scheme deletes rows that include NA and empty values.

The extended pre-processing scheme: This scheme replaces cells that include NA and empty values with the overall mean raw value.

The advanced pre-processing scheme: This scheme replaces cells that include NA and empty values with the value of 0.00000001.

The k-nearest pre-processing scheme: For each missing value, the script finds the k-nearest neighbours by means of the Euclidean metric, confined to the columns for which that protein is NOT missing.

The k-nearest pre-processing scheme: For each missing value, the script finds the k-nearest neighbours by means of the Euclidean metric, where the average distance is calculated from the non-missing coordinates. If all the neighbour values are missing in a particular element, the overall column mean for that block of proteins is used [14], [15].

The mindet pre-processing scheme: This scheme performs the imputation of left-censored missing data using a deterministic minimal value approach. For a dataset with $n$ columns corresponding to biological samples and $p$ rows corresponding to proteins, the missing entries are replaced with a minimal value observed in that sample, which is estimated as being the q-th quantile (e.g. $q=0.01$) of the observed values in that sample.

The minprob preprocessing scheme: This scheme performs the imputation of left-censored missing data by random draws from a Gaussian Distribution (GD) centred in a minimal value. Having a dataset of n columns and p rows, the mean value of the GD is set to a minimal value observed in that sample, estimated as being the q-th quantile (e.g. q = 0.01) of the observed values in the sample. The standard deviation is estimated as the median of the protein-wise standard deviations, considering only proteins which present more than 50% of recorded values.

2.4. Differential expression analysis

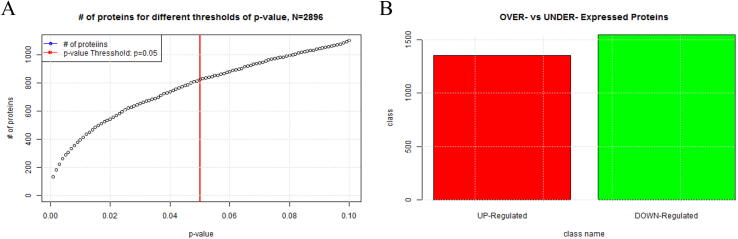
The differential expression analysis (DEA) of either protein- or gene-expression datasets employed by ProTExA, is performed by means of the LIMMA R-package [11]. The underlying package uses the Bayes Linear Modeling (BLM) approach [16], which has been widely used for the analysis of microarrays, RNA-Seq and quantitative PC. The BLM is a well-evaluated methodology adequate to provide statistically stable results for any kind and for any pair of numeric populations of values, even for very small data sets. The underlying method has been recently used by Efstathiou et al [2], on protein expression datasets with trustworthy results. Further to the above mentioned imputation schemes, ProTExA further provides a series of data normalization methods, as well as the ability to perform logarithmic transformation on the dataset under study, prior performing the LIMMA statistical package. It should be stressed that the LIMMA R-package requires the dataset under study to be first normalised and transformed into log2 scale, before performing the statistical analysis. In this line, an additional functionality by means of the Shapiro-Wilk test [17] has been also rooted into ProTExA, in order to test data normality and further inform the user whether the input requires (or not) normalisation. In analogous manner, an additional script examines and informs the user whether the dataset requires log2 transformation, accordingly. Users can perform several runs across different normalisation methods, until achieving the proper normalisation of the input dataset. At this stage of analysis, ProTExA provides additional statistical information, necessary for the understanding and evaluating the outcome of pre-processing stages. In particular, a dedicated algorithm that calculates the remaining number of proteins for different thresholds of p-value, allows to estimate the optional p-value threshold that could potentially be used for achieving an optimal filtering. Fig. 2A indicatively depicts the number of proteins for different thresholds of p-value

Fig. 2.

Evaluation of the differential expression analysis of proteins.

In the paradigm shown in Fig. 2A, it is observed that for values of p ≤ 0.05 the remaining significant proteins are less than 800 in total, suggesting that lower p-value threshold could be adequately used in order to increase the statistical significance and reduce the final protein list. Fig. 2B depicts an additional bar-chart that shows the overall number of over-expressed and under-expressed proteins-genes included in the analysis.

2.5. Obtaining top-scored proteins-genes from differential expression analysis

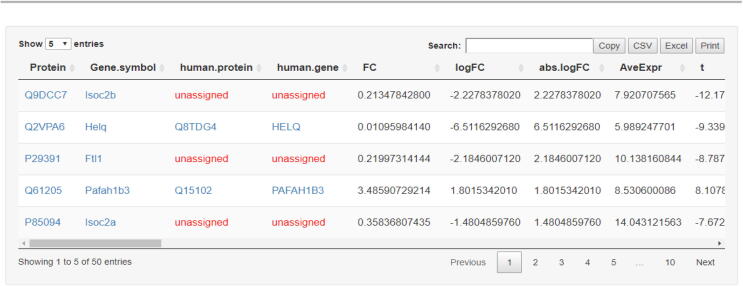
The obtained differentially expressed proteins-genes are further filtered by means of log-fold-change, p-value, sorting and other threshold-based parameters, all determined through a user-friendly interface and subjected to user’s selection criteria. For non-human protein experiments additional information is provided that includes the corresponding human proteins and their genes, to where this information is available. On the contrary, for human-based experiments this mapping involves mouse proteins and genes accordingly. Proteins that have not mapped with other organisms are characterized as “unassigned”. The final output of this process is depicted in Fig. 3, which includes the top-scored proteins, their corresponding genes and overall statistics.

Fig. 3.

Top-scored proteins obtained from differential expression analysis. The second available example was used to perform LIMMA statistics. The list includes the top-scored proteins and their statistics, sorted by means of p-value score. Protein symbols have been matched to their corresponding mouse gene symbols as provided by UniProt database, along with their human proteins and genes found, accordingly.

2.6. Creation of protein-to-protein and gene-to-gene co-expression networks

ProTExA provides an additional pipeline for creating statistically inferred protein networks for sets of filtered proteins-genes that derive from the differential expression analysis pipeline. Specifically, the top-scored proteins-genes obtained from differential expression analysis and filtering process, are forwarded to the network construction stage, where users can perform a series of co-expression network methodologies. These include the: (1) CLR (Context Likelihood or Relatedness Network) method [18], (2) ARACNE (Algorithm for the Reconstruction of Accurate Cellular Networks) [19], (3) C3NET [20], (4) the MRNET (Maximum Relevance Minimum Redundancy) [21], and (5) the WGCNA (Weighted correlation network analysis) [22]. Herein the construction of co-expression networks is performed by means of the parmigene R package [12], where descriptions and parameter setup read as follows.

The MRNET algorithm starts by selecting the variable $X_i$having the highest mutual information with the target$Y$. Then, it repeatedly enlarges the set of selected variables $S$ by taking the$X_k$that maximizes $I(X_k;Y)-mean(I(X_k;X_i))$ for all $X_i$ already in$S$. The procedure stops when the score becomes negative.

The CLR algorithm computes the score $\mathit{sqrt}({z_{\mathit{i}}}^2+{z_{\mathit{j}}}^2)$, for each pair of variables i, j, where $\mathit{zi}=max(0,(I(Xi;Xj)-mean(Xi))/sd(Xi))$ and $\mathit{mean}(Xi)$ and $\mathit{sd}(Xi)$ are the mean and the standard deviation of the mutual information values $I(Xi;Xk)$ for all $k=1,\cdots ,n$.

The ARACNEM algorithm: considers each triple of edges independently and removes the weakest one if $\mathit{MI}(i;j)<MI(j;k)\ast (1-tau)$ and$\mathit{MI}(i;j)<MI(i;k)\ast (1-tau)$, where $\mathit{MI}(i;j)$, is matrix of the mutual information tau a positive numeric value used to remove the weakest edge of each triple of nodes. By default ProTExA uses tau = 0.15.

The ARACNEA algorithm: considers each triple of edges independently and removes the weakest one if $\mathit{MI}(i;j)<MI(j;k)-eps$ and$\mathit{MI}(i;j)<MI(i;k)-eps$, where$\mathit{MI}(i;j)$, is matrix of the mutual information and eps a positive numeric value used to remove the weakest edge of each triple of nodes. By default ProTExA uses $\mathit{eps}=0.05$.

The C3NET algorithm consists of two main steps. The first step is the same as for relevance networks (RELNET), where all the non-significant mutual information values in the matrix are eliminated if statistically not significant. The second step of C3NET keeps all maximum valued mutual information values for each row in the matrix and sets the rest of the elements in the matrix zero (the diagonal of the matrix is ignored). The output is normally symmetric matrix but if the argument sym is set to FALSE then the output becomes non-symmetric. Herein, the sym argument has been set to FALSE.

The WGCNA algorithm computes the (weighted) Pearson correlation between the columns of × and the columns of y in a matrix.

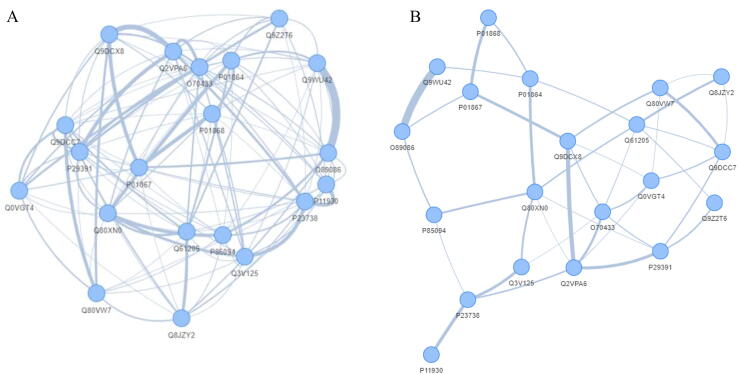
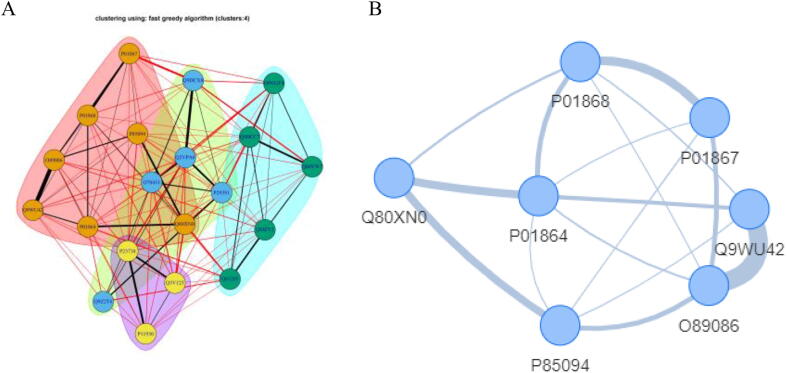
Algorithms based on mutual information concept usually connect all the examined nodes together by using the edges to characterize the weight of this connection. Thus, in most cases the obtained network may be a result of large and less informative concrete cluster, since everything is connected to everything. To handle this limitation, we further rooted additional filtering methodologies that allow the exclusion of either weak or strong edges from the network. Specifically, users can keep edges that do not exceed the overall mean edge of the network (week ones) or alternatively keep those that exceed the overall mean (strong ones). In this line, ProTExA further allows for this type of edge-filtering on the obtained networks and also provides a graphical representation that contains all the calculated network metrics/properties. Fig. 4A depicts an example of CLR protein-to-protein network as obtained from ProTExA web-tool for a set of 20 top-scored proteins, showing a strong relation between Q9WU42 and Q89086. Fig. 4B depicts the same CLR network showing only the edges that exhibit the mean edge-weight of the network.

Fig. 4.

Example of CLR protein-to-protein network (A) Overall CLR network derived from the analysis of a mouse protein experiment. (B) Filtered network showing only the edges that exhibit the mean edge-weight.

The underlying network in this case is clearer and more informative through this edge filtering, by keeping only the strongest relations between proteins. Herein, the execution of the above network inference algorithms usually fails when the given input (LIMMA output) has technical artefacts such as Inf and NA and other non-numeric values that may affect the related entropic measures used by the algorithm. Thus, we have internally applied an error-checking algorithm that fixes such issues in order to provide the optimal input as required by the specific network inference algorithm.

2.7. Employing clustering methodologies for co-expression networks

The above mentioned methodologies for co-expression networks require a large set of top-scored proteins-genes in order to be statistically meaningful. In effect this leads to the creation of large co-expression networks, difficult to be interpreted under a specific framework of analysis. Conforming to such limitation, ProTExA has been further enriched with a series of clustering algorithms that allow users to examine smaller clusters of these networks. Details on these methods read as follows:

The WALKTRAP algorithm, tries to find densely connected sub-graphs, also called communities in a graph via short random walks approach [23]. The idea is that short random walks tend to stay in the same community.

The FAST_GREEDY algorithm, tries to find dense sub-graphs, also called communities in graphs via directly optimizing a modularity score [24].

The LEADING_EIGEN algorithm tries to find densely connected sub-graphs in a graph by calculating the leading non-negative eigenvector of the modularity matrix of the graph [25].

The SPINGLASS algorithm tries to find communities in a graph in a reverse manner. A community is a set of nodes with many edges inside the community and few edges between outside it. Herein, this definition is reversed for edges having a negative weight: few negative edges inside the community and many negative edges between communities.

The edge betweeness score of an edge measures the number of shortest paths through it [26]. Herein the idea is that edges connecting separate modules potentially have high edge betweeness since all the shortest paths from one module to another must traverse through them. Thus if we gradually remove the edge with the highest edge betweeness score we will result to a hierarchical map that reveals the sub-clusters of the network.

The OPTIMAL algorithm calculates the optimal community structure of a graph, in terms of maximal modularity score, by maximizing the modularity measure over all possible partitions [27]. This can be achieved by transforming the modularity maximization into an integer programming problem.

Fig. 5A depicts a CLR network of 20 proteins, clustered in terms of the greedy optimization algorithm. Here the different colours refer to each sub-network while Fig. 5B indicatively depicts of the largest sub-cluster, marked with pink colour. The underlying sub-cluster could be considered for example as the group of proteins related to a specific disease of interest.

Fig. 5.

Co-expression protein-to-protein networks (A) Co-expression protein-to-protein network, clustered in terms of the greedy optimization algorithm. (B) Indicative plot of the largest sub-cluster is marked with pink colour. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The above mentioned methodologies can be used to separate the co-expression networks into sub-networks, and in effect to provide more comprehensive information related to a biological status being studied. ProTExA gives the possibility to the user to perform the underlying clustering either on un-weighted edges or on weighted edges accordingly, in order to compare the results. However, clustering co-expression networks may not always be a necessary process to all types of experiments especially for small networks where connectivity is biologically clear and compact.

2.8. Exporting network statistics

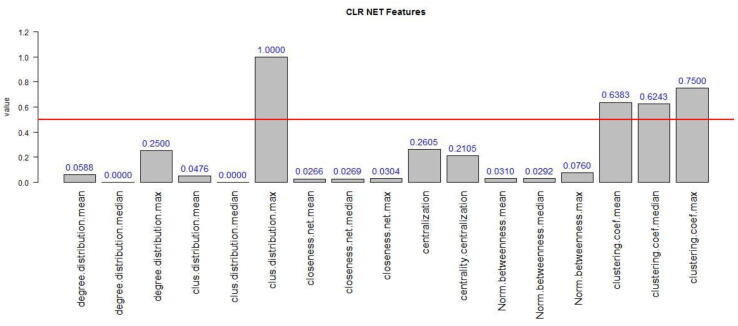
Network analysis methodologies by means of graph and complex-network theories, have become a benchmark approach towards identifying biomarkers, understanding their dynamics, their biological status and related biological mechanisms involved. Thus, in order to provide more statistics related to the complex nature of these co-expression networks, we further calculate their properties-features, using the igraph R package, for network manipulation [10]. Fig. 6 depicts a graphical representation which is automatically exported by the tool, and contains a series of network statistics-metrics. These indicatively include measures of median, mean and maximum values of: betweeness-centrality, degree distribution, closeness, and clustering coefficient. The reason for this implementation is to create a concrete web-framework of analysis adequate to provide a multilevel information content that is sufficient for further investigation and understanding.

Fig. 6.

A graphical representation of network metrics obtained from the CLR network Herein the obtained network features derive from four major categories: the degree, the betweeness, the closeness and the clustering coefficient of a network.

2.9. Enrichment analysis of differential expressed proteins-genes

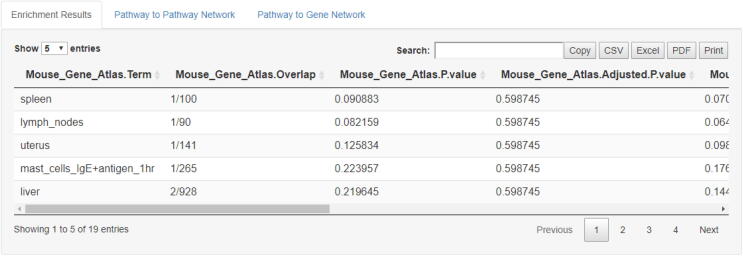
Pathway-based enrichment analysis allows for a comprehensive understanding of the molecular mechanisms related to complex diseases. In classical pathway analysis gene lists, usually obtained from any experimental-computational method, can be further analysed by relevant software tools that allow enrichment analysis to be performed based on prior knowledge gene-set libraries and pathways connected to them. Such tools may provide significant score-based information on how genes are involved into pathways and in effect, how pathways to a disease [28]. In this line, ProTExA can further perform enrichment analysis to the list of top-scored protein-genes that eventually derive from statistical analysis and filtering through the EnrichR package [13], which has been widely used to identify involved pathways from specific lists of genes. Since lists of top-scored proteins have been already mapped with their associated genes and vice versa, enrichment analysis is feasible by means of the gene symbols obtained from this mapping. ProTExA allows the user to select within a series of available database repositories to work with, depending on the biological condition under study. Filtering at pathway level can also be performed by means of specific pathway scores and thresholds. An example of top-scored pathways obtained through this type of analysis is depicted in Fig. 7. Herein, enrichment analysis was performed on the associated genes attached to the top-scored list of proteins included in the filtered sample. Analysis was performed by means of the “Mouse Gene Atlas” database supported by the EnrichR package.

Fig. 7.

Output of the enrichment analysis performed on the associated genes attached to the top-scored list of proteins. Enrichment analysis provides significant top-scored pathways sorted by specific score according to user’s selection. These include: the p-value score, the z-score and a combined score described in [13].

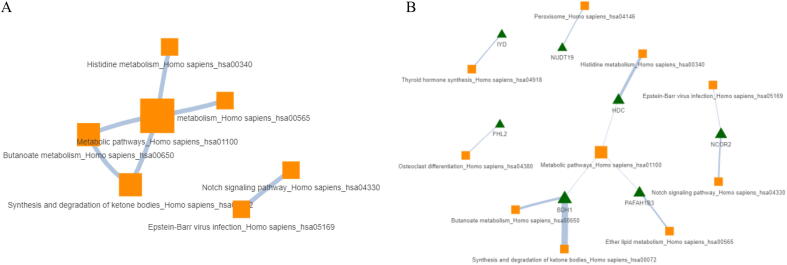
Users can, further export pathway-to-pathway and pathway-to-gene networks that are automatically constructed from the outcome of the above mentioned enrichment analysis. Fig. 8 depicts an example of these two networks accordingly. Specifically, Fig. 8A, depicts a pathway-to-pathway network for the 20 top-scored pathways, where the edges characterize the number of common genes between two pathways. The underlying commonality in calculated only for those genes that were strictly used as an input to the enrichment algorithm and not to all the available genes that are included in each pathway.

Fig. 8.

Obtained networks from enrichment analysis (A) Pathway-to-pathway network where the edges characterize the number of common genes between two pathways. (B) Pathway-to-gene network where edges characterize the calculated overlap rate between two nodes. Here the orange-squares refer to pathways, the green-triangles refer to genes and the size of each node refers to the degree. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

In analogous manner, Fig. 8B, depicts a pathway-to-gene network where the edges characterize the calculated overlap rate between two nodes, given by the following formula:

$$R=\frac{\mathit{number}ofgivengenesfoundinthepathway}{\mathit{number}oftotalavailablegenesinthepathway}$$

The above ratio describes the level of contribution of genes found, within the pathway.

3. Novelty & applications

Several research teams and laboratories dedicated in proteomics and transcriptomic data analysis, have all the appropriate equipment and tools to perform such analyses, while eminent tools such as Perseus [29], GiaPronto [30], LFQ-Analyst [31], Cytoscape StringApp [31], NetGestalt [32] and many other, can successfully perform individual analyses like some of the ones performed by ProTExA [2]. However, offering web-based services for omics data analysis, is an important forward technological step that aims to eliminate the expertise and the local resources required at a single computer level, as well as package compatibility issues, especially for stringent installations. In this line, ProTExA provides a freely available, well-designed and easy to use framework of analysis, for those that do not have the expertise and local resources to replicate specific analyses in the context of collaborative and scientific data exchanging. The tool includes the most commonly used processing stages required, starting from the analysis of pure protein-gene expression data, up to pathway discovery and creation of molecular co-expression networks. To the authors’ knowledge, there is not any non-commercial web-tool able to perform such entire workflow, both for protein and gene expression datasets, while the most comprehensive found, were those that reach at the stage of either protein or gene quantification, accordingly. Comparing with other tools at pathway discovery level, ProTExA further provides visualization of the obtained pathways, by means of pathway-to-pathway and pathway-to-gene networks, accordingly. Another significant feature is that the co-expression networks employed in ProTExA, do not draw from methodologies that use proteomics databases that include hundreds of conditions, cell lines and tissues. On the contrary, ProTExA draws from mathematical models that use entopic context and correlation-based mathematical models, to identify the level in which either protein- or gene-sets are co-expressed according to their expressions. It is worth mentioning that the top-scored outcome of proteins, genes and pathways obtained through ProTExA can be further supported and analysed by PathwayConnector [33], a recently introduced web-tool for pathway analysis. PathwayConnector draws from large database repositories like KEGG [34] and REACTOME [35], and further provides complementary pathway networks based on the functional connectivity between pathways of interest.

4. Discussion & conclusions

Casting biological systems as networks (graphs) and analysing their topology and their properties, has become a promising and useful Systems Bioinformatics approach [5], [33]. The powerful mathematical concept of the graph theory provides significant information towards understanding the organization of entities that sustain large and complex biological systems [36], [37]. Characteristically, Casas et al. (2015) who used network-based approaches to study MS-based proteomics data of spinal nerves, identified 19 biological processes potentially involved in retrograde motoneurodegeneration and neuroprotection after axonal damage [38]. The lack of integrated System Bioinformatics tools on post-proteomics and transcriptomic analysis, opens a relevant scientific field and interest on software development to this direction. In addition, the creation of co-expression networks have become a powerful approach towards understanding specific biological processes [39]. In this line, ProTExA is a valuable tool for research on post-proteomics and on post-transcriptomic data analysis, providing a bundle of network-based approaches rooted on the expression, co-expression and functional analysis of such datasets. ProTExA puts significant contribution to the understanding of protein and gene relationships through the proposed co-expression network approach, while at the same time offers a pipeline that fills a significant gap between protein-gene expressions and pathway identification.

5. Authors’ contributions

GM and GS carried out the design and the implementation of the web-tool. KS provided the data examples and evaluated the final version of the proposed tool.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.