COVID-19 scenario modelling for the mitigation of capacity-dependent deaths in intensive care

Abstract

Managing healthcare demand and capacity is especially difficult in the context of the COVID-19 pandemic, where limited intensive care resources can be overwhelmed by a large number of cases requiring admission in a short space of time. If patients are unable to access this specialist resource, then death is a likely outcome. In appreciating these ‘capacity-dependent’ deaths, this paper reports on the clinically-led development of a stochastic discrete event simulation model designed to capture the key dynamics of the intensive care admissions process for COVID-19 patients. With application to a large public hospital in England during an early stage of the pandemic, the purpose of this study was to estimate the extent to which such capacity-dependent deaths can be mitigated through demand-side initiatives involving non-pharmaceutical interventions and supply-side measures to increase surge capacity. Based on information available at the time, results suggest that total capacity-dependent deaths can be reduced by 75% through a combination of increasing capacity from 45 to 100 beds, reducing length of stay by 25%, and flattening the peak demand to 26 admissions per day. Accounting for the additional ‘capacity-independent’ deaths, which occur even when appropriate care is available within the intensive care setting, yields an aggregate reduction in total deaths of 30%. The modelling tool, which is freely available and open source, has since been used to support COVID-19 response planning at a number of healthcare systems within the UK National Health Service.

Electronic supplementary material

The online version of this article (10.1007/s10729-020-09511-7) contains supplementary material, which is available to authorized users.

Introduction

Coronavirus disease 2019 (COVID-19) is a highly contagious and virulent infectious disease caused by severe acute respiratory syndrome coronavirus 2, otherwise known as SARS-CoV-2 [1]. Given the speed at which the virus can infect populations and the severity of the resulting symptoms, it represents a significant and unprecedented challenge for many healthcare services; and one with which even the most developed countries have struggled to cope [2].

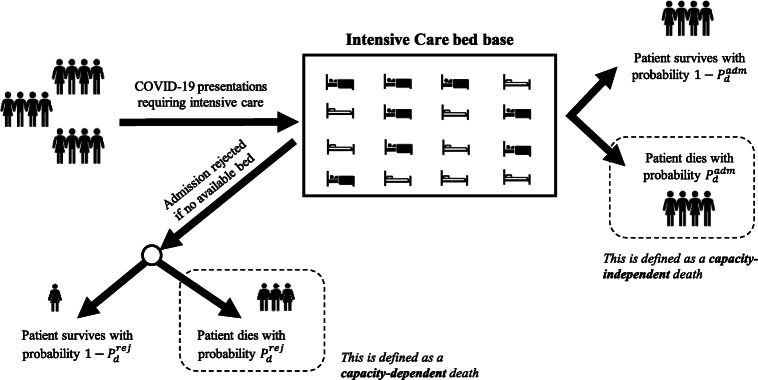
Managing a co-ordinated response to pandemics such as COVID-19 is critical. Unchecked, with a basic reproduction rate (R0) estimated at various magnitudes up to 6.5 [3, 4] and up to 14.7% of those infected requiring hospitalisation [5], the virus can propagate rapidly through a population, leading to peaks in demand for hospital care which are simply not possible to match with existing capacity [2, 3]. If, at such times, patients are unable to access the bedded care required then otherwise-avoidable death is likely to result [6]. The likelihood of this is particularly heightened when intensive care beds are required, since the necessary invasive ventilation and organ support cannot readily or safely be delivered in other settings [7]. Early case fatality rates from Wuhan are not expected to appreciate these capacity-dependent deaths (i.e. deaths that can be attributed to a patient unable to access the care they need due to lack of available capacity), since drastic efforts were taken by authorities to avoid health services becoming overwhelmed, in enforcing restrictions on movement and rapidly upscaling capacity through the building of two new hospitals [8]. Without improved treatment options, there is little that can be done to reduce COVID-19 deaths occurring when the patient has otherwise been cared for in the most appropriate hospital setting (i.e. capacity-independent deaths – see Fig. 1), and so national and local planners should focus on minimising the capacity-dependent deaths that are within their influence. That is, efforts should be made to ensure the right level of care is available to patients at the right time.

Fig. 1.

Illustrated difference between capacity-dependent and capacity-independent deaths (see Sect. 2 for further description of the probabilities $P_d^{\mathit{rej}}$ and $P_d^{\mathit{adm}}$)

The principal levers to reduce capacity-dependent deaths relate to managing the demand for and supply of intensive care resources. On the demand side, in absence of the means to treat or prevent disease, the slowing down of cases requiring admission using measures such as school closures and social distancing can reduce peak excess demand for intensive care, the so-called ‘flattening the curve’ [1]. On the supply side, efforts to create new and expand existing intensive care units increases the capacity to care for critically ill COVID-19 patients, resulting in fewer patients rejected with either no care or care in a sub-optimal setting (which increases the risk of death).

The ability to use a mathematical or computer model to experiment with ‘what if’ scenarios involving these levers is crucial to planners on the ground, in ensuring deaths over the course of the pandemic can be kept at a minimum. Public health authorities need to know what effect their policies on social distancing, home isolation and school closures (i.e. policies to reduce the effective reproduction number R from the basic reproduction number in absence of intervention R0) can have on decreasing or changing the shape over time of demand and, in turn, capacity-dependent deaths. Healthcare service planners and managers need to be cognisant of the likely benefits of their options around the flexing of bedded capacity, especially regarding the allocation between acute and intensive care beds (where the substantial efforts involved in increasing the latter must be well justified). With an appropriate model, the effect of these scenarios can be projected and used to make better informed strategic decisions when planning the response to the COVID-19 pandemic.

There has been much interest in the quantitative and mathematical modelling of COVID-19 for purposes of epidemiological forecasting [3, 9, 10], risk prediction [11], and health system vulnerability [12]. However, to the best of the authors’ knowledge there has been no explicit modelling of capacity-dependent deaths based on predicted demand. While Ferguson et al. [3] provide a detailed model of demand and the resulting deaths under various mitigation strategies, their work assumes a fixed mortality rate that is not dependent on the available capacity of the healthcare system. Our study addresses this limitation by estimating the excess mortality resulting from demand exceeding intensive care capacity under several mitigation scenarios.

Computer simulations of patient flow, demand and capacity have been used extensively to inform decision-making in healthcare [13–16]. This is especially true for the stochastic, discrete-event approach to simulation, as it is particularly suited to situations where entities (e.g. patients) ‘compete’ for limited resources such as hospital beds and operating room time [17]. Many simulation studies that have tackled questions around demand and capacity in healthcare, both under typical health system conditions (for example [18, 19]) and in periods of increased pressure such as mass casualty events [20] and winter bed crises [21, 22]. Specifically in the context of intensive care, simulation studies have addressed bed requirements by using the system dynamics simulation approach to evaluate different management policies [23], and applying analytical queuing models and simulations to the management of patient flow [24, 25]. For a general guide of how simulation modelling may be used in responding to the challenges of COVID-19, refer to [26].

This paper reports on the development and early real-life application of a purpose-built computer simulation model, designed for evaluating scenarios to mitigate capacity-dependent deaths in intensive care resulting from the COVID-19 pandemic. The remainder of this paper is structured as follows. Development of the model is covered in Sect. 2 alongside data requirements for model parameterisation and the scenarios considered for the simulation experiments. Illustrative results, obtained from application to a large teaching hospital in England at an early stage of the outbreak, are presented in Sect. 3. Finally, Sect. 4 contains a discussion on practical application, limitations, and possible further development of the model and tool.

Materials and methods

Model

The COVID-19 intensive care admission process is modelled as a multi-channel queuing system operating with loss. That is, patients requiring intensive care are rejected if there is no available service channel (bed). In Kendall’s notation [27] this is an M(t)/G/C/C queuing system: that is, in turn, a time-inhomogeneous Poisson arrivals process representing the epidemic curve for cases requiring intensive care admission; a general service distribution approximating patient length of stay in intensive care; C service channels; and a total system capacity of C patients, i.e. no space for waiting. For rejected intensive care presentations (lost arrivals), death occurs with probability $P_d^{\mathit{rej}}$ and survival with probability $1-P_d^{\mathit{rej}}$. For admitted intensive care presentations, death occurs with probability $P_d^{\mathit{adm}}$ and survival with probability $1-P_d^{\mathit{adm}}$.

Implementation of this model is through the iterative three-phased method of discrete event simulation [28]. In the case of this study, the types of simulation event consist of:

1. Arrival of patient requiring intensive care admission (unconditional event)

2. Patient admitted to intensive care (conditional event)

3. Patient died within intensive care (unconditional event)

4. Patient discharged alive from intensive care (unconditional event)

5. Patient admission rejected and patient died (conditional event)

6. Patient admission rejected and patient survived (conditional event)

The basis of the three-phased approach is in maintaining a calendar of unconditional events. The first phase is to step to the next chronological event in the calendar. This could be arrival or intensive care discharge or death (i.e. event type a, c or d as above). In the second phase the selected event is executed. In the third phase, any associated conditional event is also executed. So, for example, if a patient arrives (event type a) and there is an available service channel (e.g. a free intensive care bed) then the conditional event is that the patient is admitted (event type b) and the associated bed is flagged as unavailable. If, instead, there is no available service channel (bed) then the admission is rejected and the simulated patient either dies (event type e) or ultimately survives (event type f).

As the simulated events progress with each iteration, it is necessary to capture the state of the system over time. This keeps the event calendar up-to-date. For instance, if one of the events within an iteration involves a patient entering service (event type b), then the time at which they are discharged (sampled from the given length of stay distribution) is recorded in the calendar, as a future unconditional event of type d. Capturing the state of the system is also necessary in the generation of performance measures of interest, such as occupancy levels and patient outcomes.

During the simulation, events are iterated in line with the three-phased method until some terminating criterion is met. Here, this is given by the time at which some outcome has been reached for all simulated admissions for the given epidemic curve (for cases requiring intensive care admission), i.e. each sought admission has been either rejected or admitted and discharged or died (event types c-f). In other words, and given the time-inhomogeneous nature of the epidemic curve, this is a transient simulation model. As such, and in contrast to simulation models exploring steady-state behaviour, an otherwise necessary warm-up period is not required [29].

Running this simulation from start to finish offers just one possible explanation of how the pathway dynamics can play out and so, in order to capture the inherent stochasticity, it is necessary to perform an ensemble of replications. Each replication repeats the simulation with a different stream of random numbers from which the simulated arrivals, lengths of stay, and rejection probabilities of death and survival are generated. Outputs are then aggregated across these replications, with central estimates (based on the mean) and confidence intervals (at the 95% level) calculated for all simulation measures.

Note that the Strengthening the Reporting of Empirical Simulation Studies (STRESS) research checklist for discrete-event simulation studies (STRESS-DES) is provided within the supplementary material.

Application, data, and calibration

The model was applied to intensive care services at a major public hospital in England during the early stage of the outbreak in the UK (late March and early April 2020). Demand for intensive care admission at the hospital was estimated through local interpretation of nationwide projections contained in [3], which were made publicly available on 16 March 2020. This involved adjusting for local population size, demographics and hospital catchment area (Table 1) in our effort to interpret the national demand profiles. As similarly performed in [30], such data pre-processing was necessary given the absence of more granular projections during the early stages of the outbreak. The modelling reported in this study made use of two hypothetical strategies contained in [3] – a ‘do nothing’ and one involving ‘case isolation, home quarantine, and social distancing of those over 70’. The modelling also considers a ‘flattened’ version of this latter strategy, in order to appreciate the possibility that measures would have a greater effect than envisaged in slowing transmission of the disease, with the same level of demand but over a 50% longer period of time (Fig. 2).

Table 1.

Distribution of age within estimated hospital catchment area

Age bands	Proportion of hospital catchment
0–9	11%
10–19	10%
20–29	21%
30–39	15%
40–49	10%
50–59	10%
60–69	7%
70–79	6%
80+	11%

Fig. 2.

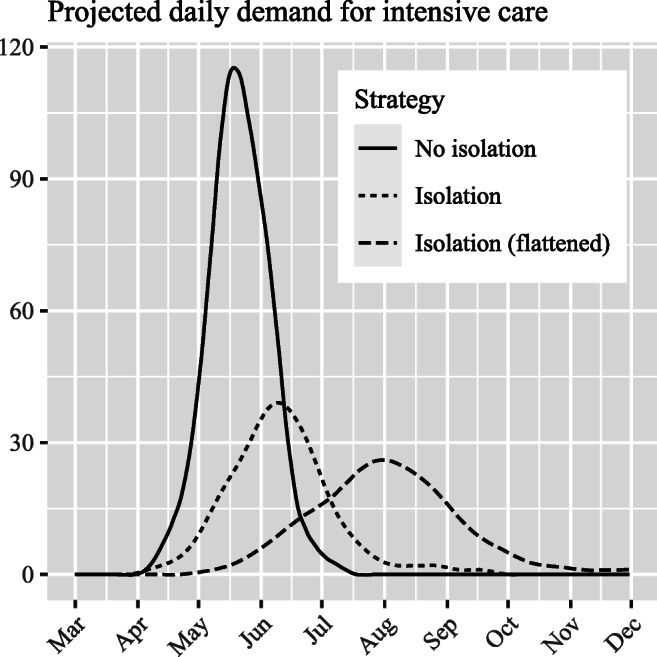
Epidemic curve for cases requiring intensive care, derived from modelling results in Ferguson et al. (2020). The No isolation strategy assumes no non-pharmaceutical intervention; Isolation strategy assumes case isolation, home quarantine, and social distancing of those over 70; and Isolation (flattened) represents a flattening of the Isolation strategy over a 50% lengthened period of time

At the collaborating hospital there are typically 45 beds available for patients requiring intensive care (21 general and 24 cardiac). In the first instance, plans were in place for capacity to be increased to a maximum of 76 beds, through making use of operating theatres and other specialist bays (which have become available due to the cancellation of routine surgery). There remained some potential to increase this number further, should additional surge capacity be required (this is considered within the scenario analysis of Sect. 3).

At the time this study was conducted, there was an insufficient number of COVID-19 patients that had been admitted to intensive care at the hospital, and so information regarding intensive care length of stay is taken from the literature. A gamma distribution (used also in fitting to COVID-19 intensive care length of stay in [30]) was parameterised based on fitting to length of stay data for 4078 COVID-19 intensive care admissions in England, Wales and Northern Ireland [31]. The shape and rate parameters were estimated at α = 1.66 and β = 0.206 respectively, giving rise to a median of 6.52 days and mean of 8.07 days (note the mean is similar to the 8 day mean used in [30]). The probability of death resulting from rejected admission to intensive care ($P_d^{\mathit{rej}}$) was also informed by the literature. Given the pivotal dependence of survival on mechanical ventilation [6] and already substantial mortality rates for cases actually receiving such intervention [31], it was assumed that all but a very small minority of rejected admissions would result in death. For the simulation study conducted here, a figure of $P_d^{\mathit{rej}}=0.99$ is used based on the clinical advice received from practicing intensive care consultants (noting the assumption that transfer to another hospital with available intensive care capacity could not take place). Finally, the probability that a COVID-19 patient admitted to intensive care dies within intensive care ($P_d^{\mathit{adm}}$) is estimated at $P_d^{\mathit{adm}}=0.507$, based on such a proportion of intensive care admissions having died as sourced from the afore-mentioned observational report representing 4078 intensive care admissions [31].

Scenario analysis

A number of scenarios relating to possible COVID-19 mitigations were modelled in order to inform planning of intensive care services at the hospital during the early stage of the outbreak. These relate to changes in the epidemic curve for cases requiring intensive care (informed by government-led strategy regarding isolation, quarantine and social distancing), capacity at the hospital in terms of number of intensive care beds, and patient length of stay in intensive care. The No isolation strategy involving no government-led effort with respect to isolation, quarantine and social distancing is considered within Scenario 1, alongside the current available capacity of 45 beds and the literature-informed gamma-distributed length of stay with mean 8.07 days [31]. Given the UK Government’s decision on 16 March 2020 to implement isolation measures, the remainder of scenarios (2 through 8) were configured on the basis of this afore-mentioned Isolation strategy (Sect. 2.2).

Scenarios 3 and 4 model the hospital’s actual planned increases in intensive care bed numbers to surge capacities of 76 and 100 respectively. Scenario 5 models the potential benefits of reducing COVID-19 length of stay by 25% through use of weaning protocols for patients receiving mechanical ventilation, as estimated in a previous study [32]. In exploring sensitivity of model outputs to length of stay, an increase of 25% was also considered (Scenario 6) in order to appreciate the effect of possible delays to discharge that reasonably may exist [33]. In appreciating the possibility that non-pharmaceutical interventions would have a greater effect than envisaged in slowing transmission of the disease under the Isolation strategy, the remainder of considered scenarios are based upon the ‘flattened’ version as introduced in Sect. 2.2 (Fig. 2). Scenarios 7 through 9 account for this in respect of the various surge capacities (45, 76, 100 beds), with Scenario 10 presenting the ‘best case’ option in bringing together this flattened demand accompanied by increased capacity to 100 beds and 25% reduced length of stay.

In order to gauge the ‘ideal world’ capacity required to readily accommodate all demand for intensive care admission, additional scenarios are considered for which no constraint on the number of beds is assumed. This is with respect to the 8.07 day mean length of stay and demand profiles equivalent to the No isolation, Isolation, and Isolation (flattened) strategies.

Simulation

Key simulation output measures of interest consist of the duration of time at maximum capacity (to inform workforce requirements), peak capacity-dependent and capacity-independent deaths per day (for mortuary planning), and total deaths over the course of the pandemic (as an ultimate marker of intervention efficacy, in balancing demand and capacity). Confidence intervals, at 95% level, were calculated based on the variation in output measure observed across the 1000 replications performed for each scenario, with each replication using a different stream of random numbers. This number of replications was selected based on the resulting reduction of simulation error to magnitudes deemed sufficiently negligible (<0.25%) when assessed against the output measures of interest (this was performed using different seeds for which the random number streams were drawn for each replication within the simulations considered). The model was implemented as a package within 64-bit R version 3.6.0. For each scenario, computational time was approximately 5 min when performed on a Windows 10 desktop computer.

Results

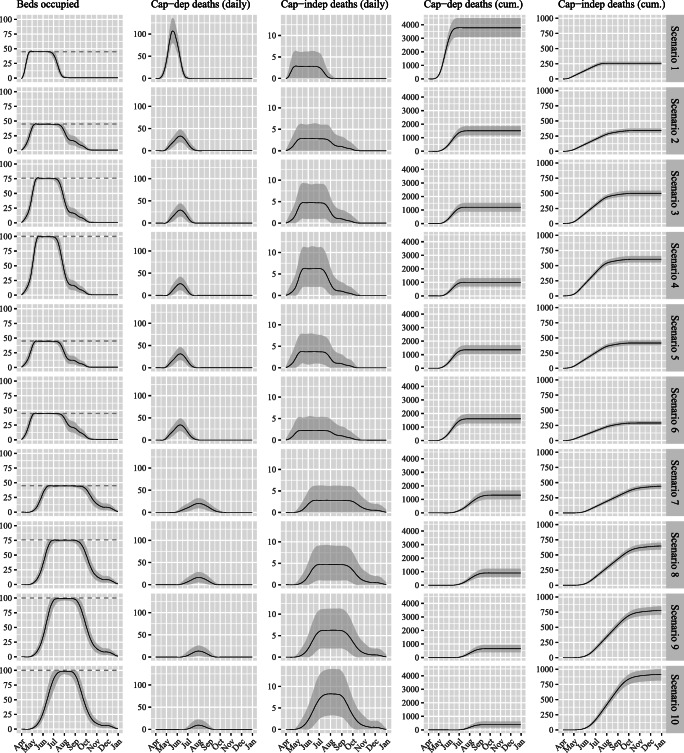
Estimates for the key output measures of interest are presented alongside each of the considered scenarios in Table 2. Transient outputs corresponding to each of these key areas of interest are presented in Fig. 3 across all scenarios, highlighting the key dynamical relationships between these variables. For instance, when full capacity is reached (left plots) then capacity-dependent deaths start to occur (middle-left plots) based on the extent to which demand continues to exceed supply; with the magnitude of this determining the rate at which deaths accumulate (middle-right plots).

Table 2.

Simulation key output measures of interest obtained over 1000 simulation replications. Strategies relate to the epidemic curves for cases requiring intensive care equivalent to those contained in Fig. 2

Scenario	Strategy	Capacity (intensive care beds)	Mean length of stay (days)	Continuous days at maximum capacity; mean (95% CIs)	Peak daily capacity-dependent deaths; mean (95% CIs)	Peak daily capacity-independent deaths; mean (95% CIs)	Capacity-dependent deaths over the pandemic; mean (95% CIs)	Capacity-independent deaths over the pandemic; mean (95% CIs)	Total deaths over the pandemic; mean (95% CIs)
1	No isolation	45	8.07	67 (55–79)	107 (79–136)	3 (0–6)	3778 (3086–4494)	257 (229–285)	4031 (3325–4761)
2	Isolation	45	8.07	76 (53–91)	33 (19–48)	3 (0–6)	1509 (1182–1853)	340 (306–377)	1849 (1500–2205)
3	Isolation	76	8.07	64 (47–77)	29 (15–45)	5 (1–9)	1202 (892–1527)	498 (453–543)	1699 (1355–2057)
4	Isolation	100	8.07	56 (41–69)	26 (12–42)	6 (2–11)	996 (702–1308)	604 (552–658)	1598 (1268–1940)
5	Isolation	45	6.05	69 (44–85)	31 (17–46)	4 (1–8)	1360 (1032–1696)	417 (377–459)	1776 (1424–2132)
6	Isolation	45	10.09	82 (59–97)	34 (21–49)	2 (0–6)	1607 (1272–1956)	290 (257–323)	1896 (1543–2257)
7	Isolation (flattened)	45	8.07	104 (42–125)	20 (9–32)	2 (0–6)	1310 (973–1655)	440 (398–481)	1750 (1405–2115)
8	Isolation (flattened)	76	8.07	82 (43–104)	16 (5–29)	5 (1–9)	907 (606–1229)	647 (588–703)	1552 (1213–1903)
9	Isolation (flattened)	100	8.07	68 (29–88)	13 (2–26)	6 (2–11)	652 (392–945)	778 (706–846)	1428 (1115–1761)
10	Isolation (flattened)	100	6.05	48 (0–74)	10 (0–22)	8 (3–14)	382 (180–627)	917 (814–1004)	1296 (1000–1614)

Fig. 3.

Simulation output results for intensive care bed occupancy and projected capacity-dependent and capacity-independent deaths (per day and cumulative) across the ten scenarios considered. Black solid lines represent the mean and grey bands the 95% confidence intervals from 1000 replications per scenario. Dashed lines represent inputted capacity associated with the respective scenarios

In the absence of any intervention to reduce the effective reproduction number (R) from the basic reproduction number (R0) through case isolation, home quarantine and social distancing (i.e. the No isolation strategy of Scenario 1), the estimated total death toll is significantly higher than in other scenarios. Employing these measures reduces capacity-dependent deaths by an estimated three-fifths and cuts the peak daily capacity-dependent deaths by 69% ceteris paribus (Scenario 2). Incorporating capacity-independent deaths (occurring within intensive care following admission), total deaths over the pandemic are reduced by 2182 (54%). Increasing capacity from 45 to 76 intensive care beds (Scenario 3) further reduces capacity-dependent deaths by 307 (20%), with total deaths reducing by a lesser 150 (8%) given the additional capacity-independent deaths that consequently occur (recalling $P_d^{\mathit{adm}}=0.507$). This also starts to reduce the number of subsequent days at maximum capacity, from 76 to 64 (16%). This is brought down further (to 56 days) should capacity increases to 100 beds be possible (Scenario 4), which also brings down capacity-dependent deaths to under 1000 and reduces total deaths by approximately 100. Curtailing mean length of stay by one-quarter appears to have a relatively small improvement to the total number of deaths (Scenario 5 c.f. Scenario 2), which is in part due to the right-skewed nature of the length of stay distribution (i.e. the number of longer-staying patients in the tail is unchanged since the shape of the distribution is presumed unaltered). When intensive care length of stay is increased by one-quarter (Scenario 6 c.f. Scenario 2), the additional 98 (6.5%) capacity-dependent deaths are offset by fewer capacity-independent deaths given the reduced intensive care throughput, resulting in a lesser 47 (2.5%) total deaths.

Should any additional government-led isolation strategies be effective in further flattening the epidemic curve for cases requiring intensive care, then a substantial reduction in peak capacity-dependent deaths from 33 to 20 would be expected (i.e. Scenario 7 c.f. Scenario 2). However, without increases to capacity this simply spreads the deaths over a longer period of time, rather than reducing the total by a significant amount (1750 c.f. 1849). To achieve a significant reduction in total deaths then any further ‘flattening’ of demand must be accompanied by increases in capacity. If first and second surge capacity levels can be met then total deaths reduce by 198 (11%) and 322 (18%) respectively (i.e. Scenarios 8 and 9 c.f. Scenario 7). Finally, if second surge bed numbers can be accompanied by the afore-mentioned one-quarter reduction in length of stay then total deaths can be reduced by 454 (26%), peak capacity-dependent deaths reduced to ten per day, and the duration of time operating at full capacity shortened by one half (Scenario 10 c.f. Scenario 7). Note that while further ‘flattening’ of demand and accompanying capacity increases lead to greater capacity-independent deaths (due to higher numbers admitted) this is more than offset by the reduction in capacity-dependent deaths, meaning total deaths are reduced.

These mortality projections can be contextualised against those theoretically achievable were intensive care bed capacity not a constraint. With an 8.07 day mean length of stay, total deaths are estimated at 2191 (95% CI 1822 to 2564) for No isolation and 1111 (920 to 1311) for both Isolation and Isolation (flattened), noting of course that these figures are composed solely of capacity-independent deaths. Thus under an Isolation (flattened) strategy with 25% reduced length of stay and 100 beds (Scenario 10), the total number of deaths is within 185 (15%) of the theoretical lower bound (at least in the absence of vaccine or treatment). The peak bed requirement corresponding to these lower bound mortality estimates under the three strategies are 853 (704 to 1012), 303 (243 to 363) and 206 (163 to 250) respectively (Fig. 4).

Fig. 4.

Simulation output results for no constraint to bed number availability. This shows the number of intensive care beds that would be required to satisfy all demand

Discussion

Application

This paper details the approach taken to evaluate the effect of various potential mitigations on COVID-19 deaths resulting from a lack of intensive care capacity at a hospital in England. Performed at an early stage of the outbreak, the analysis presented here has allowed intensivists and planners insight into the number and cause of deaths that could result under various scenarios informed through clinical opinion and early findings within the literature. In implementing the model as an open source tool, the approach has been used across a number of healthcare systems within the UK National Health Service. This has been facilitated through making the model code publicly available as an R package [34] and promoting the tool through social media and national webinar series [35].

Modelling insights have proved valuable to decision-making in a number of ways. First, it has enabled a more objective assessment of the potential gain from efforts required to convert existing clinical areas to intensive care specification. This has allowed consideration of the opportunity cost of such actions, e.g. if theatre space is used then this may limit the ability to perform emergency surgery. Second, it has facilitated consideration of the gain from investing in efforts to reduce length of stay through potentially-effective weaning protocols [32]. Third, it has enabled consideration of the effect of delays to discharge that may reasonably exist from intensive care to downstream services [33], particularly in the COVID-19 setting where other acute and community services may be overwhelmed. Fourth, it has informed an understanding of workforce requirements, through measuring the duration of time at maximum occupancy (and thus estimating staff burnout [36]). Fifth, through sharing the modelling results with public health colleagues at various stages of the modelling, it has informed the capacity requirements of temporary mortuaries within the region. And sixth, through estimating the reduction of COVID-19 related occupancy, it has facilitated consideration of the timing and scale of when certain elective surgeries may resume.

Limitations

Turning to limitations, any modelling study performed during the early stages of outbreak of a novel disease must address the lack of available data and information [26]. The modelling of this study was based upon the same projections which prompted the UK Government’s movement towards ‘lockdown’ [3]. These estimates appear to have forecasted demand for intensive care at many multiples of available supply (even at surge levels), yet it has become clear in the weeks that have followed that these projections were over-estimates [31]. The model can, however, be readily updated in response to the latest projections. Doing so has ensured modelled results have continued to reflect the best-known information at the time.

Another limitation relates to the assumption that all intensive care beds are available for newly-arriving COVID-19 patients. While elective procedures requiring post-operative intensive care have been postponed [37], there remains other sources of non-elective non-COVID-19 demand. Estimations of this, once the effect of societal isolation becomes appreciable (e.g. any reduced road traffic accidents, alcohol-related injuries), can be incorporated within the capacity parameter simply by deducting the average beds occupied by such patients.

An additional possible limitation relates to the assumption that death occurs immediately if a bed in the required setting is not available. Realistically, death is unlikely to be immediate [38], yet at an early stage of the pandemic no reliable data exists to meaningfully capture this parameter in the model. This has no effect on the ultimate number of deaths estimated, but will affect their specific timing and the thus, the peak daily number.

Further research

It is important to acknowledge that capacity has been considered only with regard to the number of beds within intensive care, and not the size or quality of clinical workforce. If the higher volumes of patients being looked after, as produced here through scenarios in which more beds are converted to intensive care specification, are not met with proportionate increases in the numbers of suitably-qualified doctors and nurses, then poorer patient outcomes (i.e. greater $P_d^{\mathit{adm}}$) and longer lengths of stay may result [39]. Further research is thus required to investigate and incorporate the effect of workforce size and skill-mix on these model parameters. On the demand side, these parameters may also be affected by the possible implementation of an intensive care triage policy, which would result in a different case-mix admitted to intensive care. Additional modelling may thus be needed to understand the effects of rejecting intensive care admissions from patient cohorts known to have negligible survival likelihood, in the interests of maintaining available beds for those known to have more favourable chances. If those patients less likely to benefit from admission are triaged-out (as considered in [6, 40]), then modelling would need to capture the different outcome and length of stay distributions for the new patient cohort. Ultimately, such a policy could potentially reduce further the total deaths over and above those considered in this study.

Further work may also investigate how the effect of discharge delays from intensive care to the acute wards can be better captured in the modelling. Firstly, any confounding in the empirically-calibrated length of stay distribution should be assessed, in examining the extent to which discharge delays are already accounted for within the length of stay data. This would require patient-level data including admission date and date ready for discharge alongside ultimate discharge date. While a 25% (2-day) addition to length of stay has been considered here (Scenario 6), further research could consider modelling the downstream acute bed base in order to assess the capacity required to reduce delays to discharge to a given length of time (with greater fidelity achievable through modelling the conjoint admission and discharge process between intensive care and the acute wards, within a pathway model similar to that of [16]).

A greater understanding of the dynamics between intensive care and the acute bed bases could also permit further work regarding the timing and magnitude of intensive care surge capacities. Converting existing specialist beds to intensive care specification for periods of time when there are relatively few COVID-19 presentations could reduce the availability or quality of service for other elective and emergency procedures. Through simulating the performance of elective pathways [41], modelling is now being performed at the authors’ organisation in order to more optimally balance the capacity allocated to these various competing demands.

Funding

No external funding has been received for this study.

Compliance with ethical standards

Conflict of interest

The authors report no conflicts of interest or competing interests.

Data/material

Model code and data used for this study is available at https://github.com/nhs-bnssg-analytics/covid-simr-hospital-application. The packaged tool for more general use is available at https://github.com/nhs-bnssg-analytics/covid-simr.