EnvCNN: A Convolutional Neural Network Model for Evaluating Isotopic Envelopes in Top-Down Mass-spectral Deconvolution

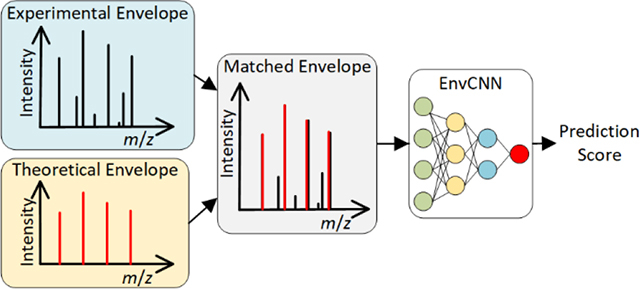
Abstract

Top-down mass spectrometry has become the main method for intact proteoform identification, characterization, and quantitation. Because of the complexity of top-down mass spectrometry data, spectral deconvolution is an indispensable step in spectral data analysis, which groups spectral peaks into isotopic envelopes and extracts monoisotopic masses of precursor or fragment ions. The performance of spectral deconvolution methods relies heavily on their scoring functions, which distinguish correct envelopes from incorrect ones. A good scoring function increases the accuracy of deconvoluted masses reported from mass spectra. In this paper, we present EnvCNN, a convolutional neural network-based model for evaluating isotopic envelopes. We show that the model outperforms other scoring functions in distinguishing correct envelopes from incorrect ones and that it increases the number of identifications and improves the statistical significance of identifications in top-down spectral interpretation.

Graphical Abstract

Introduction

Mass spectrometry (MS) has been the leading platform for protein identification, characterization, and quantitation in the last two decades^1,2. There are two main approaches in MS-based proteomics: bottom-up proteomics analyzes enzymatically digested peptides³, and top-down proteomics studies intact proteoforms^4,5. Bottom-up proteomics is the dominant technique for proteomics studies, but it has substantial limitations in identifying highly modified proteins and degraded ones^3,4. Top-down proteomics is now widely adopted by the proteomics community to analyze intact proteoforms with post-translational modifications (PTMs) and other alterations^4,6,7.

An MS spectrum consists of a list of peaks, each of which is represented by a mass to charge ratio (m/z) value and an intensity. MS data can be represented in the profile or the centroid mode. While profile data contain all of the information in raw spectra, spectral centroiding simplifies data by keeping only the local maxima of peaks. Centroid data may suffer from information loss, but it significantly reduces the time and memory requirement for mass spectral data analysis⁸. The study in this paper is focused on centroid MS data.

In MS data, owing to the occurrence of different isotopes, protein ions with the same chemical composition and the same charge state correspond to a group of peaks with different m/z values, called an isotopic envelope^9,10. A top-down mass spectrum often contains hundreds of high charge state envelopes, some of which are overlapping. Because of the complexity of top-down mass spectra, spectral deconvolution is an important preprocessing step in data analysis, which converts a spectrum into a list of monoisotopic masses by grouping spectral peaks into isotopic envelopes^9,11. Database search algorithms^12–17 match spectra to proteoforms by comparing deconvoluted masses of spectra against theoretical fragment masses of proteoforms. High accuracy in deconvoluted masses is essential to increasing proteoform identifications and improving proteoform characterization in the downstream analysis^9,18.

Many spectral deconvolution tools have been proposed^{9,10,14,16,19–23} for analyzing various types of data (Table S1, Supporting Information). While THRASH¹⁹, Decon2LS²⁰, DeconMSn²¹, and FLASHDeconv²² deconvolute profile data, the other tools process centroid data. ProMex¹⁶ and FLASHDeconv utilize envelopes with multiple charge states to determine the monoisotopic masses of precursor ions. MS-Deconv¹⁰ uses dynamic programming-based methods for deconvoluting overlapping isotopic envelopes. YADA²³ was designed to handle highly charged middle-down tandem mass spectrometry (MS/MS) data. While most tools use the Averagine model²⁴ to estimate chemical compositions of ions, ProteinGoggle²⁵ and masstodon²⁶ use chemical compositions of proteoforms and proteoform fragments from which mass spectra were generated to increase the accuracy of spectral deconvolution.

In spectral deconvolution, an isotopic envelope in a mass spectrum is converted into a monoisotopic mass with the following steps. (1) The chemical composition of an ion is estimated using the Averagine model²⁴ or obtained from the proteoform from which the spectrum was generated, and a theoretical isotopic envelope of the ion is computed using the chemical composition and a given charge state. (2) The peaks in the theoretical envelope are matched to the peaks in the spectrum to find an experimental isotopic envelope. (3) A scoring function is used to evaluate whether the theoretical and experimental envelope pair is correct. (4) If the envelope pair is correct, a monoisotopic mass is computed and reported for the envelope pair¹⁰.

A good scoring function for evaluating envelope pairs reduces errors in reported precursor masses for MS1 spectra and increases the number of correct fragment masses for MS/MS spectra. Consequently, designing scoring functions with high discrimination ability is an essential problem in spectral deconvolution. Many methods have been proposed to evaluate isotopic envelope pairs based on their peak intensities, such as the least-squares fitting¹⁹, chi-square fitting²⁰, and the dot-product function²³ (Table S1). MS-Deconv¹⁰ uses a function that combines errors in m/z values and intensities of peaks. Machine-learning methods have also been employed to train scoring functions of envelopes^9,14. However, due to noise peaks and overlapping envelopes in top-down mass spectra, it is a challenging task to design a scoring function with high discrimination capacity.

Over the past decade, deep learning has found many applications owing to the development of powerful models and the significant growth of computational resources^27,28. The proteomics community has also adopted deep learning to solve complex problems. Several deep-learning models have been proposed for predicting mass spectra from peptide sequences, such as pDeep²⁹ and pDeep2³⁰. Another application of deep-learning is to design scoring functions of the matches of peptides and mass spectra, which play an important role in enhancing the performance of peptide identification in database search^31,32 or de novo sequencing^33–35. In addition, deep learning methods have been used for predicting peptide retention time^31,36,37, predicting phosphorylation sites from peptide sequences^38,39, and identifying LC-MS features in metabolomics data analysis⁴⁰. Most of the methods use routine deep-learning models, such as convolutional neural networks (CNN), recurrent neural networks, and bidirectional long short-term memory models (Table S2).

In this study, we present an Envelope Convolutional Neural Network (EnvCNN) model for evaluating isotopic envelopes. We assessed several neural network models on a top-down MS data set of ovarian tumor cells¹⁶ and found that EnvCNN achieved the best accuracy among these models. Moreover, we tested the performance of EnvCNN on a top-down MS data set of zebrafish brain samples⁴¹ and showed that EnvCNN reported more correct deconvoluted masses and increased the number of proteoform identifications compared with the scoring function in MS-Deconv¹⁰.

Methods

Data Sets

Top-down MS data from two published studies^16,41 were used to train neural network models and evaluate their performance. The first data set¹⁶ was generated by pooling human ovarian tumor (OT) samples from five female patients. The samples were analyzed using a liquid chromatography (LC) system coupled with a Thermo Velos Orbitrap Elite mass spectrometer. The mass resolution was 240,000 (at 400 m/z) for MS1 spectra and 120,000 (at 400 m/z) for MS/MS spectra. A total of 68,711 collision-induced dissociation (CID) MS/MS spectra were collected. The second data set was generated from samples of the cerebellum and optic tectum regions of three mature female zebrafish (ZF) brains⁴¹. The samples were analyzed using a capillary zone electrophoresis (CZE) system coupled with a Q-Exactive HF mass spectrometer. MS1 and MS/MS spectra were acquired at a resolution of 240,000 (at 200 m/z) and 120,000 (at 200 m/z), respectively. The ZF data set contained 65,068 high-energy collision dissociation (HCD) MS/MS spectra. The first nine replicates of the OT data set were used for training and validating the EnvCNN model, whereas the 10th replicate of the OT data set, and the ZF data set were used for evaluating EnvCNN’s performance.

Msconvert⁴² was used to convert raw files into centroided mzML files. TopFD¹⁵ was employed to deconvolute MS and MS/MS spectra to obtain monoisotopic precursor and fragment masses. Deconvoluted spectra were searched against their corresponding protein sequence database to identify proteoform spectrum matches (PrSMs) using TopPIC¹⁵. No mass shifts were allowed in identified PrSMs. Using the target-decoy approach⁴³, PrSMs reported by database search were filtered using a spectrum-level Q-value cutoff of 0. The parameter settings of TopFD and TopPIC are listed in Tables S3 and S4. PrSMs identified by TopPIC were used to generate envelopes for training and testing the model.

Generating Envelopes

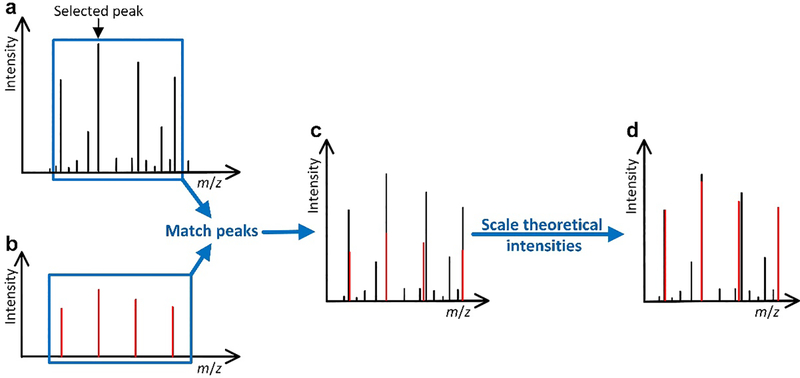
For a PrSM between a spectrum S and a protein segment P (the spectrum S may be matched to a truncated form of a protein), we generate a pair of theoretical and experimental isotopic envelopes for each deconvoluted fragment mass reported from S and then use theoretical fragment masses of P to label these envelope pairs. (See the Supporting Information for the labeling method.) The theoretical envelope of a fragment ion is computed by the Averagine model²⁴ using its monoisotopic mass and charge state. In the theoretical envelope, only high-intensity peaks are kept so that the sum of their intensities is just more than 85% of the total peak intensity. The peaks in the theoretical envelope are matched to experimental peaks in S, and a pair of theoretical and experimental peaks is reported if their m/z difference is no more than 0.02 Da. The intensities of the theoretical peaks are scaled so that the sum of the intensities of the top three theoretical peaks is the same as that of the top three experimental envelope peaks¹⁰ (Figure 1). In addition, all experimental peaks (signal and noise peaks) in the m/z interval [x-0.1, y+0.1] are reported, where x is the m/z value of the monoisotopic theoretical peak and y is the largest m/z value of the peaks in the theoretical envelope. Finally, we remove all theoretical and experimental peaks with an m/z value > x+2.9 so that the remaining peaks are enclosed in a 3 m/z interval [x-0.1, x+2.9]. The [x-0.1, x+2.9] m/z interval was selected because it includes the most intense peaks in an isotopic envelope. For an envelope with charge 1, the interval contains the first three isotopic peaks, which are often the highest. It also works for high charge envelopes as it includes the first 3c isotopic peaks for an envelope with charge c. Moreover, the 0.1 m/z at the start of the interval captures noise peaks before the monoisotopic peak.

Figure 1:

Steps for generating a theoretical envelope and an experimental envelope. (a) One peak in an experimental mass spectrum is selected for finding a theoretical envelope. (b) Theoretical distribution is obtained using the selected peak and a given charge state. (c) Peaks in the theoretical distribution are matched with the peaks in the spectrum to obtain an experimental envelope. (d) Theoretical peak intensities are scaled so that the sum of the intensities of the top three peaks in the theoretical envelope is the same as that of the top three experimental peaks.

Envelope Features

Let x and h be the m/z value and intensity of an experimental peak p. The feature for representing p is its normalized intensity I_e(p) = h/H, where H is the scaled highest peak intensity in its corresponding theoretical envelope. Let x’ and h’ be the m/z value and intensity of a theoretical peak p’. The feature representing p’ is its normalized intensity I_t(p’)= h’/H. In addition, two features are used to represent the pair between p’ and its matched experimental peak. If p’ and p are a pair of matched peaks, the first feature $S_x(p,p^{\text{'}})$ is a similarity function of x and x’: if $|x-x^{\text{'}}|\le 0.02$, then $S_x(p,p^{\text{'}})=1-\frac{|x-x^{\text{'}}|}{0.02}$; otherwise $S_x(p,p^{\text{'}})=0$. The second is the difference between the normalized peak intensities $D_y\left(p,p^{\text{'}}\right)=\left|I_e\left(p\right)-I_t\left(p\text{'}\right)\right|$. If the peak p’ does not match any experimental peak, then $S_x(p,p^{\text{'}})$ and $D_y\left(p,p^{\text{'}}\right)$ are set to 0 and I_t(p’), respectively. Let E be the theoretical envelope of p’ and S the spectrum containing p. Following the method proposed by Horn et al.¹⁹, we plot a histogram of the peak intensities of S with an interval width of $b=\mathrm{m}\mathrm{a}\mathrm{x}\left\{10,H’/1000\right\}$, where H’ is the highest peak intensity in S. We use the intensity with the maximum frequency in the histogram as the baseline intensity of S. A feature of E is the log ratio of the highest peak intensity in E and the baseline intensity of the spectrum, denoted as R_E (Table 1). The feature I_e(p) is called an experimental peak feature, and the other four are called theoretical peak features. Although R_E is a feature of the theoretical envelope, it is treated as a feature of theoretical peaks, and each peak in the theoretical envelope has the same value of R_E.

Table 1:

Features for Representing an Experimental and Theoretical Envelope Pair.

feature	description
Ie(p)	normalized intensity of a peak p in the experimental envelope
It(p’)	normalized intensity of a peak p’ in the theoretical envelope
Sx(p,p’)	piecewise function of the m/z value similarity of an experimental peak p and its matched theoretical peak p’
Dy(p,p’)	intensity difference between an experimental peak p and its matched theoretical peak p’
RE	log ratio of the highest peak intensity in the theoretical envelope and the baseline intensity of the spectrum

We use a 300 by k matrix to represent a pair of theoretical and experimental envelopes when one experimental peak feature and k-1 theoretical peak features are used (Figure 2). Let x be the m/z value of the monoisotopic peak of the experimental envelope. The m/z interval [x-0.1, x+2.9] is divided into 300 bins with size 0.01. All peaks (some are noise peaks) in the experimental envelope are converted to an array y₁, y₂, …, y₃₀₀. For $1\le i\le 300$, we set y_i to h_i/H, where h_i is the intensity of the highest peak in the ith bin (h_i = 0 if there are no peaks in the bin). All theoretical peaks are converted to a 300 by k-1 matrix. If the ith bin contains a theoretical peak, then the ith column in the matrix contains the values of the k-1 theoretical peak features. Otherwise, the column is filled with zeros. Finally, the $300\times 1$ array and $300\times (k-1)$ matrix are combined to obtain a 300 by k matrix for the representation of the envelope pair.

Figure 2:

A 300×5 matrix for representing an experimental and theoretical envelope pair with a monoisotopic m/z value of x. The m/z interval [x-0.1, x+2.9] is divided into 300 bins of size 0.01, and each peak is assigned to a bin. When a bin contains experimental peaks, the feature I_e is computed based on the intensity of the highest experimental peak in the bin. When a bin contains a theoretical peak, the features I_t, S_x, and D_y are computed based on the theoretical peak and its matched experimental peak. Finally, the feature R_E is added to all bins with theoretical peaks.

Machine Learning Models

The EnvCNN model follows the Visual Geometry Group (VGG)⁴⁴ network architecture and is comprised of 10 convolutional layers and 3 fully connected layers (Figure S1). The rectified linear unit (ReLU) activation function is used for the convolutional and the first two fully connected layers, and the sigmoid activation function for the last fully connected layer. The model was trained and tested using Keras⁴⁵ with the TensorFlow⁴⁶ backend. In model training, the loss function was binary cross-entropy and class weighting by the inverse class frequency^47,48 was used as positive and negative envelopes were not balanced. The neural network weights were initialized by the Xavier uniform initializer⁴⁹ and trained by Adam⁵⁰ with a learning rate of 1E-5. The batch size was 128. The training data was randomly split into a training set (80%) and a validation set (20%). The training process was stopped if the validation loss did not improve for 30 epochs, and the model with the smallest validation loss was reported.

Results

Envelope Pairs

The ovarian tumor (OT) data set consists of 10 replicates of the same sample. With a spectrum-level Q-value cutoff of zero, TopPIC identified 21,364 PrSMs without unknown mass shifts (see Methods), from which 2,142,027 envelope pairs were obtained. Because of the stringent Q-value cutoff, we assumed that all of the proteoform identifications were correct. On average, each spectrum contained 100 envelopes (deconvoluted monoisotopic masses).

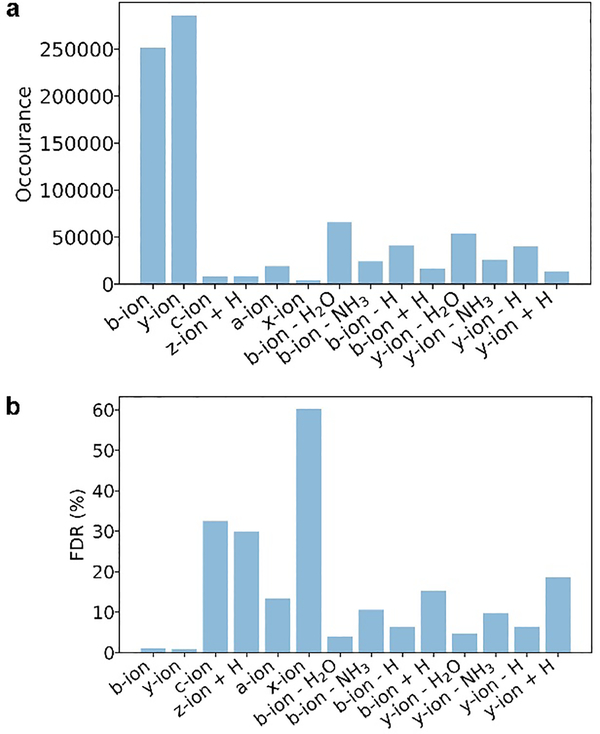
These envelope pairs were matched to 14 types of theoretical fragment masses (Table S5) using an error tolerance of 15 ppm. The total number of theoretical masses of the 21,364 PrSMs for each fragment type was 1,202,606, and the fragment types with the highest matching frequencies were b ions and y ions (Figure 3a). The target-decoy approach was used to estimate the FDR of the reported matches. The expected number of decoy matches for all of the spectra was 2,566 (see Methods), and the estimated FDRs were about 1% for matched b and y ions and larger than 3% for the other 12 types of ions (Figure 3b). Because some fragment ions, such as c and z^• ions, are seldom observed in CID and HCD spectra, the estimated FDRs of these ions may indicate that the target-decoy approach underestimated the FDRs.

Figure 3.

Matched fragments and estimated FDRs for the 14 ion types in the PrSMs identified from the OT data set. (a) Number of matched fragments for each ion type, and (b) estimated FDR for each ion type.

The envelope pairs matched to the 12 fragment types other than b and y ions were removed from the data set in order to obtain high accuracy in envelope labeling. The remaining 1,820,641 envelopes were used for model training and testing, of which 536,778 matched to b ion or y ions were labeled positive and 1,283,863 not matched to any ion were labeled negative. The ratio between positive and negative envelopes was about 1:2.4.

Evaluation Criteria

Three criteria were used for evaluating various models: balanced prediction accuracy, the area under the receiver operating characteristic (ROC) curve (AUC), and the rank-sum of positive envelope pairs. The balanced prediction accuracy of a model is the average of the positive and negative prediction accuracies⁵¹. We chose balanced prediction accuracy for evaluation because the test data were imbalanced. To compute the rank-sum of a spectrum for a model, the envelopes in the spectrum were ranked in decreasing order using their scores reported by the model, and the ranks of all positive envelopes were summed up. The rank-sums of all spectra were summed up as the rank-sum of the test data set.

Feature Selection

We used the network architecture of EnvCNN (Figure S1) to evaluate various combinations of peak features as the input of the model. These models were trained using the first replicate and evaluated using the second replicate of the OT data set.

We first compared two models in which only the experimental peak feature and one theoretical peak feature were used. The features were theoretical and experimental peak intensities in the first model and normalized peak intensities (see Methods) in the second model. The second model outperformed the first in the ROC AUC value and rank-sum (Figure S2). The second model is referred to as the base model, and the features I_t and I_e are referred to as the base features of EnvCNN. Then we compared three features of the theoretical envelope: H, H/B, and R_E=log(H/B), where H is the highest theoretical peak intensity and B is the baseline intensity of the spectrum. Each of the three features was combined with the base features to generate input matrices. The third feature achieved a better performance than the other two (Figure S3) and was chosen as a feature in EnvCNN. Combining the base features with the features S_x and D_y also improved the performance of envelope classification, and the model with the five features in Table 1 achieved the best performance of the tested models (Table 2).

Table 2:

Comparison of the Performance of Feature Combinations with the EnvCNN Model on the Second Replicate of the OT Data Set.

features	balanced accuracy (%)	AUC (%)	rank-sum
base features with Sx	79.22	87.5	1,358,494
base features with Dy	78.76	86.8	1,386352
base features with RE	77.91	87.2	1,370,810
base features with Sx, Dy and RE	79.37	87.8	1,346,183

Comparison with Other Machine-Learning Models

The EnvCNN model (Figure S1) was compared with three commonly used deep-learning models: LeNet⁵², AlexNet⁵³, and ResNet⁵⁴ (Table S6). LeNet contains two convolutional layers, one fully connected layer, and an output layer. AlexNet increases the depth of LeNet and the number of filters per layer. ResNet contains 10 convolutional layers and utilizes skip connections to deal with the diminishing gradient problem.

The first nine replicates of the OT data set were used for training, and the last replicate was used for testing the models. The method for training the three models was similar to that for the EnvCNN model (see Methods). The training data contained 479,991 positive and 1,130,523 negative envelope pairs, and the test data contained 56,787 positive and 153,340 negative envelope pairs. EnvCNN achieved the best performance in the balanced accuracy, ROC AUC, and rank-sum among the models (Table S7).

Comparison with the Scoring Function in MS-Deconv

We evaluated EnvCNN and the scoring function in MS-Deconv, referred to as the MS-Deconv score, on the last replicate of the OT data set. Compared with the MS-Deconv score, the EnvCNN model increased the ROC AUC value from 68.5% to 88.9% (Figure S4a) and reduced the rank-sum from 1,808,496 to 1,396,843. In addition, we ranked all envelopes in each PrSM based on the EnvCNN or the MS-Deconv score and counted the number of positive envelopes for each rank. Top-ranking envelopes (rank < 30 in the spectrum) reported by EnvCNN are more accurate than those reported by the MS-Deconv score (Figure S4b), showing that the discrimination ability of EnvCNN is better than the MS-Deconv score. EnvCNN achieved a high balanced accuracy of 81.13%, and the accuracy of b and y ions was even higher: 85.09% for b ions and 86.06% accuracy for y ions. The MS-Deconv score does not have a cutoff value for separating positive envelopes from negative ones and does not report prediction accuracy.

The EnvCNN model trained on the OT data set was also compared with the MS-Deconv score on the ZF data set. We obtained 692,175 positive and 1,293,994 negative envelopes from the ZF data set (see Methods). The balanced accuracy of EnvCNN was 73.52%, and the accuracy for b and y ions was 89.09% and 89.84%, respectively. The ROC AUC value of EnvCNN (80.8%) was significantly higher than the MS-Deconv score (66.4%) (Figure S5a). In addition, EnvCNN reduced the rank-sum from 19,552,895 to 16,259,277 compared with the MS-Deconv score (Figure S5b).

Proteoform identification by combining EnvCNN and database search

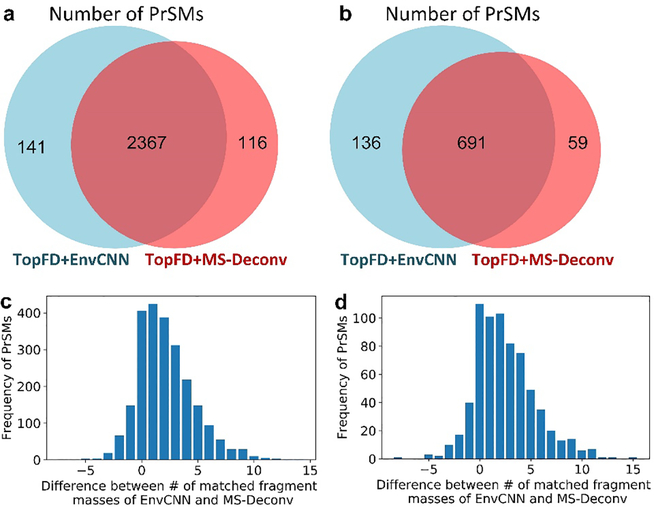
We incorporated EnvCNN into TopFD (TopFD+EnvCNN) for top-down spectral deconvolution and compared it with TopFD coupled with the MS-Deconv score (TopFD+MS-Deconv). The last replicate of the OT data set (68,711 MS/MS spectra) was deconvoluted by TopFD+EnvCNN and TopFD+MS-Deconv separately. For each spectrum, the two methods reported the same number of deconvoluted masses, which was estimated by the total number of b and y ions. The masses reported by TopFD+EnvCNN are called EnvCNN masses, and those reported by TopFD+MS-Deconv are called MS-Deconv masses. The UniProt human proteome database (UP000005640, 20,402 entries, version April 22, 2019) was concatenated with a decoy database in the database search. The deconvoluted masses reported by the two methods were searched against the human target-decoy database separately by TopPIC with a two-round method. The parameter settings of TopPIC are given in Table S8. In the first round, unexpected mass shifts were not allowed and TopPIC reported 2508 PrSMs from EnvCNN masses and 2483 PrSMs from MS-Deconv masses with a 1% Q-value cutoff (Figure 4a). In the second round, we removed the spectra identified from the first round and searched the remaining spectra against the database by allowing one unexpected mass shift in a proteoform. With a 1% Q-value cutoff, TopPIC reported 827 and 750 PrSMs from EnvCNN and MS-Deconv masses, respectively (Figure 4b). In total, TopFD+EnvCNN increased the number of identified PrSMs by about 3% from 3,233 to 3,335 compared with TopFD+MS-Deconv.

Figure 4:

Comparison of TopPIC search results for TopFD+EnvCNN and TopFD+MS-Deconv on the 10^th replicate of the OT data set. (a) PrSMs reported by TopPIC without mass shifts. (b) PrSMs reported by TopPIC when one unexpected mass shift is allowed in a proteoform. (c) Difference between the numbers of matched EnvCNN and MS-Deconv masses in PrSMs without mass shifts. (d) Difference between the numbers of matched EnvCNN and MS-Deconv masses in PrSMs each with one mass shift.

We also compared the number of matched fragment ions reported in identified PrSMs. The two deconvolution methods shared 3,058 identified spectra (2,367 without mass shifts and 691 with mass shifts). For each of the spectra, we computed the difference between the numbers of matched EnvCNN masses and MS-Deconv masses. EnvCNN reported 5,446 more matched masses than the MS-Deconv score (Figure 4c). In the 691 PrSMs with unexpected mass shifts, EnvCNN increased the number of matched masses by 2.49 on average compared with the MS-Deconv score (Figure 4d). Although the increase is not large, these matched masses may play an important role in localizing unexpected mass shifts.

We also compared the performance of EnvCNN and the MS-Deconv score using the ZF data set. The mass spectra in the data set were deconvoluted using the two methods separately, and the resulting spectra were searched against the UniProt zebrafish proteome database (UP000000437, 3,310 entries, version November 15, 2018) using TopPIC with the two-round method. In the first round, TopPIC reported 33,489 PrSMs from EnvCNN masses and identified 32,855 PrSMs from MS-Deconv masses with a 1% Q-value cutoff (Figure 5a). In the second round, TopPIC reported 18,986 PrSMs from EnvCNN masses and identified 18,540 PrSMs from MS-Deconv masses with a 1% Q-value cutoff (Figure 5b). In total, EnvCNN increased the number of identified PrSMs from 51,395 to 52,475, an increase of ~2% (Table S9). TopPIC reported 49,971 PrSMs shared by the EnvCNN and MS-Deconv methods (32,180 without mass shifts and 17,791 with mass shifts). EnvCNN reported 1.34 and 0.72 more matched masses on average than the MS-Deconv score in PrSMs without mass shift (Figure 5c) and with one unexpected mass shift (Figure 5d), respectively (Figures S6 and S7).

Figure 5:

Comparison of TopPIC search results for TopFD+EnvCNN and TopFD+MS-Deconv on the ZF data set. (a) PrSMs reported by TopPIC without mass shifts. (b) PrSMs reported by TopPIC when one unexpected mass shift is allowed in a proteoform. (c) Difference between the numbers of matched EnvCNN and MS-Deconv masses in PrSM without mass shifts. (d) Difference between the numbers of matched EnvCNN and MS-Deconv masses in PrSMs each with one mass shift.

Discussion

The performance of EnvCNN showed the ability of CNN models to accurately predict correct envelopes for top-down spectral deconvolution. EnvCNN, LeNet, AlexNet, and ResNet achieved similar prediction accuracy, but EnvCNN slightly outperformed other models. The EnvCNN model was trained using the OT data set, and its performance was evaluated using the OT and ZF data sets. The mass spectrometer used for the ZF data set was different from that for the OT data set, and the proteoforms in these two data sets were completely different. EnvCNN exhibited similar performance on both data sets, thus demonstrating the generalization ability of EnvCNN to deal with various types of data sets.

The accuracy of EnvCNN on negative data points was lower than that on positive data points (Table S10). The main reason is that negative data points had a higher error rate in labeling than positive envelopes. Although the negative data points do not match any of the 14 types of theoretical masses, some of them may be generated from internal fragments. To obtain a better training data set, manual validation or more accurate labeling methods are required.

By incorporating EnvCNN into TopFD, we increased the accuracy of deconvoluted masses and increased the number of identified PrSMs and the number of matched masses. However, the improvement is not significant. There are two cases in which the scoring function of envelopes does not significantly affect database search results. In the first case, the spectrum does not contain many fragment ions and TopFD identifies a small number of candidate envelopes. Then all candidate envelopes are reported, and the scoring function does not affect deconvolution results. In the second case, TopFD identifies many candidate envelopes from a spectrum. Then the number x of theoretical b and y ions is estimated, and only x candidate envelopes are reported. Such a spectrum can be identified using the MS-Deconv score for ranking envelopes. This might be the reason why EnvCNN did not significantly increase the number of identifications in spectral identification by database search.

In spectral deconvolution, we have to make trade-off decisions between sensitivity and specificity. In protein identification, including more masses introduces a mixed effect on the statistical significance of identifications: the matched masses will improve the significance, but the mismatched masses will reduce it. Developing methods for balancing between the sensitivity and the specificity of deconvolution results can increase spectral identifications. In proteoform characterization, it is preferred to report more matched masses by increasing sensitivity, which enable researchers to efficiently characterize modifications. Although many false-positive envelopes are also reported, a manual inspection can be used to remove the false positives.

EnvCNN still has its limitations. EnvCNN processes centroid data, not profile data. Developing a machine-learning model for profile data may further improve the accuracy of spectral deconvolution. In addition, EnvCNN evaluates only individual isotopic envelopes. To further enhance the performance of the model, we can include additional features such as the local ranking score.

Conclusions

In this paper, we proposed EnvCNN, a deep-learning neural network, for evaluating isotopic envelopes. EnvCNN outperformed existing scoring functions in distinguishing correct envelopes from incorrect. We further integrated EnvCNN with TopFD, a top-down spectral deconvolution tool, and compared its performance with the scoring function in MS-Deconv. TopPIC identified more spectra from masses reported by EnvCNN than the MS-Deconv score. In addition, EnvCNN increases the statistical significance and the number of matched masses of proteoform identifications compared with the MS-Deconv score.