From disorganized equality to efficient hierarchy: how group size drives the evolution of hierarchy in human societies

Abstract

A manifest trend is that larger and more productive human groups shift from distributed to centralized decision-making. Voluntary theories propose that human groups shift to hierarchy to limit scalar stress, i.e. the increase in cost of organization as a group grows. Yet, this hypothesis lacks a mechanistic model to investigate the organizational advantage of hierarchy and its role on its evolution. To fill this gap, we describe social organization by the distribution of individuals’ capacity to influence others. We then integrate this formalization into models of social dynamics and evolutionary dynamics. First, our results demonstrate that hierarchy strongly reduces scalar stress, and that this benefit can emerge solely because leaders and followers differ in their capacity to influence others. Second, the model demonstrates that this benefit can be sufficient to drive the evolution of leader and follower behaviours and ultimately, the transition from small egalitarian to large hierarchical groups.

1. Introduction

Start a war or negotiate peace? Invest in more capital stocks or sell shares? The fate of states, companies and organizations are shaped by their decisions. It is then surprising that only a minority of individuals are involved in the decision-making process. From companies to political parties, organizations tend to follow an ‘iron law of oligarchy’, in which larger and more productive groups switch to hierarchy where a few individuals possess most of the political power, resources and influence [1]. This transition is best illustrated by the deep overhaul of human societies initiated by the advent of agriculture 12 500 years ago. In a relatively short period of time, most human groups switched from non-hereditary and facultative forms of leadership [2,3], to hierarchical societies with one or few permanent leaders [4]. Despite this transition being well known, it is still hard to explain why human groups follow this general trend. The independent transitions to hierarchy and its pervasive presence suggest that the emergence of hierarchy is (at least partly) the result of natural selection [5]. But the emergence of hierarchy appears as a Darwinian paradox because leaders often enjoy preferential access to resources [4] and mating partners [6]. Why would any individual rationally accept a position of being a follower if the position of leader is more beneficial? One could argue that followers do not have a choice because leaders impose their dominance using coercive means. Humans have inherited traits and preferences towards hierarchy from their primate ancestors, who were organized in dominance hierarchies where individuals physically compete for rank, resources and partners [2]; but adaptations such as the capacity to form large coalitions and the development of throwing weapons led early human groups to reverse this hierarchy [7,8]. In pre-Neolithic tribes, coalitions of followers imposed strong dominance on uprising leaders and successfully avoided coercive leaders for hundreds of thousand of years [2]. Therefore, coercive theories fail to explain the emergence of hierarchy in the first place when any advanced form of coercion, e.g. armies, taxes or propaganda, was absent.

An alternative theory from political sciences proposes that in the absence of financial or military power, leaders have established their dominance by first accumulating political power, i.e. influence over collective decisions [1]. The ‘iron law of oligarchy’ states that political leaders inevitably arise as a group expands, in order to deal with the complexity of coordination. But, this allows these leaders to bias collective decisions in their favour, e.g. distribution of resources or command of a military. This theory fits well with evidence of leaders playing a prevalent role in group organization [9]. As can be seen in small scale societies [10] or in a modern share-holder meeting [11], leaders reduce the cost of organization by assigning roles to individuals, settling arguments between decision makers, and helping to decide the future course of action. However, this theory suggests that the group benefit would be enough to overcome individual selection driving everyone to become a leader rather than a follower [12]. There is clearly a conflict between individual and group interests, which makes this condition non trivial [13].

The ‘iron law of oligarchy’ proposes that a key element is scalar stress, which describes the fact that the difficulty for a group to coordinate increases with group size [1]. This relation appears in (i) psychology experiments of collective decision-making, in which larger groups reach a lesser degree of agreement [14] or take worse decisions [15], and (ii) indirectly in anthropological data showing a strong correlation between group size and probability of group fission [16], or group size and the number of political units [17]. On one side of the range, small-whale hunters of Mackenzie Inuits have one single coach to coordinate group hunting [18]. On the other extreme, complex states or companies have dozens of politicians and managers who are fully dedicated to the task of organizing. Previous work has shown that scalar stress can drive the evolution of institutionalized hierarchy [19], where a leader is appointed by a centralized process. However, rather than being ascribed, hierarchy is likely to initially emerge from the evolution of intrinsic physical and psychological traits of individuals, e.g. height [20], talkativeness and charisma [21]. Emblematic examples of such informal hierarchy are the ‘big man’ societies observed in Melanesia, in which leaders are defined by their persuasion skills rather than by an ascribed position [22]. However explaining the evolution of ‘informal’ hierarchy without supporting institutions poses an important challenge: can the group benefit of hierarchy overcome the selection pressure pushing everyone to be a leader? The lack of a mechanistic model describing the effect of hierarchy on collective decision-making has limited investigation of scalar stress as a possible solution.

The iron law of oligarchy [1] and behavioural experiments [23] suggest that the benefit of hierarchy on group coordination lies in its effect on the time a group spends to reach consensus and take a collective decision. Consensus decision-making is an efficient method for a group to coordinate, in particular to tackle tasks where learning the optimal strategy by trial and error is too costly. Examples of consensus decision-making include tribe gatherings to discuss the next camp location, councils of war to decide upcoming battle strategies, or parliamentary debates on new laws. Yet, the time spent to reach consensus (consensus time in short) is costly because individuals dedicate time to organization instead of carrying out the actual task, and because time itself can carry a cost, e.g. resources get depleted. Thus, we explicitly model the consensus decision-making and the effect of hierarchy on this process. We describe group social organization as a distribution of individuals’ influence, i.e. their capacity to modify another individual’s opinion towards their own. The scale from acephalous to highly hierarchical groups is represented by an equal to strongly positively-skewed distribution of influence. We use the term leaders and followers to describe individuals with high and low influence, respectively. This definition of hierarchy does not include the degree of inequality in resources. We allow the correlation between hierarchy and degree of inequality in resources to emerge from the model, as influential individuals can bias the distribution of resources to their advantage. The emergence of hierarchy is represented by the evolution of individual behaviours towards a minority of leaders and a majority of followers. We combine social and evolutionary dynamics to investigate the development of hierarchy and build a mechanistic formalization of the ‘iron law of oligarchy’. Using this model, we aim to answer the following question: does hierarchy limit the effect of scalar stress, and if yes, could it drive the evolution of leader and follower behaviours even if it creates inequality in resources? To do so, we consider that in absence of advanced institutions such as voting systems, collective decision-making is a sequence of communications, as observed in human groups faced with coordination problems in laboratory experiments [24] or in the real world [2,25]. Thus, we mathematically describe collective decision making by an opinion formation model, which consists of a sequence of discussions between individuals until a global consensus is reached [26].

We investigate how social organization affects scalar stress, where scalar stress is defined as the relationship between the time spent to reach consensus and group size. It has been hypothesized that scalar stress is enough to drive the evolution of stable hierarchy [27]. We test this hypothesis in the second half of the paper by explicitly integrating the consensus decision-making into an evolutionary model. We consider a population structured into patches, where individuals on a patch organize together to produce a collective good. The consensus time determines their cost of organization, and the influence of an individual on the final decision determines that individual’s share of the collective good.

2. Opinion formation model

(a). Model definition

We developed an opinion formation model based on previous work [28], which simulates a sequence of discussions between N individuals until consensus is reached. The outline of the model is represented in the electronic supplementary material, figure S1. Individuals are represented by an opinion x. The opinion x describes a generic opinion of an individual on how to realize a collective task, e.g. the next raid target, the plan of an irrigation system or the value of a law. Individuals are also described by a value of influence, α. The influence, α, is defined as the capacity of one individual to influence group decision and affects: (i) the capacity of one individual to modify the opinion of another individual towards their own opinion, (ii) the reluctance of an individual to change their opinion, and (iii) the probability that an individual talks to other individuals. These three traits, i.e. persuasiveness, stubbornness and talkativeness, are highly correlated in leaders' personalities [21] and are the key factors in explaining how leaders affect consensus decision-making [28].

Both the opinion x and the influence α are continuous variables defined on [0,1]. To facilitate the analysis of the opinion formation model, we divide individuals into two profiles: leader L, and follower F. Each profile has a fixed value of influence α such that α_L > α_F.

At the beginning of the opinion formation model, the values of opinion x are sampled from the uniform distribution between [0, 1]. Each time step is defined by one discussion event during which one speaker talks to multiple listeners. The probability P of an individual i to be chosen as a speaker is an increasing function of its α value as follows:

$$P_i(t)=\frac{{({\alpha }_i(t))}^k}{\sum _{n=1}^N{({\alpha }_n(t))}^k}.$$ 2.1

The exponent k defines how much the difference in influence is translated into a difference in the probability to talk. In the simulations we chose k = 4 so that in a group of 1000 individuals with the most extreme hierarchy, the probability that a leader is chosen as a speaker is very high (close to 90%).

The speaker talks with N_l listeners, with listeners being a subset of the total group. We assume that the number of listeners is limited because of time constraints. The listeners are randomly sampled from the other individuals in the group. We assume that every individual can be chosen as a listener, i.e. the social network is a complete network.

During a discussion event, a listener v updates its opinion to a value x′_v following the equation below, where v represents the listener and u the speaker:

$$x_{\mathrm{v}}^{\prime }=x_{\mathrm{v}}+({\alpha }_{\mathrm{u}}-{\alpha }_{\mathrm{v}})\hspace{0.17em}(x_{\mathrm{u}}-x_{\mathrm{v}}).$$ 2.2

We assume that the position of speaker gives a slight influential advantage over the listeners. Therefore, the minimum difference of influence α_u − α_v is set to a positive low value, here 0.01. This assumption is necessary to avoid a systematic convergence of individual opinions towards those of the individual with the highest α, a phenomenon not observed in real life. The individuals repeat the previous step until the following condition is true:

$${\sigma }_x<x_{\theta }.$$ 2.3

Consensus is reached when the standard deviation of the opinions σ_x is inferior to the threshold x_θ. The number of discussion events that occurred to reach consensus is called the consensus time, t*. The final decision reached, x*, is the mean of the opinions at consensus across individuals. Using this model, we aim to answer the following question: does hierarchy limit the effect of scalar stress?

(b). Analysis

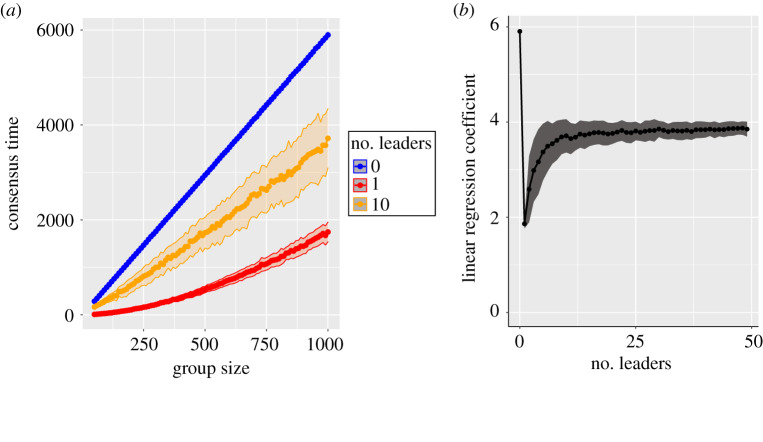
Figure 1 shows that the presence of few leaders (i) reduces the consensus time, and (ii) reduces scalar stress, which is shown by the gradient of consensus time with respect to group size being smaller. In other words, hierarchy facilitates organization by reducing the intensity of scalar stress. Importantly, the differential quality of information that leaders might posses, and which might lead to a group with hierarchy making better decisions, is not required to get this result.

Figure 1.

(a) Consensus time as a function of the size of the group for three different types of social organization: (i) 0 leaders, (ii) 1 leader and (iii) 10 leaders. (b) Scalar stress measured by the linear regression coefficient (slope) of time to reach consensus on group size as a function of number of leaders. The ribbons represent the standard deviation to highlight the high variance in the consensus time when multiple leaders are present. One hundred independent replicates have been realized for each group size and social organization. The parameters used are N_l = 30, α_L = 0.75, α_F = 0.25 and x_θ = 0.05. (Online version in colour.)

The electronic supplementary material, figure S2 shows that hierarchy reduces scalar stress and that this result is consistent across different leader and follower profiles. It shows that hierarchy with a single leader has the lowest scalar stress when the difference in influence between leaders and followers is high. Conversely, hierarchy with multiple leaders has the lowest scalar stress when the difference in influence between leaders and followers is low. This is because multiple influential leaders (i) can increase divergence by convincing followers towards extreme opinions, (ii) can convince followers from other leaders, and (iii) are slower to themselves be convinced.

The electronic supplementary material, figure S3 demonstrates that the scalar stress is strongly dependent of the number of listeners N_l. It shows that a lower number of listeners N_l results in an increase in consensus time, in particular for acephalous groups and multiple leaders hierarchy. This is because a lower number of listeners slows down the convergence of opinions. In the presence of multiple leaders, it also reduces the probability that one leader convinces the majority of the group and thus, favours the formation of clusters of different opinions built around one stubborn leader. In conclusion, our model demonstrates scalar stress, the benefit of hierarchy in reducing scalar stress, and how this benefit is amplified by limited interactions as is the case with a low number of listeners N_l.

3. Evolutionary model

(a). Model definition

We have shown that the presence of a minority of influential individuals (leaders) and a majority of influenceable individuals (followers) reduces the cost of organization and scalar stress. Can this organizational advantage be enough to drive the evolution of individuals towards leader and follower behaviours even if it creates inequality in resources?

We answer this using an evolutionary model where we describe social organization as a distribution of influence, and use opinion formation to link this distribution back to the cost of organization. The life cycle of the evolutionary model is represented in the electronic supplementary material, figure S1. We now let the trait α carried by individuals evolve. The trait α is transmitted vertically from parent to offspring, e.g. by social learning, as is common in both hunter–gatherer groups [29] and modern societies [30]. Unlike the model above, the possible values of influence α can take any value in the range [0,1]. We use the terms leader and follower to designate individuals with high and low influence, respectively. The trait α mutates following a mutation rate of μ. As α is likely to be at least partly cultural, we assume a mutation rate higher than for a classical genetic trait. When a mutation occurs, a random value is sampled from a truncated Gaussian distribution centred on the current value of the trait, with variance ${\sigma }_{\mathrm{m}}^2$.

We study the evolution of α using a standard island model with a population of individuals that is subdivided into a finite number of patches, N_p [31]. We consider that group size can vary and thus, groups can compete by differential migration. The life cycle of individuals consists of discrete and non-overlapping generations, where in each generation the following occur: (i) consensus decision-making about how to perform a task; (ii) performance of the collective task; (iii) distribution of resources obtained from the task; (iv) reproduction; and (v) migration. The first three steps determinate the reproductive success of an individual, which we denote by its fitness w.

The fitness of an individual is translated into a number of offspring, which is drawn from a Poisson distribution centred on its fitness w. After reproduction, offspring individuals migrate with a probability equal to a fixed migration rate m. Migrating individuals enter a patch chosen at random from the population (excluding their natal patch).

More formally, the fitness w of individual i on patch j at time t is described by the following equation:

$$w_{ij}(t)=\frac{r_{\mathrm{a}}}{1+(N_j(t)/K)}+r_{\mathrm{b}ij}(t),$$ 3.1

where N_j(t) is the total number of individuals on patch j. The fitness of an individual is the sum of (i) an intrinsic growth rate r_a, limited by the carrying capacity K, and (ii) an additional growth rate resulting from the extra resources produced by the collective task, r_bij(t). The additional growth rate r_bij(t) is not limited by the carrying capacity, but competition between individuals is taken into account during the distribution of collective resources. The additional growth rate r_bij(t) is calculated as follows:

$$r_{\mathrm{b}ij}(t)={\beta }_{\mathrm{r}}(1-{\text{e}}^{-{\gamma }_{\mathrm{r}}(B_j(t)p_{ij}(t))}).$$ 3.2

The term r_bij(t) is calculated from a logistic function described by γ_r and β_r, respectively the steepness and the maximum of the increase in growth rate induced by the additional resources. The additional resources are given by the total amount of benefit, B_j(t), multiplied by the share the individual receives, p_ij(t). The increase of the growth rate follows a logistic relation because of the inevitable presence of other limiting factors, e.g. space or other resources.

To produce the additional resources B_j(t), individuals first undergo a consensus decision-making process on their patch, as defined in the previous section (see equations (2.1)–(2.3)). The consensus time determines the cost of organization (equation (3.3)), and the outcome of the consensus decision-making determines the share of individuals (equation (3.4)) as explained in the following paragraphs. We do not consider that the decisions taken affect the success of the group except for the distribution of resources. We investigate the emergence of leaders defined as influential individuals, as it was done in psychology experiments [32], and as observed in psychological profiles of leaders [21]. In this case where leaders are not better at taking decisions, integrating the effects of the collective decision would only result in more noise and not qualitatively change our results. Exploring the emergence of leaders as more informed individuals can be done in further work but it is not our focus here.

After consensus is reached, all individuals on a patch take part in the collective task which produces an amount of extra resource B_j(t):

$$B_j(t)=B_j(t-1)S+\frac{{\beta }_{\mathrm{b}}}{1+{\text{e}}^{-{\gamma }_{\mathrm{b}}(N_j(t)-b_{\mathrm{mid}})}}-C_{\mathrm{t}}{t}_j^{\ast }.$$ 3.3

The benefit is calculated from a sigmoid function described by β_b, b_mid and γ_b, respectively the maximum, the group size at the sigmoid’s midpoint, and the steepness of the increase in the benefit induced by additional participants. We make the assumption of initial increasing returns to scale, where additional participants increase the benefit superlinearly [33]; but as is standard in microeconomic theory, we also make the conservative assumption that the benefit of the collective task eventually has diminishing marginal returns which overcomes the increasing returns to scale because of other limiting factors, e.g. land available or level of technology [33]. To capture the transmissibility of resources [34], we assume that a proportion S of the benefit is also present in next generation. The extra resources are discounted by a cost of organization proportional to the consensus time t*.

This cost is modulated by a parameter C_t, which describes the time constraints on group decision-making. The parameter C_t depends on the pressure of time on the task, for instance, the speed of depletion of resources or the need to build defences before an enemy arrives. To avoid studying the effect of social strategy in the collective task, which has already been extensively studied in the evolution of cooperation literature [35], we consider that all the individuals on a patch are willing to participate in the collective task once a decision is reached. The collective task simulates the numerous cooperative tasks realized during the lifetime of an individual, e.g. hunting large game or constructing an irrigation system.

The resources obtained from the collective task are distributed among all individuals on the patch. We want to test if hierarchy can emerge even if leaders receive a higher share of the collective resources, which selects against individuals becoming followers. However, leaders are not clearly designated in informal hierarchy. We assume that in the absence of coercive means, individuals can only increase their share by biasing the collective decision towards their own interests and thus, the share of an individual p_ij(t) is a function of its realized influence α_r such that:

$$p_{ij}(t)=\frac{1+\text{d}{\alpha }_{r(ij)}\hspace{0.17em}(t)}{\sum _{i=1}^{N_j}(1+\text{d}{\alpha }_{r(ij)}\hspace{0.17em}(t))}.$$ 3.4

The asymmetry of the distribution of the resources is modulated by a parameter d, which represents the level of ecological inequality. For d = 0, a patch is totally egalitarian and the influence of an individual does not affect the share of that individual. Such a scenario is close to the society of pre-Neolithic hunter–gatherers [2]. It is assumed for simplicity that d is the same for all patches, and is determined for example by the state of technology, such as food storage and military technologies. Nevertheless, different patches can have more or less despotic distributions of resources owing to different distributions of α_r values. The realized influence of an individual α_r(ij) is calculated from the difference between an individual’s initial opinion and the final decision, and measures how much the final decision is close to the individual’s interest:

$${\alpha }_{r(ij)}=1-|x_{ij}(t=0)-x_j^{\ast }|.$$ 3.5

(b). Analysis

We use this model to answer the following question: can the organizational benefit of hierarchy in the presence of scalar stress lead to the evolution of leader and follower behaviours even if it creates inequality in resources? Because of the nonlinearities of the model, we analyse it using replicated individual-based simulations.

We define hierarchy as a positively skewed distribution of influence α. The skewness is measured by the Pearson’s moment coefficient of skewness. We focus on the effect of the following parameters: (i) the level of ecological inequality d, and (ii) and the number of listeners N_l, which affects the intensity of scalar stress (electronic supplementary material, figure S3). In the electronic supplementary material, we also explore the effect of (i) the time constraints on group decision-making C_t, (ii) the migration rate m, which affects the population structure, and (iii) the absence of transmission of resources from one generation to another (S = 0). The default values of these parameters, unless otherwise specified, are for the level of inequality d = 1, the number of listeners N_l = 30, the time constraints on group decision-making C_t = 2, the migration rate m = 0.05, and the fraction of resources transmitted to next the generation S = 0.9. The default values for the remaining demographic and ecological parameters are for the number of patches N_p = 50, the initial number of individuals on each patch N_j(0) = 50, the carrying capacity K = 50, the intrinsic growth rate r_a = 2, β_b = 10 000, γ_b = 0.005, b_mid = 500, β_r = 3 and γ_r = 0.025. These values are chosen in order to allow the transition between tribe size (50–100 individuals) to small chiefdom size (500 individuals) [4], and so that additional resources lead to a clearly increased fitness. The remaining default parameter values are for the consensus threshold x_θ = 0.05, and for the mutation process, where μ_m = 0.01 and ${\sigma }_{\mathrm{m}}^2=0.01$.

The results presented are the average across patches when the result is a function of generations, and the average across patches, generations and simulations when the result is a function of a parameter. The error bars represent the standard error from the mean across replicates. The simulations are run for 10 000 generations and the first 5000 generations are ignored to limit the effects of initial conditions.

(i). The emergence of efficient hierarchy

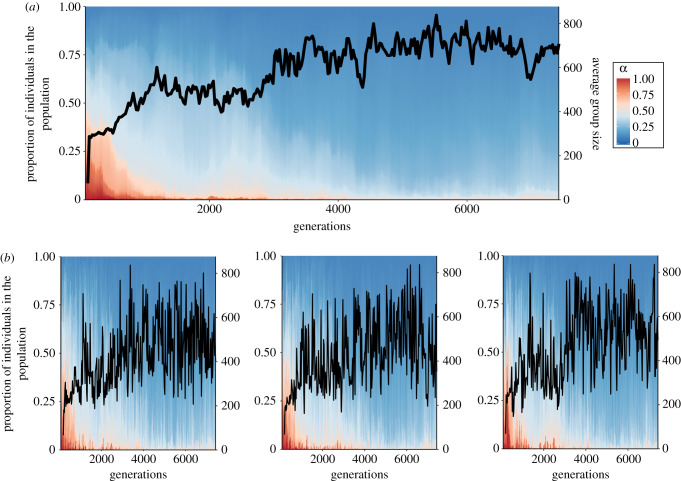
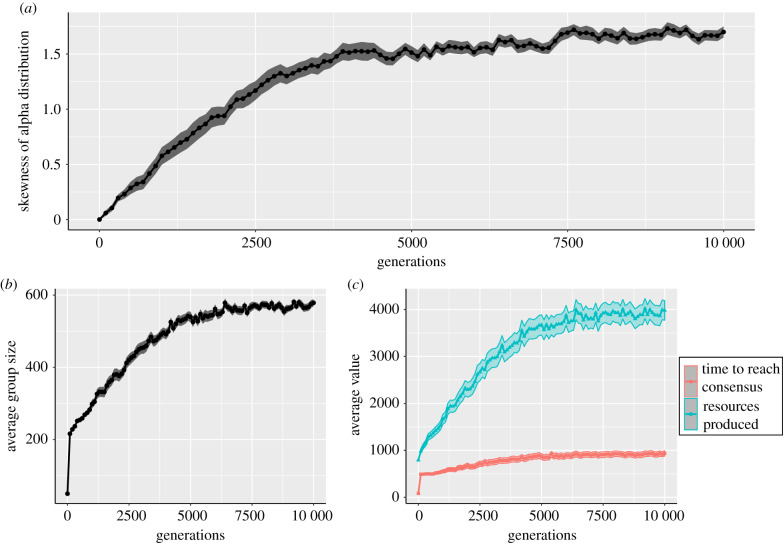
Figure 2 presents the evolution of the distribution of influence and group size as a function of generations for a single run. The results show that despite the wide range of possible distributions of influence, individuals evolve towards hierarchy, i.e. a minority of leaders with high influence and a majority of followers with low influence. In the meantime, the population grows to a large group size. Within a patch, hierarchy also evolves but the proportion of leaders and followers vary. The result is stable across replicates and in the long term as shown by figure 3a. At the start of the simulation, groups have a skewness close to 0 and a small group size because the values of influence are randomly initiated. Figure 3a demonstrates that skewness increases with time and remains at a positive value along generations. The positive skewness reflects a majority of individuals with low influence—followers—and a minority of individuals with high influence—leaders. This result is also present in absence of intergenerational transmission of resources (S = 0) as seen in the electronic supplementary material, figure S4. Overall, these results show that hierarchy can emerge from the evolution of individual behaviour and thus, hierarchy provides a clear evolutionary advantage.

Figure 2.

Evolution of the distribution of influence α, and evolution of average group size as a function of generations for the whole population (a) and three different patches (b). The plot represents results for a single run. A column at a given generation is composed of sections with each section showing the proportion (size of the section) of individuals with a given influence (colour of the section). Note that there is a small proportion of individuals with high influence at equilibrium. This proportion is low and thus, hard to discern but it is revealed by a stripe of orange and white colour at the bottom. (Online version in colour.)

Figure 3.

Evolution of (a) the average skewness of distribution of influence α, (b) average group size, and (c) average consensus time t* (red) and average additional resources produced b (blue), as a function of generations. Hierarchy is represented by a positive skewness. The values presented are the average across 32 replicates. (Online version in colour.)

The benefit of an efficient hierarchical organization is shown in figure 3c. It shows that over generations, the consensus time and the total amount of resources both increase. This is because group size increases and leads to more resources being produced owing to increasing returns to scale, but also a greater difficulty to organize. However, it can be observed in figure 3c that the increase in consensus time stabilizes before the end of the increase in extra resources. This is because individuals have evolved towards hierarchy and can maintain a low cost of organization even as the group size and the production of resources continue to increase. The benefit of hierarchy depends on the time constraints C_t, which translates the consensus time into an opportunity cost of organization. The electronic supplementary material, figure S5 shows that the level of hierarchy is proportional to the time constraints. For a low level of time constraints, the benefit of hierarchy has a negligible effect on organization and group production and thus, hierarchy does not evolve. For tasks with strong time constraints, e.g. warfare, the benefit of hierarchy is amplified and a strong hierarchy evolves.

Hierarchy evolves because it reduces the cost of organization and thus provides the creation of a surplus in group production. This surplus is distributed among the individuals and increases the number of offspring they produce. This results in hierarchical groups growing larger and exporting a larger number of migrants than groups without hierarchy. Most of these migrants are followers because most of the population within a hierarchy are followers. Ultimately, these migrants spread hierarchical organization to other groups and at the population level creates a stable skewed distribution of influence.

(ii). Hierarchy and inequality in resources

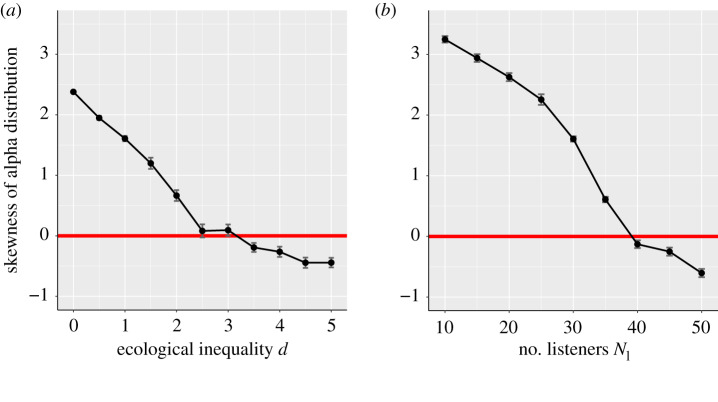
Importantly, hierarchy evolves even when the emergence of hierarchy creates inequality in resources. Hierarchy creates inequality in resources because leaders will more often bring the group decision close to their preferences and thus receive a higher share of the resources produced, and hence have a larger number of offspring compared to followers on the same patch. Inequality in resources limits the development of hierarchy because it increases the number of offspring leaders produce, and potentially drives all individuals within a group to develop high influence. This effect can be seen in figure 4a, which shows that a higher level of inequality reduces the skewness of the distribution of influence. But this is limited by the competition between leaders. In the presence of multiple leaders, a leader can get a lower share of the resource than followers if the group becomes convinced by another leader during the decision-making process. In this case, the ‘losing’ leaders are further from the final decision because they are harder to convince. However, the fact that hierarchy does not evolve for high levels of inequality shows that this competition is not always enough to stop the increase in number of leaders and the collapse of hierarchy. The second reason explaining the evolution of hierarchy despite inequality is that, even if leaders receive more resources, followers still get a higher amount of resources and offspring than they would in a group without hierarchy, because larger groups produce more resources owing to increasing returns to scale.

Figure 4.

Average skewness of the distribution of influence α across 5000 generations and across 32 replicates as a function of the level of ecological inequality d and the number of listeners N_l. (Online version in colour.)

(iii). The feedback loop between scalar stress, hierarchy and group size

We have seen previously that hierarchy reduces the consensus time but it also provides a second main advantage to group organization: it reduces scalar stress. To test the importance of this factor in the evolution of hierarchy, we look at the skewness of the distribution of influence for different values of number of listeners, N_l. Figure 4b shows that high scalar stress, i.e. low number of listeners N_l, leads to the evolution of a more skewed distribution of influence. On the other hand, a low scalar stress, i.e. here represented by a high number of listeners N_l, leads to the disappearance of hierarchy. This result shows that the benefit of reducing scalar stress is a crucial factor in the evolution of hierarchy. This is because scalar stress creates a positive feedback loop by which hierarchy increases its own benefit. On the one hand, an efficient hierarchical organization allows a group to produce a larger amount of resources and hence reach a larger size. On the other hand, hierarchy provides a stronger advantage as group size increases because the cost of organization increases less in hierarchical groups than in acephalous groups. There is a feedback loop between hierarchy leading to larger group size, and larger group size increasing the benefit of hierarchy. Eventually, this feedback loop comes to an end owing to diminishing marginal returns, i.e. other limiting factors than group size. Yet, this feedback loop amplifies the benefit that hierarchy provides to group members and favours its evolution.

To summarize, social organization is the equilibrium between two opposing forces, competition within groups where inequality pushes individuals to evolve high influence, and competition between individuals of different groups where efficient group organization pushes most individuals to evolve low influence. Looking closer, hierarchy provides one direct and one indirect benefit [13] to followers compared to individuals in acephalous groups. First, hierarchy provides a direct benefit to followers because it increases the amount of surplus resources produced and thus, it increases the fitness of followers. Second, hierarchy provides an indirect benefit to followers because it increases the group size and hence the amount of resources produced in the following generation. This increases the fitness of followers’ offspring. The contribution of each benefit is hard to distinguish but their role can be examined by investigating the effect of high migration rate, which suppresses population structure and indirect benefits to offspring on the same patch. The electronic supplementary material, figure S6 shows that, considering moderate time constraints, a high migration rate leads to the disappearance of hierarchy at equilibrium. This highlights the importance of the indirect benefit to offspring that remain on the patch in sustaining hierarchy. On the other hand, the electronic supplementary material, figure S7 shows that hierarchy evolves for any migration rate if the the time constraints are high. In this case, the direct benefit is high enough to overcome the cost of inequality in resources. In conclusion, hierarchy can evolve when time constraints are high through the immediate direct benefit of producing extra resources, but the indirect benefit resulting from the feedback loop between hierarchy, group size and scalar stress allows hierarchy to evolve over a much wider range of conditions.

4. Discussion

Group size and the resultant scalar stress have been proposed as a crucial factor to explain the emergence of hierarchy from previously egalitarian groups [16,17,19]. However, the investigation of this in models of either social dynamics or evolutionary dynamics has been limited so far because a formalization of hierarchy compatible with both types of model was lacking. To fill this gap, we have described group social organization by the distribution of an individual trait, the influence. We have looked at the effect of this distribution on the consensus time using an opinion formation model, and if this distribution can emerge from the evolution of individual behaviours in an evolutionary model.

Our results first show that hierarchy reduces the intensity of scalar stress, i.e. the increase of consensus time as group size grows. This benefit emerges solely from the difference of influence between leaders and followers. Second, the results of the evolutionary model show that hierarchy can evolve de novo in the presence of low initial inequality in resources and increasing returns to scale, which are both reasonable assumptions for the small egalitarian groups and societies present during the Neolithic transition [2,36].

This work expands on previous research in social dynamics and evolutionary dynamics by including the role of scalar stress. A previous opinion formation model shows that heterogeneity in individual persuasiveness and stubbornness can affect the time spent to reach consensus [28].

Our findings confirm this result and show that the shortest consensus time is reached for a positively skewed distribution of these traits, as observed in hierarchy. In addition, our results demonstrate that this advantage is greatly correlated with group size. A previous evolutionary model combining opinion formation and evolutionary dynamics showed that hierarchy could evolve when the cost of organization is high, for example as in warfare [37]. However, the hierarchy obtained was unstable and groups often failed to produce any resources. The model presented here demonstrates that scalar stress was a crucial missing factor which, when integrated, leads to the evolution of stable hierarchy and large groups.

Our model of informal hierarchy extends previous work on institutionalized hierarchy [19] by showing that this voluntary theory holds even in societies where political institutions are absent, and thus where inequality creates selection pressures towards leader behaviours. Furthermore, the opinion formation model developed here is a first step to move from a benefit of hierarchy that is simply assumed in the model, to a more mechanistic explanation. However, it is still missing some key aspects of group organization e.g. individual knowledge or network structure. Further work should explore how additional factors of group decision-making could amplify or reduce the role of hierarchy in organization. More broadly, our model is in line with theoretical work which proposes that hierarchy emerged because leaders fulfil an important role for the group, e.g. leaders promote cooperation by monitoring the group and punishing the defectors [38]. Importantly, the explanation explored here is not mutually exclusive with previous explanations. Rather, it can complete them. Following the previous example [38], policing in large-scale societies requires efficient decision-making to create the large number of rules [39] and to manage specialized policing forces.

Our findings predict that the level of hierarchy, i.e. skewness of the distribution of influence, should increase both with the time constraints on the tasks tackled by the group and with group size. First, there is extensive evidence that human groups tackling tasks with high time constraints such as warfare often switch to a strong hierarchical organization [40]. Second, previous reviews of ethnographic data presents evidence that group size scales with political complexity [16,17,41]. For example, the Inuit population on coastal North Alaska are composed of large groups relying on bowhead whale hunting, a complex coordination task. These populations are thus under high scalar stress and exhibit a strong hierarchy, with leaders who own the hunting equipment deciding the distribution of resources. In comparison, smaller groups of Inuits living on the Mackenzie Delta rely on individual hunting and have a less hierarchical organization [18]. However, the generality of a scenario where the cost of organization, drives the evolution of hierarchy needs to be better estimated with further work exploring the quantitative relationship between individual behaviours, group size and cost of organization, either in laboratory experiments or in real world human groups. Other than scalar stress, our findings predict that low initial inequality in resources and initial increasing returns to scale are necessary for the origin of hierarchy. Much anthropological evidence shows that inequality in resources was strongly limited in pre-hierarchical societies because of the absence of food storage technologies preventing leaders from building up a personal surplus of resources; and the absence of coercive institutions e.g. dedicated armies and tax collection [2]. Increasing returns to scale is commonly observed in modern collective actions and results from synergistic interactions between individuals, such as division of labour and specialization [42]. Archaeological evidence suggests that agriculture could have provided Neolithic society with such scalable means of production [43].

In political sciences, the ‘iron law of oligarchy’ proposes a comprehensive scenario for the emergence of hierarchy and inequality [1]. Our model, combined with previous research [19,44], shows that an evolutionary iron law of oligarchy is a plausible scenario to explain the transition to hierarchy. Expanding human groups switch to hierarchy by evolution of individual behaviours or by group decision [19] to limit the costs of large-scale organization. Later on, leaders use their influence to bias the distribution of collective benefits and costs towards their own interests [44]. Once a few individuals have monopolized economic power and political power, they can then use these advantages in order to sustain their domination [45]. The main benefit of this theory is to provide a common explanation for voluntary and coercive hierarchy. The two opposing sides of hierarchy emerge from the same mechanism, consensus decision-making, which is quicker but biased when the distribution of influence is skewed. Although the iron law was initially proposed to explain human social organization in the post industrial revolution era, our model suggests that its explanatory scope might be wider than first believed. For example, there is evidence that non-human species also use consensus decision-making to coordinate [46]. While it is hard to draw conclusions about other species with the current model, further work could tailor the model to investigate the emergence of leadership in these species.

Data accessibility

The code is available online at ‘https://github.com/CedricPerret’ in the project ‘ConsensusMod’ for the opinion formation model, and in the project ‘EvolLeadMod’ for the evolutionary model.

Authors' contributions

C.P. and S.T.P. designed the study; C.P. carried out the research; C.P., E.H. and S.T.P. wrote the manuscript.

Competing interests

The authors declare no competing financial interests.

Funding

This project is part of a PhD funded by Edinburgh Napier University.