Modeling the impact of non-pharmaceutical interventions on the dynamics of novel coronavirus with optimal control analysis with a case study

Abstract

Coronavirus disease (COVID-19) is the biggest public health challenge the world is facing in recent days. Since there is no effective vaccine and treatment for this virus, therefore, the only way to mitigate this infection is the implementation of non-pharmaceutical interventions such as social-distancing, community lockdown, quarantine, hospitalization or self-isolation and contact-tracing. In this paper, we develop a mathematical model to explore the transmission dynamics and possible control of the COVID-19 pandemic in Pakistan, one of the Asian countries with a high burden of disease with more than 200,000 confirmed infected cases so far. Initially, a mathematical model without optimal control is formulated and some of the basic necessary analysis of the model, including stability results of the disease-free equilibrium is presented. It is found that the model is stable around the disease-free equilibrium both locally and globally when the basic reproduction number is less than unity. Despite the basic analysis of the model, we further consider the confirmed infected COVID-19 cases documented in Pakistan from March 1, till May 28, 2020 and estimate the model parameters using the least square fitting tools from statistics and probability theory. The results show that the model output is in good agreement with the reported COVID-19 infected cases. The approximate value of the basic reproductive number based on the estimated parameters is ${\mathcal{R}}_0\approx 1.87$. The effect of low (or mild), moderate, and comparatively strict control interventions like social-distancing, quarantine rate, (or contact-tracing of suspected people) and hospitalization (or self-isolation) of testing positive COVID-19 cases are shown graphically. It is observed that the most effective strategy to minimize the disease burden is the implementation of maintaining a strict social-distancing and contact-tracing to quarantine the exposed people. Furthermore, we carried out the global sensitivity analysis of the most crucial parameter known as the basic reproduction number using the Latin Hypercube Sampling (LHS) and the partial rank correlation coefficient (PRCC) techniques. The proposed model is then reformulated by adding the time-dependent control variables u₁(t) for quarantine and u₂(t) for the hospitalization interventions and present the necessary optimality conditions using the optimal control theory and Pontryagin’s maximum principle. Finally, the impact of constant and optimal control interventions on infected individuals is compared graphically.

1. Introduction

The novel coronavirus infectious disease, caused by the coronavirus is commonly known as COVID-19. It has become the greatest challenge the history has ever seen. Started from Wuhan city of China earlier this year, it spread to the rest of the world in a few months and was declared a pandemic by the UN. It has paralyzed life across the globe. The main cause of the virus is yet to be discovered, but it is presumed that it has emerged in one the biggest animal market in the Chinese City of Wuhan [1], [2], [3]. So far, it has engulfed more than 210 countries of the world and according to WHO statistics, the virus has affected around 6 million people across the world and more than 300 thousand people have died so far [1], [2], [3]. The recovery rate is higher than the mortality rate. However, the ratio varies from country to country and region to region. USA is the most affected country which is the epicenter of the virus followed by Europe [2]. Scientists are struggling to discover or invent a vaccine for the treatment, but it is yet to be discovered. The question, how long it will last? is on everyone’s lips. Although research is in a very early stage and with the passage of time things will unfold. The scientists are trying to dig out the main symptoms and causes of transmission. However, according to the information available the main symptoms are high fever, severe chest pain, continuous dry coughing, body aches, headache and difficulty in the respiratory system. The spread, according to available information, is droplets, produced by an infected person during coughing and sneezing and physical contacts, etc. [4].

COVID-19 pandemic has caused great damage not only to human lives and health it has multidimensional effects. It not only exposed the weak health infrastructure even in the most advanced countries of the world, but also badly affected the world economy. Almost the entire world is on lockdown and all the economic and business activities are halted. It has shocked the largest economies of the world, i.e. China and USA where the economic slowdown is observed since the outbreak of coronavirus. The third world countries, particularly Pakistan, are the prime targets of the economic devastation. Millions of people have lost their jobs in the past few months. Poor countries are unable to repay their debts. They are even unable to support poor citizens who cannot earn their livelihood. The social and political lives of the nations are affected badly. People across the world have severed social relations. They avoid meeting each other even in the gravest times. Governments of all the countries have diverted their attention and resources to cope with the challenge of this mysterious disease and thus no political activity is visible.

Like other countries in the world, COVID-19 pandemic poses a huge threat to both humans health and economy in Pakistan. This infection is even more devastating in Pakistan because the implementation of non-pharmaceutical interventions i.e., make social-distancing and community lockdowns are certainly very tough for a society like Pakistan. The government is unable to afford a strict nationwide lockdown. The COVID-19 first case was reported on 26 February 2020 in Karachi which was a student come back from Iran. Later, only within three weeks, the infection spread in all four provinces, Gilgit-Baltistan, Azad Jammu and Kashmir, and the federal territory of Islamabad. The total number of confirmed infected cases raised to 2291 across the nation and 252 new cases were reported on 1 April. Due to the rapid growth of infected people across the country the government of Pakistan decided to put the whole nation under strict lockdown and later extended twice until 9 May, due to a worse situation. Currently, the situation in Pakistan is worse and the number of confirmed cases crossed the cases reported in mainland China. Pakistan is placed 17th in the list of highly reported infected cases and deaths by countries, territories, or areas [5], [6] with a total of more than 100,000 confirmed COVID-19 cases. About 31,000 patients are fully recovered and 1900 people lost their lives due to this deadly infection [7], [8].

Mathematical models are very useful in helping us to understand the transmission dynamics and control of emerging and re-emerging communicable diseases. One of the main challenges that mankind is facing nowadays is predicting the severity and suggest suitable public health intervention strategies to curtail the COVID-19 pandemic. Recently, a number of mathematical models have been proposed to explore the transmission patterns of COVID-19 pandemic. In [9], the authors formulated a deterministic model to explore the impact of various public interventions on the dynamic and mitigation COVID-19 in Ontario, Canada. In [10], a mathematical model based on nonlinear differential equations is presented to study the dynamics of COVID-19 infection in highly affected countries that are China, Italy, and France. A fractional-order COVID-19 model with the Atangana-Bleanu-Caputo operator is proposed by Khan and Atangana [11] and implemented the model to analyze the infection in Wuhan. The role of lockdown in the absence of effective vaccines and treatment in order to mitigate the COVID-19 pandemic is analyzed in [12]. The author has used the novel fractional-fractal operators to formulate the proposed mathematical model [12]. In [13], a transmission model is formulated to predict the cumulative COVID-19 cases in Italy, UK, and USA. The transmission dynamics of COVID-19 in Mexico are studied using mathematical and computational models in [14]. The influence of non-pharmaceutical controls, including quarantine, hospitalization or self-isolation, contact-tracing, and the use of a face mask on the dynamics of COVID-19 pandemic in the population of New York state and the entire USA is studied in detail in [15].

The present study proposes a new transmission model to analyze the dynamics and impact of non-pharmaceutical interventions on the COVID-19 in Pakistan. Initially, we develop the model without optimal control variables and provide a good fit to the reported cases and then estimate the model parameters using a nonlinear least square curve fitting approach. Further, the model is reformulated by adding two times dependent control variables. The rest of the manuscript is organized as: The mathematical formulation of the COVID-19 model is presented in Section 2. Basic mathematical analysis, including stability results of disease-free equilibrium is explored in Section 3. The model fitting to reported cases and estimation of parameters is done in Section 4. The simulation results of without optimal control model are shown in Section 5. The global sensitivity analysis and its graphical interpretation are depicted in Section 6. The optimal control problem and its analysis of the COVID-19 infection is presented in 7. Finally, a brief concluding remarks are given in Section 8.

2. Formulation of the model

This section presents a brief description of the proposed model to study the dynamics and possible control of the COVID-19 pandemic. The model is developed by dividing the whole human population at any time t, denoted by N(t) into eight mutually exclusive sub-groups depending on the disease status.  These sub-groups are  susceptible   S(t),  exposed or latent   E(t), infected with the disease symptoms (or symptomatically infectious) I(t),  asymptotically infectious   having    no clinical symptoms I_a(t), quarantined Q(t), hospitalized I_h(t), critically infected (or intensive care) patients I_c(t)  and the recovered/removed individuals   R(t), so that    

$$N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+I_a\left(t\right)+Q\left(t\right)+I_h\left(t\right)+I_c\left(t\right)+R\left(t\right).$$

 The  infected individuals showing mild symptoms of the disease are also placed in the epidemiological class I_a(t). The quarantine and isolation should be either at home or the specific centers or hospitals designated by the government. Further, the group  I_h  stand for the patients admitted into hospital also contains those with clinical symptoms of the disease who are self-isolating at home.  We further assume that hospitalized people may also transmit the infection after interacting with susceptible people. The transmission dynamics of the COVID-19 disease is expressed through the following system of the nonlinear differential equation:

$$\begin{array}{c}\frac{dS}{dt}=\Lambda -\frac{\beta (I+\psi I_a+\nu I_h)}{N}S-\mu S,\hfill \\ \\ \frac{dE}{dt}=\frac{\beta (I+\psi I_a+\nu I_h)}{N}S-(\omega +\kappa +\mu )E,\hfill \\ \\ \frac{dI}{dt}=\rho \omega E-({\zeta }_1+\mu +{\xi }_1+\eta )I,\hfill \\ \\ \frac{d{I}_a}{dt}=(1-\rho )\omega E-({\zeta }_2+\mu )I_a,\hfill \\ \\ \frac{dQ}{dt}=\kappa E-(\mu +{\varphi }_1+\delta )Q,\hfill \\ \\ \frac{d{I}_h}{dt}=\eta I+\delta Q-(\mu +{\varphi }_2+{\xi }_2+\varphi )I_h,\hfill \\ \\ \frac{d{I}_c}{dt}=\varphi I_h-(\mu +{\varphi }_3+{\xi }_3)I_c,\hfill \\ \\ \frac{dR}{dt}={\zeta }_{1}I+{\zeta }_2{I}_a+{\varphi }_{1}Q+{\varphi }_2{I}_h+{\varphi }_3{I}_c-\mu R.\hfill \end{array}$$ (1)

The corresponding initial conditions are

$$\begin{array}{c}S\left(t_0\right)=S_0\ge 0,E\left(t_0\right)=E_0\ge 0,I\left(t_0\right)=I_0\ge 0,I_a\left(t_0\right)=I_{a0}\ge 0,\hfill \\ Q\left(t_0\right)=Q_0\ge 0,I_h\left(t_0\right)=I_{h0}\ge 0,I_c\left(t_0\right)=I_{c0}\ge 0,R\left(t_0\right)=R_0\ge 0.\hfill \end{array}$$ (2)

The birth rate is denoted by Λ and the natural mortality rate in all groups is denoted by μ. The susceptible people acquired COVID-19 infection when they interact with the infected people in I, I_a and I_h compartments. The force of infection is

$$\lambda =\frac{\beta (I+\psi I_a+\nu I_h)S}{N},$$

where the parameter β shows the effective contact rate, i.e., contacts capable of leading to infection transmission and the parameter 0 ≤ ψ ≤ 1 accounts for the assumed reduction in disease transmissibility of asymptomatic infected individuals in comparison to symptomatic one. Similarly, ν is used for the infectiousness rate due to hospitalized COVID-19 patients. It is noticed from the transmission patron of COVID-19 that the asymptomatic individuals are comparatively dangerous relative to the individuals in the I_h class because they are not aware of the infection and are capable to transmit the infection. The latent individuals develop an infection after completion of incubation period and become infected at the rate ω and a fraction denoted by ρ enters to the symptomatic class after showing disease symptoms and the remanding with no (or mild) symptoms join the asymptomatic compartment I_a(t). The exposed individuals who have interaction with COVID-19 infected patients are detected (via contact-tracing) and placed in quarantine at the rate κ which further moves to hospitalized class if they are tested positive with COVID-19 infection. The symptomatically-infectious people are hospitalized at the rate η which further moves to critically-infected class I_c at the rate ϕ if they are serious and need critical care. The parameters ζ ₁ and ζ ₂ represent the recovery rates in I and I_a groups respectively. Further, the recovery rates of quarantined, hospitalized and critically infected classes are shown by ϕ ₁, ϕ ₂ and ϕ ₃ respectively. Finally, the COVID-19 induced mortality for individuals in the I, I_h and I_c classes are respectively shown by ξ ₁, ξ ₂ and ξ ₃.

For simplicity, let us denote

$$\begin{array}{ccc}\hfill k_1& =& (\omega +\kappa +\mu ),k_2=({\zeta }_1+\mu +{\xi }_1+\eta ),k_3=({\zeta }_2+\mu )\hfill \\ \hfill k_4& =& (\mu +{\varphi }_1+\delta ),k_5=(\mu +{\varphi }_2+{\xi }_2+\varphi ),k_6=(\mu +{\varphi }_3+{\xi }_3).\hfill \end{array}$$

Then, the above model (1) can be written as

$$\begin{array}{c}\frac{dS}{dt}=\Lambda -\lambda S-\mu S,\hfill \\ \\ \frac{dE}{dt}=\lambda S-k_{1}E,\hfill \\ \\ \frac{dI}{dt}=\rho \omega E-k_{2}I,\hfill \\ \\ \frac{d{I}_a}{dt}=(1-\rho )\omega E-k_3{I}_a,\hfill \\ \\ \frac{dQ}{dt}=\kappa E-k_{4}Q,\hfill \\ \\ \frac{d{I}_h}{dt}=\eta I+\delta Q-k_5{I}_h,\hfill \\ \\ \frac{d{I}_c}{dt}=\varphi I_h-k_6{I}_c,\hfill \\ \\ \frac{dR}{dt}={\zeta }_{1}I+{\zeta }_2{I}_a+{\varphi }_{1}Q+{\varphi }_2{I}_h+{\varphi }_3{I}_c-\mu R.\hfill \end{array}$$ (3)

3. Basic analytical results

We present some basic and necessary analytical results of the COVID-19 model (3) such as positivity and boundedness of the model solution, equilibria and stability of the disease-free case. Further, we establish the theoretical expression of the important biological parameter known as the basic reproduction number.    The positivity and boundedness of the model solution are presented in the following lemma.

3.1. Positivity and boundedness

Lemma 1

Let$\mathcal{P}\left(0\right)\ge 0$denotes the initial data and$\mathcal{P}\left(t\right)=(S,E,I,I_a,Q,I_h,I_c,R)$are the model variables, then all solutions of the model(3)will be non-negative for all t > 0. Furthermore,

$$\underset{t\to \infty }{\lim }supN\left(t\right)\le \Lambda /\mu .$$

Proof

Let $t_1=\sup \{t>0:\mathcal{P}\left(t\right)>0\in [0,t]\},$ then it follows from the first equation of the COVID-19 model (3):

$$\frac{dS}{dt}=\Lambda -(\lambda +\mu )S.$$ (4)

It can be further written as

$$\frac{\mathit{dS}}{\mathit{dt}}\left\{S\left(t\right)\exp (\mu t+{\int }_0^t\lambda \left(\varsigma \right)d\varsigma )\right\}=\Lambda \exp (\mu t+{\int }_0^t\lambda \left(\varsigma \right)d\varsigma ).$$

Hence,

$$\begin{array}{ccc}& & S\left(t_1\right)\exp (\mu t_1+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma )-S\left(0\right)\hfill \\ & & ={\int }_0^{t_1}\Lambda \times \exp (\mu p+{\int }_0^p\lambda \left(\varsigma \right)d\varsigma )dp.\hfill \end{array}$$ (5)

The solution of (5) can found as below

$$\begin{array}{ccc}\hfill S\left(t_1\right)& =& S\left(0\right)\exp \{-(\mu t_1+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma \left)\right\}+\exp \{-(\mu t_1+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma \left)\right\}\hfill \\ \\ & & \times {\int }_0^{t_1}\Lambda \times \exp (\mu p+{\int }_0^p\lambda \left(\varsigma \right)d\varsigma )dp>.\hfill \end{array}$$

Following a similar procedure, it can be shown that $\mathcal{P}\left(t\right)>0,$ ∀ t > 0.

In order to prove the second part we have $0<\mathcal{P}\left(0\right)\le N\left(t\right),$ and then the addition of all equations of the COVID-19 model (3) we have

$$\begin{array}{ccc}\hfill \frac{dN\left(t\right)}{dt}& =& \Lambda -\mu N\left(t\right)-{\xi }_{1}I\left(t\right)-{\xi }_2{I}_h\left(t\right)-{\xi }_3{I}_c\hfill \\ \\ & \le & \Lambda -\mu N\left(t\right).\hfill \end{array}$$

Hence,

$$\underset{t\to \infty }{\lim }sup\left\{N\left(t\right)\right\}\le \Lambda /\mu .$$

 □

Invariant region

The dynamics of the COVID-19 mathematical model (3) will be studied in the following closed and biologically feasible region.

$$\Delta \subset {\mathbb{R}}_{+}^8,$$

where,

$$\Delta =\{(S,E,I,I_a,Q,I_h,I_c,R)\in {\mathbb{R}}_{+}^8:S+E+I+I_a+Q+I_h+I_c+R\le \Lambda /\mu \}.$$

Lemma 2

The region defined in the closed set$\Delta \subset {\mathbb{R}}_{+}^8,$is positively invariant for the model(3)with non-negative initial conditions in${\mathbb{R}}_{+}^8$.

Proof

As in Lemma 1, it follows from the summation of all equations of the COVID-19 model (3),

$$\frac{dN\left(t\right)}{dt}\le \Lambda -\mu N\left(t\right).$$ (6)

It is clear that

$$\frac{dN\left(t\right)}{dt}\le 0,ifN\left(0\right)\ge \frac{\Lambda }{\mu }.$$

The solution of and (6) is given in the following inequality,

$$N\left(t\right)\le N\left(0\right)e^{-\mu t}+\frac{\Lambda }{\mu }(1-e^{-\mu t}).$$

In particular, N(t) ≤ Λ/μ, if N(0) ≤ Λ/μ. Therefore, the region Δ is positively invariant as well as attracts all the possible solution trajectories in ${\mathbb{R}}_{+}^8$. □

3.2. The basic reproduction number

The propose model (3) has a disease free equilibrium (DFE), given by

$${\mathcal{W}}_0=(S^0,0,0,0,0,0,0)=(\Lambda /\mu ,0,0,0,0,0,0,0).$$

Next, we investigate the most important and crucial threshold quantity known as the basic reproduction number and generally denoted by ${\mathcal{R}}_0$. This parameter measures the average number of new COVID-19 infected cases generated by a typical infected individual when introduced into a completely susceptible population. The most common approach used to obtain ${\mathcal{R}}_0$ is the next-generation method presented in [16].  The next generation  matrices obtained from the model (3) are  given as follows:

$$\mathcal{F}=\left(\begin{array}{c}\frac{\beta (I+\psi I_a+\nu I_h)S}{N}\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right),\mathcal{V}=\left(\begin{array}{c}{k}_{1}E\\ k_{2}I-\rho \omega E\\ k_3{I}_a-(1-\rho )\omega E\\ k_{4}Q-\kappa E\\ k_5{I}_h-\eta I-\delta Q\\ k_6{I}_c-\varphi I_h\end{array}\right).$$

The corresponding Jacobian matrices F and V evaluated at DFE is given as below:

$$\begin{array}{ccc}\hfill F& =& \left(\begin{array}{cccccc}0& \beta & \beta \psi & 0& \beta \nu & 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right),\hfill \\ \hfill V& =& \left(\begin{array}{cccccc}{k}_1& 0& 0& 0& 0& 0\\ -\rho \omega & k_2& 0& 0& 0& 0\\ -(1-\rho )\omega & 0& k_3& 0& 0& 0\\ -\kappa & 0& 0& k_4& 0& 0\\ 0& -\eta & 0& -\delta & k_5& 0\\ 0& 0& 0& 0& -\varphi & k_6\end{array}\right).\hfill \end{array}$$

Hence, utilizing the definition ${\mathcal{R}}_0=\rho \left(F{V}^{-1}\right)$ (where ρ(.) represents the spectral radius), we derived the following expression for the basic reproduction number:

$${\mathcal{R}}_0=\frac{\beta (k_4\omega (\rho k_3(\eta \nu +k_5)+(1-\rho )k_2{k}_5\psi )+\kappa \delta k_2{k}_3\nu )}{k_1{k}_2{k}_3{k}_4{k}_5}.$$

Interpretation of ${\mathcal{R}}_0$

In order to interpret the basic reproductive quantity we split the expression for ${\mathcal{R}}_0$ as follows:

$${\mathcal{R}}_0={\mathcal{R}}_{0i}+{\mathcal{R}}_{0a}+{\mathcal{R}}_{0h},$$

where,

$${\mathcal{R}}_{0i}=\frac{\beta \omega \rho }{k_1{k}_2},{\mathcal{R}}_{0a}=\frac{\beta \omega (1-\rho )\psi }{k_1{k}_3},{\mathcal{R}}_{0h}=\frac{\beta (k_4\omega \rho \eta +k_2\kappa \delta )\nu }{k_1{k}_2{k}_4{k}_5}.$$ (7)

The first term ${\mathcal{R}}_{0i}$ in (7) shows the average number of new  COVID-19 infections generated by symptomatically-infectious individuals in the I class.  This term  contains  the product of the infection rate in the I class (the disease transmission rate), β, the fraction of exposed people  that completed the incubation period and move to the symptomatic stage ($\frac{\rho \omega }{k_1}$) and  the average period spend  in the I compartment $\left(\frac{1}{k_2}\right)$.   The second constituent reproduction number ${\mathcal{R}}_{0a}$ represents the number of new COVID-19 infection cases generated by asymptomatically-infectious individuals in class I_a.  It is the product of infectious rate due to asymptomatic COIVD-19 individuals (βψ),   the fraction of latent people that completed the incubation period and move to the asymptomatic stage ($\frac{\rho (1-\omega )}{k_1}$) and the average period spent in the asymptomatic class  $\left(\frac{1}{k_3}\right)$.

Similarly, the third constituent reproduction number ${\mathcal{R}}_{0h}$ expresses the new COVID-19 infection cases generated by hospitalized/isolated individuals.  In particular, the first term in  ${\mathcal{R}}_{0h}$ represents the contribution into the hospitalized class by symptomatic infectious individuals (in class I). It is the product of infectious rate due to hospitalized individuals (βν),  the fraction of latent individuals that completed the incubation period and move to the asymptomatic stage ($\frac{\rho (1-\omega )}{k_1}$), the portion of individuals that left the symptomatic class  I  and move to the hospitalized class I_h ($\frac{\eta }{k_2}$), and the average duration in the hospitalized class ($\frac{1}{k_5}$). Finally,    the second term in   ${\mathcal{R}}_{0h}$ expresses the contribution of quarantined individuals into the hospitalized class.

3.3. Stability of disease free equilibrium

In this part, we will prove the local and global stability of the model around the DFE. The epidemiological implication of the stability result of DFE case is that a small influx of COVID-19 infections cases will not generate a COVID-19 outbreak if ${\mathcal{R}}_0<1$.

Theorem 1

The DFE, ${\mathcal{W}}_0$of the model(3)is locally asymptotically stable if${\mathcal{R}}_0<1$and unstable otherwise.

Proof

The Jacobian matrix $J_{{\mathcal{W}}_0}$ obtained at the DFE ${\mathcal{W}}_0$ is as follows:

$$J_{{\mathcal{W}}_0}=\left(\begin{array}{cccccccc}-\mu & 0& -\beta & -\beta \psi & 0& -\beta \nu & 0& 0\\ 0& -k_1& \beta & \beta \psi & 0& \beta \nu & 0& 0\\ 0& \rho \omega & -k_2& 0& 0& 0& 0& 0\\ 0& (1-\rho )\omega & 0& -k_3& 0& 0& 0& 0\\ 0& \kappa & 0& 0& -k_4& 0& 0& 0\\ 0& 0& \eta & 0& \delta & -k_5& 0& 0\\ 0& 0& 0& 0& 0& \varphi & -k_6& 0\\ 0& 0& {\zeta }_1& {\zeta }_2& {\varphi }_1& {\varphi }_2& {\varphi }_3& -\mu \end{array}\right).$$

Clearly, from the above Jacobian matrix $J_{{\mathcal{W}}_0},$ the eigenvalues $-\mu ,$ $-\mu$ and $-k_6$ have negative real part. There remanning eigenvalues can be obtained through the equations given below:

$${\Pi }^5+C_1{\Pi }^4+C_2{\Pi }^3+C_3{\Pi }^2+C_4\Pi +C_5=0.$$ (8)

The coefficients involved in (8) are as follow:

$$\begin{array}{ccc}\hfill C_1& =& k_1+k_2+k_3+k_4+k_5,\hfill \\ \hfill C_2& =& k_2{k}_3+k_1{k}_4+k_2{k}_4+k_3{k}_4+k_1{k}_5+k_2{k}_5+k_3{k}_5+k_4{k}_5\hfill \\ & & +k_1{k}_2(1-{\mathcal{R}}_{0i})+k_1{k}_3(1-{\mathcal{R}}_{0a}),\hfill \\ \hfill C_3& =& k_2{k}_3{k}_4+k_1{k}_3{k}_5+k_2{k}_3{k}_5+k_2{k}_4{k}_5+k_3{k}_4{k}_5\hfill \\ & & +k_1{k}_2{k}_5(1-{\mathcal{R}}_{0i}-{\mathcal{R}}_{0h_1})+k_1{k}_2{k}_3(1-{\mathcal{R}}_{0a}-{\mathcal{R}}_{0i})\hfill \\ & & +k_1{k}_2{k}_4(1-{\mathcal{R}}_{0i})+k_1{k}_3{k}_4(1-{\mathcal{R}}_{0a})+k_1{k}_4{k}_5(1-{\mathcal{R}}_{0a}-{\mathcal{R}}_{0h_2}),\hfill \\ \hfill C_4& =& k_2{k}_3{k}_4{k}_5+k_1{k}_2{k}_4{k}_5(1-{\mathcal{R}}_{0i}-{\mathcal{R}}_{0h})\hfill \\ & & +k_1{k}_2{k}_3{k}_5(1-{\mathcal{R}}_{0i}-{\mathcal{R}}_{0a}-{\mathcal{R}}_{0h_1})+k_1{k}_3{k}_4{k}_5(1-{\mathcal{R}}_{0a}-{\mathcal{R}}_{0h_2})\hfill \\ & & +k_1{k}_2{k}_3{k}_4(1-{\mathcal{R}}_{0i}-{\mathcal{R}}_{0a}),\hfill \\ \hfill C_5& =& k_1{k}_2{k}_3{k}_4{k}_5(1-{\mathcal{R}}_0),\hfill \end{array}$$

where,

$${\mathcal{R}}_{0h_1}=\frac{\beta \omega \rho \eta \nu }{k_1{k}_2{k}_5},and{\mathcal{R}}_{0h_2}=\frac{\beta \kappa \delta \nu }{k_1{k}_4{k}_5}.$$

Clearly, C_j for $j=1\dots ,5$ are all positive if ${\mathcal{R}}_0<1$. Further, it is easy to show the remaining Routh-Hurtwiz condition for the fifth order polynomial (8). Thus, the DFE is locally asymptotically stable if ${\mathcal{R}}_0<1$. □

The global dynamics of DFE, ${\mathcal{W}}_0$ of the COVID-19 transmission model is studied in the following result.

Theorem 2

The system(3)at${\mathcal{W}}_0$is globally asymptotically stable if${\mathcal{R}}_0<$1, and unstable for${\mathcal{R}}_0>$1.

Proof

Let we consider the following Lyapunov function, in order to prove the required result:

$$\mathcal{Z}\left(t\right)={\mathcal{B}}_{1}E+{\mathcal{B}}_{2}I+{\mathcal{B}}_3{I}_a+{\mathcal{B}}_{4}Q+{\mathcal{B}}_5{I}_h.$$

where ${\mathcal{B}}_i,$ for $i=1,2,\cdots ,5,$ used for some unknown positive constants. Differentiating the function $\mathcal{Z}\left(t\right)$ with respect to t and using the solutions of system (3), we obtain:

$$\begin{array}{ccc}\hfill \frac{d\mathcal{Z}\left(t\right)}{dt}& =& {\mathcal{B}}_1\{\frac{\beta S(I+\psi I_a+\nu I_h)}{N}-k_{1}E\}+{\mathcal{B}}_2\{\rho \omega E-k_{2}I\}\hfill \\ & & +{\mathcal{B}}_3\{(1-\rho )\omega E-k_3{I}_a\}\hfill \\ & & +{\mathcal{B}}_4\{\kappa E-k_{4}Q\}+{\mathcal{B}}_5\{\eta I+\delta Q-k_5{I}_h\}\hfill \\ & & \le {\mathcal{B}}_1\{\beta (I+\psi I_a+\nu I_h)-k_{1}E\}+{\mathcal{B}}_2\{\rho \omega E-k_{2}I\}\hfill \\ & & +{\mathcal{B}}_3\{(1-\rho )\omega E-k_3{I}_a\}\hfill \\ & & +{\mathcal{B}}_4\{\kappa E-k_{4}Q\}+{\mathcal{B}}_5\{\eta I+\delta Q-k_5{I}_h\},asS/N<1.\hfill \\ & =& \{{\mathcal{B}}_1\beta +{\mathcal{B}}_5\eta -{\mathcal{B}}_2{k}_2\}I+\{{\mathcal{B}}_1\beta \psi -{\mathcal{B}}_3{k}_3\}{I}_a\hfill \\ & & +\{{\mathcal{B}}_2\rho \omega +(1-\rho )\omega {\mathcal{B}}_3+\kappa {\mathcal{B}}_4-{\mathcal{B}}_1{k}_1\}E\hfill \\ & & +\{{\mathcal{B}}_1\beta \nu -{\mathcal{B}}_5{k}_5\}{I}_h+\{{\mathcal{B}}_5\delta -{\mathcal{B}}_4{k}_4\}Q\hfill \\ & =& \{{\mathcal{B}}_1\beta +{\mathcal{B}}_5\eta -{\mathcal{B}}_2{k}_2\}I+\{{\mathcal{B}}_1\beta \psi -{\mathcal{B}}_3{k}_3\}{I}_a\hfill \\ & & +\{{\mathcal{B}}_1\beta \nu -{\mathcal{B}}_5{k}_5\}{I}_h+\{{\mathcal{B}}_5\delta -{\mathcal{B}}_4{k}_4\}Q\hfill \\ & & +{\mathcal{B}}_1{k}_1\{\frac{{\mathcal{B}}_2\rho \omega +(1-\rho )\omega {\mathcal{B}}_3+\kappa {\mathcal{B}}_4}{{\mathcal{B}}_1{k}_1}-1\}E.\hfill \end{array}$$

Now choosing

$${\mathcal{B}}_1=1,{\mathcal{B}}_2=\frac{\beta (k_5+\nu \eta )}{k_2{k}_5},{\mathcal{B}}_3=\frac{\beta \psi }{k_3},{\mathcal{B}}_4=\frac{\beta \nu \delta }{k_4{k}_5},{\mathcal{B}}_5=\frac{\beta \nu }{k_5}.$$

We obtained after some simplification

$$\frac{d\mathcal{Z}\left(t\right)}{dt}\le k_1({\mathcal{R}}_0-1)E.$$ (9)

Hence, it is obvious that if ${\mathcal{R}}_0<1$ then $\frac{d\mathcal{Z}\left(t\right)}{dt}<0$. Therefore, the largest compact invariant set in Δ is the singleton set ${\mathcal{W}}_0$ and using the LaSalle’s invariant principle [17], ${\mathcal{W}}_0$ is globally asymptotically stable in Δ. □

4. Model fitting and parameter estimation process

The present section investigates the data fitting using model (3) to the confirmed reported COVID-19 infected cases in Pakistan. The disease situation in Pakistan is becoming worse day by day and currently, the cumulative reported cases are higher than China.   In this study we consider the COVID-19  confirmed cases from March 01, 2020, till May  28, 2020, reported in Pakistan. The data is obtained from [7], [8].   In order to parameterize the model, we utilized two approaches: Some of the demographic parameters are estimated from the literature.   We assume  the time unit is days and the estimation procedure of   the parameters is as follows:

• •Natural death rate μ: The average life span of Pakistani people are 67.79 years [18], therefore, we have $\mu =1/67.79$ per year.
• •The birth rate Λ: The total population of Pakistan estimated by UN for the year 2020 is about N(0)=220,309,834 [18], therefore, the parameter Λ is obtained from $\Lambda /\mu =N\left(0\right),$ and it is assumed that this is the limiting population in the disease absence, so that $\Lambda =8939$ per day.
• •Mortality rate due to coronavirus ξ ₁: The death rate due to this novel infection in Pakistan is 2.2% so far [8], therefore the COVID-19 induced mortality rate is estimated as ${\xi }_1=0.022.$

The remaining biological  parameters are fitted   from the reported infected cases plotted in Fig. 1 . To do this we used the non-linear  least-square curve fitting technique followed in [19], [20]. We  briefly present the main steps in this statistical technique.

Fig. 1.

The cumulative COVID-19 infected cases reported in Pakistan from March 01 till May 28, 2020.

4.1. Non-linear least square method

In order to present the main theme of the algorithm,  firstly,   the model (3)  can be comprehensively expressed as

$$\frac{d\mathcal{Y}}{dt}=\mathcal{F}(t,\mathcal{Y},\theta ),\mathcal{Y}\left(t_0\right)={\mathcal{Y}}_0.$$ (10)

The function $\mathcal{F}$ depends on time t, the vectors of dependent or state  variables  $\mathcal{Y}$ and unknown parameters θ to be estimated. The purpose of using the least square technique is to estimate  the best values  of model  parameter which is obtain   by minimizing the error between   the reported  data points ${\tilde{y}}_{t_l}$ and the solution of the model $y_{t_l}$ associated with the model parameters θ. The objective function used in the minimization  procedure   is given as

$$\widehat{\theta }=\sum _{l=1}^n{(y_{t_l}-{\tilde{y}}_{t_l})}^2.$$ (11)

Where n denotes the  available actual data points. To obtain the model parameters,  we aimed to minimize the following objective function

$$\{\begin{array}{c}\min \widehat{\theta }\hfill \\ subjecttoEq.\left(10\right).\hfill \end{array}$$ (12)

For more detail about this technique please see [19], [21] and reference therein.

4.2. Model fitting results

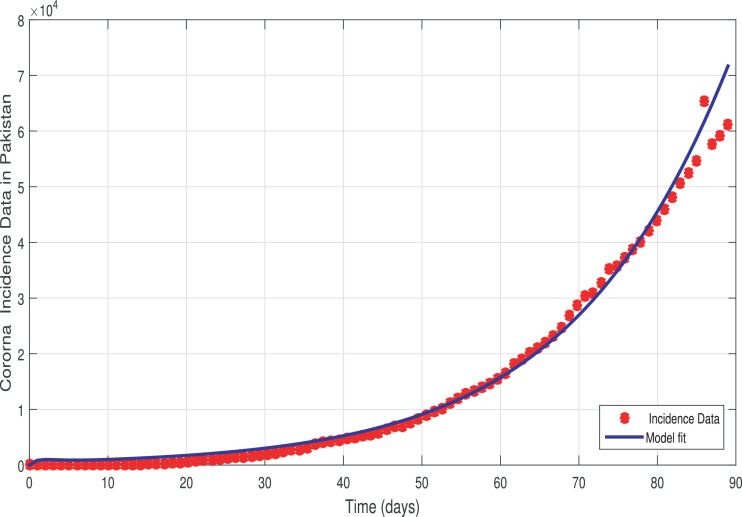
We investigate the proposed model fit to the reported COVID-19 infected cases in Pakistan using the above approach. The reported cases are shown in Fig. 1.  The model is solved using ode45 (RK4 technique) package which is a solver for the initial value problem in Matlab. Then, we implemented the   lsqcurvefit package to fit the model to real data and to estimate the parameters. The best fit to the reported data via our model is depicted in Fig. 2 .  It can be seen that the model simulation is in good agreement with the real data. The estimated and fitted parameters are given in Table 1 .   The approximate value of the reproduction number based on the estimated parameters is  ${\mathcal{R}}_0\approx 1.87$.

Fig. 2.

Data fitting to the reported cases using model (3).

Table 1.

Numerical values and description for the estimated and fitted parameters.

Parameter	Description	Value (per day)	Source
Λ	Birth rate	μ × N(0)	Estimated
μ	Natural death rate	1/(67.7 × 365)	[18]
ξ1	Infection induced death rate in I class	0.022	[8]
ψ	Relative transmissibility of asymptomatic class	0.7892	Fitted
ω	Incubation period	0.2403	Fitted
ρ	The proportion of asymptomatic infection	0.2929	Fitted
η	Hospitalization rate in I class	0.4015	Fitted
ξ2	Disease induced death rate in Ih class	0.0290	Fitted
ξ3	Disease induced death rate in Ic class	0.4897	Fitted
ϕ1	Removal or recovery rate of Q	0.4971	Fitted
ϕ2	Removal or recovery rate of Ih	0.5967	Fitted
ϕ3	Removal or recovery rate of Ic	0.0458	Fitted
ζ1	Recovery rate of I	0.6214	Fitted
ζ2	Recovery rate of Ia	0.0806	Fitted
κ	Rate at which exposed people are quarantined	0.3922	Fitted
β	Disease transmission coefficient	0.6594	Fitted
δ	Rate at which quarantined people are hospitalized	0.1368	Fitted
ν	Relative transmissibility of hospitalized class	0.6526	Fitted
ϕ	Rate at which hospitalized individuals join Ic class	0.4937	Fitted

5. Numerical simulation and discussion

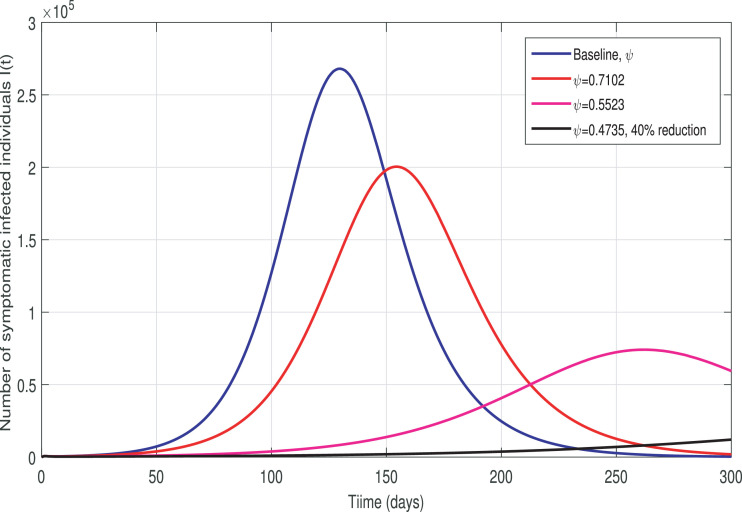
This section is devoted to  perform the simulation results of the COVID-19 transmission model (3). The model is solved numerically using ode45 Package in Matlab which is base on the Range-Kutta fourth-order method. The estimated parameter values given in Table 1  are utilized in the simulation process in order to study the impact of various possible non-pharmaceutical interventions against the spread of COVID-19   in Pakistan.      In the graphical results, the various non-pharmaceutical control parameters are taken at their baseline values given in Table 1  (unless otherwise stated in captions).   The effect of parameter β  that represents the impact of effective contacts is shown in Fig. 3 . We have analyzed the impact of baseline social-distancing, mild social-distancing (10% reduction in β),   moderate social-distancing  (30% reduction in β)  and comparatively strict social-distancing  (35% reduction in β) on the disease transmission.  It is observed from Fig. 3 that the enhancement in social-distancing significantly reduced the burden of cumulative new infected cases. It is further observed that the implementation of a highly-effective social-distancing strategy (i.e., at least 35% reduction in β) dramatically reduces the cumulative new infected cases. Thus, this graphical interpretation suggests that strict social-distancing measures that reduces the contacts between people including staying 2 m apart or more preferably staying at home should be implemented by the government. The impact of parameter ψ representing  the infectiousness rate due to asymptomatically-infected individuals is depicted in Fig. 4 . It can be seen that the reduction in   ψ also significantly reduces the cumulative number of newly confirmed COVID-19 infected cases. This interpretation shows that the people who do not even know that they are infected (i.e., those with mild or no symptoms), are significantly contributing the disease burden.  Further, the influence of parameter ν  the infectiousness rate due to COVID-19 patients admitted in the hospital are depicted in Fig. 5 .  It is observed that the reduction in this parameter has no reasonable impact on disease transmission.   Obviously, the hospitalized COVID-19 patients are isolated and no one is allowed to meet him. The health care facilities are also supposed to follow strict Standard Operating Procedure (SOP)   during the treatment and look after of hospitalized patients. Therefore, these infected individuals do not contribute greatly to the disease burden.

Fig. 3.

Effective contact rate β (a measure of social-distancing effectiveness) on the number of new COVID-19 infected cases.

Fig. 4.

Effective contact rate ψ on the number of new COVID-19 infected cases.

Fig. 5.

Effective contact rate ν on the number of new COVID-19 infected cases.

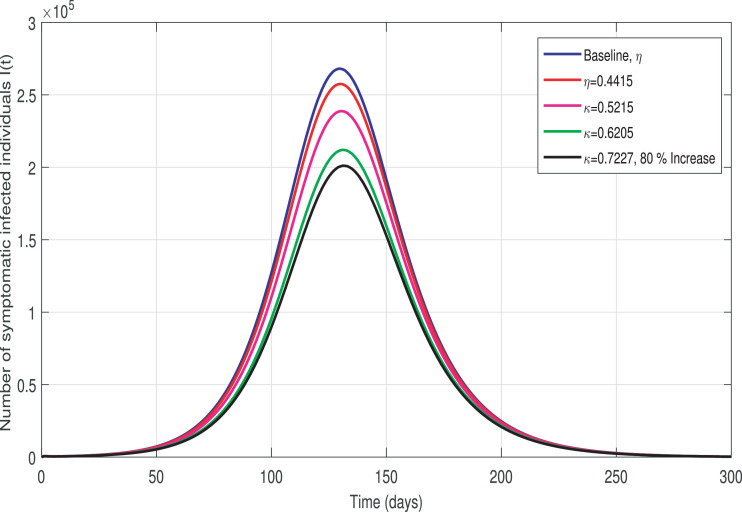
We further simulate the COVID-19 model (3) by using the baseline parameter tabulated in Table 1 and various of κ by increasing with different levels i.e, mild, moderate, and strict rates. The resulting behavior is depicted in Fig. 6 showing that a strict quarantine or contact-tracing policy (up to 70% enhancement to its baseline) is needed to reduce the disease burden in Pakistan.  Finally, the impact of hospitalization or self-isolation of tested positive cases (η) is plotted in Fig. 7 .  It is observed that this strategy is comparatively less effective than social-distancing and quarantine interventions. These graphical  interpretations emphasize that  once a COVID-19 infected case is diagnosed via testing, that case must be rapidly isolated and his/her contacts quickly traced (via effective contact-tracing) and placed in quarantine.

Fig. 6.

Effect of quarantine rate κ to the COVID-19 infected cases.

Fig. 7.

Effect of isolation/hospitalization rate η to the COVID-19 infected cases.

6. Global threshold’s sensitivity analysis

Global sensitivity analysis is one of the important aspects of mathematical modeling not only for epidemic models but in all sciences. The global sensitivity analysis of the threshold quantity ${\mathcal{R}}_0$ is used to measure the effect of changes in the dominant factors of the model and to point out the most influential parameters of the model that greatly influence the prevalence of infection. Furthermore, the sensitivity results provide a pathway to set effective and suitable control strategies to curtail the disease in a community. More specifically, this analysis is helpful to explore how the initial inputs to the model contribute to the system outputs.

A Latin-hypercube sampling approach (LHS) coupled with the partial rank correlation coefficient (PRCC) is commonly used for this purpose [22]. This technique provides PRCC and the corresponding p-values for each parameter the use of which can help estimate the level of uncertainty in an epidemic model. The higher  PRCC and smaller  p-value of a parameter indicating that it has a substantial effect on simulation behavior.   The graphical PRCC results of the COVID-19 model associated parameters taken in this analysis are shown in   Fig. 8 ,  while the numerical values of PRCC and corresponding p-values  are placed in Table 2 .  It is observed from Table 2 and  Fig. 8 that β is considered to be the most sensitive parameter with high PRCC value with a positive sign followed by ψ,  ν, and ω.  Moreover,  μ and  κ, ξ ₁   and η  have competitively higher PRCC   with   negative sign and zero p-values.

Fig. 8.

Global sensitivity analysis and PRCC results for ${\mathcal{R}}_0$.

Table 2.

The PRCC and p values of various parameters relative to ${\mathcal{R}}_0$.

Parameter	PRCC values	p values
ψ	0.6770	0.0000
β	0.9144	0.0000
ν	0.3576	0.0000
κ	0.4226	0.0000
ω	0.3320	0.0000
ρ	0.2244	0.0000
η	-0.3863	0.0000
μ	-0.6693	0.0000
ϕ	-0.1340	0.2513
ξ1	-0.4483	0.0000
ξ2	-0.3075	0.0000

7. Optimal control problem

Previously, we analyzed the impact of non-pharmaceutical interventions with constant rates. In this section we formulate an optimal control problem   for COVID-19 with the inclusion of two time dependent controls in the model (3). The resulting control problem is presented in (13). These controls are chosen on the basis of global sensitivity results. The  control variable u ₁(t) is used for the enhancement of effective contact-tracing policy to quarantine the exposed individuals which was previously taken as a constant parameter. The time dependent control variable u ₂(t) is used to enhance the hospitalization or self-isolation of diagnosed COVID-19 infected cases (following testing).   Thus, the resulting control model after incorporating the aforementioned  control  variables is formulated via the following system:

$$\begin{array}{c}\frac{dS}{dt}=\Lambda -\frac{\beta (I+\psi I_a+\nu I_h)}{N}S-\mu S,\hfill \\ \\ \frac{dE}{dt}=\frac{\beta (I+\psi I_a+\nu I_h)}{N}S-(\omega +\mu )E-\kappa (1+u_1\left(t\right))E,\hfill \\ \\ \frac{dI}{dt}=\rho \omega E-({\zeta }_1+\mu +{\xi }_1)I-\eta (1+u_2\left(t\right))I,\hfill \\ \\ \frac{d{I}_a}{dt}=(1-\rho )\omega E-({\zeta }_2+\mu )I_a,\hfill \\ \\ \frac{dQ}{dt}=\kappa (1+u_1\left(t\right))E-(\mu +{\varphi }_1+\delta )Q,\hfill \\ \\ \frac{d{I}_h}{dt}=\eta (1+u_2\left(t\right))I+\delta Q-(\mu +{\varphi }_2+{\xi }_2+\varphi )I_h,\hfill \\ \\ \frac{d{I}_c}{dt}=\varphi I_h-(\mu +{\varphi }_3+{\xi }_3)I_c,\hfill \\ \\ \frac{dR}{dt}={\zeta }_{1}I+{\zeta }_2{I}_a+{\varphi }_{1}Q+{\varphi }_2{I}_h+{\varphi }_3{I}_c-\mu R.\hfill \end{array}$$ (13)

subject to the non-negative initial conditions. In order to minimize this COVID-19 infection, we are aimed to minimize the cost function given as:

$$J(u_1,u_2)={\int }_0^{T_f}\{A_{1}E+A_{2}I+A_3{I}_h+\frac{1}{2}(A_4{u}_1^2+A_5{u}_2^2)\}\mathit{dt},$$ (14)

where the expressions A_i for $i=1,2,\cdots ,5,$ are the constants and representing the balancing cost factors while T_f represents the final time. We consider the quadratic objective functional because the intervention is nonlinear, for more details see the work and references therein [20], [23], [24], [25].

Onward our main objective is to investigate an optimal controls $u_1^{*},$ $u_2^{*}$ for quarantine and hospitalization respectively such that

$$J(u_1^{*},u_2^{*})=\underset{\Omega }{min}\left\{J(u_1,u_2)\right\}.$$

The associated control set is given by

$$\Omega =\{(u_1,u_2):[0,T_f]\to [0,1],(u_1,u_2)isaLebesguemeasurable\}.$$

The Lagrangian and Hamiltonian for the above optimal control system is defined by

$$\mathcal{L}=A_{1}E+A_{2}I+A_3{I}_h+\frac{1}{2}(A_4{u}_1^2+A_5{u}_2^2).$$ (15)

and

$$\begin{array}{cc}\mathcal{H}=\hfill & A_{1}E+A_{2}I+A_3{I}_h+\frac{1}{2}(A_4{u}_1^2+A_5{u}_2^2)\hfill \\ & +{\lambda }_1[\Lambda -\frac{\beta (I+\psi I_a+\nu I_h)}{N}S-\mu S]\hfill \\ & +{\lambda }_2[\frac{\beta (I+\psi I_a+\nu I_h)}{N}S-(\omega +\mu )E-\kappa (1+u_1\left(t\right))E]\hfill \\ & +{\lambda }_3[\rho \omega E-({\zeta }_1+\mu +{\xi }_1)I-\eta (1+u_2\left(t\right))I]\hfill \\ \\ & +{\lambda }_4[(1-\rho )\omega E-({\zeta }_2+\mu )I_a]\hfill \\ \\ & +{\lambda }_5[\kappa (1+u_1\left(t\right))E-(\mu +{\varphi }_1+\delta )Q]\hfill \\ \\ & +{\lambda }_6[\eta (1+u_2\left(t\right))I+\delta Q-(\mu +{\varphi }_2+{\xi }_2+\varphi )I_h]\hfill \\ \\ & +{\lambda }_7[\varphi I_h-(\mu +{\varphi }_3+{\xi }_3)I_c]\hfill \\ \\ & +{\lambda }_8[{\zeta }_{1}I+{\zeta }_2{I}_a+{\varphi }_{1}Q+{\varphi }_2{I}_h+{\varphi }_3{I}_c-\mu R].\hfill \end{array}$$ (16)

where λ_j, for $j=1,2\cdots ,8,$ are the adjoint variables.

7.1. Optimal control solution

We use the Pontryagin’s maximum principle [26] in order to solve the COVID-19 optimal control problem (13). To do this, let $u_1^{*},$ $u_2^{*}$ are the desired optimal solution then, the corresponding conditions of Pontryagin’s maximum principle used in solution process are as follows:

$$\{\begin{array}{c}\frac{dz}{dt}=-\frac{\partial }{\partial {\lambda }_j}\mathcal{H}(t,{{\mathrm{u}}_{\mathrm{j}}}^{*},{\lambda }_j),\hfill \\ \\ \frac{\partial }{\partial \mathrm{u}}\mathcal{H}(t,{{\mathrm{u}}_{\mathrm{j}}}^{*},{\lambda }_j)=0,\hfill \\ \\ \frac{d{\lambda }_j\left(t\right)}{dt}=-\frac{\partial }{\partial z}\mathcal{H}(t,{{\mathrm{u}}_{\mathrm{j}}}^{*},{\lambda }_j).\hfill \end{array}$$ (17)

Utilizing the conditions mentioned above (17), we present the solution of optimality system in the following theorem.

Theorem 3

The optimal controls$u_1^{*},$$u_2^{*}$and the solutions S*, E*, I*, $I_a^{*},$Q*, $I_h^{*},$$I_c^{*}$and R* of the corresponding control system(13)that minimize the objective functional J(u₁, u₂) over Ω. There exists adjoint variables λ_i, where $i=1,2,\cdots ,8,$ along with transversality conditions ${\lambda }_i\left(T_f\right)=0$ such that

$$\begin{array}{ccc}\hfill \frac{d{\lambda }_1}{dt}& =& \frac{\beta (I^{*}+\psi I_a^{*}+\nu I_h^{*})(N^{*}-S^{*})}{{N^{*}}^2}({\lambda }_1-{\lambda }_2)+\mu {\lambda }_1,\hfill \\ \hfill \frac{d{\lambda }_2}{dt}& =& -A_1+\frac{\beta (I^{*}+\psi I_a^{*}+\nu I_h^{*})S^{*}}{{N^{*}}^2}({\lambda }_2-{\lambda }_1)-\rho \omega {\lambda }_3\hfill \\ & & -(1-\rho )\omega {\lambda }_4+(1+u_1)\kappa ({\lambda }_2-{\lambda }_5)+(\omega +\mu ){\lambda }_2,\hfill \\ \hfill \frac{d{\lambda }_3}{dt}& =& -A_2+\frac{\beta (N^{*}-(I+\psi I_a^{*}+\nu I_h^{*}))S^{*}}{{N^{*}}^2}({\lambda }_1-{\lambda }_2)\hfill \\ & & +(1+u_2)\eta ({\lambda }_3-{\lambda }_6)+({\zeta }_1+\mu +{\xi }_1){\lambda }_3-{\zeta }_1{\lambda }_8,\hfill \\ \hfill \frac{d{\lambda }_4}{dt}& =& \frac{\beta (\psi N^{*}-(I+\psi I_a^{*}+\nu I_h^{*}))S^{*}}{{N^{*}}^2}({\lambda }_1-{\lambda }_2)+{\zeta }_2({\lambda }_4-{\lambda }_8)+\mu {\lambda }_4,\hfill \\ \hfill \frac{d{\lambda }_5}{dt}& =& \frac{\beta (I^{*}+\psi I_a^{*}+\nu I_h^{*})S^{*}}{{N^{*}}^2}({\lambda }_2-{\lambda }_1)+\delta ({\lambda }_5-{\lambda }_6)+{\varphi }_1({\lambda }_5-{\lambda }_8)+\mu {\lambda }_5,\hfill \\ \hfill \frac{d{\lambda }_6}{dt}& =& -A_3+\frac{\beta (\nu N^{*}-(I+\psi I_a^{*}+\nu I_h^{*}))S^{*}}{{N^{*}}^2}({\lambda }_1-{\lambda }_2)+\varphi ({\lambda }_6-{\lambda }_7)\hfill \\ & & +{\varphi }_2({\lambda }_6-{\lambda }_8)+({\xi }_2+\mu ){\lambda }_6,\hfill \\ \hfill \frac{d{\lambda }_7}{dt}& =& \frac{\beta (I^{*}+\psi I_a^{*}+\nu I_h^{*})S^{*}}{{N^{*}}^2}({\lambda }_2-{\lambda }_1)+{\varphi }_3({\lambda }_7-{\lambda }_8)+({\xi }_3+\mu ){\lambda }_7,\hfill \\ \hfill \frac{d{\lambda }_5}{dt}& =& \frac{\beta (I^{*}+\psi I_a^{*}+\nu I_h^{*})S^{*}}{{N^{*}}^2}({\lambda }_2-{\lambda }_1)+\mu {\lambda }_8.\hfill \end{array}$$ (18)

Furthermore, the associated optimal controls $u_1^{*}$ and $u_2^{*}$ are given by

$$\begin{array}{c}{u}_1^{*}=\min \{1,\max (0,\frac{\kappa E^{*}({\lambda }_2-{\lambda }_5)}{A_4}\left)\right\},\hfill \\ u_2^{*}=\min \{1,\max (0,\frac{\eta I^{*}({\lambda }_3-{\lambda }_6)}{A_5}\left)\right\}.\hfill \end{array}$$ (19)

Proof

The desired results (18) and the transversality conditions are obtained by utilizing the conditions specified in (17) for the Hamiltonian function given (16) and with the settings $S=S^{*},$ $E=E^{*},$ $I=I^{*},$ $I_a=I_a^{*},$ $Q=Q^{*},$ $I_h=I_h^{*},$ $I_c=I_c^{*}$ and $R=R^{*}$. Further, to obtain the equations (19) for the control characterization, we use the condition $\frac{\partial \mathcal{H}(t,{{\mathrm{u}}_{\mathrm{j}}}^{*},{\lambda }_j)}{\partial {\mathrm{u}}_{\mathrm{j}}}=0$ given in (17) for $j=1,2,$ and the equations (19) are presented. □

7.2. Simulation of the control problem

We present and discuss the graphical results of the COVID-19 model (3) with constant quarantine and hospitalization/isolation control measures and the model (13) with time dependent control interventions and compared both results. To perform the simulations, both models are solved numerically using the RK4 technique. The estimated and fitted parameters given in Table 2 are used in the simulation results. The time level is considered up to 150 units (days). The weight and balancing constants are chosen as $A_1=0.001,$ $A_2=0.01,$ $A_3=0.001,$ $A_4=300,$ and $A_5=200$. It should be noticed that the weight constants values taken in the simulations are theoretical as they were chosen only to carried out the control strategies developed in this study.

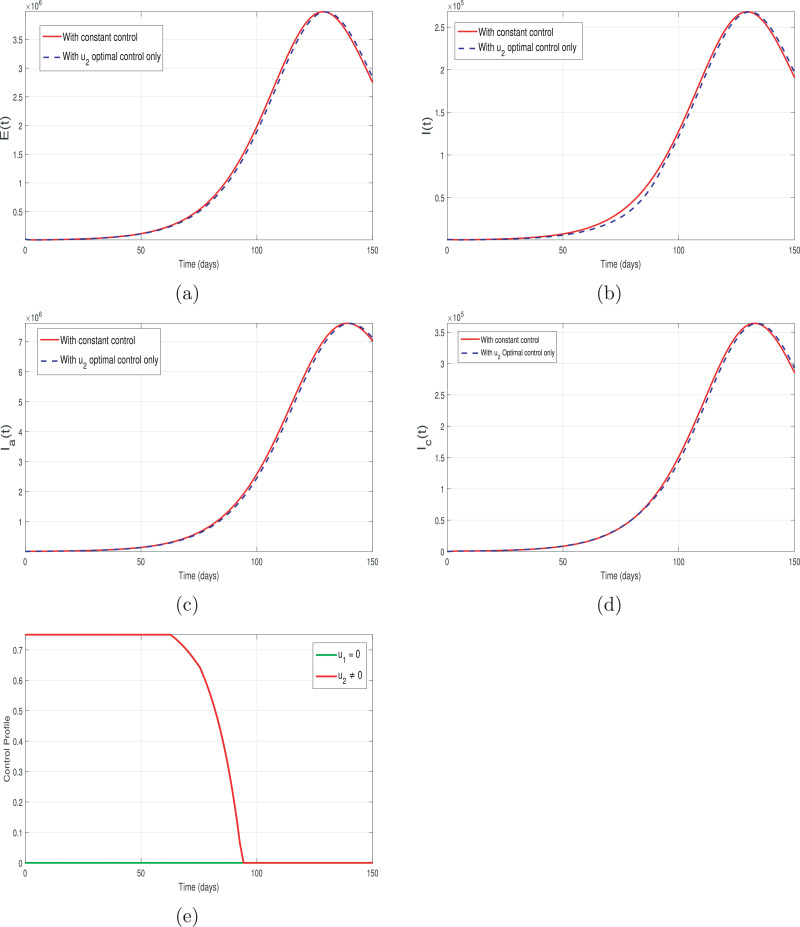
In Fig. 9 (a-d), we have depicted the impact of hospitalization control only and keeping the quarantine or case tracing control inactive (i.e., $u_1=0$ and u ₂ ≠ 0). The control profile for this strategy is shown in Fig. 9 (e). It is observed that although the control u ₂ is kept 100% for the first 70 days, but still it has no significant impact on the different infected individuals as seen Fig. 9 (a-d). Thus, only the hospitalization or self-isolation intervention is not enough for the control of COVID-19 pandemic in Pakistan.

Fig. 9.

Graphical results of the model (13) with hospitalization control only i.e., $u_1=0$ and u₂ ≠ 0.

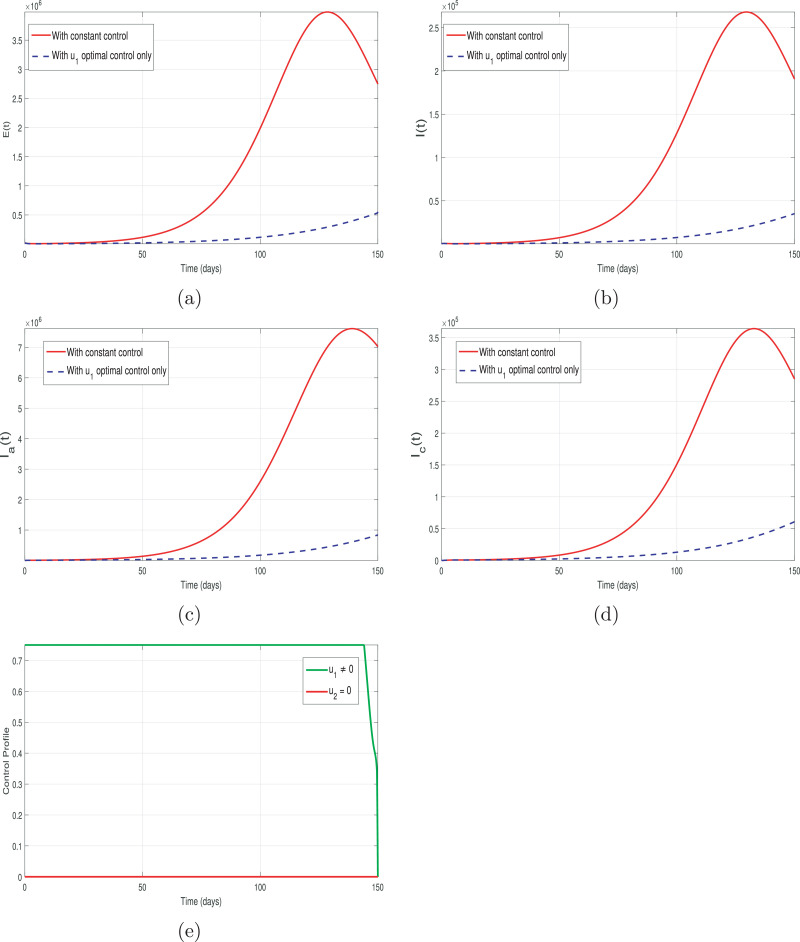
The impact of only quarantine optimal control by keeping the hospitalization control zero (i.e., u ₁ ≠ 0 and $u_2=0$) is shown in Fig. 10 (a-d). The corresponding control profile for this case is depicted in Fig. 10 (e). It can be seen that maintaining a strict quarantine control is very effective in minimizing the spread of the COVID-19 infection.

Fig. 10.

Graphical results of the model (13) with quarantine optimal control only i.e., u₁ ≠ 0 and $u_2=0$.

Finally, the impact of both optimal controls on the dynamics of COVID-19 burden is analyzed. The graphical results are depicted in Fig. 11 (a-d), while the control profile is shown in Fig. 11 (e). It can be observed from Fig. 11 (a-d) that the number of exposed, symptomatically-infected, asymptomatically-infected, and critically-infected individuals are decreasing very significant when the optimal quarantined and hospitalization controls are applied rather than the constant case. The effectiveness can be viewed from the difference between the peaks of the two graphs. From the control profile depicted in Fig. 11 (e), it can be seen that the control u ₁ is kept initially at 100% for 140 days and gradually reduces towards the end of the intervention, while the control u ₂ is set to 55% and then immediately increases to 90% in the initial days and then gradually reduced during the rest of the intervention.

Fig. 11.

Graphical results of the model (13) with both optimal controls i.e., u₁ ≠ 0 and u₂ ≠ 0.

8. Conclusion

The COVID-19 pandemic has rapidly spread out to most of the regions of the world and has severe public health and socio-economic burden in developed and devolving countries including Pakistan. The number of reported cases in Pakistan is increasing and more than 100,000 confirmed cases have been reported till 05 June 2020. In the absence of a safe and effective vaccine or antiviral, the whole human’s community is being focused on the use of non-pharmaceutical interventions against the COVID-19 pandemic. In this study, we formulated a mathematical model in order to study the dynamics of COVID-19 pandemic in Pakistan, and used it to assess the community-wide impact of the various control and mitigation strategies. Initially, we developed the model and presented some mathematical analysis, including positivity and stability results of the disease-free equilibrium. It is proven that the disease-free equilibrium is stable both locally and globally when ${\mathcal{R}}_0<1$. The model is parameterized from the COVID-19 confirmed cases reported till May 28, 2020 in Pakistan while some parameters are estimated from literature. The findings show that the model predicted infected curve is in good agreement to the real infected cases. The estimated numerical value of the basic reproduction is obtained as ${\mathcal{R}}_0\approx 1.87$ showing the alarming situation of the pandemic in Pakistan. The control and mitigation strategies should be implemented to bring the threshold quantity ${\mathcal{R}}_0$ to a value less than unity. After the estimation of model parameters, we simulated the model to explore the effectiveness of various control strategies implemented in Pakistan. Firstly, we presented the impact of three effectiveness levels (i.e., low or mild, moderate and strict) of social-distancing in curtailing the burden of COVID-19. The simulation results revealed that although the implementation of mild social-distancing decreased the COVID-19 burden significantly (as measured in terms of shifting and lowering the peak of daily infected cases), still a strict social-distancing measures should be implemented and maintained for an extended period of time to avoid a significant outbreak in Pakistan. Further, we simulated the model to assess the effect of various levels of quarantine and hospitalization or self-isolation interventions. With a highly-effective quarantine intervention (enhanced by 70% to its baseline value) a dramatic reduction in the pandemic peak was observed. On the other hand increase of hospitalization intervention of confirmed cases had no significant influence on the pandemic burden. Finally, the proposed COVID-19 model is reformulated by the inclusion of two time-dependent control variables in order to assess the impact of optimal control measures on disease dynamics. We simulated the control model and compared the effect of constant and optimal time-dependent control measures on disease burden. It is observed from the simulation results of the control COVID-19 model that the infected individuals significantly decrease with the implementation of both time-dependent control measures.

Although it is impressive that Pakistan ramps up daily diagnostic COVID-19 testing and contact tracing to have a realistic measure of the burden of the nationwide pandemic and emphasize personal hygiene and hand washing, physical-distancing, wearing face masks in public. Still, this study suggests that the implementation of basic non-pharmaceutical interventions, particularly social-distancing, quarantine (or self-isolation or stay at home) should be strictly observed in the future to avoid the worse scenario in Pakistan. It is also believe that the present study will be beneficial to the decision-making in combating the disease. In the near future, we will extend the present model by introducing the fractional operators with local and nonlocal kernel to gain more insights about the dynamics of COVID-19 pandemic.

CRediT authorship contribution statement

Saif Ullah: Writing - original draft, Data curation, Software, Methodology, Conceptualization. Muhammad Altaf Khan: Visualization, Investigation, Supervision, Validation, Writing - review & editing.

Declaration of Competing Interest

No conflict of interest exists regarding the publications of this paper.