Critical phenomena in the temperature-pressure-crowding phase diagram of a protein

Abstract

In the cell, proteins fold and perform complex functions through global structural rearrangements. Function requires a protein to be at the brink of stability to be susceptible to small environmental fluctuations, yet stable enough to maintain structural integrity. These apparently conflicting behaviors are exhibited by systems near a critical point, where distinct phases merge—a concept beyond previous studies indicating proteins have a well-defined folded/unfolded phase boundary in the pressure-temperature plane. Here, by modeling the protein phosphoglycerate kinase (PGK) on the temperature (T), pressure (P), and crowding volume-fraction (ϕ) phase diagram, we demonstrate a critical transition where phases merge, and PGK exhibits large structural fluctuations. Above the critical point, the difference between the intermediate and unfolded phases disappears. When ϕ increases, the critical point moves to lower T_c. We verify the calculations with experiments mapping the T-P-ϕ space, which likewise reveal a critical point at 305 K and 170 MPa that moves to lower T_c as ϕ increases. Crowding places PGK near a critical line in its natural parameter space, where large conformational changes can occur without costly free energy barriers. Specific structures are proposed for each phase based on simulation.

I. INTRODUCTION

Complex processes in nature often arise at an order-disorder transition [1–4]. In proteins, this complexity arises from an almost perfect compensation of entropy by enthalpy: molecular interactions that create structural integrity are on the same scale as thermal fluctuations from the environment. The resulting marginal stability of proteins suggests that they could behave like fluids near a critical point [5] – their structures fluctuate considerably subject to small perturbations without overcoming a large activation barrier.

The concept of first order and critical phase transitions does not rigorously apply to nano-objects such as proteins, but is a useful one to classify folding transitions. For example, folding of small model proteins has been described as an abrupt, cooperative transition between the folded and unfolded phase for some proteins (the below-critical point scenario), or as a gradual barrier-less ‘downhill’ transition for other proteins (the above-critical point scenario) [6]. Even though critical behavior of proteins has been previously hinted [7–9], there has not been a direct observation of a critical point where one of these abrupt transitions simply disappears at T_c and P_c. In larger proteins, such as PGK ([10] in section S1), the situation can get even more complex: different parts or ‘domains’ of a large protein are more likely to be able to undergo separate order-disorder events [11], delicately poised between folded and partially unfolded structures to carry out their functions [12].

Proteins must fold and function while crowded by surrounding macromolecules [13], which perturb the structure of the proteins at physiological conditions in the cell. The volume exclusion from macromolecules [14], which places shape and size (or co-volume) [15,16] constraints on the conformational space (Fig. 1A), complicates protein folding and dynamics in living cells [17]. How the competing properties of a protein arise – being both stable yet dynamically sensitive to its environment – is largely unknown; however, we show that the crowded environment provides a unique solution by placing PGK near a critical regime.

FIG 1.

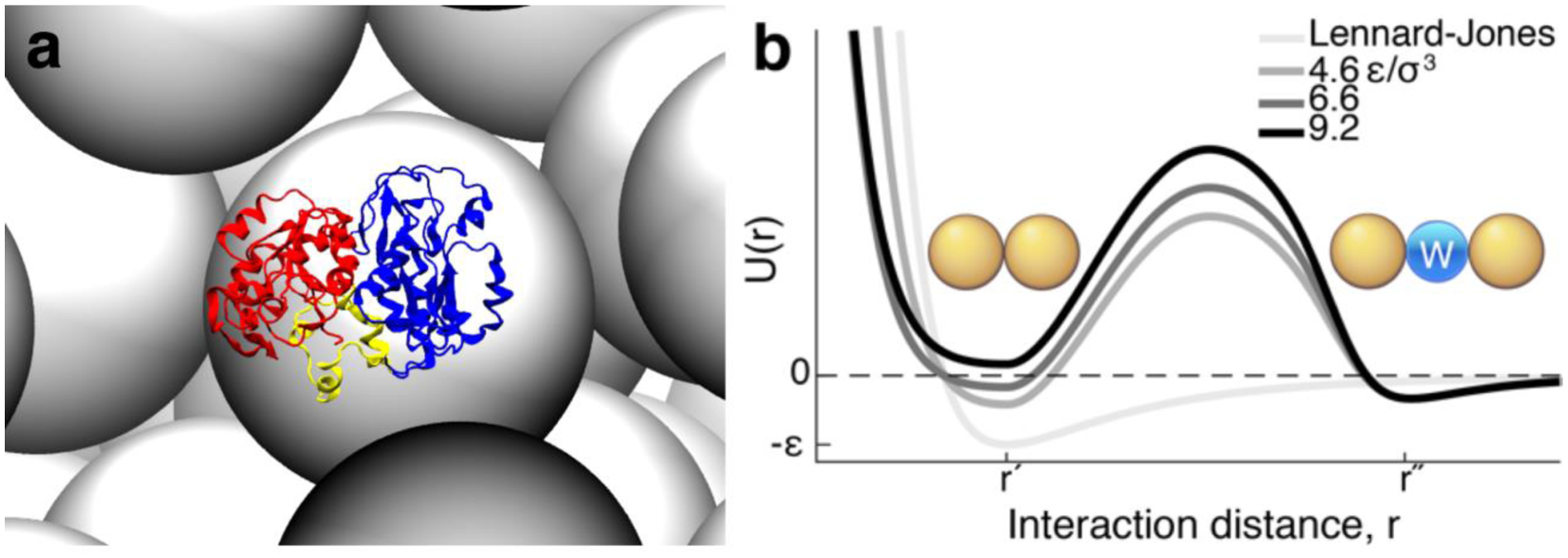
PGK surrounded by crowders and the desolvation potential between residues. (A) A snapshot from the coarse-grained molecular simulation of PGK’s spherical compact state (Sph) surrounded by crowders (gray) at the volume fraction of 40%. N-, C-domain, and hinge are in red, blue, and yellow respectively. (B) The pressure-dependent desolvation potential at σ³P/ε = 4.6, 6.6, and 9.2, contains a desolvation barrier with a width (|r′ − r″|) the size of a water molecule (blue). This incorporates the entropic cost of expelling a solvent molecule between two residues (gold). The Lennard-Jones potential is plotted in light grey for comparison.

We use pressure P, temperature T, and crowder-excluded volume fraction ϕ, to map PGK’s folding energy landscape [12,18] and its critical regime on the T-P-ϕ phase diagram. Temperature can induce heat unfolding by favoring states of high conformational entropy, or cold unfolding by favoring reduced solvent entropy when hydrating core amino acids in the protein [19,20]. Since folded proteins contain heterogeneously distributed small, dry cavities due to imperfect packing of their quasi-fractal topology [21–23], high pressure also induces unfolding by introducing water molecules (as small granular particles) into the cavities in protein structures, leading to reduced overall solvent-accessible volume of the unfolded protein [24]. Finally, in the presence of high crowding (large excluded volume fraction ϕ), compact desolvated (crystal) states are favored over less compact solvated (unfolded) states [12].

To investigate the opposing impact of macromolecular volume exclusion and solvation water on protein conformation, we utilized a minimalist protein model that incorporates the free energy cost of expelling a water molecule between a pair of residues in a contact (desolvation potential) [25]. This potential has a barrier that separates two minima that account for a native contact and a water-mediated contact. As pressure increases, the desovlation barrier increases and the free energy gap between the two minima tilts to favor the water-mediated contact, leading to an unfolding of a protein. We previously employed a similar model in molecular dynamics simulations to investigate compact conformations of PGK induced by macromolecular crowding [12] (Fig. 1 and [10] in section S2.2). Despite the model’s simplicity without capturing all the chemistry in a residue, this desolvation model predicts a folding mechanism involving water expulsion from the hydrophobic core, which has been observed by all-atomistic molecular dynamics [26] and validated by experiments in which the volume or polarity of amino acids is changed by mutation [27]. By studying the competition of temperature, pressure and crowding on the energy landscape, we are able to observe a rich ensemble of PGK states on a P-ϕ phase diagram (Fig. 2). By using scaling arguments from polymer physics, we derive a critical line, where the costly barrier between two phases disappears, on the isochore surface. As a consequence of being near the critical regime, PGK exhibits large structural fluctuations at physiologic conditions, which may be advantageous for enzymatic function.

FIG 2.

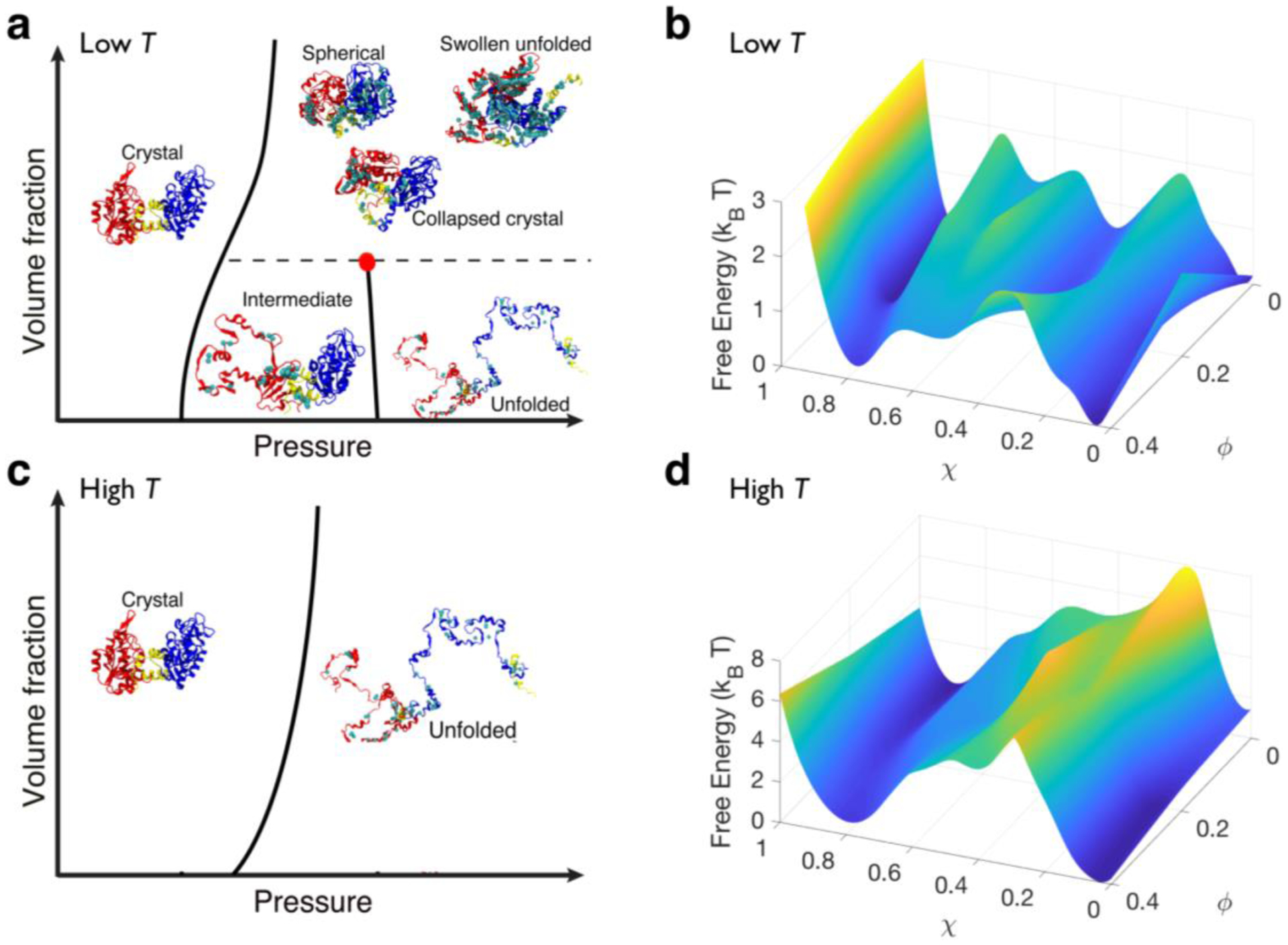
Solvation and crowding give rise to a rich phase diagram of PGK. (A & C) Schematics of PGK’s behavior in the crowding volume fraction-pressure (ϕ – P) phase plane and (B & D) corresponding free energy with respect to the overlap (χ) and crowding volume fraction (ϕ) at the folding pressure at low (A-B) and high (C-D) temperatures. Lines represent the division between distinct configurational phases that are separated by a free energy barrier from simulations at ϕ = 0, 0.2, and 0.4, and pressures from σ³P/ε = 10⁻³ to 23. Collapsed crystal (CC), spherical (Sph), and swollen unfolded (SU) states are indistinguishable in terms of free energy. These configurations were reconstructed from coarse-grained models to all-atomistic protein models for illustration purposes using SCAAL [28]. N-, C-domain, and hinge are in red, blue, and yellow respectively. A cyan sphere was inserted in between residues to show water-mediated contacts were formed.

To test our computational model, we observe structural transitions of PGK by fluorescence to construct the experimental T-P-ϕ phase diagram (Fig. 3). Experiment verifies the predicted existence of a critical point which moves to a lower temperature T_c as the crowding volume fraction ϕ is increased. Finally, a unified phase diagram is presented (Fig. 4) using analytically derived equation for T_c(ϕ) mapped onto the experimental results. Our current investigation is transforming the typical “structure-function” problem in proteins to a novel paradigm of a “structure-function-environment” relationship, and is a step toward developing universal thermodynamic principles of protein folding in living cells.

FIG 3.

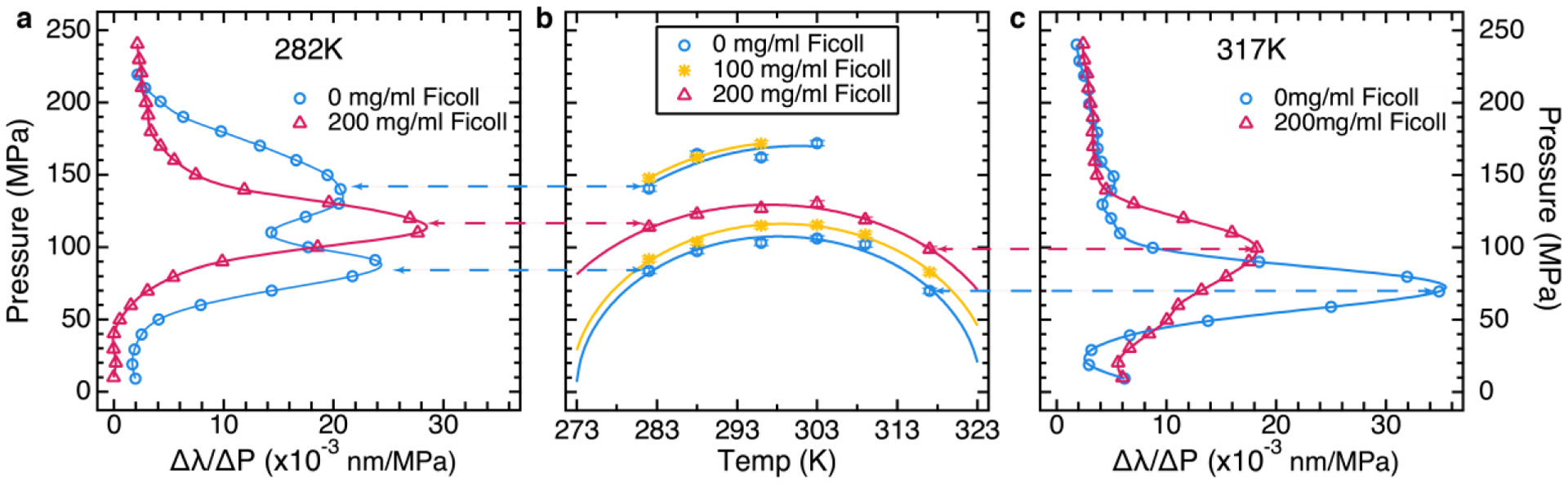
Experimental P-T-ϕ phase diagram of PGK (full data in [10]). (A) The derivative of the mean tryptophan fluorescence wavelength vs. pressure of PGK at 282 K calculated from fluorescence spectra. Two of six Ficoll concentrations are shown. The markers show the data points and the solid line shows a cubic spline interpolation. The blue curve (0 mg/ml Ficoll) has two peaks as pressure increases, signifying two transitions; the magenta curve (200 mg/ml Ficoll) has only one peak point, signifying only one transition when pressure is applied. The dashed lines point from transition midpoints to the corresponding point in the phase diagram. (B) P-T-ϕ phase diagram obtained by fitting the fluorescence data to obtain the inflection points of λ_m(P) (peaks in the derivative ∂λ_m/∂P). Three of six Ficoll concentrations are shown. Circles represent midpoint pressures measured at 282, 288, 296, 303, 309 and 317K in absence of Ficoll (0 mg/ml), asterisks represent transitions for the middle ficoll concentration (100 mg/ml) and triangles represent transitions for the highest Ficoll concentration (200 mg/ml). At high T, or upon increasing Ficoll concentration, the second (higher P) transition disappears, mapping out a critical point that moves to lower T_c at higher Ficoll concentration. Solid elliptical curves going through the circles are fits to eq. [1] representing the ΔG = 0 curves. (C) Equivalent data as in (A) at 317 K. Note that the second (higher P) transition is never present at high T.

FIG 4.

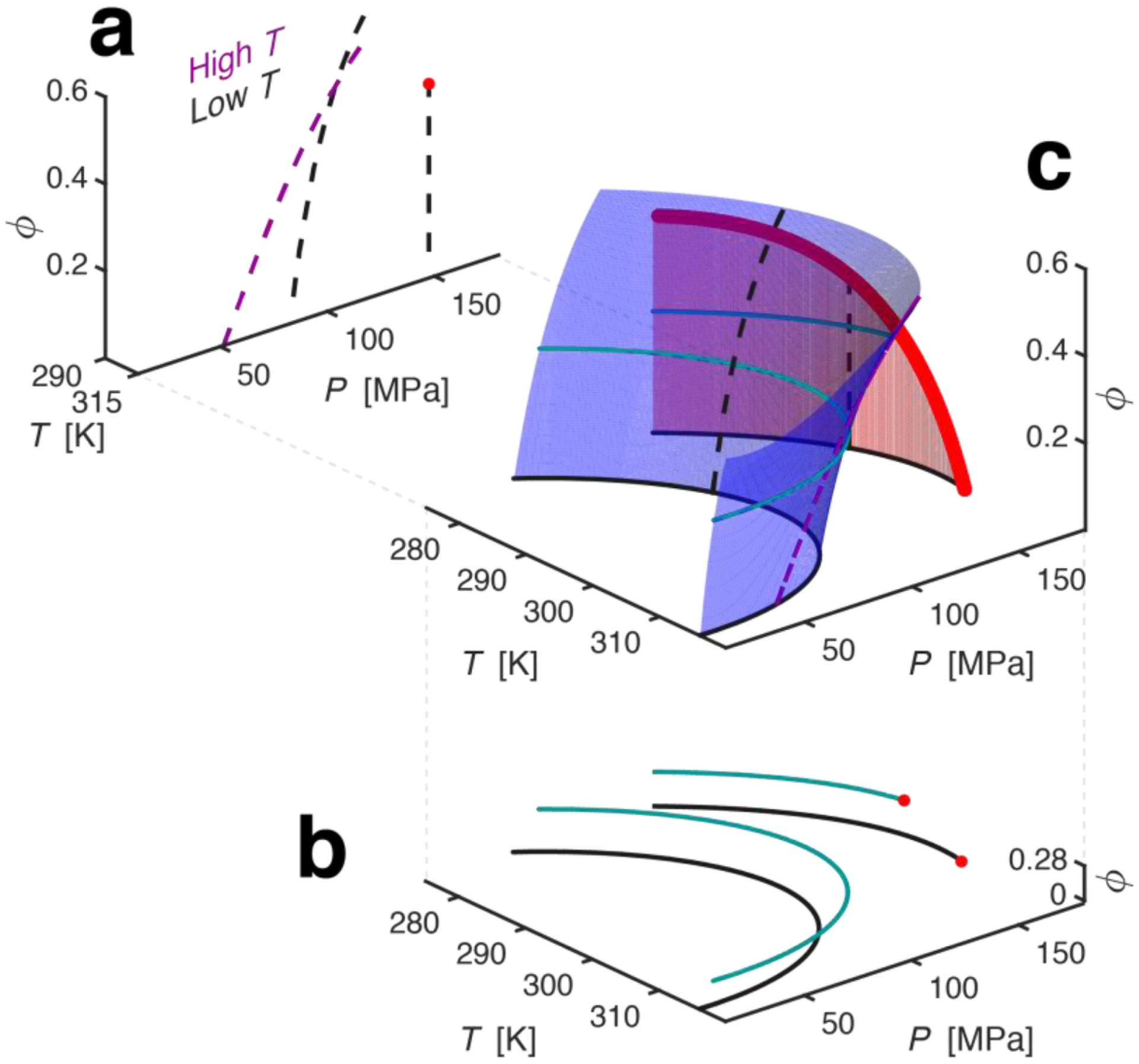
T-P-ϕ phase diagram of PGK from theory mapped onto the experimental data. (A) PGK’s ϕ-P phase plane at high (magenta) and low (black) T. Dotted lines represent the division between distinct configurational phases. The red circle signifies a critical point. (B) Slices of P-T phase diagram observed experimentally. Data in black – no Ficoll 70, data in cyan– 100 mg/mL Ficoll 70. Note that I-U coexistence curve terminates at the critical point (in red) and shifts T_c to a lower temperature in the presence of Ficoll 70. Solid elliptical curves going through the circles are the fits representing the ΔG = 0 curves. (C) A pressure-temperature-crowding phase diagram of PGK. The blue and red surfaces are the C-I (or C-U, depending on T and ϕ) and I-U coexistence surfaces respectively. The dashed magenta and black line are the ϕ-P cross-section from Fig 4A, and the solid black and cyan are the P-T cross-section from Fig 4B. The bold, red, line bordering the red surface is a critical line.

II. RESULTS AND DISCUSSION

A. T-P-ϕ phase diagram of PGK from simulation

We investigated the conformations of PGK, a large, 415 amino acid, two-domain protein ([10] in section S1 for more information on PGK), in an environment that includes cell-like excluded volume. From prior FRET experiments and molecular simulations, we gained knowledge of several PGK conformations that denote a phase diagram in the ϕ-T plane [12]. It includes C (crystal structure), CC (collapsed crystal), Sph (spherical compact state), and U (unfolded structures). In the C state, there is a linker that separates the N-terminal and C-terminal domains, resembling an open “pacman”. The CC state is a closed “pacman”. The Sph state involves a twisting of one of the domains with respect to the other and becomes more spherical than the CC state. A complete description of the structures of these states is in Supplemental Material [10] section S3.

By changing hydrostatic pressure and volume fraction of crowders at several temperatures, we have identified two new states on the ϕ-P isothermal phase plane (Fig. 2): I (folding intermediate), and SU (swollen compact unfolded structure). The criteria to define the six distinctive conformations are in Table S3.1 [10]. The I state is an ensemble of structures containing one folded domain (C-terminus) and one unfolded domain (N-terminus), making a specific prediction as to which domain is least stable on its own (N-terminal). SU is completely denatured, but exhibits a large number of water-mediated contacts (Fig. 1B). Thus, the SU state is structurally more compact than the U state.

The microscopic mechanism of pressure-induced unfolding of PGK depends on the temperature T and volume fraction ϕ of Ficoll 70 crowders. Ficoll 70 is a neutral crowding agent that is computationally modelled as hard spheres. Fig. 2 shows the P-ϕ phase plane at low T (a) and high T (c). At sufficiently low T and ϕ = 0 (no crowders) the unfolding of PGK is a multi-state transition between folded state C (Fig. 2 A&B) and unfolded state U via an intermediate state I. We capture the folding process using the overlap parameter χ ([10] for definition), which characterizes similarity to the crystal structure. In Fig. 2B, χ ranges from 0 for the C state to 1 for the U state, with the I state at about 0.35. The state I is a consequence of the heterogeneous distribution of cavities, causing a localized pressure-denaturation. Small packing differences between the domains are revealed by pressure. Since the sum total of cavity volume of the N-terminal domain (≈171 ų) is larger than of the C-terminal domain (≈132 ų), the former is more vulnerable to high pressure. Moreover, two anti-parallel β-strands m and n of the N-terminal domain are totally exposed to the solvent ([10] in section S5 and Fig S1.1). Under high pressure, they act as a channel for water to fill the N-terminal domain’s cavities. Therefore, the dominant intermediate contains an unfolded N-terminal domain and a folded C-terminal domain.

At sufficiently high T (Fig. 2C) or high ϕ (Fig. 2A, above the red critical point), the transition between folding and unfolding versus pressure exhibits only two states, without the folding intermediate I. As the limited void formed by the density fluctuations of crowders inhibits extended unfolded conformations [29], macromolecular crowding favors compact states like the spherical state Sph [28]. PGK’s domains collapse from C to Sph and CC states when the linker “cracks” [11] and forms a disordered hinge. High pressure competing with crowding gives rise to compact unfolded conformations where up to half of the contacts becomes swollen with water that forms a “wet interface” (swollen unfolded states, SU). Without extended unfolded conformations in the U state, the protein only needs to subtly reduce its volume as if it expels water molecules out of this wet core to return to the Sph state. There are effectively no barriers between the Sph, CC, and SU states, which are thus located in the same region of the phase diagram (see Figures 2A and 2B, and S5.2 [10]). This data supports the theory that protein dynamics is governed by the solvent motion [30], and water inside the protein “lubricates” the transitions between conformations without significant free energy costs [25].

Thus, our model predicts that PGK undergoes a critical transition with a value of T_c that decreases as ϕ is increased: crowding makes the folding of PGK apparent two-state at both low and high T, whereas lack of crowding produces a multi-state transition below T_c.

B. T-P-ϕ phase diagram of PGK from experiment

To validate the computed phase diagram, we measured the P-T phase diagram of PGK at various Ficoll 70 crowder concentrations to obtain the full P-T-ϕ information experimentally (Fig. 3). While one cannot expect the exact temperatures and pressures to agree, identical topologies of the experimental and computed phase diagrams validate the general conclusions from theory. Changes of state were detected by tryptophan fluorescence because tryptophan mean fluorescence wavelength is sensitive to water exposure as the protein unfolds. We scanned T from 283 to 318 K at constant P, and P from 0 to 250 MPa at constant T with 0, 25, 50, 100, 150, and 200 mg/mL of Ficoll concentration (ϕ = 0 to ≈ 0.56) to cover the complete phase diagram. Each transition produces a sigmoidal step in the plot of mean tryptophan fluorescence wavelength λ_m vs. P (Fig. S2.1 [10]). Singular value decomposition analysis ([10] in section S4) also strongly supports the conclusions obtained from analyzing λ_m.

In the absence of crowder at sufficiently low T (Fig. 3A, blue trace), there are two steps in λ_m as a function of pressure, signaling two separate transitions among three states. These steps are easily revealed by plotting ∂λ_m/∂P and identifying peaks (see Fig 3A, and Fig. S2.1 [10]). We assign the first peak to the C to I transition, the second to the I to U transition. At sufficiently high T, at ≥ 303 K and ≈170 MPa, one of the peaks disappears (Fig. 3C, blue trace), leaving only one transition between two states. We assign this to a direct transition from C to U from Fig. 2C, corresponding to a critical point at T_c = 306±3 K. Finally, when crowder is added, T_c moves to lower temperature, until the apparent three-state transition is no longer observed at all at 200 mg/ml Ficoll (Fig. 3AC, red traces). We assign this to the transition between C and SU/Sph/CC from Fig. 2A. Accurate transition midpoints (T_m, P_m, ϕ_m) were obtained from each trace by fitting to sigmoidal two- or three-state models (solid curves in Fig. 3A&C; see Appendix B; all data traces are shown [10] in section S4.)

We constructed T-P planes of the phase diagram at all crowder concentrations as follows: First, the transition midpoints were plotted on P-T slices at constant ϕ as shown in Fig. 3B. These points correspond to zero free energy difference, ΔG = 0, for the first-order transition, where concentrations of C and I, I and U, or C and U (depending on the location on the phase diagram) are equal. Then the transitions were fitted to Hawley’s elliptical P-T phase curve for proteins [31],

$$\Delta G=\frac{1}{2}\Delta \beta {\left(P-P_0\right)}^2+\Delta \alpha \left(T-T_0\right)\left(P-P_0\right)-{\Delta \text{C}}_P\left[T\left(\text{ln}\frac{T}{T_0}-1\right)+T_0\right]+{\Delta \text{V}}_0\left(P-P_0\right)-{\Delta \text{S}}_0\left(T-T_0\right)+{\Delta \text{G}}_0,$$ (1)

at each value of ϕ (fits for all ϕ and parameter definitions in [10] section S4). Here Δβ, Δα, ΔC_p, ΔV₀, and ΔS₀, signify changes in compressibility, thermal expansion coefficient, heat capacity, volume, and entropy, respectively. The resulting experimental phase diagram in Fig. 3B agrees with the computational data as both exhibit two pressure transitions at low T, one at high T, and a shift from two to three transitions at a value of T_c that decreases with increased crowding.

The simulation predicts that in the state I, the N-terminus would be unfolded and the C-terminus folded. We truncated the protein to the N-terminal domain, and indeed found it to be unfolded with long tryptophan fluorescence wavelength and no cooperative transition (Fig. S4.4 [10]). It is known from the literature [32] that the C-terminal domain of PGK is stable by itself. These two observations combined strongly support the computational assignment of the intermediate I to a state with the N-terminal domain largely unfolded, and the C-terminal domain largely folded. Thus, experiment and theory are in agreement both on the disappearance of a phase at high T or high ϕ, as well as the general structural features of an intermediate I formed at low crowding.

C. Unified T-P-ϕ phase diagram of PGK from theory and experiment

The three-dimensional T-P-ϕ phase diagram in Fig. 4C presents a unified picture of the computational and experimental results. In addition, Fig. 4A shows a computational low and high T slice in the ϕ-P plane, and Fig. 4B shows an experimental low ϕ and high ϕ slice in the P-T plane. As temperature increases, the second transition surface terminates in a critical line (bold red line on the red I-U coexistence surface in Fig. 4C). As the crowding volume fraction increases, the critical point shifts towards lower temperatures. Thus, above ϕ = ϕ_c ≈ 0.5 or above T = T_c⁰ ≈ 306 K the pressure-induced folding transition contains only two apparent phases. Whereas at low ϕ and T, PGK exhibits apparent three-state folding.

To quantitate the unified phase diagram, we modified Hawley’s theory by incorporating the free energy change due to crowding to construct the first transition surface (blue surface in Fig 4). We treat the folded and unfolded proteins as effective hard spheres and utilized scaled particle theory (SPT) to estimate the change in folding free energy as the difference between the insertion free energy for the folded and the unfolded states to first order approximation. As for the critical line on the second transition surface (in red in Fig 4), we used scaling arguments to derive the equation for the critical line,

$$P-P_c=a_1\left(T-T_c\left(\varphi \right)\right)+a_2{\left(T-T_c\left(\varphi \right)\right)}^2+\mathcal{O}\left(\Delta T^3\right),$$ #(2)

by treating the proteins U to I transition similar to in the coil-globule transition of theory [33,34]. Here,

$$T_c\left(\varphi \right)=T_c^0{\left(1-\frac{\varphi }{{\varphi }_c}\right)}^{\gamma },$$ #(3)

where T_c⁰ is the critical temperature without crowding, ϕ_c is the critical crowding volume fraction, P_c (≈ 170 MPa) is the critical pressure at T_c⁰, and $a_1={\frac{dP}{dT}|}_{T=T_c^0}$ and $a_2=\frac{d^{2}P}{d{T}^2}{|}_{T=T_c^0}$. From the fitting, we found γ = 0.40 with a possible range from 0.41 to 0.39 when including the margin of error. This is the predicted scaling exponent of a polymer collapse due to crowders, γ = 2/5 [35,36] (see Appendix C). From this phase diagram, we can see the protein moves through a rich space of structural states, suggesting different folding mechanisms that depend on how the phase diagram is traced out [37,38].

D. Consequences of criticality

In Fig. 5, we explore the impact of pressure and crowding on the folding of PGK. The consequences of the critical regime are revealed by the ensemble distributions of the cavity volume (conjugate variable of P) and co-volume (conjugate variable of ϕ) [15,16] from our simulations (also see Fig. S5.1 [10]). In the critical regime, small perturbations in crowding volume fraction, pressure, or temperature will greatly affect the system.

FIG 5.

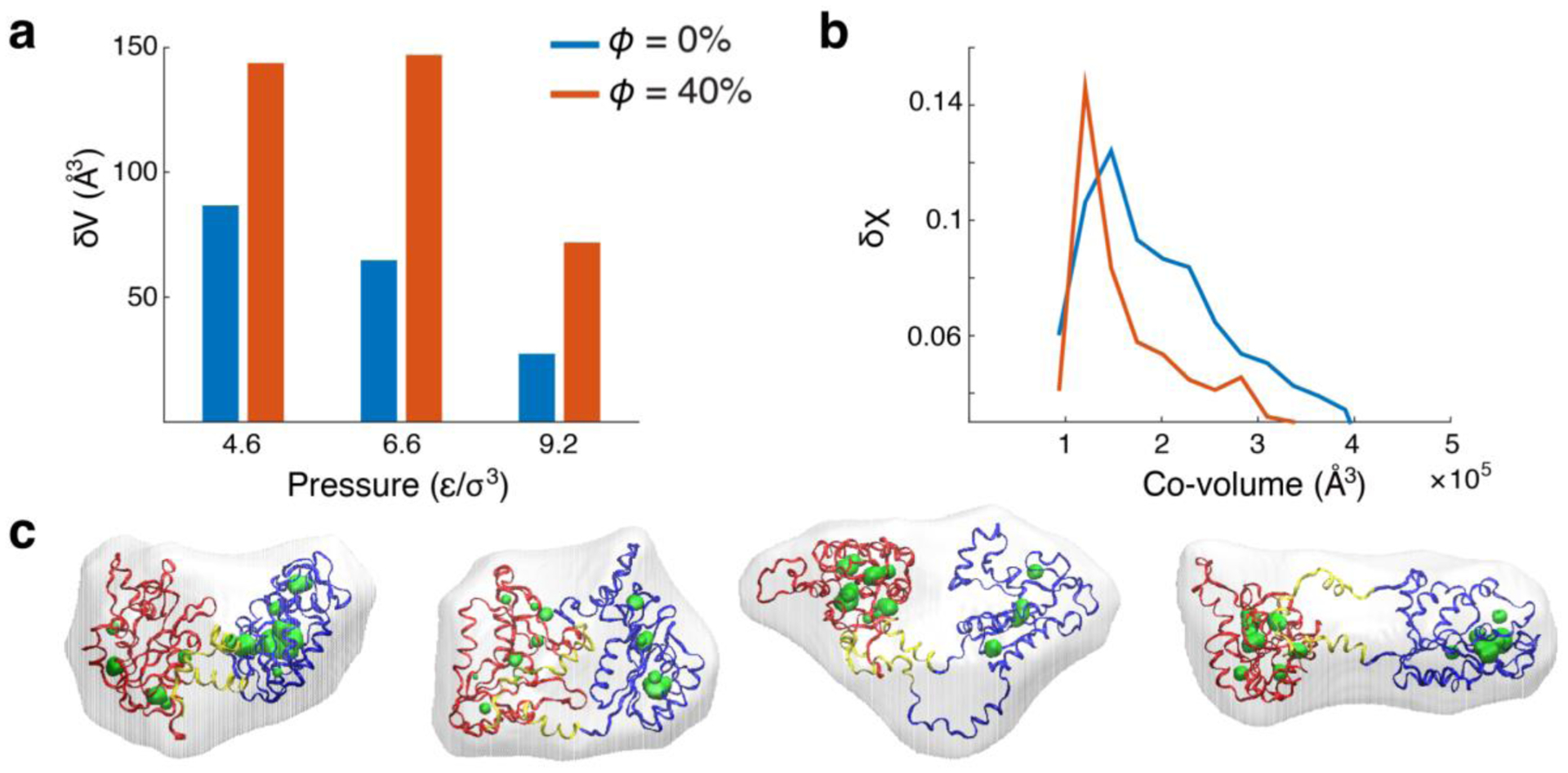
Volume and structural fluctuations near critical regime. (A) Volume fluctuations (or proportionally compressibility) of PGK at k_BT/ε = 0.97 and pressures 4.6, 6.6, and 9.2 ε/σ³ with (orange) and without (blue) crowding. (B) Overlap fluctuations, δχ² = 〈χ²〉 − 〈χ〉², as a function of co-volume at pressure 6.6 ε/σ³. (C) Conformations from the ensemble in presence of crowding at k_BT/ε = 0.97 and σ³P/ε = 6.6 with co-volumes ≈1.1 ×10⁵ ų and cavities ≈200 ų. Most left conformation is a crystal state. The following structures from left to right have a χ = 0.31, 0.38 and 0.48. N-, C-domain, and hinge are in red, blue, and yellow respectively. Co-volumes are shown as translucent surfaces surrounding the protein and cavity surfaces are shown in green.

We investigate the response of the ensembles near the conformational distribution of structures close to the critical region by comparing the volume fluctuations (or proportionally, the compressibility) and structural fluctuations in the presence and absence of crowding agent. PGK has larger cavity volume fluctuations (δV² = 〈V²〉 − 〈V〉²) (Fig. 5A) at ϕ = 0.4 with a peak at 6.6 ε/σ³ than that of ϕ = 0. We suspected that the critical regime is between at ϕ = 0.2 and 0.4 and between pressure 4.6 ε/σ³ and 6.6 ε/σ³ at a temperature of 0.97 ε/ k_BT in the computational model, which qualitatively agrees with the experiment. Even though the cavity volume fluctuations are large in the presence of crowders, structures lie in a narrow range of co-volumes, making them indistinguishable to macromolecular crowding effects if shape can be neglected to 0^th order (Fig. 5B). A sample of the diverse structures with similar cavity volumes and co-volumes are shown in Fig. 5C.

Not only does crowding shift the population of structures to more compact states such as CC or Sph (Fig. 2 and [12]), where the two ligand binding sites (for ADP and 1,3-DPG) come into close proximity of each other, but it also increases the structural fluctuations of the compact states by bringing PGK closer to the critical regime, as shown in Fig. 5. Both of these properties would most likely facilitate enzymatic activity. This is corroborated by previous FRET experiments that show an increase in PGK’s enzymatic activity as Ficoll 70 concentration increases [12]. These results suggest that criticality assists the enzymatic function of a protein.

III. CONCLUSION

In summary, we have shown direct evidence of equilibrium critical-like behavior on the T-P-ϕ phase diagram of a protein by computational simulations, by fluorescence spectroscopy, and by a theoretical argument based on polymer theory. Above the critical line in Fig. 4C (by increasing T and/or ϕ at P_c ≈ 170 MPa), the difference between the intermediate I and unfolded U phases disappears. This is due to the disappearance of the free energy barrier between the two phases (Fig 2B), and is validated by the high-pressure fluorescence measurements (Fig 3).

What is the origin of this critical behavior in proteins? Firstly, proteins are biopolymers that often undergo an abrupt or first-order-like transition to a compacted folded state from an expanded unfolded state or coil at a certain temperature (T_F). Secondly, the coil-globule transition seen in other polymers is a continuous transition at a certain temperature (T_θ). Therefore, the first order transition in protein folding must be occurring near the collapse transition (T_F ≈ T_θ), meaning it normally is tricritical [7]. In our system, the pressure perturbation may cause T_F ≠ T_θ, separating the continuous and first-order transitions. When going from a continuous to a first-order transition, there are signatures of passing through a critical point [39,40]. Finally, when ϕ is high (ϕ > ϕ_c), the protein is collapsed even when it is unfolded resulting in no collapse transition. Our theoretical model in Eq. (3) and Appendix C captures this postulation of basis of criticality in proteins.

Furthermore, our computational and experimental results are in accord with the capillarity picture of folding [41], which posits a wetting interface between folded and unfolded parts of a protein, giving rise to a rich state space. Strong macromolecular crowding, which drives conformational changes to favor spherical states, roughens that wetting interface, allowing cavities to spread throughout the conformation of the protein, with two major consequences. A roughened interface reduces activation barriers for folding, driving multi-state transitions towards apparent two-state transitions. It also creates a critical state where heterogeneous conformations coexist, as the front of wetting interface moves across the protein.

We conclude that large structural fluctuations (Fig 5) and merging of protein phases are consequences of being close to a critical point (Fig 4C). At such a point, the barrier separating states vanishes (here: between I and U). Critical behavior has been proposed for protein folding at the onset of downhill folding [8], but its manifestation has been difficult to demonstrate computationally and experimentally [42]. Macromolecular crowding shifts the critical point to a lower temperature (Eq. (3)), indicating that such criticality could be physiologically important [3,4]: a protein near a critical state could access a wide range of conformations without large activation barriers for functional purposes inside the cell.

Further work will be needed to provide stronger evidence for the universality of critical behavior in proteins. Due to their complexity, proteins are not like other conventional condensed matter systems, and conventional tools, such as finite size scaling [43] or renormalization group theory [44], are not easily applicable. Our investigation is a starting point toward developing universal principles of protein folding relevant to the environmental perturbations inside living cells, and also inspiration to create new tools to understand critical phenomena in these complex systems.

APPENDIX A: SIMULATION MODEL

The emergence of structure and function from a protein sequence makes the modeling of proteins from first principle (ab initio models) computationally and theoretically prohibitive. Therefore, experimentally derived structural information is needed (even in models termed “all-atom”, which refine ab initio force field parameters to fit experimentally known structures) to capture key features in protein folding and dynamics [45]. A structure-based model is one of the minimalist protein models to incorporate experimentally derived structural information [46] to investigate the mechanism of protein folding dynamics. It is often utilized as the “ideal gas” of protein folding for the investigation of a wide range of folding mechanisms [2,47]. This model renders an energy landscape [48] with minimal frustration and contains a dominant basin of attraction, corresponding to an experimentally determined configuration [49]. This “necklace and beads” model carries the added bonus of being computationally inexpensive, enabling long-timescale simulations to be obtained for our large protein and macromolecular crowding system. Additionally, structure-based models tend to capture unfolded protein scaling laws better than all-atom models [50], which is necessary to correctly characterize the various non-crystal states of PGK. Lastly, high pressure is known to unfold proteins on a longer time scale; therefore, structure-based, minimalist-model simulations provide statistically significant results. Similar to adding specific complexity to the ideal gas model to study specific phenomena, we add the desolvation barrier [25] to the native interactions that accounts for the free energy cost to expel a water molecule in the first hydration shell between two hydrophobic residues [51] to study pressure unfolding, leading to the appearance of a partially folded intermediate. The use of this model has been validated in other systems [27]. The Hamiltonian of this structure-based protein model is as follows:

$${\mathcal{H}}_p\left(\Gamma ,{\Gamma }^0\right)=\sum _{i<j}{K}_r{}^{{\left(r_{ij}-r_{ij}^0\right)}^2}{\delta }_{j,i+1}+\sum _{i\in \text{angles}}{K}_{\theta }{}^{{\left({\theta }_i-{\theta }_i^0\right)}^2}+\sum _{i\in \text{dihedrals}}{K}_{\varphi }\left(\left\{1-\text{cos}\left[{\varphi }_i-{\varphi }_i^0\right]\right\}+\frac{1}{2}\left\{1-\text{cos}\left[3\left({\varphi }_i-{\varphi }_i^0\right)\right]\right\}\right)+\sum _{\begin{array}{c}i,j\in \text{native}\\ \left|i-j\right|>4\end{array}}U\left(r_{ij}\right)+\sum _{i,j\notin \text{native}}ϵ{\left(\frac{\sigma }{r_{ij}}\right)}^{12}$$ (4)

where Γ is a configuration of the set r, θ, ϕ. The r_ij term is the distance between i^th and j^th residues, θ is the angle between three consecutive beads, and ϕ is the dihedral angle defined over four sequential residues. δ is the Kronecker delta function. Γ⁰ = {{r⁰},{θ⁰},{ϕ⁰}} is obtained from the crystal structure configuration. Lastly, U(r_ij) is desolvation potential. Crowders are modeled as hard spheres. The complete descriptions of a structure-based protein model, desolvation potential, and simulations of PGK in a periodic cubic box of Ficoll 70 are provided in the Supplemental Material [10]. All simulations were performed using GROMACS 2016.3 molecular dynamics software [52].

APPENDIX B: HIGH PRESURE FLUORESCENCE EXPERIMENT METHODS

Fluorescence experiments were carried out at high pressure using a high-pressure cell (ISS High-Pressure Cell System) on a fluorimeter (JASCO FP8300). A computerized high-pressure generator (Pressure BioSciences Inc. HUB440) was used to pressurize the fluorescence cell. We used a rectangular quartz cuvette with a path length of 6 mm and deionized water was used as pressurizing fluid. The pressure was raised from 0.1 MPa to 250 MPa at a rate of 10 MPa/min and held at intervals of 10 MPa for a 5 min wait time to allow sample equilibration. Fluorescence spectra from 300 to 450 nm were acquired in the middle of the wait time and an in-built proportional-integral-derivative (PID) feedback loop was used to obtain accurate pressures (within 5 bars of target pressure). The temperature was controlled using an external water-circulating bath. To construct a complete P-T-ϕ phase diagram, fluorescence measurements were done at 6 different Ficoll concentrations ([Ficoll] = 0, 25, 50, 100, 150 and 200 mg/ml), each at 6 different temperatures T ranging from from 282K to 317K (9°C to 44°C). Equilibrium traces of mean fluorescence wavelength vs. pressure (e.g. Fig. 3 left) were fit to a two-state or three-state thermodynamic model (see Supplementary Material [10]), depending on whether the derivative (Fig. S1.2 [10]) of the titration curve identified one or two transitions (An inflection point in the fluorescence vs. P trace at given T and [Ficoll] produces a peak in the derivative). The fitted transition midpoints (P, T, ϕ) were then plotted in a phase diagram (e.g. Fig. 3 middle) and fitted to Eq. (1). See [10] for complete data and fitting parameters.

APPENDIX C: CONSTRUCTION OF PHASE DIAGRAM

We derived the critical line on the P-T-ϕ phase diagram using arguments based on the coil-globule transition [33,34] of a polymer. Beginning with a Landau-Ginsberg free energy [53], F = −r(T,ϕ)Ψ² + sΨ⁴ + F₀, to describe the critical transition, where Ψ is the order parameter, which is a scaled and shifted R_g (radius of gyration) so that Ψ = − Ψ₀ for the I state and Ψ = + Ψ₀ for the U state. Since pressure is only involved with the first-order transitions, it can be ignored for now. At the critical temperature, the barrier between the I and U states vanishes, meaning r = 0; therefore, a reasonable function is r(T,ϕ) = r₀[T − T_c(ϕ)], where the critical temperature T_c is a function of ϕ. To find the ϕ dependence of T_c, we used the scaling relationship

$$\frac{R_g{\left(\varphi \right)}^2}{R_g{\left(0\right)}^2}~{\left(1-c_0\varphi \right)}^{\gamma },$$ #(5)

which relates R_g at a given ϕ to R_g without crowders for the collapse of a coil to globule transition [35]. The scaling exponent γ, is shown to be 2/5 in Refs [35,36]. Since the collapse of the polymer, or in our case the protein, is dependent on ϕ, and since Ψ² ~ R_g(ϕ)²/R_g(0)², the critical temperature T_c(ϕ) causing the free energy barrier between I and U to disappear must also scale as Eq. (5), giving Eq. (3). We fit Eq. (3) to the experimental critical point values at all Ficoll 70 concentrations to find γ and ϕ_c. We fit Eq. (2) to experimental values of the I to U transition surface to find the Taylor expansion coefficients.

Lastly, we modified Hawly’s equation [31] to fit the C to I (or U, depending on T and ϕ) transition surface. Similar to Minton’s theory [16], we added a ϕ-dependent ΔG_crowd(ϕ) term to Eq. (1),

$$\Delta G_{\mathit{\text{crowd}}}\left(\varphi \right)=g\left(\frac{\varphi }{1-\varphi }\right)+\mathcal{O}\left({\varphi }^2\right),$$ #(6)

which treats the folded and unfolded proteins as effective hard spheres and employs scaled particle theory (SPT) to estimate the change in folding free energy as the difference between the insertion free energy for the folded and the unfolded states [54].