Exploring Disordered Morphologies of Blends and Block Copolymers for Light-Emitting Diodes with Mesoscopic Simulations

Abstract

Recently, disordered blends of semiconducting and insulating polymers have been used to prepare light-emitting diodes with increased luminous efficiency. Because the thermodynamic stability of the disordered phase in blends is limited, equivalent diblock copolymers (BCPs) could be an alternative. However, the choice between disordered blends and BCPs requires understanding structural differences and their effect on charge carrier transport. Using a hybrid mesoscopic model, we simulate blends and equivalent BCPs of two representative semiconducting and insulating polymers: poly(p-phenylene vinylene) (PPV) and polyacrylate. The immiscibility is varied to mimic annealing at different temperatures. We find stable or metastable disordered morphologies until we reach the mean-field (MF) spinodal. Disordered morphologies are heterogeneous because of thermal fluctuations and local segregation. Near the MF spinodal, segregation is stronger in BCPs than in the blends, even though the immiscibility, normalized by the MF spinodal, is the same. We link the spatial distribution of PPV with electric conductance. We predict that the immiscibility (temperature at which the layer is annealed) affects electrical percolation much stronger in BCPs than in blends. Differences in the local structure and percolation between blends and BCPs are enhanced at a high insulator content.

1. Introduction

Organic light-emitting diode technology is an active research area owing to its compatibility with lighting and display applications. Especially, for polymeric active materials with their excellent film-forming properties, device fabrication based on cost-effective solution processing becomes feasible. Such a polymer light-emitting diode (PLED) typically comprises¹ a thin ∼100 nm layer of a light-emitting semiconducting polymer situated between two electrodes, of which at least one is transparent. A PLED generates light through² radiative decay of excitons, formed in the semiconductor upon recombination of holes and electrons, injected at the anode and cathode. Balanced transport of these oppositely charged carriers is of paramount importance to reach optimal device performance.

Unfortunately, in commonly used disordered polymeric semiconductors, electron transport—unlike hole transport—is limited by trap states, likely caused by chemical impurities.³ The resulting disbalance in transport strongly reduces¹ device performance because of losses via trap-assisted recombination and cathode quenching. The problem can be addressed by blending the semiconducting polymer with an insulating polymer.⁴ This approach is motivated by the theoretical prediction of Mark and Helfrich (MH)⁵ that the trap-limited current density scales as J ∼ N/N_t^r, where N and N_t are the densities of transport and trapping sites, respectively. The exponent r is a measure of the width of the energetic distribution of the trap states. For disordered visible light-emitting semiconductors,^4,6r ≥ 4 typically. For the first approximation, blending with an insulator reduces both N and N_t by the average volume fraction of the semiconducting polymer ϕ̅_A (0 < ϕ̅_A < 1). Hence, the electron current density increases to J_blend ≈ ϕ̅_A^(1–r)J. It has been shown that diluting the semiconductor with 90% of an insulator doubles the luminous efficiency of the PLED.^4,6

Although the concept of alleviating trapping by blending has been convincingly demonstrated, the fabrication of smooth and homogeneous films is subject to considerable optimization. It is believed⁶ that trap reduction is more effective when the active layer is solidified from a disordered blend to guarantee intimate mixing between the semiconductor and insulator. However, polymer blends are prone to macroscopic phase separation: the strength of immiscibility is proportional to the chain length, so that even weak incompatibilities between monomers are amplified. For example, for the semiconductor:insulator system, poly[2-methoxy-5-(2-ethylhexyloxy)-1,4-phenylenevinylene] (MEH-PPV):polystyrene trap elimination is not observed if the molecular weight (MW) of polystyrene exceeds ∼10 kg/mol (with an average MW of MEH-PPV of ∼300 kg/mol) because of segregation of the blend into phases of the pure polymers.⁶ An apparently straightforward way to avoid phase separation is to push the blend outside the miscibility gap by significantly increasing the fraction of the insulator. However, the density of the current drops significantly for small ϕ̅_A because of the loss of percolating pathways for charge transport.

One possibility to increase the range of processing temperatures where disordered phases are stable is to link semiconductor and insulator homopolymers into an “equivalent” diblock-copolymer (BCP). The rationale is simple: covalently linked blocks of dissimilar polymers cannot segregate into macroscopic phases (as homopolymers do), but microphase separate into regular domain patterns.⁷⁻⁹ Because of the entropy losses caused^9,10 by stretching of blocks inside domains and localization of block junctions at domain interfaces, microphase separation in BCPs requires stronger immiscibility (which for mixtures with upper critical solution temperature (UCST) behavior is equivalent to lower temperatures) than phase separation in the equivalent blends. For example, consider compositional and conformational symmetric blends of homopolymers composed of N monomers each. Monomer/monomer incompatibility is quantified by the Flory–Huggins (FH) parameter, which in the simplest case has only an enthalpic contribution: χ = B/T (B is a constant and T is the temperature). For a symmetric blend, the phase transition from disordered to the macroscopically separated phase occurs¹¹ within mean-field (MF) at χN = 2. In contrast, for an equivalent BCP comprising 2N monomers, the phase transition from the disordered state to an ordered microdomain structure, that is, order–disorder transition (ODT), occurs⁷ within MF at 2χN ≃ 10.49. Hence, in this example, substituting a blend by a BCP reduces the threshold temperature, below which the disordered phase is unfavorable thermodynamically, by 2.5 times.

The idea to replace blends by BCPs requires detailed investigation because disordered blends and BCPs are structurally not equivalent. Let us first recapitulate some similarities. At thermodynamic equilibrium, in both materials, disordered phases are characterized by local segregation of different constituents, fluctuations in composition, and correlations. These heterogeneities span a broad range of scales:^12,13 from atomistic to mesoscopic. Mesoscopic composition fluctuations are suppressed¹⁴ for chain lengths N → ∞ but cannot be neglected for the chain lengths used in typical applications. In general, for both systems, correlation lengths and strength of composition fluctuations increase upon approaching the phase transition.

However, phase transitions in blends and BCPs belong to different universality classes: three-dimensional (3D) Ising^12,14−17 and Brazovskii,^18,19 respectively. Depending on ϕ̅_A, the phase transition in blends is first order (off-critical ϕ̅_A) or second order (critical ϕ̅_A). For critical ϕ̅_A, the correlation length and magnitude of composition fluctuations diverge at the phase transition, following 3D Ising critical exponents.^12,14−17 In BCPs, the Brazovskii mechanism always leads¹⁹ to a first-order ODT, for which reason such divergences do not occur. This mechanism also modifies¹⁹⁻²¹ in BCP the “topology” of the phase diagram near ODT (comparing to MF predictions). Moreover, in disordered blends, mesoscopic heterogeneities are characterized by a single length scale, corresponding to the correlation length of composition fluctuations. In contrast, in a disordered BCP, there is²² an additional length scale on the order of the average chain extension, related to the wavelength of the emerging microphase-separated structure. This feature of BCPs is signified by a Lorentzian-like shaped structure factor of composition fluctuations.⁷ Interestingly,^23,24 near the ODT, disordered phases of lamellar- and cylinder-forming BCPs with short chains contain bicontinuous random networks. Each network is enriched in one of the blocks. Fluctuations of the network topology provide additional entropy, stabilizing the disordered phase.²⁴ It is unknown whether structural differences of disordered phases in blends and BCPs lead to differences in charge transport dynamics and, if so, which structures are more suitable for PLED applications.

Here, we use computer simulations to investigate the morphology of the disordered phase of blends of semiconducting and insulating homopolymers in comparison to that of their equivalent BCPs. We aim to qualitatively understand how structural differences between the two systems may affect charge transport. Ideally, such studies should use all-atom representations because charge transport is sensitive to both atomistic and mesoscopic polymer arrangement. However, the equilibration of dense polymeric mixtures on device-relevant length scales is unfeasible in all-atom simulations^25,26 because of the vast number of degrees of freedom and slow dynamics. So far, all-atom simulations of blends or copolymers related to organic electronics have considered oligomers and rather small systems (containing up to a few tens of oligomers). Representative studies can be found in refs (27−33). However, to model disordered PLED layers, simulations must consider realistically long chains—we just saw that in disordered polymer mixtures, the chain length is a “thermodynamic” parameter, intrinsically linked to the structure of heterogeneities.

Alternatively, one can use computationally efficient models that do not resolve a microscopic structure but capture generic features driving mesoscopic polymer assembly and can be applied to study morphologies on large scales. Our work is based on such a model. Polymers are represented by discrete worm-like chains (WLC) which account for different molecular flexibilities of semiconducting and insulating homopolymers (blocks). Nonbonded interactions are described by two functionals that are quadratic in instantaneous local densities of different monomer species. The first functional captures the limited compressibility of polymer liquids,³⁴ whereas the second, a FH-like expression, describes repulsion of unlike monomers. Such generic models are standard for theoretical studies of multicomponent polymeric systems.³⁵⁻³⁹ To investigate phase behavior of materials relevant for organic electronics, these models have been frequently applied⁴⁰⁻⁴³ within MF. However, MF cannot describe the structure of disordered phases because it neglects fluctuations and correlations. To capture these features, we use the mesoscopic model as a framework for particle-based pseudo-dynamical Monte Carlo (MC) simulations by transforming the density functional into pairwise potentials⁴⁴ via a particle-to-mesh (PM) scheme.⁴⁴⁻⁴⁷

We set the parameters of the model to values typical for poly(para-phenylene-vinylene) (PPV) derivatives and polyacrylates, representing two families of organic semiconductors and insulators. We focus on PPV polymers that are short enough to be semiflexible and control dilution by varying the length of polyacrylate chains (blocks). The MC simulations are used to prepare disordered morphologies of blends and BCPs for different dilutions and strength of PPV:polyacrylate immiscibility. The latter covers the entire phase space where the disordered phase is stable or metastable in our simulations and reaches up to the MF spinodal. We estimate the MF spinodal from the random phase approximation^7,48 (RPA) adjusted to include the WLC architecture and compressibility. Varying immiscibility is analogous to varying the processing temperature of an actual PLED active layer, prior to solidification.

Our mesoscopic model describes polymers in the liquid state. We assume that solidification is fast enough to consider active layers as structurally equivalent to vitrified configurations of liquid blends or BCPs. Hence, we infer the properties in the solid state from structural analysis of liquid morphologies. First, we analyze the local structure of disordered blends and their equivalent BCPs in terms of fluctuations in local composition, as well as strength of local segregation between PPV and polyacrylate monomers. We identify differences in the local structure of the two materials, which are more pronounced near the phase transitions from disordered to macroscopically-separated (blends) and microphase-separated (BCPs) states and for higher polyacrylate content. Next, we use a phenomenological percolation model to explore the influence of global polymer arrangement on macroscopic electrical conductance. The analysis finds intriguing differences between blends and BCPs concerning how annealing conditions—magnitude of FH parameter or, equivalently, temperature—influence electrical percolation of their disordered morphologies.

2. Simulation Method

2.1. Polymer Description

Our mesoscopic model represents an atomistic system containing n_A PPV and n_B polyacrylate homopolymers or blocks in a volume V. For both polymers, the general chemical structure of a monomer is shown in Figure 1a. For brevity, we indicate the chemical identity of a homopolymer (or BCP block) with subscripts α = A for PPV and α = B for polyacrylate. Each homopolymer (block) is made of m_α atomistic monomers; the MW of each monomer is M_α. The mass densities of pure PPV and polyacrylate phases are given by 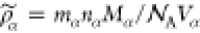, where V_α are the volumes that would be occupied by atomistic PPV and polyacrylate homopolymers (blocks) in their pure phase. 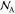is the Avogadro number.

Figure 1.

(a) Chemical structure of PPV (top) and polyacrylate (bottom) monomers. For PPV, R₁ and R₂ stand for alkyl substituents. For polyacrylates, R₃ is a small nonpolar moiety while R₄ denotes a −H or −CH₃ group. (b) Scheme used to map PPV (shown in an all trans configuration) on the discrete WLC model. Each atomistic monomer (gray sphere) is mapped on one interaction center (solid circle) placed at a junction or end-point of the WLC. (c) Top: sketch showing the representation of PPV and polyacrylate homopolymers in blends by WLC with N_A (solid circles) and N_B (open circles) beads, respectively. Angles between WLC bonds are controlled by stiffness parameters ϵ_α, while bond lengths are fixed to b_α. Bottom: coarse-grained representation of PPV-b-polyacrylate BCPs obtained by covalently linking the WLC of PPV and polyacrylate homopolymers.

Our coarse-graining procedure conserves n_α and V_α. In PPV:polyacrylate blends, each atomistic polymer is mapped onto a discrete WLC comprising N_α interaction centers, beads, connected by bonds with fixed length b_α. The bonded potential of the WLC is defined by

1

where β = 1/k_BT and u(s) is a unit vector along the s-th bond. Parameter ϵ_α controls the stiffness of the WLC.

The discrete WLC conserves two physical length scales of an actual polymer: persistence length l_p,α and contour length L_α. This requirement imposes two constraints⁴⁹ on the parameters N_α, b_α, and ϵ_α

2

and

3

In general, the constraints expressed via eqs 2 and 3 are satisfied⁴⁹ by an infinite number of combinations of N_α and b_α. In this study, we obtain unique mapping by introducing two additional requirements.

First, to facilitate qualitative studies of charge transport, it is reasonable to use for the WLC, describing the electrically active component, a level of discretization which is comparable to the actual polymer. Based on earlier studies,^49,50 we assign physical meaning to A-type beads, assuming that each of them represents an actual (atomistic) PPV monomer (see Figure 1b). Second, we choose for the insulator N_B such that the pure phase of coarse-grained polyacrylates has the same average number density of beads as the pure phase of the coarse-grained PPV, that is, we impose the constraint n_AN_A/V_A = n_BN_B/V_B ≡ ρ₀. This specific choice of N_B facilitates the definition of nonbonded interactions, realizing a generic equation-of-state of a compressible polymer liquid, cf. eq 7. These two requirements lead to the relationships

4

Provided that l_p,α, L_α, m_α, M_α, and ρ̃_α of actual polymers are known, eqs 2–4 fully define the mapping of PPV and polyacrylate homopolymers on our mesoscopic model. We provide these material-specific parameters in Section 2.2.

For BCPs, the WLC description of blocks is identical to that of the corresponding homopolymers, as illustrated in Figure 1c. We connect a PPV and a polyacrylate block by a covalent bond with length b_B. The stiffness parameter controlling the angles formed by this covalent bond with its two neighboring bonds is set to ϵ_B. Although this choice is somewhat arbitrary, we expect that penalizing the angle between the last PPV and the linking bond by ϵ_A, instead of ϵ_B, will not substantially affect our results. The reasons are twofold: our flexible polyacrylate blocks are long (cf. Section 2.2) and we focus on disordered phases. To support this statement, we have considered BCP molecules in the ideal chain limit, that is, where only bonded βH_b interactions are present, adopting the two different scenarios for the stiffness of the linkage. As demonstrated in the Supporting Information, we found that the orientational correlations of polyacrylate bonds with respect to the last PPV bond, for both scenarios, decay to zero along the contour of the polyacrylate WLC after a comparable number of bonds (counted from the link). Moreover, the distributions of the end-to-end distance of the BCP for the two cases are very similar (cf. Supporting Information). Modeling shorter BCPs might require more chemistry-specific choices for the mesoscopic description of the linkage. For instance, in a microphase-separated state, the architecture of the linkage might influence the orientation of the blocks with respect to the interface.

2.2. Material-Specific Parameters and Systems Studied

The parameterization of our model requires as an input a few quantities related to MWs, chain architecture, and conformations of actual PPV derivatives and polyacrylates. To specify these input quantities, we choose the PPV derivative poly[2-methoxy-5-(3′,7′-dimethyloctyloxy)-1,4-phenylenevinylene] (MDMO-PPV) and poly(methylmethacrylate) (PMMA) as model systems. We emphasize that the conjugated polyaromatic backbone, as well as the alkyl substitution pattern of MDMO-PPV, is representative for a broad range of nonpolar polymeric (luminescent) semiconductors commonly applied in optoelectronics. Similarly, PMMA represents a class of synthetically well-accessible insulating polymers, of which the polarity (and hence solubility with PPV) can be easily tuned by varying the alkoxy groups of the ester moieties. Hence, the parameterization established on the basis of MDMO-PPV and PMMA can be considered, at least, as qualitatively representative of a broad range of nonpolar polymeric semiconductor:insulator mixtures.

We focus on the special case of blends with n_A = n_B, that is, equimolar mixtures. We make this choice to facilitate direct comparison with their equivalent BCPs, where n_A = n_B by default. The atomistic PPV homopolymers (blocks) underlying the WLC model have m_A = 24 monomers. The MW of an MDMO-PPV monomer is M_A ≃ 288 g/mol, and we use for the mass density⁵¹ ρ̃_A = 0.91 g/cm³. We stress that considering such rather short PPV polymers is relevant from an experimental point of view. Typically, PPV derivatives exhibit poor solubility and processability if the MW is high.⁵² For this reason, synthetic strategies have focused on suppressing the chain length and coupling defects,⁵³ in order to arrive at well-processable materials while exhibiting a high charge carrier mobility.

Different levels of dilution are realized by parameterizing the WLC model such that it describes long atomistic polyacrylate chains with m_B = 70, 138, and 300. The MW of each atomistic PMMA monomer is M_B ≃ 100 g/mol, and we set the mass density to ρ̃_B = 1.09 g/cm³, which is a representative value for the polyacrylate family.⁵⁴ Blending PPV with these three polyacrylates induces dilutions that approximately correspond to mass ratios of 1:1, 1:2, and 1:4. In the following, all modeled blends and BCPs will be indexed by these three mass ratios.

Having specified m_A, M_A, and ρ̃_A, it is straightforward to calculate the average number density of coarse-grained beads ρ₀ = 1.9 nm^–3. The amounts of homopolymers (blocks) comprising a sample with volume V are

5

The last set of material-specific parameters is persistence lengths and contour lengths, required as input for the RHS of eqs 2 and 3. Experimental data on the persistence length of MDMO-PPV are not available, so we set l_p,A = 6 nm. This choice is motivated by data⁵⁵ on the persistence length of MEH-PPV, which has the same conjugated backbone and similar substitution pattern as MDMO-PPV. For PMMA, we choose an experimentally known⁵⁶ value of persistence length l_p,B = 0.8 nm. The provided persistence lengths illustrate that PPV derivatives are significantly less flexible than polyacrylates. Finally, contour lengths are obtained from L_α = m_αl_α, where l_α stands for the end-to-end distance of either atomistic monomer when the polymer is in the all-trans conformation. We estimate l_A = 0.657 nm and l_B = 0.268 nm based on the chemical structures of the PPV and polyacrylate backbone (see Figure 1a), as well as geometric parameters such as bond lengths and angles. The latter are available from atomistic force-fields.^57,58Table 1 summarizes the parameters of the WLC models for all homopolymers and BCPs considered in this study.

Table 1. Parameters Characterizing the Discrete WLC Used in This Study.

dilutions	bA (nm)	bB (nm)	NA	NB	ϵA	ϵB
1:1		0.937		20		0.99
1:2	0.657	0.923	24	40	9.6	1.01
1:4		0.923		87		1.01

2.3. Nonbonded Interactions

Nonbonded interactions are described using a simple PM scheme.⁴⁴⁻⁴⁷ The continuum space of the simulation cell, where the coordinates of coarse-grained beads are defined, is discretized through a cubic mesh with spacing ΔL. In PM schemes, ΔL determines the range of nonbonded interactions. We use ΔL = 1.8 nm which is comparable to the Kuhn segment of the polyacrylate chains l_k,B ≃ 2l_p,B, that is, the length scale below which our most flexible chains can be considered (approximately) as stiff. The vector c_m defines the position of the m-th node of the mesh. A particle-based configuration of the system—defined through the instantaneous set of bead coordinates—can be transformed into instantaneous fields of densities at the nodes of the lattice. For example, the density of PPV beads is defined as

6

N_A(tot) is the total number of PPV beads and r_i is the position of the i-th PPV bead in the system. The function Π(r_i, c_m) assigns beads to grid nodes and is defined as Π = 1 when −ΔL/2 ≤ d_γ < ΔL/2 and Π = 0 otherwise. d_γ are distances along the three Cartesian directions (denoted by γ) between the grid point at c_m and the position of the i-th bead. A similar expression is used to calculate the polyacrylate density ρ̂_B(c_m) from the coordinates r_j of N_B(tot) polyacrylate beads (j = 1, ..., N_B(tot)). Our choice of Π(r_i, c_m) corresponds to a “zero-order” PM scheme.^47,59

The effective Hamiltonian of nonbonded interactions reads

7

The first term in eq 7 limits local fluctuations in total density.³⁴ Their magnitude, that is, the compressibility of the liquid is set by κ. Based on exploratory runs, we employ κ = 10. This choice allows for reasonably high MC acceptance rates (cf. Section 2.4), while maintaining sufficiently low isothermal compressibility for the coarse-grained polymer. For our model, it is straightforward to estimate the isothermal compressibility as κ_T = 1/k_BTκρ₀. For simplicity, we omit in this MF estimate^44,49,60 a small contribution from chain translational entropy. For the representative temperature, T = 423 K, we obtain κ_T ≃ 9 × 10^–9 Pa^–1. This value is only marginally larger than the compressibility of actual polymeric liquids, typically found⁶¹ in the range 10^–9 to 10^–10 Pa^–1. Previous studies have demonstrated that for models, similar to the one used in our work, the MF estimation of κ_T is quite accurate.⁴⁴ In the Supporting Information, we calculate κ_T directly from long-wavelength density fluctuations and demonstrate that, indeed, it is very close to the MF estimate. The nonbonded potential introduced in eq 7 is sufficient for a generic description of a liquid with limited compressibility and is consistent with our mesoscopic representation where coarse-grained beads of PPV and polyacrylate have the same number density, ρ₀. For more detailed studies, asymmetries in monomer volume can be captured by slightly more complex effective Hamiltonians.⁶²

The second term in eq 7 captures the incompatibility of PPV and polyacrylate beads. The degree of incompatibility is controlled by χ. We emphasize that χ is literally a “bare” parameter of pairwise interactions between beads.⁶³ It should not be confused with an effective FH parameter χ_e that would enter the mixing free energy in a MF theory (hypothetically) parameterized to match some observables in our simulations. Because a single coarse-grained configuration in our model is underpinned by a large number of averaged-out microstates, βH_nb and related “bare” parameters are free-energy-like quantities. Modeling actual blends or BCPs under specified thermodynamic conditions would require a state-dependent χ. Because of the molecular complexity of the studied materials and drastic coarse-graining, nontrivial state dependence is expected. For example, bare χ will have a more sophisticated temperature dependence, χ(T), than the simple ∼1/T scaling (indicating only enthalpic effects). These χ(T) are analogous to more complicated dependencies on temperature, known⁶⁴⁻⁶⁶ for effective χ_e parameters. However, to mimic annealing at different temperatures, it is sufficient to vary χ considering it as a free input parameter, without specifying χ(T). We only assume that the dependence χ(T) is identical for blends and BCP made of the same material. Of course, specifying χ(T) becomes necessary for rephrasing observations made for different χ in terms of actual temperature variations. For this purpose, we adopt a classical scenario⁶⁶ assuming that our mixtures follow a UCST behavior, that is, we postulate that decreasing temperature increases bare χ and vice versa. The assumption of UCST behavior of PPV-containing blends and BCPs is supported by previous work⁶⁷⁻⁶⁹ and expected based on the absence of strong directional interactions between the unlike monomers.

Equations 6 and 7 provide a particle-based definition of nonbonded interactions and complete the definition of our particle-based model, together with eq 1. Direct substitution of eqs 6 into 7 and straightforward algebra demonstrate⁴⁴ that βH_nb is equivalent to a standard sum of pairwise potentials acting between beads. These potentials are anisotropic and translationally noninvariant because of the grid.

2.4. Simulation Protocol

The particle-based model defined by eqs 1, 6, and 7 provides a framework for pseudo-dynamical MC simulations in the canonical ensemble. Our simulation protocol is inspired by a processing procedure, which is employed during lab-scale experiments where PLED active layers are manufactured by spin-coating. To reduce nonequilibrium morphological features, caused by fast drying, spin-coated layers are annealed at elevated temperatures (after the solvent has evaporated). After annealing, the structure of morphologies is solidified by rapid quenching. Multicomponent polymer systems are characterized by slow kinetics, originating from the combination⁷⁰ of thermodynamic barriers to mixing of different species, chain entanglements, and segmental friction (which depends on local environment). Therefore, nonequilibrium states may even survive long annealing durations. For our materials, we assume that it is possible to qualitatively mimic the effects of thermodynamic barriers on morphology formation using an MC algorithm which reproduces Rouse-like pseudo-dynamics.

We employ the standard crankshaft MC move,⁷¹ also named⁷² “flip”, where we randomly chose the rotation angle^71,72 from the interval [0, 2π]. The generalization of the crankshaft move to chain ends (end-rotation move) is straightforward. The coordinates of the “flipped” bead in the new and old position, r^(new) and r^(old), are used to calculate the change in the bonded energy Δ(βH_b) (cf. eq 1). These coordinates serve also to identify the cells affected by the move; their amount is either zero (if the new position of the bead is found in the same cell as before) or two. The new densities, ρ_A,B^new(c_m), of PPV or polyacrylate beads (depending on the species of the displaced bead) are calculated in the affected cells. Considering the old density ρ_A,B(c_m) in the same cells, it is straightforward to calculate the difference in the nonbonded energy Δ(βH_nb) (cf. eq 7). The Metropolis criterion is applied to accept the move with probability p_acc = min{1, exp[−Δ(βH_b) – Δ(βH_nb)]}. The acceptance rate of the flip move averaged over both chain species is about 50%.

Assuming that the spin-coated structure used as a starting point for annealing experiments is disordered, we initiate our pseudo-dynamic MC simulations from configurations of disordered melts. Each MC run imitates an annealing process performed at a specific temperature. To mimic the implementation of different annealing temperatures in experiments, we consider a broad range of χ-values. We scan the region 0 ≤ χ ≤ χ_max with step Δχ = 0.029 and identify the χ-values for which each blend or BCP remains disordered (details follow in Section 3.1 and Section 3.2).

Orthogonal to the electrodes, PLED active layers are finite systems with a typical thickness of ∼100 nm. Therefore, we perform the simulations in cubic samples with edge lengths L ≈ 100 nm. Periodic boundary conditions (PBCs) are employed in all Cartesian directions. In the following, we report results obtained for samples with L = 6 R_e, with R_e as the root-mean-square end-to-end distance of a BCP. In actual units, this choice is equivalent to L ≃ 74 nm (1:1 dilution) and L ≃ 101 nm (1:4 dilution). To provide a better feeling for the sizes of the modeled systems, we mention that the samples at 1:1 and 1:4 dilutions contain about 7.8 × 10⁵ and 1.9 × 10⁶ monomers, respectively. To estimate the influence of finite size effects when the system size is varied around ∼100 nm, we also consider samples with L = 5 R_e and 7 R_e (for each dilution). For each χ, the starting configuration is obtained from samples equilibrated at χ = 0. The annealing runs are long: the number of MC cycles is equivalent (at least) to 10 τ_rel for BCPs and 25 τ_rel for blends. The characteristic relaxation “time” τ_rel is the number of MC cycles needed for the autocorrelation function of the end-to-end vector of PPV homopolymers (in blends) or PPV-b-polyacrylate chains (in BCP) to decay to zero, when χ = 0. For example, in 1:4 blends and BCPs, τ_rel approximately corresponds to 5 × 10⁴ and 2 × 10⁵ MC cycles, respectively. We define one MC cycle as the total number of individual MC crankshaft moves for which each monomer was given the opportunity to move, on the average, once (i.e., each MC cycle comprises a number of MC moves that equals the number of monomers in the system).

3. Results and Discussion

3.1. RPA Spinodals

Accurately locating the phase transition for each blend and BCP is outside the scope of our work. Such calculations would require advanced sampling techniques beyond the simple MC pseudo-dynamics realized in this study, as well as sophisticated finite-size scaling methods specific to first-order phase transitions.⁷³⁻⁷⁵ However, we need to estimate a region of χ-values where we can assume that the disordered phase is stable in our simulations.

We approximate the boundary of the region of bare χ-values where the disordered phase can be considered as stable in our simulations by the value of the bare χ at the MF spinodal, χ_s. To determine χ_s, we calculate within RPA the structure factor of composition fluctuations. In these RPA calculations, the polymer architecture is described with the same molecular model as in the simulations, that is, eq 1. However, to allow for analytically tractable calculations, the discrete density operators and functional of nonbonded interactions are replaced by their continuum analogs: in eqs 6 and 7, we substitute Π(r_i, c_m) by δ(r – r_i) (where r is a point in continuum space) and 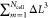by ∫dr. Most steps of our RPA calculation are standard and similar to previous studies that included compressibility effects^44,76,77 or continuum WLC architectures.⁷⁸ A summary of the RPA calculations is presented in the Supporting Information, where we also provide the final expression for the RPA structure factor, S_RPA(q,κ,χ). This expression is involved because in our compressible and asymmetric mixtures, density and composition fluctuations are coupled. One special feature of our RPA calculations is the determination of the structure factors of ideal (unperturbed) chains that enter S_RPA(q,κ,χ) (cf. Supporting Information). In RPA calculations based on Gaussian chain models, the structure factors of ideal chains are analytically expressed through appropriate Debye functions.^7,48 Because such analytical expressions are not available for our discrete WLC model, we obtain the structure factors of ideal chains numerically from a large ensemble of single chain conformations. This ensemble is generated for WLC of PPV homopolymers, polyacrylate homopolymers, and BCPs, by adjusting our MC algorithm to sample conformations of ideal chains. Specifically, for this MC sampling, we retain the bonded potential βH_b,α and deactivate the nonbonded interactions βH_nb.

RPA invokes several approximations.^13,63,79,80 Part of these simplifications occurs on small scales, where RPA neglects local correlations, for example, monomer packing, and local fluctuations, present in the statistical mechanics of the coarse-grained model. To correct^{13,63,79−81} for these local approximations, the bare parameters κ and χ entering S_RPA must be “renormalized”. Namely, the scattering in MC simulations should be approximated by S_RPA(q,κ_e,χ_e) where the effective parameters are defined through functions κ_e = κ_e(κ,χ) and χ_e = χ_e(κ,χ). The renormalized κ_e and χ_e encapsulate contributions from local correlations and fluctuations. Even with renormalized parameters κ_e and χ_e, the RPA accuracy is still limited^13,63,80 for finite chain lengths by approximations made on larger scales, such as assuming ideal chain statistics at χ = 0 and neglecting long wavelength fluctuations (essentially the MF nature of the theory). With the chosen value of bare κ, the compressibility in our simulations is already small. Therefore, we assume that κ_e ≃ κ and consider only χ_e ≠ χ. Provided that the function χ_e(χ) is known, χ_s is extracted from the divergence of the scattering, that is, from the condition 1/S_RPA(q*,κ,χ_e(χ_s)) = 0, where q* is the modulus of the wavevector at which the structure factor has a maximum.

To estimate χ_e(χ), we calculate, in our simulations, the structure factor

8

In eq 8, the Cartesian components of the scattering vectors q comply with PBC, that is, q_γ = 2πk_γ/L_box, where k_γ are integers. Angular brackets denote an average over system configurations and orientations of vector q, at given χ; accordingly, q = |q|. For each χ, we average over 10 configurations taken from 10 independent annealing runs, after the number of MC cycles becomes larger than 25 τ_rel (blends) and 10 τ_rel (BCP). Figure 2 presents 1/S(q̃*,χ) (open squares) extracted for blends and BCP, for two compositions: 1:1 (top panels) and 1:4 (bottom panels). For the blends, q̃* = 0, whereas for the BCPs, q̃* is finite. The “tilde” in the notation q̃* indicates that, in general, the location of the scattering peak in simulations and RPA is different.

Figure 2.

Structure factors (black squares) and order parameters (blue open squares) calculated from MC simulations for blends and BCPs at different dilutions indicated in each panel. Black solid lines show the RPA prediction: 1/S_RPA(q*,λχ_s), where λ is a renormalization coefficient (see main text and Figure 3). Black dashed lines indicate the location of RPA spinodals χ_s. In blend 1:1, blend 1:4, BCP 1:1, and BCP 1:4, χ_s = 0.1182, 0.1205, 0.3169, and 0.2406, respectively.

For each system, we assume that χ_e is proportional to the bare parameter χ, that is, χ_e = λχ. This simple renormalization can be understood as follows.^79,80,82 Within RPA, the average energy (per monomer) penalizing mixing of unlike monomers is reduced to a MF term of random mixing E_AB = χϕ_Aϕ_B. This MF term does not account for basic correlations that are present in the MC simulations. Importantly, random mixing neglects the fact that chain connectivity in weakly compressible polymer melts expels intermolecular monomers from the neighborhood of a test monomer and, consequently, reduces AB contacts. The prefactor λ corrects for the reduced effective coordination number of monomers. This linear renormalization of bare χ is expected to be valid⁸⁰⁻⁸² for small χ. We do not consider more sophisticated nonlinear^80,81,83,84 renormalization which might be necessary for larger χ.

The renormalization coefficient λ is extracted separately for each blend and BCP, by simultaneously fitting S_RPA(q,λχ) to a set of structure factors calculated from simulations conducted at several small χ. We start with χ = 0 and choose empirically the largest χ in the set. The choice is based on exploratory fits, taking into account that the quality of RPA deteriorates when immiscibility increases. Our fit minimizes the mean-squared error: δS² = ∑_{χ}∑_{q}[S_RPA(q,λχ) – S(q,χ)]²/N_χN_q. The first summation is performed over the set of small χ; N_χ is the total number of χ-values in this set. The second summation is performed over N_q moduli of wave vectors for which the S(q,χ) is available from simulations (for given χ). The good quality of the fits is illustrated in Figure 3a,b, considering as examples 1:1 blends and 1:1 BCP, respectively. The two panels present the original structure factors calculated from simulations (symbols) for several χ (indicated in the legends) and the fitted RPA prediction (red lines).

Figure 3.

Examples of structure factors calculated from simulations (symbols) at χ-values indicated by the legends, compared with RPA predictions (red solid lines). The latter are plotted based on an effective parameter χ_e = λχ. For each mixture, the renormalization coefficient λ is a single fit parameter extracted by simultaneously fitting the RPA result to the set of structure factors available at the different χ-values (see main text). (a) Structure factors for blends 1:1, where RPA predictions are obtained with λ = 0.734. The inset illustrates the linear relationship between 1/S(q) and q² in the regime of small q. (b) Structure factors for BCP 1:1. The RPA predictions are obtained with λ = 0.615.

In structurally symmetric systems with flexible chains, local correlations are affected by the polymerization degree N, for example, the intermolecular correlation hole becomes more shallow as N increases, so that λ is also an N-dependent quantity. For these systems, the N-dependence of λ is known.^79,80 It can be used to determine the effective FH parameter in the limit of infinitely long chains χ_e = λ_∞χ, by extrapolating a sequence of λ extracted for different N to N → ∞. For blends and BCPs as those considered in our study, such extrapolation procedures are currently not available. χ_e extracted from the procedure outlined in the previous paragraph implicitly encapsulates local effects from system-specific features such as composition, asymmetry in the molecular structure, and chain length.

In all panels of Figure 2, we present the functions 1/S_RPA(q*,λχ) (solid black line) calculated from RPA after substituting the fitted λ. Interestingly, in BCP, the RPA provides a reasonable approximation for the peak of S_RPA(q*) for immiscibilities well beyond the range of χ used to fit the entire structure factor (cf. Figure 3). The required MF spinodal χ_s is found at 1/S_RPA(q*,λχ_s) = 0 and is indicated in the panels of Figure 2 by a vertical dashed line.

3.2. Order Parameter

How reliable is our approach to assume that the disordered phase is stable in our simulations for χ < χ_s ? The answer would have been simple for symmetric systems. There, within MF, the phase transition occurs at the critical point where the MF binodal and MF spinodal touch. Because fluctuations stabilize the disordered phase, the χ at which the phase transition actually happens is larger than MF χ_s. Hence, for χ ≤ χ_s, the disordered phase is stable. The case of first-order transitions in our asymmetric systems is less straightforward. Thermal fluctuations still shift the actual binodal to higher χ, comparing to the MF binodal. However, because the MF binodal and MF spinodal are now separated by the metastability region, χ where the phase transition actually happens may still be smaller than χ_s. Such cases have been observed experimentally.⁸⁵ Therefore, the condition χ < χ_s does not guarantee the thermodynamic stability of the disordered phase, which motivates us to quantify the degree of order in our morphologies as a function of χ.

We consider the MC trajectories accumulated at every χ and calculate the order parameter⁸⁶

9

Here, angular brackets denote an average over the same configurations that were used to calculate S(q,χ). The advantage of using the order parameter ψ is its sensitivity to order:⁸⁶ in a disordered phase (where correlations are short-ranged), ψ∼V^–1, whereas in an ordered phase, ψ∼V⁰.

Figure 2a,b presents (open blue squares) ψ as a function of χ in the 1:1 and 1:4 blends. Figure 2c,d provides similar plots for the 1:1 and 1:4 BCPs. We do not display results for the 1:2 systems because they are qualitatively similar to the 1:4 case (cf. Supporting Information). In all plots, ψ increases substantially only when χ ≥ χ_s, demonstrating that we can indeed consider morphologies with χ < χ_s as disordered. Actually, we expect that in our simulations, some of the disordered morphologies near χ_s are only metastable; long-lived metastability is facilitated by the slow Rouse-like pseudo-dynamics.

As expected (cf. Introduction), Figure 2 demonstrates that blends become ordered at lower values of χ than their equivalent BCPs; in terms of actual experiments, this behavior is equivalent to PPV:polyacrylate blends becoming ordered at higher temperatures (than the BCPs). Therefore, to compare these different materials on a common basis, it is meaningful to refer the strength of segregation not to χ = 0 but to their respective MF spinodals. In the following, all results will be reported in terms of the normalized χ̃ = χ/χ_s.

3.3. Local Composition in Blends and BCP

We identify qualitative differences in the structure of disordered morphologies of our blends and BCPs by analyzing the local environment of PPV and acrylate monomers. Inspired by earlier studies^87,88 of symmetric blends and BCPs, we calculate the volume fraction ϕ_A of PPV monomers in the surroundings of each PPV and acrylate monomer. This volume fraction equals a number fraction calculated as^87,88 ϕ_A = Σ_A/(Σ_A + Σ_B). Here, Σ_A and Σ_B are, respectively, the number of intermolecular PPV and acrylate neighbors of a test (PPV or acrylate) monomer. Considering intermolecular neighbors only filters out⁸⁸ effects from trivial contributions to monomer concentration in the local environment caused by chain connectivity.

We calculate Σ_A and Σ_B by summing particles that are found in a spherical control volume centered at the test particle, that is, we sum particles that are closer than a cutoff radius, r_c. To obtain physically meaningful information on the local environment, unbiased by the sublattice structure (see discussion in Section 3.4 and the Supporting Information) we choose r_c = 2ΔL, which is larger than the lattice spacing.

Figure 4 presents the probability distribution P_α(ϕ_A) quantified around PPV (α = A, circles) and acrylate (α = B, lines) monomers. We report results for the 1:1 and 1:4 dilution (left and right panels, respectively). For each dilution, two representative segregations are considered: far (χ̃ = 0) and near the MF spinodal (χ̃ = 0.84). For χ̃ = 0 (cf. Figure 4a,b), the distributions P_A(ϕ_A) are indistinguishable from P_B(ϕ_A) in both blends and BCPs. The slight difference in the width of the distributions calculated in blends and BCPs suggests that local composition fluctuations in the former are somewhat stronger than in the latter. For χ̃ = 0 the maximum of all distributions is found at the average number fraction of PPV monomers in the system (indicated by the vertical dashed line). In Figure 4c,d, the distributions P_A(ϕ_A) and P_B(ϕ_A) become distinguishable, demonstrating that the local segregation in the disordered phase increases as χ becomes larger. This trend is consistent with previous studies.^87,88 For the more asymmetric 1:4 systems, the difference in local segregation between blends and BCPs becomes evident even from simple visual inspection of their morphologies. As an illustration, the left column of Figure 5 shows instantaneous configurations of the 1:4 blend and the 1:4 BCP, that have been considered in Figure 4d. In the BCP morphology, PPV blocks (yellow color) show a stronger tendency for clumping together, comparing to the blend. To demonstrate more clearly, the segregation in these configurations, we divide the simulation box into cubic cells with length 2ΔL, calculate the number density of PPV monomers in each cell, and extract the instantaneous density distribution. The right column of Figure 5 shows a random slice of the 3D density distribution for the blend and the BCP. We observe that the density distribution in the BCP is more heterogeneous than in the blend.

Figure 4.

Probability distributions P_α(ϕ_A) for the volume fraction of PPV monomers in a spherical volume surrounding a test PPV (α = A, circles) or polyacrylate (α = B, lines) monomer. Each of the four panels compares the distributions P_α(ϕ_A) for blends and BCPs at the same composition and normalized χ̃ value, indicated in the panel. Vertical dashed lines correspond to the average volume fraction of PPV monomers in a completely homogeneous mixture.

Figure 5.

Left column: representative configurations of a 1:4 blend (top) and a 1:4 BCP (bottom) obtained from our hybrid simulations at χ̃ = 0.84. PPV and polyacrylate chains (blocks) are colored with yellow and blue, respectively. Right column: two slices of the instantaneous 3D contour plot of the local number density of PPV monomers calculated for the configuration of the blend (top) and BCP (bottom).

For a more quantitative comparison of local environments in blends and BCPs, it is useful to consider the quantity

10

Here, we introduce an additional index to indicate the type of the material (blend or BCP) where P_A(ϕ_A) was calculated. The meaning of ΔI(ϕ_A) is transparent: it quantifies the difference between BCPs and blends in probability to observe a local volume fraction larger than ϕ_A.

Figure 6a,b shows plots of ΔI(ϕ_A) at several representative values for χ̃, for dilutions 1:1 and 1:4, respectively. The plots demonstrate that for segregations χ̃ > 0.5, the probability to observe large values of ϕ_A is higher in BCPs than in blends, for the same distance from the MF spinodal. In other words, the local segregation in the disordered morphologies of BCPs is stronger. This trend is more pronounced in the more asymmetric 1:4 mixtures [the data for ΔI(ϕ_A) obtained for the 1:2 dilution are consistent with this statement, cf. Supporting Information].

Figure 6.

Difference between BCPs and blends in probability to observe, in the surroundings of a test PPV monomer, a volume fraction of PPV monomers larger than ϕ_A, cf. eq 10. In both panels, the probability difference is denoted by ΔI(ϕ_A) and is plotted as a function of the threshold value ϕ_A. Panel (a) shows ΔI(ϕ_A) calculated for BCPs and blends with dilution 1:1 found at the same normalized χ̃, indicated by the legends. Panel (b) is similar to (a) but refers to BCPs and blends with dilution 1:4.

Finding stronger local segregation in disordered BCPs than in blends (at the same χ̃ and dilution) suggests that in the latter, the effect of electron trap alleviation by blending may be more pronounced than in the former. However, we emphasize that the MH relation for the trap-limited current density⁵ (cf. Introduction) is not sufficient for verifying this hypothesis. Although the MH model has served to explain in what way a trap-limited current in an organic semiconductor is enhanced by spatially separating transport and trap sites,^4,6 it remains to be a macroscopic theory. By construction, it considers only the global average of the semiconductor concentration and overlooks any effects related to local inhomogeneities in composition.

3.4. Percolation Analysis

In this section, we identify structural differences between disordered blends and BCPs concerning the spatial distribution of the charge-conducting PPV component over large scales. Our approach attempts to establish a qualitative link to electric conductivity. The analysis assumes that we are dealing with solid-state structures corresponding to vitrified instantaneous configurations of an annealed morphology. Whenever we refer to χ, we implicitly mean the value of χ (equivalently the temperature) at which annealing was performed. Because we are interested in disordered morphologies, we focus on the range 0 ≤ χ̃ ≤ 1.

We identify conducting clusters of PPV monomers through a percolation analysis based on quantitative charge transport models.⁸⁹⁻⁹¹ First, we take into account that our PPV homopolymers (blocks) are semiflexible because they are only slightly longer than a single PPV Kuhn segment. Considering the restricted conformational freedom, we make the approximation that there are no conjugation breaks along the entire PPV backbone of the homopolymers or blocks. Therefore, each PPV homopolymer (block) is a single charge-carrier transport site. Within this picture, electric conductivity is limited only by factors disrupting interchain charge transfer. To group transport sites into conductive clusters, we postulate that charges can hop between two PPV homopolymers (blocks) only if the minimum distance between these homopolymers (blocks) is smaller than a hopping threshold d. With this criterion in hand, it is straightforward to identify the conductive clusters using an “ants-in-labyrinth” algorithm⁹² with PBC. We determine the minimum distance of two PPV homopolymer (blocks) by comparing the distances within all possible intermolecular pairs formed by their monomers.

From the perspective of the Miller–Abrahams model,⁹³⁻⁹⁷ it is tempting to interpret d as a characteristic cutoff distance at which the charge tunneling probability between two conjugated segments has exponentially decayed to an extent that they can be considered as electrically decoupled.⁹⁸ However, the nanoscale structure of morphologies in our model and real materials differs significantly because of drastic coarse graining, soft potentials, and grid-based calculation of interactions. Therefore, it is not meaningful to quantitatively compare d at which percolation occurs in our samples with length scales typical to charge transport in real systems, such as the localization length.⁹⁹d should rather be seen as a phenomenological parameter. Still, we can quantify similarities or differences across morphologies, for example, by systematically comparing the properties of conducting clusters identified at a value of d which is fixed across different systems.

We focus on the spanning probability, P_s, and percolation probability, P_c. A cluster is classified as spanning when it connects two opposite sides of the sample, at least, along one of the three Cartesian directions. The spanning probability is calculated as the frequency of observing a spanning cluster in a set of independent morphologies obtained for a fixed set of system parameters, that is, class of material (blend or BCP), degree of dilution, and χ. Specifically, P_s = n_s/n_o where n_s is the number of spanning clusters observed in n_o independent simulations. The error in estimating P_s is given by¹⁰⁰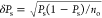. We follow the customary convention of the percolation theory¹⁰¹ and define P_c as the probability that a randomly picked PPV bead belongs to a spanning cluster. That is, P_c = N_s/N_A(tot), where N_s is the number of PPV beads forming the spanning cluster.

Percolation transitions are subjected to finite system size effects.⁷⁴ In an infinite system, P_s is a step function of the geometrical parameter controlling percolation, that is, P_s is zero or unity, whereas in finite systems it grows and saturates smoothly around the percolation threshold. In this work, we are explicitly interested in a percolation analysis that includes effects of a finite system size because (as has been elaborated previously) PLED layers themselves have finite dimensions, especially in the vertical coordinate.

Figure 7a–d presents contour plots quantifying P_s as a function of d and χ̃ for blends and BCPs. Mixtures with weight fraction 1:1 are presented in Figure 7a,c while the 1:4 case is addressed in Figure 7b,d. For each (d, χ̃) pair, P_s has been extracted from 10 independent morphologies. The resolution of the color map is consistent with the error estimate δP_s. For each fixed χ̃, P_s varies with d as expected. Small d lead to P_s = 0, that is, the systems are always nonconducting, whereas a large d results in P_s = 1, that is, the systems are always conducting. Between the two extremities, there is a rather narrow region of d-values where 0 < P_s < 1. In our contour plots, this region is indicated by the multicolored band and stems from finite system size effects.

Figure 7.

Contour plots quantifying the probability, P_s, to observe a spanning PPV cluster in disordered blends and BCPs as a function of normalized χ̃ and hopping threshold d. Blue and red colors correspond to low and high probabilities, respectively. The type of the mixture is indicated at each panel.

For χ̃ = 0, the percolation transition in our blends and BCPs occurs at about the same value for d, provided that the degree of dilution is the same. This trend is consistent with the local environment analysis for χ̃ = 0 (cf. Figure 4a,b) where the distribution P_A(ϕ_A) in blends was found to be only marginally broader than in their corresponding BCPs. However, P_s behaves qualitatively different for blends and BCPs when χ̃ > 0. In blends, we observe that the position of the d-boundary, separating nonconducting and conducting regimes, changes with χ̃ only weakly. In contrast, for the BCPs, the boundary shifts substantially toward smaller d, as χ̃ increases to reach χ̃ = 1. This effect is particularly evident for the 1:4 BCP, where the boundary shifts between χ̃ = 0 and χ̃ = 1 by about 15%. These qualitative differences in the behavior of P_s in blends and BCPs are consistent with our conclusions from Figures 4 and 6 that disordered blends are locally less segregated than BCPs (as χ̃ increases toward χ̃ = 1). The observation that increasing χ̃ strongly promotes the formation of a percolating PPV phase in BCPs is consistent with the build-up of a disordered fluctuating network-like morphology.^23,24

In Figure 7a–d, all changes in percolation occur for d ≪ ΔL. PM schemes are characterized⁵⁹ by artificial packing of material below the smallest physical scale of the model ΔL, manifested by density variations within individual grid cells. For our model, the sublattice structure is quantified in the Supporting Information. To verify that the observed trends do not originate from the model-specific sub-lattice polymer packing but stem from generic physical mechanisms, we performed an alternative, more coarse-grained, percolation analysis.¹⁰² As elaborated in the Supporting Information, this analysis involves length scales larger than ΔL and excludes, therefore, artefacts from sublattice polymer packing. The percolation behavior extracted from the coarser analysis is fully consistent with the trends reported in Figure 7a–d (cf. Supporting Information).

Although d acts in Figure 7a–d as an adjustable phenomenological parameter, we can make qualitative estimates concerning effects of annealing temperature on the conductance of disordered PLED layers, prepared in experiments. Namely, the weak dependence of percolation threshold on χ̃ in blends suggests the following hypothesis. Suppose that the concentration of insulating polymer is such that there is no flow of current through active layers prepared by annealing the blend at a given temperature. Then, it is unlikely that macroscopic conductance will be recovered by preparing the layers at lower annealing temperatures (but still above the phase transition). The situation in BCPs is radically different. Because increasing χ̃ substantially reduces the maximum hopping length required for percolation, annealing these materials at lower temperatures may recover conductance. The practical consequence of the finite system size effects on the percolation transition in both blends and BCPs (multicolored bands in Figure 7) can be understood as follows: if, because of materials parameters or processing conditions, PLED layers are found near a percolation transition, their electronic properties may not be reproducible: conducting and nonconducting samples will be randomly mixed within a single batch.

Further differences in percolation properties of disordered blends and BCPs are found by comparing percolation probabilities. Figure 8a,b present P_c as a function of χ̃ in blends and BCPs for dilutions 1:1 and 1:4, respectively. P_c is calculated from the continuum-space percolation analysis setting the hopping thresholds to d = 0.26 nm (dilution 1:1) and d = 0.38 nm (dilution 1:4). These choices ensure percolation even when χ̃ = 0 (cf. Figure 7a–d). For all compositions, the plots in Figure 8a,b demonstrate that P_c in BCP is larger than in blends, when the strength of the segregation in the disordered phase is (approximately) χ̃ > 0.4. For the more asymmetric compositions, the situation reverses in the region of weaker segregation χ̃ < 0.4. There, the percolating clusters in blends are somewhat larger than those in BCP. We have verified that P_c calculated from the lattice-based percolation analysis show similar trends.

Figure 8.

Percolation probability, P_c, plotted as a function of normalized χ̃. P_c is obtained from continuum-space percolation analysis for (a) 1:1 and (b) 1:4 blends and BCP. Error bars correspond to standard deviation from the mean value. The hopping threshold d used to calculate P_c is indicated on each panel.

We remind that in our simulations blends and BCPs, at the same dilution, have the same physical size and number of particles. Therefore, they are compared in Figures 7 and 8 on equal basis, as far as finite system size effects are concerned. We performed the same analysis for systems with box sizes L = 5 R_e and 7 R_e. As expected, increasing L makes the percolation transitions sharper; the multicolored bands in Figure 7 become narrower. At the same time, the overall shape of the boundary between blue (nonpercolating) and red (percolating) areas is conserved. In other words, increasing the system size does not change our conclusions, provided that L stays on the scale of ∼100 nm.

4. Summary and Outlook

We performed mesoscopic computer simulations of disordered morphologies of blends of semiconducting and insulating homopolymers and their equivalent BCP melts. Polymers were coarse-grained into discrete WLCs, and nonbonded interactions were introduced through a quadratic, generic functional of instantaneous local densities of monomers of different chemical species. The functional accounts for limited compressibility and repulsion between unlike monomers. The strength of repulsion is controlled by a bare⁶³ FH-like parameter, χ. We transformed the functional-based definition of interactions into particle-based potentials via a simple PM scheme⁴⁴⁻⁴⁷ and sampled the configurational space with local MC moves that realize Rouse-like pseudo-dynamics. The model was parameterized to mimic characteristic conformational and volumetric properties of PPV and polyacrylates—two typical families of semiconducting and insulating polymers relevant to PLED applications.

The hybrid approach enabled the simulation of samples with dimensions on the order of 100 nm, which is the typical thickness of active layers in an actual PLED, for a broad range of χ-values. We found that for the Rouse-like pseudo-dynamics used in our simulations, the disordered phase is stable or metastable for 0 ≤ χ < χ_s. The upper boundary χ_s is the MF spinodal obtained from the standard RPA theory, which we adapted to the specific features of our model: WLC architecture and compressibility. We analyzed the structure of the disordered morphologies on local and more global scales, focusing on the spatial distribution of the electrically active PPV component.

Structural analysis demonstrated the local heterogeneity of disordered morphologies because of thermal fluctuations in composition, as well as segregation of PPV and polyacrylate monomers. We found that the local segregation near the MF spinodal is stronger in BCPs than in the equivalent blends. This qualitative difference between blends and BCP is stronger for higher compositional asymmetries, that is, higher fractions of insulating homopolymers or blocks in the mixture. Our BCP did not show a clear tendency to form spherical domains at high χ because the surplus of acrylate was not sufficiently high. Therefore, we cannot conclude whether the observed difference between BCP and blends persists for very asymmetric compositions. In this case, BCPs can micellize in the disordered phase.^8,23,103,104

Our observations on the heterogeneity of disordered morphologies highlight the phenomenological character of effective medium charge-transport models⁴ based on the MH formalism.⁵ These models only yield effective transport and trap site densities when fitted against experimental current–voltage data. However, global averaging of composition in combination with a one-dimensional drift-diffusion model is insufficient to explain how a reduction in trapping depends on local morphological details of the active layer of the PLED. The present mesoscopic description of morphologies could be combined with an advanced model for charge-carrier dynamics^97,105−107 to provide for a more appropriate description of the effect of composition heterogeneity on trap elimination. Such a model is necessary because a nonhomogeneous composition automatically leads to spatial inhomogeneities in charge distribution, local electric field, and hence, carrier mobility.

Instead of employing sophisticated models of charge-transport, we used a simplified percolation analysis to qualitatively link the global distribution of the PPV component with macroscopic electric conductance. Strikingly, we found that the χ—equivalently the temperature—at which the disordered morphology is annealed prior to solidification, has a stronger influence on electrical percolation in BCPs than in their equivalent blends. Specifically, if there is no flow of current through a disordered BCP morphology prepared by annealing at low χ (high temperatures), it might be still possible to recover conductivity by preparing the morphology at higher χ (lower temperatures) which are near (but do not cross) the ODT. For an equivalent blend, it is less likely that one can switch between conducting and nonconducting morphologies simply by changing the χ (temperature) of annealing. Similar to local segregation, the differences between blends and BCPs with respect to their electrical percolation increase as the compositional asymmetry of the mixture becomes larger. The percolation analysis also suggests an unexpected consequence of finite size effects related to the limited thickness of active layers. Because finite size effects smoothen the percolation transition, the macroscopic current conductance of layers annealed under conditions, for example, temperatures, close to this transition may be erratic.

Here, we considered isotropic systems and neglected the confined film geometry of actual PLED layers. Even in disordered polymer blends and BCPs, confinement profoundly affects the microstructure: the boundaries of the film modify polymer conformations and are usually enriched in one component. Of course, conjecturing local environment and percolation properties in these anisotropic regions from “bulk-like” systems is not valid. However, we believe that our analysis can provide useful insights into structural differences between blends and BCPs in the interior of PLED layers, that is, their bulk-like part. The part of the layer that can be considered as bulk is largely determined by the decay of compositional perturbations into the film, characterized^108−110 by a correlation length ξ. The quantity ξ relates directly^108−110 to the correlation length of bulk composition fluctuations and is, therefore, proportional to the size of the chains quantified, for example, by the average end-to-end distance, R_e. The prefactor in this proportionality depends on the incompatibility of unlike monomers—for symmetric systems, within MF,^108,111 ξ diverges as one approaches^108,109,111 the phase transition. For strongly asymmetric systems (the focus of our work), simulations¹⁰⁹ suggest that the changes of ξ as a function of incompatibility are less pronounced. For conjugated polymers similar to those considered in our study, the typical thickness of PLED layers is equivalent to several R_e. Therefore, for thermodynamic conditions away from the phase transition, we expect these layers to have an extended bulk-like region. At higher χ, the isotropic approximation for the interior of the layers deteriorates for symmetric systems (because of the significant increase of ξ) but might be still reasonably accurate for the application-relevant case of asymmetric blends and BCPs.

The model described in this study can be extended^44,46,112 to include free polymer surfaces and polymer/solid interfaces. This extension will allow for a more realistic mesoscopic description of PLED layers at comparable costs of computation. However, we emphasize that explicit considerations of film geometry will significantly expand the parameter space. Indeed, interfacial phenomena, for example, surface segregation and conformational changes, are driven by a complex balance¹¹³ between various entropic and enthalpic factors, which change across different systems. Therefore, the choice of the relevant parameters of the model, for example, the strength of effective interactions with film boundaries becomes much more material-specific. Inevitably, the scenarios that can be considered at each simulation study are rather limited.

Our modeling results suggest that, from a fundamental point of view, it is of interest to study the electronic behavior of blend- or BCP-based devices of which the active layer has been processed in the disordered phase near the phase transition. To our knowledge, such studies are currently lacking. Structure–conductivity relationships on both sides of the phase transition have been explored experimentally for other polymer-based systems, such as ion-conducting mixtures.¹¹⁴

The summarized results illustrate the kind of material-design questions that can be addressed by mesoscopic models of mixtures containing semiconducting polymers. Generally, for many types of devices in organic electronics, the active layer comprises a mixture of (at least) two functional species, whether or not covalently linked. For instance, these species can be a semiconductor and an insulator, an electron donor and an electron acceptor, a semiconducting and a ferroelectric polymer, or a host and a dopant or energy transfer dye. The optimal morphology of such multicomponent active layers depends on the operational characteristics of the device. Whereas some rely on intimate contact between the components, for example, if efficient charge transfer is a dominating prerequisite, others require a morphology compatible with processes occurring on mesoscopic length scales, such as exciton diffusion or local electric field modulation. Lastly, because device operation typically relies on charge transport at macroscopic length scales, long-range electrical percolation between “active units”, for example, conjugated segments, usually is essential.

Therefore, to evaluate the suitability of morphology based on a certain mixture for a specific device application, one requires reasonable estimates of spatial distributions of functional components on meso- and macroscopic length scales. Our mesoscopic model serves this purpose. It enables generation, analysis, and comparison of morphologies¹¹⁵ not only as a function of mixture composition but also as a function of chain architecture and polydispersity.

In relation to our current findings, we note that the nontrivial structure of disordered BCP morphologies, especially close to ODT, makes them potentially interesting for other devices. For instance, the motivation of using donor(D)–acceptor(A) BCPs,^116,117 or BCP compatibilizers¹¹⁵ in organic photovoltaic (OPV), has focused on ordered phases, following the philosophy of obtaining thermodynamically relaxed microstructures that provide for stable domains with dimensions commensurate with the exciton diffusion length.^116,117 However, despite exhibiting enhanced thermal stability compared to classical blends, such BCP-based OPV cells have never outperformed blend-based devices. With this respect, so far, possible advantages of stabilized disordered D–A BCP morphologies near the ODT have not been explored.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.9b02402.

• Results for effects of stiffness of the link between blocks in BCPs; details of RPA calculation and structure factors; details on sublattice polymer packing; alternative lattice-based percolation analysis; and results for blends and BCPs at dilution 1:2 (PDF)

The authors declare no competing financial interest.