Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 27;14(5):5337–5347. doi: 10.1021/acsnano.9b07820

Temporal Evolution of Superlattice Contraction and Defect-Induced Strain Anisotropy in Mesocrystals during Nanocube Self-Assembly

Martin Kapuscinski †,*, Michael Agthe ‡, Zhong-Peng Lv †, Yingxin Liu †, Mo Segad †, Lennart Bergström †,*
PMCID: PMC7343289  PMID: 32338498

Abstract

graphic file with name nn9b07820_0007.jpg

Understanding and controlling defect formation during the assembly of nanoparticles is crucial for fabrication of self-assembled nanostructured materials with predictable properties. Here, time-resolved small-angle X-ray scattering was used to probe the temporal evolution of strain and lattice contraction during evaporation-induced self-assembly of oleate-capped iron oxide nanocubes in a levitating drop. We show that the evolution of the strain and structure of the growing mesocrystals is related to the formation of defects as the solvent evaporated and the assembly process progressed. Superlattice contraction during the mesocrystal growth stage is responsible for the rapidly increasing isotropic strain and the introduction of point defects. The crystal strain, quantified by the Williamson–Hall analysis, became more anisotropic due to the formation of stress-relieving dislocations as the mesocrystal growth was approaching completion. Understanding the formation of the transformation of defects in mesocrystals and superlattices could assist in the development of optimized assembly processes of nanoparticles with multifunctional properties.

Keywords: self-assembly, nanocube, mesocrystal, time-resolved SAXS, strain anisotropy, defect, superlattice contraction

Assembly of nanoparticles into superlattices or mesocrystals is a promising pathway to produce nanostructured materials with tunable properties.1−4 Superlattices that display not only a long-range translational order but also atomic coherence, i.e., mesocrystals, are materials with unique properties that are attractive for optoelectronic and biomedical applications.5−9 Assembly of polyhedral nanocrystals into structurally diverse mesocrystals is controlled by the composition, size, and shape of the nanoparticles and the conditions during assembly.5−7 Several methods are used to assemble nanoparticles, with the evaporation-driven increase of the particle concentration being the most widely used.10−12

Significant advances in the synthesis of nanoparticles with well-defined sizes and shapes and optimization of the assembly conditions have generated superlattices and mesocrystals with an impressive structural diversity.1,13,14 Investigations on how defects evolve and how they influence and modulate the structure and properties of self-assembled superlattices have, however, been less frequent and limited to studies on close-packed arrays of spheres. For instance, studies on colloidal crystals of micron-sized spheres have shown that defects such as vacancies, dislocations, and grain boundaries can generate nonlinear stress fields that affect the mechanical properties of the ordered assemblies.15 Schall et al. used laser diffraction microscopy in combination with nanoindentation to probe the stress-induced nucleation and dynamics of dislocations in face-centered cubic (fcc) colloidal crystals.16,17 It has also been shown that premelting, i.e., melting of colloidal crystals below the bulk melting temperature, occurs at grain boundaries and dislocations.18 Studies on defects in superlattices of several hundred nanometer large spherical particles have shown that stacking faults of fcc and hexagonal close-packed opals can influence the photonic band structure,19 and anisotropic strain can break the lattice symmetry and induce a transition from an fcc to a monoclinic opal phase, which allows formerly forbidden scattering peaks to appear.20

Ex situ electron microscopy has been used to probe various types of defects in CdSe nanorod liquid crystals grown at the interphase of a subphase,21 in solution22,23 or on a substrate24 and in thin quasicrystalline and periodic, binary superlattices of spherical particles that were grown on a carbon substrate.25,26 Mayence et al. used 3D small-angle electron diffraction tomography to show stacking faults in spherical Pd nanoparticle superlattices and made analogies to dislocations in close-packed metals.27 Time-resolved small-angle X-ray scattering (SAXS) and grazing-incidence SAXS (GISAXS) have previously mainly been used to give insight into the structural evolution of mesocrystals.10,13,28,29 Mirkin and co-workers showed in a SAXS study that annealing DNA-capped gold nanoparticle superlattices close to their melting temperature resulted in a reduction of the microstrain and increased domain size.30 Probing defects in superlattices of anisotropic nanoparticles in real time, which display shape-dependent properties and produce superlattices with a much larger structural diversity than spherical nanoparticles,31 is unexplored.

Here, we have used SAXS to study the temporal evolution of strain and structure during evaporation-induced self-assembly of superparamagnetic magnetite nanocubes (NCs) with edge lengths of 6.8 nm (NC068) and 9.1 nm (NC091) in an evaporating levitating droplet. We used the Gualtieri equation32 to estimate the nucleation and crystal growth rate and showed that the assembly of the NCs in the shrinking levitating drop is diffusion-controlled. Analysis of the time-resolved SAXS data by the Williamson–Hall (WH) method33 showed that lattice contraction and infrequent size mismatch resulted in an increasing isotropic strain during the mesocrystal growth stage. The crystal strain became more anisotropic and resulted in the formation of dislocations toward the end of mesocrystal growth.

Results and Discussion

We used time-resolved SAXS to follow the formation and growth of mesocrystals of superparamagnetic magnetite NCs by evaporation-driven self-assembly in a levitating drop that slowly shrinks as the solvent evaporates (Figure 1).34 We used an acoustic levitator (Figure 1a) to trap a colloidal droplet between two pressure nodes of an acoustic standing wave that is created between a sonotrode and a reflector (Figure 1b), which allows mesocrystal formation to be investigated in a substrate-free environment.35−37 The colloidal dispersions contained oleic-acid-capped, truncated magnetite NCs (Figure 1b and Figure S1) with edge lengths of 6.8 (NC068) or 9.1 nm (NC091). The NCs were dispersed in a 3:1 toluene/decane mixture at a concentration of 3 mgmagnetite mL–1. The relatively slow evaporation of the toluene/decane mixture, which is significantly slower than pure toluene,34 in combination with the high time resolution of the SAXS instrument (ID02, ESRF), allowed us to probe and analyze in detail the evolution of size and strain during the different stages of mesocrystal formation and growth.

Figure 1.

Figure 1

Open in a new tab

Schematic overview of the experimental setup and representative time-resolved SAXS data. (a) Experimental setup showing the acoustic levitator, a microscope camera, the incoming X-ray beam, and the scattered X-ray beam, which was detected simultaneously by a wide-angle X-ray scattering (WAXS) and a SAXS detector. (b) High-resolution transmission electron microscopy images of NC068 and NC091 (scale bars = 5 nm) and schematic illustration and images of the shrinking droplet levitated between two pressure nodes of the standing ultrasonic wave (blue curve). (c) Excerpt of time-resolved SAXS data showing the different stages of mesocrystallization of iron oxide NCs with edge lengths of 6.8 nm (NC068). The crystallization process consists of three stages, where the NCs are in dispersed (purple), clustered (red), and crystalline states (blue). SAXS data of assembled mesocrystals (MC) of (d) NC068 (MCNC068) and (e) NC091 (MCNC091).The orange lines indicate the peak positions of a simple cubic superlattice, and the purple lines correspond to the peak positions of a face centered cubic structure.

The intensity I(q) of X-rays scattered at a small angle relate to the structural properties of the nanoparticles and the interaction and correlation between them, which is commonly formalized as the product of the form factor P(q) and the structure factor S(q); I(q) = P(q)S(q). The SAXS patterns of dilute dispersions of NC068 and NC091 displayed only form factor contributions to the scattered intensity, suggesting that the NCs were well-dispersed and did not form aggregates at low particle concentrations (Figure 1c, purple curves). The nanocube sizes and polydispersities were estimated by fitting a cubic model to the form factor, giving values of 6.8 ± 0.3 nm for NC068 and 9.1 ± 0.5 nm for NC091 (Figure S2), which corresponds very well to the edge lengths measured with transmission electron microscopy.10,11 The deviation from the cuboidal model at low scattering angles in the SAXS patterns measured in the levitating drops at times exceeding 1180 and 800 s for the NC068 and NC091 dispersions, respectively, indicates that clusters were formed in the shrinking levitating drops (Figure 1c, red curves). The absence of any structural peaks suggests that the NC clusters were disordered. Increasing the particle concentration by the evaporation-driven shrinkage of the levitating droplet eventually resulted in the formation of NC assemblies with both positional and orientational long-range order, i.e., mesocrystals (MCs), as indicated by the sharp diffraction peaks in the small-angle (low q) regime (Figure 1c, blue curves). The structural 100 peak of the mesocrystal was first observed after 1294 and 910 s for MCNC068 and MCNC091, respectively. In the following discussion, the time for the first observation of a structural peak, i.e., when mesocrystals are first formed, will be designated as tMC.

Indexing the reflections in the small-angle regime showed that both NC068 and NC091 crystallized in a simple cubic (SC) structure (Figure 1d,e). The mesocrystal MCNC068, however, exhibited a second crystal phase, where the NCs also assembled into an fcc structure. The SC phase appeared to be dominant based upon the more well-pronounced peaks compared to the fcc phase and the fact that the structural 100 peak of the SC lattice was observed first. The lattice parameter aSC of the SC structures of MCNC068 and MCNC091 were aSC,MCNC068 = 10.8 nm and aSC,MCNC091 = 12.9 nm, which corresponds well to the edge length of the constituent NCs, including the oleic acid length of 2 nm38 bound to each nanocube facet in a face-to-face orientation of the NCs. For the fcc structure of the mesocrystals MCNC068, we found afcc,MCNC068 = 16.0 nm.

The partial scattering invariant Q*, obtained from the integral 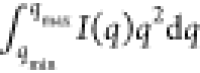Inline graphic over 0.035 < q < 3.74 nm–1, increased with increasing volume fraction of the NCs in the shrinking droplet (Figure 2). Similar to previous studies on the assembly in shrinking levitating drops,34 we observed a maximum and subsequent decrease of Q* with time. The time when Q* reaches its maximum value corresponds well to tMC, i.e., the time when the first structural peaks appeared (Figure 2). The subsequent decrease of Q* suggests that the nanoparticle volume fraction decreased in the irradiated volume of the shrinking droplet, which may be attributed to an accumulation of mesocrystals at the liquid–air interface.34 The critical volume fractions of the NCs at tMC could be estimated from the initial particle concentration and the droplet size and were ϕC,NC068 = 0.171 ± 0.003 (Figure 2a) and ϕC,NC091 = 0.066 ± 0.008 (Figure 2b), respectively. The higher volume fraction necessary to initiate the formation of mesocrystals of the smaller NCs (NC068) compared to the larger NC091 corresponds to smaller average interparticle center-to-center distances for the beginning of mesocrystal formation of 19.5 nm for NC068 compared to 33.5 nm for NC091. The self-assembly process is a two-step process where the formation of ordered mesocrystals is preceded by clustering, as reported previously and discussed in more detail later. The average center-to-center distances between two nanocubes at the time when clustering was observed (Figure 1c, red curves) are about 24.5 and 39 nm for NC068 and NC091, respectively (Figure S3). The lower center-to-center distance necessary to induce clustering and crystallization for the smaller nanocubes can be attributed to the weaker interparticle van der Waals interactions.

Figure 2.

Figure 2

Open in a new tab

Partial scattering invariant Q* (red circles) and volume fraction of iron oxide ϕNC (blue squares) during evaporation-driven self-assembly of (a) NC068 and (b) NC091. The vertical black line indicates the beginning of mesocrystal formation, tMC.

We used the WH method to probe the temporal evolution of the size of the growing mesocrystals and the defect-induced strain within the mesocrystals during self-assembly.33 Williamson and Hall assumed the peak width to be a sum of the contributions from microstrain and crystallite size in the form

graphic file with name nn9b07820_m002.jpg 1

Here, qC is the peak position in reciprocal space, D is the mean crystal size, K is a shape factor, which is given a value of 0.9, and ε is the apparent strain defined as ε = Δd/d̅, where Δd is the distribution of interplanar spacings, and d̅ is the average interplanar spacing. The peak width, w, is defined as the full width at half-maximum. In order to determine w and qC, we fitted the structural reflections of the SC structures of MCNC068 and MCNC091 with pseudo-Voigt functions of the form y = y0 + A[μL(x) + (1 – μ)G(x)], where y0 is the baseline, A the amplitude, and L(x) and G(x) represent the Lorentzian and Gaussian parts of the function with their corresponding fractions μ and (1 – μ), respectively. Plotting w against qC should result in a linear relationship according to eq 1, where the microstrain and the crystallite size are related to the slope and the intercept with the ordinate, respectively.

We have also evaluated crystal growth using the Gualtieri equation, which treats the increase of a fraction α of a crystalline phase as a combination of nucleation and crystal growth:32

graphic file with name nn9b07820_m003.jpg 2

where a is the reciprocal of the nucleation rate constant, kN = 1/a, b is a parameter related to the mechanism of nucleation, kg is the crystal growth rate constant, and the exponent n is related to the dimension of crystal growth. The probability PN that a number of nuclei N are formed at a time t – tMC is described by

graphic file with name nn9b07820_m004.jpg 3

During the early growth stage for MCNC068, the WH plots of the h00 and h1l reflections displayed an overlapping linear behavior (Figure 3a), which indicates isotropic microstrain and crystallite dimensions. The linear fits of the h00 and the h1l peaks in the WH plot differed significantly for the first time about 96 s after structural peaks first appeared (Figure 3b). Due to the lack of well-pronounced higher orders of the h1l reflections (110, 111, 210, 211; Figure 1d), a precise statement of the crystallite dimensions and microstrain along any other specific direction than ⟨100⟩ is not possible; thus, these four reflections are considered together using the notation h1l. The different slopes of the linear fits of the h00 and the h1l peaks indicate anisotropic strain, and the difference increased as the mesocrystals grew (Figure 3c). Typical defects known to induce anisotropic peak broadening in crystals are edge and screw dislocations.39 The difference in the slopes of the linear fits (solid and dashed line in Figure 3b,c) indicate that microstrain is lower along the ⟨100⟩ direction compared to the ⟨h1l⟩ direction. Further, the h11 (111, 211) peaks were separated from the h10 peaks (110, 210) in the WH plot (Figure 3c), indicating different strain and size along these directions.

Figure 3.

Figure 3

Open in a new tab

Williamson–Hall analysis of time-resolved SAXS patterns of growing mesocrystals: (a–c) MCNC068 (red squares) and (d–f) MCNC091 (blue circles). The h00 and h1l reflections are displayed as filled and empty symbols, respectively. Linear fits for h00 and h1l reflections of MCNC068 at different times after structural peaks first appeared, t – tMC: (a) 36 s, (b) 96 s, and (c) 384 s. Linear fits for h00 and h10 reflections of MCNC091 at t – tMC: (d) 8 s, (e) 49 s, and (f) 145 s.

The WH plots of MCNC091 (Figure 3d–f) show that the separation of the h00 (100, 200) from the h10 peaks (110, 210) in the WH plot is observable already at the early growth stage (Figure 3d). Due to the lack of well-pronounced higher-order diffraction peaks for the MCNC091 system (Figure 1e), the slopes and intercepts of the WH plots are only indicative; however, both the h00 and h10 peaks showed slopes close to zero, indicating that microstrain was insignificant during the initial stage of mesocrystal growth. Hence, the peak broadening is expected to be mainly caused by the formation of anisotropic mesocrystals. Isotropic strain was induced during the later stages of the growth process, as indicated by the higher but parallel slopes and decreasing intercepts of the WH plots (Figure 3e), whereas the difference of the slopes of the linear fits of the h00 and h10 peaks, as the mesocrystals continue to grow (Figure 3f), may indicate the presence of anisotropic strain during the final stage of mesocrystal growth.

Figure 4a shows that the time-dependent increase of the crystallite size, D, determined from the intercepts in the WH plots, corresponds well to the increasing fraction of crystalline phase during the MCNC068 mesocrystal growth stage, estimated from the normalized time-dependent peak area, A100. The mesocrystal growth stage, which is defined as the time from the first observation of the structural 100 peak until A100, shows no further increase (tA100,max – tMC) and lasted 66 s, and its duration is indicated by the red solid line in Figure 4a. The probability for nucleation, PN (Figure 4a, purple line), which was estimated by fitting the temporal evolution of A100 with the Gualtieri equation (eq 2) (Figure 4a, black line), peaks at around 25 s and covers a significant part of the mesocrystal growth stage of MCNC068. The volume-weighted domain size D increases constantly throughout the growth process (Figure 4a), including the period before and after 25 s, where the nucleation probability is predicted to peak, which suggests that the growth of the already formed mesocrystals dominates over the formation of new, small mesocrystals.

Figure 4.

Figure 4

Open in a new tab

Temporal evolution of the size, lattice parameter, and strain of the growing mesocrystals MCNC068 and scanning electron microscopy images of the generated mesocrystals. (a) Gualtieri fit (black line) of the normalized peak area A100 (blue squares) and the resulting probability for nucleation PN (light purple line, eq 3). The crystallite size, D, along ⟨100⟩ (dark purple circles) and ⟨h1l⟩ (open orange circles) was obtained from the intercepts of the linear fits in the WH plots. (b) NC separation distance d100 (black triangles), calculated as d100 = 2π/qC, and microstrain ε along ⟨100⟩ (dark purple diamonds) and ⟨h1l⟩ (open orange diamonds) obtained from the slopes of the linear fits in the WH plots. The end of the mesocrystal growth stage (red solid lines) and the end of lattice contraction (red dashed line) are marked in both (a) and b). (c) Scanning electron micrograph of the resulting mesocrystals. Spherical, partly hollow mesocrystals were produced, as observed from the cross section of a spherical mesocrystal. (d) Magnified image displays well-ordered NCs in the mesocrystal, as indicated by the fast Fourier transform (inset) but contains a large number of vacancies.

The microstrain ε (Figure 4b), obtained from the WH analysis, of MCNC068 increased but remained isotropic during the mesocrystal growth stage. The crystallite size along ⟨100⟩ and ⟨h1l⟩ were similar throughout the postgrowth stage, indicating that the mesocrystallites were isotropic, which was corroborated by scanning electron microscopy (SEM) (Figure 4c), showing that the MCNC068 mesocrystals were spherical and displayed a high degree of order (Figure 4d, inset); however, the mesocrystal also contains a large number of vacancies, as seen from the cross section (Figure 4d).

The microstrain ε along ⟨100⟩ decreased much more than along ⟨h1l⟩ during the postgrowth phase, which shows that the relaxation of the strain was anisotropic (Figure 4b). The NC separation distance d100 (i.e., the lattice constant; calculated by d100 = 2π/qC,100, with qC,100 being the 100 peak position) in the mesocrystal attained its maximum value at the beginning of the mesocrystal growth stage and then decreased as the mesocrystals grew. The lattice parameter for the mesocrystals continued to contract after the mesocrystal growth stage has ended (Figure 4b). The contraction of the MCNC068 mesocrystals reached a steady state with unchanged d100, ε, and D about 225 s after the structural 100 peak was first observed, as indicated by the red dashed line in Figures 4a,b.

The temporal evolution of the size, lattice parameter, and strain of the growing mesocrystals MCNC091 (Figure 5a,b) differed significantly from the growth and subsequent contraction of the mesocrystals assembled from smaller nanocubes, MCNC068 (Figure 4). The mesocrystal growth stage is more than twice as long for MCNC091 (145 s) than for MCNC068 (66 s). The crystallite size D of MCNC091 differed significantly along ⟨100⟩ and ⟨h10⟩ at all times, which shows that the mesocrystals are anisotropic throughout the mesocrystal growth and contraction stage. Indeed, SEM showed (Figure 5c and Figure S4) that cuboidal mesocrystals were formed with dimensions in relatively good agreement with a D value along ⟨100⟩ of about 500 nm for the fully grown (and contracted) mesocrystals (Figure 5a). The mesocrystal displays, despite being well-ordered (Figure 5d, fast Fourier transform inset), many surface defects, such as vacancies, kinks, and steps.

Figure 5.

Figure 5

Open in a new tab

Temporal evolution of the size, lattice parameter, and strain of the growing mesocrystal MCNC091 and images of the generated mesocrystal. (a) Gualtieri fit (black line) of the normalized peak area A100 (blue squares) and the resulting probability for nucleation PN (purple line, eq 3). The crystallite size D along ⟨100⟩ (purple circles) and ⟨h10⟩ (open orange circles) was obtained from the intercepts of the linear fits in the WH plots. (b) NC separation distance d100 (black triangles) and the microstrain ε along ⟨100⟩ (dark purple diamonds) and ⟨h10⟩ (open orange diamonds) obtained from the slopes of the linear fits in the WH plots. The end of the mesocrystal growth stage is indicated with a red solid line. (c) SEM micrograph depicts a cuboidal-shaped mesocrystal. (d) Magnified image of the mesocrystal surface displays a large number of defects. The fast Fourier transform (inset) shows a high degree of order of the nanocubes.

The nucleation period for MCNC091 (Figure 5a, purple line) is of similar duration as the nucleation period for MCNC068 (Figure 4a), and the probability for nucleation PN reached its maximum after 24.7 and 20.0 s for MCNC068 and MCNC091, respectively, corresponding to nucleation rates kN,MCNC068 = 0.04 s–1 and kN,MCNC091 = 0.05 s–1. The crystal growth rates obtained from the Gualtieri fits were kg,MCNC068= 0.14 s–1 and kg,MCNC091 = 0.017 s–1. Hence, although the nucleation rates were similar for MCNC068 and MCNC091, the crystal growth rate for MCNC068 was an order of magnitude faster than that for MCNC091. The formation of the MCNC091 mesocrystals displays overlapping periods of nucleation and crystal growth only during the initial growth stage followed by a period of about 100 s of only crystal growth. The similar nucleation rates for MCNC068 and MCNC091 can be explained by the pre-existence of dense, but disordered, nanocube clusters prior to crystallization that rapidly transform into mesocrystals, which corroborates that the mesocrystals form by a two-step process.34 The transition rate from disordered clusters to well-ordered mesocrystals is independent of the NC size as the nucleation rates for MCNC068 and MCNC091 show. The critical size, however, at which the transition takes place, cannot be easily extracted from the SAXS data. The large difference in crystal growth rate constants suggests that mesocrystal growth is diffusion-controlled and hence depends on the average size of the NCs and the NC number density in the dispersion.

The strain along ⟨h10⟩ and ⟨100⟩ was isotropic during the initial mesocrystal growth stage (first 60 s) and reached its maximum simultaneously with D at around 100 s. The strain decreased close to the end of the crystal growth stage and during the postgrowth stage, but the decrease was larger along ⟨100⟩ than ⟨h10⟩, resulting in the development of anisotropic strain (Figure 5b). The NC separation distance d100 within the MCNC091 mesocrystals decreased continuously from a value of 13.5 nm at the beginning of mesocrystal formation to 12.9 nm at the end of the measurement when MCNC091 reached its steady-state, consolidated structure (Figure 5b). The lattice contraction, i.e., the shrinkage of the unit cell, is related to the expulsion of solvent associated with the oleic acid capping molecules. The lattice contraction during the rapid incorporation of new NCs into the crystal lattice of the growing mesocrystals probably depends on the distance from the core, with the NCs that assemble at the surface of the growing mesocrystal having more solvent associated with the capping layer compared to the NCs in the core of the mesocrystal. The decrease of the crystallite size D of both MCNC068 and MCNC091 (Figures 4a and 5a) shows that the mesocrystals shrink during the postgrowth stage.

The analysis of the time-resolved SAXS data has shown that the emergence and relaxation of isotropic and anisotropic strain in the mesocrystals depend on the size and polydispersity of the assembling nanocubes and the “age” of the growing and contracting mesocrystals. The isotropic strain in the mesocrystals is related to a nonuniform lattice contraction (Figure 6a). The relaxation of the strain during the postgrowth stage indicates that the lattice spacing throughout the mesocrystal becomes more uniform as the solvent expulsion stage reaches completion. Size mismatches in the mesocrystal due to the occurrence of smaller or larger NCs could also result in strained areas in the mesocrystal (Figure 6a). The lower polydispersity of the smaller nanocubes NC068 results indeed in lower strain values for NC068 compared to those for NC091 (Figures 4b and 5b).

Figure 6.

Figure 6

Open in a new tab

Schematic representation of growth-induced strain and stress-induced dislocations in mesocrystals. (a) Schematic illustration of a growing mesocrystal. The lattice spacing d100 is smaller in the center compared to the perimeter of the mesocrystal, indicated by the red-pink color scale, as the solvent is entirely expulsed from the center but still surrounds NCs closer to the perimeter of the mesocrystal, indicated by the differently blue-shaded areas. The incorporation of NCs with slightly different sizes can result in strained areas in the mesocrystal (purple cubes). (b) Shrinkage stress acting on the mesocrystals at the liquid–air interface; the red arrows indicate the direction of the stress. (c) TEM micrograph of a thin slice obtained from MCNC091 showing an edge dislocation with a ⟨100⟩ Burgers vector. (d) Illustration of a slip plane (red plane) as well as shear forces (red arrows) that result in the formation of edge dislocations in mesocrystals (left). 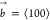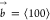The resulting edge dislocation (right) has a Burgers vector Inline graphic. (e) Illustration of slip plane (yellow) and shear forces (yellow arrows) that induce the formation of a screw dislocations (left). The resulting screw dislocation (right) has a Burgers vector Inline graphic.

The transition from isotropic to anisotropic strain occurred during the late stages of the mesocrystal growth or during the postgrowth stage for both MCNC068 and MCNC091. Anisotropic strain is related to the formation of defects.39 Many studies on metals and colloidal crystals have shown that dislocations can be induced by stress. For instance, Suresh et al. showed that the stress needed to induce a dislocation in thin copper and aluminum films correlates with the mechanical properties, in particular, the shear strength of the different metals.40,41 Schall et al. showed that the nucleation of a stress-induced dislocation in an initially defect-free colloidal crystal causes a strain relief.16,17

Inhomogeneous lattice contraction and size mismatch that are the major sources of isotropic strain (Figure 6a) can nucleate dislocations to relieve the generated internal stress. Previous studies on growing nanoparticles have shown that the large stresses that are generated due to variations of interatomic distances can result in the formation of dislocations at a critical nanoparticle size.42,43 The internal stress needed for a dislocation to form can be estimated from σI = Yε, where the Young’s modulus Y of the mesocrystals can be approximated to the previously measured value of gold superlattices of 1 GPa.44 The point where the strain becomes anisotropic (Figures 4b and 5b), which is caused by the formation of dislocations, relates to a stress σI of about 5 MPa for both MCNC068 and MCNC091. External stresses in a drying dispersion droplet that are caused by the increasing curvature and the surface tension of the liquid were found to result in cracking and wrinkling effects in colloidal crystals,45 which suggests that such drying stresses can be transferred to the mesocrystals located close to or attached to the liquid–air interface. The decrease of the scattering invariant Q* during the mesocrystal growth stage (Figure 2) indicates that a large fraction of the formed mesocrystals accumulated at the interface and are therefore expected to be affected by the shrinkage stress (Figure 6b).

The shrinkage stress σS can be estimated using the Laplace equation:

graphic file with name nn9b07820_m005.jpg

with γ being the surface tension of the liquid and r being the radius of the droplet. The shrinkage stress acting on the mesocrystals at the interface at the time when anisotropic strain was observed (when only decane remains; γ = 24 mN m–1) is estimated to range between 200 and 300 Pa for MCNC068 and MCNC091, which is several orders of magnitude smaller than the internal stresses needed to form a dislocation.

The presence of different defects in the mesocrystals was confirmed by ex situ microscopy. SEM images of the surface of mesocrystals displayed a large number of steps, kinks, and vacancies (Figure 5d). Edge dislocations could be observed by ex situ TEM in a thin slice prepared by focused ion beam (FIB) from the inside of a single mesocrystal MCNC091 (Figure 6c). Selected area electron diffraction patterns of a defect-free region (Figure S5a) and a region containing a dislocation (Figure S5b) show, in both cases, alignment of the nanocubes with respect to their atomic lattices, which suggests that the alignment was not perturbed by the presence of a dislocation. In SC crystals, the edge and screw dislocations that are most likely to occur have a Burgers vector 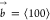Inline graphic (Figure 6d,e). The energy per unit length of a dislocation EL of an edge or screw dislocation can be approximated with

graphic file with name nn9b07820_m007.jpg

where the energy is proportional to the shear modulus G of the mesocrystals, the square of the length of the Burgers vector b, which is equal to the lattice parameter of the unit cell d100, and the length of the dislocation line L. Liu et al. used molecular dynamics simulations and showed that the shear modulus of gold nanoparticle superlattices is around 100 MPa and depends on the length of the capping agent and its capability to deform under shear stress but not on the size of the nanoparticle.44 As both NC068 and NC091 are capped with oleic acid, we do not expect large differences between the shear moduli of MCNC068 and MCNC091. The larger Burgers vector in MCNC091 compared to that in MCNC068 can be compensated by the smaller mesocrystal sizes of MCNC091 compared to MCNC068 and hence the maximum length of a dislocation line and its energy. Thus, it is reasonable to expect that the energy necessary to induce a dislocation is similar for MCNC068 and MCNC091. Estimates of critical shear stresses yield values around G/30, which correspond well with experimental values for dislocation-free crystals.46 Shear moduli for MCNC068 and MCNC091 assumed to be about 100 MPa44 result in estimates of critical shear stresses of about 3 MPa, which corresponds well with the previous estimates based on the Young’s modulus. Hence, our estimates of the critical stress to form a dislocation and the shear stress indicate that the relatively low critical shrinkage stress of a few hundred Pa is not sufficient to induce dislocations, and that the main source of dislocations is most likely the internal stress generated by superlattice contraction and NC size mismatch. Because the critical stress ultimately depends on the intrinsic shear modulus of the mesocrystal, increasing the shear modulus by decreasing the length of the capping agent and thus its ability to deform under shear stress could increase the critical shear stress. Minimizing the occurrence of size mismatches by minimizing the polydispersity of the nanoparticles could allow for growth of mesocrystals with less defects.

Ungár and co-workers developed a modified WH model that can be used to extract information on the crystal size and dislocation density.47−50 By using Ungár’s dislocation-modified function to describe the peak widths for the mesocrystals, we additionally verified the presence of dislocations in the mesocrystals (Supporting Information Method 1 and Figure S6). The modified WH model takes into account the average contrast factor C̅ of the dislocations, which depends on the elastic constants of the crystal, in particular, the Zener anisotropy ratio, Inline graphic, where c11, c12, and c44 are the elastic constants of a cubic crystal. The ratio AZ indicates whether a material has isotropic (AZ = 1) or anisotropic (AZ ≠ 1) elastic properties. It has been shown that the most compliant crystal direction displays the largest peak strain broadening and vice versa, and that peak strain broadening of cubic crystals is maximal for either the ⟨100⟩ (AZ > 1) or the ⟨111⟩ (AZ < 1) direction.51 The WH plots (Figure 3) show that the h00 peaks display the lowest strain broadening (Figure 3), which suggests that the ⟨100⟩ direction is the stiffest for both MCNC068 and MCNC091. These results can be understood when considering the surfactant’s ability to deform under stress in these specific directions. Whereas uniaxial stress in the ⟨100⟩ direction results in interdigitation of the oleic acid chains (Figure S7a), stress in the ⟨111⟩ direction causes partly a shear deformation of the surfactants (Figure S7b). The difference in stiffness in these specific directions can thus be compared to the difference of the Young’s and the shear modulus of nanoparticle superlattices, where the Young’s modulus is expected to be 1 order of magnitude larger than the shear modulus and can be significantly increased by surfactant interdigitation.44

Conclusions

An acoustic levitation device in combination with time-resolved SAXS was used to probe self-assembly of oleate-capped iron oxide NCs in a levitating drop. By fitting the Gualtieri equation to the increase of a crystalline phase during the main growth stage, we have shown that nanocube self-assembly is mainly diffusion-controlled. The size mismatch due to the polydispersity of the NCs and the superlattice contraction was related to the increasing isotropic strain during the mesocrystal growth stage. The occurrence of a strain anisotropy that increased with time at the end of the mesocrystal growth or in the postgrowth stage was related to the formation of dislocations, which was confirmed by ex situ microscopy. Estimates of the magnitude of internal and external stresses showed that the internal stresses created by the inhomogeneous superlattice contraction and size mismatches are probably responsible for the formation of dislocations that result in the development of an anisotropic strain. By considering the dependence of peak strain broadening on the average contrast factor of the dislocations and the Zener anisotropy ratio, we showed that the most compliant mesocrystal direction is the ⟨111⟩ direction. The study shows that, in originally dislocation-free mesocrystals, the nucleation of dislocations, which affect the mechanical and physical properties of the mesocrystals, ultimately depends on the internal strain and stresses created during the growth stage. Our study suggests that the density of dislocations could be reduced by using shorter capping agents to increase the shear modulus of the mesocrystal.

Methods

Nanocube Synthesis and Dispersion Preparation

The detailed preparation of iron oxide NCs capped by oleic acid (OA) was described previously.1 In brief, Fe3O4 NCs with edge lengths of 6.8 ± 0.3 nm (NC068) and 9.1 ± 0.4 nm (NC091) were synthesized by dissolving 10 mmol of an iron oleate precursor in 50 mL of a 1-octadecene (90%, Sigma-Aldrich)/1-hexadecene (99%, TCI) mixture (3:2 for NC068 and 9:1 for NC091), then adding 5 mmol sodium oleate (97%, TCI) and oleic acid (99% TCI). The mixture was degassed for 30 min at 140 °C and then heated at 3 °C min–1 and refluxed at 308 °C for 25 min and 316 °C for 30 min for the synthesis of NC068 and NC091, respectively. After reflux, the mixture was cooled to room temperature. The mother liquor was washed with a toluene/ethanol mixture and centrifuged several times to remove excess organics. The purified dispersion was dried under vacuum to yield a paste with an iron oxide content of 48 wt % for NC068 and 41 wt % NC091.

For the time-resolved self-assembly experiments, 6.22 mg (NC068) and 7.29 mg (NC091) of the NC pastes were redispersed in 0.75 mL of toluene and 0.25 mL of decane to obtain dispersions with a concentration of 3 mgiron oxide mL–1. Small amounts of oleic acid were added to the dispersions (0.2 mgOA mgpaste–1 for NC068; 0.05 mgOA mgpaste–1 for NC091), and the dispersions were then sonicated for 30 min.

Time-Resolved Scattering and Video Microscopy

Time-resolved small- and wide-angle X-ray scattering (SAXS/WAXS) experiments were carried out at the ID02 beamline at the European Synchrotron Radiation Facility (ESRF), Grenoble, France. The data were recorded by two CCD detectors, Rayonix MX-170HS and Rayonix LX-170HS, with covering ranges of 0.035 < q < 3.74 nm–1 and 11.42 < q < 50.44 nm–1, respectively. The time-resolved data were acquired with an exposure time of 30 ms per frame, resulting in a time resolution of 2 s. The data were automatically reduced after exposure by an online data reduction routine included in the SPEC acquisition program. The dispersion droplet was irradiated by a rectangular beam with a spot size of 76 × 290 μm2 and a wavelength λ = 1 Å.

We fitted a cubic form factor to the 1D small-angle scattering profile of the initial dispersion in SASView 4.1.2 to obtain a size distribution of the dispersed nanocrystals (Figure S2). The polydispersity was fitted by a Gaussian distribution function. Fitting the cubic form factor resulted in an average edge length of 6.8 ± 0.3 and 9.1 ± 0.5 nm for NC068 and NC091, respectively.

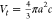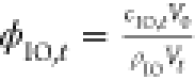The colloidal droplet was injected into an acoustic levitator (model 13K11, tec5, Oberursel, Germany), and the shrinking droplet was recorded with a microscope camera. The recorded video was decomposed into image frames using the program VirtualDub 1.10.4. The image frames were processed using ImageJ,52 and the time-dependent volume of the oblate ellipsoidal drop was estimated using Inline graphic, with a being the horizontal and c being the vertical radius of the shrinking droplet. The time-dependent volume fraction of the iron oxide core was calculated with Inline graphic, where cIO,t and ρIO = 5.15 g cm–3 are the time-dependent concentration of the inorganic iron oxide core and the density of magnetite, respectively, and V0 is the initial droplet volume. We calculated the volume fraction of the NCs ϕNC,t by assuming a 2 nm wide oleic acid layer on each NC facet.

Scanning Electron Microscopy

SEM micrographs were recorded using a JEOL JSM-7000F (JEOL, Japan; Uacc = 15 kV, WD = 10 mm) equipped with a Schottky-type field emission gun (FEG). Prior to SEM imaging, the organic residues were removed by heating the sample under an argon atmosphere in a tube furnace at 2 °C min–1 to 500 °C and holding at that temperature for 2 h.

Transmission Electron Microscopy

TEM images were recorded using a JEOL JEM-2100F (JEOL, Japan) equipped with a Schottky-type FEG (point resolution: 0.19 nm, spherical aberration Cs = 0.5 mm) operated at an accelerating voltage of 200 kV. Selected area electron diffraction patterns were recorded on a Themis Z (Thermo Fischer Scientific, USA) equipped with a Schottky-type FEG (point resolution: 0.06 nm).

Focused Ion Beam

A thin slice from a single mesocrystal was obtained by an FEI Nova NanoLab 600 (FEI Company, USA) at 30 kV and 30 pA using Ga ions. Prior to FIB milling, Pt was deposited on the mesocrystal. The mesocrystal slice was subsequently removed from a silicon substrate and transferred to a TEM sample holder (Omniprobe, USA) using a nanomanipulator (Omniprobe, USA).

Acknowledgments

We acknowledge the Swedish Research Council (VR, Grant No. 2015-05350) for funding this work. We thank H. Voisin and P. Munier for assistance with beam time preparations and data acquisition. We would like to acknowledge A. Kentaro Inge and J. Grins for scientific discussions, and P. Jansson for technical assistance with the acoustic levitator. We thank T. Church for helpful input and linguistic revision. We are grateful to T.S. Plivelic for providing the acoustic levitator. We thank R. Prasath Babu from KTH for technical assistance with FIB, and A. Ashok for assistance with TEM. The experiments were performed on beamline ID02 at the European Synchrotron Radiation Facility (ESRF), Grenoble, France. We are grateful to L. Sharpnack, M. Sztucki, and T. Narayanan for providing assistance in using beamline ID02.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.9b07820.

  • Further experimental and theoretical details, including WAXS data, cubic form factor fitted SAXS curves, the average center-to-center distances, a size histogram of MCNC091, peak broadening analyzed with the modified WH method, and a schematic illustration for direction-dependent mechanical properties in simple cubic mesocrystals (PDF)

Author Contributions

M.A. and L.B. conceived the study. M.K., M.A., Z.-P.L., and L.B. planned and designed the SAXS experiments. M.K., M.A., Z.-P.L., Y.L., and M.S. conducted the SAXS experiments. M.K. performed the data analysis and interpretation of the data. M.K. and L.B. wrote the manuscript. All of the authors discussed the results and commented on the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nn9b07820_si_001.pdf (659.9KB, pdf)

References

  1. Wetterskog E.; Agthe M.; Mayence A.; Grins J.; Wang D.; Rana S.; Ahniyaz A.; Salazar-Alvarez G.; Bergström L. Precise Control over Shape and Size of Iron Oxide Nanocrystals Suitable for Assembly into Ordered Particle Arrays. Sci. Technol. Adv. Mater. 2014, 15, 055010 10.1088/1468-6996/15/5/055010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Wetterskog E.; Klapper A.; Disch S.; Josten E.; Hermann R. P.; Rücker U.; Brückel T.; Bergström L.; Salazar-Alvarez G. Tuning the Structure and Habit of Iron Oxide Mesocrystals. Nanoscale 2016, 8, 15571–15580. 10.1039/C6NR03776C. [DOI] [PubMed] [Google Scholar]
  3. Wang D.; Li J.; Cao X.; Pang G.; Feng S. Hexagonal Mesocrystals Formed by Ultra-Thin Tungsten Oxide Nanowires and Their Electrochemical Behaviour. Chem. Commun. 2010, 46, 7718–7720. 10.1039/c0cc01835j. [DOI] [PubMed] [Google Scholar]
  4. Hu B.; Wu L.-H.; Liu S.-J.; Yao H.-B.; Shi H.-Y.; Li G.-P.; Yu S.-H. Microwave-Assisted Synthesis of Silver Indium Tungsten Oxide Mesocrystals and Their Selective Photocatalytic Properties. Chem. Commun. 2010, 46, 2277–2279. 10.1039/b921455k. [DOI] [PubMed] [Google Scholar]
  5. Bergström L.; Sturm (née Rosseeva) E. V.; Salazar-Alvarez G.; Cölfen H. Mesocrystals in Biominerals and Colloidal Arrays. Acc. Chem. Res. 2015, 48, 1391–1402. 10.1021/ar500440b. [DOI] [PubMed] [Google Scholar]
  6. Ma M.-G.; Cölfen H. Mesocrystals - Applications and Potential. Curr. Opin. Colloid Interface Sci. 2014, 19, 56–65. 10.1016/j.cocis.2014.03.001. [DOI] [Google Scholar]
  7. Zhou L.; O’Brien P. Mesocrystals - Properties and Applications. J. Phys. Chem. Lett. 2012, 3, 620–628. 10.1021/jz2015742. [DOI] [PubMed] [Google Scholar]
  8. Gamarra L.; Silva A.C.; Oliveira T. R.; Mamani J. B.; Malheiros S. M. F.; Malavolta L.; Pavon L. F.; Sibov T. T.; Amaro Jr E; Gamarra L. Application of Hyperthermia Induced by Superparamagnetic Iron Oxide Nanoparticles in Glioma Treatment. Int. J. Nanomed. 2011, 6, 591–603. 10.2147/IJN.S14737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Laurent S.; Dutz S.; Häfeli U. O.; Mahmoudi M. Magnetic Fluid Hyperthermia: Focus on Superparamagnetic Iron Oxide Nanoparticles. Adv. Colloid Interface Sci. 2011, 166, 8–23. 10.1016/j.cis.2011.04.003. [DOI] [PubMed] [Google Scholar]
  10. Agthe M.; Wetterskog E.; Bergström L. Following the Assembly of Iron Oxide Nanocubes by Video Microscopy and Quartz Crystal Microbalance with Dissipation Monitoring. Langmuir 2017, 33, 303–310. 10.1021/acs.langmuir.6b03570. [DOI] [PubMed] [Google Scholar]
  11. Kapuscinski M.; Agthe M.; Bergström L. Time-Resolved Viscoelastic Properties of Self-Assembling Iron Oxide Nanocube Superlattices Probed by Quartz Crystal Microbalance with Dissipation Monitoring. J. Colloid Interface Sci. 2018, 522, 104–110. 10.1016/j.jcis.2018.03.034. [DOI] [PubMed] [Google Scholar]
  12. Lv Z.-P.; Kapuscinski M.; Bergström L. Tunable Assembly of Truncated Nanocubes by Evaporation-Driven Poor-Solvent Enrichment. Nat. Commun. 2019, 10, 4228. 10.1038/s41467-019-12237-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Disch S.; Wetterskog E.; Hermann R. P.; Salazar-Alvarez G.; Busch P.; Brückel T.; Bergström L.; Kamali S. Shape Induced Symmetry in Self-Assembled Mesocrystals of Iron Oxide Nanocubes. Nano Lett. 2011, 11, 1651–1656. 10.1021/nl200126v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Li R.; Zhang J.; Tan R.; Gerdes F.; Luo Z.; Xu H.; Hollingsworth J. A.; Klinke C.; Chen O.; Wang Z. Competing Interactions between Various Entropic Forces toward Assembly of Pt3Ni Octahedra into a Body-Centered Cubic Superlattice. Nano Lett. 2016, 16, 2792–2799. 10.1021/acs.nanolett.6b00564. [DOI] [PubMed] [Google Scholar]
  15. Lin N. Y. C.; Bierbaum M.; Schall P.; Sethna J. P.; Cohen I. Measuring Nonlinear Stresses Generated by Defects in 3D Colloidal Crystals. Nat. Mater. 2016, 15, 1172–1176. 10.1038/nmat4715. [DOI] [PubMed] [Google Scholar]
  16. Schall P.; Cohen I.; Weitz D. A.; Spaepen F. Visualizing Dislocation Nucleation by Indenting Colloidal Crystals. Nature 2006, 440, 319–323. 10.1038/nature04557. [DOI] [PubMed] [Google Scholar]
  17. Schall P.; Cohen I.; Weitz D. A.; Spaepen F. Visualization of Dislocation Dynamics in Colloidal Crystals. Science 2004, 305, 1944–1948. 10.1126/science.1102186. [DOI] [PubMed] [Google Scholar]
  18. Alsayed A. M.; Islam M. F.; Zhang J.; Collings P. J.; Yodh A. G. Premelting at Defects within Bulk Colloidal Crystals. Science 2005, 309, 1207–1210. 10.1126/science.1112399. [DOI] [PubMed] [Google Scholar]
  19. Vlasov Y. A.; Astratov V. N.; Baryshev A. V.; Kaplyanskii A. A.; Karimov O. Z.; Limonov M. F. Manifestation of Intrinsic Defects in Optical Properties of Self-Organized Opal Photonic Crystals. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2000, 61, 5784–5793. 10.1103/PhysRevE.61.5784. [DOI] [PubMed] [Google Scholar]
  20. Kontogeorgos A.; Snoswell D. R. E.; Finlayson C. E.; Baumberg J. J.; Spahn P.; Hellmann G. P. Inducing Symmetry Breaking in Nanostructures: Anisotropic Stretch-Tuning Photonic Crystals. Phys. Rev. Lett. 2010, 105, 233909. 10.1103/PhysRevLett.105.233909. [DOI] [PubMed] [Google Scholar]
  21. Diroll B. T.; Greybush N. J.; Kagan C. R.; Murray C. B. Smectic Nanorod Superlattices Assembled on Liquid Subphases: Structure, Orientation, Defects, and Optical Polarization. Chem. Mater. 2015, 27, 2998–3008. 10.1021/acs.chemmater.5b00355. [DOI] [Google Scholar]
  22. Li L. S.; Walda J.; Manna L.; Alivisatos A. P. Semiconductor Nanorod Liquid Crystals. Nano Lett. 2002, 2, 557–560. 10.1021/nl0255146. [DOI] [Google Scholar]
  23. Baranov D.; Fiore A.; Van Huis M.; Giannini C.; Falqui A.; Lafont U.; Zandbergen H.; Zanella M.; Cingolani R.; Manna L. Assembly of Colloidal Semiconductor Nanorods in Solution by Depletion Attraction. Nano Lett. 2010, 10, 743–749. 10.1021/nl903946n. [DOI] [PubMed] [Google Scholar]
  24. Li L. S.; Alivisatos A. P. Semiconductor Nanorod Liquid Crystals and Their Assembly on a Substrate. Adv. Mater. 2003, 15, 408–411. 10.1002/adma.200390093. [DOI] [Google Scholar]
  25. Bodnarchuk M. I.; Shevchenko E. V.; Talapin D. V. Structural Defects in Periodic and Quasicrystalline Binary Nanocrystal Superlattices. J. Am. Chem. Soc. 2011, 133, 20837–20849. 10.1021/ja207154v. [DOI] [PubMed] [Google Scholar]
  26. Talapin D. V.; Shevchenko E. V.; Bodnarchuk M. I.; Ye X.; Chen J.; Murray C. B. Quasicrystalline Order in Self-Assembled Binary Nanoparticle Superlattices. Nature 2009, 461, 964–967. 10.1038/nature08439. [DOI] [PubMed] [Google Scholar]
  27. Mayence A.; Wang D.; Salazar-Alvarez G.; Oleynikov P.; Bergström L. Probing Planar Defects in Nanoparticle Superlattices by 3D Small-Angle Electron Diffraction Tomography and Real Space Imaging. Nanoscale 2014, 6, 13803–13808. 10.1039/C4NR04156A. [DOI] [PubMed] [Google Scholar]
  28. Weidman M. C.; Smilgies D.-M.; Tisdale W. A. Kinetics of the Self-Assembly of Nanocrystal Superlattices Measured by Real-Time In Situ X-ray Scattering. Nat. Mater. 2016, 15, 775–781. 10.1038/nmat4600. [DOI] [PubMed] [Google Scholar]
  29. Lu C.; Akey A. J.; Dahlman C. J.; Zhang D.; Herman I. P. Resolving the Growth of 3D Colloidal Nanoparticle Superlattices by Real-Time Small-Angle X-Ray Scattering. J. Am. Chem. Soc. 2012, 134, 18732–18738. 10.1021/ja307848h. [DOI] [PubMed] [Google Scholar]
  30. Senesi A. J.; Eichelsdoerfer D. J.; Brown K. A.; Lee B.; Auyeung E.; Choi C. H. J.; MacFarlane R. J.; Young K. L.; Mirkin C. A. Oligonucleotide Flexibility Dictates Crystal Quality in DNA-Programmable Nanoparticle Superlattices. Adv. Mater. 2014, 26, 7235–7240. 10.1002/adma.201402548. [DOI] [PubMed] [Google Scholar]
  31. Glotzer S. C.; Solomon M. J. Anisotropy of Building Blocks and Their Assembly into Complex Structures. Nat. Mater. 2007, 6, 557–562. 10.1038/nmat1949. [DOI] [PubMed] [Google Scholar]
  32. Gualtieri A. F. Synthesis of Sodium Zeolites from a Natural Halloysite. Phys. Chem. Miner. 2001, 28, 719–728. 10.1007/s002690100197. [DOI] [Google Scholar]
  33. Williamson G. K.; Hall W. H. X-ray Line Broadening from Filed Aluminium and Wolfram. Acta Metall. 1953, 1, 22–31. 10.1016/0001-6160(53)90006-6. [DOI] [Google Scholar]
  34. Agthe M.; Plivelic T. S.; Labrador A.; Bergström L.; Salazar-Alvarez G. Following in Real Time the Two-Step Assembly of Nanoparticles into Mesocrystals in Levitating Drops. Nano Lett. 2016, 16, 6838–6843. 10.1021/acs.nanolett.6b02586. [DOI] [PubMed] [Google Scholar]
  35. Vandaele V.; Lambert P.; Delchambre A. Non-Contact Handling in Microassembly: Acoustical Levitation. Precis. Eng. 2005, 29, 491–505. 10.1016/j.precisioneng.2005.03.003. [DOI] [Google Scholar]
  36. Leiterer J.; Leitenberger W.; Emmerling F.; Thünemann A. F.; Panne U. The Use of an Acoustic Levitator to Follow Crystallization in Small Droplets by Energydispersive X-ray Diffraction. J. Appl. Crystallogr. 2006, 39, 771–773. 10.1107/S0021889806024915. [DOI] [Google Scholar]
  37. Klimakow M.; Leiterer J.; Kneipp J.; Rössler E.; Panne U.; Rademann K.; Emmerling F. Combined Synchrotron XRD/Raman Measurements: In Situ Identification of Polymorphic Transitions during Crystallization Processes. Langmuir 2010, 26, 11233–11237. 10.1021/la100540q. [DOI] [PubMed] [Google Scholar]
  38. Zhang L.; He R.; Gu H. C. Oleic Acid Coating on the Monodisperse Magnetite Nanoparticles. Appl. Surf. Sci. 2006, 253, 2611–2617. 10.1016/j.apsusc.2006.05.023. [DOI] [Google Scholar]
  39. Ungár T. Microstructural Parameters from X-ray Diffraction Peak Broadening. Scr. Mater. 2004, 51, 777–781. 10.1016/j.scriptamat.2004.05.007. [DOI] [Google Scholar]
  40. Suresh S.; Nieh T. G.; Choi B. W. Nano-Indentation of Copper Thin Films on Silicon Substrates. Scr. Mater. 1999, 41, 951–957. 10.1016/S1359-6462(99)00245-6. [DOI] [Google Scholar]
  41. Gouldstone A.; Koh H. J.; Zeng K. Y.; Giannakopoulos A. E.; Suresh S. Discrete and Continuous Deformation during Nanoindentation of Thin Films. Acta Mater. 2000, 48, 2277–2295. 10.1016/S1359-6454(00)00009-4. [DOI] [Google Scholar]
  42. Yacaman M. J.; Ascencio J. A.; Liu H. B.; Gardea-Torresdey J. Structure Shape and Stability of Nanometric Sized Particles. J. Vac. Sci. Technol., B: Microelectron. Process. Phenom. 2001, 19, 1091–1103. 10.1116/1.1387089. [DOI] [Google Scholar]
  43. Zhang Q.; Xie J.; Yu Y.; Yang J.; Lee J. Y. Tuning the Crystallinity of Au Nanoparticles. Small 2010, 6, 523–527. 10.1002/smll.200902033. [DOI] [PubMed] [Google Scholar]
  44. Liu X. P.; Ni Y.; He L. H. Elastic Properties of Gold Supracrystals: Effects of Nanocrystal Size, Ligand Length, and Nanocrystallinity. J. Chem. Phys. 2016, 144, 144507. 10.1063/1.4946029. [DOI] [PubMed] [Google Scholar]
  45. Van Der Kooij H. M.; Van De Kerkhof G. T.; Sprakel J. A Mechanistic View of Drying Suspension Droplets. Soft Matter 2016, 12, 2858–2867. 10.1039/C5SM02406D. [DOI] [PubMed] [Google Scholar]
  46. Hull D.; Bacon D. J.. Introduction to Dislocations, 5th ed.; Elsevier: Oxford, U.K., 2011; pp 14, 158. [Google Scholar]
  47. Ungár T.; Dragomir I.; Révész Á.; Borbély A. The Contrast Factors of Dislocations in Cubic Crystals: The Dislocation Model of Strain Anisotropy in Practice. J. Appl. Crystallogr. 1999, 32, 992–1002. 10.1107/S0021889899009334. [DOI] [Google Scholar]
  48. Ungár T.; Tichy G. The Effect of Dislocation Contrast on X-ray Line Profiles in Untextured Polycrystals. Phys. Status Solidi A 1999, 171, 425–434. . [DOI] [Google Scholar]
  49. Ungár T. Strain Broadening Caused by Dislocations. Mater. Sci. Forum 1998, 278–281, 151–156. 10.4028/www.scientific.net/MSF.278-281.151. [DOI] [Google Scholar]
  50. Ungár T.; Borbély A. The Effect of Dislocation Contrast on X-ray Line Broadening: A New Approach to Line Profile Analysis. Appl. Phys. Lett. 1996, 69, 3173–3175. 10.1063/1.117951. [DOI] [Google Scholar]
  51. Leineweber A. Understanding Anisotropic Microstrain Broadening in Rietveld Refinement. Z. Kristallogr. Cryst. Mater. 2011, 226, 905–923. 10.1524/zkri.2011.1413. [DOI] [Google Scholar]
  52. Schneider C. A.; Rasband W. S.; Eliceiri K. W. NIH Image to ImageJ: 25 Years of Image Analysis. Nat. Methods 2012, 9, 671–675. 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn9b07820_si_001.pdf (659.9KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES