Abstract
The high degree of parallelism of today’s computing systems often requires executing applications and their tasks in parallel due to a limited scaling capability of individual applications. In such scenarios, considering the differing importance of applications while scheduling tasks is done by assigning priorities to the tasks. However, priorities may lead to starvation in highly utilized systems. A solution is offered by aging mechanisms that raise the priority of long waiting tasks. As modern systems are often dynamic in nature, we developed a two-level aging mechanism and analyzed its effect in the context of 6 dynamic scheduling algorithms for heterogeneous systems. In the context of task scheduling, aging refers to a method that increases the priority of a task over its lifetime. We used a task-based runtime system to evaluate the mechanism on a real system in two scenarios. The results show a speed up of the average total makespan in 9 out of 12 conducted experiments when aging is used with the cost of additional waiting time for the applications/jobs with higher priority. However, the job/application with the highest priority is still finished first in all cases. Considering the scheduling algorithms, Minimum Completion Time, Sufferage, and Relative Cost benefit in both experiments by the aging mechanism. Additionally, no algorithm significantly dominates all other algorithms when total makespans are compared.
Keywords: Dynamic task scheduling, Task priorities, Heterogeneous architectures
Motivation
Modern computing systems used in fields like embedded and high performance computing feature a high degree of parallelism and are often equipped with additional accelerators, e.g. GPUs. This parallelism can be used to execute different functionality or applications in parallel as not all applications are able to exploit the available computational power due to a lack of scaling capability. However, executing multiple applications and their corresponding tasks in parallel can be problematic if a certain quality of service is required or expected for a subset of the applications. A common way to express differing importance of applications or functionality in non-safety-critical systems is to assign priorities accordingly. In highly utilized systems though, static task priorities can lead to the starvation of certain tasks. Starvation can be avoided by applying aging mechanisms. Aging refers to the technique of raising the priority of tasks that have waited a certain amount of time in the system for execution. This is not to be confused with hardware aging, where the fault rate of a hardware component increases over its lifetime.
Today’s computing systems are often dynamic in nature, which means that the set of tasks to be executed does not remain static, and tasks’ start times may be unknown as they may be triggered by signals or user interactions. Therefore, we focus on dynamic scheduling algorithms and add an adaptive aging mechanism that considers the current system state and load.
Generally, heterogeneous architectures present many challenges to application developers. A state-of-the-art solution is offered by task-based runtime systems that abstract from the underlying system and provide helpful functionality for developers. To utilize these features, we integrate our work into an existing task-based runtime system, the Embedded Multicore Building Blocks (EMB ), an open-source runtime system and library developed by Siemens. In summary, we make the following contributions:
), an open-source runtime system and library developed by Siemens. In summary, we make the following contributions:
We integrate 6 dynamic scheduling algorithms into a task-based runtime system and add the ability to consider task priorities.
We develop a two-level adaptive aging mechanism to extend the scheduling module.
We evaluate the algorithms without and with aging on a real system and investigate their behavior in terms of different metrics.
We analyze the effect of aging in these experiments.
The remainder of this paper is structured as follows: In Sect. 2 we briefly discuss the problem statement and the necessary fundamentals of our work. EMB is shortly introduced in Sect. 3. Section 4 presents the extensions made to EMB
is shortly introduced in Sect. 3. Section 4 presents the extensions made to EMB and the scheduling algorithms we implemented. The experimental setup and the obtained results are presented in Sect. 5. Finally, we discuss related work (Sect. 6) and conclude with directions for future work (Sect. 7).
and the scheduling algorithms we implemented. The experimental setup and the obtained results are presented in Sect. 5. Finally, we discuss related work (Sect. 6) and conclude with directions for future work (Sect. 7).
Fundamentals and Problem Statement
The basic scheduling problem comprises a set of n tasks 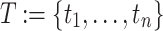 that has to be assigned to a set of m processing units
that has to be assigned to a set of m processing units 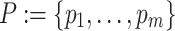 . Next to mapping a task
. Next to mapping a task 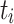 to a processing unit
to a processing unit 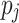 , scheduling also includes the assignment of an ordering and time slices. In the case of heterogeneous systems, the processing units
, scheduling also includes the assignment of an ordering and time slices. In the case of heterogeneous systems, the processing units 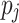 may have different characteristics, which can lead to varying executions times for a single task on different units [22]. Scheduling problems are generally considered to be NP-hard [10].
may have different characteristics, which can lead to varying executions times for a single task on different units [22]. Scheduling problems are generally considered to be NP-hard [10].
As there is no algorithm that can solve all scheduling problems efficiently, there exist many heuristics. Generally, these can be classified into static and dynamic algorithms [20]. The main difference is that static algorithms make all decisions before a single task is executed, whereas dynamic algorithms schedule tasks at runtime. Hence, static algorithms have to know all relevant task information beforehand, while dynamic ones do not need full information and are able to adapt their behavior.
This work targets tasks that may potentially create infinite task instances for execution and whose start times may be unknown. Therefore, we focus on dynamic scheduling algorithms. Additionally, we allow adding priorities to tasks. In general, task priorities can be set before runtime for every instance of this task and remain static over its lifecycle, or they are dynamically set for every task instance at runtime and may change over time [5]. The earliest deadline first (EDF) algorithm [9] is a well-known example with dynamic task priorities. Each task instance is assigned the priority 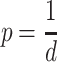 when it arrives in the system, where d is the deadline of this instance. Contrary to EDF, rate-monotonic scheduling [16] assigns static priorities. Each task is assigned the priority
when it arrives in the system, where d is the deadline of this instance. Contrary to EDF, rate-monotonic scheduling [16] assigns static priorities. Each task is assigned the priority 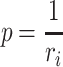 , where
, where 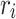 is the period of task
is the period of task 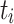 . In this work, an application developer is allowed to assign a static priority to a task, which is then used for all instances of this task. However, we also utilize an aging mechanism that is allowed to increase the priority of a single task instance in order to improve fairness if the waiting time of an instance is considered too long. In addition, it has to be noted that we do not support task preemption.
. In this work, an application developer is allowed to assign a static priority to a task, which is then used for all instances of this task. However, we also utilize an aging mechanism that is allowed to increase the priority of a single task instance in order to improve fairness if the waiting time of an instance is considered too long. In addition, it has to be noted that we do not support task preemption.
Embedded Multicore Building Blocks
EMB [21] is a C/C++ library and runtime system for parallel programming of embedded systems.1 One of the challenges EMB
[21] is a C/C++ library and runtime system for parallel programming of embedded systems.1 One of the challenges EMB aims to solve is to reduce the complexity of heterogeneous and parallel architectures for application developers. EMB
aims to solve is to reduce the complexity of heterogeneous and parallel architectures for application developers. EMB builds on MTAPI, a task model that allows several implementation variants for a user-defined task. An application developer defines a specific functionality (kernel), e.g., a matrix multiplication, and is then allowed to provide one or multiple implementations for this task. Thereby, the application development can be separated from implementing specific kernels and the underlying hardware. These kernels targeting specific accelerators can then be optimized by hardware experts.
builds on MTAPI, a task model that allows several implementation variants for a user-defined task. An application developer defines a specific functionality (kernel), e.g., a matrix multiplication, and is then allowed to provide one or multiple implementations for this task. Thereby, the application development can be separated from implementing specific kernels and the underlying hardware. These kernels targeting specific accelerators can then be optimized by hardware experts.
MTAPI additionally allows a developer to start tasks and to synchronize on their completion, where the actual execution is controlled by the runtime system. Thereby, the developer has to guarantee that only tasks that are ready to execute and have their dependencies fulfilled are started. MTAPI’s tasks are more light-weight than a thread and distributed among worker threads for execution. Execution takes place concurrently to other tasks that have been started and it is allowed to start new tasks within a task.
In previous work, we already extended EMB to support sophisticated scheduling on heterogeneous architectures [2]. For this purpose, we added a general processing unit abstraction that allows grouping identical units into groups. All processing units are represented by an OS-level worker thread that is used to execute the tasks mapped to this processing unit. Furthermore, we added a monitoring component to EMB
to support sophisticated scheduling on heterogeneous architectures [2]. For this purpose, we added a general processing unit abstraction that allows grouping identical units into groups. All processing units are represented by an OS-level worker thread that is used to execute the tasks mapped to this processing unit. Furthermore, we added a monitoring component to EMB that monitors task execution. In the current version, the component measures task execution times including potentially necessary data transfers. The measurements are stored within a history database with the task’s problem size as key. The stored data is then used to predict execution times of upcoming tasks to improve scheduling decisions. Finally, we added an abstract scheduler module and six dynamic scheduling heuristics for heterogeneous architectures to EMB
that monitors task execution. In the current version, the component measures task execution times including potentially necessary data transfers. The measurements are stored within a history database with the task’s problem size as key. The stored data is then used to predict execution times of upcoming tasks to improve scheduling decisions. Finally, we added an abstract scheduler module and six dynamic scheduling heuristics for heterogeneous architectures to EMB .
.
As of yet, necessary data transfers for the execution on accelerators are not considered separately. This means that a task executed on an accelerator always transfers its data on and off the accelerator regardless of its predecessor and successor tasks. The high-level architecture of EMB can be seen in Fig. 1.
can be seen in Fig. 1.
Fig. 1.
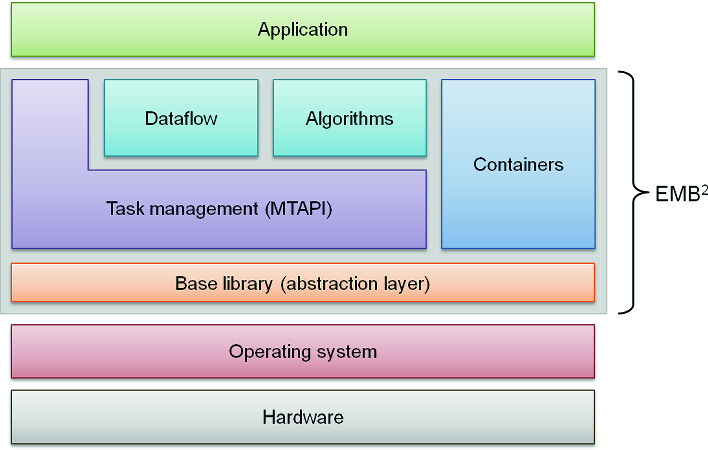
High-level architecture of EMB [21]
[21]
Dynamic Scheduling Algorithms
This section presents the extensions added to EMB to support task priorities, the algorithms that have been integrated into EMB
to support task priorities, the algorithms that have been integrated into EMB , and the adaptive aging mechanism used to increase fairness.
, and the adaptive aging mechanism used to increase fairness.
We selected the algorithms on the basis of their runtime overhead, since scheduling decisions have to be made as fast as possible in dynamic systems, their implementation complexity, and their ability to work with limited knowledge about the set of tasks to be executed. The selected heuristics can be classified into immediate and batch mode. Immediate mode considers tasks in a fixed order, only moving on to the next task after making a scheduling decision. In contrast, batch mode considers tasks out-of-order and so delays task scheduling decisions as long as possible, thereby increasing the pool of potential tasks to choose from.
EMB Extensions
Extensions
Both the abstract scheduler module and each processing unit abstraction created for [2] comprise queues to store tasks. The scheduler queue stores all tasks ready to execute, while the processing unit queues store all tasks assigned to this specific unit. For EMB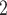 to be able to support different task priorities, each queue was replaced by a set of queues with one queue for every priority level. Assigned tasks and tasks ready to execute are then stored in queues according to their current priority.
to be able to support different task priorities, each queue was replaced by a set of queues with one queue for every priority level. Assigned tasks and tasks ready to execute are then stored in queues according to their current priority.
Immediate Mode Heuristics
Minimum Completion Time (MCT). [1] combines the execution time of a task 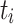 with the estimated completion time ct of the already assigned tasks of a processing unit
with the estimated completion time ct of the already assigned tasks of a processing unit 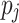 . In total, MCT predicts the completion time ct of a task
. In total, MCT predicts the completion time ct of a task 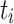 and assigns
and assigns 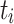 to the processing unit
to the processing unit 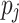 that minimizes ct of
that minimizes ct of 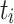 .
.
Batch Mode Heuristics
Min-Min. [12] extends the idea of MCT by considering the complete set of currently ready-to-execute tasks. The heuristic then assigns the task 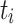 that has the earliest completion time to the processing unit
that has the earliest completion time to the processing unit 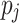 that minimizes the completion time of
that minimizes the completion time of 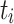
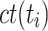 . In general, the core idea is to schedule shorter tasks first to encumber the system for as short a time as possible. This can lead to starvation of larger tasks if steadily new shorter tasks arrive in the system.
. In general, the core idea is to schedule shorter tasks first to encumber the system for as short a time as possible. This can lead to starvation of larger tasks if steadily new shorter tasks arrive in the system.
Max-Min. [15] is a variant of Min-Min and based on the observation that Min-Min often leads to large tasks getting postponed to the end of an execution cycle, needlessly increasing the total makespan because the remaining tasks are too coarse-granular to partition equally. So, Max-Min schedules the tasks with the latest minimum completion time first, leaving small tasks to pad out any load imbalance in the end. However, this can lead to starvation of small tasks if steadily new longer tasks arrive.
RASA. [18] is a combination of both Min-Min and Max-Min. It uses them alternatively for each iteration, starting with Min-Min if the number of resources is odd, and Max-Min otherwise.
Sufferage. [15] ranks all tasks ready-to-execute according to their urgency based on how much time the task stands to lose if it does not get mapped to its preferred resource. The ranking is given by the difference between the task’s minimum completion time and the minimum completion time the task would achieve if the fastest processing unit would not be available.
Relative Cost (RC). [17] uses the new metric rc, which divides ct of a task 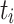 by its average ct over all processing units, to rank tasks. RC both uses a static and a dynamic variant of the relative cost metric to compute the final metric. The static variant is defined as
by its average ct over all processing units, to rank tasks. RC both uses a static and a dynamic variant of the relative cost metric to compute the final metric. The static variant is defined as 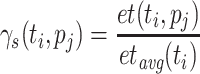 , where
, where 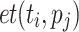 is the execution time of task
is the execution time of task 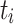 on processing unit
on processing unit 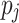 , and
, and 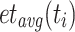 is the average execution time of
is the average execution time of 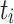 over all processing units.
over all processing units. 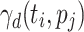 , the dynamic variant is defined as
, the dynamic variant is defined as 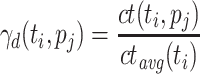 , where
, where 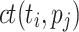 is the completion time of
is the completion time of 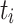 on
on 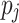 , and
, and 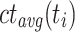 is the average ct of
is the average ct of 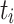 over all processing units. The second variant is dynamic as ct is updated after each time a task is mapped to a processing unit. The variants are then combined into
over all processing units. The second variant is dynamic as ct is updated after each time a task is mapped to a processing unit. The variants are then combined into 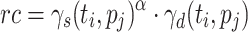 , where
, where 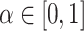 determines the effect of the static costs. In this work, we use
determines the effect of the static costs. In this work, we use 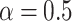 . RC then maps the task with minimum rc to
. RC then maps the task with minimum rc to 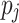 that minimizes
that minimizes 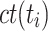 .
.
Aging Mechanism
We added a two-level aging mechanism to the scheduling module of EMB to avoid starvation of tasks. The first level was integrated directly into the scheduler module. Tasks ready to execute are stored into priority-specific ready-queues. Therefore, if there are n distinct priority levels, n separate ready-queues are created. Each time the scheduler is activated, each non-empty queue with a priority lower than the set maximum priority is checked for potential aging candidates if at least two times the amount of active processing units of tasks are currently ready to execute. So, the aging mechanism is only activated if at least
to avoid starvation of tasks. The first level was integrated directly into the scheduler module. Tasks ready to execute are stored into priority-specific ready-queues. Therefore, if there are n distinct priority levels, n separate ready-queues are created. Each time the scheduler is activated, each non-empty queue with a priority lower than the set maximum priority is checked for potential aging candidates if at least two times the amount of active processing units of tasks are currently ready to execute. So, the aging mechanism is only activated if at least 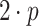 tasks are currently enqueued with p being the number of active processing units. A task in a ready-queue is selected for priority promotion if the task is older than the average task waiting time multiplied with a threshold factor
tasks are currently enqueued with p being the number of active processing units. A task in a ready-queue is selected for priority promotion if the task is older than the average task waiting time multiplied with a threshold factor 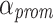 . After a task is promoted to a new priority queue by increasing its priority, the task is pushed to the back of the queue and its waiting time reset.
. After a task is promoted to a new priority queue by increasing its priority, the task is pushed to the back of the queue and its waiting time reset.
The second level of the aging mechanism targets the processing units’ waiting queues. Each processing unit possesses priority-specific queues, where assigned tasks are stored. Again, if there are n distinct priority levels, each processing unit possesses n separate waiting queues. A task is assigned to the priority level, which it last had in the scheduler. As long as a processing unit is active, i.e. at least one waiting queue is non-empty, each non-empty queue with a priority lower than the set maximum priority is checked for potential aging candidates. Again, a task in a waiting queue is selected for priority promotion if the task is older than the average queue waiting time multiplied with a threshold factor 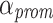 . Actually, different threshold factors
. Actually, different threshold factors 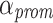 can be used. However in this work, we use
can be used. However in this work, we use 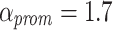 for both levels. This value was determined empirically as a compromise to reduce overall priority promotion while still enabling the promotion for long-waiting tasks. Again, the waiting time of a task is reset after a promotion and it is pushed to the back of the new queue.
for both levels. This value was determined empirically as a compromise to reduce overall priority promotion while still enabling the promotion for long-waiting tasks. Again, the waiting time of a task is reset after a promotion and it is pushed to the back of the new queue.
Experiments
As benchmarks we considered two different scenarios with all benchmark tasks providing both a CPU and a GPU OpenCL implementation. The first scenario consists of three independent heterogeneous tasks with differing priorities and has already been used in our previous work [2]. This benchmark resembles dynamic systems as the task instances are started sporadically, thereby adding a random component to the starting point of a task instance.
For the second scenario, we execute two benchmarks of the Rodinia benchmark suite [4], hotspot3D and particlefilter, in parallel with different priorities. Both benchmarks distribute their work over several parallel tasks.
All experiments were conducted ten times with and without aging. For each experiment, we measured the makespan of each application or job, and the total makespan of all tasks. We then computed the average, the minimum, and the maximum. The makespan is defined as the time from start to finish of an application or task. Additionally, we measured the flow time of each task and again computed the average, the minimum, and the maximum. The flow time of 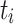 is defined as
is defined as 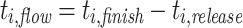 , where
, where 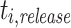 is the release time or system arrival time of
is the release time or system arrival time of 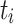 and
and 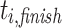 is the finish time of
is the finish time of 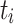 . So,
. So, 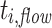 is basically the time
is basically the time 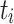 spends in the system. It has to be noted that the flow time is usually dominated by a task’s waiting time. This potentially leads to large differences between minimum, average, and maximum values.
spends in the system. It has to be noted that the flow time is usually dominated by a task’s waiting time. This potentially leads to large differences between minimum, average, and maximum values.
Experimental Setup
The experiments were performed on a server with two Intel Xeon E5-2650 v4 CPUs with 12 cores at 2.2 GHz each and dynamic voltage and frequency scaling enabled, an NVIDIA Tesla K80, and 128 GB of 2.4 GHz DDR4 SDRAM DIMM (PC4-19200). The software environment includes Ubuntu 18.04.3, the Linux 4.15.0-74.84-generic kernel, glibc 2.27, and the nvidia-410.48 driver. EMB was compiled with the GCC 7.4.0 compiler. We limited EMB
was compiled with the GCC 7.4.0 compiler. We limited EMB to 16 CPU cores for the experiments in order to increase the system load and simulate a highly utilized system.
to 16 CPU cores for the experiments in order to increase the system load and simulate a highly utilized system.
The scheduling algorithms presented in Sect. 4 operate in the so-called pull mode. In pull mode, the scheduler gets triggered iff at least one processing unit is idle. We chose this mode because it allows the scheduler to collect a set of tasks, which is needed to benefit from the batch mode heuristics.
Independent Heterogeneous Jobs
We chose three video-processing tasks that have both an OpenCL and a CPU implementation for the first scenario:
J
 (Mean): A
(Mean): A  box blur.
box blur.J
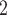 (Cartoonify): Performs a Sobel operator with a threshold selecting black pixels for edge regions and discretized RGB values for the interior. The Sobel operator consists of two convolutions with different
(Cartoonify): Performs a Sobel operator with a threshold selecting black pixels for edge regions and discretized RGB values for the interior. The Sobel operator consists of two convolutions with different 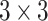 kernels followed by the computation of an Euclidean norm.
kernels followed by the computation of an Euclidean norm.J
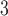 (Black-and-White (BW)): A simple filter which replaces (R,G,B) values with their greyscale version
(Black-and-White (BW)): A simple filter which replaces (R,G,B) values with their greyscale version 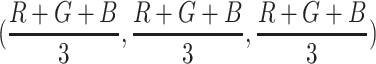 .
.
All operations were applied to the kodim23.png test image. The three operations execute for 72.8 ms, 165.97 ms, and 11.4 ms on the CPU and 3.4 ms, 3.1 ms, and 3.1 ms on the GPU. We assigned Mean the priority 1, Cartoonify the priority 2, and Black-and-White the priority 0 with 2 being the highest and maximum priority in the system. A sporadic profile was used to create task instances of these three jobs. New task instances were released with a minimum interarrival time of  s, where k is the parameter to control the load, plus a random delay drawn from an exponential distribution with parameter
s, where k is the parameter to control the load, plus a random delay drawn from an exponential distribution with parameter 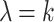 . By varying k, we can generate a range of different loads. The evaluation workload consists of 3000 tasks corresponding in equal proportions to instances of all three jobs. We conducted the experiment for
. By varying k, we can generate a range of different loads. The evaluation workload consists of 3000 tasks corresponding in equal proportions to instances of all three jobs. We conducted the experiment for 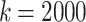 to simulate a heavily utilized system. The results of the makespan measurements can be seen in Table 1.
to simulate a heavily utilized system. The results of the makespan measurements can be seen in Table 1.
Table 1.
Makespan results of the independent heterogeneous jobs experiment
| MCT | Min-Min | Max-Min | Suff | RASA | RC | ||
|---|---|---|---|---|---|---|---|
| Cartoonify | min w/o aging | 1.43 s | 1.46 s | 1.45 s | 1.46 s | 1.42 s | 1.44 s |
| min w/ aging | 1.68 s | 1.64 s | 1.79 s | 1.51 s | 1.79 s | 1.59 s | |
| avg w/o aging | 1.49 s | 1.56 s | 1.54 s | 1.53 s | 1.59 s | 1.52 s | |
| avg w/aging | 1.88 s | 1.87 s | 2.22 s | 1.68 s | 2.25 s | 1.82 s | |
| max w/o aging | 1.64 s | 1.70 s | 1.65 s | 1.74 s | 1.78 s | 1.65 s | |
| max w/ aging | 2.38 s | 2.24 s | 3.67 s | 2.23 s | 3.71 s | 2.69 s | |
| Mean | min w/o aging | 2.17 s | 2.31 s | 2.35 s | 2.36 s | 2.29 s | 2.35 s |
| min w/ aging | 2.20 s | 2.69 s | 2.46 s | 2.48 s | 2.43 s | 2.70 s | |
| avg w/o aging | 2.29 s | 2.45 s | 2.49 s | 2.48 s | 2.51 s | 2.46 s | |
| avg w/ aging | 2.37 s | 2.86 s | 2.71 s | 2.60 s | 2.62 s | 2.85 s | |
| max w/o aging | 2.55 s | 2.82 s | 2.70 s | 2.86 s | 2.93 s | 2.70 s | |
| max w/ aging | 2.57 s | 3.08 s | 3.23 s | 2.68 s | 3.14 s | 3.06 s | |
| BW | min w/o aging | 2.38 s | 2.75 s | 2.79 s | 2.83 s | 2.68 s | 2.85 s |
| min w/ aging | 2.28 s | 2.42 s | 2.72 s | 2.52 s | 2.35 s | 2.56 s | |
| avg w/o aging | 2.51 s | 2.92 s | 2.98 s | 2.95 s | 2.96 s | 2.97 s | |
| avg w/ aging | 2.46 s | 2.57 s | 2.98 s | 2.74 s | 2.58 s | 2.80 s | |
| max w/o aging | 2.77 s | 3.27 s | 3.23 s | 3.32 s | 3.38 s | 3.27 s | |
| max w/ aging | 2.70 s | 2.74 s | 3.23 s | 2.84 s | 2.75 s | 2.99 s | |
| Total | min w/o aging | 2.38 s | 2.75 s | 2.79 s | 2.83 s | 2.68 s | 2.85 s |
| min w/ aging | 2.31 s | 2.69 s | 2.72 s | 2.62 s | 2.52 s | 2.70 s | |
| avg w/o aging | 2.51 s | 2.92 s | 2.98 s | 2.95 s | 2.96 s | 2.97 s | |
| avg w/ aging | 2.47 s | 2.86 s | 3.03 s | 2.74 s | 2.82 s | 2.90 s | |
| max w/o aging | 2.77 s | 3.27 s | 3.23 s | 3.32 s | 3.38 s | 3.27 s | |
| max w/ aging | 2.70 s | 3.08 s | 3.67 s | 2.82 s | 3.71 s | 3.06 s |
They show that for 5 out of 6 algorithms the average total makespan is improved by adding the aging mechanism, with Max-Min being the only algorithm where the makespan increases by 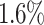 . On average over all algorithms, the average makespan is improved by about
. On average over all algorithms, the average makespan is improved by about 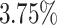 . Sufferage profits the most with an improvement of about
. Sufferage profits the most with an improvement of about 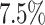 . Considering the single applications, aging increases the average makespan for Cartoonify by about
. Considering the single applications, aging increases the average makespan for Cartoonify by about 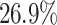 and for Mean by about
and for Mean by about 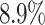 compared to a decrease of
compared to a decrease of 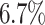 for Black-and-White. Especially for Max-Min and RASA, which uses Max-Min, the average makespan of Cartoonify suffers from an increase of over
for Black-and-White. Especially for Max-Min and RASA, which uses Max-Min, the average makespan of Cartoonify suffers from an increase of over 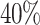 . Other noteworthy results are an increase of over
. Other noteworthy results are an increase of over 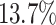 for the maximum measured total makespan for Max-Min and of over
for the maximum measured total makespan for Max-Min and of over 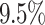 for RASA, which correlates with an increase of
for RASA, which correlates with an increase of 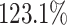 and
and 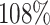 respectively for Cartoonify. Comparing the algorithms, MCT achieves the best average total makespan with and without aging while Max-Min achieves the worst result in both cases. Sufferage gets the second best results in both cases.
respectively for Cartoonify. Comparing the algorithms, MCT achieves the best average total makespan with and without aging while Max-Min achieves the worst result in both cases. Sufferage gets the second best results in both cases.
Further, we obtained results for the flow time 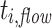 of each task instance
of each task instance 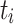 and then computed the minimum, average and maximum flow time for all three jobs. Table 2 lists the results.
and then computed the minimum, average and maximum flow time for all three jobs. Table 2 lists the results.
Table 2.
Flow time results of the independent heterogeneous jobs experiment
| MCT | Min-Min | Max-Min | Suff | RASA | RC | ||
|---|---|---|---|---|---|---|---|
| Cartoonify | min w/o aging | 1.54 ms | 1.61 ms | 1.46 ms | 1.49 ms | 1.46 ms | 1.48 ms |
| min w/ aging | 1.77 ms | 2.00 ms | 1.47 ms | 1.56 ms | 1.51 ms | 1.61 ms | |
| avg w/o aging | 214.01 ms | 239.59 ms | 222.93 ms | 229.04 ms | 233.67 ms | 220.88 ms | |
| avg w/ aging | 477.43 ms | 355.65 ms | 427.44 ms | 230.28 ms | 730.11 ms | 202.69 ms | |
| max w/o aging | 1047.54 ms | 948.90 ms | 1500.34 ms | 1137.52 ms | 1000.74 ms | 1124.99 ms | |
| max w/ aging | 1306.71 ms | 1553.85 ms | 3624.45 ms | 1454.86 ms | 3313.17 ms | 1838.82 ms | |
| Mean | min w/o aging | 1.81 ms | 1.72 ms | 1.62 ms | 1.72 ms | 1.64 ms | 1.64 ms |
| min w/ aging | 2.99 ms | 6.05 ms | 1.65 ms | 1.81 ms | 1.66 ms | 1.79 ms | |
| avg w/o aging | 1073.45 ms | 1208.23 ms | 1206.62 ms | 1261.46 ms | 1145.06 ms | 1226.23 ms | |
| avg w/ aging | 904.87 ms | 1092.57 ms | 1030.84 ms | 1073.86 ms | 886.34 ms | 1213.63 ms | |
| max w/o aging | 1498.08 ms | 2570.64 ms | 2708.11 ms | 2513.19 ms | 2180.18 ms | 2605.41 ms | |
| max w/ aging | 1459.64 ms | 26617.62 ms | 3196.53 ms | 1904.88 ms | 2830.09 ms | 2883.13 ms | |
| BW | min w/o aging | 1.41 ms | 1.69 ms | 1.33 ms | 1.41 ms | 1.44 ms | 1.57 ms |
| min w/ aging | 1.76 ms | 1.76 ms | 1.49 ms | 1.37 ms | 1.48 ms | 1.73 ms | |
| avg w/o aging | 1744.71 ms | 2085.71 ms | 2085.25 ms | 2142.52 ms | 2016.48 ms | 2123.33 ms | |
| avg w/ aging | 1400.28 ms | 1333.99 ms | 1946.73 ms | 1587.36 ms | 1263.95 ms | 1517.70 ms | |
| max w/o aging | 2365.10 ms | 2823.32 ms | 3116.59 ms | 2914.91 ms | 2817.72 ms | 3026.06 ms | |
| max w/ aging | 2089.93 ms | 2161.86 ms | 3210.39 ms | 2321.71 ms | 2402.84 ms | 2666.41 ms |
The results show a significant increase, by 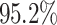 on average, in the average flow time for Cartoonify in 5 out of 6 experiments, with RC being the exception. For Cartoonify, this correlates with an increase in the maximum flow time for each algorithm. In contrast, the average flow time for both Mean and Black-and-White decreases for each algorithm by
on average, in the average flow time for Cartoonify in 5 out of 6 experiments, with RC being the exception. For Cartoonify, this correlates with an increase in the maximum flow time for each algorithm. In contrast, the average flow time for both Mean and Black-and-White decreases for each algorithm by 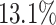 on average and
on average and 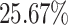 on average, respectively. This shows the effect of the aging mechanism as the waiting time for task instances of both jobs is reduced by increasing their priority. For Black-and-White, this also correlates with a decrease in the maximum flow time measured.
on average, respectively. This shows the effect of the aging mechanism as the waiting time for task instances of both jobs is reduced by increasing their priority. For Black-and-White, this also correlates with a decrease in the maximum flow time measured.
Parallel Applications
The second scenario consists of two Rodinia benchmark applications, Hotspot3D and Particlefilter, executed in parallel. Hotspot3D iteratively computes the heat distribution of a 3D chip represented by a grid. In every iteration, a new temperature value depending on the last value, the surrounding values, and a power value is computed for each element. We chose this computation as kernel function for a parallelization with EMB and parallelized it over the z-axis. The CPU implementation then further splits its task into smaller CPU specific subtasks. This is done manually and statically by the programmer to use the underlying parallelism of the multicore CPU and still have a single original CPU task that handles the same workload as the GPU task. For the evaluation, we used a
and parallelized it over the z-axis. The CPU implementation then further splits its task into smaller CPU specific subtasks. This is done manually and statically by the programmer to use the underlying parallelism of the multicore CPU and still have a single original CPU task that handles the same workload as the GPU task. For the evaluation, we used a 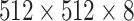 grid with the start values for temperature and power included in the benchmark, and 1000 iterations. The average runtime on the CPU is 5.03 ms and 7.36 ms on the GPU.
grid with the start values for temperature and power included in the benchmark, and 1000 iterations. The average runtime on the CPU is 5.03 ms and 7.36 ms on the GPU.
Particlefilter is a statistical estimator of the locations of target objects given noisy measurements. Profiling showed that findIndex() is the best candidate for a parallelization. findIndex() computes the first index in the cumulative distribution function array with a value greater than or equal to a given value. As findIndex() is called for every particle, we parallelized the computation by dividing the particles into work groups. The CPU implementation again further divides those groups into subtasks. We used the standard parameters 128 for both matrix dimensions, 100 for the number of frames, and 50000 for the number of particles for the evaluation. The average task runtime on the CPU is 17.8 ms and 6.5 ms on the GPU. Table 3 shows the makespan results without and with aging respectively for this experiment.
Table 3.
Makespan results of the Rodinia benchmarks experiment
| MCT | Min-Min | Max-Min | Suff | RASA | RC | ||
|---|---|---|---|---|---|---|---|
| Particlefilter | min w/o aging | 26.46 s | 26.52 s | 25.97 s | 26.57 s | 26.62 s | 25.61 s |
| min w/ aging | 27.25 s | 25.96 s | 26.37 s | 26.82 s | 26.23 s | 26.42 s | |
| avg w/o aging | 27.61 s | 27.73 s | 27.82 s | 27.72 s | 27.56 s | 27.85 s | |
| avg w/ aging | 27.76 s | 27.17 s | 27.49 s | 27.61 s | 27.62 s | 27.67 s | |
| max w/o aging | 28.79 s | 27.92 s | 28.83 s | 28.54 s | 28.79 s | 29.56 s | |
| max w/ aging | 28.62 s | 28.37 s | 28.55 s | 28.97 s | 29.15 s | 29.47 s | |
| Hotspot3D | min w/o aging | 26.84 s | 27.82 s | 29.91 s | 30.52 s | 26.63 s | 30.22 s |
| min w/ aging | 26.27 s | 25.37 s | 26.02 s | 25.93 s | 25.33 s | 27.82 s | |
| avg w/o aging | 30.93 s | 30.59 s | 31.44 s | 31.38 s | 30.71 s | 31.78 s | |
| avg w/ aging | 30.70 s | 30.59 s | 30.03 s | 30.96 s | 30.64 s | 30.93 s | |
| max w/o aging | 32.60 s | 32.18 s | 32.02 s | 32.28 s | 32.09 s | 33.46 s | |
| max w/ aging | 31.81 s | 31.91 s | 31.71 s | 32.47 s | 31.83 s | 33.16 s | |
| Total | min w/o aging | 26.84 s | 27.82 s | 29.91 s | 30.52 s | 26.63 s | 30.22 s |
| min w/ aging | 27.42 s | 26.68 s | 26.62 s | 26.82 s | 26.48 s | 27.82 s | |
| avg w/o aging | 30.93 s | 30.59 s | 31.44 s | 31.38 s | 30.71 s | 31.78 s | |
| avg w/ aging | 30.81 s | 30.72 s | 30.09 s | 31.05 s | 30.76 s | 30.93 s | |
| max w/o aging | 32.60 s | 32.18 s | 32.02 s | 32.28 s | 32.09 s | 33.46 s | |
| max w/ aging | 31.81 s | 31.91 s | 31.71 s | 32.47 s | 31.83 s | 33.16 s |
Overall, the average total makespan is improved by a speed up of about 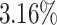 when aging is used and the average total makespan improves for 4 out of 6 algorithms, with Min-Min and RASA being the exceptions. In this scenario Max-Min improves most by using aging with a speed up of about
when aging is used and the average total makespan improves for 4 out of 6 algorithms, with Min-Min and RASA being the exceptions. In this scenario Max-Min improves most by using aging with a speed up of about 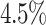 . The individual average makespans decrease by
. The individual average makespans decrease by 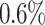 for Particlefilter and by
for Particlefilter and by 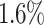 for Hotspot3D. It is also noteworthy that the minimum obtained makespan of Hotspot3D decreases by over
for Hotspot3D. It is also noteworthy that the minimum obtained makespan of Hotspot3D decreases by over 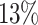 for both Max-Min and Sufferage. When the algorithms are compared, Min-Min achieves the best average total makespan without aging and Max-Min the best result with aging, with Min-Min getting the second best result.
for both Max-Min and Sufferage. When the algorithms are compared, Min-Min achieves the best average total makespan without aging and Max-Min the best result with aging, with Min-Min getting the second best result.
Again, we additionally monitored the flow time 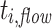 for all task instances
for all task instances 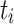 and computed the minimum, average, and maximum over all instances for both applications. The results are shown in Table 4.
and computed the minimum, average, and maximum over all instances for both applications. The results are shown in Table 4.
Table 4.
Flow time results of the Rodinia benchmarks experiment
| MCT | Min-Min | Max-Min | Suff | RASA | RC | ||
|---|---|---|---|---|---|---|---|
| Particlefilter | min w/o aging | 4.58 ms | 4.56 ms | 4.52 ms | 4.92 ms | 4.59 ms | 4.34 ms |
| min w/ aging | 4.29 ms | 4.37 ms | 4.68 ms | 4.65 ms | 4.18 ms | 4.45 ms | |
| avg w/o aging | 42.16 ms | 42.10 ms | 43.93 ms | 43.61 ms | 42.19 ms | 42.21 ms | |
| avg w/ aging | 43.35 ms | 41.98 ms | 43.46 ms | 41.69 ms | 42.66 ms | 43.47 ms | |
| max w/o aging | 564.30 ms | 568.94 ms | 606.79 ms | 663.52 ms | 528.12 ms | 723.96 ms | |
| max w/ aging | 636.67 ms | 506.50 ms | 490.95 ms | 639.28 ms | 651.32 ms | 543.53 ms | |
| Hotspot3D | min w/o aging | 2.34 ms | 1.96 ms | 2.15 ms | 1.92 ms | 1.94 ms | 1.67 ms |
| min w/ aging | 1.63 ms | 1.65 ms | 1.62 ms | 1.63 ms | 2.33 ms | 1.62 ms | |
| avg w/o aging | 13.33 ms | 13.06 ms | 13.27 ms | 13.16 ms | 13.25 ms | 13.49 ms | |
| avg w/ aging | 13.31 ms | 13.28 ms | 13.16 ms | 13.31 ms | 13.17 ms | 13.37 ms | |
| max w/o aging | 932.72 ms | 801.60 ms | 838.39 ms | 686.93 ms | 648.79 ms | 819.58 ms | |
| max w/ aging | 709.43 ms | 674.13 ms | 656.37 ms | 938.87 ms | 664.43 ms | 735.07 ms |
The results show a decrease in the minimum and maximum flow time of Hotspot3D for 5 and 4 algorithms, respectively. This correlates with shorter waiting times caused by a priority raise. The averages roughly remain unchanged. This can be explained by the much larger number of tasks for Hotspot3D, which are executed after Particlefilter is finished and thereby dominate the average for Hotspot3D.
Related Work
Known existing task-based runtime systems such as HALadapt [14], the TANGO framework [8], and HPX [11] do not employ task priorities to distinguish application importance. StarPU [3], though, supports assigning a priority per processing unit type to a task. Compared to our work, StarPU does not adapt priorities at runtime.
Task or job scheduling algorithms with priorities are usually employed in the context of real-time systems, especially hard real-time systems with strict deadlines. These algorithms can be classified by the way they assign priorities [5]. Algorithms like EDF [9] or least laxity first (LLF) [6] assign each task instance a different priority. Thereby, EDF assigns each instance an individual static priority based on its deadline (see Sect. 2), whereas the priorities assigned by LLF are dynamically adapted as the laxity, the remaining time until a task has to be started to fulfill its deadline, decreases over time [5]. Contrary to this, algorithms like RMS [16] set a static priority that applies to each instance. The work of this paper differs from these algorithms as our tasks do not possess deadlines. In our work, an application developer is allowed to set a priority for a task that then applies to each instance. However, we additionally utilize an aging mechanism to increase fairness, i.e. priorities may be dynamically adapted.
Similarly to EDF, list scheduling algorithms [22–24] prioritize and then order individual task instances by computing metrics like the upward rank used by the heterogeneous earliest finish time (HEFT) heuristic.
Kim et al. [15] consider task priorities and deadlines in the context of dynamic systems, where the arrival of tasks is unknown. The paper uses three priority levels, high, medium, low, that can be assigned to task instances. The priorities are combined with the tasks’ deadlines to compute the worth of executing a task. Thereby, a scheduling order is created. In contrast to our approach, priorities are not dynamically adapted to avoid starvation.
Aging mechanisms have been employed in several other works. Kannan et al. [13] implemented three priority queues and task instances get promoted to a higher priority level after a fixed time interval. Similarly, the priority of a task also gets promoted at fixed time intervalls in [19]. In [7], a counter is decreased after high priority tasks are executed. If a threshold is reached, a low priority task is executed next.
Conclusion and Future Work
In this work, we developed an adaptive aging mechanism and integrated it in combination with six different dynamic scheduling algorithms into the task-based runtime system EMB . We evaluated the scheduling algorithms in two scenarios with task priorities, a benchmark consisting of three independent heterogeneous jobs with a sporadic profile, and two Rodinia benchmarks executed in parallel. Thereby, the experiments were conducted without and with the developed aging mechanism to examine its effects.
. We evaluated the scheduling algorithms in two scenarios with task priorities, a benchmark consisting of three independent heterogeneous jobs with a sporadic profile, and two Rodinia benchmarks executed in parallel. Thereby, the experiments were conducted without and with the developed aging mechanism to examine its effects.
The results show a slight improvement in total average makespan (average speed up of 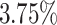 and
and 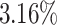 ) for 5 out of 6 algorithms in the first and for 4 out of 6 algorithms in the second scenario. As expected, this correlates with an increase in the average makespan for the applications with higher priorities caused by additional waiting time (the total time spent in queues in the scheduler and processing unit). This is also reflected in the flow time measurements. The average increase of
) for 5 out of 6 algorithms in the first and for 4 out of 6 algorithms in the second scenario. As expected, this correlates with an increase in the average makespan for the applications with higher priorities caused by additional waiting time (the total time spent in queues in the scheduler and processing unit). This is also reflected in the flow time measurements. The average increase of 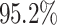 for the average flow time of the Cartoonify benchmark is exemplary for this statement. However, the average flowtime and the average makespan of the application/job with the highest priority remain lowest over all applications/jobs in all experiments. In return, the aging mechanism reduces the waiting time which is reflected by improvements of the average makespan and the average flow time of the job/application with the lowest priority (
for the average flow time of the Cartoonify benchmark is exemplary for this statement. However, the average flowtime and the average makespan of the application/job with the highest priority remain lowest over all applications/jobs in all experiments. In return, the aging mechanism reduces the waiting time which is reflected by improvements of the average makespan and the average flow time of the job/application with the lowest priority (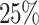 decrease in average flowtime for black-and-white). A comparison between the scheduling algorithms shows that no algorithm dominates the other ones considering the average total makespan. MCT, Sufferage, and RC, though, are able to profit in all experiments by using aging.
decrease in average flowtime for black-and-white). A comparison between the scheduling algorithms shows that no algorithm dominates the other ones considering the average total makespan. MCT, Sufferage, and RC, though, are able to profit in all experiments by using aging.
In summary, our adaptive aging mechanism slightly improves the overall makespan in most experiments while reducing the time a low priority task has to wait for its execution, thereby increasing fairness, and still securing the fastest execution and shortest time spent in the system for the job with the highest priority. In the future, supplemental evaluations are necessary to further solidify these conclusions. Furthermore, additional optimization goals next to fairness and makespan, like energy consumption, have to be considered.
Footnotes
Contributor Information
André Brinkmann, Email: brinkman@uni-mainz.de.
Wolfgang Karl, Email: wolfgang.karl@kit.edu.
Stefan Lankes, Email: slankes@eonerc.rwth-aachen.de.
Sven Tomforde, Email: st@informatik.uni-kiel.de.
Thilo Pionteck, Email: thilo.pionteck@ovgu.de.
Carsten Trinitis, Email: carsten.trinitis@tum.de.
Thomas Becker, Email: thomas.becker@kit.edu.
Tobias Schüle, Email: tobias.schuele@siemens.com.
References
- 1.Armstrong, R., Hensgen, D., Kidd, T.: The relative performance of various mapping algorithms is independent of sizable variances in run-time predictions. In: Seventh Proceedings of the Heterogeneous Computing Workshop (HCW 1998), pp. 79–87, March 1998. 10.1109/HCW.1998.666547
- 2.Becker T, Karl W, Schüle T. Evaluating dynamic task scheduling in a task-based runtime system for heterogeneous architectures. In: Schoeberl M, Hochberger C, Uhrig S, Brehm J, Pionteck T, editors. Architecture of Computing Systems - ARCS 2019. Cham: Springer; 2019. pp. 142–155. [Google Scholar]
- 3.Bramas B. Impact study of data locality on task-based applications through the Heteroprio scheduler. PeerJ Comput. Sci. 2019;5:e190. doi: 10.7717/peerj-cs.190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Che, S., et al..: Rodinia: a benchmark suite for heterogeneous computing. In: Proceedings of the 2009 IEEE International Symposium on Workload Characterization (IISWC), IISWC 2009, pp. 44–54. IEEE Computer Society, Washington, DC (2009). 10.1109/IISWC.2009.5306797
- 5.Davis RI, Burns A. A survey of hard real-time scheduling for multiprocessor systems. ACM Comput. Surv. 2011;43(4):1–44. doi: 10.1145/1978802.1978814. [DOI] [Google Scholar]
- 6.Dertouzos ML, Mok AK. Multiprocessor online scheduling of hard-real-time tasks. IEEE Trans. Softw. Eng. 1989;15(12):1497–1506. doi: 10.1109/32.58762. [DOI] [Google Scholar]
- 7.Dhivya., P., Sangamithra., V., KamalRaj, R., Karthik, S.: Improving the resource utilization in grid environment using aging technique. In: Third International Conference on Computing, Communication and Networking Technologies (ICCCNT 2012). pp. 1–5, July 2012. 10.1109/ICCCNT.2012.6395912
- 8.Djemame, K., et al.: TANGO: transparent heterogeneous hardware architecture deployment for energy gain in operation. CoRR abs/1603.01407 (2016). http://arxiv.org/abs/1603.01407
- 9.Garey MR, Johnson DS. Computers and Intractability: A Guide to the Theory of NP-Completeness. New York: W. H. Freeman & Co.; 1990. [Google Scholar]
- 10.Graham, R., Lawler, E., Lenstra, J., Kan, A.: Optimization and approximation in deterministic sequencing and scheduling: a survey. In: Hammer, P., Johnson, E., Korte, B. (eds.) Discrete Optimization II, Annals of Discrete Mathematics, vol. 5, pp. 287–326. Elsevier (1979)
- 11.Heller, T., Diehl, P., Byerly, Z., Biddiscombe, J., Kaiser, H.: HPX - An open source C++ Standard Library for Parallelism and Concurrency. In: Proceedings of OpenSuCo 2017 (OpenSuCo 2017), Denver, Colorado, USA, November 2017, p. 5 (2017)
- 12.Ibarra OH, Kim CE. Heuristic algorithms for scheduling independent tasks on nonidentical processors. J. ACM. 1977;24(2):280–289. doi: 10.1145/322003.322011. [DOI] [Google Scholar]
- 13.Kannan, G., Thamarai Selvi, S.: Nonpreemptive priority (NPRP) based job scheduling model for virtualized grid environment. In: 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE), vol. 4, pp. V4-377–V4-381, August 2010. 10.1109/ICACTE.2010.5579461
- 14.Kicherer M, Nowak F, Buchty R, Karl W. Seamlessly portable applications: managing the diversity of modern heterogeneous systems. ACM Trans. Archit. Code Optim. 2012;8(4):42:1–42:20. doi: 10.1145/2086696.2086721. [DOI] [Google Scholar]
- 15.Kim JK, et al. Dynamically mapping tasks with priorities and multiple deadlines in a heterogeneous environment. J. Parallel Distrib Comput. 2007;67(2):154–169. doi: 10.1016/j.jpdc.2006.06.005. [DOI] [Google Scholar]
- 16.Liu CL, Layland JW. Scheduling algorithms for multiprogramming in a hard-real-time environment. J. ACM. 1973;20(1):46–61. doi: 10.1145/321738.321743. [DOI] [Google Scholar]
- 17.Wu, M.-Y., Shu., W: A high-performance mapping algorithm for heterogeneous computing systems. In: Proceedings 15th International Parallel and Distributed Processing Symposium. IPDPS 2001, pp. 6 pp, April 2001
- 18.Parsa S, Entezari-Maleki R. RASA: a new task scheduling algorithm in grid environment. World Appl. Sci. J. 2009;7:152–160. [Google Scholar]
- 19.Pathan, R.M.: Unifying fixed- and dynamic-priority scheduling based on priority promotion and an improved ready queue management technique. In: 21st IEEE Real-Time and Embedded Technology and Applications Symposium, pp. 209–220 (2015)
- 20.Rajak, N., Dixit, A., Rajak, R.: Classification of list task scheduling algorithms: a short review paper. J. Ind. Intell. Inf. 2 (2014). 10.12720/jiii.2.4.320-323
- 21.Schuele, T.: Embedded Multicore Building Blocks: Parallel Programming Made Easy. Embedded World (2015)
- 22.Topcuoglu, H., Hariri, S., Wu, M.-Y.: Task scheduling algorithms for heterogeneous processors. In: Proceedings of the Eighth Heterogeneous Computing Workshop (HCW 1999), pp. 3–14, April 1999. 10.1109/HCW.1999.765092
- 23.Xu Y, Li K, Hu J, Li K. A genetic algorithm for task scheduling on heterogeneous computing systems using multiple priority queues. Inf. Sci. 2014;270:255–287. doi: 10.1016/j.ins.2014.02.122. [DOI] [Google Scholar]
- 24.Zhao H, Sakellariou R. An experimental investigation into the rank function of the heterogeneous earliest finish time scheduling algorithm. In: Kosch H, Böszörményi L, Hellwagner H, editors. Euro-Par 2003 Parallel Processing; Heidelberg: Springer; 2003. pp. 189–194. [Google Scholar]


