Automatic Brain Extraction for Rodent MRI Images

Abstract

Rodent models are increasingly important in translational neuroimaging research. In rodent neuroimaging, particularly magnetic resonance imaging (MRI) studies, brain extraction is a critical data preprocessing component. Current brain extraction methods for rodent MRI usually require manual adjustment of input parameters due to widely different image qualities and/or contrasts. Here we propose a novel method, termed SHape descriptor selected Extremal Regions after Morphologically filtering (SHERM), which only requires a brain template mask as the input and is capable of automatically and reliably extracting the brain tissue in both rat and mouse MRI images. The method identifies a set of brain mask candidates, extracted from MRI images morphologically opened and closed sequentially with multiple kernel sizes, that match the shape of the brain template. These brain mask candidates are then merged to generate the brain mask. This method, along with four other state-of-the-art rodent brain extraction methods, were benchmarked on four separate datasets including both rat and mouse MRI images. Without involving any parameter tuning, our method performed comparably to the other four methods on all datasets, and its performance was robust with stably high true positive rates and low false positive rate. Taken together, this study provides a reliable automatic brain extraction method that can contribute to the establishment of automatic pipelines for rodent neuroimaging data analysis.

1. Introduction

Brain extraction, with the purpose of extracting the brain tissue from the surrounding tissues in magnetic resonance imaging (MRI) images, is a critical component in neuroimaging data processing. This component is also a prerequisite for other neuroimaging data analysis procedures such as brain registration/normalization, brain tissue segmentation, as well as quantification of regional volume and cortical thickness.

A number of automated brain extraction methods have been proposed for human MRI structural (T1- or T2-weighted) images (Avants et al. 2011; Cox 1996; Doshi et al. 2013; Eskildsen et al. 2012; Heckemann et al. 2015; Huang et al. 2006; Iglesias et al. 2011; Leung et al. 2011; Smith 2002), as well as rodent structural (T1- or T2- weighted) and diffusion weighted images (Chou et al. 2011; Delora et al. 2016; Lee et al. 2009; Li et al. 2013; Oguz et al. 2011, 2014; Roy et al. 2018; Wood et al. 2013). Unlike human MRI data acquisition, which has been highly standardized, rodent MRI images are acquired with a wide range of setups and imaging parameters, which can result in large variations in intensity profiles, contrast, spatial resolution, field of view (FOV) and signal-to-noise ratio (SNR). Consequently, brain extraction methods used for rodent MRI data typically require manual fine tuning of parameters in separate studies with various image modalities and qualities, and tend to perform sub-optimally with inappropriate parameters (Fig. S1). Considering that rodent models are increasingly important in translational neuroimaging studies, and rodent imaging data are expanding exponentially (Denic et al. 2011; Hoyer et al. 2014; Jonckers et al. 2015; Liu et al. 2019), manual adjustment during brain extraction can be time-consuming and inefficient. Therefore, an automatic brain extraction method that can cope with various imaging modalities and qualities is highly desirable.

In addition to cumbersome manual adjustment, current brain extraction methods can have unstable performance in processing rodent images. For instance, template/atlas-matching techniques match the subject images or image patches to a library of template images or atlases containing prior probabilistic information of tissue types through sequential affine and nonlinear image registrations (Ashburner and Friston 2000; Avants et al. 2011; Eskildsen et al. 2012; Heckemann et al. 2015; Lee et al. 2009; Leung et al. 2011; Oguz et al. 2011). These techniques usually provide accurate results in human images (Eskildsen et al. 2012; Esteban et al. 2019), but the performance can be inconsistent when being applied to rodent brain images, possibly due to sub-optimal rigid registration (Oguz et al. 2014), and/or a larger portion of non-brain tissue in rodents relative to humans. In addition, deep learning methods require substantial manually labeled data and their performance can be affected by the similarity between the training dataset and the data to analyze (Kleesiek et al. 2016; Roy et al. 2018). Other techniques such as deformable surface model (Li et al. 2013; Oguz et al. 2014; Smith 2002; Wood et al. 2013; Zhang et al. 2011), level-set methods (Cheng et al. 2005; Huang et al. 2007), morphological operations (Chou et al. 2011; Oguz et al. 2014; Shattuck et al. 2001; Shattuck and Leahy 2002), edge detection (Shattuck and Leahy 2002), and artificial neural network (Chou et al. 2011; Murugavel and Sullivan 2009) need to rely on the contrast between brain tissue and surrounding non-brain tissue, which can vary between different MRI pulse sequences (Chou et al. 2011; Li et al. 2013; Murugavel and Sullivan 2009; Oguz et al. 2011; Wood et al. 2013). These factors can all contribute to variable performance of current brain extraction methods in processing rodent images.

Here we propose a novel automatic rodent brain extraction method, termed SHape descriptor selected Extremal Regions after Morphologically filtering (SHERM), which only uses a brain template mask as the input and can robustly extract brain tissue in distinct MRI datasets. The method relies on the fact that the shape of the rodent brain is highly consistent across individuals, and uses shape descriptors, which can identify brain mask candidates that match the shape of the brain template, as an effective tool for automatic rodent brain extraction. We benchmarked four state-of-the-art rodent brain extraction methods, Rodent Brain Extraction Tool (RBET) (Wood et al. 2013), three dimensional pulse coupled neural networks (3D-PCNN) (Chou et al. 2011), Rapid Automatic Tissue Segmentation (RATS) (Oguz et al. 2014), and BrainSuite (Shattuck and Leahy 2002), on four separate datasets including anisotropic T1- and T2-weighted rat structural images, anisotropic T1-weighted mouse structural images, and isotropic T2-weighted mouse structural images.

2. Materials and Methods

2.1. Method design

A. Overview of workflow

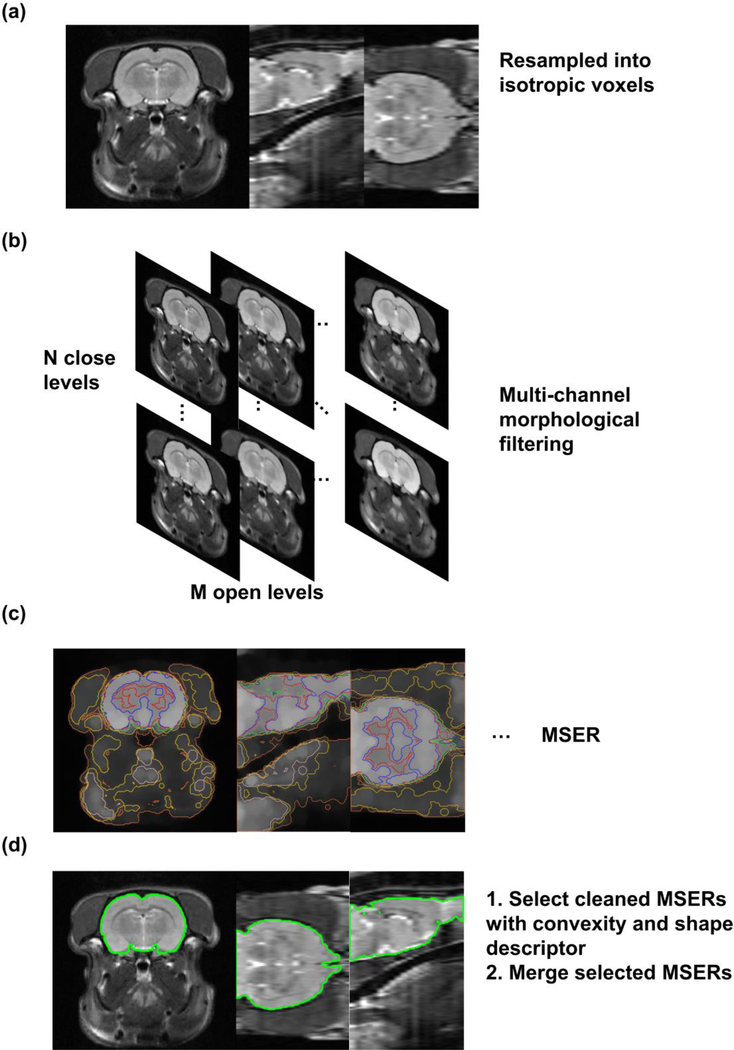
The method we proposed combined morphological operation, blob feature detection, and a shape descriptor. First, rodent head MRI images, if containing anisotropic voxels, were resampled into isotropic voxels using tri-cubic interpolation (Fig. 1a). Second, images were filtered with morphological operations of multiple kernel sizes so that morphological features in the image (e.g. boundaries and skeletons) of multiple scales were intensified. This step resulted in a multi-channel output for a given image (Fig. 1b). Third, blob features called maximally stable extremal regions (MSERs) (Matas et al. 2004), which were connected regions with uniform internal gray values and large gradients at boundaries, in these output images were extracted (Fig. 1c). Fourth, these MSERs were screened by convexity and evaluated by a shape descriptor. A set of MSERs with the shape matching that of the brain template were selected and merged to generate the brain mask (Fig. 1d).

Fig. 1.

Pipeline of the SHERM method. (a) Input images, if having anisotropic voxels, are resampled into isotropic voxels. (b) Images are morphologically opened and closed with ball kernels of multiple radii. (c) MSERs are computed in filtered images. (d) A set of cleaned MSERs with the shapes matching those of the template were selected, and merge to generate the brain mask.

B. Multi-channel morphological filtering on grayscale images

In the morphological operation, we used a grayscale image I and a structural element H as inputs, where H was a ball with the radius r and kernel size (2r+1) × (2r+1) × (2r+1). Values within the ball were ones and values outside of the ball were zeros. Morphological erosion on I with H can be written as

$$(I\ominus H)(u,v,w)=\underset{H(i,j,k)=1}{min}\{I(u+i,v+j,w+k)\}$$ (1)

, where u, v, w, i, j, and k indicate voxel locations. Similarly, morphological dilation on I with H can be written as

$$(I\oplus H)(u,v,w)=\underset{H(i,j,k)=1}{max}\{I(u+i,v+j,w+k)\}$$ (2)

The morphological opening, defined as (A ⊝ B) ⊕ B (erosion followed by dilation), enlarges dark regions on dark background and shrinks bright regions on bright background, whereas the morphological closing, defined as (A ⊕ B) ⊖ B (dilation followed by erosion) does the opposite.

Images were morphologically opened with kernels of N different sizes and then morphologically closed with kernels of M different sizes, which generated M × N output channels for an image (Fig 1b). The purpose of this step was to open the dark gap around the brain tissue (consisting of the skull and cerebrospinal fluid) and to close the dark gaps within the brain, such as the white matter in T2-weighted images.

C. Maximally Stable Extremal Region (MSER)

The concept of MSER was proposed by Matas et al. (Matas et al. 2004). The goal was to detect blob features, which are connected regions that have relatively uniform internal gray values and large gradient at boundaries, by considering the overall gradient intensities at the boundary of a region. An extremal region of an image is a connected region R with all voxels in the region larger than (called maximally extremal region) or smaller than (called minimally extremal region) a threshold l. A stable extremal region is an extremal region that does not appreciably change when the intensity threshold l changes. A set of extremal regions R_l can be constructed by selecting the intensity threshold l from a set of values. Then, this set of extremal regions R_l can be depicted by a tree as smaller minimally/maximally extremal regions emerge as intensity threshold l increases/decreases. In other words, a minimally extremal region R_l is a child of another minimally extremal region R_l+1 as R_l ⊂ R_l+1. A branch of the tree consists of a series of descendant regions that have only one child, and thus, an extremal region grows as threshold increases or decreases until it merges with another extremal region. For each branch, we can define a maximally stable extremal region. The stability can be measured by a stability score

$$S=\frac{volume\left(R_{l+\mathrm{\Delta }}-R_l\right)}{volume\left(R_l\right)}$$ (3)

, which represents how much R_l changes in volume as the intensity threshold increases from l to l + Δ. The smaller the stability score is, the more stable the region is. Therefore, our method searched for a local minimum of the stability score in each branch and the corresponding region was the MSER of the branch.

D. Clean MSERs

First, MSERs were morphologically opened by a ball kernel with the radius twice of the voxel size. If MSERs were separated into multiple disconnected regions (based on the 6-connectivity measure), only the largest one was kept. For anisotropic images, MSER masks were resized to the original resolution, and ‘slice-wise connected’ 3D regions in these masks were then extracted.

Slice-wise connectivity was defined as connectivity between 2D regions on adjacent slices, quantified by the ratio between their connected (i.e. overlapped) area and their averaged area.

$$\mathrm{Slice}-\mathrm{wise}\mathrm{Connectivity}=\frac{2\left|R_i\cap R_j\right|}{\left|R_i\right|+\left|R_j\right|}$$ (4)

, where R_i and R_j are 2D regions in adjacent slices. A slice-wise connected 3D region is a 3D region, in which the slice-wise connectivity of every pair of its 2D regions on adjacent slices was greater than a threshold (0.1 in our implementation). As shown in Fig. 2, this method can successfully separate brain and non-brain regions.

Fig. 2.

The use of 3D slice-wise connectivity in images with anisotropic resolution. Brain (green) and non-brain (blue and yellow) regions are separated by slice-wise connectivity, shown on the same un-interpolated image. The arrow points to the overlapped region used to define the slice-wise connectivity (Eq. 4).

Finally, the extracted regions were morphologically closed by a ball kernel with the radius twice the size of the in-plane resolution to close up irregular boundaries, and holes in resulting regions were then filled.

E. MSER selection with shape discrimination

This step aimed to select a set of MSERs with the shape matching that of the template. First, we used the convexity (Sonka et al. 2007) to screen MSERs. Convexity of a region is defined as the ratio between its volume and that of its convex hull, which is the smallest convex polyhedron that contains the region. MSERs with convexity smaller than 0.85 were discarded. The threshold was determined by the minimal convexity of rat and mouse brain atlases truncated by various FOVs.

Then, shapes of the MSERs were compared to that of the template using a shape descriptor, which was the distances from voxels in the MSERs to their longest (first) principal axis sampled on a polar grid (Fig. 3). The distances were sampled on a polar coordinate system around the longest principal axis with digitized grids on the radial coordinate r and the angular coordinate φ. The zero angular line aligned with either the second or the third principal axis. The directions of the three orthogonal principal axes of the MSERs were calculated by applying the principal component analysis (PCA) on the covariance matrix of [x, y, z], where x, y, z ∈ ℝ ⁿ were column vectors of coordinates of n voxels in each MSER, and the directions of the principal components were the directions of the axes. In our implementation, we evenly split the range of r (0 to the maximum r) into 10 intervals and split the range of φ (0–2π) into 20 intervals, which resulted in a 200-bin histogram of within-MSER voxels’ distances to the first principal axis. The scale of the histogram was normalized by the MSER’s projected area on the plane orthogonal to the first principal axis to account for potential difference in brain size. The distance between two shape descriptors was defined as the L1 norm of the element-wise difference between the two, which measured the shape similarity of the MSER to the template.

Fig. 3.

Construction of the shape descriptor. (a) Principal axes computed by PCA. (b) Sampling the distance from voxels in the 3D mask to the first principal axis using grids on a polar coordinate system (showed by red dashed lines). (c) Examples of shape descriptors. Distance between the template and MSER1 is 0.166; distance between the template and MSER2 is 0.634.

The descriptor is invariant to the position and orientation of the MSER, except that a flipped or 180-degree rotated region would have a different descriptor from its original region if the region is asymmetric. Therefore, all images needed to be reoriented before processing to match the orientation of the template, which were done automatically using the header of NIfTI or DICOM files.

Subsequently, we identified a set of MSERs that had the shape descriptors similar to that of the template. Specifically, we first identified the MSER that had the shape descriptor (denoted as SD₀) closest to that of the template (denoted as SD_tmp). Then we selected a set of MSERs, whose shape descriptor SD satisfied the following criterion:

$${\left|\left|{\left|\left|SD-S{D}_{\text{tmp}}\right|\right|}_1-{\left|\left|S{D}_0-S{D}_{\text{tmp}}\right|\right|}_1\right|\right|}_1<0.05*{\Vert S{D}_{\text{tmp}}\Vert }_1$$ (5)

These MSERs were merged using their union as the final brain mask.

2.2. Method Implementation

The method was implemented in MATLAB (version: 2018b) (Mathworks, Natick, MA, USA). The source code is available at https://github.com/liu-yikang/SHERM-rodentSkullStrip.

Morphological operations were implemented by calling the built-in functions imopen and imclose in MATLAB. Radii of opening and closing kernels ranged from 0.2 mm to 0.7 mm, and from 0.2 mm to 0.5 mm, respectively, with the step sizes the same as the in-plane spatial resolution.

MSER was implemented by calling the MATLAB interface of the VLFeat package (version: 0.9.20) (Vedaldi and Fulkerson 2010). The input parameters of MSER were: MaxArea = 1900 mm³/volume for the FOV of rat images and 500 mm³/volume for the FOV of mouse images, MinArea = 1500 mm³/volume for the FOV of rat images and 300 mm³/volume for the FOV of mouse images, MinDiversity = 0.05, MaxVariation = 0.5, and Delta = 1. The first two parameters indicate the brain size relative to the FOV. MinDiversity means that if the relative area variation of two nested regions was below the threshold, the more stable one was selected. MaxVariation set the maximum stable score allowed. MinDiversity was set small and MaxVariation was set large so that the method could provide more MSERs for selection and handle images of various modalities and qualities. Delta, the step length of intensity threshold, was set minimum for the same purpose. For the shape discrimination, volume of the convex hull and PCA were computed by calling the built-in function convhull and pca in MATLAB, respectively. Multi-channel morphological filtering and MSER cleaning were implemented in parallel using parfor in MATLAB. To reduce computational cost, MSERs of very small or large volumes were discarded before shape discrimination. The range for rat and mouse data were 1500–1900 mm³ and 300–550 mm^3, respectively.

2.3. Evaluation and Benchmarking

A. Dataset

We used four separate datasets to benchmark our method with other methods.

The first two datasets consisted of ten T1-weighted and seven T2-weighted brain images of Long-Evans rats (280–360g), respectively, acquired on a 7T Bruker 70/30 BioSpec running ParaVision 6.0.1 (Bruker, Billerica, MA) with a custom-built volume coil at the High Field MRI Facility at the Pennsylvania State University. Rapid imaging with refocused echoes (RARE) sequence was used for both datasets. Imaging parameters of T1-weighted images were: repetition time (TR) = 1500 ms; echo time (TE) = 8 ms; matrix size = 256 × 256; FOV = 3.2 × 3.2 cm2; slice number = 20; slice thickness = 1 mm. Imaging parameters of T2-weighted images were: TR = 4200 ms; TE = 30 ms; matrix size = 256 × 256; FOV = 3.2 × 3.2 cm2; slice number = 20; slice thickness = 1 mm.

The third dataset consisted of twelve T1-weighted brain images of C57BL/6J mice (23–27g), acquired on the same 7T Bruker scanner with different custom-built volume coil. The RARE sequence was used with parameters: TR = 1500 ms; TE = 8 ms; matrix size = 128 × 128; FOV = 1.6 × 1.6 cm2; slice number = 20; slice thickness = 0.75 mm.

For these three datasets, animals were first acclimated to the MRI scanning environment for four to seven days to minimize motion and stress during imaging (Liang et al. 2011). Before imaging, animals were anesthetized using 2% isoflurane, secured into a head restrainer with a built-in coil, and placed into a body tube. Isoflurane was discontinued after the setup and rats/mice were fully awake during imaging. All experiments were approved by the Institutional Animal Care and Use Committee (IACUC) of the Pennsylvania State University.

The fourth dataset was from the MRM NeAt database (Y. Ma et al. 2005; Yu Ma 2008), consisting of nine T2-weighted images of C57BL/6J male mice (25–30g), acquired on a 9.4T/210 mm horizontal bore magnet (Magnex), with a birdcage coil for transmission and a surface coil for receiving. A 3D large flip angle (145°) spin echo sequence was used (number of excitations = 1; TE = 7.5ms; TR = 400 ms; 0.1 mm isotropic resolution).

The template used for rat and mouse images was the brain mask from Waxholm Space atlases of the Sprague Dawley rat brain (Papp et al. 2014) and the C57BL/6 mouse brain (Johnson et al. 2010), respectively.

All images were corrected for intensity non-uniformity using the Non-parametric Non-uniform intensity Normalization (N3) method (Sled et al. 1998). Images from the MRM NeAt database were denoised by a Gaussian kernel with the standard deviation of one voxel size before processing.

B. Benchmarked Methods

Four other state-of-the-art rodent brain extraction methods including RBET (version: Jan-2014) (Wood et al. 2013), 3D-PCNN (version: Aug-2017) (Chou et al. 2011), RATS (version: Sep-2014) (Oguz et al. 2014), and BrainSuite (version:19a) (Shattuck and Leahy 2002) were also tested under multiple input parameters. For each dataset, the input parameters that provided the best averaged performance on the dataset were used. Images with anisotropic spatial resolutions were resampled into isotropic voxels by tri-cubic interpolation before being processed by these methods.

Table 1 summarizes the ranges of input parameters tested and the best value chosen (bracketed) for each dataset and each method. For RBET, the head radius was fixed at 6 mm for rats and 3 mm for mice; the center of gravity of initial mesh surface was fixed at the empirical brain centroid. For 3D-PCNN, the brain volume ranges for rats and mice were set at 1500–1900 mm³ and 300–500 mm³, respectively. For RATS, the brain volume for rats and mice was set at 1650 mm³ and 380 mm³, respectively. Other input parameters used the corresponding default values for the four methods.

Table 1.

Range of input parameters tested (three numbers are minimum, step size and maximum, respectively) and the best values (bracketed) for each method on each dataset.

	RBET fractional intensity threshold	3D-PCNN radius of structural element (mm)	RATS intensity threshold (normalized by image maximum)	BrainSuite diffusion constant; diffusion iteration; edge constant; erosion size (voxel)
D1 (T1 rat, AN)	0.1:0.05:0.35 [0.3]	0.5:0.25:1.25 [1]	0.120:0.036:0.264 [0.192]	15:5:30 [30] 2:2:6 [6] 0.5:0.1:0.9 [0.7] 1:1:4 [4]
D2 (T2 rat, AN)	0.1:0.05:0.35 [0.25]	0.5:0.25:1.25 [0.5]	0.107:0.046:0.290 [0.153]	15:5:30 [25] 2:2:6 [2] 0.5:0.1:0.9 [0.6] 1:1:4 [4]
D3 (T1 mouse, AN)	0.1:0.05:0.35 [0.3]	0.5:0.25:1.25 [1]	0.183:0.061:0.427 [0.244]	15:5:30 [25] 2:2:6 [6] 0.5:0.1:0.9 [0.7] 1:1:4 [3]
D4 (T2 mouse, ISO)	0.1:0.05:0.35 [0.1]	0.4:0.2:1 [0.4]	0.025:0.012:0.074 [0.037]	15:5:30 [30] 2:2:6 [6] 0.5:0.1:0.9 [0.8] 1:1:4 [3]

AN: anisotropic resolution; ISO: isotropic resolution.

Manually drawn masks or the masks available from the atlases were used as the ‘ground truth’ to evaluate the accuracy of all methods. Masks were drawn slice-by-slice in MRIcron (https://www.nitrc.org/projects/mricron). Individuals who drew the masks had adequate knowledge of rodent brain anatomy and were blind to results from all tested methods.

The Jaccard index, true-positive rate (TPR), and false-positive rate (FPR) used in (Chou et al. 2011) were used to evaluate the performance of all methods:

$$\mathrm{Jaccard}\mathrm{index}=\frac{\left|M_{auto}\cap M_{manual}\right|}{\left|M_{auto}\cup M_{manual}\right|}$$ (6)

$$\text{TPR}=\frac{\left|M_{auto}\cap M_{manual}\right|}{\left|M_{manual}\right|}$$ (7)

$$\text{FPR}=\frac{\left|M_{auto}-M_{auto}\cap M_{manual}\right|}{\left|V-M_{manual}\right|}$$ (8)

, where M_auto and M_manual are automatically and manually extracted brain regions, respectively, and 𝑉 is the total volume of all voxels greater than 5% of the maximum intensity. In addition, to measure the performance stability, we calculated the variances of these three metrics across all tested images (i.e. four datasets combined) for each method. We then performed F tests to compare variances of SHERM to those of other methods.

3. Results

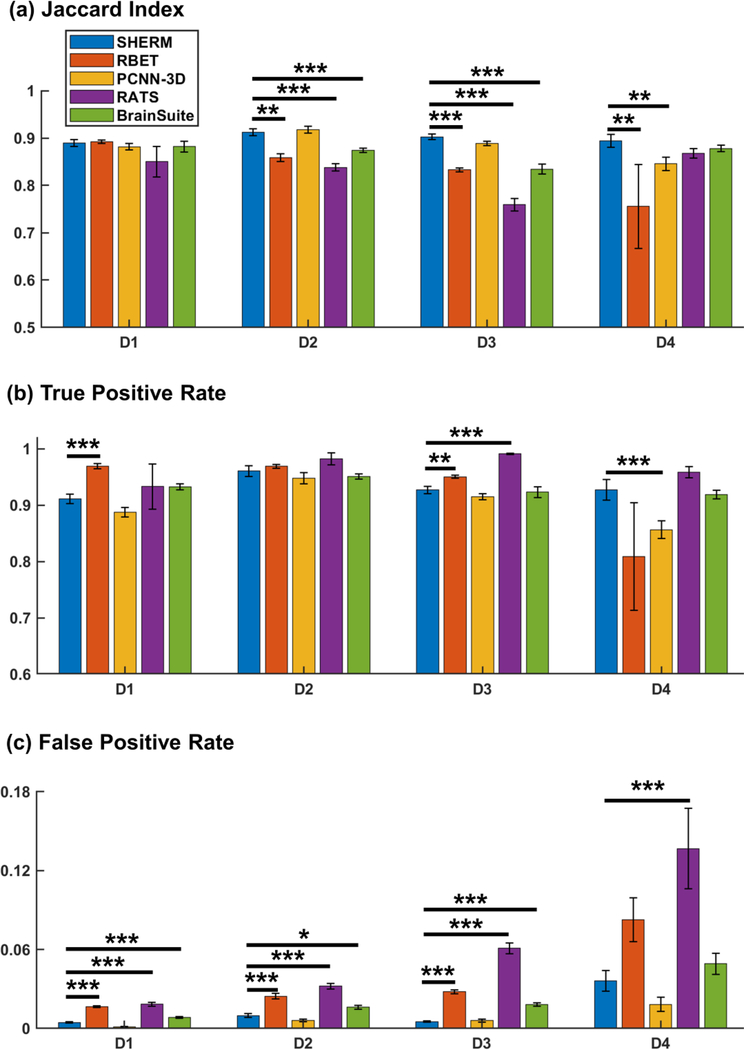
Fig. 4 shows benchmarking results of the proposed method SHERM and four cutting-edge methods, RBET, 3D-PCNN, RATS, and BrainSuite. Results reported in the other four methods were obtained with manually optimized input parameters (Table 1). Two-sided Wilcoxon rank sum test was used to compare the three metrics (Jaccard index, TPR, and FPR) among these results. Our data showed that the Jaccard indices were comparable among all four methods on Dataset 1. SHERM’s Jaccard indices were higher than RBET in Datasets 2, 3 and 4, higher than 3D-PCNN in Dataset 4, higher than RATS in Datasets 2 and 3, and higher than BrainSuite in Dataset 3. In terms of TRP, SHERM’s performance was worse than RBET in Datasets 1 and 3, better than 3D-PCNN in Dataset 4, and worse than RATS in Datasets 3. However, the performance of SHERM in FPR was superior to RBET in Datasets 1, 2 and 3, comparable to 3D-PCNN in all datasets, superior to RATS in all datasets, and superior to BrainSuite in Datasets 1, 2, and 3. Overall, these results indicate that SHERM’s performance was comparable versus other cutting-edge methods, and was somewhat more conservative.

Fig. 4.

Benchmarking of SHERM, RBET, 3D-PCNN, RATS, and BrainSuite. *p<0.01; **p<0.005; ***p<0.001. P values were not corrected. D1: T1-weighted rat images, anisotropic resolution; D2: T2-weighted rat images, anisotropic resolution; D3: T1-weighted mouse images, anisotropic resolution; D4: T2-weighted mouse images, isotropic resolution.

Table 2 shows the performance stability of SHERM compared to other methods, which was measured by the variances of the Jaccard index, TPR, and FPR across all images. SHERM had smaller variances in all the three metrics compared to RBET and RATS, whereas had larger variance in TPR compared to 3D-PCNN and larger variance in FPR compared to BrainSuite.

Table 2.

Performance stability test.

	RBET	3D-PCNN	RATS	BrainSuite
Jaccard Index	0.0374***	0.5684	0.1646***	0.6153
	(0.0000)	(0.0521)	(0.0000)	(0.0810)
TPR	0.2422***	2.8735**	0.0765***	0.8076
	(0.0000)	(0.0014)	(0.0000)	(0.2683)
FPR	0.0556***	0.6946	0.4701*	1.9647*
	(0.0000)	(0.1464)	(0.0154)	(0.0264)

F-tests on variances of the three metrics (Jaccard index, TPR, and FPR) between SHERM and other methods.

^*p<0.05

^**p<0.005

^***p<0.001

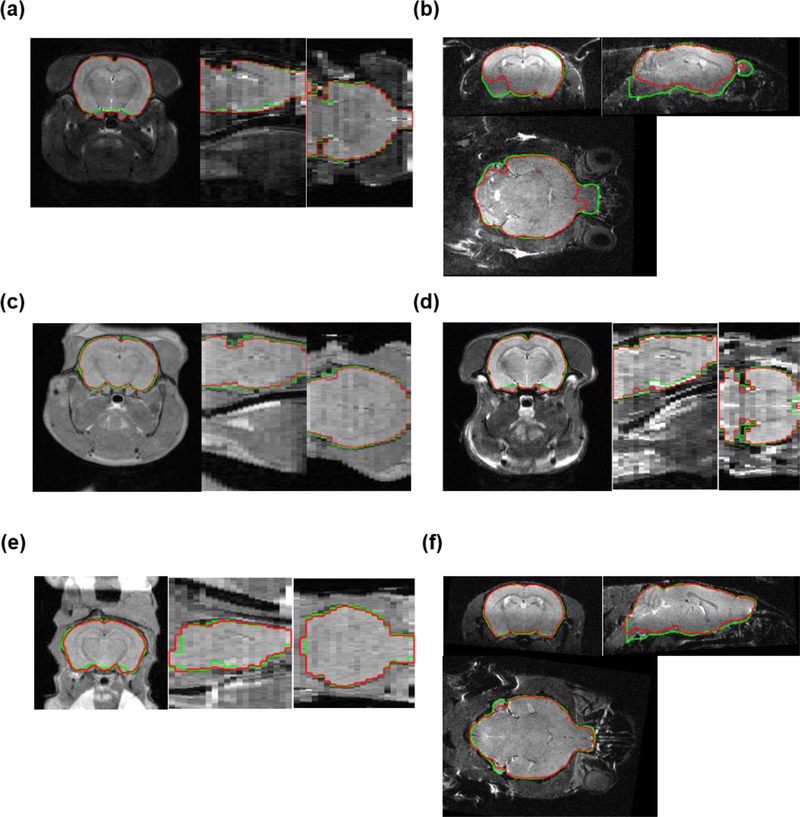
Fig. 5 shows representative examples of the best (from D2), worst (from D4), and four typical cases (one from each dataset) of our proposed method SHERM, measured by the Jaccard index. Overall, each brain mask obtained by SHERM aligned well with the corresponding ground truth. When magnetic field inhomogeneity was severe (Fig. 5b), N3 correction improved but failed to completely correct the signal homogeneity and SHERM failed to identify the brain regions with low signal intensity. However, such case only occurred once in nine T2-weighted mouse images acquired with a surface coil. For images with relatively homogeneous signal intensity, mis-segmentation tended to occur at the ventral brain, cerebellum and caudal midbrain, since morphological operations were intrinsically incapable of handling fine structures. However, mis-segmentation in these regions should have limited impact on other image processing procedures such as image registration.

Fig. 5.

Representative brain masks extracted with SHERM. Green lines show brain masks drawn manually or from atlases; red lines show automatically computed brain masks. (a, b) The best and worst cases in all datasets. (c-f) One typical case from each dataset.

The computation time varied across separate datasets. All tests were run on a desktop computer with a CentOS 7 system (https://www.centos.org), an AMD Ryzen 7 1700 8-core CPU, and 32 GB RAM. For T1- and T2- weighted rat images, the computation time of SHERM was around 3 minutes; for T1-weighted mouse images, the computation time was around 40 seconds; and for T2-weighted mouse images, the computation time was around 4 minutes. Computation time of RBET, 3D-PCNN, RATS, and BrainSuite varied by datasets and input parameters. Generally, BrainSuite took less than 10 seconds, RBET and RATS took less than 3 minutes, whereas 3D-PCNN took from 10 to 30 minutes.

4. Discussion

4.1. Significance of automatic brain extraction in rodent MRI images

Neuroimaging in rodents has become increasingly important for neuroscience research, translational medicine, and pharmaceutical development. Compared to neuroimaging studies in humans, rodent studies can be combined with other well-established pre-clinical tools (e.g. optogenetics) that allow for mechanistically elucidating neural mechanisms, testing effects of drugs and deriving causal relationship between brain function and behaviors (Dopfel and Zhang 2018; Liang et al. 2014, 2015, 2017). However, unlike human neuroimaging studies, where available automatic processing pipelines have facilitated large-scale investigations of human brain anatomy and function (Esteban et al. 2019; Glasser et al. 2013), an automatic data processing pipeline is still lacking for rodent brain images, which has impeded the expansion of rodent neuroimaging studies. To establish such a pipeline, the brain extraction, which is required for other processing steps such as brain co-registration and motion correction, is key to the overall quality of data processing. The current automatic brain extraction methods cannot cope with images from various imaging protocols and scanners without manual parameter adjustment. As shown in Table 1, optimal parameters varied across datasets. Even with manual parameter tuning, the performance of currently available methods may vary across datasets. Consequently, an automatic brain extraction method with robust performance is highly desirable for high throughput processing of exponentially increased rodent neuroimaging data, especially given that the rodent neuroimaging protocols and devices are not as standardized as the human’s.

4.2. Reliability of multi-channel morphological filtering and shape descriptors

The success of our proposed method relies on the reliability of multi-channel morphological filtering and shape descriptors. The range of morphological kernel sizes needs to be wide enough so that the MSERs pertaining to the brain mask should all be included, and the shape descriptor should be sensitive and specific enough to identify these MSERs.

Since morphological operations mainly act on gaps around and within the brain, their kernel sizes should match the gap width. For images of adult rats and mice, they should be covered by the opening and closing kernels we chose, ranging from 0.2 mm to 0.7 mm, and from 0.2 mm to 0.5 mm, respectively. For images of younger rats or mice, the kernel sizes should be smaller. Users can always choose a wider range of kernel sizes at the expense of longer computation time.

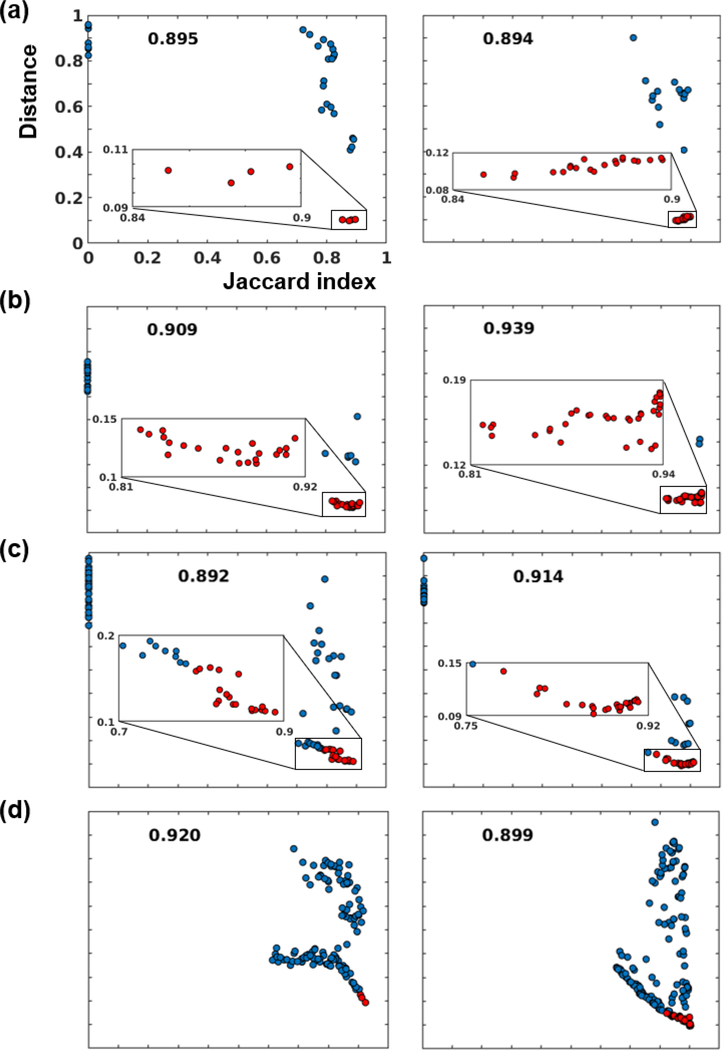
Incomplete brain coverage (i.e. the portion of the brain covered in the FOV) could potentially harm the reliability of the shape descriptor. Considering that the datasets we tested on had various brain coverage (Fig. 5) and the template we used was a whole-brain mask, we evaluated this issue by randomly choosing two head images from each dataset (i.e. 8 head images in total) and plotting the Jaccard index between every cleaned and convexity-screened MSER and its corresponding ‘ground-truth’ brain mask, against the L1-norm distance between their shape descriptors and the template shape descriptor. As shown in Fig. 6, the Jaccard index was overall inversely correlated with the shape descriptor distance across all animals, which indicates the reliability of the shape descriptor. However, when brain coverage was incomplete (images in Fig. 6a and 6b had the least brain coverage, followed by those in 6c, whereas those in 6d had the full brain coverage), the shape descriptor failed to distinguish the best MSER from other similar but suboptimal MSERs, though the MSER with the lowest distance still had a tolerable Jaccard index (> 0.85). We further improved the results by merging a set of MSERs that had distances close to the minimum distance (Eq. 5), indicated by red dots in Fig. 6. The resulting brain mask had Jaccard indices close to that of the optimal MSER, as indicated by the number at the top of each subplot. This is because the MSERs selected by the convexity thresholding and the shape descriptor were rather conservative, supported by Fig. 4. Thus, merging a set of conservative masks gave a mask with higher Jaccard index.

Fig 6.

The relationship between the Jaccard index and shape descriptor distance. Each subplot indicates MSERs from an image. (a), (b), (c), and (d) are two samples from dataset D1, D2, D3, D4, respectively. Red dots indicate selected MSERs to be merged into the final brain mask. The Jaccard indices of final brain masks were labeled at the top of each subplot.

4.3. Application to atypical brains

Rodent brains in stroke, tumor, traumatic, and transgenetic models may have altered image contrast and brain shapes. In these situations, SHERM might perform differently for separate cases and future experiments are necessary to document these performances. However, we argue that SHERM might still be robust for a wide range of applications. SHERM will fail if either MSERs other than the brain region are selected by the shape descriptor or none of the MSERs is the brain region. If it is possible to generate the brain template by choosing a representative image from the dataset, the former scenario should rarely happen. The latter scenario could happen when the brain boundary is blurred by tumors (Boult et al. 2018) or injury (Krukowski et al. 2018). In other cases where alterations do not significantly impact the brain boundary (Totenhagen et al. 2017; Zheng et al. 2015), SHERM should still perform well even with large internal contrast changes.

4.4. Potential limitations

The advantage of the proposed method is its ability to extract the brain tissue in images of various modalities without human intervention, including T1- and T2-weighted images, images with anisotropic or isotropic resolutions, and images acquired with either a volume or a surface coil. However, it has to be noted that the method tends to generate inaccurate segmentation at fine structures such as the ventral brain, cerebellum, and caudal midbrain. Also, it by itself may not be enough for applications such as cortical thickness calculation, which should involve more accurate brain segmentation techniques such as atlas-based segmentation (Eskildsen et al. 2012). The robustness of our method, nonetheless, should increase the performance and reduce the computation costs of these following steps.

5. Conclusion

We proposed an automatic rodent brain extraction method named SHERM that was shown to perform robustly on data of various modalities and qualities. The method can contribute to the establishment of automatic pipelines for rodent neuroimaging data analysis.

Information Sharing Statement

We used four separate datasets in the present study to benchmark our method with other methods. Among them, three datasets were acquired in the lab, and the fourth dataset was from the MRM NeAt database (Y. Ma et al. 2005; Yu Ma 2008). Raw data associated with any figures can be provided upon request. There is no restrictions on data availability.