Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Jun 23;5(26):15835–15842. doi: 10.1021/acsomega.0c00773

Thermodynamic and Dynamic Modeling of the Boron Species in Aqueous Potassium Borate Solution

Dan Li †, Guangli Zhou †, Shuangshuang Gu †, Tao Zhang †, Lingzong Meng †,‡,*, Yafei Guo ‡, Tianlong Deng ‡
PMCID: PMC7345394  PMID: 32656404

Abstract

graphic file with name ao0c00773_0007.jpg

The concentration of B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42– in the solution and the solubilities in the system KCl–K2SO4–K2B4O7–H2O and its subsystems were calculated on the basis of the Pitzer model. The mole fraction of the four boron species is mainly affected by m(B) in the solution but less by m(Cl–) and m(SO42–). m(Cl–) and m(SO42–) mainly affect the solubility of K2B4O5(OH)4·2H2O. The calculated solubilities in the system KCl–K2B4O7–H2O agree well with the experimental data. The results show that the standard chemical potentials of K2B4O5(OH)4·2H2O at 298.15 K obtained in this work is reliable. The transformation between the boron species at 298.15 K was also conducted with the density functional theory (DFT) method. The results affirm that the boron species can transform other boron species as the boron concentration in the solution changes.

1. Introduction

The salt lake brine resources with high concentrations of boron and potassium are widely distributed in the Qaidam basin of China.1 There are many boron species in aqueous borate solution and the dissolution behavior of boron species is very intricate. At least six polyborate species such as B(OH)3, B(OH)4–, B3O3(OH)4–, B3O3(OH)52–, B4O5(OH)42–, and B5O6(OH)4– exist in the aqueous borate solutions.2−6 On the basis of standard chemical potentials (μ0/RT) of different boron species and pH data, the concentration of various boron species in the different borate solutions can be calculated. In the calculation, the activity coefficients of boron ions were considered as 1.0, which may cause relative errors if the concentration of boron species in the solutions is not very low.2−5 At low total boron concentrations, boron species exist in aqueous solution as B(OH)3 and B(OH)4–. As the total boron concentration increases in solution, boron can coordinate to three or four oxygen atoms, which allows a variety of theoretical structures to exist, and several different polyborate species have been hypothesized to exist in solution.7−9

The Pitzer electrolyte solution theory and Harvie–Weare (HW) equations (Pitzer model),10,11 which is described in our previous study,12,13 was widely used in the solubility calculation of the brine systems containing borate.9,14,15 The concentration of various boron species can be calculated if the parameters and standard chemical potentials of boron species are known. In the literature,8,9 the concentration of B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42– in the solution saturated with Na2B4O5(OH)4·8H2O or NaB(OH)4·2H2O and solubilities in the system containing borate or B(OH)3 were calculated. However, the calculation for the systems containing potassium borate was not reported in the literature. The Pitzer binary parameters of potassium borate, some Pitzer mixing parameters between two anions, and standard chemical potentials of boron species were given in the literature.8 However, the Pitzer mixing parameters ψAA′K, which represents the interactions among the two boron anions and K+, were not reported in the literature. In this work, the concentration of B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42– in the solution and the solubilities in the system KCl–K2SO4–K2B4O7–H2O and its subsystems were calculated with the Pitzer model. The transformation between boron ions at 298.15 K was also conducted with the density functional theory (DFT) method.

2. Results and Discussion

The compositions of different boron species at equilibrium and solubilities in the system KCl–K2SO4–K2B4O7–H2O and its subsystems were calculated on the basis of the Pitzer model. The model assumes that there are four boron species corresponding to B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42– in the solution of the system K+//Cl–, SO42–, borate–H2O. The Pitzer parameters for boron ions and standard chemical potentials (μ0/RT) of boron species in the above systems were obtained from Felmy and Weare.8 The other parameters and μ0/RT of the systems were obtained from Harvie et al.16 All of the Pitzer parameters and μ0/RT used in the calculation in the systems K+//Cl–, SO42–, and borate–H2O are tabulated in Tables S1, S2, and S3 in the Supporting Information. The parameters λ between B(OH)3 and other ions were not used in the calculation. The calculated results with λ are nearly the same as those without λ. Therefore, the parameters λ were not considered in this study. The Pitzer mixing parameters ψAA′K for the K+//Cl–, SO42–, and borate–H2O systems were not reported in the literature.8 Moreover, so many parameters cannot be fitted with the thermodynamic properties in the literature. Therefore, the Pitzer mixing parameters were assumed to be zero in the model. The boron ion B5O6(OH)4– was not mentioned in the solubility calculation because of a lack of parameters for B5O6(OH)4–. The experimental data were used to evaluate the model.

2.1. K2B4O7–H2O System

The mole fractions for different boron species at different K2B4O7 concentrations calculated by the Pitzer model are shown in Figure 1. The mole fraction for B4O5(OH)42– (x(B4O5(OH)42–)) can be calculated with eq 1 and eq 2.

2.1. 1
2.1. 2

In eq 1 and eq 2, B, B0, B–, B3–, and B42– represent the total boron in the solution, B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42–, respectively. The m and x are the concentration (mol·kg–1) and the mole fraction of the boron species, respectively.

Figure 1.

Figure 1

Open in a new tab

Variation in the distribution of boron species with m(B) in the system K2B4O7–H2O at 298.15 K with the Pitzer model. ○, B4O5(OH)42–; ▲, B3O3(OH)4–; □, B(OH)4–; ●, B(OH)3; I, unsaturated solution; and II, solution saturated with K2B4O7·4H2O.

In Figure 1, x(B4O5(OH)42–) increased with an increase in m(B). When m(B) is more than 0.4 mol·kg–1, x(B4O5(OH)42–) is the biggest among the four boron species. x(B3O3(OH)4–) first increased and reached the maximum value with m(B) of about 0.5 mol·kg–1 and then x(B3O3(OH)4–) decreased smoothly. x(B(OH)4–) and x(B(OH)3) always decreased with increasing m(B). When K2B4O5(OH)4 dissolved in the solution, B4O5(OH)42– hydrolyzes to B3O3(OH)4–, B(OH)4–, and B(OH)3. The results in Figure 1 show that the mole fraction of B4O5(OH)42– for hydrolysis decreased with increasing the concentration of K2B4O5(OH)4 in the solution. In Figure 1, the saturated concentration of K2B4O7 is about 0.68 mol·kg–1 (with m(B) about 2.72 mol·kg–1 in Figure 1). However, the supersaturated solution of K2B4O7 was obtained in the literature,17,18 and the maximum concentration of K2B4O7 can reach 1.2477 mol·kg–1.18 Therefore, the mole fraction of the four boron species were also calculated in the supersaturated solution of K2B4O7.

The solubility of K2B4O7–H2O is given in many literatures.19−21 The solubility from Wang et al.19 (mass fraction = 0.1341), which is the same as that from Lepeshkov et al.20 and nearly the same as that from Jin et al.21 was used in this study. The μ0/RT for K2B4O5(OH)4·2H2O at 298.15 K was lacking in the literature.8 Therefore, the Pitzer parameters at 298.15 K, μ0/RT for K2B4O5(OH)4·2H2O at 303.15 K, and μ0/RT for other species at 298.15 K from Felmy and Weare8 were used to calculate the solubility for the K2B4O7–H2O system. The calculated solubility for the K2B4O7–H2O system was 0.1487, which shows a remarkable deviation with the experimental data (0.1341). Therefore, the μ0/RT for K2B4O5(OH)4·2H2O at 298.15 K was fitted with experimental solubility for the K2B4O7–H2O system and the parameters at 298.15 K. The standard chemical potentials and ln Ksp for K2B4O5(OH)4·2H2O at 298.15 K are −1663.65 and −5.309, respectively.

2.2. KCl–K2B4O7–H2O System

The solubilities of the KCl–K2B4O7–H2O system, which were reported in the literature,20 were used to evaluate the Pitzer model. The system belongs to the simple eutectic type, with only two crystallization regions corresponding to KCl and K2B4O5(OH)4·2H2O found in the system. The calculated and experimental phase diagrams are plotted in Figure S1 in the Supporting Information. The calculated solubilities in the invariant point saturated with KCl and K2B4O5(OH)4·2H2O (w(KCl) = 0.2513; w(K2B4O7) = 0.0290) were in good agreement with the experimental data (w(KCl) = 0.2514; w(K2B4O7) = 0.0276). The agreement between the experimental and calculated solubility data in Figure S1 shows that the ln Ksp for K2B4O5(OH)4·2H2O obtained in this work is reliable for the solubility calculation. The Pitzer mixing parameters ψAA′K can be considered as zero in the solubility calculation in this study.

The mole fractions for different boron species in this ternary system calculated with the Pitzer model are shown in Figure 2. m(B) and m(Cl–) were used as the abscissa in Figure 2a,b, respectively. In the region I saturated with KCl, the xi for the four boron species varies obviously as m(B) increases. However, the xi for the four boron species changes smoothly with a small change in the region II saturated with K2B4O5(OH)4·2H2O. The xi diagram in Figure 2a for the system KCl–K2B4O7–H2O is similar to that in Figure 1 for the system K2B4O7–H2O. The results show that the xi for the four boron species is mainly affected by the total m(B) in the solution but less affected by m(Cl–). The main difference in Figures 1 and 2a is the saturated solubility for K2B4O5(OH)4·2H2O in the two systems K2B4O7–H2O and KCl–K2B4O7–H2O. m(B) of the solution saturated with K2B4O5(OH)4·2H2O in the ternary system is much smaller than that in the binary system, which is mainly caused by the salting-out effect from KCl in the solution. m(B) of the solution decreases as m(Cl–) increases. Therefore, the curves in Figure 2a,b show a nearly opposite trend.

Figure 2.

Figure 2

Open in a new tab

Variation in the distribution of boron species with m(B) (a) and m(Cl–) (b) in the system KCl–K2B4O7–H2O at 298.15 K. ○, B4O5(OH)42–; ▲, B3O3(OH)4–; □, B(OH)4–; ●, B(OH)3; I, solution saturated with KCl; and II, solution saturated with K2B4O7·4H2O.

2.3. K2SO4–K2B4O7–H2O System

The experimental solubilities of the K2SO4–K2B4O7–H2O system at 298.15 K have not been reported in the literature. Therefore, the experimental solubilities in this ternary system at 313.15 K22 were used to evaluate the Pitzer model. The calculated solubility curves at 298.15 K and experimental data at 313.15 K in the system are shown in Figure S2. The changing trend for the calculated solubility curves is similar to the experimental results, which shows that the model is reliable for solubility calculation in the ternary system.

On the basis of the calculated concentration for different boron species in this ternary system, the diagrams of mole fractions for the four boron species with m(B) or m(SO42–) as the abscissa are plotted in Figure 3a,b, respectively. The xi diagram in Figure 3a for the system K2SO4–K2B4O7–H2O is also similar to that in Figure 1 for the system K2B4O7–H2O, which shows that the xi for the four boron species is mainly affected by the total m(B) in the solution but less affected by m(SO42–).

Figure 3.

Figure 3

Open in a new tab

Variation in the distribution of boron species with m(B) (a) and m(SO42–) (b) in the system K2SO4–K2B4O7–H2O at 298.15 K. ○, B4O5(OH)42–; ▲, B3O3(OH)4–; □, B(OH)4–; ●, B(OH)3; I, solution saturated with K2SO4; and II, solution saturated with K2B4O7·4H2O.

2.4. KCl–K2SO4–K2B4O7–H2O System

The experimental solubilities in the system at 298.15 K have not been reported in the literature; the calculated dry-salt diagram is shown in Figure S3. The dry-salt phase diagram consists of three crystallization zones (KCl, K2SO4, and K2B4O5(OH)4·2H2O), three univariant solubility curves cosaturated with KCl + K2SO4, KCl + K2B4O5(OH)4·2H2O and K2SO4 + K2B4O5(OH)4·2H2O, and one invariant point E cosaturated with KCl, K2SO4, and K2B4O5(OH)4·2H2O. The crystallization areas increase in the sequence KCl, K2B4O5(OH)4·2H2O, and K2SO4. The points A, B, and C are the invariant points in the ternary systems KCl–K2B4O7–H2O, KCl–K2SO4–H2O, and K2SO4–K2B4O7–H2O, respectively.

The xi diagram for the four boron species is shown in Figure 4 using m(B), m(Cl–), or m(SO42–) as the abscissa. The xi diagram using m(B) as the abscissa are nearly the same in the four systems K2B4O7–H2O, KCl–K2B4O7–H2O, K2SO4–K2B4O7–H2O, and KCl–K2SO4–K2B4O7–H2O. The xi diagram using m(Cl–) as the abscissa in Figure 4b in the quaternary system are the same as that in the ternary system KCl–K2B4O7–H2O in Figure 4b. However, the xi diagram using m(SO42–) as the abscissa in Figure 4c differs from that in Figure 3b. In the curves AE and BE saturated with K2B4O5(OH)4·2H2O, the xi for the four boron species are almost constant. The results show that the xi are mainly affected by m(B) but rarely by m(Cl–) and m(SO42–). m(Cl–) and m(SO42–) mainly affect the solubility of K2B4O5(OH)4·2H2O. Therefore, the xi diagram in Figure 1 shows that the binary system K2B4O7–H2O can be used to describe the variation trend of xi in the more complicated system containing K2B4O5(OH)4·2H2O.

Figure 4.

Figure 4

Open in a new tab

Variation in the distribution of boron species with m(B) (a), m(Cl–) (b), and m(SO42–) (c) in the system KCl–K2SO4–K2B4O7–H2O at 298.15 K. ○, B4O5(OH)42–; ▲, B3O3(OH)4–; □, B(OH)4–; ●, B(OH)3; and A, B, C, and E, invariant points for the systems KCl–K2B4O7–H2O, KCl–K2SO4–H2O, K2SO4–K2B4O7–H2O, and KCl–K2SO4–K2B4O7–H2O.

2.5. Boron Species Transformation Calculation

From the above-calculated results with the Pitzer model, the boron species can transform into other boron species as the concentration of boron changes. The transformation process between the boron ions was calculated with the DFT method. With the decrease in boron concentration, the concentrations of boron species with fewer oxygen atoms increase. With the structure of B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42– in the literature,2 the whole hydrolysis process of B4O5(OH)42– and B3O3(OH)4– was calculated by the DFT method. The optimized Cartesian coordinates (Å) and enthalpies (au, including zero-point energy correction) of the species B4O5(OH)42–, H2O, B3O3(OH)4–, B(OH)4–, and B(OH)3 and key transition states TSi (i = 1–9) are listed in Table S4. The hydrolysis process of B4O5(OH)42– and B3O3(OH)4– were calculated and are shown in Figures 5 and 6.

Figure 5.

Figure 5

Open in a new tab

Optimized structures (distance in Å) and their relative entropy (energy in kcal·mol–1) of the B4O5(OH)42– hydrolytic process.

Figure 6.

Figure 6

Open in a new tab

Optimized structures (distance in Å) and their relative entropy (energy in kcal·mol–1) of the B3O3(OH)4– hydrolytic process.

As shown in Figure 5, one water molecule attacks B4O5(OH)42– via a conventional four-center transition state, TS1, providing a six-membered intermediate. This step has an entropy energy barrier of 28.2 kcal·mol–1. TS2 derived from B4O5(OH)42– attacked by two water molecules (path 2) could yield a six-membered intermediate with water coordination. This process has an energy barrier of 19.8 kcal·mol. It is computationally found that TS2 is lower in entropy than TS1 by 8.4 kcal·mol–1. This suggests that path 2 is more favorable. Subsequently, the newly formed intermediate further goes through B–O cleavage and hydrolysis via TS3–TS5 to yield B3O3(OH)4– and B(OH)4–. Overall, the reaction could feasibly take place from the view of DFT calculations. The hydrolysis process for B3O3(OH)4– in Figure 6 is nearly the same as that in Figure 5 for B4O5(OH)42–. The pathway (2) for B3O3(OH)4– with attack from two water molecules was chosen for further calculation. After many steps of attack via two water molecules and B–O cleavage, B(OH)3 and B(OH)4– were finally obtained. It should be noted that the intermediate from TS9 in Figure 6 undergoes B–O cleavage three times to form B(OH)3 and B(OH)4–, but the critical complex is not shown in Figure 6 because of its simple process.

From the energy in Table S4 in the Supporting Information, the ΔH≠ in the pathway (2) and its reverse process is not very high in both processes, which shows that water molecules can easily attack the boron species and form the critical complex mentioned in Figures 5 and 6. Moreover, the water molecule can be also easily dissolved from the cyclic critical complex. The B–O bond can be easily formed and broken. The calculated results affirm that the boron species can transform each other as the boron concentration in the solution changes. The concentration of polyborate ions containing more B–O bonds increases as the boron concentration in the solution increases. However, the concentration of polyborate ions containing less B–O increases as the boron concentration in the solution decreases.

3. Conclusions

The concentrations of B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42– in the solution and the solubilities in the system KCl–K2SO4–K2B4O7–H2O and its subsystems were calculated on the basis of the Pitzer model. The model assumes that there are four boron species corresponding to B(OH)3, B(OH)4–, B3O3(OH)4–, and B4O5(OH)42– in the solution. The mole fraction of the four boron species is mainly affected by m(B) in the solution but rarely by m(Cl–) and m(SO42–). x(B4O5(OH)42–) increases, while x(B(OH)3) and x(B(OH)4–) decrease as m(B) increases in the solution. m(Cl–) and m(SO42–) mainly affect the solubility of K2B4O5(OH)4·2H2O. The calculated solubilities in the system KCl–K2B4O7–H2O agree well with the experimental data. The results show that the Pitzer model is reliable for solubility calculation in the system KCl–K2SO4–K2B4O7–H2O. The transformation between the boron species at 298.15 K was also performed with the DFT method. The results affirm that the boron species can transform each other as the boron concentration in the solution changes. The results of the Pitzer model and the DFT calculation for the systems containing various boron species in this study are essential for the development of universal solubility models for brine systems containing borate.

4. Computational Methods

4.1. Thermodynamic Model

The Pitzer model containing the Pitzer parameters and μ0/RT of different species was applied in calculating the thermodynamic properties of aqueous electrolyte solutions in this study. Take the solution saturated with K2B4O5(OH)4·2H2O in the system for example, the dissolution equilibrium equations for the Pitzer model used in the calculation are as follows:

4.1. 3

In the Pitzer model, the relationship between boron species can be represented with eq 4 and eq 5.

4.1. 4
4.1. 5

The solubility product constant of K2B4O5(OH)4·2H2O (KK2) at a stated temperature and pressure is shown in eq 6. The equilibrium constants for eq 4 and eq 6, which can be calculated with the μ0/RT from the literature,8,16 are shown in eq 7 and eq 4.

4.1. 6
4.1. 7
4.1. 8

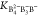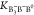In eq 6–eq 7, K2 represents K2B4O5(OH)4·2H2O. Inline graphic and Inline graphic are the equilibrium constant equations for eq 7 and eq 6. Additionally, γi represents the activity coefficient of the ions. The water activity aw is a function of the osmotic coefficient ø through eq 9.

4.1. 9

where Mw is the molar mass of water and the sum covers all of the solute species. ø is the osmotic coefficient for the solvent.

According to the Pitzer model, the activity and osmotic coefficients are parametric functions of β(0), β(1), β(2), CØ, θAA′, and ψAA′C; β(0), β(1), β(2), and CØ are the parameters of a single salt; θAA′ represents the interaction between the two ions with the same sign; and ψAA′C represents the interactions among the three ions, in which the sign of the third ion is different from the first two ions. Combining the charge conservation and matter conservation equations, the compositions of different boron species at equilibrium and solubilities for the system KCl–K2SO4–K2B4O7–H2O and its subsystems can be calculated with the above equations with the Pitzer parameters and μ0/RT of different species.

4.2. DFT Calculations

The boron species can transform into other boron ions as the boron concentration changes. The transformation process between the boron ions was calculated with the DFT method. All calculations were performed with Gaussian 09 program.23 The M06-2x functional,24,25 which often shows better performance in the treatment of weak interaction systems, was used for geometry optimization and frequency calculations in the water phase (ε = 78.36), with the CPCM solvation model without any symmetry or geometrical constraints. The 6-311++G(2df,2pd) basis set was used for C, H, N, O, and S atoms. The energy in the solution, which is derived from these calculations including Gibbs free energy correction from the frequency calculation, was used for the description of energy profiles.26 The three-dimensional molecular structures are visualized by CYLView.27

Acknowledgments

This work was jointly funded by the National Natural Science Foundation of China (U1507112, 21773170, and U1607123), the Foundation of Tianjin Key Laboratory of Marine Resources and Chemistry at TUST (2018-04), the Innovative Research Team in Tianjin Colleges and Universities (TD13-5008), and Yangtze Scholars and Innovative Research Team of the Chinese University (IRT_17R81).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00773.

  • Pitzer binary and mixing parameters, μ0/RT of species in the systems K+//Cl–, SO42–, and borate–H2O, and details of the DFT calculations, experimental and calculated phase diagrams of the systems KCl–K2B4O7–H2O, K2SO4–K2B4O7–H2O, and KCl–K2SO4–K2B4O7–H2O (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c00773_si_001.pdf (144KB, pdf)

References

  1. Li W.; Dong Y. P.; Song P. S.. Exploitation and Comprehensive Utilization of Salt Lake Resources (in Chinese); Chemical Industry Press: Beijing, 2012. [Google Scholar]
  2. Zhou Y. Q.; Fang C. H.; Fang Y.; Zhu F. Y. Polyborates in aqueous borate solution: A Raman and DFT theory investigation. Spectrochim. Acta, Part A 2011, 83, 82–87. 10.1016/j.saa.2011.07.081. [DOI] [PubMed] [Google Scholar]
  3. Ge H. W.; Fang C. H.; Fang Y.; Zhou Y. Q.; Zhu F. Y.; Liu H. Y.; Yang Z. X.; Tang Y. L. Density, Electrical Conductivity, pH, and Polyborate Distribution of LiB(OH)4, Li2B4O5(OH)4, and LiB5O6(OH)4 Solutions. J. Chem. Eng. Data 2014, 59, 4039–4048. 10.1021/je500683z. [DOI] [Google Scholar]
  4. Zhou Y. Q.; Fang C. H.; Fang Y.; Zhu F. Y. Volumetric and Transport Properties of Aqueous NaB(OH)4 Solutions. Chin. J. Chem. Eng. 2013, 21, 1048–1056. 10.1016/S1004-9541(13)60561-3. [DOI] [Google Scholar]
  5. Ge H. W.; Zhou Y. Q.; Liu H. Y.; Fang Y.; Fang C. H. Molecular interactions in aqueous solutions of polyborates at different acidity based on the Raman spectroscopy data at 25 °C. Russ. J. Phys. Chem. A 2017, 91, 1925–1931. 10.1134/S0036024417100119. [DOI] [Google Scholar]
  6. Fang C. H.; Fang Y.; Zhou Y. Q.; Zhu F. Y.; Liu H. Y.; Zhang W. Q. Recent Progress on Structure of Aqueous Polyborate Solutions. J. Salt Lake Res. 2019, 27, 11–40. [Google Scholar]
  7. Wang P. M.; Kosinski J. J.; Lencka M. M.; Anderko A.; Springer R. D. Thermodynamic modeling of boric acid and selected metal borate systems. Pure Appl. Chem. 2013, 85, 2117–2144. 10.1351/pac-con-12-07-09. [DOI] [Google Scholar]
  8. Felmy A. R.; Weare J. H. The prediction of borate mineral equilibria in natural waters: Application to Searles Lake, California. Geochim. Cosmochim. Acta 1986, 50, 2771–2783. 10.1016/0016-7037(86)90226-7. [DOI] [Google Scholar]
  9. Chen L. L.; Li D.; Guo Y. F.; Deng T. L.; Meng L. Z. Experimental Data and Thermodynamic Model in the Salt–Water Ternary System (NaBO2 + Na2B4O7 + H2O) at T = 298.15 K and p = 0.1 MPa. J. Chem. Eng. Data 2019, 64, 5878–5885. 10.1021/acs.jced.9b00780. [DOI] [Google Scholar]
  10. Pitzer K. S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. A. 1973, 77, 268–277. 10.1021/j100621a026. [DOI] [Google Scholar]
  11. Harvie C. E.; Weare J. H. The prediction of mineral solubilities in natural waters: the Na–K–Mg–Ca–Cl–SO4–H2O system from zero to high concentration at 25 °C. Geochim. Cosmochim. Acta 1980, 44, 981–997. 10.1016/0016-7037(80)90287-2. [DOI] [Google Scholar]
  12. Meng L. Z.; Gruszkiewicz M. S.; Deng T. L.; Guo Y. F.; Li D. Isothermal evaporation process simulation using Pitzer model for the quinary system LiCl–NaCl–KCl–SrCl2–H2O at 298.15 K. Ind. Eng. Chem. Res. 2015, 54, 8311–8318. 10.1021/acs.iecr.5b01897. [DOI] [Google Scholar]
  13. Meng L. Z.; Deng T. L.; Guo Y. F.; Li D.; Yang L. Measurement and thermodynamic model study on solid + liquid equilibria and physicochemical properties of the ternary system MgBr2 + MgSO4 + H2O at 323.15 K. Fluid Phase Equilib. 2013, 342, 88–94. 10.1016/j.fluid.2013.01.004. [DOI] [Google Scholar]
  14. Yang L.; Meng L. Z.; Ge T. J.; Li D.; Deng T. L.; Guo Y. F. Solubility Measurement and Thermodynamic Modeling of Solid–Liquid Equilibria in the MCl–M2B4O7–H2O (M = Li, Na) Systems. J. Chem. Eng. Data 2019, 64, 4510–4517. 10.1021/acs.jced.9b00561. [DOI] [Google Scholar]
  15. Zhang N.; Guo Y. F.; Liu Y. H.; Wang S. Q.; Deng T. L. Thermodynamic Phase equilibria in the Aqueous Ternary System (LiCl + LiBO2 + H2O) at 308 K: Experimental Data and predictions using Pitzer Model. J. Chem. Eng. Jpn. 2016, 49, 324–331. 10.1252/jcej.15we045. [DOI] [Google Scholar]
  16. Harvie C. E.; Møller N.; Weare J. H. The prediction of mineral solubilities in natural waters: The Na-K-Mg-Ca-H-Cl-SO4-OH-HCO3-CO3-CO2-H2O system to high ionic strengths at 25 °C. Geochim. Cosmochim. Acta 1984, 48, 723–751. 10.1016/0016-7037(84)90098-X. [DOI] [Google Scholar]
  17. Zhu F. Y.The Properties and Structures of Aqueous Potassium Borate Solutions. Doctoral dissertation; Xining, 2013. [Google Scholar]
  18. Li L. J.; Yao Y.; Song P. S. The Pitzer Ion -interaction Model for the K2B4O7–H2O System at 298.15 K (in Chinese). J. Salt Lake Res. 2004, 12, 23–28. [Google Scholar]
  19. Wang S.-q.; Zhao D.; Song Y.; Shi Z.; Guo Y. F.; Deng T. L. Solubility, Density, and Refractive Index in the Ternary System (K2B4O7 + Mg2B6O11 + H2O) at 298.15 K. Russ. J. Inorg. Chem. 2019, 64, 661–665. 10.1134/S003602361905019X. [DOI] [Google Scholar]
  20. Lepeshkov I. N.; Bodaleva N. V.; Kotova L. T. Solubility in system KCl–K2B4O7–H2O at 25 °C. Zh. Neorg. Khim. 1963, 8, 2600–2601. [Google Scholar]
  21. Jin Z. L.; Sun B.; Li G.; Li W. Study on the Ternary System K+, Mg2 +/B4O72––H2O at 25 °C(in Chinese). J. Salt Lake Res. 2004, 12, 19–22. [Google Scholar]
  22. Vin C. C.; Shen Y. L.; Shen J. M.; Shen H. C.; Liu T. T. Solubility in system K2SO4–K2B4O7–H2O at 30°C. Sciemia Sinica 1965, 14, 407. [Google Scholar]
  23. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam N. J.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, revision A.02; Gaussian, Inc: Wallingford, CT, 2009.
  24. Zhao Y.; Truhlar D. G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
  25. Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  26. Cossi M.; Rega N.; Scalmani G.; Barone V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
  27. Legault C. Y.CYLview, 1.0b; Université de Sherbrooke. http://www.cylview.org,2009.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c00773_si_001.pdf (144KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES