Monitoring Protein–Protein Interactions in the Cyanobacterial Circadian Clock in Real Time via Electron Paramagnetic Resonance Spectroscopy

Abstract

The cyanobacterial circadian clock in Synechococcus elongatus consists of three proteins, KaiA, KaiB, and KaiC. KaiA and KaiB rhythmically interact with KaiC to generate stable oscillations of KaiC phosphorylation with a period of 24 h. The observation of stable circadian oscillations when the three clock proteins are reconstituted and combined in vitro makes it an ideal system for understanding its underlying molecular mechanisms and circadian clocks in general. These oscillations were historically monitored in vitro by gel electrophoresis of reaction mixtures based on the differing electrophoretic mobilities between various phosphostates of KaiC. As the KaiC phospho-distribution represents only one facet of the oscillations, orthogonal tools are necessary to explore other interactions to generate a full description of the system. However, previous biochemical assays are discontinuous or qualitative. To circumvent these limitations, we developed a spin-labeled KaiB mutant that can differentiate KaiC-bound KaiB from free KaiB using continuous-wave electron paramagnetic resonance spectroscopy that is minimally sensitive to KaiA. Similar to wild-type (WT-KaiB), this labeled mutant, in combination with KaiA, sustains robust circadian rhythms of KaiC phosphorylation. This labeled mutant is hence a functional surrogate of WT-KaiB and thus participates in and reports on autonomous macroscopic circadian rhythms generated by mixtures that include KaiA, KaiC, and ATP. Quantitative kinetics could be extracted with improved precision and time resolution. We describe design principles, data analysis, and limitations of this quantitative binding assay and discuss future research necessary to overcome these challenges.

The circadian clock of the cyanobacterium Synechococcus elongatus regulates global gene expression¹ and provides a selective growth advantage.² The fact that transcriptional and translational oscillations (TTO) are unnecessary to drive posttranslational oscillations (PTOs)³ sets this clock apart from circadian clocks from other organisms.⁴ Indeed, in vitro reconstitution of the core oscillator proteins, KaiA, KaiB, and KaiC (Figure 1a), generates an autonomous macroscopic circadian rhythm of sequential KaiC phosphorylation–dephosphorylation at residues Ser-431 (S431) and Thr-432 (T432) in the presence of ATP^5,6 mirroring in vivo oscillations,⁷ making the Kai system a unique model system for studying circadian clock systems in general.

Figure 1.

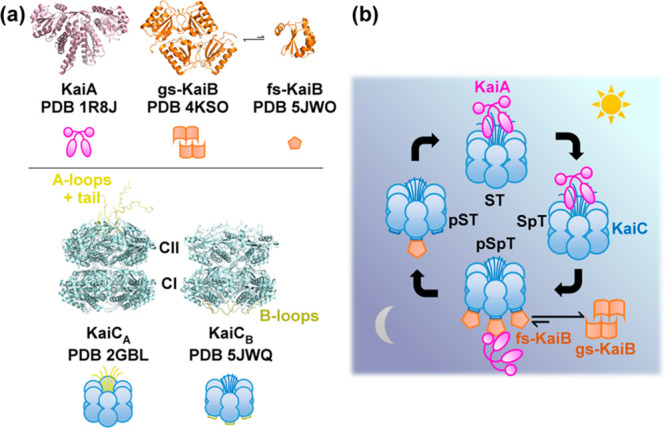
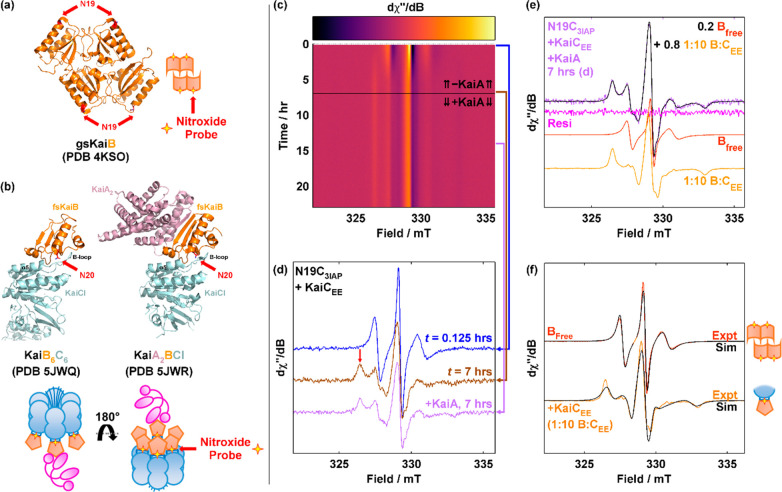
Overview of the core Kai oscillator. (a) Representative crystal structures and simplified representations of isolated clock components KaiA (magenta), KaiB [orange, ground state (gs) vs fold-switched (fs) states], and KaiC (blue, KaiA-binding competent state KaiC_A vs KaiB-binding competent state KaiC_B). The crystal structure of KaiC_B (Protein Data Bank entry 5JWQ) was obtained from the KaiC homologue in Thermosynechococcus elongatus. All other crystal structures were obtained from S. elongatus. For KaiC, the KaiA-binding A-loops and tail (yellow) and KaiB-binding B-loops (olive) are highlighted in both the crystal structures and simplified representations. (b) Model of events governing circadian oscillations in the Kai clock. Input and output pathways are not shown.

KaiC belongs to the AAA+ ATPase family and consists of two homologous domains, CI and CII (Figure 1a).⁸ CI possesses slow ATPase activity,⁹⁻¹¹ with its activity correlated with the frequencies of both TTO and PTO.¹⁰ On the other hand, CII contains two phosphorylation sites, S431 and T432, that undergo ordered phosphorylation as S/T → S/pT → pS/pT → pS/T → S/T (p, phosphorylated).^5,6 This order is dictated by phosphorylation-dependent CII ring dynamics¹² and CI–CII ring stacking interactions.¹³ The autophosphatase activity of CII is atypical in that ATP is regenerated from ADP and pS431 or pT432 as an intermediate prior to hydrolysis.¹⁴

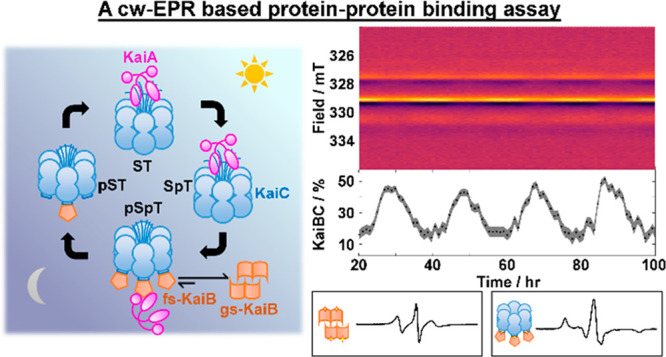
In the absence of KaiA or KaiB, KaiC autophosphatase activity dominates, leading to an unphosphorylated KaiC_ST resting state.⁵ To drive autokinase activity in KaiC, KaiA, a domain-swapped homodimer (Figure 1a),¹⁵ interacts with the C-terminal residues (“A-loops” and tail) of KaiC during the day (Figure 1a,b)^16,17 as a KaiAC complex. This KaiA–KaiC interaction promotes nucleotide exchange in KaiC and consequently autokinase activity in CII.^18,19 As CII progresses from S/T to pS/pT, corresponding to the day-to-night transition, the CII ring tightens, withdrawing its A-loops,¹² which decreases the binding affinity between KaiA and KaiC²⁰ and suppresses the autokinase activity in KaiC. This decrease in affinity is critical to maintaining macroscopic phase coherence.²⁰ Concurrently, the CII and CI rings of KaiC stack¹³ such that CI adopts a posthydrolysis conformation that exposes its “B-loops” to KaiB binding (Figure 1b),^10,21 a step that marks the beginning of clock resetting.²² The interchanging competences for KaiA and KaiB binding by two conformations of KaiC²³ are designated here as KaiC_A and KaiC_B, respectively. Curiously, the conformation of KaiB that can bind to CI in this KaiBC complex differs from KaiB as crystallized in that the former has a thioredoxin fold and is termed fold-switched KaiB (fs-KaiB),^21,24 whereas the latter possesses an uncommon tetrameric state and is termed ground-state KaiB [gs-KaiB (Figure 1a)].^25,26 The tetramer and monomer have been shown to interconvert reversibly under native conditions,²⁷ whereas the mechanism of fold switching within monomerized KaiB remains elusive. On fold switching, a β-strand (β2) together with a newly formed α-helix (α3) in fs-KaiB is capable of KaiA binding, thereby stabilizing KaiA in an “autoinhibited” conformation where the CII-binding motif of KaiA is blocked.^21,28 The KaiB–KaiC_pS(p)T binary complex can thus recruit KaiA to form a ternary KaiABC nighttime complex,^21,28 suppressing further KaiC phosphorylation and forming a negative feedback loop. Subsequent autodephosphorylation of KaiC_pS(p)T during the night enables resetting of KaiC to KaiC_ST and prepares the proteins for the next day. As the Kai system consists of discrete molecules, intrinsic stochastic noise can lead to desynchronization of the population.²⁹ To combat this, populations of KaiC synchronize via intersubunit allosteric interactions,^23,30 phosphorylation-dependent KaiA–KaiC binding affinities,^20,31 and monomer shuffling.^32,33

Biochemical circadian rhythms of the Kai clock were first revealed by sodium dodecyl sulfate–polyacrylamide gel electrophoresis (SDS–PAGE) in which KaiC phosphostates in SDS-quenched reaction samples were quantitatively resolved.⁵⁻⁷ As KaiC phosphodistribution represented only one facet of the Kai oscillator, coimmunoprecipitation assays^5,23 and native mass spectrometry²⁷ were developed in parallel in attempt to quantify relevant protein–protein interactions over the oscillations. However, the discontinuous nature of these assays meant that multiple samples had to be prepared to provide time-domain information. More recently, fluorescence correlation spectroscopy (FCS) and fluorescence polarization/anisotropy (FA) have been employed to study KaiB binding by fluorophore tagging, producing tagged proteins using either cell free synthesis^34,35 or site-directed mutagenesis.^24,36 Fluorescence assays are an improvement to previous discontinuous methods as the fluorescence signals could be continuously monitored provided the fluorophore tags are not photobleached. However, the myriad of stoichiometries existing in Kai reaction mixtures, tetrameric²⁶ and monomeric KaiB²⁴ and (sub)stoichiometric KaiBC and KaiABC complexes,^20,27,28 invalidate models that assume two species with differing molecular weights. Thus, fluorescence signals via either FCS or FA are not directly comparable to coimmunoprecipitation results, limiting their usefulness. Here, we introduce site-directed spin labeling–electron paramagnetic resonance (SDSL–EPR)³⁷ to probe real-time evolution of KaiB–KaiC interactions. SDSL–EPR provides an alternative to fluorescence assays by providing comparable time resolution while avoiding ambiguities in stoichiometry inherent to fluorescence-based methods. Furthermore, interaction specificity is maintained, allowing quantitative binding information comparable to coimmunoprecipitation or native-PAGE. In the following section, we discuss in detail the sample preparation and data analysis necessary to obtain reproducible results. Then, we describe the design principles to site-directed spin labeling. Once the theoretical background has been laid, we implement cw-EPR to the Kai system and demonstrate that cw-EPR gives complementary information to existing methods. Finally, we outline the limitations of this quantitative binding assay and discuss future research and instrumentation necessary to overcome these challenges.

Materials and Methods

Cloning, Protein Expression, Purification, and Fluorescence/Spin Labeling

All genes were cloned into pET-28b using the NdeI/HindIII sites for production of SUMO fusion proteins. Details of the cloning protocol have been described previously.^12,13 Proteins were expressed in Escherichia coli BL21(DE3) (Novagen) and purified by Ni-NTA affinity chromatography and size-exclusion chromatography as described previously.^12,13 6-Iodoacetamidofluorescein (6IAF) labeling of KaiB was performed according to a previous report.²⁴ A modified protocol for 3-iodoacetamido-PROXYL (3IAP) labeling of KaiB was performed as follows. A 5-fold excess of tris(2-carboxyethyl)phosphine (TCEP) was added to a purified aliquot of unlabeled KaiB (typically 100 μM) and incubated at room temperature for 15 min in labeling buffer [20 mM Tris and 150 mM NaCl (pH 8.0)], followed by overnight incubation of a 10-fold excess of 3IAP in the dark at 4 °C using a 200 mM 3IAP stock solution in DMSO. The difference in concentrations between the spin-label and TCEP is critical to a high labeling efficiency; TCEP is known to directly react with iodoacetamide-based fluorescent dyes³⁸ and is inferred to do the same to 3IAP, decreasing its effective concentration. After labeling, excess 3IAP was removed with a HiPrep 26/10 desalting column (GE Healthcare Life Sciences). The sample was then concentrated using Amicon ultrafiltration stirred cells fitted with 10 kDa cutoff membranes.

Protein Characterization

The concentrations of stock protein solutions were determined via a Bradford assay using bovine serum albumin (Thermo Fisher). All concentrations refer to the monomer unless otherwise stated. The labeling efficiencies of all spin-labeled KaiB samples were determined by electrospray ionization high-resolution liquid chromatography mass spectrometry [ESI-HR-LCMS (Figure S1)] using an LTQ Orbitrap XL mass spectrometer equipped with an electrospray ionization source (ThermoFisher, San Jose, CA) operating in positive ion mode. Fifty microliter portions of spin-labeled KaiB samples (400 μg/mL) were desalted using Zeba Spin Desalting Columns (ThermoFisher). LCMS was performed on a C18 column eluted with gradient of 0.1% formic acid in water to 0.1% formic acid in acetonitrile. The LCMS data were then analyzed using MagTran.³⁹ The labeling efficiency was determined by fitting the transformed spectrum with Gaussian lines and determining the peak areas of both labeled and unlabeled proteins. Samples that were not at least 95% labeled on the basis of LCMS peak areas were relabeled by repeating the labeling protocol described above.

Sample Preparations for In Vitro Kai Protein Reactions

All reactions were performed at 30 °C in reaction buffer [20 mM Tris, 150 mM NaCl (pH 8.0), 0.5 mM EDTA, 5 mM MgCl₂, and 1 mM ATP]. The in vitro 1× oscillator was carried out using 1.2 μM KaiA, 3.5 μM KaiB, and 3.5 μM KaiC. Fluorescence samples were prepared as 100 μL samples with additional 50 nM KaiB-K25C-6IAF included as described previously.³⁶ For real-time cw-EPR characterization, 10–40 μL samples were prepared by replacing WT-KaiB with spin-labeled KaiB. KaiC_S431E,T432E (KaiC_EE) phosphomimetic reactions were performed with a 1× or 5× protein concentration without supplementing extra ATP. KaiB was added to KaiC_EE and incubated for 7 h (5×) or 1 day (1×), after which KaiA was added to the KaiB/KaiC_EE reaction mixture to a final Kai protein concentration of 4.6× (5×) or 0.9× (1×) relative to the 1× oscillator. Native-PAGE samples were prepared as 200 μL reaction mixtures at a 1× protein concentration and incubated at 30 °C overnight. Twenty microliters of the sample was then removed at predefined time points and mixed with 20 μL of 2× native-PAGE buffer [62.5 mM Tris, 20% (w/v) glycerol, 0.01% (w/v) bromophenol blue, 1 mM ATP, and 5 mM MgCl₂ (pH 6.8)] to give final KaiB and KaiC_EE concentrations of 1.75 μM. The samples were frozen in a −80 °C freezer and then thawed over ice for 3 min prior to loading.

Native-PAGE

Thawed samples were electrophoresed at 60 V for 30 min followed by 140 V for 135 min using hand-cast 6% Tris-glycine mini gels with a 4% stacking gel in ATP-supplemented native-PAGE running buffer (25 mM Tris, 192 mM glycine, 1 mM ATP, and 5 mM MgCl₂) in an electrophoresis cell surrounded by ice–water. Gels were incubated in 0.5% SDS in 7.5% acetic acid, stained in SYPRO Orange (Fisher Scientific, Waltham, MA), and imaged using a BioSpectrum AC Imaging System (UVP, Upland, CA). Image contrast adjustment and densitometry were performed on ImageJ (National Institutes of Health). Formation of the KaiB–KaiC_EE complex was estimated by normalizing the BC_EE complex band intensity against the sum of band intensities of the BC_EE complex and free KaiC_EE (Figure S2).

Fluorescence Anisotropy (FA) Measurements

FA measurements of 1× oscillators (Figure S3) and phosphomimetic reactions (Figure S13) using 6IAF-labeled samples were performed at 30 °C on a BMG Clariostar plate reader (BMG LABTECH, Cary, NC) with an excitation wavelength of 492 nm and an emission wavelength of 530 nm.

EPR Spectroscopy

X-Band cw-EPR (9.2 GHz) spectra were recorded using a Bruker ECS 106 spectrometer equipped with an SHQE cavity. In vitro reaction spectra were recorded at 30 °C using 2 G modulation at a 100 kHz modulation frequency with a conversion time of 40 ms and a time constant of 20 ms. Scan times were approximately 7.5 min per spectrum. Samples were loaded into custom sample tubes by sealing one end of glass pipets (10 μL, Fisher Scientific) or rectangular miniature hollow tubing (20–40 μL, VitroCom, Mountain Lakes, NJ) to ensure a high quality factor (Q) and to suppress sample heating. For near-rigid limit samples for determination of g and A, the spin-labeled samples were mixed with WT-KaiB and equilibrated overnight followed by dilution to a final concentration of 17.5 μM labeled KaiB, 157.5 μM WT-KaiB, and 20% (w/w) sucrose (20 Bx), 100 μL (4 mm inside diameter, Wilmad, Vineland, NJ), and the spectra were recorded at −40 °C and 1 G modulation. Temperature control was achieved using an FTS XR401 Air-jet Crystal Cooler (SP Scientific, Stone Ridge, NY). Real-time temperature monitoring in the sample cavity was achieved using an external type T thermocouple (Omega Inc.) connected to a Universal Thermocouple Connector Direct USB to PC Connection (Omega Inc.) on a separate computer. The thermocouple readings inside the EPR sample tube and Air-jet outlet were consistent, ruling out microwave heating of the sample. The microwave frequency was continuously monitored externally via an EIP 578B frequency counter (National Instruments, Santa Clara, CA) connected to a separate computer.

EPR Data Preprocessing

Prior to data analysis, the EPR data were (1) microwave frequency drift corrected and (2) background subtracted as follows. Unlike previous spin labeling and spin trapping studies in which spectral acquisition is usually complete within hours, the Kai clock oscillates over a duration of days. The length of the acquisition process enables extensive averaging yet poses an additional challenge that the resonance microwave frequency of the resonance cavity can drift over time due to electronic imperfections, cavity and/or ambient-temperature changes, and sample evaporation. For a given spin system, this microwave frequency drift is manifested as a shift in the spectrum predicted by considering the Hamiltonian (H̑).

1a

where μ_B is the Bohr magneton, B is the incident magnetic field, and g is the g factor. S and I are the electron and nuclear spin quantum numbers, respectively, and the energy states are coupled by an anisotropic hyperfine matrix A that is incompletely averaged by motion. For a single nitroxide component with an isotropic rotational correlation time (τ_c), a modest simulated frequency drift of 0.5 MHz over a 4 day period (Figure S4a) could lead to observable differences between the spectra at 0 h and 96 h (Figure S4b). Because similar levels of microwave frequency drift were observed in our experiments (Figure S4a), a correction (Figure S4c,d) was applied by either multiplying the magnetic field of each spectrum by the ratio of their microwave frequencies (eq 1b) or adding a linear term proportional to their frequency difference (eq 1c) followed by interpolation using MATLAB interpolation routine interp1:

1b

1c

Both correction schemes reduced the difference spectra to the noise level. The estimated error due to microwave frequency correction is 2 orders of magnitude smaller than the magnetic field intervals used (see the Supplementary Text for details). While microwave frequency correction is theoretically impossible as the Zeeman term of the spin Hamiltonian is linearly dependent on frequency whereas hyperfine is not and the g and A tensors are transition-dependent, with this difference forming the basis of multifrequency EPR,⁴⁰ we found this protocol to be a reasonable compromise to allow quantitative analysis over extended experimental durations.

To perform background subtraction, the background spectrum (B_bg) was first acquired using sample cells containing reaction buffer only. Then, the background spectrum was subtracted from the data (Figure S5). As the cw-EPR signal intensity is directly proportional to the resonator quality factor (Q),⁴¹ intersample variations in Q could lead to variations in intensity in both the signal of interest originating from the spin-label and the resonator cavity background (Figure S5a,b). The signal intensity could also fluctuate due to microwave frequency detuning. Thus, the magnitude of background subtraction (w) applied was determined individually for each spectrum Y by considering only magnetic field positions that are not within the span of the nitroxide spectrum (null window, Figure S5b). This background subtraction is hence a linear regression problem to determine the weight of the background (w):

2

Once w is determined, the correction is applied to the entire spectrum to recover the background and baseline-corrected spectrum (Figure S5c).

Determination of EPR Spin System Parameters

Simulations and least-squares fitting (LSQ) were carried out with EasySpin toolbox (version 4.5.5) and Optimization Toolbox in MATLAB (Mathworks Inc., Natick, MA) using the routine chili for slow-motion cw-EPR spectra by solving the stochastic Liouville equation with rotational eigenfunctions as a basis.⁴² The feasibility of changes in the rotational correlation time (τ_c) in distinguishing spin components was illustrated by simulating slow-motion spectra over isotropic τ_c values from 0.01 to 100 ns (Figure 2b and Table S1).

Figure 2.

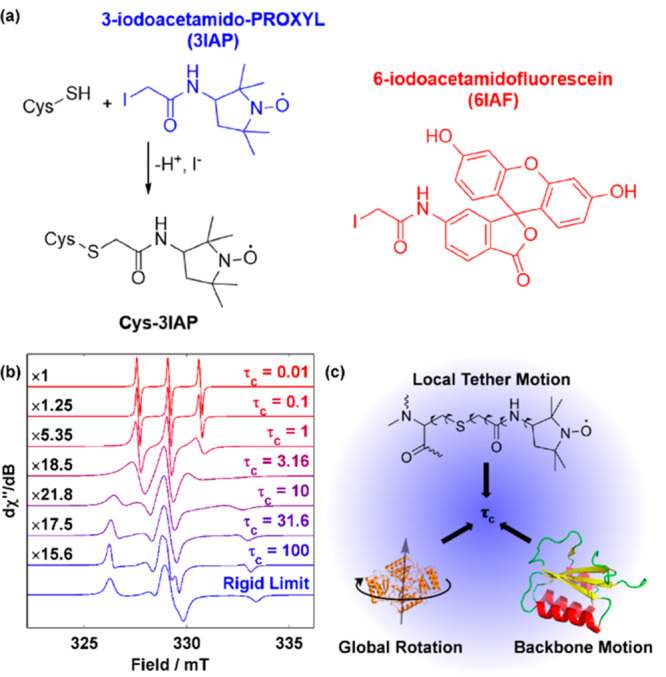
cw-EPR is a strategy for detecting and quantifying intermediates in the Kai clock. (a) Spin labeling reaction used to attach a nitroxide probe onto proteins of interest showing the spin-label 3-iodoacetamido-PROXYL (3IAP, blue) used in this work. The fluorophore 6-iodoacetamido-fluorescein (6IAF, red), also used in this work for fluorescence assays, is also shown for comparison. (b) Simulated nitroxide spectra as a function of mobility normalized by the maximum transition intensity. The scaling factor is shown to the left of each trace, whereas the isotropic rotational correlation time (τ_c in nanosecond) is shown at the right. Simulation details can be found in Table S1. (c) Three types of motions contribute to the experimentally observed rotational correlation time (τ_c), which reflects the mobility of the probe.

The best fits [P_opt (Table S2)] for spin system parameters (P) were determined by interfacing the EasySpin functions pepper (to determine g and A tensors for frozen samples) or chili (to determine rotational correlation times for ambient-temperature samples)⁴² with MATLAB nonlinear least-squares (NLLS) routine lsqnonlin using the objective function obj(spectrum, P) defined below:

3a

For frozen samples, P(pepper) consists of rhombic g and A tensors as well as Gaussian and Lorentzian line widths, totaling eight parameters (Figure S8a). For ambient-temperature N19C_3IAP and its corresponding KaiBC_EE samples, P(chili) consists of a rotational correlation time (a = 1, 2, or 3) parameters (Figures S8b,c and S9). The use of lsqnonlin in place of Easyspin native NLLS function esfit⁴² led to (i) reduced computational time, (ii) allowed user-defined lower and upper bounds for spin parameters as opposed to the [center ± vary] scheme, and (iii) enabled calculation of confidence intervals of spin parameters via the Jacobian matrix using the MATLAB function nlparci. We note that the Jacobian matrix-derived uncertainty measured only the depth or flatness of the local minimum in the objective function landscape with respect to P and thus could underestimate its uncertainty due to insufficient modeling or correlations in P. An alternative scheme was implemented via case resampling bootstrapping by magnetic field bootstrapping. In this scheme, the spectrum was first fitted as described above to obtain the best fit for P_opt. Then, 200 bootstrap spectra were generated via randomly selecting magnetic field positions with replacement and performing NLLS using only the magnetic field positions specified and P_opt as a guess. The resultant fits P* were then used to estimate the uncertainty in P. The (1–2α) confidence interval ([L, U]) of P will then have the form

3b

where P_(0.01γ)^* refers to the γth quantile of P*.

To facilitate ambient-temperature simulations, the g and A tensors were first determined in the near-rigid limit at −40 °C in a 20% (w/w) sucrose (20 Bx) solution using the EasySpin function pepper (Figure S8a) with their uncertainties estimated as described above. The 30 °C spectra were then fitted with fixed g and A tensors with reduced line widths while floating their rotational correlation time(s). For both free and KaiC-bound KaiB, their spectra were simulated with isotropic, axial, and rhombic rotational correlation times in that order (Figure 3f and Figure S8b,c). For selectivity testing of KaiB with respect to direct KaiB–KaiA binding (Figure S9), spectral subtraction was employed by subtracting the spectrum of free KaiB from the reaction spectrum of a 10-fold excess of KaiA and the resultant spectrum was simulated as described above (also see the Supplementary Text). The necessity of rotational anisotropy in simulations was tested via an F-test and AIC computed using the formulas below:

4a

4b

where NRMSD refers to the normalized root-mean-square deviation and is the square root of the residual sum of squares (RSS), normalized by the sum of squares of the background-corrected spectra. For AIC model selection, the quantity of adjustable parameters is equal to k + 2 due to the contribution from isotropic rotation and noise. The AIC is calculated by

4c

where the log-likelihood ln(L̑) is computed by

4d

Due to the possibility for the slight temperature- and local environment-dependent nature of g and A, the spin parameters were further floated within small constraints to better fit the data and compared with the results derived from floating only the rotational correlation time (Figure S8b,civ). It was observed that significantly better fits were obtained by floating g and A, but the values obtained deviated from those of typical nitroxide spin-labels in aqueous solutions determined from multifrequency studies⁴⁰ and thus were not further considered.

Figure 3.

KaiB-N19C-3IAP (N19C_3IAP) reports KaiB–KaiC binding. (a) Crystal structure of tetrameric KaiB [Protein Data Bank (PDB) entry 4KSO] with N19 highlighted in red. (b) Crystal structures of KaiB₆C₆ (PDB entry 5JWQ, chains E and F) and KaiA₂BCI (PDB entry 5JWR, chains A, B, E, and F) with N20 (PDB entries 5JWQ and 5JWR, T. elongatus) highlighted in red. Residue numbers of KaiB in PDB entries 5JWQ and 5JWR are offset from those of S. elongatus by +1. Color code: orange, KaiB; sky blue, KaiC; magenta, KaiA. Pictorial representations of the location of N19(N20) where 3IAP is installed are shown below the respective PDB codes. (c and d) cw-EPR spectra of N19C_3IAP (5×, 17.5 μM) incubated with KaiC_EE (17.5 μM) for 7 h and then spiked with KaiA (6 μM). Panel c shows a surface plot, whereas panel d shows a stacked plot at selected times. The red vertical arrow in panel d indicates B = 326 mT. (e) Reproduction of the experimental spectrum of N19C_3IAP with KaiC_EE and KaiA (7 h spectrum, lilac as in panel d)) with experimental spectra of free N19C_3IAP (red) and N19C_3IAP incubated with a 10-fold excess of KaiC_EE (12 h, orange). (f) Overlay of spectral simulations (black) of free (red) and KaiC_EE-bound (orange) N19C_3IAP using rhombic rotational correlation times. See Table S2 for simulation parameters.

Quantitative Weight Fitting for N19C_3IAP

The microwave frequency drift-corrected real-time cw-EPR data Y_1024×n were simulated by varying the weights (w_ij) of the r components as represented by the matrix multiplication in eq 5, where B_1024×r corresponds to the spectra of the r components and w_ij corresponds to the weight of the ith species in the jth spectrum (i = 1–r; j = 1–n):

5

where ε represents the residual of the fit. The background-corrected spectra of 35 μM spin-labeled KaiB in reaction buffer and 17.5 μM KaiB (5×) in equilibrium with a 10-fold excess of KaiC_EE were taken as B_{free,unscaled} and B_bound, respectively. In general, two spectra may differ in total intensity due to differences in concentration/volume due to experimental design and/or pipetting error, sample alignment, Q factor, or other unexplained factors. The B_{free,unscaled} and B_bound obtained thus cannot be directly used for quantification and must be scaled or normalized. Double integration-based normalization was avoided due to known numerical instability and susceptibility to noise (see Figure S10a).⁴³ Instead, the spectra were normalized by using the real-time kinetic data of KaiB in the presence of a 10-fold excess of KaiC_EE. The real-time data can be written as

6

where θ is the scaling factor to scale B_free. B_bound is set to be the mean of all spectra in the window t = 12–24 h where there is complete binding. Under these conditions, w_t tends toward unity as binding goes to completion as the spectrum is dominated by B_bound. The equation implies that w_t and θ(1 – w_t) can be solved via linear regression (Figure S10b). As B_{free,unscaled} is not scaled, the weight coefficients do not add up to unity. θ can then be solved via linear regression by plotting θ(1 – w_t) against 1 – w_t (Figure S10c). B_free is then scaled by θ (Figure S10d).

In addition to B_free and B_bound, background spectrum B_bg and constant/linear correction terms B_b0 and B_b1 were included. Thus, for a cw-EPR spectrum Y_j that contains two components KaiB_free and KaiB_bound, the equation is overdetermined (1024 equations, 5 unknowns). The corresponding normal equation is

7a

The shape of each component can be found in Figure S11c. The weights are reported as ratios to total nitroxide content (a_ij).

7b

We noted that simulations of spectra from technical replicates using experimental spectra of pure KaiB and KaiBC_EE as basis spectra (B) occasionally led to slight magnetic field offsets (“B-shift”) that could not be accounted for even after correcting for changes in microwave frequency. We reason that these differences were due to (1) minor variations in magnetic shielding between experiments, (2) removing and reinserting the variable-temperature Dewar, and/or (3) ambient-temperature drift leading to minor magnetic field output. To determine the variation in “B-shift” over time, 20 μM 4-hydroxy-TEMPO (TEMPOL) was used as a spin standard (Figure S6a). It was found that the spectrum drifted horizontally over a 3 day period even after accounting for microwave frequency drift (Figure S4a,b). This drift was correlated to ambient-temperature changes and had a period of ∼24 h but with a lag of 5 h (Figure S6b), hinting that the origin of this time-dependent “B-shift” was potentially due to periodic drift in (1) magnet temperature, (2) expansion or contraction near the magnet, and/or (3) circuit load on the electrical outlets supplying the magnet, all of which can result in variations in magnetic field output.

Because minor shifts in the magnetic field abscissa directly impact spin quantification (Figure S6c), the experimental spectra were shifted horizontally (B′) to account for this difference. The discrete form of this shift can be written as a matrix operator P below:

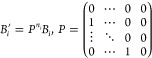8a

As the optimal shift (in millitesla) is unlikely to be an integer multiple of the magnetic field unit, the magnitude of the shift n_i may take any real value s and is achieved via interpolation. Hence, quantitative cw-EPR at any time t becomes a nonlinear problem of 1024 equations and r + 1 unknowns:

8b

Hence, simultaneously solving for w_t and s_t yields the weights of each component and the “B-shift” provided that the spectra of the components were known and “B-shift” corrected. However, eq 5 did not explicitly take “B-shift” into account. Accordingly, eq 5 is modified to the following:

9

where Y_t and s_t are the spectrum and “B-shift” magnitude at time t, respectively, w_it is the weight of the ith component at time t, and s_i is the component-dependent shift. The term s_i accounts for the intersample “B-shift” contribution due to changes in sample placement and thus effective magnetic field experienced at the sample, whereas s_t accounts for intrasample “B-shift” due to fluctuations in magnetic field output that was found to correlate with ambient temperature (Figure S6b). Nonlinear least squares is used to solve for w_it, s_i, and s_t simultaneously by considering data at multiple time points (t_n) using the components B_{free,unscaled}, B_bound, and B_bg. This results in 1024 × n equations and 3n (w_it) + (3 – 1)(s_i) + n(s_t) unknowns with initial guesses for w_ij obtained via linear regression and s_i and s_t set to zero. Only r – 1 components require a non-zero s_i as s_i and s_t co-vary and s_i=1 is hence defined to be zero. The fitted w_it is then used to compute θ (eq 6) for scaling, whereas s_i is used to shift the B components for further quantitative analysis (eq 8b).

Uncertainty Analysis in Quantitative Real-Time cw-EPR Kai Reactions

There are three contributions to the observed variance in the data: (1) spin model/spectral line shape uncertainty, (2) noise-induced uncertainty, and (3) other random errors, including pipet errors and protein batch-to-batch variability.

(1) Spin Model/Spectral Line Shape Uncertainty (σ_model). Although experimental spectra were used for fitting of all real-time spectra, giving rise to well-defined line shapes, the necessity of scaling B_free relative to B_bound introduces error in the form of uncertainty in scaling factor θ. As θ is determined via linear regression (eq 6), the confidence interval in θ can be readily obtained by standard linear regression formulas and implemented by MATLAB function regress.

(2) Noise-Induced Uncertainty (σ_S/N). Real data are noisy and thus give rise to uncertainty in quantification. The weights of B_free and B_bound are simultaneously determined with “B-shift” via nonlinear regression (see eq 8b). Uncertainty can thus be estimated via the Jacobian matrix and MATLAB function nlparci.

(3) Other Random Errors (σ_r). Other random errors include protein batch-to-batch variations, pipetting error, and other unknown sources of error. This error can be observed when comparing results obtained between technical replicates.

For phosphomimetic reactions, the overall uncertainty is then computed as

10a

The modeling or line shape uncertainty error is intrinsic to the data processing. On the other hand, performing multiple technical replicates simultaneously measures σ_r and σ_S/N.

For oscillator reactions, direct averaging of multiple replicates can lead to cancellations in oscillations due to minor variations in period and/or phasing. Thus, calculation of the inter-replicate standard error of the mean (SEM) was not performed. Instead, the error reported does not contain inter-replicate uncertainty:

10b

Uncertainty estimates from the Jacobian matrix obtained from nonlinear least-squares correspond to weights (w) to be converted to fractions (a). This propagation is done via

11

where w_i in eq 11 corresponds to the weight of component i in the spectrum and a_i corresponds to the ratio of component i to the overall concentration. Notice that the first term is common for all values of i and j whereas the second term is a correction term arising from the i = j case in the summation. The final 95% confidence interval (CI) is calculated by

12

where a̅ is the best estimate for a and t_0.975,df and z are t and z values, respectively, for the 95% confidence interval, where df refers to the degrees of freedom in the evaluation of θ.

In experiments in which the binding velocity was desired to be computed (see Figures S11 and S12), a Savitzky–Golay filter was applied via Easyspin function savgol to simultaneously smooth and differentiate the binding kinetic curve using seven-point window and quadratic polynomials.

Circadian Oscillation Rhythm Period and Waveform Analysis

The extracted KaiB binding kinetics were further analyzed by curve fitting to mFourfit⁴⁴ (MFF) by modeling the kinetic trace f(t) as a sum of cosines as shown below using lsqnonlin as the interface:

13a

where the constant C, amplitude A_j, phase angle φ_j, and period T are adjustable parameters and the residual term ε is minimized. The quantity of cosines used can be adjusted by changing q. The number of adjustable parameters is thus equal to 3 + 2q. To prevent overfitting, the corresponding AIC was computed at each q by

13b

Confidence intervals in amplitude and period were determined with nlparci. To ascertain the period of oscillation, the maximum entropy spectral analysis (MESA)⁴⁵ and Lomb–Scargle periodogram⁴⁶ were computed and compared with the period obtained via MFF (Figure S15b,c).

Results

cw-EPR Strategies for Quantifying Complex Mixtures

As cw-EPR spectra of mixtures are additive, quantitative kinetics can be extracted from real-time cw-EPR experiments with spin-labeled proteins if the spectra of underlying components are known. Thus, successful cw-EPR quantification is contingent upon design and/or discovery of spectroscopic handles that respond to relevant interactions. Because none of the Kai proteins contain paramagnetic centers necessary for direct cw-EPR characterization, a spin-label in the form of nitroxide can be introduced via bioconjugation to provide this handle. This is most conveniently done via site-directed mutagenesis to cysteine followed by labeling with a cysteine-reactive reagent that bears the nitroxide moiety (Figure 2a). In this regard, KaiB is an ideal candidate for spin labeling due to its lack of native cysteine residues as compared to KaiA (six cysteines per monomer) or KaiC (three cysteines per monomer).

There are multiple strategies for designing a labeling site such that the nitroxide spectroscopic handle will respond to binding once installed on the protein of interest by exploiting various spin-based phenomena. One such strategy is to install spin-labels that are close to one another in a multimeric protein, resulting in spin exchange⁴⁷ and/or dipolar broadening⁴⁸ that broadens the spectra and thus differentiates monomeric versus multimeric species. Another strategy that is exploited in this work is the mobility dependence of the width of the nitroxide spectrum. Unlike the free nitroxide molecule in solution that tumbles freely, a protein-bound nitroxide moiety exhibits a reduced level of global tumbling. Motions originating from the connecting tether and protein backbone dominate. As the motion slows from rapid tumbling toward the rigid limit, the ¹⁴N hyperfine anisotropy is no longer averaged out by the motion and the cw-EPR spectrum broadens (Figure 2b). This mobility as quantified by the rotational correlation time (τ_c) of a spin-labeled residue is a combination of local and global motions (Figure 2c), changes in which are directly reflected in cw-EPR spectra (Figure 2b). Thus, a successful spin labeling site should lead to either (a) a nitroxide tether that becomes motionally restricted or (b) a change in secondary structure on protein–protein binding. In theory, the global protein tumbling motion (Figure 2c) should contribute to experimentally observed mobility as predicted by the Stokes–Einstein relation (SE, τ_c^SE):

14

where η is the dynamic viscosity of the buffer (assumed to be equal to that of water at 30 °C), V is the estimated volume of the crystal structures, ν̅_p (= 0.73 cm³ g^–1) is the partial specific volume, M_p is the molecular weight of the protein, k_B is the Boltzmann constant, and T is the temperature in kelvin. In practice, τ_c^SE often underestimates global rotation by a factor of 2 due to the negligible level of hydration.⁴⁹ This puts a lower limit on the molecular mass of the protein in question as nitroxide spectra stemming from spin-labeled proteins smaller than this limit will be influenced by both local mobility and global rotation. The parallel contributions from both local and global motions complicate interpretations as spectral changes can no longer be attributed to only local binding events.

Site Design and Other Practical Considerations in SDSL–cw-EPR for Probing KaiB–KaiC Binding

Like fluorescence anisotropy (FA),³⁶ the success of EPR spin labeling-based assays is dependent on the labeling site. In the former, site design is guided by two potentially conflicting principles that both local rotational effects (“propeller effects”) and binding affinity interference should be minimized.⁵⁰ In the latter, it is precisely the changes in local rotational motion that enable a meaningful binding assay as reflected by nitroxide line shape changes while also taking advantage of the smaller footprint of a nitroxide moiety compared to common fluorophores (Figure 2a). To that end, we chose KaiB-N19 (Figure 3a) as the mutation site for studying KaiB–KaiC binding without interference from KaiA. N19 is located at the N-terminal cap of KaiB-α1 and is close to the KaiB-CI binding interface in published crystal structures (Figure 3a).²¹ However, it is pointed away from the KaiB–KaiA binding interface in the ternary KaiABC complex (Figure 3b).²¹ Hence, we hypothesized that the N19C mutant of KaiB when spin-labeled will report a decrease in flexibility on KaiB–KaiC binding but that further binding to KaiA will not report the ternary KaiABC complex as a spectroscopically distinct species.

To generate the spin-labeled KaiB-N19C-3IAP construct (N19C_3IAP hereafter), a 5-fold excess of TCEP was first added to unlabeled KaiB to reduce preformed disulfide bonds that prevent cysteine-iodoacetamide bioconjugation. Then, a 10-fold excess of 3IAP was added. The labeling efficiency can be checked by intact mass spectrometry (Figure S1). As the EPR signal intensity varies with the quantity of spins in a sample, the labeling reaction should be repeated on samples with low labeling efficiencies to drive the labeling reaction toward completion to provide an optimal signal-to-noise (S/N) ratio. The more commonly used spin-labels S-(1-oxyl-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methylmethanesulfonothioate (R1) and 4-maleimido-TEMPO (4MT) were avoided because they release free PROXYL via disulfide exchange when encountering free thiols⁵¹⁻⁵³ and undergo maleimide hydrolysis to the more flexible succinamic acid ester (SAT),^54,55 respectively, rendering them unsuitable for functional assays that span multiple days.

Despite the enhanced reactivity between N19C_3IAP and KaiC_EE as compared to WT-KaiB as revealed by native-PAGE (Figure S2) on mutagenesis and spin labeling, wild-type KaiB could be completely replaced by N19C_3IAP without significantly altering the period of the Kai oscillator based on our previously developed FA assay using 6IAF-labeled KaiB-K25C as a fluorescence reporter [K25C_6IAF (Figure S3)].³⁶ Our spin-labeled KaiB mutants are thus robust functional surrogates for wild-type KaiB and therefore suitable as reporters of the Kai clock.

The Spin-Labeled Construct Provides a Selective Response to KaiB–KaiC Binding

To test our hypothesis that N19C_3IAP provides a spectroscopic handle for quantifying KaiB–KaiC binding without interference due to ternary KaiABC complex formation, N19C_3IAP was first reacted with a stoichiometric amount of KaiC_EE and then the mixture was spiked with KaiA after 7 h (Figure 3c,d). KaiC_EE, a KaiC_pSpT phosphomimetic, was chosen as the KaiC surrogate as S431 phosphorylation was shown to be necessary for KaiBC complex formation, and KaiC_EE outperformed KaiC_EA in binding to KaiB.²³ As spectra from the same sample were collected at 7.5 min intervals over 24 h, 192 spectra were recorded and displayed as a surface plot (Figure 3c). Comparison between cw-EPR spectra recorded immediately after mixing N19C_3IAP and KaiC_EE versus that of a sample that had been incubated for 7 h (Figure 3d and Figure S7) revealed the formation of a slowly tumbling species in the latter as indicated by the appearance of a peak at 326 mT that is identified as originating from KaiB–KaiC interactions. The intensity of this peak reached a maximum in approximately 6 h (Figure 3c), in agreement with native-PAGE (Figure S2). When the sample was spiked with KaiA, the intensity of the slowly tumbling species decreased marginally but no new spectroscopically distinct species were visually discernible (Figure S7a). Furthermore, the real-time KaiB–KaiC_EE–KaiA reaction spectra could be satisfactorily reproduced as a linear combination of the spectrum of pure N19C_3IAP and that of N19C_3IAP in a 10-fold excess of KaiC_EE (Figure 3e and Figure S7b). This implies that cw-EPR of N19C_3IAP does not distinguish between various KaiA_2jB_iC₆ complexes (i = 1–6, and j = 0–i),^27,28,56 and thus, the spectra derived from N19C_3IAP and KaiC can be used as a readout reflecting the fraction of KaiC-bound KaiB independent of KaiA forming a complex with KaiBC.

To investigate the origin of the observed equivalence of cw-EPR spectra of N19C_3IAP in KaiABC complexes of various stoichiometries, spectral simulations were applied to analyze the rotational motion of the KaiB-bound spin-labels. The best fits for free and KaiC_EE-bound N19C_3IAP are shown in Figure 3f. The g and A tensors determined at the near-rigid limit at −40 °C using 20% (w/w) sucrose (Figure S8a and Table S2) are highly comparable to those obtained via W-band cw-EPR (94 GHz) of 3IAP⁵⁷ as well as multifrequency studies of the related spin-label R1.⁴⁰ Although the Brownian-motion model oversimplifies the spin-labeled systems in question as global rotation, backbone, and local tether motions are all known to contribute to rotational diffusion (Figure 2c), experimental spectra of both free and KaiC_EE-bound N19C_3IAP acquired at 30 °C could be satisfactorily simulated via such treatment and hence justify its application. The effective isotropic correlation times (τ_c^iso,eff) of both forms of N19C_3IAP are shorter than their Stokes–Einstein (SE) estimates [τ_c^SE (Figure S8b,c and Tables S2 and S3)]. Similar observations have been demonstrated with 3IAP-labeled IDPs⁵⁷ and R1-labeled lysozyme.⁴⁰ As typical rotational correlation times estimated by SE often underestimate τ_c^iso by a factor of 2 for globular proteins,⁴⁹ our simulations imply that the combined motions of the nitroxide tethers and protein backbone in both free and KaiC-bound KaiB exhibit high flexibility as the tethered nitroxide probe moves faster than global rotational motion. The experimentally observed τ_c^eff is thus attributed to the combined motions of the nitroxide tether and protein backbone and explains the independence of the spectral signature to N19C_3IAP–KaiC binding stoichiometry.

For the sake of completeness, we also reacted N19C_3IAP with KaiA in the absence of KaiC to determine its spectral sensitivity to direct KaiA–KaiB interactions (Figure S9). It has previously been reported that KaiA could bind to WT-KaiB in trace quantities in the form of KaiA₂B₁ based on native mass spectrometry.²⁸ Separately, mutations that destabilize tetrameric gs-KaiB via either the G88A mutation²⁴ or C-terminal deletions²⁰ have been shown to enhance direct KaiA–KaiB interactions. On the basis of these observations, it is deduced that KaiB likely adopts the fs-KaiB conformation in the KaiA₂B₁ complex. To determine if N19C_3IAP responds to direct KaiA–KaiB interactions, cw-EPR spectra of 17.5 μM N19C_3IAP, corresponding to 5× in vitro oscillator, in the presence of varying concentrations of KaiA were compared. The cw-EPR spectrum in the presence of 6 μM KaiA (5×) could not be discerned from that of N19C_3IAP alone (Figure S9a). There are three possibilities to this observation. (a) KaiB and KaiA do not interact at all. (b) They interact, but X-band cw-EPR of N19C_3IAP treats the KaiA-bound KaiB population as spectroscopically equivalent to free KaiB. (c) They interact to give a spectroscopically distinct species, but the limited S/N ratio renders detection impossible. The last scenario may be attributed to (i) weak interactions at the physiologically relevant KaiA:KaiB ratio (1:3) and/or (ii) the high degree of cw-EPR spectral similarity between free and KaiA-bound N19C_3IAP due to insignificant changes in local mobility. In an attempt to distinguish the three scenarios and drive KaiA–KaiB interactions, we increased the KaiA:KaiB ratio to 10:1 and observed subtle changes in the h_–1 transition region as well as slight broadening in the central transition (Figure S9b), ruling out possibilities (a) and (b). Subtraction and simulation studies indicate that this motional component constitutes at least 7% of the total signal under excess KaiA loading (Figure S9c, Table S4, and the Supplementary Text). Because this ratio is unphysiological as ratios of 1:3²⁹ to 1:30²² have been reported in vivo, little insight into the biological relevance of direct KaiA–KaiB interactions can be gained. Nevertheless, the selectivity of the spectroscopic response of N19C_3IAP to KaiB–KaiC interactions is established.

Quantitative Interpretation of KaiB–KaiC Binding

Because N19C_3IAP is the only EPR-active species in the experiments described above, the fraction of KaiB in KaiC-bound KaiB relative to total KaiB is equal to its contribution (weight) normalized by the total weight of the spectrum. It was found above that the N19C_3IAP reaction spectra could be explained by two components, free and KaiC-bound KaiB (Figure 3e). The former was readily obtained by acquiring the spectrum of N19C_3IAP alone, whereas the latter was obtained by adding it to a 10-fold excess of KaiC_EE (Figure S7b). Quantitative kinetics with N19C_3IAP could thus be extracted using these two spectra as basis spectra.

We first applied this strategy to analyze the KaiB–KaiC_EE binding data to obtain a binding progression curve. The extracted kinetics exhibited sigmoidal kinetics (Figure 4a and Figures S11 and S12). Qualitatively, the sigmoidal kinetics observed in our experiments rules out the possibility of single-step KaiB–KaiC binding and is consistent with previous studies that indicate binding cooperativity among KaiB subunits²⁷ as well as gating via KaiB fold switching and/or CI ATPase activity.²⁴ To quantify binding latency, we determined the time taken to reach the maximum rate of binding (t_v,max) to be 0.9 ± 0.2 h [SEM; n = 6 (Figure 4b and Figures S11 and S12)]. Compared to native-PAGE (Figure S2), the nondestructive nature of ambient-temperature cw-EPR allows kinetics to be determined using a single sample. This contrasts with native-PAGE in which the sample is adulterated by the loading buffer and consumed during electrophoresis, rendering the need to prepare multiple samples flash frozen at predetermined times. The improved time resolution of cw-EPR over native-PAGE allows identification of sigmoidal kinetics in N19C_3IAP–KaiC_EE binding that is not observed in native-PAGE.

Figure 4.

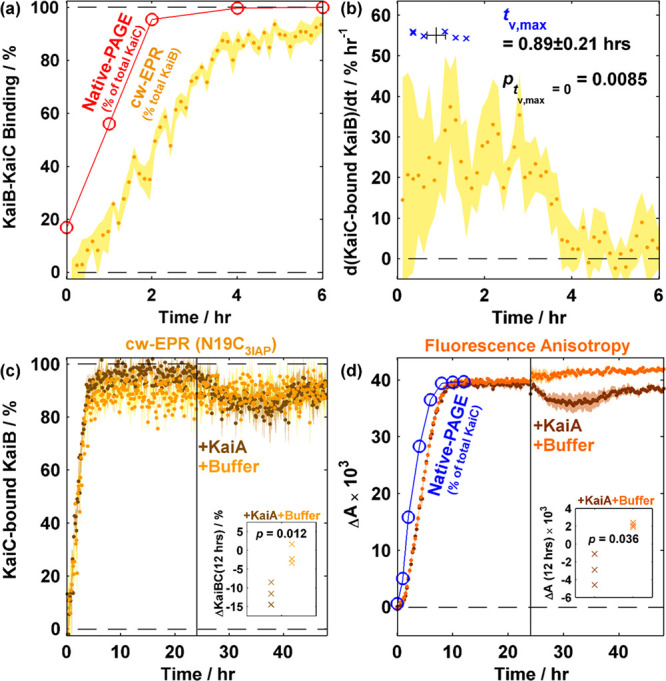
cw-EPR is an orthogonal method for quantitatively assaying KaiB–KaiC binding as illustrated by KaiB–KaiC_EE binding followed by KaiA spiking at 24 h. (a) Overlay of N19C_3IAP–KaiC_EE binding kinetics obtained via native-PAGE (red empty circles) and cw-EPR (yellow filled circles) from 0 to 6 h. (b) Rate of formation of KaiC-bound KaiB (yellow circles) and time at maximum binding velocity (t_v,max, blue crosses). For panels a and b, the shaded area (cw-EPR) and error bars (t_v,max) indicate SEM (n = 6). (c) Overlay of N19C_3IAP–KaiC_EE cw-EPR binding kinetics followed by spiking with KaiA (brown) or buffer (yellow) at 24 h. Shaded areas show the SEM (n = 3). (d) Overlay of WT-KaiB–KaiC_EE fluorescence anisotropy-based binding kinetics using 50 nM KaiB-K25C-6IAF (K25C_6IAF) as a fluorescence probe with KaiA (brown) or buffer (orange) spiking at 24 h. Shaded areas show the SEM (n = 3). Insets in panels c and d show two-tailed t-tests comparing the effects of KaiA vs buffer spiking after 12 h of spiking. cw-EPR data were binned in 2 h bins prior to performing the t-test.

Curiously, an apparent offset of approximately 1 h was observed between kinetics derived from cw-EPR versus native-PAGE (Figure 4a). As KaiC (58 kDa) is larger than KaiB (11 kDa), the native-PAGE band intensity is likely dominated by KaiC in KaiBC complexes. Furthermore, native-PAGE electrophoretic mobility is a function of protein conformation. We interpret the discrepancy in native-PAGE and either cw-EPR or FA (Figure 4d and Figure S13, vide infra) as originating from the former being sensitive to KaiC conformational changes in KaiB binding. This discrepancy is consistent with the multistep nature of KaiB–KaiC binding based on native mass spectrometric identification of substoichiometric KaiBC complexes.²⁷ However, the possibility of in-gel KaiB–KaiC binding during electrophoresis cannot be ruled out.

We further analyzed the KaiB–KaiC_EE binding data when the steady-state mixtures were subjected to KaiA spiking (Figure 4c and Figures S11 and S12). On the basis of previous studies, the addition of KaiA to an equilibrated mixture of KaiB and KaiC_EE would lead to a ternary mixture of KaiB-containing species: KaiB, KaiBC_EE, and KaiABC_EE.²⁰ As demonstrated above, cw-EPR of N19C_3IAP is insensitive to KaiABC complexes due to the lack of formation of spectroscopically distinct species at physiologically relevant concentrations. Thus, the slight increase in the mobile component’s intensity after KaiA was added to the preequilibrated mixture of N19C_3IAP and KaiC_EE provides unequivocal evidence that KaiA can antagonize KaiBC_EE interactions slowly (Figures 3d and 4c and Figures S11 and S12). On the contrary, interpretation of the K25C_6IAF FA data (Figure 4d and Figure S13) is complicated by the presence of at least three KaiB-containing species even under the assumption that KaiBC complexes of all stoichiometries (KaiB_iC₆, where i = 1–6) have identical fluorescence anisotropies. Because there is little theoretical basis to assume that K25C_6IAF in the ternary KaiABC_EE complex possesses an FA identical to that of the binary KaiBC_EE complex, the use of FA to quantify KaiB–KaiC_EE binding in the presence of KaiA is akin to solving an underdetermined system of equations. Nevertheless, if these assumptions hold, we anticipate that formation of the ternary complex would marginally increase the observed anisotropy whereas KaiB–KaiC interaction antagonization should reduce the anisotropy. The observed decrease in anisotropy could thus be interpreted qualitatively as KaiBC_EE complex antagonization, a fortuitous conclusion that agrees with cw-EPR-derived kinetics (Figure 4c and Figures S11 and S12). This KaiA spiking experiment highlights the potential ambiguity in extracting kinetics from single-wavelength FA data. On the other hand, cw-EPR benefits from the use of the magnetic field as a second abscissa, offering the possibility of statistically testing the quantity of components via rank analysis⁵⁸ and quantifying more than two components if warranted. Thus, cw-EPR of spin-labeled KaiB offers an orthogonal and quantitative method for probing KaiB–KaiC binding while eliminating interference due to ambiguity in variable Kai protein stoichiometries.

Application to Oscillator Reactions

Equipped with the knowledge that N19C_3IAP probes KaiB–KaiC binding, we measured the time dependence of KaiB binding in the in vitro oscillator using real-time cw-EPR (Figure 5 and Figures S14–S16) using N19C_3IAP as a spin-labeled surrogate for WT-KaiB.

Figure 5.

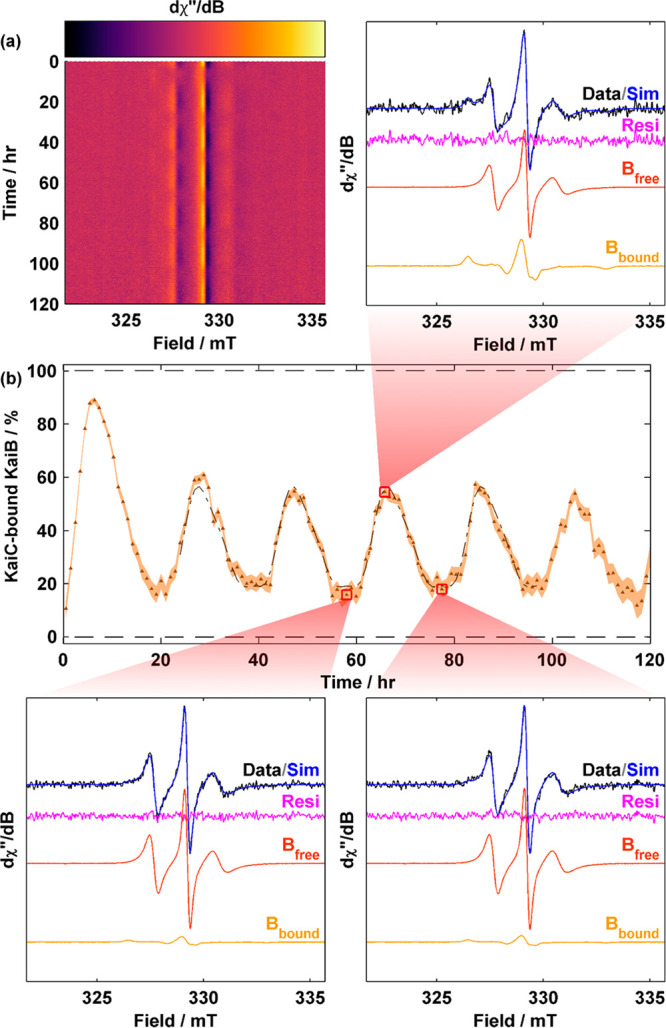
Observation of KaiB–KaiC binding and dissociation throughout the Kai oscillations via cw-EPR. (a) Surface plot of cw-EPR spectra of N19C_3IAP 1× oscillator (3.5 μM N19C_3IAP, 3.5 μM KaiC, and 1.2 μM KaiA). (b) cw-EPR-based kinetics of KaiC-bound KaiB as a function of time. Data were binned in 1 h bins. The shaded area indicates the 95% CI. A fit to the sum of cosines is overlaid as a dashed–dotted line (see Table S5). Selected spectra at three time points (red squares) with their respective fit are displayed.

The cw-EPR spectra of N19C_3IAP in the reconstituted oscillator demonstrated periodic time dependence as seen in height oscillations of the central (h₀) transition at B₀ = 329.1 mT as well as broader features corresponding to h_–1 and h₊₁ transitions that are out of phase with the h₀ transition (Figure 5a and Figure S14a). The periodic spectral variations indicate periodic KaiB binding–unbinding events. Although individual spectra at a 1× concentration were very noisy, reasonable fits using experimental spectra of pure KaiB and KaiBC_EE were still possible after binning (Figure 5b and Figure S14b) and enabled quantitative determination of binding progression with high reproducibility (Figure S15). Using a sum of cosines via mFourfit⁴⁴ (Figure S16), we determined the phenomenological amplitude of oscillation to be 41.7 ± 3.4% [SEM; n = 4 (Figure 5b, Figure S15, and Table S5], slightly smaller than 50% as determined by FCS by Goda et al.³⁴ We reasoned that the minor discrepancy is due to a smaller translational diffusion coefficient of the ternary KaiABC complex compared to KaiBC that leads to amplitude overestimation in a two-component model. However, the difference in reactivity between WT-KaiB and N19C_3IAP revealed by native-PAGE (Figure S2) may also contribute to the difference in amplitudes. The overall shape of the binding curve is consistent with previous literature³⁴ that revealed that (i) KaiB binding occurs over a shorter time span than KaiB unbinding and (ii) the duration of minimally bound KaiB (trough) is wider than the duration of maximally bound KaiB (peak) (Figure 5b, Figure S16, and Table S5). We note that a two-component model for describing FCS data is likely inappropriate as FCS is based on the translational diffusion time, which is in turn dependent on the molecular weights of various KaiABC complexes with various stoichiometries, and previous native mass spectrometry results²⁷ point toward this fact. On the other hand, for sufficiently large proteins where global rotational motion is slow, cw-EPR is dependent on only the local nitroxide tether and protein backbone motion. Thus, a two-component model is appropriate for N19C_3IAP (Figure 3e).

Discussion

Implications of cw-EPR Results for the Current Model of the Kai Oscillator

The discovery of N19C_3IAP as a KaiB–KaiC interaction selective probe allowed binding kinetics to be observed in real time. The improved time resolution and theoretical support for selectivity offer an orthogonal window into the understanding of the Kai system.

Our cw-EPR and FA data suggest that the KaiB–KaiC_EE interaction is weakly antagonized by KaiA transiently (Figure 4c,d). As pointed out above, the existence of more than two KaiB-containing species prevents interpretation of K25C_6IAF FA as KaiB–KaiC binding when KaiA is present. Nevertheless, the consistency between these two techniques at differing labeling sites implies that this transient KaiA antagonization is unlikely to be a probe or technique-based artifact. The observed antagonization is surprising given that KaiA is known to be sequestered during the night state as a ternary KaiABC complex when S431 is phosphorylated.²⁰ As KaiA was observed to impact KaiB–KaiC binding in a phospho-state-dependent manner as determined by immunoprecipitation SDS–PAGE,²³ with an increasing level of KaiA leading to a nonlinear response in KaiC_pSpT–KaiB binding, the real-time observations presented in this study were not unreasonable. KaiA has been shown to act as a nucleotide exchange factor for KaiC,^18,19 the latter of which has only been crystallized in conjunction with KaiB in a post-ATP hydrolysis state.²¹ We speculate that this transient KaiA-induced KaiBC antagonization is due to interactions between KaiA and A-loops on CII. This interaction weakens the CII ring integrity, which in turn weakens CII–CI ring stacking interactions.¹³ As ring stacking stabilizes the posthydrolysis state of CI, weakened stacking promotes the prehydrolytic state of CI, which destabilizes KaiBC interactions. This antagonization occurs over 12 h, but the KaiBC population recovers on longer time scales as the spiked KaiA is sequestered into a KaiABC complex. This observation is consistent with exclusive activities of CI and CII rings that are reciprocally regulated.²³ Further experiments are necessary to evaluate the plausibility and molecular mechanism of this pathway and its relevance in clock resetting.

Limitations of cw-EPR as an Analytical Technique for Studying Protein–Protein Interactions

Prior to this work, SDSL–EPR has been used to determine the secondary structure⁵⁹ and oligomeric state⁴⁷ of membrane proteins as well as folding of both globular⁶⁰ and intrinsically disordered proteins.⁵³ Our current work illustrates that cw-EPR can be an analytical technique for studying protein–protein interactions in real time. However, there are two limitations that can limit the usefulness of cw-EPR in quantification and generalization to other systems to be discussed below.

(1) Site Design for Spin Labeling. Unlike FA where the fluorescence probe can be attached to surface residues or either terminus of the protein of interest,⁵⁰ the requirement for a change in the local environment (Figure 2c) for a corresponding spectral change in the nitroxide cw-EPR spectrum poses a unique problem. Researchers are often limited by existing crystal structures and biochemical intuition in designing mutants for probe conjugation while minimizing perturbations to biochemical reactivity. In this work, we showed that N19C_3IAP was selective with respect to KaiB–KaiC interactions but the mutagenesis and labeling also enhanced KaiB’s reactivity (Figure S2). SDSL is thus not necessarily a conservative mutation, and orthogonal functional assays should be employed to test the spin-labeled constructs’ reactivity. Nevertheless, considering the potential of SDSL–EPR in resolving multiple species in real time by using magnetic field as the second abscissa, its application could be extended if this barrier in site design is lowered. We envision that future researchers should be able to design SDSL–EPR probe sites based on molecular dynamics (MD) simulations.⁶¹⁻⁶⁵ To that end, multiple strategies have been implemented to directly compute the cw-EPR spectra of spin-labeled proteins from MD simulations.⁶²⁻⁶⁵ However, screening of multiple sites via a full MD simulation can be computationally demanding. Alternatively, rotamer libraries have previously been computed for multiple nitroxide spin-labels as coarse-grain approximations to the true dynamics of the nitroxide moiety to aid in designing probe sites for favorable distance measurements.^61,66 Computed within the rotamer library-based calculations are metrics such as nitroxide partition function Z, which measures the tightness of the site and root-mean-square deviation of the midpoint of the N–O group from the mean position, both of which might be correlated with nitroxide mobility. As only a single biologically active mutant was described in this work, there are insufficient data to correlate our results with MD or rotamer library predictions. Nevertheless, we anticipate that such a correlation can be established in the future with additional data and increasingly efficient schemes in computing nitroxide molecular dynamics.

(2) Sensitivity and Throughput. A second limitation to developing an SDSL–EPR-based biochemical assay is the limited sensitivity and throughput of cw-EPR. SDSL–cw-EPR at ambient temperatures has previously been performed with proteins at high concentrations⁴⁰ (∼1 mM) to allow a sufficient S/N ratio. For practical biological assays, the protein concentration is often kept low to mimic physiological conditions and reduce the level of aggregation. This trade-off in sample concentration renders a low S/N ratio and ambiguity in spectral interpretation. In the context of the Kai clock, increasing the concentration of the Kai oscillator can lead to an increased level of ATP consumption and premature failure of the oscillator due to ATP depletion.⁶⁷ This contrasts with routine fluorescence assays in which nanomolar probe concentrations coupled with optical plate readers provide decent S/N ratios with high throughput. The S/N ratio limitation highlights the urgency for innovative detection schemes to improve cw-EPR sensitivity. In that respect, we anticipate that rapid-scan EPR⁶⁸ coupled with imaging⁶⁹ can satisfy both requirements of increased S/N ratio and throughput at physiological concentrations.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.biochem.0c00279.

• Tables S1–S5, Figures S1–S16, and Supplementary Text (PDF)

Accession Codes

S. elongatus (PCC 7942) KaiC, UnitProt entry Q79PF4; S. elongatus (PCC 7942) KaiB, UnitProt entry Q79PF5; S. elongatus (PCC 7942) KaiA, UnitProt entry Q79PF6.

Author Present Address

^∇ Y.-G.C.: Monash Biomedicine Discovery Institute, Monash University, Clayton, VIC 3800, Australia.

This work was supported by grants from the U.S. National Science Foundation (NSF-MCB-1615752 to R.D.B. and NSF-HRD-1547848 to CREST, the Center for Cellular and Biomolecular Machines at the University of California, Merced, CA), the National Institutes of Health (GM107521 to A.L.), and the Army Research Office (W911NF-17-1-0434 to A.L.).

The authors declare no competing financial interest.