Forecasting Retinal Nerve Fiber Layer Thickness from Multimodal Temporal Data Incorporating OCT Volumes

Abstract

Purpose

The purpose of this study was to develop a machine learning model to forecast future circumpapillary retinal nerve fiber layer (cpRNFL) thickness in eyes of healthy, glaucoma suspect, and glaucoma participants from multimodal temporal data.

Design

Retrospective analysis of a longitudinal clinical cohort.

Participants

Longitudinal clinical cohort of healthy, glaucoma suspect, and glaucoma participants.

Methods

The forecasting models used multimodal patient information including clinical (age and intraocular pressure), structural (cpRNFL thickness derived from scans as well as deep learning-derived OCT image features), and functional (visual field test parameters) data and the intervisit interval for prediction of cpRNFL thickness at the next visit. Four models were developed based on the number of visits used (n = 1 to 4). Longitudinal data from 1089 participants (mean observation period, 3.65±1.73 years) was used with 80% of the cohort for the development of the models. The results of our models were compared with those of a commonly adopted linear regression model, which we refer to here as linear trend-based estimation (LTBE).

Main Outcome Measures

The mean absolute difference and Pearson’s correlation coefficient between the true and forecasted values of the cpRNFL in the healthy, glaucoma suspect, and glaucoma patients.

Results

The best forecasting model of cpRNFL was obtained using 3 visits and incorporated deep learning-derived OCT image features. The mean error was 1.10±0.60 μm, 1.79±1.73 μm, and 1.87±1.85 μm in eyes of healthy, glaucoma suspect, and glaucoma participants, respectively. Our method significantly outperformed the LTBE model for glaucoma suspect and glaucoma participants (P < 0.001), which showed a mean error of 1.55±1.16 μm, 2.4±2.67 μm, and 3.02±3.06 μm in the 3 groups, respectively. The Pearson’s correlation coefficient between the forecasted value and the measured thickness was ρ = 0.96 (P < 0.01), ρ = 0.95 (P < 0.01), and ρ = 0.96 (P < 0.01) for the 3 groups, respectively.

Conclusions

The performance of the proposed forecasting model for cpRNFL is consistent across glaucoma suspect and glaucoma patients, which implies the robustness of the developed model against the disease state. These forecasted values may be useful to personalize patient care by determining the most appropriate intervisit schedule for timely interventions.

Glaucoma is a chronic and irreversible neurodegenerative ocular disorder in which the optic nerve is damaged progressively, leading to deterioration in vision and quality of life.¹ It will have affected approximately 80 million individuals worldwide by 2020.² Being mostly asymptomatic, glaucoma patients usually are unaware of their disease until a notable visual loss occurs at a later stage. Therefore, early detection of glaucoma is challenging. After diagnosis, the current clinical challenge is to assess accurately the rate of aggressiveness of glaucoma progression to choose appropriate disease management strategies (medication, surgery, or both) because the progression rate is largely variable from individual to individual. Previous works suggest that the progressive thinning of circumpapillary retinal nerve fiber layer (cpRNFL) thickness measured by OCT is useful for prediction of future visual field (VF) loss in patients with glaucoma.^3–5 Therefore, the ability to forecast the cpRNFL value for future visits is useful in early stratification of patients who are at risk of losing VF more rapidly.

Assessing the progression of the disease using cpRNFL thickness has been performed in a variety of ways, including the use of preset thresholds of change observed across visits (event analysis) or by computing the rate of change (trend analysis).⁶ Guided progression analysis^4,7 has been used to estimate the rate of cpRNFL thickness changes based on 4 consecutive visits. Other approaches^8–10 have aimed to differentiate between stable and progressive patients but did not forecast estimates of the cpRNFL or VF. For example, cpRNFL thickness and visual function measurements were used jointly to classify individual eyes as either stable or progressive over time.¹⁰

More recently, principal component analysis features of retinal nerve fiber layer (RNFL) thickness maps were used to predict the stability of a patient’s disease.¹¹ Similar to previous works, stability was defined with respect to a small cohort of healthy individuals and the progression was determined using 4 visits. This approach highlighted the advantages of machine learning to predict the mean RNFL and mean deviation (MD) from VF tests, but their model used only baseline data from a single visit and did not leverage the available temporal information.

In another method, longitudinal structural and functional data were used to develop a glaucoma progression model.^12,13 This approach incorporated the variable intervisit durations into a continuous-time model that provided predictions regarding the future transitions of individual patients. This model was able to provide insights into the patient’s future state (defined by mean RNFL and MD), and while continuous in time, used discrete phases of mean RNFL thickness and MD values.

Clinical assessment of the aggressiveness of glaucoma can be subjective, varies by patient, and can be gauged only through a comprehensive assessment of each patient. Therefore, tools that can forecast the state of the patient accurately at the next visit in terms of clinically useful biomarkers, such as cpRNFL thickness, would be a practical solution to support clinicians. The proposed method is unique in its use of a deep learning network to extract relevant image features from raw OCT image data. Note, these features are not segmented retinal thickness, but rather represent an abstraction of data in the OCT volumes that are relevant for forecasting the cpRNFL thickness accurately at a future time point. This was used in combination with structural and VF measurements from multiple visits to develop a forecasting model for cpRNFL thickness. This model also incorporates a variable visit-interval term allowing for forecasts to be generated at multiple future dates, such as 3, 6, 9, or 12 months ahead of the last visit. This multimodal forecasting model ensures the inclusion of all available patient information obtained by various methods to imitate the comprehensive assessment conducted in clinical practice. With inclusion of raw OCT volumes in the analysis, our proposed approach takes full advantage of all the information included in the cube and not within the RNFL alone. Moreover, given that the temporal data analysis is applied not only to glaucoma patients, but also to healthy control participants and glaucoma suspect participants, our model inherently learns changes associated with natural aging in addition to those associated with glaucoma.

Methods

Patient Population

This observational study was approved by the institutional review boards at New York University and the University of Pittsburgh and adhered to the tenets of the Declaration of Helsinki. Participants diagnosed with glaucoma or as glaucoma suspects as well as healthy participants were enrolled to the study. All participants provided informed consent and underwent a comprehensive ophthalmic examination, including best-corrected visual acuity, slit-lamp biomicroscopy, intraocular pressure (IOP) measurement, gonioscopy, funduscopic examination, VF testing, and OCT scanning. The participants were included in the study according to the following inclusion criteria: best-corrected visual acuity of 20/60 or better and refractive error between −6.00 and +3.00 diopters. Participants were excluded based on the following exclusion criteria: history of intraocular surgery or any ocular pathologic features that may affect OCT scanning, retinal layer thickness measurements, or both.

Clinical Diagnosis

Our study included participants diagnosed with glaucoma or as glaucoma suspects at the baseline visit. Glaucoma suspect eyes were defined as eyes with normal VF with any of the following criteria: asymmetric optic nerve head (ONH) cupping, large global ONH cupping or a local neuroretinal rim notch, RNFL defect, or the contralateral eye of unilateral glaucoma patient. Glaucomatous eyes were those with glaucomatous VF defects (at least 2 consecutive abnormal VF test results) and abnormal ONH findings as detailed for the glaucoma suspects.

Visual Field Testing

All participants underwent Swedish interactive thresholding algorithm standard achromatic 24–2 perimetry (Humphrey Field Analyzer; Zeiss, Dublin, CA). A reliable VF test was defined as one with less than 30% fixation losses, false-positive responses, or false-negative responses. Abnormal VF tests were defined as tests featuring a cluster of 3 or more adjacent points in the pattern deviation plot depressed by more than 5 dB or 2 adjacent points depressed more than 10 dB, and pattern standard deviation or glaucoma hemifield test results outside normal limits. The visual field index and MD from 2 consecutive visits were used as functional measurements.

OCT Testing

Spectral-domain OCT scans and IOP measurements were acquired from both eyes of 651 glaucoma patients, 404 glaucoma suspects, and 34 healthy controls using a commercial OCT device (Cirrus HD-OCT; Zeiss). The scans were acquired on the ONH using the ONH cube 200×200 imaging protocol, where each volume contained 200×200×1024 voxels (voxel size of 30×30×1.95 μm and was acquired from a region 6×6×2 mm). OCT scans with signal strengths less than 7 were excluded.

Forecasting the Retinal Nerve Fiber Layer Thickness at Future Visits

The forecasting models developed here aimed to analyze data from multiple visits to forecast the RNFL thickness parameters. Figure 1 illustrates the process. Let m_i be a vector that includes features (structural thickness, MD of visual field tests, etc.) obtained at the ith visit and a_i be the age of the participant at the ith visit. The feature vector for the i^th visit then was constructed as f_i = [m_i, a_i, Δt_i], where the visit interval Δt_i = a_{i + 1} − a_i is the time difference between the 2 consecutive visits. The temporal feature vector was constructed by concatenating the feature vectors from multiple visits, that is, F_N = [f_i, … f_N] for the N available visits. The corresponding target to be forecasted was Y_{N + 1} = [RT_global, RT_sup, RT_temp, RT_nas, RT_inf], which represents the mean cpRNFL thickness and the cpRNFL thickness in the superior, temporal, nasal, and inferior quadrants, respectively for (N + 1)th visit. We then trained a discriminative regression model G such that Y_{N + 1} = G(F_N) correlating the temporal feature vector to the target mean cpRNFL thickness values using the training data. The training of the model G(F_N) was carried out by taking a particular number of visits (N + 1) for each patient in which the first N visits were used to create a temporal feature vector F_N and the cpRNFL parameters of the (N + 1)th visit were used to generate the response Y_{N + 1}. In the test phase, if more than N visits were available, then the last N visits could be used to construct F_N to obtain the forecast for the future date. The future forecast date could be set using the visit interval Δt_N = a_{N + 1} − a_N, where a_{N + 1} denotes the age of the participant at the forecast date and a_N is the age of the participant at the Nth visit.

Figure 1.

Illustration showing structural and functional measurement features used by the machine learning regressor. cpRNFL = circumpapillary retinal nerve fiber layer; IOP = intraocular pressure; MD = mean deviation; VF = visual field.

Two forecasting models were developed and evaluated. The first forecasting model (FM) used (1) clinical glaucoma biomarkers segmented and quantified from the OCT volumes, namely, the global mean cpRNFL, mean cpRNFL thickness in the 12 clock hours and 4 quadrants, cup-to-disc ratio, cup volume, and rim area; (2) clinical test results, namely, the VF MD and IOP; and (3) other demographic information, such as age at visits, the interval between visits, and baseline diagnosis (healthy, glaucoma suspect, or glaucoma).

The second model used abstract image features extracted directly from the OCT scans using a 3-dimensional convolutional neural network (3D-CNN). The convolutional neural network (CNN) is an architecture that is capable of generating feature representation at increased levels of abstraction via multiple layers of processing,¹⁴ and they have been used successfully in retinal image analysis.^15,16 The architecture of the 3D-CNN used to augment the feature set is shown in Figure 2. The 3D-CNN was designed to analyze a single OCT scan and extract the features that are relevant for forecasting of cpRNFL parameters. This was achieved by training it to estimate jointly the cpRNFL parameters of the input OCT volume and the visual function parameters Yi = [RT_global, RT_sup, RT_temp, RT_nas, RT_inf, MD, visual field index]. The cascade of operations such as 3-dimensional convolutions and other nonlinear operations (such as rectified linear units, batch normalization,¹⁷ and max pooling) generate features that have semantic meaning with increased levels of abstraction at successive levels of the network. The training of the 3D-CNN used the mean square error loss as the objective function computed between the ground truth cpRNFL thickness and the visual function parameters and predicted cpRNFL thickness and visual function parameters. The Adam optimizer¹⁸ was used to train the network in multiple iterations using a batch size of 16 and initial learning rate of 1e − 3. After being trained, the 3D-CNN model estimated the cpRNFL parameters of the input OCT volume. The main purpose of the 3D-CNN model was to convert OCT volume to a lower dimensional feature representation that correlated with both cpRNFL structure and the visual function parameters. The extracted 3D-CNN features then were used by the forecasting model. The 3D-CNN features for the input OCT volume could be computed by taking the 64-dimensional feature response from the penultimate layer of the 3D-CNN as show in Figure 2.

Figure 2.

Diagram showing training of the 3-dimensional (3D) convolutional (Conv) neural network and the architecture of the network. The number of filters used by convolution and fully connected layers are shown. BatchNorm = batch normalization; MD = mean deviation; RELU = rectified linear units; RT = retinal thickness; VF = visual field.

The forecasting model that used the augmented feature set (referred to subsequently as FM + CNN) is illustrated in Figure 3. In FM + CNN, the trained 3D-CNN model was used to extract the CNN feature vector (D_i) for all the visits for the participants. This was carried out by feeding each image in the training set to the 3D-CNN model and taking the 64-dimensional response from the penultimate fully connected layer. We then concatenated the extracted CNN feature vector (D_i) with the measurement feature vector (m_i), age (a_i), and the forecast interval (Δt_i) for each visit to obtain an augmented feature vector f_i = [D_i, m_i, a_i, Δt_i] for each participant. These extracted features at N visits were concatenated further to obtain the temporal feature vector F_N. A machine learning–based forecasting model then was trained to learn a mapping from the temporal feature vector space (F_N) to the cpRNFL thickness parameters for the next visit Y_{N + 1}.

Figure 3.

Illustration showing the forecasting model that used the augmented feature set. cpRNFL = circumpapillary retinal nerve fiber layer; 3D-CNN = 3-dimensional convolutional neural network.

Comparison of Regressors

The forecasting model FM can be designed to use data from 1 to N number of visits in combination with any regressor. Thus, the first experiment aimed to establish (1) the optimal number of visits needed to forecast the cpRNFL thickness parameters as accurately as possible and (2) the best regressor for the task. For this, the FM model was trained using different numbers of visits = [1, 2, 3, 4] as well as different regression methods, including linear support vector machine¹⁹; linear relevance vector machine,²⁰ which uses Bayesian learning for regression; linear regression (LR); lasso linear regression, which uses the L₁ penalty to improve the sparsity of the model; and gradient boosting machine²¹ regressor.

A total of 1089 participants were included in this study; 859 participants were used for training, whereas the remaining 230 participants made up the test set. Thus, the FM was evaluated on data that were not encountered previously during the training process. To evaluate the performance of the predictive models, we calculated the mean absolute error (MAE) and mean relative error (MRE) between the forecasted and the ground truth thickness values:

$$MAE=\frac{1}{M}\sum _{i=1}^M\left|y_i-{\mathrm{z}}_{\mathrm{i}}\right|;MRE=\frac{1}{M}\sum _{i=1}^M\frac{\left|y_i-z_i\right|}{y_i}$$

where y is the ground truth retinal thickness, z is the predicted retinal thickness, and M is the total number of test samples. Additionally, the Pearson’s correlation coefficient was computed for the forecasted and ground truth retinal thicknesses:

$$R=\frac{\sum y_i{z}_i-N\overline{y}\overline{z}}{\surd \left(\sum y_i^2-N{\overline{y}}^2\right)\surd \left(\sum z_i^2-N{\overline{z}}^2\right)}$$

Evaluating the Impact of the Convolutional Neural Network–Derived Features

The impact of the CNN-derived abstract image OCT features on the forecasting model’s performance also was evaluated for a number of visits n = [1, 2, 3, 4]. Various regressors also were tested in the FM + CNN model as detailed above. The MAE and MRE were used to evaluate the performance of the system. Additionally, the Pearson’s correlation coefficient was computed between the forecasted and ground truth retinal thicknesses.

Comparison with Linear Trend-Based Estimation

The best regressor in the above experiment was identified, and the model then was compared with the linear trend-based estimation (LTBE) model that was created by linearly regressing the cpRNFL thickness against the duration of the follow-ups. The LTBE model uses the cpRNFL thickness measurements from 4 visits to predict the measurement at the fifth visit. The MAE and Pearson’s correlation coefficient were computed between the forecasted and ground truth retinal thicknesses. Finally, the LTBE approach was compared with the FM and FM + CNN using a 1-way analysis of variance test.

Results

In this study, the participants were monitored longitudinally over a period of 3.57±1.69 years. The number of visits of participants varied from 3 to 30, and the mean intervisit interval was 9.7±9.0 months. The demographics and summary of the tests conducted are detailed in Table 1. A 2-way analysis of variance indicated that there were no significant differences in age among the 3 cohorts.

Table 1.

Baseline Characteristics of Participants, Including the Mean Deviation from 24–2 Perimetry (Humphrey Field Analyzer) and the Global Mean of the Circumpapillary Retinal Nerve Fiber Layer Obtained from OCT Images

Characteristic	Healthy	Glaucoma Suspect	Glaucoma
Gender
Male	17	177	298
Female	24	228	345
No. of visits	3–24	3–24	3–30
Encounters
Right eye	166	1549	3060
Left eye	171	1576	2925
Age (yrs)
Mean ± SD	61.37±11.82	59.99±13.02	63.29±12.64
Range (minimum–maximum)	22–89	19–88	21–94
Baseline MD (dB)
Mean ± SD	−0.71±1.65	−1.72±3.22	−5.49±7.05
Range (minimum–maximum)	−9.9 to 2.8	−28.5 to 2.85	−32.95 to 2.17
Baseline mean cpRNFL (μm)
Mean ± SD	87.9±9.15	83.0±0.9	74.15±14.5
Range (minimum–maximum)	68–116	48–124	41–126

cpRNFL = circumpapillary retinal nerve fiber layer; dB = decibels; MD = mean deviation; SD = standard deviation.

Table 2 shows the MAE and MRE for forecasting the thickness values for the fourth visit by observing the 3 prior visits for different group of participants using the FM (only structural and functional measurements) and relevance vector machine regression model. The MAE for forecasting global mean cpRNFL thickness was 2.21±2.11 μm overall, 1.58±0.93 μm for healthy participants, 2.01±1.87 μm for glaucoma suspects, and 2.44±2.34 μm for glaucoma patients.

Table 2.

Forecasting Errors^* across Regions and Groups Obtained Using the Forecasting Model (only Measurements Features)

Diagnosis	Global Mean	Temporal	Superior	Nasal	Inferior
Healthy
MAE	1.58 (0.93)	1.23 (0.82)	2.88 (2.43)	0.91 (0.69)	1.71 (0.99)
MRE	1.75 (1.07)	2.20 (1.47)	2.56 (2.27)	1.32 (1.04)	1.43 (0.86)
Suspects
MAE	2.01 (1.87)	2.27 (2.91)	3.43 (2.79)	2.80 (2.33)	2.92 (2.45)
MRE	2.45 (2.33)	3.58 (4.35)	3.42 (2.66)	4.36 (3.84)	2.90 (2.43)
Glaucoma
MAE	2.44 (2.34)	3.08 (2.87)	3.51 (2.88)	3.54 (3.03)	3.45 (2.75)
MRE	3.53 (3.46)	5.66 (5.26)	4.35 (3.63)	5.59 (4.86)	4.57 (4.14)
All
MAE	2.21 (2.11)	2.63 (2.89)	3.45 (2.82)	3.10 (2.73)	3.14 (2.59)
MRE	2.96 (2.98)	4.56 (4.89)	2.85 (3.21)	4.86 (4.42)	3.68 (3.48)

MAE = mean absolute error; MRE = mean relative error.

Data are mean (standard deviation).

^*MAE in micrometers and MRE in percent.

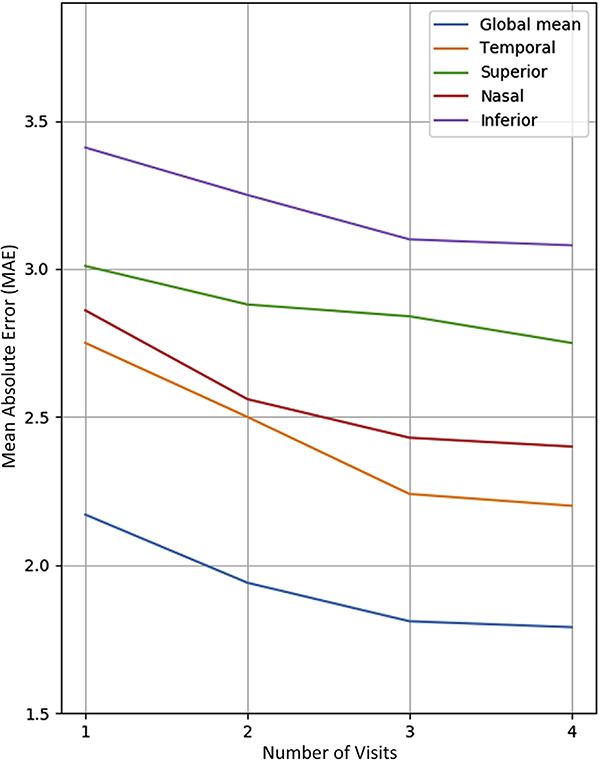
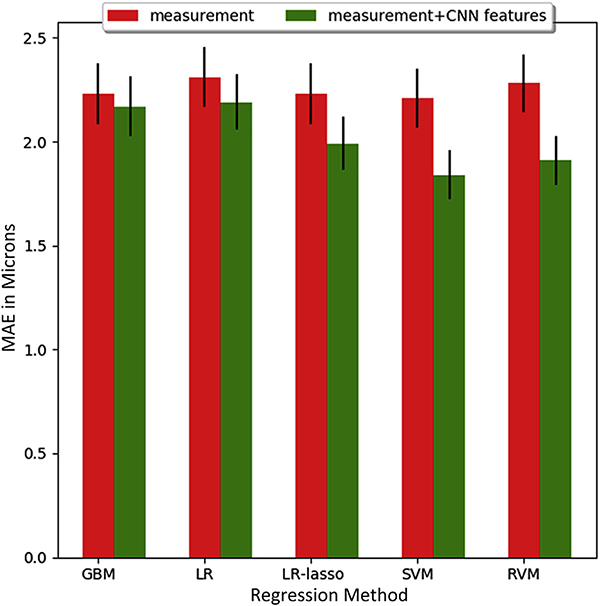
Table 3 shows how forecasting performance improved by incorporating the 3D-CNN features into our dataset. This inclusion improved the forecasting for all participant groups and most of the spatial regions of the retina. Overall, the MAE for forecasting the global mean cpRNFL was 1.81±1.77 μm for all participants, 1.10±0.60 μm for healthy participants, 1.79±1.73 μm for glaucoma suspects, and 1.87±1.85 μm for glaucoma patients. With regard to region, the best improvements were obtained for the nasal (2.56±2.20 μm; P < 0.001) and superior (2.69±2.33 μm; P < 0.01) quadrants, whereas the temporal quadrant did not show notable improvement (P = 0.64). We also observed that the forecasting performance did not improve significantly when more than 3 visits were used as input to the model, as shown in Figure 4. This choice of regressor did not have a significant impact on the MAE for the FM model, whereas the relevance vector machine model gave the lowest MAE for the FM + CNN, as shown in Figure 5. In analyzing the features used by the regressors, the top 10 significant features were found to be global mean thickness; age at visit; mean thickness at clock hours 3, 7, and 8; mean thickness at the superior and nasal quadrants; and 3 CNN feature components.

Table 3.

Forecasting Errors^* across Regions and Patient Groups Using Linear Relevance Vector Machine Regression with Measurement Features Augmented with Convolutional Neural Network Features

Diagnosis	Global Mean	Temporal	Superior	Nasal	Inferior
Healthy
MAE	1.10 (0.60)	0.97 (0.91)	3.28 (2.13)	1.26 (1.44)	1.72 (1.01)
MRE	1.22 (0.69)	1.76 (1.68)	2.91 (2.05)	1.90 (2.26)	1.42 (0.85)
Suspects
MAE	1.79 (173)	2.18 (2.60)	2.77 (2.35)	2.39 (2.11)	2.88 (2.36)
MRE	2.19 (2.11)	3.55 (3.92)	2.83 (2.52)	3.75 (3.49)	2.85 (2.34)
Glaucoma
MAE	1.87 (1.85)	3.01 (2.83)	2.59 (2.31)	2.83 (2.29)	3.33 (2.54)
MRE	2.73 (2.81)	5.34 (4.26)	3.14 (2.57)	4.34 (3.50)	4.42 (3.71)
All
MAE	1.81 (1.77)	2.44 (2.68)	2.69 (2.33)	2.56 (2.20)	3.06 (2.45)
MRE	2.44 (2.47)	4.36 (4.57)	2.98 (2.59)	4.01 (3.58)	3.58 (3.30)

MAE = mean absolute error; MRE = mean relative error.

Data are mean (standard deviation).

^*MAE in micrometers and MRE in percent.

Figure 4.

Line graph showing the effect of the number of visits on the mean absolute error (MAE) of the relevance vector machine-based forecasting model that used the augmented feature set model in forecasting global mean circumpapillary retinal nerve fiber layer (cpRNFL) and mean cpRNFL for 4 sectors.

Figure 5.

Bar graph showing the performance (mean absolute error [MAE] and standard error) of different regression methods for the mean circumpapillary retinal nerve fiber layer using the 2 methods (forecasting model and forecasting model that used the augmented feature set) using 3 visits. The regression methods in the figure refer to the gradient boosting machine (GBM), multivariate linear regression (LR), multivariate linear regression with lasso (LR-lasso), support vector machine (SVM), and relevance vector machine regressor (RVM). CNN = convolutional neural network.

Table 4 compares the MAE observed in the FM and FM + CNN (that uses measurement and measurements together with OCT-CNN features) with the existing LTBE method for forecasting global mean cpRNFL thickness values for different participant groups. We observed that our method (with n = 3) resulted in lower MAE of 1.87 (1.85) than the LTBE approach (with n = 4), which showed a mean error of 3.02±3.06 μm in the forecast of the global mean cpRNFL thickness values in glaucoma patients. Similarly, for glaucoma suspects, our method produced a lower MAE of 1.79±1.73 μm than the LTBE method, which showed an error of 2.40±2.67 μm. An analysis of variance test revealed that the errors for the 3 methods were significantly different for glaucoma (P < 0.001) and glaucoma suspects (P = 0.035). For healthy participants, no significant difference could be detected (P = 0.64).

Table 4.

Mean Absolute Error Computed for the Global Mean Circumpapillary Retinal Nerve Fiber Layer Thickness Forecasting Using 3 Methods: Linear Trend-Based Estimation, Forecasting Model (Measurement Features Only), and the Forecasting Model That Used the Augmented Feature Set

Diagnosis	Linear Trend-Based Estimation	Measurement Features	Measurement Features plus Convolutional Neural Network Features	P Value*
Healthy	1.55 (1.16)	1.58 (0.93)	1.10 (0.60)	0.64
Glaucoma suspect	2.40 (2.67)	2.01 (1.87)	1.79 (1.73)	0.035
Glaucoma	3.02 (3.06)	2.44 (2.34)	1.87 (1.85)	<0.001
All	2.66 (2.86)	2.21 (2.11)	1.81 (1.77)	<0.001

Data are mean (standard deviation) in micrometers.

^*One-way analysis of variance of 3 errors.

Table 5 compares the MAE observed in cpRNFL estimation from 3D-CNN with the cpRNFL forecasting from FM + CNN on the test set. We observed that estimation error of 3D-CNN is 2.71±2.36 μm compared with the forecasting error of measurements and 3D-CNN features extracted from OCT volumes (FM-CNN) of 1.81±1.77 μm for global mean cpRNFL. Our forecasting model gave a lower MAE because it can leverage OCT features and multimodal data at multiple visits to forecast the cpRNFL parameters of the next visit.

Table 5.

Mean Absolute Error Computed for the Circumpapillary Retinal Nerve Fiber Layer Thickness Estimation Using the 3-Dimensional Convolutional Neural Network Model and Circumpapillary Retinal Nerve Fiber Layer Forecasting Using the Forecasting Model That Used the Augmented Feature Set

Diagnosis	3-Dimensional Convolutional Neural Network	Forecasting Model That Used the Augmented Feature Set	P Value*
Global mean	2.71 (2.36)	1.81 (1.77)	<0.001
Temporal	4.05 (3.81)	2.44 (2.68)	<0.001
Superior	4.56 (4.65)	2.69 (2.33)	<0.001
Nasal	4.31 (3.97)	2.56 (2.20)	<0.001
Inferior	4.94 (4.42)	3.06 (2.45)	<0.001

Data are mean (standard deviation) in micrometers.

^*Paired t test between the errors.

Table 6 compares the MAE of FM + CNN by excluding the categorical feature “diagnosis” from the input feature. We observed that FM-CNN without diagnosis as an input feature showed slightly higher error of 1.83±1.75 μm than with the diagnosis as input feature of 1.81±1.77 μm, but the difference was not statistically significant (P = 0.96).

Table 6.

The Effect of Diagnosis on Forecasting Performance

	Forecasting Model That Used the Augmented Feature Set
Diagnosis	Without Initial Diagnosis as a Feature	With Initial Diagnosis as a Feature	P Value*
Healthy	1.28 (0.83)	1.10 (0.60)	0.67
Glaucoma suspect	1.84 (1.70)	1.79 (1.73)	0.88
Glaucoma	1.85 (1.84)	1.87 (1.85)	0.89
All	1.83 (1.75)	1.81 (1.77)	0.96

Mean absolute error computed for the global mean circumpapillary retinal nerve fiber layer thickness forecasting using the measurements and 3-dimensional convolutional neural network features extracted from OCT volume model with the initial diagnosis as input feature and without the initial diagnosis as input feature.

Data are mean (standard deviation) in micrometers.

^*Paired t test.

Figure 6 shows the scatterplot of the predictions versus the ground truth for the mean cpRNFL thickness values from our model along with the R² score (top of the figure) associated with each plot. It can be observed that the first method that used measurements explains only 95% of variance in prediction, whereas the second method that uses measurements with OCT-CNN features explains 97% of the variance. The LTBE model uses 4 follow-up visits but explains only 92% of variance of variance. The scatterplots of predictions versus ground truth for all 4 quadrants for the FM is shown in Figure 7, and those for FM + CNN are shown in Figure 8. With regard to region, we observed that the inclusion of the OCT-CNN features greatly improved the prediction in the nasal region, with the R² value improving from 0.87 to 0.91 (P < 0.001), and in the superior region, with the R² value improving from 0.95 to 0.97 (P = 0.013).

Figure 6.

Scatterplots showing the forecasted mean retinal nerve fiber layer thickness values versus true measurements for 3 models: (A) forecasting model using only measurements, (B) Forecasting model + convolutional neural network (FM + CNN) using measurement features plus 3-dimensional CNN features, and (C) the linear trend-based estimation approach.

Figure 7.

Scatterplots showing the forecasted mean circumpapillary retinal nerve fiber layer thickness values versus true measurements for 4 quadrants using the forecasting model (measurements only).

Figure 8.

Scatterplots showing the predicted average retinal nerve fiber layer thickness values versus true measurements for 4 quadrants the measurements and 3-dimensional convolutional neural network (CNN) features extracted from OCT volumes.

Discussion

Forecasting the future mean cpRNFL outcomes and measuring its rate of change across as few visits as possible will serve as the new way for observing and managing patients with glaucoma. For example, patients with rapid RNFL thinning may require more frequent follow-up visits and a lower target IOP because they are more likely to show visual field loss. Herein, we demonstrated the ability of a machine learning technique to forecast the cpRNFL thickness reliably using as few as 3 visits. Our method acts as a personalized progression model that can be used to design the intervisit schedules for individual participants, which enables practicing more efficient personalized medicine.

Our approach to predicting glaucoma progression is different from the conventional approaches^10–12 in which the output is dichotomized to progression or nonprogression. The conventional approach is influenced heavily by the definition of progression, which can vary wildly from individual to individual and also varies among studies. Our approach provides clinicians a more practical forecast of the value of measurements at the next visit. Because the intervisit duration is one of the input variables, this forecast can be created for varying intervals. For instance, forecasts can be created for the next 12 months at 3-month intervals. This information then can be used by clinicians to decide how aggressive the treatment or intervention should be. When the expected error of forecasting is small, as in the present results, this is more robust and reliable because it eliminates the concern of the fit between a given individual and arbitrary criteria for glaucoma progression.

Although previous approaches have predicted the future state of patients in terms of progressive versus stable,¹² to our best knowledge, this is the first technique that leverages raw OCT volumes and combines them with clinical, structural, and functional measurements longitudinally to forecast the future cpRNFL thickness of participants regardless of disease states. Deep learning is an inherently data-driven technique. The network used here was trained to identify features that are most relevant for estimating the cpRNFL without any additional guidance. The improvement noted in the performance of the model when these features were included indicates that not only did these abstract features assist the forecasting process, but also that potentially untapped pieces of information exist within the OCT volumes. Another significant contribution here is a technique that can use data from a single visit, whereas LTBE requires a minimum of 4 visits.

Overall, the forecasted values obtained from the 2 models, FM and FM + CNN, were highly correlated with the true values. Furthermore, these correlation numbers were high regardless of the severity of glaucoma, that is, healthy, glaucoma suspect, or glaucoma. In general, we found that the forecasting performance for the global mean cpRNFL was more accurate than that of the individual sectors. This is likely because the thickness measurements recorded from the scanner across quadrants are noisier than that of the global mean cpRNFL thickness because of signal variability as well as the registration variability.

One of the limitations of this proposed method is its reliance on the structural measurement and functional tests together with raw OCT volumes to make the predictions. Occasionally, not all measurements are available for patients, which clinically would translate into a poor forecast. Also, our study included a limited number of healthy individuals who were observed for the same duration as the glaucoma patients. Thus, the finding that the inclusion of the OCT-CNN features did not improve the forecasting performance significantly for this group is not entirely surprising. Despite this shortcoming of the study, the forecasts for the healthy controls (using both proposed models) were significantly better than those obtained using the LTBE method. Another limitation here was the number of patients available with a large number of follow-up visits (>5). Although using 3 visits has in fact produced a lower error than other techniques, it is difficult to state conclusively that 3 visits produces the best possible forecast. Forecasts of the visual function also are missing currently from our model. In future work, we intend to extend the current models to include visual functional parameters, thus providing a more complete outlook for individual patients.

In summary, our method allows for the future prediction of cpRNFL thickness in glaucoma patients as well as glaucoma suspects. Quantification of the cpRNFL value for the future visits is important for estimating disease progression and allows for the early identification of patients at risk of vision loss.

Abbreviations and Acronyms

CNN

convolutional neural network

cpRNFL

circumpapillary retinal nerve fiber layer

FM

forecasting model

FM + CNN

forecasting model that used the augmented feature set

FM-CNN

measurements and 3-dimensional convolutional neural network features extracted from OCT volumes

IOP

intraocular pressure

LTBE

linear trend-based estimation

MAE

mean absolute error

MD

mean deviation

MRE

mean relative error

ONH

optic nerve head

RNFL

retinal nerve fiber layer

VF

visual field

3D-CNN

3-dimensional convolutional neural network