Socially optimal lockdown and travel restrictions for fighting communicable virus including COVID-19

Abstract

This paper examines the socially optimal lockdown and travel (social activity) restriction policies for communicable virus including COVID-19. In our simple model, we exploit the remarkable similarity in the structure of external costs causing market failure between the socially optimal choices of the COVID-19 pandemic case and the socially optimal urban traffic congestion level. By identifying this similarity, the results obtained from our simple model allow for future pandemic researchers to use the well-established research methodologies for designing socially optimal traffic levels and associated policy tools to find the socially optimal lockdown and travel restrictions. The key results obtained from our COVID-19 model are: (1) individuals do not internalize the external cost of infection risks they impose on others and health care system when making their own travel (social-activity) decisions; In order to induce individual travel decision makers to internalize this external cost, the government actions are necessary; The travel restrictions via lockdown or monetary penalty is one form of such actions; (2) the existence of external cost implies that the socially optimal length of lockdown is always longer than the privately optimal length of the lockdown period; (3) the strictness of the travel restriction and the amount of violation penalty should be higher in the areas with high population density and in larger cities because the external cost of spreading virus by a traveler would be higher. The monetary penalty in this model resembles the classical Pigouvian tax, which should increase with the city's population, people density, and economic prosperity; (4) when a government subsidizes or fully covers medical expenses of COVID-19 patients, stricter travel restrictions with heavier penalties are required. This is to avoid crowding out of the health care system.

Highlights

• •Individuals do not internalize the external cost of infection risks they impose on others and health care system.
• •To induce individual travel decision makers to internalize this external cost, the government actions are necessary.
• •The existence of external cost implies that the socially optimal length of lockdown is always longer than the privately optimal length.
• •The strictness of travel restriction and the violation penalty should be higher with high population density.
• •Monetary penalty resembles the classical Pigouvian tax, which should increase with the city's population and economic prosperity.

1. Introduction

Since the first COVID-19 case was recorded in Wuhan China on December 9th, 2019, the virus had quickly spread to the rest of world, mostly facilitated by the global air travel to the major cities in Europe, the US, and elsewhere (Huang et al., 2020; Zhang et al., 2020a). The pandemic hubs then quickly switched from Asia to the US (e.g., New York) and Europe (Italy, Spain, the UK etc.). Due to the absence of coronavirus vaccine or any effective medical treatment, a country had two available options:

• (a)Developing a “herd immunity” to COVID-19, which comes with high fatality rate, especially endangering elderly population (e.g. US and UK policies at the beginning of the crisis, presently Sweden and Brazil).
• (b)Implementing social distancing measures by prohibiting face-to-face interaction, shutting down nonessential services and imposing fines on violators.

Although there are differences in timing and strictness of the restrictions, most countries in the world (with the exception of a few e.g. South Korea and Sweden) have imposed a lockdown of social and economic activities. For example, activities include but not limited to: (a) prohibition of social contacts and closure of schools, sports, outside leisure, etc.; (b) stopping gastronomical services, social and cultural events; (c) closing of non-essential retail shops, regulating various services to minimize contacts.

Wuhan imposed a total lockdown on January 23rd, 2020. Over ten million people were quarantined at homes and banned from traveling for social activities. As a result of the strict lockdown policies, the infection and deaths rates got stabilized. Since late March the city did not report any new confirmed cases and it re-opened on April 8th.

On the contrary, some European countries did not implement strict lockdown and travel restrictions. Sweden, for example, was one of the countries where the lockdown measures were not imposed. People voluntarily adjusted their outdoor travel without government interventions (Born et al., 2020). However, Sweden experienced a spike of COVID-19 cases since late March with 46,814 confirmed cases as of mid-June (Google, 2020).

Similarly, the US did not have effective lockdown or domestic travel restrictions at early stages of the virus transmission. As a result, the US has the largest number of confirmed COVID-19 cases and deaths in the world (Google, 2020). The lockdown periods in the US began on March 16th, 2020. Each state independently decided when to start and end the lockdown period. For example, Georgia was one of the last states to begin the lockdown on April 3rd (BBC, 2020). Studies suggest that the late lockdown decisions in the US costed approximately 36,000 more lives (New York Times, 2020). Thus, lockdown and social distancing rules appear to be the most effective way to contain the spread of COVID-19 domestically and globally (Chinazzi et al., 2020; Lau et al., 2020; Zhang et al., 2020b).

Any communicable virus, specifically COVID-19, is transmitted through person-to-person interaction. There are two types of COVID-19 patients: symptomatic and asymptomatic. Asymptomatic individuals can be virus carriers without even knowing it. As a result, the risk of infection creates a negative externality of individual's travel decisions on others. Although the fear of getting the infection can deter individual's travel and social activity, each individual will not voluntarily account for his/her external risk cost imposing on all others (negative externality cost to society). Thus, the number of trips would be larger than socially optimal in the absence of lockdown or other travel restrictions.

Many cities or countries impose a penalty or a fine for violating the lockdown guidelines to account for the external cost of infection risk to be imposed on others. New York, for example, implemented a $1,000 fine for violators of the lockdown order (Breuninger et al., 2020). While, Italy imposed both criminal and civil penalties on violators (Reynolds, 2020).

The external cost of infection risk is analogous to the well-known urban traffic congestion theory. That is, an individual driver only considers his/her private costs which include driving and delay time costs he/she experiences while ignoring the additional congestion delay his/her own decision to drive imposes on other drivers. As a result, a privately optimal travel quantity would be larger than the socially optimal. This leads to a ‘market failure’. The analysis of urban traffic congestion and related policies to deal with it have been well established over a century. The key parts are succinctly summarized, for example, in the seminal work of Walters (1961). Many studies including Small (2013) have explored the relationship between private, external and social marginal congestion costs. Optimal regulatory policies have also been discussed, such as traffic restriction (Viard and Fu, 2015; Gu et al., 2017; Li et al., 2019), Pigouvian congestion tolls, etc. (Arnott, 2007; Proost and Van Dender, 2008). Empirical investigations have also been conducted to verify or quantify the effects of these policies to control urban traffic congestion (e.g. Cravioto et al., 2013; Rizzi & De La Maza, 2017; Santos, 2017; Cipriani et al., 2019).

Given the remarkable similarities in the structure of external costs and associated market failure between socially optimal travel choices during the pandemic and the socially optimal urban traffic congestion level, we borrow urban traffic congestion economic models to examine the socially optimal lockdown period and travel restriction/ban or penalties amid COVID-19 pandemic. More essentially, the determining factors of the optimal policies can be investigated as well. This model would help policy makers determine the optimal lockdown and travel restrictions given city's population size, density and economic viability.

Our paper hopes to make two contributions to the literature. First, by linking infection risk and urban congestion external costs, we link the economic analysis of communicable disease control with the framework of urban traffic congestion analysis. As a result, our simple model allows future researchers to use well-advanced research methodologies for designing socially optimal urban traffic levels and associated policy tools on the socially optimal lockdown and travel restrictions to contain communicable diseases. Second, our modelling analysis sheds a light on various determining factors of socially optimal lockdown and travel restriction policies. It can help governments adjust their policies for cities with heterogenous characteristics.

The remainder of the paper is organized as follows. Section 2 specifies the economic model of lockdown and travel restrictions amid COVID-19 pandemic. Then privately optimal travel quantity during the COVID-19 pandemic is solved and discussed in subsection 2.1. The socially optimal lockdown and travel restriction policies are solved and discussed in subsection 2.2. The policy implications and practicality of the proposed model will also be elaborated. Section 3 concludes the paper.

2. Model specification

Assume a city with population $N$ and area size $K$ (square meters). Many studies assume quadratic consumer utility function (e.g., Singh and Vives, 1984), including the transport economics literature (e.g., Fu and Zhang, 2010; Xia et al., 2019). We also assume that a representative individual has a quadratic utility function for travel expressed as,

$$U_i=a{q}_i-\frac{1}{2}b{q}_i^2$$ (1)

The parameter $a$ captures the overall utility level of a trip. $a$ is higher for more economically developed regions, as people derive more benefits by traveling, ceteris paribus. The parameter $b$ measures the travel demand elasticity regarding the travel cost. The total number of trips in the city is $Q=\sum _{i=1}^N{q}_i$, where $i=\mathrm{1,2}\dots ,N$. This model assumes symmetric (homogenous) conditions for all people, such that they have the same utility and infection risk/cost structures. The population are also assumed to be uniformly distributed. These are of course simplifications to make the model focused on the main economic insights and trade-offs.

The people density for social activity is $\frac{Q}{K}$, a ratio of the total travelers to the city area size. An individual's infection risk of COVID-19 per travel (for social activity) is positively related to such people density $\frac{Q}{K}$. Referring to the road congestion literature, we adopt a power law (quadratic function) to model the infection risk per travel, as ${\left(\frac{Q}{K}\right)}^2$. For each individual, his/her infection risk is calculated as the infection risk per travel multiplied by the number of trips (frequency), which can be expressed as ${\left(\frac{Q}{K}\right)}^2{q}_i$.1 The infection leads to two types of costs imposed on each individual:

• 1)The “medical cost” paid by an individual to get the treatment, expressed as $\lambda {\left(\frac{Q}{K}\right)}^2{q}_i$, with the parameter $\lambda$ indicating a medical service fee charged by the hospital. In countries where treatments for COVID-19 patients are free of charge, such as China and South Korea, the term $\lambda {\left(\frac{Q}{K}\right)}^2{q}_i$ is equal to zero.
• 2)The “health cost” expressed as $\mu {\left(\frac{Q}{K}\right)}^2{q}_i$, which captures suffering of illness and residual effect of COVID-19 on health (probably in the long run). The current data suggests that elderly patients have a higher death toll, such that a city/country with larger elderly population has a higher value of $\mu$ on average.

Thus, the total infection cost of one individual is $(\mu +\lambda ){\left(\frac{Q}{K}\right)}^2{q}_i$.

2.1. Private optimum

An individual maximizes his or her net utility by maximizing the difference between the gross travel utility and the infection risk cost,2

$$\underset{q_i}{\text{Max}}a{q}_i-\frac{1}{2}b{q}_i^2-(\mu +\lambda ){\left(\frac{Q}{K}\right)}^2{q}_i$$ (2)

The First-order Condition (FOC) is,

$$\underset{M{U}_i}{a-b{q}_i}-\underset{MP{C}_i}{\left[(\mu +\lambda ){\left(\frac{Q}{K}\right)}^2+2(\mu +\lambda )\frac{Q}{K^2}{q}_i\right]}=0$$ (3)

where $M{U}_i$ in Eq. (3) is the individual's marginal utility of travel; and $MP{C}_i$ is the private marginal cost of infection risk for individual $i$.

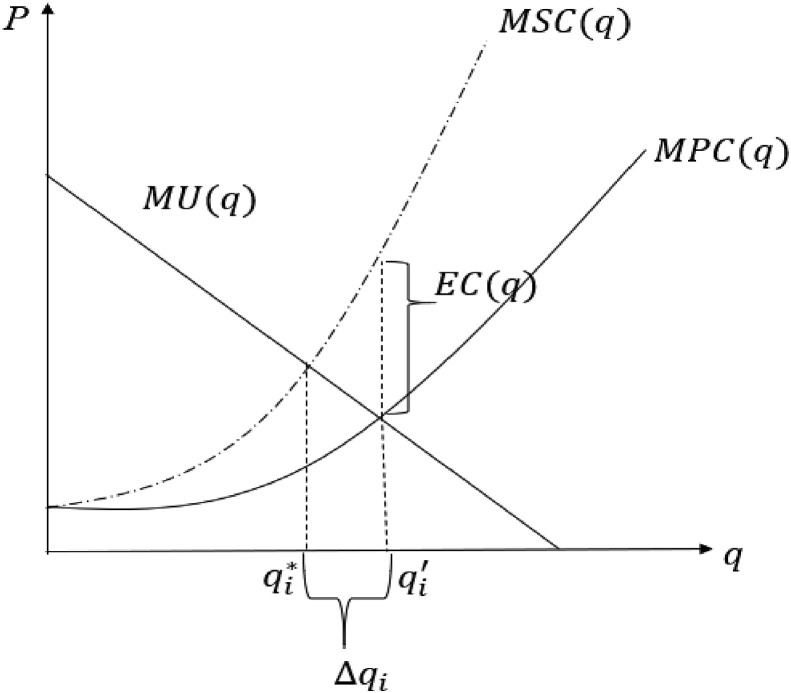
As $Q=q_i+\sum _{j\ne i}^N{q}_j$, the private marginal cost of infection risk $MP{C}_i=\left[(\mu +\lambda ){\left(\frac{Q}{K}\right)}^2+2(\mu +\lambda )\frac{Q}{K^2}{q}_i\right]$ is also a quadratic function of $q_i$. Fig. 1 illustrates that $MP{C}_i$ is a convex function of $q_i$, such that it also increases at a faster speed with travel quantity $q_i$.

Fig. 1.

The private and social marginal costs of infection risk after imposing the symmetry

Solving for FOC, $M{U}_i=MP{C}_i$, by assuming the symmetry at equilibrium (i.e., $q_i=q_j$ for $i\ne j$), we obtain the private optimal travel quantity for each individual $i$ as follows,

$$q_i^{\text{'}}=\frac{K\left(\sqrt{4a(\mu +\lambda )N\left(N+2\right)+b^2{K}^2}-bK\right)}{2(\mu +\lambda )N(N+2)}>0$$ (4)

The comparative statics are $\frac{\partial q_i^{\text{'}}}{\partial N}<0$;$\frac{\partial q_i^{\text{'}}}{\partial \lambda }=\frac{\partial q_i^{\text{'}}}{\partial \mu }<0$; $\frac{\partial q_i^{\text{'}}}{\partial K}>0$; $\frac{\partial q_i^{\text{'}}}{\partial a}>0$ (with proof shown in Appendix 1). The above results lead to the following propositions.

Proposition 1.1

Even without travel restrictions or a city lockdown, people living in more populous or crowded cities (i.e., larger $N$ or smaller $K$) will voluntarily reduce their travel frequency more than in smaller cities because of the higher infection risk.

Proposition 1.2

without travel restrictions or a city lockdown, people will reduce their travel quantities if they are more vulnerable, for example, the elderly (i.e., higher $\mu$) or people who bear higher medical cost themselves (i.e., higher $\lambda$).

2.2. Social optimum

When the government considers optimal travel restrictions via city lockdown, it has to consider social welfare, which accounts for the infection cost faced by the entire population, and the medical cost incurred by the health care system. The social welfare can be expressed as follows,

$$SW=\sum _{j=1}^N\left[a{q}_j-\frac{1}{2}b{q}_j^2-(\mu +\lambda ){\left(\frac{Q}{K}\right)}^2{q}_i\right]+\sum _{j=1}^N\left[\lambda {\left(\frac{Q}{K}\right)}^2{q}_i-\rho {\left(\frac{Q}{K}\right)}^2{q}_i\right]$$ (5)

The first part of the right-hand side (RHS) is the total net utility of all the individuals. The second term of RHS is the net economic profit or loss of the health care system. Parameter $\rho$ reflects the actual cost incurred by the health care system. Many countries adopt the public health care system, such that citizens are insured by participating in the public health insurance program, where governments provide subsidy or free treatments for the communicable diseases.3 This indicates $\rho >\lambda$. Even in the US, where people pay medical fees themselves, the insured patients are partially covered. The government's social welfare maximization problem is as follows, which determines the optimal travel restrictions,

$$\underset{q_1,q_{2,\dots }{q}_N}{\text{Max}}SW=\sum _{j=1}^N\left[a{q}_j-\frac{1}{2}b{q}_j^2-(\mu +\rho ){\left(\frac{Q}{K}\right)}^2{q}_j\right]$$ (6)

It is noted that medical fees paid by patients become the revenue of the health care system, thus internalized in the social welfare expression. FOC regarding $q_i$ is as follows,

$$\underset{M{U}_i}{a-b{q}_i}-\underset{MP{C}_i}{\left[(\mu +\mathrm{\lambda }){\left(\frac{Q}{K}\right)}^2+2(\mathrm{\lambda }+\mu )\frac{Q}{K^2}{q}_i\right]}-\underset{MS{C}_i}{\underset{E{C}_i}{\left[(\rho -\lambda )\left({\left(\frac{Q}{K}\right)}^2+2\frac{Q}{K^2}{q}_i\right)+2(\mu +\rho )\frac{Q}{K^2}\sum _{j\ne i}^N{q}_j\right]}}=0$$ (7)

When comparing the socially optimal FOC (as in Eq. (7)) with the privately optimum condition in Eq. (3), the government considers the external cost of infection risk imposed by each individual $i$ on other people and the health care system, which is the term $E{C}_i=(\rho -\lambda )\left({\left(\frac{Q}{K}\right)}^2+2\frac{Q}{K^2}{q}_i\right)+2(\mu +\rho )\lambda \frac{Q}{K^2}\sum _{j\ne i}^N{q}_j$ in Eq. (7). More specifically, the term $(\rho -\lambda )\left({\left(\frac{Q}{K}\right)}^2+2\frac{Q}{K^2}{q}_i\right)$ is the additional marginal medical cost caused by an individual $i$’s infection on the health care system (i.e., government's subsidy); and the term $2(\mu +\rho )\frac{Q}{K^2}\sum _{j\ne i}^N{q}_j$ is the marginal cost of infection risk imposed on other individuals' suffering of illness and health care system. This is also exhibited in Fig. 1. Thus, governments have to internalize the external marginal cost of infection risk caused by each individual's travel.

The socially optimal travel quantity $q_i^{\ast }$is reached when the private marginal utility of travel equals to the marginal social cost of the infection risk, which is $M{U}_i=MS{C}_i=MP{C}_i+E{C}_i$.

After imposing symmetry assumption on individuals (i.e., $q_i=q_j$ for $i\ne j$), the socially optimal travel quantity can be calculated as follows,

$$q_i^{\ast }=\frac{K\left(\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}-bK\right)}{6N^2(\mu +\rho )}>0$$ (8)

Similar to the comparative statics of the private optimum travel quantity, we also have $\frac{\partial q_i^{\ast }}{\partial N}<0$; $\frac{\partial q_i^{\ast }}{\partial K}>0$; $\frac{\partial q_i^{\ast }}{\partial a}>0$. Moreover, we have $\frac{\partial q_i^{\ast }}{\partial \rho }<0$, such that the social optimal travel quantity decreases with the health care system's cost to treat the patient.

It can be proved that $q_i^{\ast }<q_i^{\text{'}}$ (see Appendix 2 for proof). This suggests that the socially optimal travel quantity (frequency) is smaller than the privately optimal level. This leads to the following Proposition 2.

Proposition 2

It is socially optimal for the government to restrict people’s travel by imposing lengthy lockdown and strict travel (social activity) restrictions, in order to correct for the external cost of the infection risk imposed by individual’s travel on the others and health care system.

The difference between privately and socially optimal travel quantity $\Delta q_i=q_i^{\text{'}}-q_i^{\ast }$ can be used to measure the strictness of travel restrictions or city lockdown.

We also have the following comparative statics: $\frac{\partial \Delta q_i}{\partial N}>0;\frac{\partial \Delta q_i}{\partial K}<0$; (see Appendix 3 for proof). Therefore, we have the following Proposition 3.1.

Proposition 3.1

Travel restrictions or a city lockdown should be stricter in more populous cities (i.e., larger $N$), more crowded areas (i.e., smaller $K$), and more economically vital cities (i.e., larger $a$).

Moreover, we also have $\frac{\partial \Delta q_i}{\partial \rho }>0$ and $\frac{\partial \Delta q_i}{\partial \lambda }<0$ (see Appendix 3 for a proof). This leads to the following Proposition 3.2.

Proposition 3.2

Travel restrictions or a city lockdown should be stricter if the burden or a medical cost incurred by the health care system is higher (i.e., larger $\rho$), or when a citizen only pays a smaller amount of medical fees (i.e., smaller $\lambda$). That is, when the government subsidizes the health care system.

Proposition 3.2 demonstrates that it is essential to lockdown cities/states as early as possible in countries with limited health care resources to avoid crowding out of public health institutions. Thus, crowding out of health care systems at early stages of COVID-19 outbreak in Wuhan and Italy illustrates the importance of lockdown restrictions.

Travel restrictions or a city lockdown should be implemented by limiting the number of social activities or only allowing essential travel. For example, during the pandemic, all residential communities in most Chinese cities were closed. In Wuhan, all people were quarantined at home and any essential trips were administered by the government-assigned cars. In Italy, France and most European countries, individuals had to carry a printed permit to prove that their travel is essential and in some cases violators were arrested. To effectively enforce the lockdown and travel restrictions, monetary penalty (i.e., fines) can also be imposed. Monetary penalties have been implemented in many cities in Europe and Canada. For example, in Vancouver, Canada, individuals and businesses who do not comply with the social distancing and lockdown guidelines can be fined up to $50,000 (Mangione, 2020). Such a penalty resembles the classical Pigouvian tax or congestion toll, which equals to an individual’s external cost of the infection risk imposed on others (i.e.$E{C}_i$).

Specifically, the optimal monetary penalty $t_i^{\ast }$ is calculated as follows,

$$t_i^{\ast }=E{C}_i\left(q_i^{\ast }\right)=\frac{\left[3N\left(\mu +\rho \right)-(N+2)(\mu +\mathrm{\lambda })\right]{\left(\sqrt{12a\left(\mu +\rho \right)\lambda N^2+b^2{K}^2}-bK\right)}^2}{36N^3{(\mu +\rho )}^2}$$ (9)

We also have the following comparative statics: $\frac{\partial t_i^{\ast }}{\partial N}>0;\frac{\partial t_i^{\ast }}{\partial K}<0$; $\frac{\partial t_i^{\ast }}{\partial a}>0$;$\frac{\partial t_i^{\ast }}{\partial \lambda }<0$ (see Appendix 4 for proof). These lead to the following Proposition 4.

Proposition 4

A monetary penalty that enforces the lockdown and travel restrictions increases with city population (i.e., larger $N$), people density (i.e., smaller $K$), and the economic prosperity (i.e., larger $a$), but decreases with higher medical fees paid by the citizen (i.e., higher $\lambda$)

The explanation of Proposition 4 is intuitive:

• 1) when a city population is large or crowded, the external cost of infection is high, such that a government is required to implement heavier fines to enforce travel restrictions.
• 2) when a city is more economically developed (i.e., higher $a$), people have a greater incentive to go out, thus a larger penalty is required.
• 3) when people bear a larger share of medical expenses (i.e., higher $\lambda$), they tend to self-discipline and thus require a lower penalty.

3. Conclusion

This paper demonstrates a theoretical model to determine a socially optimal lockdown strictness and travel restrictions for a city, state or a country. We use an urban traffic congestion economic model to analyze a socially optimal lockdown strictness and travel restrictions during the pandemic such as COVID-19. While individuals account for their private costs when participate in social activities, they do not internalize the external cost of infection risk they impose on others. For this reason, policy makers should intervene to implement a socially optimal lockdown period and travel restrictions in order to contain a communicable disease like the case of COVID-19.

This model utilizes already well-established literature on the urban traffic congestion analysis in order to do policy choice and analysis for the communicable disease control (e.g. COVID-19). This opens a door for future researchers on communicable viruses or diseases for the possibility of exploiting the well-established methodologies and research tools available in the urban congestion analysis and policy choices. Our model can be extended to incorporate more realistic determining factors of the optimal travel restriction polices. For example, the risk attitude of the infection risk should be considered, with different risk aversion attitudes among distinct population groups, and between citizens and the government. Moreover, more specific heterogenous characteristics (asymmetric features) of different groups of people could be modeled. Lastly, the detailed city landscape and population distributions can be further examined through a more rigorous model. In addition, various empirical studies may be conducted to verify the model predictions to design appropriate policy options for cities with different area size, population, people density, economic prosperity, etc.

CRediT authorship contribution statement

Tae Hoon Oum: Conceptualization, Methodology, Writing - original draft, Validation. Kun Wang: Formal analysis, Investigation, Writing - original draft, Writing - review & editing.

Appendix. Mathematic Proofs

• 1.The proof of comparative statics $\frac{\partial {\mathit{q}}_{\mathit{i}}^{\text{'}}}{\partial \mathit{N}}<0$;$\frac{\partial {\mathit{q}}_{\mathit{i}}^{\text{'}}}{\partial \mathit{\lambda }}=\frac{\partial {\mathit{q}}_{\mathit{i}}^{\text{'}}}{\partial \mathit{\mu }}<0$ $\frac{\partial {\mathit{q}}_{\mathit{i}}^{\text{'}}}{\partial \mathit{K}}>0$; $\frac{\partial {\mathit{q}}_{\mathit{i}}^{\text{'}}}{\partial \mathit{a}}>0$

The positive marginal utility $M{U}_i\left(q_i^{\text{'}}\right)>0$ suggests the following condition,

$$\frac{2a\left(\mu +\mathrm{\lambda }\right)N\left(N+2\right)+b^2{K}^2-bK\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}}{2N(N+2)\left(\mu +\lambda \right)}>0$$ (A1)

Thus, we have $2a\left(\mu +\mathrm{\lambda }\right)N\left(N+2\right)+b^2{K}^2-bK\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}>0$.

Then,

$$\frac{\partial q_i^{\text{'}}}{\partial N}=\frac{-\left(N+1\right)K\left[2a\left(\mu +\mathrm{\lambda }\right)N\left(N+2\right)+b^2{K}^2-bK\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}\right]}{{\left[N(N+2)\right]}^2(\mu +\mathrm{\lambda })\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}}<0$$ (A2)

$$\frac{\partial q_i^{\text{'}}}{\partial \lambda }=\frac{\partial q_i^{\text{'}}}{\partial \mu }=\frac{-K\left[2a\left(\mu +\mathrm{\lambda }\right)N\left(N+2\right)+b^2{K}^2-bK\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}\right]}{2{\left[N(N+2)\right]}^2(\mu +\mathrm{\lambda })\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}}<0$$ (A3)

$$\frac{\partial q_i^{\text{'}}}{\partial K}=\frac{{\left[\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}-bK\right]}^2}{2{\left[N(N+2)\right]}^2(\mu +\mathrm{\lambda })\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}}>0$$ (A4)

$$\frac{\partial q_i^{\text{'}}}{\partial a}=\frac{K}{\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}}>0$$ (A5)

Analogously, we can show $\frac{\partial q_i^{\ast }}{\partial N}<0$; $\frac{\partial q_i^{\ast }}{\partial K}>0$; $\frac{\partial q_i^{\ast }}{\partial a}>0$.

For $\frac{\partial q_i^{\ast }}{\partial \rho }$, we have its expression as,

$$\frac{\partial q_i^{\ast }}{\partial \rho }=\frac{-K\left[6a\left(\mu +\rho \right)N^2+b^2{K}^2-bK\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}\right]}{6N^2{\left(\mu +\rho \right)}^2\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}}<0$$ (A6)

It is noted that $6a\left(\mu +\rho \right)N^2+b^2{K}^2-bK\sqrt{12a\left(\mu +\rho \right)N^2+b^2{K}^2}>0$ because $M{U}_i\left(q_i^{\ast }\right)>0$.

• 2.The proof of ${\mathit{q}}_{\mathit{i}}^{\ast }<{\mathit{q}}_{\mathit{i}}^{\text{'}}$.

We can prove this relation just by examining the FOCs of private and social optimum, without using the closed-form expressions of $q_i^{\ast }$ and $q_i^{\text{'}}$.

The FOC of the social optimum suggests,

$$a-b{q}_i^{\ast }-\left[(\mu +\mathrm{\lambda }){\left(\frac{N{q}_i^{\ast }}{K}\right)}^2+2(\mathrm{\lambda }+\mu )\frac{N{q_i^{\ast }}^2}{K^2}\right]-\left[(\rho -\lambda )\left({\left(\frac{N{q}_i^{\ast }}{K}\right)}^2+2\frac{N{q_i^{\ast }}^2}{K^2}\right)+2(\mu +\rho )\frac{N(N-1){q_i^{\ast }}^2}{K^2}\right]=0$$ (A7)

Since the term $\left[(\rho -\lambda )\left({\left(\frac{N{q}_i^{\ast }}{K}\right)}^2+2\frac{N{q_i^{\ast }}^2}{K^2}\right)+2(\mu +\rho )\frac{N(N-1){q_i^{\ast }}^2}{K^2}\right]>0$, we have,

$$a-b{q}_i^{\ast }-\left[\left(\mu +\mathrm{\lambda }\right){\left(\frac{N{q}_i^{\ast }}{K}\right)}^2+2\left(\mathrm{\lambda }+\mu \right)\frac{N{q_i^{\ast }}^2}{K^2}\right]>0$$ (A8)

The FOC of the private optimum suggests,

$$a-b{q}_i^{\text{'}}-\left[\left(\mu +\mathrm{\lambda }\right){\left(\frac{N{q}_i^{\text{'}}}{K}\right)}^2+2\left(\mathrm{\lambda }+\mu \right)\frac{N{q}_i^{\text{'}2}}{K^2}\right]=0$$ (A9)

As the function $a-b{q}_i-\left[\left(\mu +\mathrm{\lambda }\right){\left(\frac{N{q}_i}{K}\right)}^2+2\left(\mathrm{\lambda }+\mu \right)\frac{N{q}_i^2}{K^2}\right]$ is a decreasing function of $q_i$, we must have $q_i^{\ast }<q_i^{\text{'}}$.

Next, we can also show $q_i^{\ast }<q_i^{\text{'}}$ using their closed-form expressions,

$$\Delta q_i=q_i^{\text{'}}-q_i^{\ast }=\frac{K\left[\begin{array}{l}3N\left(\mu +\rho \right)\left(\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}-bK\right)-\hfill \\ (\mu +\lambda )(N+2)\left(\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}-bK\right)\hfill \end{array}\right]}{6N^2(\mu +\mathrm{\lambda })\left(N+2\right)\left(\mu +\rho \right)}$$ (A10)

As can be seen in Fig. 1, after imposing the symmetry, the marginal private/social marginal cost of infection risk is shown. The social marginal cost ($MSC\left(q\right)$) is higher than the private marginal cost ($MPC\left(q\right))$, because of the external cost ($EC\left(q\right))$. Fig. 1 suggests that $MSC\left(q_i^{\text{'}}\right)>MPC\left(q_i^{\ast }\right)$. By comparing expressions for $MSC\left(q_i^{\ast }\right)$ and $MPC\left(q_i^{\text{'}}\right)$, we can obtain the condition for the numerator of $\Delta q_i>0$, which is. Thus $\Delta q_i>0$

3. Proof of $\frac{\partial \Delta {\mathit{q}}_{\mathit{i}}}{\partial \mathit{N}}>0;\frac{\partial \Delta {\mathit{q}}_{\mathit{i}}}{\partial \mathit{K}}<0$; $\frac{\partial \Delta {\mathit{q}}_{\mathit{i}}}{\partial \mathit{a}}>0$; $\frac{\partial \Delta {\mathit{q}}_{\mathit{i}}}{\partial \mathit{\rho }}>0$; $\frac{\partial \Delta {\mathit{q}}_{\mathit{i}}}{\partial \mathit{\lambda }}$

The expressions of $\frac{\partial \Delta q_i}{\partial N},\frac{\partial \Delta q_i}{\partial K}$ are somewhat complicated. But it can be shown that $\frac{\partial q_i^{\ast }}{\partial N}<\frac{\partial q_i^{\text{'}}}{\partial N}$ with some reasonable algebraic derivations, such that $\frac{\partial \Delta q_i}{\partial N}>0$. Similarly, it can be proved that $\frac{\partial q_i^{\ast }}{\partial K}>\frac{\partial q_i^{\text{'}}}{\partial K}$, such that $\frac{\partial \Delta q_i}{\partial K}<0$. The numerical verification has also been done by assigning different values of $N$ and $K$, thus, it proves that the result holds.

In addition, we have,

$$\frac{\partial \Delta q_i}{\partial a}=\frac{K\left[\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}-\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}\right]}{\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}}>0$$ (A11)

$$\frac{\partial \Delta q_i}{\partial \rho }=\frac{K\left[6a\left(\mu +\rho \right)N^2+b^2{K}^2-bK\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}\right]}{6N^2{\left(\mu +\rho \right)}^2\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}}>0$$ (A12)

$$\frac{\partial \Delta q_i}{\partial \lambda }=\frac{-K\left[2a\left(\mu +\mathrm{\lambda }\right)N\left(N+2\right)+b^2{K}^2-bK\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}\right]}{2{\left[N(N+2)\right]}^2(\mu +\mathrm{\lambda })\sqrt{4a\left(\mu +\lambda \right)N\left(N+2\right)+b^2{K}^2}}<0$$ (A13)

• 4.Proof of $\frac{\partial {\mathit{t}}_{\mathit{i}}^{\ast }}{\partial \mathit{N}}>0;\frac{\partial {\mathit{t}}_{\mathit{i}}^{\ast }}{\partial \mathit{K}}<0$; $\frac{\partial {\mathit{t}}_{\mathit{i}}^{\ast }}{\partial \mathit{a}}>0$;$\frac{\partial {\mathit{t}}_{\mathit{i}}^{\ast }}{\partial \mathit{\lambda }}<0$

$$\frac{\partial t_i^{\ast }}{\partial N}=\frac{\begin{array}{l}\left[\sqrt{12a\left(\mu +\rho \right)N^2+b^2{K}^2}-bK\right]\hfill \\ \left[6a\left(\mu +\rho \right)\left(\mu +\rho \right)N^2+bK\left(\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}-bK\right)\left(3N\left(\mu +\rho \right)-(N+2)\left(\mu +\lambda \right)\right)\right]\hfill \end{array}}{18N^4{\left(\mu +\rho \right)}^2\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}}>0$$ (A14)

$$\frac{\partial t_i^{\ast }}{\partial K}=\frac{-b{\left[\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}-bK\right]}^2\left(3N\left(\mu +\rho \right)-(N+2)\left(\mu +\lambda \right)\right)}{18N^3{\left(\mu +\rho \right)}^2\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}}<0$$ (A15)

$$\frac{\partial t_i^{\ast }}{\partial a}=\frac{\left[\sqrt{12a\left(\mu +\rho \right)N^2+b^2{K}^2}-bK\right]\left(3N\left(\mu +\rho \right)-(N+2)\left(\mu +\lambda \right)\right)}{3N(\mu +\rho )\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}}>0$$ (A16)

$$\frac{\partial t_i^{\ast }}{\partial \lambda }=\frac{-(N+2){\left[\sqrt{12a(\mu +\rho )N^2+b^2{K}^2}-bK\right]}^2}{36N^3{\left(\mu +\rho \right)}^2}<0$$ (A17)