Abstract
Accurate ET0 estimation is of great significance in effective agricultural water management and realizing future intelligent irrigation. This study compares the performance of five Boosting-based models, including Adaptive Boosting(ADA), Gradient Boosting Decision Tree(GBDT), Extreme Gradient Boosting(XGB), Light Gradient Boosting Decision Machine(LGB) and Gradient boosting with categorical features support(CAT), for estimating daily ET0 across 10 stations in the eastern monsoon zone of China. Six different input combinations and 10-fold cross validation method were considered for fully evaluating model accuracy and stability under the condition of limited meteorological variables input. Meanwhile, path analysis was used to analyze the effect of meteorological variables on daily ET0 and their contribution to the estimation results. The results indicated that CAT models could achieve the highest accuracy (with global average RMSE of 0.5667 mm d-1, MAE of 4199 mm d-1and Adj_R2 of 0.8514) and best stability regardless of input combination and stations. Among the inputted meteorological variables, solar radiation(Rs) offers the largest contribution (with average value of 0.7703) to the R2 value of the estimation results and its direct effect on ET0 increases (ranging 0.8654 to 0.9090) as the station’s latitude goes down, while maximum temperature (Tmax) showes the contrary trend (ranging from 0.8598 to 0.5268). These results could help to optimize and simplify the variables contained in input combinations. The comparison between models based on the number of the day in a year (J) and extraterrestrial radiation (Ra) manifested that both J and Ra could improve the modeling accuracy and the improvement increased with the station’s latitudes. However, models with J could achieve better accuracy than those with Ra. In conclusion, CAT models can be most recommended for estimating ET0 and input variable J can be promoted to improve model performance with limited meteorological variables in the eastern monsoon zone of China.
Introduction
Reference evapotranspiration (ET0) is an essential factor in both of hydrological and ecological process [1–5]. Since ET0 plays a crucial role in calculating crop water requirement, water budgeting and agricultural water management, accurate estimation of ET0 is very meaningful and also serves as the foundation of realizing water-saving irrigation and intelligent irrigation. Methods of obtaining ET0 can be generally divided into three types: experimental method, empirical models and numerical simulations. Although experimental determination can measure ET0 directly, it can hardly be popularized due to its tedious operation steps and strong regional limitations [6–8]. Now days, FAO-56 Penman-Monteith (FAO-56 PM) model is generally regarded as the most authentic method for estimating ET0 in semiarid and humid regions and the estimation result is also widely used as the target to validate other models in areas where ET0 data are not available [9–12]. However, the meteorological variables required by FAO-56 PM model for estimating ET0 are difficult to obtain or fully available in most regions, which makes it difficult to be implemented. According to the principle of selecting ideal model for estimating ET0 proposed by Shih [13], ideal models should be based on minimal input variables with acceptable accuracy. Therefore, empirical models based on less meteorological variables have evolved to enhance the practicality of empirical models over the years [12,14–16], which can be generally classified as temperature-based, radiation-based, pan evaporation-based, mass transfer-based and combination type [4]. Among all these empirical models, Hargreaves-Samani model [17] requires the least meteorological variables input and has already been proved its accuracy around the world, which makes it the most popular empirical model. Other empirical models based on simplified Penman-Monteith model and solar radiation, such as Priestley-Taylor model [18], Irmak model [19] and Makkink model [20], have also been implemented in areas where full meteorological factors can hardly be obtained. However, these methods usually have such regional limitation and poor portability that they are not suitable to be applied for accurate estimation directly without taking localization approach.
By introducing intelligent algorithms for analyzing the non-linear relationship between meteorological variables and ET0, numerical simulation method using machine learning and deep learning have been advanced greatly. Since Kuma first investigated artificial neural network (ANN) models for estimating ET0 [21], this kind of method has attracted more and more researchers because of its short time, high precision and strong generalization ability. These algorithms can be generally classified as artificial neural networks-based [9,22–25], tree-based [7,26,27], kernel-based [28,29], heuristic-based [27,30,31] and hybrid algorithm-based [32,33].
To further improve the accuracy of machine learning algorithm in ET0 estimation, ensemble learning has drawn attention from more and more researchers. The core idea of ensemble learning is to combine several ‘weak learners’ to build a new ‘strong learner’, so as to reduce bias, variance and improve prediction results. Common ensemble learning models like Random Forest [34], Gradient Boosting Decision Tree [35] and Extreme Gradient Boosting models [36] have already widely used in various classification and regression problems [3,37–39] based on the characteristics of simple structure and high accuracy.
This study provides a comparison of five Boosting-based models to find out the best Boosting-based for estimating daily ET0 under the condition of limited input variables in the eastern monsoon zone of China. Therefore, the main purpose of this study produced as follows: (1) to compare the accuracy and stability of Boosting-based models with various input combinations across different climate zones; (2) to find an effective approach for improving the modeling accuracy under the condition of limited input variables.
Material and methods
Study area and data description
Geographically, the eastern monsoon zone of China is located in the east of the Great Khingan Mountains, south of the Inner Mongolia Plateau and east of the eastern edge of the Tibetan Plateau, including the second-level Loess Plateau, Sichuan Basin, Yunnan-Guizhou Plateau and the Hengduan Mountain area, as well as the third-level coastal plain and hilly areas. The climate types of the eastern monsoon zone include temperate monsoon climate, subtropical monsoon climate and tropical monsoon climate. This study area is significantly affected by the ocean monsoon in summer and the cold air flow from the north in winter. The annual average temperature changes significantly with latitude, showing a decreasing trend from south to north. This zone accounts for about 45% of the country's land area and 95% of the Chinese total population. As the eastern monsoon zone servers as one of the main farming areas of China, the research on the estimation model of ET0 can provide scientific basis for the accurate prediction of crop water demand in this region and improve the utilization efficiency of agricultural water resources, which is of great significance to the sustainable utilization of water resources.
According to the climate type and latitude distribution range of the eastern monsoon zone, 10 meteorological stations (Harbin, Shenyang, Yan 'an, Jinan, Nanjing, Changsha, Chengdu, Kunming, Nanning and Guangzhou) were selected as research stations. To be more specific, Harbin, Shenyang, Yan 'an, Jinan belong to the temperate monsoon zone (TMZ), Nanjing, Changsha, Chengdu, Kunming belong to the subtropical monsoon zone (SMZ) and Nanning, Guangzhou belong to the tropical monsoon zone (TPMZ).
In order to test and verify the accuracy and stability of Boosting-based models for ET0 estimation, daily meteorological variables, including maximum(Tmax), and minimum(Tmin) air temperature, relative humidity (RH), wind speed at 2 m height (U2) and solar radiation (Rs) from 1997 to 2016 continuously, were selected as the training and testing data set. The above meteorological data was obtained from the National Meteorological Information Center (NMIC) of China Meteorological Administration (CMA) with good quality and high precision and the missing data was interpolated through PYTHON KNN interpolation method in data pre-processing. The annual average values of the main meteorological variables at above stations during the study period were illustrated in Table 1.
Table 1. The annual average of the main meteorological variables of 10 stations during the study period.
| Climate zone | Station | Longitude | Latitude | Altitude | Tmax | Tmin | U2 | RH | Rs | Pr |
|---|---|---|---|---|---|---|---|---|---|---|
| (E) | (N) | (m) | (°C) | (°C) | (m s-1) | (%) | (MJ m-2 d-1) | (mm yr-1) | ||
| TMZ | Harbin | 126.5 | 45.8 | 165.5 | 10.0 | -1.6 | 2.8 | 65.7 | 13.9 | 535.0 |
| Shenyang | 123.5 | 41.7 | 74.8 | 14.5 | 2.4 | 2.9 | 61.8 | 14.6 | 621.1 | |
| Yan‘an | 109.5 | 36.6 | 1275.8 | 16.5 | 3.4 | 2.6 | 53.1 | 15.4 | 497.2 | |
| Ji’nan | 116.7 | 36.6 | 95.6 | 20.1 | 7.9 | 2.5 | 58.6 | 15.1 | 650.4 | |
| SMZ | Nanjing | 118.8 | 32.1 | 25.5 | 21.5 | 10.9 | 2.6 | 73.0 | 13.8 | 1090.7 |
| Changsha | 112.9 | 28.2 | 90.4 | 22.7 | 13.2 | 2.1 | 77.6 | 11.9 | 1465.3 | |
| Chengdu | 104.1 | 30.6 | 617.2 | 22.2 | 12.1 | 1.6 | 68.7 | 11.7 | 939.6 | |
| Kunming | 102.8 | 24.9 | 1938.5 | 22.4 | 10.3 | 2.5 | 68.6 | 16.3 | 836.1 | |
| TPMZ | Nanning | 108.4 | 22.8 | 160.4 | 27.1 | 17.4 | 2.5 | 76.4 | 13.4 | 1373.1 |
| Guangzhou | 113.3 | 23.1 | 64.3 | 27.1 | 17.8 | 2.3 | 77.3 | 13.5 | 1776.7 |
Where Pr is annual average precipitation.
All daily meteorological data were normalized to fall between 0 and 1 to improve the convergence rate of the model and minimize the influence of absolute scale. The normalization equation is as follows [3,24,26]:
| (1) |
Where Xnorm is the normalized value, X0, Xmin, and Xmax are the real value, the minimum value, and the maximum value of the same variable, respectively.
FAO-56 Penman-Monteith model
Since it is difficult to obtain the practical ET0 data in this study area, ET0 values calculated by the FAO-56 Penman-Monteith model are regarded as the target for training and testing the Boosting-based models, which is a widely used and acceptable practice in this case [2,8,22,30,40].
The FAO-56 PM model is expressed as:
| (2) |
Where ET0 is reference evapotranspiration (mm d-1), Rn is net radiation (MJ m-2 d-1), G is soil heat flux density (MJ m-2 d-1), Tmean is mean air temperature at 2 m height (°C), es is saturation vapor pressure (kPa), ea is actual vapor pressure (kPa), Δ is slope of the saturation vapor pressure function (kPa °C-1), γ is psychometric constant (kPa °C-1), U2 is wind speed at 2 m height (m s-1).
Boosting-based models
Boosting algorithm is a category of the ensemble learning algorithm. The principle of the Boosting algorithm is to first train a weak learner1 from the training set with the initial weight and then update the weight according to the error. When the weight becomes higher, samples with high error rate are more valued in the latter weak learner 2. After adjusting the weight based on the training set, the repetition of single weak learner is performed until the number of weak learners reaches the predetermined number. Finally, the weak learners are integrated through the set strategy (usually by weighted averaging) to obtain the final strong learner for regression or classification purpose [41].
In 1997, Freund proposed the first practical Boosting algorithm-Adaptive Boosting [42], which laid the foundation for Boosting from an idea to a practical approach. Subsequently, Friedman introduced the idea of gradient descent into the Boosting algorithm and then proposed the Gradient Boosting algorithm [35] which is more practical and can handle different loss functions. Based on the above research, Boosting-based model has been continuously developed by researchers and has already been widely used in classification and regression problems. In this study, five Boosting-based models, Adaptive Boosting (ADA), Gradient Boosting Decision Tree(GBDT), Extreme Gradient Boosting(XGB), Light Gradient Boosting Decision Machine(LGB) and Gradient boosting with categorical features support(CAT), are employed to compare their performance of estimating ET0 value. All codes of Boosting-based models introduced in this study were written in Python and performed in a laptop with Intel Core i7-9750H CPU @2.60GHz, NVDIA GeForce GTX 1660Ti GPU and 16GB of RAM. For evaluating the performance of each model at the same level of model structure and complexity, only ‘n_estimators’ and ‘learning_rate’ were set to 500 and 0.05 respectively and other hyper parameters were set to default.
Adaptive Boosting (ADA)
The first boosting algorithm, Adaptive Boosting (ADA) was proposed by Freund [42]. AdaBoost assigns equal initial weights to all training data for weak learns training, then updates the weight distribution according to the prediction results. To be more specific, higher weights are assigned to mispredicted samples while lower weights are given to samples predicted correctly, which makes the next training step more focused on mispredicted samples to reduce bias. Above process is repeated until the specified number of iterations or the expected error rate is reached, then all predicted results of the weak learners are added linearly with weights as the final result. The detailed calculation procedures of ADA are described as follows:
For the given dataset , the steps of ADA model for regression problem can be expressed as follows:
(1) Initialize the weight distribution of the training samples as follows:
For i = 1,2,3…M
| (3) |
(2) For k (k = 1,2,3…K), taking Dk as the training set of weak learner fk(x) and calculating the following indicators:
(a) Maximum error:
| (4) |
(b) Relative error of each sample:
| (5) |
(c) Regression error rate:
| (6) |
(d) Weight of weak learner fk(x):
| (7) |
(e) Weight distribution of samples is updated as:
| (8) |
Where Zk is normalizing factor:
| (9) |
(3) The final strong learner is obtained as:
| (10) |
Where g(x) is the median of all αmfm(x), m = 1,2,3…M.
Although ADA is no longer suitable for the current scenario of large sample, high-latitude data usage, its appearance has turned Boosting idea from an initial conjecture into a practical algorithm, which greatly promoted the development of subsequent Boosting-based algorithms.
Gradient Boosting Decision Tree (GBDT)
The Gradient Boosting Decision Tree (GBDT) is an iterative decision tree algorithm, proposed by Friedman [35]. The weak learners in GBDT model have strong dependencies between each other and are trained by progressive iterations based on the residuals. The results of all weak learners are added together as the final result, which makes GBDT have great advantages in over-fitting and computational cost fields and also insensitive to data set missing and can reduce bias at the same time. The detailed calculation procedures of GBDT are described as follows:
For the given dataset , the steps of GBDT model for regression problem can be expressed as follows:
(1) Initialize the weak learner:
| (11) |
Where L(yi, γ) is the loss function.
(2) For m (m = 1,2,3…M) sample in the training set, the residual along the gradient direction is written as:
| 12 |
Where n is the number of the estimators (‘n_estimators), n = 1,2,3…,N.
(3) Taking (xi, rim) i = 1,2,3…,m as the training data of the weak learner n and the leaf node region is Rnj, j = 1,2,3…,J. For this new weak learner, the optimal negative gradient fitting value of each leaf node is calculated as follows:
| (13) |
(4) The model is updated as:
| (14) |
(5) The final strong learner is obtained as:
| (15) |
Extreme Gradient Boosting (XGB)
Extreme Gradient Boosting (XGB) is an improved algorithm based on GBDT algorithm [36]. Different from the original GBDT model, XGB model obtains the residual by performing second-order Taylor expansion on the cost function, and adds a regularization term to control the complexity of the model at the same time. The addition of regularization terms reduces the variance of the model and makes the model more simplified, making XGB model superior to original GBDT model in terms of weighing the bias-variance tradeoff and preventing overfitting. Also, XGB supports multiple cost functions and parallel operations on feature granularity.
The specific calculation procedures of XGB are described as follows:
(1) Define the objective function as follows:
| (16) |
Where C is a constant term, which can be commonly omitted and R(fk) is the regularization term at the k time iteration, defined as follows:
| (17) |
Where α is complexity of leaves, T is the number of the leaves, η is the penalty parameter and ωj is the output result of each leaf node.
(2) Introduce second-order Taylor series of objective function and adopt the mean square error as the loss function, the objective function can be described as follows:
| (18) |
Where is fk, gi and hi is the first and second derivative of loss function, respectively.
the output result of each leaf node.
(3) Determine the final loss value by summing the loss values of leaf nodes. Therefore, the objective function can be expressed as:
| (19) |
Where , , and Ij indicates all samples in leaf node j.
Light Gradient Boosting Decision Machine (LGB)
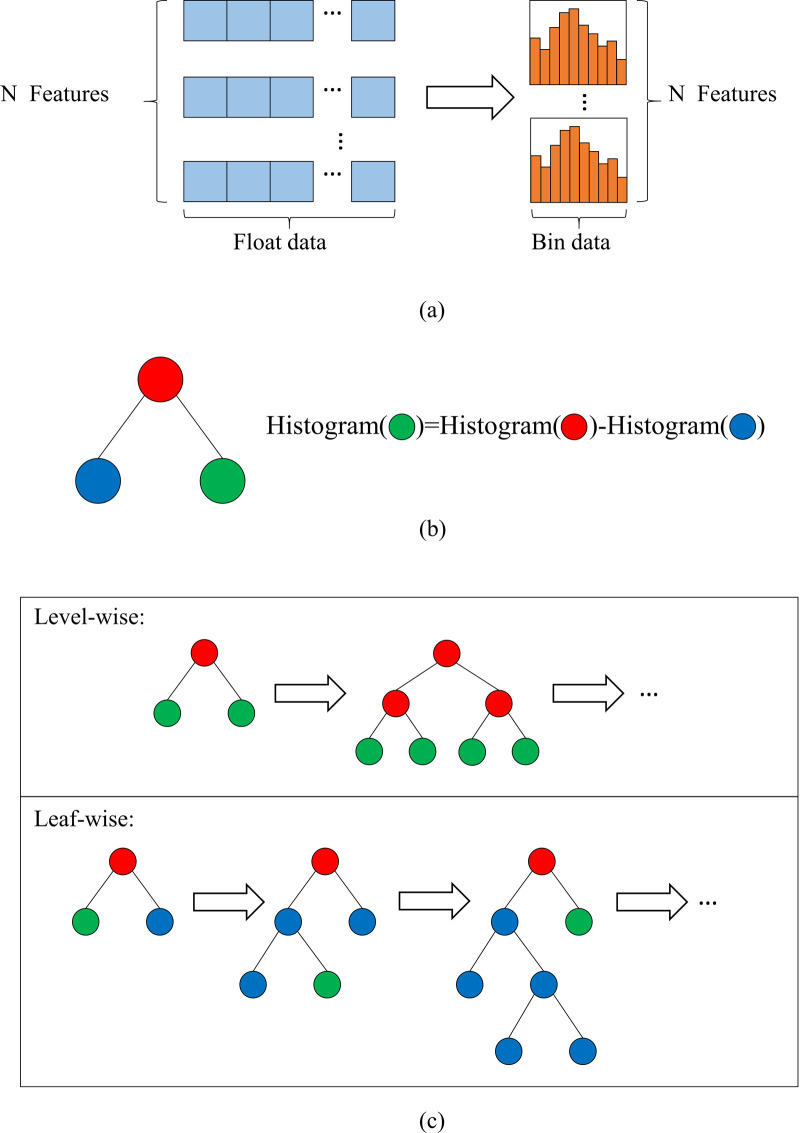
Light Gradient Boosting Decision Machine (LGB) is a novel algorithm from Microsoft [43], which has the advantages of lower memory consumption, higher precision and faster training efficiency. Traditional Boosting-based algorithms need to scan all the sample points for each feature to select the best segmentation point, which leads to the model taking too much time in the large sample and high latitude data condition. In order to solve the above problems and further improve the efficiency and scalability of the model, LGB introduces the Gradient-based One-Side Sampling(GOSS) and Exclusive Feature Bundling(EF-B) algorithm. Fig 1 illustrates the special strategy adopted by LGB algorithm and detailed introduction is as follows:
Fig 1. Special process of LGB algorithm.
(a) Histogram-based algorithm; (b) Obtain difference value by histogram value; (c) Level-wise and leaf-wise strategies.
The GOSS algorithm does not use all sample points to calculate the gradient, but instead reserves the sample points with large gradients and performs random sampling on the sample points with small gradients to complete the data sampling in order to maintain the accuracy of information gain. Information gain indicates the expected reduction in entropy caused by splitting the nodes based on attributes, which can be described as follows:
| (20) |
| (21) |
Where En(B) is the information entropy of the collection B, pd is the ratio of B pertaining to category d, D is the number of categories, v is the value of attribute V and Bv is the subset of B for which attribute has value v.
As shown in Fig 1A, the EF-B uses a histogram-based approach, which can discrete floating-point eigenvalues into k integers and construct a histogram of k width. In this way, optimal segmentation point can be found based on the discrete value of histogram with lower memory consumption. In addition, Fig 1B also manifests that the histogram of a single leaf can be obtained by contrasting the histogram of its parent node with that of its sibling node in LGB algorithm, which further increases the speed of the model.
The general process of level-wise and leaf-wise strategies is shown in Fig 1C. Compared with the level-wise strategy, the limited leaf-wise strategy used by LGB could be more effective because it only split at the leaf with the largest information gain and the limited depth can prevent overfitting effectively.
Gradient boosting with categorical features support (CAT)
Gradient boosting [44] with categorical features support (CAT) introduces a modified target-based statistics (TBS) to use all data set for training and avoid potential overfitting problem by performing random permutations. To be more specific, CAT first randomly sorts all samples, and then takes a value from a category-based feature. Each sample's feature is converted to a numerical value by taking an average value based on the category label that precedes the sample, and adding priority and weight coefficients of priority. In the process of building new weak learners, CAT first uses the gradient of the sample points before the sample Xn to estimate the model, and then uses these models to calculate the gradient of Xn and update the model. Moreover, CAT uses the oblivious tree as the weak learner, and the index of each leaf node in the oblivious tree can be encoded as a binary vector of length equal to the depth of the tree, which further enhance the model’s ability to resist overfitting.
Compared with XGB and LGB, CAT has following main contributions:
Categorical features can be handled automatically by using TBS before training process.
Feature dimensions can be enriched by combining the category features according to the relationship between different ones.
Overfitting problem can be better resisted by adopting complete oblivious tree.
Calibration and validation of the models
This study considered limited meteorological variables input combinations as the combination of air temperature data (Tmax and Tmin) with Rs, RH and U2 respectively. In addition, Since extraterrestrial radiation (Ra) is commonly applied to improve the modeling accuracy for estimating ET0 with limited input meteorological variables and it is closely related to the geographic data of the station and the number of the days in a year(J), this study also employed J as the input variable to compare with the modeling accuracy improvement brought by Ra and J.
As summarized above, six input meteorological variables combinations were shown in Table 2, these combinations are: (1) Tmax, Tmin, Rs; (2) Tmax, Tmin, RH; (3) Tmax, Tmin, U2; (4) Tmax, Tmin; (5) Tmax, Tmin, Ra and (6) Tmax, Tmin, J.
Table 2. The input meteorological variables combinations for different models.
| Input combination | Input variables | Model abbreviation | ||||
|---|---|---|---|---|---|---|
| ADA | GBDT | XGB | LGB | CAT | ||
| M1 | Tmax, Tmin, Rs | ADA1 | GBDT1 | XGB1 | LGB1 | CAT1 |
| M2 | Tmax, Tmin, RH | ADA2 | GBDT2 | XGB2 | LGB2 | CAT2 |
| M3 | Tmax, Tmin, U2 | ADA3 | GBDT3 | XGB3 | LGB3 | CAT3 |
| M4 | Tmax, Tmin | ADA4 | GBDT4 | XGB4 | LGB4 | CAT4 |
| M5 | Tmax, Tmin, Ra | ADA5 | GBDT5 | XGB5 | LGB5 | CAT5 |
| M6 | Tmax, Tmin, J | ADA6 | GBDT6 | XGB6 | LGB6 | CAT6 |
10-fold cross validation method was used to better evaluate the accuracy of the model and reduce the randomness brought by test samples, and the average value of 10-fold cross-validation result is used as the final performance of the model. In addition, meteorological data from 1997 to 2011, 2012 to 2016 were used as the training and testing set respectively, with a different proportion of training and testing sets from that of 10-fold cross validation stage to analyze model accuracy on daily scale.
Performance criteria
Present study introduced root mean square error (RMSE), mean absolute error (MAE) and adjusted R2 (Adj_R2) to evaluate performance of the models [4,24,26,28,45].
| (22) |
| (23) |
| (24) |
| (25) |
Where and are ET0 values estimated by FAO-56 PM and other models respectively. and are the mean values of the ET0 values estimated by FAO-56 PM model and other models respectively. N and P are the number of test samples and variables, respectively. i is the number of i-th step, n is the number of the total steps. RMSE is in mm day-1, with the value range from 0 (optimum value) to +∞ (worst value). MAE is in mm/d, with the value range from 0 (optimum value) to +∞ (worst value). R2 and Adj_R2 are dimensionless, with the value range from 1 (optimum value) to −∞ (worst value).
Results
Comparison of different Boosting-based models with various input combinations on daily scale
The performances of Boosting-based models with daily different meteorological variables inputs at Harbin, Shenyang, Yan 'an, Jinan, Nanjing, Changsha, Chengdu, Kunming, Nanning and Guangzhou stations were illustrated in Tables 3–12, respectively. Tables manifested that the tested models generally had similar performance ranking across 10 stations. For brevity, Harbin, Changsha and Guangzhou were chosen as representatives of TMZ, SMZ and TPMZ respectively to describe in detail.
Table 3. Performance of Boosting-based models during 10-fold cross validation and testing stages at Harbin station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.5748 | 0.4715 | 0.9019 | 0.5400 | 0.4140 | 0.9042 |
| GBDT1 | 0.4523 | 0.2994 | 0.9400 | 0.3942 | 0.2790 | 0.9489 |
| XGB1 | 0.4354 | 0.2937 | 0.9444 | 0.3769 | 0.2784 | 0.9533 |
| LGB1 | 0.4335 | 0.2890 | 0.9449 | 0.3721 | 0.2694 | 0.9545 |
| CAT1 | 0.4288 | 0.2871 | 0.9461 | 0.3699 | 0.2662 | 0.9550 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.6108 | 0.4857 | 0.8883 | 0.6400 | 0.5263 | 0.8654 |
| GBDT2 | 0.4511 | 0.2994 | 0.9401 | 0.4270 | 0.2843 | 0.9401 |
| XGB2 | 0.4411 | 0.3051 | 0.9427 | 0.4228 | 0.2994 | 0.9413 |
| LGB2 | 0.4385 | 0.2950 | 0.9433 | 0.4261 | 0.2925 | 0.9403 |
| CAT2 | 0.4334 | 0.2919 | 0.9446 | 0.4123 | 0.2844 | 0.9441 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.7052 | 0.5417 | 0.8537 | 0.6934 | 0.5441 | 0.8420 |
| GBDT3 | 0.6268 | 0.4417 | 0.8838 | 0.6091 | 0.4275 | 0.8781 |
| XGB3 | 0.6108 | 0.4348 | 0.8899 | 0.5955 | 0.4286 | 0.8834 |
| LGB3 | 0.6091 | 0.4324 | 0.8906 | 0.5885 | 0.4211 | 0.8862 |
| CAT3 | 0.5997 | 0.4259 | 0.8940 | 0.5811 | 0.4132 | 0.8890 |
| Tmax, Tmin | ||||||
| ADA4 | 0.7432 | 0.5585 | 0.8373 | 0.7524 | 0.5557 | 0.8141 |
| GBDT4 | 0.6911 | 0.4821 | 0.8596 | 0.6508 | 0.4656 | 0.8609 |
| XGB4 | 0.6817 | 0.4905 | 0.8636 | 0.6488 | 0.4804 | 0.8618 |
| LGB4 | 0.6709 | 0.4803 | 0.8684 | 0.6269 | 0.4516 | 0.8709 |
| CAT4 | 0.6586 | 0.4657 | 0.8726 | 0.6228 | 0.4466 | 0.8726 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.6812 | 0.5107 | 0.8632 | 0.6806 | 0.5286 | 0.8478 |
| GBDT5 | 0.5581 | 0.3706 | 0.9086 | 0.5358 | 0.3668 | 0.9057 |
| XGB5 | 0.5330 | 0.3584 | 0.9168 | 0.5094 | 0.3563 | 0.9147 |
| LGB5 | 0.5291 | 0.3543 | 0.9181 | 0.5019 | 0.3460 | 0.9172 |
| CAT5 | 0.5224 | 0.3507 | 0.9201 | 0.4957 | 0.3385 | 0.9193 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.6429 | 0.4783 | 0.8782 | 0.6426 | 0.4856 | 0.8643 |
| GBDT6 | 0.5394 | 0.3600 | 0.9147 | 0.5185 | 0.3536 | 0.9117 |
| XGB6 | 0.5235 | 0.3539 | 0.9197 | 0.5075 | 0.3554 | 0.9153 |
| LGB6 | 0.5228 | 0.3516 | 0.9199 | 0.4928 | 0.3424 | 0.9202 |
| CAT6 | 0.5122 | 0.3473 | 0.9231 | 0.4897 | 0.3395 | 0.9212 |
Table 12. Performance of Boosting-based models during 10-fold cross validation and testing stages at Guangzhou station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.4997 | 0.4115 | 0.7624 | 0.5269 | 0.4457 | 0.7515 |
| GBDT1 | 0.3890 | 0.2610 | 0.8539 | 0.3751 | 0.2614 | 0.8740 |
| XGB1 | 0.3778 | 0.2577 | 0.8618 | 0.3620 | 0.2613 | 0.8827 |
| LGB1 | 0.3760 | 0.2557 | 0.8629 | 0.3585 | 0.2562 | 0.8849 |
| CAT1 | 0.3708 | 0.2516 | 0.8664 | 0.3528 | 0.2533 | 0.8886 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.6114 | 0.5029 | 0.6453 | 0.5971 | 0.4804 | 0.6808 |
| GBDT2 | 0.5396 | 0.4172 | 0.7228 | 0.5243 | 0.3938 | 0.7539 |
| XGB2 | 0.5334 | 0.4186 | 0.7292 | 0.5013 | 0.3846 | 0.7750 |
| LGB2 | 0.5253 | 0.4068 | 0.7374 | 0.5005 | 0.3783 | 0.7757 |
| CAT2 | 0.5193 | 0.4036 | 0.7432 | 0.4891 | 0.3697 | 0.7858 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.7658 | 0.6215 | 0.4457 | 0.7854 | 0.6315 | 0.4478 |
| GBDT3 | 0.6596 | 0.5088 | 0.5866 | 0.6558 | 0.5006 | 0.6149 |
| XGB3 | 0.6422 | 0.4990 | 0.6086 | 0.6341 | 0.4875 | 0.6400 |
| LGB3 | 0.6407 | 0.4988 | 0.6106 | 0.6296 | 0.4853 | 0.6451 |
| CAT3 | 0.6322 | 0.4906 | 0.6207 | 0.6167 | 0.4760 | 0.6596 |
| Tmax, Tmin | ||||||
| ADA4 | 0.7593 | 0.6152 | 0.4558 | 0.7797 | 0.6181 | 0.4561 |
| GBDT4 | 0.7109 | 0.5574 | 0.5210 | 0.6976 | 0.5467 | 0.5645 |
| XGB4 | 0.6944 | 0.5501 | 0.5439 | 0.6736 | 0.5365 | 0.5940 |
| LGB4 | 0.6872 | 0.5422 | 0.5542 | 0.6654 | 0.5255 | 0.6038 |
| CAT4 | 0.6794 | 0.5336 | 0.5625 | 0.6555 | 0.5169 | 0.6156 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.7622 | 0.6171 | 0.4512 | 0.7871 | 0.6389 | 0.4453 |
| GBDT5 | 0.6737 | 0.5221 | 0.5688 | 0.6547 | 0.5084 | 0.6162 |
| XGB5 | 0.6592 | 0.5125 | 0.5874 | 0.6427 | 0.5037 | 0.6302 |
| LGB5 | 0.6566 | 0.5110 | 0.5904 | 0.6365 | 0.4990 | 0.6373 |
| CAT5 | 0.6494 | 0.5036 | 0.5992 | 0.6249 | 0.4879 | 0.6504 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.7580 | 0.6138 | 0.4574 | 0.7875 | 0.6386 | 0.4449 |
| GBDT6 | 0.6450 | 0.4946 | 0.6047 | 0.6294 | 0.4838 | 0.6453 |
| XGB6 | 0.6312 | 0.4865 | 0.6217 | 0.6127 | 0.4760 | 0.6639 |
| LGB6 | 0.6282 | 0.4843 | 0.6252 | 0.6083 | 0.4738 | 0.6687 |
| CAT6 | 0.6171 | 0.4745 | 0.6382 | 0.5909 | 0.4560 | 0.6874 |
Table 4. Performance of Boosting-based models during 10-fold cross validation and testing stages at Shenyang station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.6376 | 0.5208 | 0.8792 | 0.6089 | 0.4706 | 0.8795 |
| GBDT1 | 0.5315 | 0.3657 | 0.9184 | 0.4912 | 0.3413 | 0.9216 |
| XGB1 | 0.5173 | 0.3630 | 0.9225 | 0.4785 | 0.3399 | 0.9256 |
| LGB1 | 0.5139 | 0.3567 | 0.9236 | 0.4721 | 0.3307 | 0.9276 |
| CAT1 | 0.5020 | 0.3506 | 0.9272 | 0.4656 | 0.3255 | 0.9295 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.6737 | 0.5374 | 0.8635 | 0.6533 | 0.5281 | 0.8613 |
| GBDT2 | 0.5224 | 0.3571 | 0.9202 | 0.4875 | 0.3350 | 0.9228 |
| XGB2 | 0.5085 | 0.3603 | 0.9242 | 0.4813 | 0.3417 | 0.9247 |
| LGB2 | 0.5071 | 0.3528 | 0.9246 | 0.4801 | 0.3309 | 0.9251 |
| CAT2 | 0.5027 | 0.3485 | 0.9259 | 0.4763 | 0.3311 | 0.9264 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.7903 | 0.6300 | 0.8157 | 0.7637 | 0.6239 | 0.8104 |
| GBDT3 | 0.6644 | 0.4896 | 0.8695 | 0.6189 | 0.4626 | 0.8755 |
| XGB3 | 0.6488 | 0.4820 | 0.8758 | 0.5992 | 0.4545 | 0.8833 |
| LGB3 | 0.6477 | 0.4797 | 0.8763 | 0.5933 | 0.4481 | 0.8856 |
| CAT3 | 0.6334 | 0.4711 | 0.8814 | 0.5894 | 0.4491 | 0.8871 |
| Tmax, Tmin | ||||||
| ADA4 | 0.8371 | 0.6621 | 0.7935 | 0.8270 | 0.6298 | 0.7779 |
| GBDT4 | 0.7469 | 0.5449 | 0.8375 | 0.7002 | 0.5226 | 0.8408 |
| XGB4 | 0.7419 | 0.5578 | 0.8391 | 0.6952 | 0.5368 | 0.8430 |
| LGB4 | 0.7218 | 0.5371 | 0.8485 | 0.6633 | 0.5031 | 0.8571 |
| CAT4 | 0.7087 | 0.5263 | 0.8532 | 0.6584 | 0.4994 | 0.8592 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.7546 | 0.5880 | 0.8322 | 0.7240 | 0.5741 | 0.8297 |
| GBDT5 | 0.6150 | 0.4283 | 0.8924 | 0.5693 | 0.4098 | 0.8947 |
| XGB5 | 0.5879 | 0.4166 | 0.8992 | 0.5506 | 0.4017 | 0.9015 |
| LGB5 | 0.5835 | 0.4122 | 0.9009 | 0.5460 | 0.3945 | 0.9031 |
| CAT5 | 0.5731 | 0.4073 | 0.9043 | 0.5446 | 0.3928 | 0.9036 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.7419 | 0.5807 | 0.8381 | 0.7088 | 0.5623 | 0.8367 |
| GBDT6 | 0.5970 | 0.4191 | 0.8959 | 0.5626 | 0.4021 | 0.8971 |
| XGB6 | 0.5794 | 0.4130 | 0.9019 | 0.5462 | 0.3987 | 0.9030 |
| LGB6 | 0.5752 | 0.4087 | 0.9034 | 0.5439 | 0.3921 | 0.9039 |
| CAT6 | 0.5684 | 0.4068 | 0.9057 | 0.5385 | 0.3921 | 0.9058 |
Table 5. Performance of Boosting-based models during 10-fold cross validation and testing stages at Yan’an station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.6368 | 0.5079 | 0.8905 | 0.6544 | 0.5167 | 0.8700 |
| GBDT1 | 0.5508 | 0.4074 | 0.9180 | 0.5198 | 0.3963 | 0.9180 |
| XGB1 | 0.5338 | 0.3975 | 0.9230 | 0.4962 | 0.3842 | 0.9252 |
| LGB1 | 0.5299 | 0.3930 | 0.9241 | 0.4876 | 0.3777 | 0.9278 |
| CAT1 | 0.5251 | 0.3895 | 0.9254 | 0.4829 | 0.3732 | 0.9292 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.6503 | 0.5274 | 0.8851 | 0.6819 | 0.5633 | 0.8588 |
| GBDT2 | 0.5592 | 0.3997 | 0.9156 | 0.5238 | 0.3809 | 0.9167 |
| XGB2 | 0.5361 | 0.3935 | 0.9225 | 0.5126 | 0.3826 | 0.9202 |
| LGB2 | 0.5377 | 0.3893 | 0.9219 | 0.5166 | 0.3804 | 0.9190 |
| CAT2 | 0.5280 | 0.3830 | 0.9248 | 0.5016 | 0.3679 | 0.9236 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.8212 | 0.6553 | 0.8172 | 0.8121 | 0.6559 | 0.7998 |
| GBDT3 | 0.6703 | 0.5010 | 0.8785 | 0.6402 | 0.4793 | 0.8756 |
| XGB3 | 0.6560 | 0.4919 | 0.8836 | 0.6262 | 0.4714 | 0.8810 |
| LGB3 | 0.6524 | 0.4890 | 0.8849 | 0.6211 | 0.4655 | 0.8829 |
| CAT3 | 0.6411 | 0.4817 | 0.8888 | 0.6117 | 0.4597 | 0.8864 |
| Tmax, Tmin | ||||||
| ADA4 | 0.8948 | 0.7024 | 0.7832 | 0.8925 | 0.6975 | 0.7583 |
| GBDT4 | 0.8265 | 0.6165 | 0.8160 | 0.7883 | 0.5962 | 0.8115 |
| XGB4 | 0.8096 | 0.6191 | 0.8232 | 0.7723 | 0.6023 | 0.8190 |
| LGB4 | 0.8013 | 0.6078 | 0.8275 | 0.7480 | 0.5736 | 0.8302 |
| CAT4 | 0.7890 | 0.5960 | 0.8323 | 0.7372 | 0.5642 | 0.8351 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.7998 | 0.6248 | 0.8269 | 0.7930 | 0.6194 | 0.8091 |
| GBDT5 | 0.6810 | 0.4994 | 0.8756 | 0.6599 | 0.4852 | 0.8678 |
| XGB5 | 0.6614 | 0.4888 | 0.8819 | 0.6354 | 0.4720 | 0.8774 |
| LGB5 | 0.6598 | 0.4878 | 0.8825 | 0.6275 | 0.4668 | 0.8804 |
| CAT5 | 0.6499 | 0.4818 | 0.8860 | 0.6157 | 0.4566 | 0.8849 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.7835 | 0.6064 | 0.8340 | 0.7825 | 0.6067 | 0.8141 |
| GBDT6 | 0.6742 | 0.4964 | 0.8774 | 0.6494 | 0.4812 | 0.8720 |
| XGB6 | 0.6550 | 0.4870 | 0.8842 | 0.6326 | 0.4720 | 0.8785 |
| LGB6 | 0.6523 | 0.4844 | 0.8852 | 0.6209 | 0.4633 | 0.8830 |
| CAT6 | 0.6397 | 0.4755 | 0.8896 | 0.6118 | 0.4570 | 0.8864 |
Table 7. Performance of Boosting-based models during 10-fold cross validation and testing stages at Nanjing station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.5564 | 0.4663 | 0.8590 | 0.5494 | 0.4638 | 0.8597 |
| GBDT1 | 0.3918 | 0.2850 | 0.9315 | 0.3605 | 0.2721 | 0.9396 |
| XGB1 | 0.3832 | 0.2816 | 0.9345 | 0.3505 | 0.2658 | 0.9429 |
| LGB1 | 0.3798 | 0.2784 | 0.9356 | 0.3476 | 0.2630 | 0.9438 |
| CAT1 | 0.3740 | 0.2743 | 0.9376 | 0.3406 | 0.2593 | 0.9461 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.6397 | 0.5326 | 0.8157 | 0.5993 | 0.4761 | 0.8330 |
| GBDT2 | 0.5462 | 0.3969 | 0.8665 | 0.5175 | 0.3749 | 0.8755 |
| XGB2 | 0.5269 | 0.3923 | 0.8757 | 0.4994 | 0.3762 | 0.8840 |
| LGB2 | 0.5264 | 0.3880 | 0.8760 | 0.4970 | 0.3659 | 0.8851 |
| CAT2 | 0.5194 | 0.3830 | 0.8793 | 0.4917 | 0.3602 | 0.8876 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.7774 | 0.6195 | 0.7265 | 0.7634 | 0.6113 | 0.7290 |
| GBDT3 | 0.6851 | 0.5174 | 0.7893 | 0.6453 | 0.4913 | 0.8064 |
| XGB3 | 0.6647 | 0.5042 | 0.8016 | 0.6226 | 0.4792 | 0.8198 |
| LGB3 | 0.6613 | 0.5021 | 0.8038 | 0.6130 | 0.4722 | 0.8252 |
| CAT3 | 0.6548 | 0.4956 | 0.8076 | 0.6065 | 0.4642 | 0.8290 |
| Tmax, Tmin | ||||||
| ADA4 | 0.9803 | 0.7305 | 0.5812 | 0.7509 | 0.6003 | 0.7380 |
| GBDT4 | 0.7695 | 0.5441 | 0.7446 | 0.6737 | 0.5172 | 0.7891 |
| XGB4 | 0.6927 | 0.5365 | 0.7849 | 0.6583 | 0.5171 | 0.7986 |
| LGB4 | 0.6785 | 0.5170 | 0.7940 | 0.6359 | 0.4901 | 0.8121 |
| CAT4 | 0.6699 | 0.5081 | 0.7992 | 0.6274 | 0.4820 | 0.8171 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.7482 | 0.5925 | 0.7474 | 0.7352 | 0.5801 | 0.7487 |
| GBDT5 | 0.6311 | 0.4661 | 0.8215 | 0.6141 | 0.4575 | 0.8247 |
| XGB5 | 0.6106 | 0.4534 | 0.8328 | 0.5935 | 0.4470 | 0.8362 |
| LGB5 | 0.6062 | 0.4501 | 0.8352 | 0.5875 | 0.4431 | 0.8395 |
| CAT5 | 0.6014 | 0.4453 | 0.8379 | 0.5738 | 0.4298 | 0.8469 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.7645 | 0.6077 | 0.7359 | 0.7557 | 0.6005 | 0.7345 |
| GBDT6 | 0.6243 | 0.4609 | 0.8253 | 0.6072 | 0.4536 | 0.8286 |
| XGB6 | 0.6030 | 0.4479 | 0.8370 | 0.5850 | 0.4433 | 0.8408 |
| LGB6 | 0.5980 | 0.4454 | 0.8397 | 0.5781 | 0.4387 | 0.8446 |
| CAT6 | 0.5914 | 0.4380 | 0.8431 | 0.5665 | 0.4244 | 0.8508 |
Table 8. Performance of Boosting-based models during 10-fold cross validation and testing stages at Changsha station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.4275 | 0.3527 | 0.8976 | 0.4433 | 0.3658 | 0.8894 |
| GBDT1 | 0.2865 | 0.2037 | 0.9536 | 0.2715 | 0.1989 | 0.9585 |
| XGB1 | 0.2790 | 0.2011 | 0.9559 | 0.2641 | 0.1952 | 0.9607 |
| LGB1 | 0.2790 | 0.1994 | 0.9559 | 0.2654 | 0.1935 | 0.9604 |
| CAT1 | 0.2746 | 0.1959 | 0.9573 | 0.2569 | 0.1881 | 0.9628 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.6134 | 0.4873 | 0.7908 | 0.5861 | 0.4568 | 0.8066 |
| GBDT2 | 0.5744 | 0.4212 | 0.8161 | 0.5355 | 0.3968 | 0.8386 |
| XGB2 | 0.5528 | 0.4121 | 0.8298 | 0.5141 | 0.3879 | 0.8512 |
| LGB2 | 0.5531 | 0.4098 | 0.8296 | 0.5086 | 0.3805 | 0.8544 |
| CAT2 | 0.5462 | 0.4040 | 0.8338 | 0.5021 | 0.3731 | 0.8581 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.7151 | 0.5802 | 0.7143 | 0.7130 | 0.5798 | 0.7138 |
| GBDT3 | 0.6466 | 0.4789 | 0.7667 | 0.6281 | 0.4700 | 0.7779 |
| XGB3 | 0.6258 | 0.4693 | 0.7816 | 0.6041 | 0.4586 | 0.7945 |
| LGB3 | 0.6257 | 0.4684 | 0.7818 | 0.6018 | 0.4553 | 0.7961 |
| CAT3 | 0.6176 | 0.4623 | 0.7873 | 0.5978 | 0.4480 | 0.7988 |
| Tmax, Tmin | ||||||
| ADA4 | 0.7174 | 0.5808 | 0.7129 | 0.6982 | 0.5617 | 0.7257 |
| GBDT4 | 0.6622 | 0.4968 | 0.7558 | 0.6394 | 0.4870 | 0.7700 |
| XGB4 | 0.6484 | 0.5009 | 0.7659 | 0.6319 | 0.4954 | 0.7754 |
| LGB4 | 0.6421 | 0.4913 | 0.7713 | 0.6197 | 0.4753 | 0.7840 |
| CAT4 | 0.6335 | 0.4813 | 0.7767 | 0.6117 | 0.4672 | 0.7895 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.7158 | 0.5807 | 0.7138 | 0.7172 | 0.5841 | 0.7104 |
| GBDT5 | 0.6276 | 0.4606 | 0.7802 | 0.6169 | 0.4533 | 0.7858 |
| XGB5 | 0.6053 | 0.4487 | 0.7956 | 0.5938 | 0.4444 | 0.8015 |
| LGB5 | 0.6035 | 0.4477 | 0.7969 | 0.5912 | 0.4407 | 0.8032 |
| CAT5 | 0.5943 | 0.4394 | 0.8030 | 0.5834 | 0.4321 | 0.8084 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.7163 | 0.5798 | 0.7133 | 0.7133 | 0.5782 | 0.7136 |
| GBDT6 | 0.6188 | 0.4540 | 0.7863 | 0.6081 | 0.4530 | 0.7918 |
| XGB6 | 0.5978 | 0.4430 | 0.8007 | 0.5896 | 0.4437 | 0.8043 |
| LGB6 | 0.5962 | 0.4415 | 0.8018 | 0.5870 | 0.4392 | 0.8061 |
| CAT6 | 0.5870 | 0.4324 | 0.8079 | 0.5754 | 0.4271 | 0.8136 |
Table 9. Performance of Boosting-based models during 10-fold cross validation and testing stages at Chengdu station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.5473 | 0.4533 | 0.8515 | 0.5506 | 0.4556 | 0.8458 |
| GBDT1 | 0.3697 | 0.2630 | 0.9323 | 0.3640 | 0.2583 | 0.9326 |
| XGB1 | 0.3595 | 0.2585 | 0.9360 | 0.3543 | 0.2528 | 0.9361 |
| LGB1 | 0.3582 | 0.2556 | 0.9364 | 0.3516 | 0.2508 | 0.9371 |
| CAT1 | 0.3521 | 0.2499 | 0.9385 | 0.3413 | 0.2439 | 0.9407 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.5962 | 0.4731 | 0.8247 | 0.5907 | 0.4662 | 0.8225 |
| GBDT2 | 0.5552 | 0.4074 | 0.8476 | 0.5501 | 0.4005 | 0.8461 |
| XGB2 | 0.5425 | 0.4042 | 0.8545 | 0.5201 | 0.3891 | 0.8624 |
| LGB2 | 0.5370 | 0.3978 | 0.8574 | 0.5235 | 0.3852 | 0.8606 |
| CAT2 | 0.5337 | 0.3943 | 0.8592 | 0.5109 | 0.3746 | 0.8672 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.6889 | 0.5560 | 0.7665 | 0.6831 | 0.5553 | 0.7626 |
| GBDT3 | 0.6100 | 0.4645 | 0.8166 | 0.6092 | 0.4681 | 0.8112 |
| XGB3 | 0.5914 | 0.4548 | 0.8277 | 0.5908 | 0.4595 | 0.8224 |
| LGB3 | 0.5898 | 0.4529 | 0.8286 | 0.5881 | 0.4576 | 0.8240 |
| CAT3 | 0.5835 | 0.4483 | 0.8323 | 0.5753 | 0.4455 | 0.8316 |
| Tmax, Tmin | ||||||
| ADA4 | 0.7012 | 0.5602 | 0.7582 | 0.7124 | 0.5639 | 0.7419 |
| GBDT4 | 0.6482 | 0.4973 | 0.7933 | 0.6495 | 0.5004 | 0.7855 |
| XGB4 | 0.6369 | 0.4984 | 0.8006 | 0.6376 | 0.5016 | 0.7933 |
| LGB4 | 0.6288 | 0.4910 | 0.8060 | 0.6330 | 0.4933 | 0.7963 |
| CAT4 | 0.6197 | 0.4808 | 0.8110 | 0.6206 | 0.4820 | 0.8042 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.6824 | 0.5470 | 0.7703 | 0.6857 | 0.5549 | 0.7608 |
| GBDT5 | 0.6159 | 0.4711 | 0.8125 | 0.6267 | 0.4753 | 0.8002 |
| XGB5 | 0.5944 | 0.4593 | 0.8256 | 0.5967 | 0.4606 | 0.8189 |
| LGB5 | 0.5948 | 0.4588 | 0.8253 | 0.5953 | 0.4587 | 0.8197 |
| CAT5 | 0.5869 | 0.4521 | 0.8300 | 0.5795 | 0.4474 | 0.8292 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.6739 | 0.5376 | 0.7760 | 0.6697 | 0.5414 | 0.7719 |
| GBDT6 | 0.6135 | 0.4689 | 0.8141 | 0.6180 | 0.4750 | 0.8057 |
| XGB6 | 0.5963 | 0.4599 | 0.8247 | 0.5943 | 0.4594 | 0.8203 |
| LGB6 | 0.5949 | 0.4590 | 0.8255 | 0.5916 | 0.4574 | 0.8219 |
| CAT6 | 0.5881 | 0.4531 | 0.8294 | 0.5800 | 0.4500 | 0.8288 |
Table 10. Performance of Boosting-based models during 10-fold cross validation and testing stages at Kunming station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.4682 | 0.3851 | 0.8682 | 0.4675 | 0.3742 | 0.8841 |
| GBDT1 | 0.3507 | 0.2514 | 0.9264 | 0.3735 | 0.2696 | 0.9260 |
| XGB1 | 0.3415 | 0.2469 | 0.9301 | 0.3648 | 0.2624 | 0.9294 |
| LGB1 | 0.3408 | 0.2457 | 0.9303 | 0.3655 | 0.2616 | 0.9291 |
| CAT1 | 0.3338 | 0.2417 | 0.9331 | 0.3557 | 0.2538 | 0.9329 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.4430 | 0.3525 | 0.8816 | 0.5061 | 0.3937 | 0.8642 |
| GBDT2 | 0.4156 | 0.3253 | 0.8962 | 0.4346 | 0.3354 | 0.8998 |
| XGB2 | 0.4039 | 0.3168 | 0.9020 | 0.4199 | 0.3262 | 0.9065 |
| LGB2 | 0.4028 | 0.3158 | 0.9025 | 0.4166 | 0.3236 | 0.9079 |
| CAT2 | 0.3977 | 0.3106 | 0.9049 | 0.4110 | 0.3173 | 0.9104 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.5864 | 0.4690 | 0.7933 | 0.6212 | 0.4958 | 0.7953 |
| GBDT3 | 0.4982 | 0.3868 | 0.8503 | 0.5096 | 0.4015 | 0.8622 |
| XGB3 | 0.4887 | 0.3807 | 0.8559 | 0.4982 | 0.3925 | 0.8683 |
| LGB3 | 0.4871 | 0.3791 | 0.8569 | 0.4998 | 0.3941 | 0.8675 |
| CAT3 | 0.4785 | 0.3721 | 0.8618 | 0.4890 | 0.3819 | 0.8732 |
| Tmax, Tmin | ||||||
| ADA4 | 0.6290 | 0.5001 | 0.7630 | 0.6779 | 0.5351 | 0.7564 |
| GBDT4 | 0.5791 | 0.4494 | 0.7988 | 0.5890 | 0.4603 | 0.8161 |
| XGB4 | 0.5665 | 0.4437 | 0.8076 | 0.5785 | 0.4570 | 0.8226 |
| LGB4 | 0.5633 | 0.4398 | 0.8103 | 0.5720 | 0.4476 | 0.8266 |
| CAT4 | 0.5542 | 0.4314 | 0.8157 | 0.5620 | 0.4387 | 0.8325 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.6152 | 0.4864 | 0.7731 | 0.6373 | 0.5038 | 0.7845 |
| GBDT5 | 0.5087 | 0.3899 | 0.8448 | 0.5250 | 0.4059 | 0.8538 |
| XGB5 | 0.5007 | 0.3828 | 0.8498 | 0.5118 | 0.3947 | 0.8611 |
| LGB5 | 0.4996 | 0.3829 | 0.8504 | 0.5162 | 0.3982 | 0.8587 |
| CAT5 | 0.4914 | 0.3766 | 0.8551 | 0.4906 | 0.3768 | 0.8724 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.5392 | 0.4227 | 0.8254 | 0.5712 | 0.4467 | 0.8269 |
| GBDT6 | 0.4735 | 0.3662 | 0.8654 | 0.4933 | 0.3831 | 0.8709 |
| XGB6 | 0.4607 | 0.3561 | 0.8726 | 0.4772 | 0.3716 | 0.8792 |
| LGB6 | 0.4602 | 0.3558 | 0.8729 | 0.4772 | 0.3719 | 0.8792 |
| CAT6 | 0.4507 | 0.3486 | 0.8780 | 0.4624 | 0.3592 | 0.8866 |
Table 11. Performance of Boosting-based models during 10-fold cross validation and testing stages at Nanning station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.5397 | 0.4489 | 0.7728 | 0.5938 | 0.5139 | 0.7500 |
| GBDT1 | 0.4300 | 0.3023 | 0.8540 | 0.4247 | 0.3110 | 0.8721 |
| XGB1 | 0.4152 | 0.2952 | 0.8638 | 0.4043 | 0.3040 | 0.8841 |
| LGB1 | 0.4149 | 0.2935 | 0.8640 | 0.4016 | 0.3003 | 0.8857 |
| CAT1 | 0.4105 | 0.2916 | 0.8667 | 0.3932 | 0.2942 | 0.8904 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.5919 | 0.4837 | 0.7254 | 0.6139 | 0.4964 | 0.7327 |
| GBDT2 | 0.5260 | 0.4050 | 0.7812 | 0.4995 | 0.3778 | 0.8231 |
| XGB2 | 0.5169 | 0.4029 | 0.7893 | 0.4900 | 0.3797 | 0.8298 |
| LGB2 | 0.5104 | 0.3946 | 0.7942 | 0.4796 | 0.3649 | 0.8369 |
| CAT2 | 0.5060 | 0.3902 | 0.7978 | 0.4768 | 0.3638 | 0.8388 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.7424 | 0.6064 | 0.5696 | 0.7750 | 0.6370 | 0.5742 |
| GBDT3 | 0.6539 | 0.5113 | 0.6642 | 0.6455 | 0.5088 | 0.7045 |
| XGB3 | 0.6412 | 0.5036 | 0.6774 | 0.6376 | 0.5039 | 0.7118 |
| LGB3 | 0.6399 | 0.5023 | 0.6788 | 0.6377 | 0.5050 | 0.7116 |
| CAT3 | 0.6344 | 0.4972 | 0.6842 | 0.6323 | 0.4984 | 0.7165 |
| Tmax, Tmin | ||||||
| ADA4 | 0.7500 | 0.6074 | 0.5613 | 0.7671 | 0.6218 | 0.5830 |
| GBDT4 | 0.7145 | 0.5614 | 0.5995 | 0.7165 | 0.5661 | 0.6362 |
| XGB4 | 0.6923 | 0.5490 | 0.6247 | 0.6903 | 0.5587 | 0.6623 |
| LGB4 | 0.6903 | 0.5470 | 0.6280 | 0.6812 | 0.5478 | 0.6712 |
| CAT4 | 0.6847 | 0.5417 | 0.6327 | 0.6747 | 0.5444 | 0.6774 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.7374 | 0.5984 | 0.5752 | 0.7689 | 0.6298 | 0.5808 |
| GBDT5 | 0.6694 | 0.5241 | 0.6466 | 0.6677 | 0.5308 | 0.6839 |
| XGB5 | 0.6538 | 0.5146 | 0.6635 | 0.6482 | 0.5221 | 0.7021 |
| LGB5 | 0.6553 | 0.5168 | 0.6622 | 0.6472 | 0.5217 | 0.7030 |
| CAT5 | 0.6486 | 0.5108 | 0.6686 | 0.6401 | 0.5164 | 0.7095 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.7472 | 0.6066 | 0.5638 | 0.7834 | 0.6411 | 0.5648 |
| GBDT6 | 0.6390 | 0.4957 | 0.6792 | 0.6405 | 0.5047 | 0.7092 |
| XGB6 | 0.6236 | 0.4849 | 0.6948 | 0.6221 | 0.4959 | 0.7256 |
| LGB6 | 0.6245 | 0.4863 | 0.6941 | 0.6222 | 0.4949 | 0.7255 |
| CAT6 | 0.6165 | 0.4810 | 0.7011 | 0.6062 | 0.4833 | 0.7395 |
As shown in Table 3, CAT models generally achieved the best performance (on average RMSE of 0.5259 mm d-1, MAE of 0.3614 mm d-1 and Adj_R2 of 0.9168) among all the tested models with all input combinations at Harbin station (TMZ), followed by LGB (on average RMSE of 0.5430 mm d-1, MAE of 0.3671 mm d-1 and Adj_R2 of 0.9142) and XGB (on average RMSE of 0.5376 mm d-1, MAE of 0.3727 mm d-1 and Adj_R2 of 0.9128). The GBDT models could also achieve acceptable precision (on average RMSE of 0.5618 mm d-1, MAE of 0.3883 mm d-1 and Adj_R2 of 0.9041), while the original ADA models had the relatively worst performance (on average RMSE of 0.6597 mm d-1, MAE of 0.5077 mm d-1 and Adj_R2 of 0.8704).
During the 10-fold cross validation stage, models with M1(Rs) input (with RMSE ranged from 0.4288–0.5748 mm d-1, MAE ranged from 0.2871–0.4715 mm d-1, Adj_R2 ranged from 0.9019–0.9461) and M2(RH) input (with RMSE ranged from 0.4334–0.6108 mm d-1, MAE ranged from 0.2919–0.4857 mm d-1, Adj_R2 ranged from 0.8883–0.9446) performed the best. When only Tmax and Tmin data were inputted, models based on M4 input achieved the worst precision (with RMSE ranged from 0.4288–0.5748 mm d-1, MAE ranged from 0.2871–0.4715 mm d-1, Adj_R2 ranged from 0.8373–0.8726), followed by models based on M3(U2) input (with RMSE ranged from 0.5997–0.7052 mm d-1, MAE ranged from 0.4259–0.5417 mm d-1, Adj_R2 ranged from 0.8537–0.8940). It is worth to see that models based on M5(Ra) and M6(J), which are combinations of temperature data with Ra and J respectively, could achieve better performance than models based on M4 and even models based on M3 input. In addition, models based on M6 (with RMSE ranged from 0.5122–0.6429 mm d-1, MAE ranged from 0.3473–0.4783 mm d-1, Adj_R2 ranged from 0. 8782–0.9231) could obtain slightly better accuracy than models based on M5 (with RMSE ranged from 0.5224–0.6812 mm d-1, MAE ranged from 0.3507–0.5107 mm d-1, Adj_R2 ranged from 0.8632–0.9201).
The performance of tested models at Changsha station (SMZ) was demonstrated in Table 6. The accuracy ranking of various Boosting-based models was same as that of Harbin station, which was in the order of CAT, LGB, XGB, GBDT and ADA. However, the overall simulation accuracy suffered a slight decrease compared with the performance of models at Harbin station, the average Adj_R2 value of ADA, GBDT, XGB, LGB and CAT decreased by 13.02%, 11.22%, 10.00%, 10.00% and 9.72% respectively. Particularly, models based on M1 combination achieved the best precision (with RMSE ranged from 0.2746–0.4275 mm d-1, MAE ranged from 0.1959–0.3527 mm d-1, Adj_R2 ranged from 0.8976–0.9573),which was far ahead of models with other input combinations. The above results could also be found in the testing stage.
Table 6. Performance of Boosting-based models during 10-fold cross validation and testing stages at Ji’nan station.
| Models | 10 Fold cross validation results | Testing results | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | Adj_R2 | RMSE | MAE | Adj_R2 | |
| mm/d | mm/d | mm/d | mm/d | |||
| Tmax, Tmin, Rs | ||||||
| ADA1 | 0.7516 | 0.6139 | 0.8547 | 0.6986 | 0.5436 | 0.8637 |
| GBDT1 | 0.6115 | 0.4357 | 0.9047 | 0.5679 | 0.4050 | 0.9100 |
| XGB1 | 0.5977 | 0.4309 | 0.9089 | 0.5423 | 0.3940 | 0.9179 |
| LGB1 | 0.5924 | 0.4249 | 0.9106 | 0.5359 | 0.3870 | 0.9198 |
| CAT1 | 0.5861 | 0.4198 | 0.9124 | 0.5259 | 0.3789 | 0.9228 |
| Tmax, Tmin, RH | ||||||
| ADA2 | 0.8077 | 0.6538 | 0.8315 | 0.7889 | 0.6382 | 0.8262 |
| GBDT2 | 0.6413 | 0.4586 | 0.8952 | 0.6132 | 0.4384 | 0.8950 |
| XGB2 | 0.6143 | 0.4513 | 0.9034 | 0.5860 | 0.4360 | 0.9041 |
| LGB2 | 0.6124 | 0.4444 | 0.9042 | 0.5769 | 0.4209 | 0.9071 |
| CAT2 | 0.6044 | 0.4388 | 0.9066 | 0.5766 | 0.4204 | 0.9072 |
| Tmax, Tmin, U2 | ||||||
| ADA3 | 0.8731 | 0.6815 | 0.8043 | 0.8215 | 0.6502 | 0.8115 |
| GBDT3 | 0.7067 | 0.5301 | 0.8717 | 0.6672 | 0.5015 | 0.8757 |
| XGB3 | 0.6931 | 0.5226 | 0.8767 | 0.6472 | 0.4891 | 0.8830 |
| LGB3 | 0.6907 | 0.5206 | 0.8776 | 0.6454 | 0.4877 | 0.8837 |
| CAT3 | 0.6811 | 0.5126 | 0.8810 | 0.6334 | 0.4755 | 0.8880 |
| Tmax, Tmin | ||||||
| ADA4 | 0.9552 | 0.7496 | 0.7658 | 0.9106 | 0.7133 | 0.7686 |
| GBDT4 | 0.8563 | 0.6407 | 0.8135 | 0.8108 | 0.6155 | 0.8166 |
| XGB4 | 0.8500 | 0.6508 | 0.8159 | 0.7829 | 0.6107 | 0.8289 |
| LGB4 | 0.8330 | 0.6297 | 0.8240 | 0.7651 | 0.5826 | 0.8366 |
| CAT4 | 0.8204 | 0.6183 | 0.8287 | 0.7471 | 0.5705 | 0.8442 |
| Tmax, Tmin, Ra | ||||||
| ADA5 | 0.8630 | 0.6652 | 0.8089 | 0.8226 | 0.6402 | 0.8111 |
| GBDT5 | 0.7330 | 0.5349 | 0.8626 | 0.6907 | 0.5090 | 0.8668 |
| XGB5 | 0.7139 | 0.5236 | 0.8698 | 0.6723 | 0.4996 | 0.8738 |
| LGB5 | 0.7099 | 0.5200 | 0.8713 | 0.6629 | 0.4916 | 0.8773 |
| CAT5 | 0.7042 | 0.5146 | 0.8734 | 0.6520 | 0.4847 | 0.8813 |
| Tmax, Tmin, J | ||||||
| ADA6 | 0.8357 | 0.6445 | 0.8215 | 0.7851 | 0.6114 | 0.8279 |
| GBDT6 | 0.7259 | 0.5306 | 0.8654 | 0.6957 | 0.5156 | 0.8649 |
| XGB6 | 0.7044 | 0.5182 | 0.8732 | 0.6643 | 0.4957 | 0.8768 |
| LGB6 | 0.6978 | 0.5126 | 0.8757 | 0.6569 | 0.4898 | 0.8795 |
| CAT6 | 0.6877 | 0.5060 | 0.8791 | 0.6479 | 0.4801 | 0.8828 |
Table 12 showed the performance of tested models at Guangzhou station (TPMZ). Same performance ranking of tested models could also be found at Guangzhou station, but overall simulation accuracy suffered a more significant decrease, the average Adj_R2 value of ADA, GBDT, XGB, LGB and CAT decreased by 38.39%, 30.08%, 27.83%, 27.43 and 26.73% respectively, compared with those of models at Harbin station. In terms of effect of input combinations on modeling accuracy, models with M5 (with RMSE ranged from 0.6494–0.7622 mm d-1, MAE ranged from 0.5036–0.6171 mm d-1, Adj_R2 ranged from 0.4512–0.5992) performed slightly worse than models with M3 (with RMSE ranged from 0.6322–0.7658 mm d-1, MAE ranged from 0.4906–0.6215 mm d-1, Adj_R2 ranged from 0.4457–0.6207), while models with M6 (with RMSE ranged from 0.6171–0.7580 mm d-1, MAE ranged from 0.4745–0.6138 mm d-1, Adj_R2 ranged from 0.4574–0. 6382) still performed better than models with M3, while the effect of the other input combinations was generally the same as that of Harbin station and Changsha station.
In conclusion, CAT models could offer the highest accuracy among all tested models no matter under what input combination or at which station, followed by LGB and XGB models, which could also achieve relatively satisfactory precision. There is no doubt CAT1 based on Rs obtained the best performance and be highly recommend for estimating daily ET0 in this study area. However, CAT5 and CAT6 models based on only temperature data and partial geographic data could achieve acceptable accuracy with fewest meteorological variables, which can be regarded as more cost-effective and more conducive to promotion and application.
Comparison of model accuracy stability with different input combinations across 10 stations
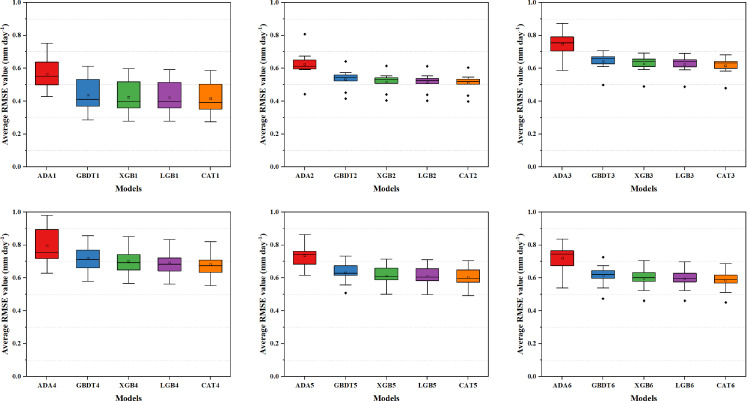
Fig 2 demonstrated the average RMSE values of Boosting-based models with various input combinations across 10 stations as a box plot. Because of the modeling accuracy of ADA models were much worse than the other Boosting-based models, the stability comparison employed in present study mainly focuses on GBDT, XGB, LGB and CAT models. Among the tested models, CAT model not only achieved the smallest average RMSE value, but also the most concentrated distribution of RMSE values regardless of the input combinations, which indicated that the CAT model had the best precision stability. The stability of the other three models is basically the same, thus the modeling accuracy should be the primary consideration when selecting one model for estimating ET0 among these 3 models. In terms of the effect of input combinations, taking CAT models as example, the RMSE values of CAT model based on M2 input obtained the minimal fluctuation (with RMSE ranged from 0.4334–0.6044) across 10 stations, followed by models based on M3, M6, M5, M4 and M1. It's also worth noting that although the accuracy of models with M1 input was the highest in each station, the accuracy gap between stations across different climate zones was the largest (with RMSE ranged from 0.2746–0.5861), which may as a result of the differences in the Rs distribution among each station and the different contribution of Rs to daily ET0 across various climate zones.
Fig 2. Average RMSE values of Boosting-based models at 10 stations under different input combinations.
The results of path analysis between meteorological variables and ET0 at 10 stations
Path analysis is a method proposed by Sewell Wright for studying the direct and indirect effects of independent variables on dependent variables and quantitatively analyzing the mutual influence degree of factors. Therefore, this study introduced path analysis to analyze the effect of Tmax, Tmin, RH, U2 and Rs on daily ET0. The results of path analysis between meteorological variables and ET0 across all stations were shown in Table 13.
Table 13. Path analysis between meteorological variables and ET0 at 10 stations.
| Meteorological Variables | Correlation Coefficient | Direct Effect | Indirect Effect | Contribution to R2 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Tmax | Tmin | RH | U2 | RS | Sum | ||||
| Harbin | |||||||||
| Tmax | 0.860 | 0.544 | - | 0.976 | -0.318 | -0.085 | 0.670 | 0.316 | 0.142 |
| Tmin | 0.787 | 0.003 | 0.976 | - | -0.216 | -0.097 | 0.567 | 0.784 | 0.000 |
| RH | -0.614 | -0.184 | -0.318 | -0.318 | - | -0.125 | -0.628 | -0.430 | 0.026 |
| U2 | 0.034 | 0.087 | -0.085 | -0.097 | -0.125 | - | -0.077 | -0.053 | 0.007 |
| RS | 0.865 | 0.390 | 0.670 | 0.567 | -0.628 | -0.077 | - | 0.475 | 0.749 |
| Shenyang | |||||||||
| Tmax | 0.829 | 0.565 | - | 0.968 | -0.016 | -0.039 | 0.598 | 0.264 | 0.164 |
| Tmin | 0.726 | 0.050 | 0.968 | - | 0.130 | -0.056 | 0.461 | 0.675 | 0.000 |
| RH | -0.442 | -0.236 | -0.016 | 0.130 | - | -0.087 | -0.527 | -0.205 | 0.038 |
| U2 | 0.117 | 0.136 | -0.039 | -0.056 | -0.087 | - | -0.040 | -0.019 | 0.018 |
| RS | 0.843 | 0.362 | 0.598 | 0.461 | -0.527 | -0.040 | - | 0.480 | 0.710 |
| Yan’an | |||||||||
| Tmax | 0.822 | 0.310 | - | 0.943 | -0.156 | -0.138 | 0.597 | 0.512 | 0.142 |
| Tmin | 0.673 | 0.256 | 0.943 | - | 0.068 | -0.148 | 0.388 | 0.417 | 0.004 |
| RH | -0.581 | -0.252 | -0.156 | 0.068 | - | -0.208 | -0.642 | -0.330 | 0.033 |
| U2 | 0.124 | 0.140 | -0.138 | -0.148 | -0.208 | - | 0.030 | -0.015 | 0.020 |
| RS | 0.870 | 0.420 | 0.597 | 0.388 | -0.642 | 0.030 | - | 0.450 | 0.757 |
| Jinan | |||||||||
| Tmax | 0.799 | 0.396 | - | 0.946 | -0.051 | -0.060 | 0.600 | 0.403 | 0.127 |
| Tmin | 0.643 | 0.190 | 0.946 | - | 0.176 | -0.124 | 0.417 | 0.453 | 0.002 |
| RH | -0.513 | -0.290 | -0.051 | 0.176 | - | -0.223 | -0.532 | -0.223 | 0.052 |
| U2 | 0.240 | 0.187 | -0.060 | -0.124 | -0.223 | - | 0.098 | 0.053 | 0.032 |
| RS | 0.856 | 0.366 | 0.600 | 0.417 | -0.532 | 0.098 | - | 0.490 | 0.732 |
| Nanjing | |||||||||
| Tmax | 0.765 | 0.294 | - | 0.936 | 0.015 | -0.137 | 0.504 | 0.471 | 0.144 |
| Tmin | 0.592 | 0.248 | 0.936 | - | 0.254 | -0.080 | 0.300 | 0.344 | 0.004 |
| RH | -0.485 | -0.299 | 0.015 | 0.254 | - | 0.135 | -0.524 | -0.186 | 0.038 |
| U2 | -0.091 | 0.133 | -0.137 | -0.080 | 0.135 | - | -0.237 | -0.224 | 0.017 |
| RS | 0.866 | 0.519 | 0.504 | 0.300 | -0.524 | -0.237 | - | 0.347 | 0.750 |
| Changsha | |||||||||
| Tmax | 0.776 | 0.012 | - | 0.930 | 0.019 | -0.176 | 0.610 | 0.764 | 0.070 |
| Tmin | 0.629 | 0.392 | 0.930 | - | 0.296 | -0.062 | 0.430 | 0.237 | 0.000 |
| RH | -0.343 | -0.227 | 0.019 | 0.296 | - | 0.239 | -0.378 | -0.117 | 0.012 |
| U2 | -0.133 | 0.133 | -0.176 | -0.062 | 0.239 | - | -0.265 | -0.266 | 0.015 |
| RS | 0.927 | 0.701 | 0.610 | 0.430 | -0.378 | -0.265 | - | 0.226 | 0.859 |
| Chengdu | |||||||||
| Tmax | 0.793 | 0.260 | - | 0.948 | -0.203 | -0.002 | 0.595 | 0.532 | 0.104 |
| Tmin | 0.639 | 0.146 | 0.948 | - | 0.029 | 0.028 | 0.426 | 0.493 | 0.001 |
| RH | -0.589 | -0.229 | -0.203 | 0.029 | - | -0.115 | -0.504 | -0.360 | 0.043 |
| U2 | 0.097 | 0.149 | -0.002 | 0.028 | -0.115 | - | -0.140 | -0.052 | 0.022 |
| RS | 0.895 | 0.583 | 0.595 | 0.426 | -0.504 | -0.140 | - | 0.312 | 0.801 |
| Kunming | |||||||||
| Tmax | 0.741 | 0.117 | - | 0.839 | -0.368 | -0.018 | 0.515 | 0.624 | 0.114 |
| Tmin | 0.374 | 0.289 | 0.839 | - | 0.102 | -0.165 | 0.114 | 0.085 | 0.008 |
| RH | -0.806 | -0.398 | -0.368 | 0.102 | - | -0.362 | -0.732 | -0.408 | 0.060 |
| U2 | 0.345 | 0.156 | -0.018 | -0.165 | -0.362 | - | 0.205 | 0.189 | 0.023 |
| RS | 0.878 | 0.462 | 0.515 | 0.114 | -0.732 | 0.205 | - | 0.416 | 0.771 |
| Nanning | |||||||||
| Tmax | 0.643 | 0.222 | - | 0.878 | 0.265 | -0.306 | 0.587 | 0.421 | 0.042 |
| Tmin | 0.402 | 0.256 | 0.878 | - | 0.579 | -0.263 | 0.409 | 0.146 | 0.006 |
| RH | -0.367 | -0.443 | 0.265 | 0.579 | - | -0.220 | -0.131 | 0.075 | 0.088 |
| U2 | -0.045 | 0.213 | -0.306 | -0.263 | -0.220 | - | -0.342 | -0.258 | 0.071 |
| RS | 0.865 | 0.645 | 0.587 | 0.409 | -0.131 | -0.342 | - | 0.220 | 0.748 |
| Guangzhou | |||||||||
| Tmax | 0.527 | 0.104 | - | 0.874 | 0.383 | -0.418 | 0.502 | 0.423 | 0.001 |
| Tmin | 0.270 | 0.348 | 0.874 | - | 0.694 | -0.293 | 0.285 | -0.078 | 0.069 |
| RH | -0.349 | -0.476 | 0.383 | 0.694 | - | -0.127 | -0.178 | 0.127 | 0.036 |
| U2 | -0.209 | 0.173 | -0.418 | -0.293 | -0.127 | - | -0.400 | -0.382 | 0.021 |
| RS | 0.909 | 0.741 | 0.502 | 0.285 | -0.178 | -0.400 | - | 0.168 | 0.826 |
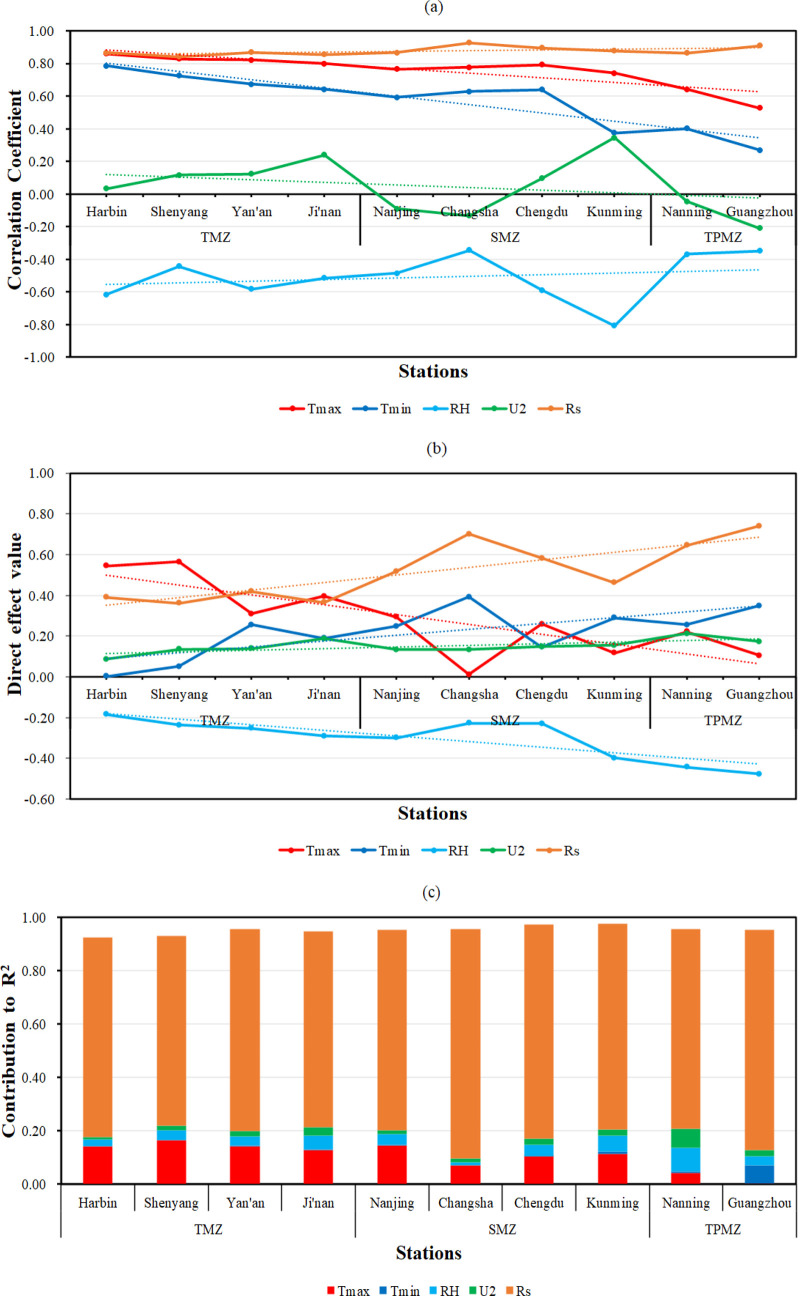
It could be found from Table 13 that except for RH and U2, the other 3 meteorological variables all had positive correlation coefficient to ET0 at all 10 stations. As illustrated in Fig 3A, the dashed line is the trend line of its corresponding meteorological variables. At stations in TMZ, the correlation coefficient of Tmax, Tmin, RH, U2 and Rs were 0.799–0.860,0.643–0.787,-0.442- -0.614,0.034–0.240 and 0.843–0.865 respectively. When it comes to stations in SMZ, the correlation coefficient of Tmax, Tmin, RH, U2 and Rs were 0.741–0.793,0.374–0.639,-0.343- -0.806, -0.091–0.345 and 0.866–0.927 respectively. And the correlation coefficient of Tmax, Tmin, RH, U2 and Rs were 0.527–0.643,0.270–0.402,-0.349- -0.367, -0.045–0.209 and 0.865–0.909 respectively at stations in TPMZ. It’s obvious to see that from Harbin station to Guangzhou station, the correlation coefficient of Tmax, Tmin, RH and U2 with ET0 showed decrease trend in general, while only Rs were on the contrary (increased from 0.749 at Harbin station to 0.826 at Guangzhou station), which indicated that the overall contribution of Rs on ET0 increased significantly and became more and more crucial for accurately estimating ET0 as the latitude of the station goes down in this study area.
Fig 3. Path analysis results of meteorological variables to daily ET0 across different stations.
(a) Correlation coefficient between meteorological variables and ET0 at 10 stations; (b) Direct effect of meteorological variables on ET0 at 10 stations; (c) The contribution of meteorological variables to R2 value at 10 stations.
The direct effects tendency of Tmax, Tmin, RH, U2 and Rs on ET0 across 10 stations was shown in Fig 3B. At Harbin station, Tmax contributed the largest direct effect (0.544), which was 0.154 more than Rs (0.390), but the direct effect of Tmin was almost none, only 0.003. As the station’s latitude goes down, the direct effect of Tmax showed a significant decrease, the direct effect of Tmin, RH (absolute value) and Rs had apparent rise, and that of U2 showed a slight rise. When it comes to Guangzhou station, the direct effect of Tmax only left 0.104, while the direct effect of Rs rose to 0.711 and Tmin exceeded Tmax to 0.348. This trend is similarly reflected in the overall contribution of variables to R2. It can be seen from Fig 3C, specially, as the second most contributing variable (0.142) at Harbin station, Tmax reduced to the least contributing variable (0.001)at Guangzhou station. On the contrary, Tmin, which is the least contributing variable at Harbin station (0.000), could offer a contribution to R2 of 0.069 at Guangzhou station. Other meteorological variables also gradually increase the contribution to the R2 of ET0 estimation results, as the latitude goes from north to south.
In conclusion, Rs had the greatest contribution to ET0, followed by Tmax, Tmin and RH, while U2 generally had the least effect on daily ET0. These results provided an explanation for the difference in the modeling accuracy of models with same input condition between stations across different climate zones and could also offer a reliable reference for selecting appropriate input combination for ET0 estimation in different climate zones.
Discussion
Effect of Ra and J on improving model accuracy
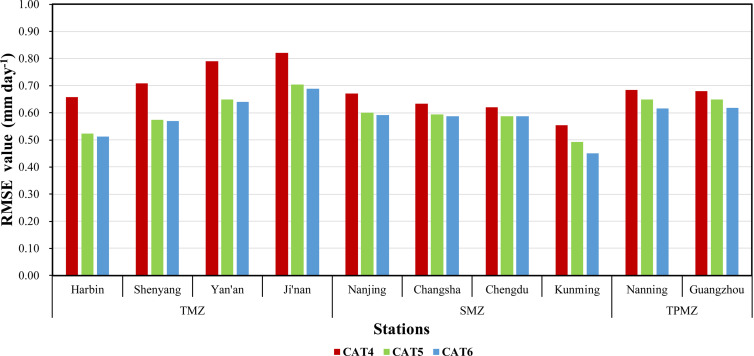
Ra has been proved that it can improve the estimation accuracy of daily ET0 when only limited meteorological variables are available [26,46–48]. As shown in Fig 4, taking CAT models as examples, CAT4 based on only temperature data could only obtain an average RMSE value ranging from 0.5542–0.8204 mm day-1, while the average RMSE values of CAT5 and CAT6 ranged from 0.4914–0.7042 mm day-1and 0.4507–0.6877 mm day-1 respectively. Compared with CAT4, employing Ra could make the average RMSE value decrease by 20.67%, 19.14%, 17.63%, 14.17%, 10.22%, 6.18%, 5.29%, 11.34%, 5.26% and 4.42% from Harbin to Guangzhou station, while using J could make that decreased by 22.22%, 19.79%, 18.93%, 16.18%, 11.72%, 7.33%, 5.10%, 18.67%, 9.95% and 9.17% respectively. It is obvious to see that CAT6 performed even better than CAT5 and this kind of improvement on modeling accuracy decreased as the station’s latitude decreases. This phenomenon may as a result of meteorological conditions of the stations in this study area are generally quite stable and ET0 is the result of the coupling effect of various meteorological variables, so J contains more overall information and variation pattern of ET0 than the single calculated Ra.
Fig 4. Comparison of the RMSE value of CAT4, CAT5 and CAT6 across 10 stations.
To sum up, the result of employing Ra with only temperature data for estimating ET0 in present study was also same as previous. As a parameter to calculate Ra, J could also improve the modeling accuracy with limited inputs and was even better than Ra. Therefore, models based on J input can be recommended for estimating ET0 when partial meteorological variables and geographical data are absent.
Strategy for selecting proper input combination at different stations
According to Tables 3–12 and the results of path analysis in 3.3, we can optimize the meteorological variables involved in the input combination at different stations. For example, Tmin has the least contribution to R2 and smallest direct effect on daily ET0 at Harbin station, thus Tmin could be removed from these input combinations without reducing the modeling accuracy. Similarly, Tmax could be removed from the input combinations at Guangzhou station due to the fact that it could hardly make contribution to the R2 value of the estimation results. The different model performance between various stations could also be explained by the path analysis results. Taking CAT models in 10-fold validation stage as examples, the correlation coefficient of RH and U2 at Kunming station are much higher than those at other stations, thus CAT2 model (with RMSE of 0.3977 mm d-1, MAE of 0.3106 mm d-1 and Adj_R2 of 0.9168) and CAT3 model (with RMSE of 0.4785 mm d-1, MAE of 0.3721 mm d-1 and Adj_R2 of 0.8618) achieved the highest precision compared with CAT2 and CAT3 models at other stations. In conclusion, the selection of the input combination for estimating daily ET0 should be based on the importance and contribution of meteorological variables at each single station, so as to make use of available meteorological variables more effectively to obtain better accuracy.
Conclusion
This study investigated 5 Boosting-based models, including original Adaptive Boosting(ADA), Gradient Boosting Decision Tree(GBDT), Extreme Gradient Boosting(XGB), Light Gradient Boosting Decision Tree (LGB) and Gradient boosting with categorical features support(CAT), for accurately estimating daily ET0 value with 6 different meteorological variables input combinations at 10 stations across the eastern monsoon zone of China. The results indicated that the CAT models had the highest accuracy and stability over all tested models under the same input combinations across all stations. And the LGB and XGB models could achieve very close accuracy, while original ADA models produced the worst performance. Under the condition of limited meteorological variables input, Rs definitely plays the most important role for accurately estimating daily ET0 value which makes the models based on M1 provide the best accuracy regardless of which station. Model with M2 input combination could offer the second highest precision, while models based on M4 (only temperature data) had the worst estimation accuracy. However, when Ra and J were employed with temperature data, the modeling accuracy increased significantly. The accuracy of models based on M6 generally ranked the third place (better than models with M3 input) and models based on M5 ranked the fifth place (much better than models with M4 input). Thus, in terms of improving the accuracy of the models with limited meteorological variables, J has better effect than Ra and is more easier to obtain in this study and the improvement brought by employing J was more and more significant as the latitude of the stations increases compared with employing Ra.
In summary, the CAT could be most highly recommended for estimating daily ET0 and J can be highly recommended for improving the accuracy of models when limited meteorological variables are available or geographical information is absent in the eastern monsoon zone of China.
Acknowledgments
We sincerely thank the National Climatic Centre of the China Meteorological Administration for providing the daily meteorological database used in this study.
Data Availability
The data underlying the results presented in the study are available fromNational Meteorological Information Center (NMIC) of China Meteorological Administration (CMA) (http://data.cma.cn/).
Funding Statement
This study is financially supported by National Natural Science Foundation of China (No: 51609064) and the Fundamental Research Funds for the Central Universities (B19020185).
References
- 1.Allen R, Pereira L, Raes D, Smith M. Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56; FAO-Food and Agriculture Organization of the United Nations, Rome (http://www. fao. org/docrep). ARPAV (2000), La caratterizzazione climatica della Regione Veneto, Quad. Geophysics. 1998;156: 178.
- 2.Antonopoulos VZ, Antonopoulos A V. Daily reference evapotranspiration estimates by artificial neural networks technique and empirical equations using limited input climate variables. Comput Electron Agric. 2017. 10.1016/j.compag.2016.11.011 [DOI] [Google Scholar]
- 3.Wu L, Fan J. Comparison of neuron-based, kernel-based, tree-based and curve-based machine learning models for predicting daily reference evapotranspiration. PLoS One. 2019. 10.1371/journal.pone.0217520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tabari H, Grismer ME, Trajkovic S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig Sci. 2013. 10.1007/s00271-011-0295-z [DOI] [Google Scholar]
- 5.Gu Z, Qi Z, Burghate R, Yuan S, Jiao X, Xu J. Irrigation Scheduling Approaches and Applications: A Review. J Irrig Drain Eng. 2020. 10.1061/(asce)ir.1943-4774.0001464 [DOI] [Google Scholar]
- 6.Allen RG, Jensen ME, Wright JL, Burman RD. Operational estimates of reference evapotranspiration. Agron J. 1989;81: 650–662. [Google Scholar]
- 7.Feng Y, Cui N, Gong D, Zhang Q, Zhao L. Evaluation of random forests and generalized regression neural networks for daily reference evapotranspiration modelling. Agric Water Manag. 2017. 10.1016/j.agwat.2016.07.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Falamarzi Y, Palizdan N, Huang YF, Lee TS. Estimating evapotranspiration from temperature and wind speed data using artificial and wavelet neural networks (WNNs). Agric Water Manag. 2014. 10.1016/j.agwat.2014.03.014 [DOI] [Google Scholar]
- 9.Xu JZ, Peng SZ, Zhang RM, Li DX. Neural network model for reference crop evapotranspiration prediction based on weather forecast. Shuili Xuebao/Journal Hydraul Eng. 2006. [Google Scholar]
- 10.Khoshhal J, Mokarram M. Model for prediction of evapotranspiration using MLP neural network. Int J Environ Sci. 2012;3: 1000. [Google Scholar]
- 11.Tabari H. Evaluation of reference crop evapotranspiration equations in various climates. Water Resour Manag. 2010. 10.1007/s11269-009-9553-8 [DOI] [Google Scholar]
- 12.Kisi O. Comparison of different empirical methods for estimating daily reference evapotranspiration in Mediterranean climate. J Irrig Drain Eng. 2013;140: 4013002. [Google Scholar]
- 13.Shih SF. Data requirement for evapotranspiration estimation. J Irrig Drain Eng. 1984;110: 263–274. [Google Scholar]
- 14.Allen RG. Self-calibrating method for estimating solar radiation from air temperature. J Hydrol Eng. 1997. 10.1061/(ASCE)1084-0699(1997)2:2(56) [DOI] [Google Scholar]
- 15.Alexandris S, Stricevic R, Petkovic S. Comparative analysis of reference evapotranspiration from the surface of rainfed grass in central Serbia, calculated by six empirical methods against the Penman-Monteith formula. Eur Water. 2008;21: 17–28. [Google Scholar]
- 16.Jensen M, Haise H. Estimating Evapotranspiration from Solar Radiation. Proc Am Soc Civ Eng J Irrig Drain Div. 1963. [Google Scholar]
- 17.Hargreaves GH, Samani ZA. Reference crop evapotranspiration from temperature. Appl Eng Agric. 1985;1: 96–99. [Google Scholar]
- 18.PRIESTLEY CHB, TAYLOR RJ. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon Weather Rev. 1972. [DOI] [Google Scholar]
- 19.Irmak S, Irmak A, Allen RG, Jones JW. Solar and net radiation-based equations to estimate reference evapotranspiration in humid climates. J Irrig Drain Eng. 2003. 10.1061/(ASCE)0733-9437(2003)129:5(336) [DOI] [Google Scholar]
- 20.Makkink GF. Testing the Penman formula by means of lysismeters. Int Water Eng. 1957. [Google Scholar]
- 21.Kumar M, Raghuwanshi NS, Singh R, Wallender WW, Pruitt WO. Estimating evapotranspiration using artificial neural network. J Irrig Drain Eng. 2002. 10.1061/(ASCE)0733-9437(2002)128:4(224) [DOI] [Google Scholar]
- 22.Abdullah SS, Malek MA, Abdullah NS, Kisi O, Yap KS. Extreme Learning Machines: A new approach for prediction of reference evapotranspiration. J Hydrol. 2015;527: 184–195. 10.1016/j.jhydrol.2015.04.073 [DOI] [Google Scholar]
- 23.Kişi Ö. Evapotranspiration modeling using a wavelet regression model. Irrig Sci. 2011. 10.1007/s00271-010-0232-6 [DOI] [Google Scholar]
- 24.Feng Y, Cui N, Zhao L, Hu X, Gong D. Comparison of ELM, GANN, WNN and empirical models for estimating reference evapotranspiration in humid region of Southwest China. J Hydrol. 2016. 10.1016/j.jhydrol.2016.02.053 [DOI] [Google Scholar]
- 25.Zheng H, Yuan J, Chen L. Short-Term Load Forecasting Using EMD-LSTM neural networks with a xgboost algorithm for feature importance evaluation. Energies. 2017. 10.3390/en10081168 [DOI] [Google Scholar]
- 26.Fan J, Yue W, Wu L, Zhang F, Cai H, Wang X, et al. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric For Meteorol. 2018. 10.1016/j.agrformet.2018.08.019 [DOI] [Google Scholar]
- 27.Kisi O. Modeling reference evapotranspiration using three different heuristic regression approaches. Agric Water Manag. 2016. 10.1016/j.agwat.2016.05.010 [DOI] [Google Scholar]
- 28.Kişi O, Çimen M. Evapotranspiration modelling using support vector machines. Hydrol Sci J. 2009. 10.1623/hysj.54.5.918 [DOI] [Google Scholar]
- 29.Wu L, Huang G, Fan J, Zhang F, Wang X, Zeng W. Potential of kernel-based nonlinear extension of Arps decline model and gradient boosting with categorical features support for predicting daily global solar radiation in humid regions. Energy Convers Manag. 2019. 10.1016/j.enconman.2018.12.103 [DOI] [Google Scholar]
- 30.Malik A, Kumar A, Kisi O. Monthly pan-evaporation estimation in Indian central Himalayas using different heuristic approaches and climate based models. Comput Electron Agric. 2017;143: 302–313. 10.1016/j.compag.2017.11.008 [DOI] [Google Scholar]
- 31.Shiri J, Nazemi AH, Sadraddini AA, Landeras G, Kisi O, Fakheri Fard A, et al. Comparison of heuristic and empirical approaches for estimating reference evapotranspiration from limited inputs in Iran. Comput Electron Agric. 2014. 10.1016/j.compag.2014.08.007 [DOI] [Google Scholar]
- 32.Mosavi A, Edalatifar M. A Hybrid Neuro-Fuzzy Algorithm for Prediction of Reference Evapotranspiration. Lecture Notes in Networks and Systems. 2019. 10.1007/978-3-319-99834-3_31 [DOI] [Google Scholar]
- 33.Mohammadi B, Mehdizadeh S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric Water Manag. 2020. 10.1016/j.agwat.2020.106145 [DOI] [Google Scholar]
- 34.Breiman L. Random forests. Mach Learn. 2001. 10.1023/A:1010933404324 [DOI] [Google Scholar]
- 35.Friedman JH. Greedy function approximation: A gradient boosting machine. Ann Stat. 2001. 10.2307/2699986 [DOI] [Google Scholar]
- 36.Chen T, Guestrin C. Xgboost: A scalable tree boosting system. Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. ACM; 2016. pp. 785–794.
- 37.Wang S, Fu Z, Chen H, Ding Y, Wu L, Wang K. Simulation of Reference Evapotranspiration Based on Random Forest Method. Nongye Jixie Xuebao/Transactions Chinese Soc Agric Mach. 2017. 10.6041/j.issn.1000-1298.2017.03.038 [DOI] [Google Scholar]
- 38.Huang G, Wu L, Ma X, Zhang W, Fan J, Yu X, et al. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J Hydrol. 2019. 10.1016/j.jhydrol.2019.04.085 [DOI] [Google Scholar]
- 39.Fan J, Ma X, Wu L, Zhang F, Yu X, Zeng W. Light Gradient Boosting Machine: An efficient soft computing model for estimating daily reference evapotranspiration with local and external meteorological data. Agric Water Manag. 2019. 10.1016/j.agwat.2019.05.038 [DOI] [Google Scholar]
- 40.Allen RG, Pereira LS, Raes D, Smith M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Fao, Rome. 1998;300: D05109.
- 41.Freund Y, Schapire R, Abe N. A short introduction to boosting. Journal-Japanese Soc Artif Intell. 1999;14: 1612. [Google Scholar]
- 42.Freund Y, Schapire RE. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J Comput Syst Sci. 1997. 10.1006/jcss.1997.1504 [DOI] [Google Scholar]
- 43.Ke G, Meng Q, Finley T, Wang T, Chen W, Ma W, et al. LightGBM: A highly efficient gradient boosting decision tree. Adv Neural Inf Process Syst. 2017;2017–Decem: 3147–3155. [Google Scholar]
- 44.Prokhorenkova L, Gusev G, Vorobev A, Dorogush AV, Gulin A. Catboost: Unbiased boosting with categorical features. Advances in Neural Information Processing Systems. 2018. [Google Scholar]
- 45.Landeras G, Ortiz-Barredo A, López JJ. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain). Agric water Manag. 2008;95: 553–565. [Google Scholar]
- 46.Valiantzas JD. Temperature-and humidity-based simplified Penman’s ET0 formulae. Comparisons with temperature-based Hargreaves-Samani and other methodologies. Agric Water Manag. 2018. 10.1016/j.agwat.2018.06.028 [DOI] [Google Scholar]
- 47.Yu T, Cui N, Zhang Q, Hu X. Applicability evaluation of daily reference crop evapotranspiration models in Northwest China. Paiguan Jixie Gongcheng Xuebao/Journal Drain Irrig Mach Eng. 2019. 10.3969/j.issn.1674-8530.18.0256 [DOI] [Google Scholar]
- 48.Feng Y, Peng Y, Cui N, Gong D, Zhang K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput Electron Agric. 2017. 10.1016/j.compag.2017.01.027 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data underlying the results presented in the study are available fromNational Meteorological Information Center (NMIC) of China Meteorological Administration (CMA) (http://data.cma.cn/).