Constrained Optimization for the Selection of Influenza Vaccines to Maximize the Population Benefit: A Demonstration Project

Abstract

Background

Influenza is an infectious disease causing a high annual economic and public health burden. The most efficient management of the disease is through prevention with vaccination. Many influenza vaccines are available, with varying efficacy and cost, targeting different age groups. Therefore, strategic decision-making about which vaccine to deliver to whom is warranted to improve efficiency.

Objective

We present the use of a constrained optimization (CO) model to evaluate targeted strategies for providing influenza vaccines in three adult age groups in the USA.

Methods

CO was considered for identifying an influenza vaccine provision strategy that maximizes the benefits at constrained annual budgets, by prioritizing vaccines based on return on investment. The approach optimizes a set of predefined outcome measures over several years resulting from an increasing investment using the best combination of influenza vaccines.

Results

Results indicate the importance of understanding the relative differences in benefits for each vaccine type within and across age groups. Scenario and threshold analyses demonstrate the impact of changing budget distribution over time, price setting per vaccine type, and selection of outcome measure to optimize.

Conclusion

Significant gains in cost efficiency can be realized for a decision maker using a CO model, especially for a disease like influenza with many vaccine options. Testing the model under different scenarios offers powerful insights into maximum achievable benefit overall and per age group within the predefined constraints of a vaccine budget.

Electronic supplementary material

The online version of this article (10.1007/s40258-019-00534-y) contains supplementary material, which is available to authorized users.

Key Points for Decision Makers

While the number of influenza vaccines available on the market is expected to stay high, health authorities struggle with prioritizing the introduction of new vaccines in view of real-life budgetary limitations in their regions.

We developed a methodology for assessing which influenza vaccines should be introduced and in what chronological order (i.e., vaccine ranking) to achieve the greatest possible benefit while still complying with the constraints of a multi-year financial plan.

This optimization method makes a justifiable economic argument by comparing the results generated by this model with those generated from a process where no programmed vaccine selection was made (i.e., an “uninformed” selection process).

We applied this model to the USA setting and explain in detail the model working and its relevance.

Introduction

Seasonal influenza is a highly contagious infectious disease causing illness across all age groups and social classes, and inducing a significant disease burden that depends on the combination of circulating virus strains and the measures taken to tackle the ensuing public health problem [1]. Prevention through vaccination is considered the best option for reducing influenza-related morbidity and mortality since anti-viral drugs are only effective when they are administered during early disease stages and influenza is often diagnosed in later stages [2].

Nevertheless, the regular viral mutation processes complicate the development of the vaccines and require annual vaccination with a vaccine customized to each season-specific wildtype strain circulation [3]. To overcome eventual weak responses, researchers developed adjusted vaccines with a higher dose of antigen, improved adjuvants, and/or more strains, resulting in many influenza vaccines being available on the market today [4].

Estimates of the total annual economic disease burden are not frequently reported at country level in the literature, except for in the USA, where the burden measured at different time points remains high [5–8]. Therefore, the Advisory Committee on Immunization Practices (ACIP) in the USA expanded its recommendations for influenza vaccination from specific high-risk groups to the entire population [9, 10] without recommending a specific vaccine over the other. The UK is following the same strategy [11], but the other European countries have not.

Given the widespread vaccine recommendation and the variation between vaccines’ effectiveness, cost, and age indication, healthcare payers and decision-makers could benefit from an economic evaluation method and model that identify a strategy for implementing an overall influenza vaccine program in the most cost-efficient way across the whole population.

The proposed method uses constrained optimization (CO) to identify the best combination of vaccines across the age groups for optimizing health outcomes, while considering multiple constraints [12]. The proposed model, an influenza-specific CO model, called the Portfolio Model for Management of Flu-Vaccines (PMMFV), has been developed, and addresses the specific needs listed above.

What follows is a detailed explanation of the model and its application to the USA, where data on influenza disease are available and multiple influenza vaccines are approved.

The aim of this study was not to make recommendations about specific strategies for the USA or other countries to follow; the exercise gives hints on what to expect and how to explore additional useful information with such a model. The influenza vaccine market is dynamic and versatile with the selection of available vaccines changing yearly, and local demographics and constraints vary considerably. The model construct and data inputs need to be adapted and adjusted to local conditions to better assess local recommendations for being more cost and allocative efficient in an overall influenza vaccination program.

Methods

The PMMFV allows for including six influenza vaccines to be administered to different age groups by year. It optimizes a specific measure of overall public health impact with a combination of vaccines given some constraints. These constraints reflect limitations on the maximum spending for influenza vaccination per year and a feasible coverage per age group. Measures of public health impact include influenza cases, medical visits, hospitalization-days, deaths, quality-adjusted life years (QALYs), and disease-management costs due to influenza.

The model considers up to ten vaccination strategies at a time, where a strategy is defined by an age group and a specific vaccine attributed to it. Only vaccines approved for each age group are considered. Vaccines are defined by their effectiveness in preventing symptomatic influenza for each targeted age group and by the total cost of vaccinating one person. A maximum budget for spending across all age groups for each year is specified, and its allocation to the vaccination strategies is optimized for achieving a maximum reduction impact on disease burden over the model’s time horizon. The mathematical formulation of the functional objective of outcome optimization is available in Supplementary Material Table A1.

Baseline Numbers

Outcomes in the absence of any vaccination are calculated using a multi-cohort model (Microsoft Excel, Microsoft, Redmond, WA, USA) following the annual progression of the total population until the end of the selected time horizon or until individuals reach the age of 100 years, whichever comes first.

The number of influenza cases in the total population is calculated annually, measuring the total disease burden, as well as influenza-related outcomes: medical visits, hospitalization days, and deaths. Each year, the number of medical visits and hospitalization days are multiplied by their unit costs to obtain the total annual cost of disease management. Annual mortality-related QALY-loss is estimated by multiplying influenza deaths per year of age with their quality-adjusted life expectancy at the age of death [13]. The annual number of cases per age group are multiplied by their QALY-loss per influenza case and the annual number of hospitalization-days by their incremental QALY-loss to obtain the total morbidity-related QALY-loss. Those totals are then summed with mortality-related QALY-loss to obtain total annual QALY-loss.

The effect of vaccination is implemented via a reduction in the number of influenza cases versus those that occur in the absence of vaccination. It is determined by the effect of the vaccine in the targeted age group as well as by the coverage achieved. Adverse events (AEs) associated with vaccination are not considered in the analysis.

Methods for Identifying the Strategies to be Selected

The PMMFV first calculates for each of the ten vaccination strategies the total cumulative vaccination cost and the maximum achievable reduction in the selected outcome over a pre-specified time horizon, in the absence of any constraint.

A strategy is considered as being dominated and eliminated from further assessment if an alternative for that same age group results in higher cumulative gains at an equal or lower vaccination cost. The remaining strategies are then ranked by their return on investment (ROI), measured by the estimated reduction in the outcome measure selected per dollar spent in vaccination.

Within the same age group, a lower ranked vaccine implies that it provides more benefits (i.e., is more effective) than a higher ranked vaccine but requires a relatively higher investment compared with its relative benefit gains.

Funding allocation starts with the vaccination strategy having the highest ROI, i.e., being ranked first, until (1) its vaccine coverage reaches the maximum achievable coverage for that age group, or (2) the entire vaccination budget is spent, whichever event occurs first.

If budget remains after the first-ranked strategy is funded to maximum achievable coverage level, the second ranked vaccination strategy is considered. If this vaccination strategy targets another age group, the same funding principle is applied. If the second-ranked strategy targets the same age group as the first-ranked strategy, the first-ranked vaccine will be replaced by the more expensive one and only the incremental budget required to switch between vaccines will be allocated to that age group.

This process is consecutively repeated throughout the range of ranked vaccines until all the vaccination budget is spent. Hence, as soon as the maximum achievable coverage of an age group is attained with the highest ranked vaccine, the optimization algorithm will consider the next option with the highest ROI so that either it is initiating vaccination in another age group and then the absolute benefits and vaccination costs of this vaccination strategy are accounted for, or it is replacing the already implemented vaccine with the next ranked one in the same age group and then only its marginal benefits and the incremental cost of switching to the next ranking vaccine are accounted for.

To demonstrate the application of the PMMFV, an analysis for the USA was conducted with a 10-year budget time horizon. Estimates for model inputs defining the population and the vaccines were derived from published literature.

Population

The population sizes by age at the start of the analysis are derived from the Centers for Disease Control and Prevention (CDC) [14]. Each subsequent year, a new birth cohort (with the same size as those aged < 1 year in the initial population) is added and the remaining population is aged by 1 year and reduced in size due to all-cause mortality and influenza-related mortality [6, 15]. Disease-specific mortality reduction in cardio-vascular or pulmonary disease due to influenza is not considered. Migration is not considered.

The population is divided into ten age groups (0–5 months, 6 months–1 year, 2 years, 3 years, 4 years, 5–8 years, 9–17 years, 18–49 years, 50–64 years, and 65–99 years). These age boundaries were determined by specific age-dependent influenza vaccine recommendations and/or differences in vaccine efficacy estimates. For each age group, all individuals or only a defined at-risk subgroup can be targeted for vaccination.

The example analysis presented here only considers influenza vaccination targeted to three adult age groups in the USA: 18–49 years, 50–64 years, and 65–99 years. If all age groups and all options were considered it would have been more difficult to clarify the selection procedures made by the model.

Vaccination Strategies

The ten strategies included in this analysis are presented in Table 1. The different vaccines considered are quadrivalent influenza vaccine [QIV] [16], recombinant QIV [17], trivalent influenza vaccine [TIV] [18], TIV-high dose [HD] [19], QIV cell culture-derived [20], and adjuvanted TIV [21].

Table 1.

Vaccination strategies considered in this example analysis

Vaccination strategy	Age group, population vaccinated (years)	Vaccine name	Maximum achievable coverage (%)a	Vaccine effectiveness (%)b	Cost of vaccination (per person)c,d
TIV 18–49 years	18–49	TIV	35.0	62.0	$38.35
QIV 18–49 years	18–49	QIV	35.0	64.7	$38.67
TIV 50–64 years	50–64	TIV	45.0	62.0	$38.35
QIV 50–64 years	50–64	QIV	45.0	64.7	$38.67
Adj TIV 50–64 years	50–64	Adj TIV	45.0	73.7	$68.96
QIV 65 years+	65–99	QIV	65.0	61.5	$38.67
QIV CCD 65 years+	65–99	QIV CCD	65.0	61.5	$45.67
Recom QIV 65 years+	65–99	Recom QIV	65.0	73.7	$58.34
TIV HD 65 years+	65–99	TIV high dose	65.0	69.2	$67.82
Adj TIV 65 years+	65–99	Adj TIV	65.0	73.7	$68.96

Adj adjuvant, CCD cell culture-derived, HD high–dose, Recom Recombinant, TIV trivalent influenza vaccine, QIV quadrivalent influenza vaccine, CDC Centers for Disease Control and Prevention, CPT Current Procedural Terminology, WAC wholesale acquisition cost

^aBased on approximate influenza coverage rates achieved in the US over the last 10 seasons [23]

^bSee Appendix Table A1 for vaccine effectiveness calculations by age and vaccine type. Vaccine effectiveness = % reduction in influenza cases. Those numbers can change significantly from year to year in absolute but also in relative value due to potential mismatch

^cIncludes the cost of vaccine and vaccine administration. Cost of vaccine is based on an average vaccine price across all available vaccines by vaccine type (e.g., QIV vaccines in the USA in 2018–2019) from the CDC Vaccine Price List for Adults, private price [24]. Vaccine administration costs ($20.88) are based on CPT code 90471 [25]

^dRed Book 2018, Fluad 2018–2019 formula weighted average cost (of WAC) price is used for Adj TIV [26] (“IBM Micromedex RED BOOK” 2018). Fluzone high-dose 2018–2019 formula WAC is used for TIV High dose. Afluria 2018–2019 formula WAC is used for TIV vaccines, as no TIV vaccines are listed in 2018–2019 CDC Vaccine Price List, and no other TIV vaccines had 2018–2019 formulas listed in Red Book

All TIVs include an average annual risk of a mismatch (i.e., not optimally covering the circulating influenza B virus strains) of 53.1%, calculated based on CDC surveillance data in the USA [22]. The risk of mismatch lowers expected vaccine effectiveness compared to that of QIVs, which better cover all circulating strains (see Supplementary Material Table A2 for calculation).

Data Inputs

Table 2 lists the additional data requirements for the PMMFV together with their estimates applied in this example analysis. Those inputs include symptomatic influenza incidence rates, clinical pathways of influenza cases, unit costs associated with disease management, and QALY losses associated with influenza outcomes.

Table 2.

Influenza-related parameter estimates used in the example analysis

Parameter	Age group			References
	18–49 years	50–64 years	65–99 years
Annual per-person clinical influenza incidence in the absence of vaccination (all symptomatic cases)	0.073	0.073	0.093	Average over 9 seasons [27–29]
% of clinical cases requiring GP visit or outpatient treatmenta	38.4%	38.4%	43.3%	Average over 9 seasons [27–29]
% of clinical cases requiring hospitalization	0.7%	0.7%	4.9%
% of clinical cases resulting in death	0.009%	0.134%	1.17%	[6]
Costs (2018 US$)b				[6]; inflated from 2003 US$ to 2018 US$ using medical care component of CPI
Cost per GP visit/outpatient treatment	$343	$548	$579
Cost per hospitalization	$37,261	$45,717	$22,661
QALY losses				Derived from [22]
QALYs lost per influenza case	0.0060	0.0063	0.0048
Incremental QALYs lost per hospitalized case	0.0054	0.0052	0.0045

CPI consumer price index, GP general practitioner, US$ United States dollars, QALY quality-adjusted life year

^aCalculated as residual 1 minus the probability of hospitalization minus the probability of a non-medically attended case

^bNo incremental costs are assigned to influenza-related deaths, to avoid double counting: the cost of death is assumed to be covered in the average cost estimates for outpatient treatment and hospitalization

Maximum budgets for vaccination are defined for each calendar year included in the time horizon of 10 years. In this case, we started with a low vaccination budget of US$1.5 billion in Year 1. This budget was annually increased by a fixed amount of US$570 million, ultimately resulting in a vaccination budget of US$6.63 billion in Year 10, the amount that is exactly sufficient to fully cover the most expensive vaccines for all three age groups.

Costs and outcome measures in the model were not discounted since nominal budgets were evaluated each year and no overall value assessment of the vaccination program was considered.

Optimization of Influenza Vaccine Budget Investments

We applied the objective of minimizing QALY losses (equivalent to maximizing QALY gains) over a time horizon of 10 years, within the constraints of the annually defined vaccination budget and the maximum achievable vaccination coverage in each of the three targeted age groups. The model was used to determine the annual coverages of each vaccination strategy that minimize the QALY losses.

We then compared the outcome results of the optimized set of strategies with those resulting from an alternative allocation of the same annual budget to a random selection of vaccination strategies, irrespective of their ROI, i.e., vaccination strategies were ranked randomly and budgets were sequentially allocated according to this uninformed ranking. This comparison will demonstrate the potential benefits of an optimized versus a random approach to allocating a budget.

Scenario, Threshold, and Additional Analyses

Scenario analyses were conducted for the example to assess the impact of the following on the optimal set of vaccine strategies: (1) higher annual vaccination budgets by doubling the amount; (2) reducing the level of vaccine mismatch for TIVs to that of QIVs and; (3) optimizing each of the other options for health outcome measures, including minimizing influenza cases, medical visits, hospitalization days, deaths, and disease-management costs.

We performed threshold analyses to determine the vaccination cost at which the dominated TIV high-dose 65 years+ vaccination strategy, was no longer dominated by the alternatives.

Finally, we calculated the incremental costs of funding the combination of the most effective strategy in each age group at maximum achievable coverage versus the combination of the second most effective alternative in each age group. The intent was to balance the marginal benefits achieved with the most effective but costlier vaccines against their supplementary budget requirement.

Results of Example Analysis

Outcomes for Each Strategy with 100% Vaccine Coverage

Table 3 reports the maximum QALYs to be gained by applying the most efficacious vaccination strategy at 100% coverage in each age group, the maximum achievable gain per vaccination strategy, the relative maximum contribution of each vaccination strategy in attaining the maximum achievable QALY gains across all age groups, the vaccination cost with 100% vaccine coverage, the percentage gain in QALYs per US$10 billion invested, and the percentage gain per 100 million vaccinated persons.

Table 3.

Cumulative QALY gains and required vaccination costs for each of the ten vaccination strategies at 100% coverage and over the time-horizon of 10 years

	Maximum achievable QALYs gained, i.e., with the most effective vaccination strategy at 100% coverage	Vaccination strategy
		TIV 18–49 years	QIV 18–49 years	TIV 50–64 years	QIV 50–64 years	Adj TIV 50–64 years	QIV 65 years+	QIV CCD 65 years+	Recom QIV 65 years+	TIV HD 65 years+	Adj TIV 65 years+
# vaccinees		1,371,807,436	1,371,807,436	620,921,647	620,921,647	620,921,647	580,675,667	580,675,667	580,675,667	580,675,667	580,675,667
Age groups and QALYs gained		Maximum achievable QALYs by vaccination strategy at 100% coverage
18–49 years	636,318	609,632	636,318
50–64 years	1,212,329			1,019,832	1,064,483	1,212,329
65–99 years	5,363,847						4,476,302	4,476,302	5,362,494	5,032,342	5,363,847
Total QALYs gained for 18–99 years	7,212,494
Relative maximum achievable QALYs vs. 18–99 years		8.45%	8.82%	14.14%	14.76%	16.81%	62.06%	62.06%	74.35%	69.77%	74.37%
Vaccination cost		$52,608,815,160	$53,047,831,345	$23,812,131,251	$24,011,040,080	$42,820,030,302	$22,454,728,035	$26,516,585,100	$33,891,769,276	$39,393,300,421	$40,062,669,268
Relative QALY gain per $10 billion invested		1.61%	1.66%	5.94%	6.15%	3.93%	27.64%	23.41%	21.94%	17.71%	18.56%
Relative QALY gain per 100 million vaccinees		0.62%	0.64%	2.28%	2.38%	2.71%	10.69%	10.69%	12.80%	12.02%	12.81%

Bold numbers show the relative QALY gain per US dollar invested and per vaccinated person highest for that age group

Adj adjuvanted, CCD cell culture-derived, HD high-dose, Recom recombinant, QIV quadrivalent influenza vaccine, TIV trivalent influenza vaccine, QALY quality-adjusted life year

The highest QALY gain from vaccination is achieved in the oldest age group despite their smallest population size. The relative QALY gain per US dollar invested and per vaccinated person is therefore highest for that age group (bold numbers in Table 3). Among the strategies targeting the elderly, the relative gain per dollar invested (ROI) is highest for QIV 65 years+ (27.64%) and lowest for TIV HD 65 years+ (17.71%).

Optimization Results

Of the ten strategies considered, only six were allocated funding during the time horizon of 10 years (QIV 65 years+, QIV 50–64 years, QIV 18–49 years, Recombinant QIV 65 years+, Adjuvanted TIV 65 years+ and Adjuvanted TIV 50–64 years) (Fig. 1). The remaining ones were excluded because they were dominated by other strategies (TIV 18–49 years, TIV 50–64 years, QIV cell culture-derived 65 years+, and TIV High Dose 65 years+), i.e., they could not provide a higher number of QALYs gained compared with an alternative vaccination strategy with a better ROI in the same age group. In each age group, the top-ranked vaccine based on ROI was QIV (i.e., strategies QIV 65 years+, QIV 50–64 years, QIV 18–49 years, respectively). The eldest age group was first selected for vaccination because the highest ROI of vaccination is achieved in that age group.

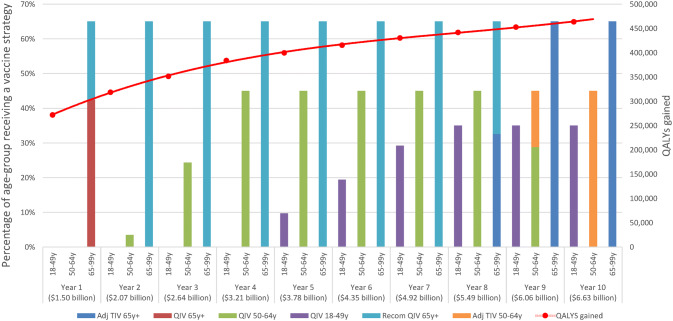
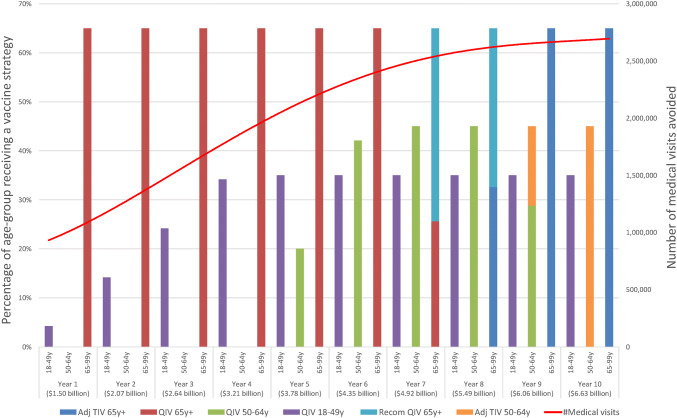
Fig. 1.

Annual vaccination strategy coverage (bars) and QALYs gained (solid red line) resulting from the best allocation of funding to minimize QALY losses from influenza. Adj adjuvanted, Recom recombinant, QIV quadrivalent influenza vaccine, TIV trivalent influenza vaccine, QALY quality-adjusted life year

Figure 1 shows that with a budget of US$1.5 billion in the first year and an annual increase of US$570 million over the remaining time horizon, its allocation across vaccination strategies changes over time. In Year 1, the maximum achievable coverage of 65% was obtained for the oldest age group; with a combination of QIV and the more-expensive-but-more-effective recombinant QIV, 272,068 QALYs were gained, which is the maximum gain that can be achieved with a vaccination budget of US$1.5 billion. The higher budget in Year 2 resulted in a complete replacement of QIV by the more expensive recombinant QIV in the 65 years+ age group. The remaining budget was allocated to the 50–64 years age group where QIV was initiated as being the subsequent option with the highest ROI.

With annually increasing budget, the maximum achievable coverage in the 50–64 years age group was reached with QIV in Year 5. With the remaining budget, vaccination with QIV was initiated in the youngest age group. From Year 8 onwards, all age groups reached their maximum achievable coverage and both recombinant QIV 65 years+ and QIV 50–64 years were gradually replaced by costlier strategies that could provide additional QALY gains but at a lower ROI. The annually increased funds were shifted to those costlier strategies so that by Year 10 the most expensive non-dominated strategies of Adjuvanted TIV 65 years+, QIV 18–49 years and Adjuvanted TIV 50–64 years were funded, resulting in a total of 463,591 QALY gains, which is the maximum achievable with a vaccination budget of US$6.63 billion in Year 10.

Despite a linear annual increase in funding, the resulting increase in QALYs (dotted line in Fig. 1) slows down over time, reflecting decreasing marginal returns from the strategies funded in later years. This observation is logical, given that the strategies funded first have the highest ROI.

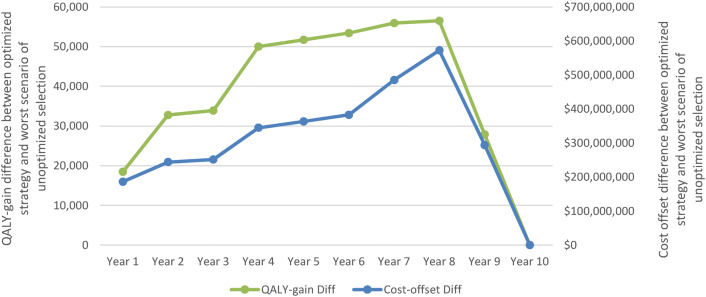
When comparing the optimized allocation to the worst scenario of unoptimized conditions while keeping the budget equivalent, we found that the benefits of considering ROI varied over the time horizon as well as for the selected outcome measure to maximize (e.g., savings in disease management costs). The worst selection, different from the allocation focusing on benefit maximization, never resulted in better outcomes in any calendar year of the time horizon (Fig. 2). When sufficient budget was available in Year 10 to fund the most effective but most expensive strategies for all three age groups, the same allocation was applied in both methods and the resulting outcomes were the same.

Fig. 2.

QALY gain difference and disease management cost-offset difference between an optimized vaccination strategy versus the worst scenario of unoptimized condition, with the same total budget allocation over time as described in Fig. 1. Diff difference in outcome between strategies: optimized versus random allocation, QALY quality-adjusted life year

Scenario, Threshold, and Additional Analyses

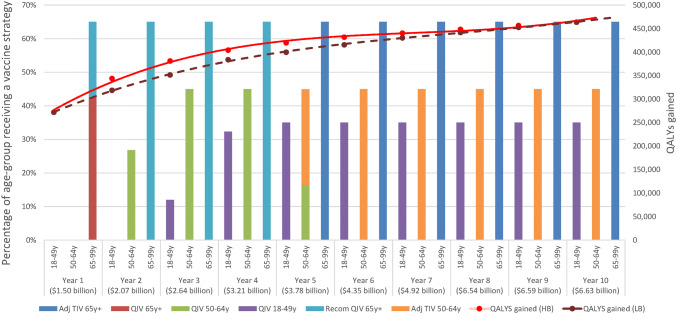
Increasing the annual vaccination budget resulted in an earlier funding of the more expensive (and more effective) non-dominated vaccination strategies. Figure 3 represents a situation in which the annual budget increase is twice as high as in the base-case, i.e., US$1,140 million instead of US$570 million. In this situation, the maximum benefit will be reached earlier (Fig. 3: solid red line representing higher budget versus brown dotted line representing lower base-case budget; dotted line is equal to the solid red line in Fig. 1). Depending on the amount of budget increase, the total number of different vaccination strategies implemented during the time horizon of 10 years can be reduced from six to three (not shown in the figure). The latter represents a situation in which the budget in Year 1 is already sufficiently high to attain the maximum achievable coverage in each age group with the most expensive non-dominated vaccine.

Fig. 3.

Annual vaccination strategy coverage (bars) and associated QALYs gained (red solid line (higher fund) and brown dotted line (lower fund)) resulting from best allocation of the funding at start to minimize QALY losses from influenza with an increased annual vaccination budget compared with base-case. Adj adjuvanted, Recom recombinant, QIV quadrivalent influenza vaccine, TIV trivalent influenza vaccine, QALY quality-adjusted life year, HB high budget, LB lower (base-case) budget

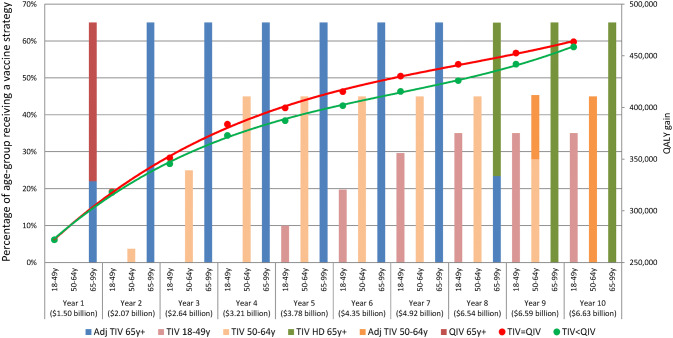
When varying the TIV’s degree of mismatch with the circulating B-strains in the two age groups < 65 years, we found that with a perfect match resulting in TIV’s effectiveness being equivalent to QIV’s, the model ranked the TIVs before QIVs. QIV will be dominated by TIV because of its slightly higher price. TIVs normally include an average annual risk of a mismatch (i.e., not optimally covering the circulating influenza B virus strains) of 53.1%, calculated based on CDC surveillance data in the USA [22], and a perfect match with circulating B-strains is in fact rare. The risk of mismatch lowers the expected vaccine effectiveness compared with QIVs, that better covers all circulating strains (see Supplementary Material Table A1 for calculation). Figure 4 indicates what happens when TIV dominates with the QALY-gain equivalent to the selection of QIV (red line). The green line is the QALY-gain when TIV has the average mismatch (note: the coverages reflected in the bar chart only reflect those of a situation with perfect match). In a situation of a perfect match between the cheaper TIVs and circulating B-strains, more budget remains available to spend on non-dominated lower ranking vaccination strategies that are more efficacious but at a relatively higher cost. This is reflected in more QALY gains compared to a situation where QIV dominates TIV because of its lower efficacy in a situation with average mismatch.

Fig. 4.

Annual vaccination strategy coverage (bars) resulting from the best allocation of TIV with perfect match (equal effectiveness as QIV) in < 65-year-old adults to minimize QALY losses from influenza. Adj adjuvanted, Recom recombinant, QIV quadrivalent influenza vaccine, TIV trivalent influenza vaccine, QALY quality-adjusted life year

Meanwhile, the shift from QIV 65 years+ to Recombinant QIV 65 years+ as seen in Fig. 1 before funding TIV vaccination in another age group, was instigated by the better ROI of replacing QIV with Recombinant QIV among those elderly compared with the ROI of initiating any vaccine in any younger age group.

When the model optimized alternate outcome measures (e.g., minimizing the number of influenza cases), the vaccination strategies funded over the time horizon varied. The budget allocation differed for an approach where influenza cases or outpatient medical visits were minimized compared with those where other outcomes were optimized (e.g., minimize influenza hospitalizations, minimize influenza deaths, maximize QALYs gained). The reason for these differences is likely due to the more equal spread of the former across the different age groups compared with the latter outcomes. For instance, hospitalizations are much more frequent in the elderly, by which more offset can be obtained within that age group when introducing a vaccine and by which a costlier vaccine can be used within that age group.

The difference between the outcome measures selected and the vaccine selection is illustrated in the comparison of Fig. 1 with Fig. 5. In the latter figure, medical visits were minimized. Like the allocation strategy aiming to minimize QALY losses (Fig. 1), the QIV strategies were funded first. When medical visits were minimized, however, the youngest age group was funded earlier and in the 65 years+ age group replacement of the QIV vaccine by a costlier one occurred later in time. We also observed that alternative objectives resulted in higher incremental increases in the objective with increased funding (as represented by a steeper slope of the red line in Fig. 5).

Fig. 5.

Annual strategy coverage and QALYs resulting from the best allocation of funding to minimize medical visits for influenza. Adj adjuvanted, Recom recombinant, QIV quadrivalent influenza vaccine, TIV trivalent influenza vaccine

In the base-case analysis, TIV high-dose 65 years+ strategy was dominated and hence excluded from funding. In a threshold analysis, we found that the cost per vaccinee for this strategy should be decreased from US$67.82 to US$50 to become eligible for funding. However, it was only funded in Year 1, with the initial vaccination budget of US$1.5 billion; with the base-case budget increase, it was immediately replaced by the second ranking vaccine in the same age group. To be allocated a funding for 3 years before being replaced, the cost per vaccinee should be further reduced to US$45.

When comparing the ROI of the adoption of the most effective non-dominated strategies (Adjuvanted TIV 65 years+, Adjuvanted TIV 50–64 years, and QIV 18–49 years) during the 10-year investment period at maximum achievable coverage with their second best alternative (Recombinant QIV 65 years+, QIV 50–64 years for the two oldest age groups, respectively; all alternatives for 18–49 years are dominated), we found that the incremental funding in vaccination was US$193,869 per QALY gained (Table 4).

Table 4.

Incremental analysis between the two best overall vaccination strategies

Strategy	Accumulated funding in vaccinationa/years	Accumulated QALY gains	Incremental funding in vaccinationa/QALY gained
Most effective non-dominated strategies (Adj TIV 65 years+, Adj TIV 50–64 years+ QIV 18–49 years+)	$570,000,000a × 9 = $5,130,000,000	189,956
Next best alternative (Recom QIV 65 years+, QIV 50–64 years, QIV 18–49 years)	$430,000,000a × 9 = $3,870,000,000	183,456
Difference	$1,260,000,000	6499	$193,869

Adj adjuvanted, Recom recombinant, QIV quadrivalent influenza vaccine, TIV trivalent influenza vaccine, QALY quality-adjusted life year

^aExcludes incremental savings in disease management costs induced by most effective non-dominated strategies compared to the next best alternative

Discussion

Many influenza vaccines are available, and new ones are coming [30]. The PMMFV, using an optimization heuristic, identifies the most cost-efficient strategy across different age groups to maximize a preselected beneficial outcome cumulative over a finite time horizon. It applies CO methods that are underutilized in health economics to inform healthcare decision making [31, 32]. The approach links budget allocation to an overall health gain for the population that should be maximized by proposing the best combination of interventions. The model looks at different age groups that differ in influenza epidemiology, evaluates the outcome on an annual basis, selects vaccination strategies for maximizing health gains, and replaces them if additional budget becomes available. The analysis presents the ROI from a budget-holder perspective and considers a defined budget for vaccination and benefits to be maximized over a defined time horizon.

The data inputs applied in the model could vary in real-life as the influenza environment is dynamic in vaccine exposure, price setting, and impact on burden of disease with annual variations in epidemiology. However, a CO analysis can still result in more efficient decisions than the conventional cost-effectiveness analysis (CEA) in which budget constraints are masked through a willingness-to-pay threshold selection [12].

Many different scenarios can be tested with a CO model and their results may be very informative for a decision maker. Those scenarios may include a change in budget allocation, optimal annual budget distribution when the optimization is focused to reach a minimum target in benefits (e.g., reduction of 15% influenza mortality), required starting budget, price setting per vaccine type, prioritization of vaccination for those who are most in need of prevention, outcome measures aimed to be maximized, or constraints that are specific for local environments.

CO brings a variety of different factors to be considered into one analysis. If the price of a vaccine is high, it is likely to be dominated unless its superior effectiveness justifies the increase when compared to the ROI of available alternatives. If dominated, it will be excluded for not being efficient enough to be financed within the allocated budget. When excess budget is available, the model may fund a better and more expensive vaccine, replacing the one being first selected because of a higher ROI at a lower cost. The decision maker is then informed about the additional budget required to achieve a more ambitious health goal, and must determine if the incremental benefit justifies the incremental cost. The attractiveness of CO modelling is to provide an overview in a broad availability of options rather than a narrow look at one product-specific intervention.

A portfolio approach of different options for managing a specific problem has been applied in many different domains outside healthcare such as forest management, fishery planning, or the search for ecological equilibrium, to name a few [33]. These methods have been applied to healthcare recently but are still underutilized [34]. This could be caused by a past focus on evaluations of one intervention at a time compared with standard of care and not in combination. CEA is a form of optimization in that an outcome is searched for and the intervention that gains more outcome for an acceptable extra price is selected [35]. However, CEA is not constrained and therefore has some shortcomings when considering allocation-related decisions. For example, it does not directly indicate how much additional budget is required when selecting a more expensive vaccine and therefore an additional budget impact analysis will be required.

The attractiveness of CO modelling is that it brings the different options into one analysis so that a more complete and informed decision can be made by understanding the different consequences for different target populations at once. For instance, a more expensive vaccine can generate sufficient gains within its specific target group indication that it becomes cost-effective and hence eligible for funding; when considering the entire population, however, there might be more gains achieved by implementing a less expensive vaccine in another target group with the same amount of money instead, thereby fulfilling the criteria of constrained budget in a better way.

This approach is very informative to budget holders such as insurance companies or third-party payers because they often work with fixed budgets and aim to maximize the benefits of investments to satisfy their members. The number of members under insurance coverage defines the budget made available for investments, and how much they likely want to invest in prevention versus treatment or how much control they want to over infections. In these situations, a CO model can be developed within a specific disease area (influenza, pneumococcal disease, malaria, HPV [36]) or per disease domain (infectious diseases [37], diabetes [38], cancer [39]), when different intervention options exist, precise budgets are known, and the constraints are well specified.

Limitations

There are limitations with the model as constructed. First, simplifications were made for demonstration. For example, while the model could include indirect costs, the current analysis only considered direct medical costs; as a result, the societal impact was not considered. Second, annual mortality in the population is slightly overestimated as influenza-associated mortality is already included in the all-cause mortality data and the resulting natural mortality calculations thereof in the annual model cohorts. Third, the ranking process considers the ROI of each vaccination strategy in isolation. By only considering the ROI of the vaccination strategies in the allocation process, the model cannot account for what health authorities may consider an easier way of working by selecting the same vaccine for all age groups. Fourth, the shelf-life and wastage are not considered in the analysis. Fifth, potential AEs associated with vaccination are not included, but the differences in AE rates between the vaccine types considered are unclear and, in the USA, with only one exception, ACIP equally recommends all vaccines marketed in the USA.

In addition, the heuristic used to solve the optimization problem with a ranking approach is not a conventional way of analyzing optimization models. The optimization normally relies on linear or non-linear programming using the simplex method or other well-established algorithms to solve the equations. The heuristic is explained in detail in Sect. 2.2. The simplicity of the ranking analysis method, the ability to implement it into a spreadsheet, and the possibility to easily check whether the proposed solution matches the expected result, made it an attractive and useful option.

Also, herd effect was not applied in the PMMFV, as we have done in other portfolio models through approximations of increased vaccine effectiveness and/or vaccine coverage rate [34]. It was not considered as an option because if one vaccine is more effective, its herd effect will be more pronounced, thereby inflating its ROI without affecting its sequence in the ranking.

Finally, it should be noted that the overall benefit could be larger than what is measured as the effect of vaccination on the influenza-attributable excess mortality in cardio-vascular or pulmonary disease has not been considered here and the age group younger than 18 years was not evaluated.

Conclusion

The PMMFV is a helpful instrument for decision makers working under budget constraints, limited vaccination coverage rates, and still searching for optimizing overall health gains when different options exist and the best combination of options must be sought. This CO analysis simultaneously considers available budget and disease/vaccine specifics in the entire population to improve allocation-based decisions. It may indicate where in an overall assessment the extra investment in extra gain is worth its value.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author Contributions

All authors participated in the design or implementation or analysis, interpretation of the study, and the development of the manuscript. All authors had full access to the data and gave final approval before submission.

Data Availability Statement

GSK makes available anonymized individual participant data and associated documents from interventional clinical studies that evaluate medicines, upon approval of proposals submitted to http://www.clinicalstudydatarequest.com. To access data for other types of GSK-sponsored research, for study documents without patient-level data and for clinical studies not listed, please submit an enquiry via the website.

Compliance with Ethical Standards

Conflict of interest

B. Standaert and P. Buck are employees of the GSK group of companies and declare restricted shares ownership in the GSK group of companies. I. Van Vlaenderen, L.A. Van Bellinghen, S. Talbird, K. Hicks, and J. Carrico declare that their institutions have received fees from the GSK group of companies during the conduct of the study reported here as well as for projects outside the submitted work.

Funding

GlaxoSmithKline Biologicals SA funded this study (GSK study identifier: HO-17-18476) and all costs associated with the development of related publications.