Comparative phase imaging of live cells by digital holographic microscopy and transport of intensity equation methods

Abstract

We describe a microscopic setup implementing phase imaging by digital holographic microscopy (DHM) and transport of intensity equation (TIE) methods, which allows the results of both measurements to be quantitatively compared for either live cell or static samples. Digital holographic microscopy is a well-established method that provides robust phase reconstructions, but requires a sophisticated interferometric imaging system. TIE, on the other hand, is directly compatible with bright-field microscopy, but is more susceptible to noise artifacts. We present results comparing DHM and TIE on a custom-built microscope system that allows both techniques to be used on the same cells in rapid succession, thus permitting the comparison of the accuracy of both methods.

1. Introduction

Digital Holographic Microscopy (DHM) is an established real-time, high resolution quantitative phase contrast imaging technique. It is based on the interferometric detection of phase changes of a light wave that passes through, or is reflected from, a microscopic sample. The intensity of light passing through a nearly transparent sample, such as a cell, changes little, but the light slows down inside the sample in proportion to its index of refraction, resulting in a significant phase change. DHM converts these phase changes into intensity variations, which are recorded by an imaging detector. Since the phase change indicates a change in the optical path length, or optical thickness, a height profile of the sample can be deduced. It is, therefore, especially advantageous in mapping the height profile of mostly transparent samples (“pure phase” objects), such as individual cells grown in a monolayer on a transparent surface [1–8].

Other useful properties of digital holographic microscopic imaging are the ability to numerically focus on a surface of the sample from a single image frame, and the ability to digitally correct for various imperfections in the imaging system. For example, the curvature mismatch between the reference and object beams can be numerically compensated [1,2,9–14] and the process for such numerical compensation can be automated (as discussed below), significantly simplifying the operation of a digital holographic microscope.

DHM uses a high-resolution digital camera to acquire a hologram. After the intensity information is recorded, it is encoded as an array of numbers representing the intensity of the optical field. To extract the phase map of the cell from the hologram, it is necessary to numerically propagate the optical field along the direction perpendicular to the hologram plane, until the object is in focus. In this work, this is done using angular spectrum method. By calculating the final complex optical field and extracting the phase, the optical thickness map of the cells is created. Coupled with many phase unwrapping algorithms, DHM is becoming a routine method for inspection of microstructures [15] and biological systems on a nanometer scale [8].

DHM allows simultaneous measurement of thickness of individual cells and monitoring of many cells within the field of view with nearly real-time resolution. In principle, the speed at which the digital holograms are acquired is limited only by the frame rate of the camera, although numerical propagation and, in some cases, software-based phase unwrapping may require substantial processing power, especially for larger images of samples with complicated height profiles.

Transport of intensity equation (TIE) phase imaging is, like DHM, a high resolution computational imaging technique capable of near-real-time 3D surface and thickness reconstructions [16–18]. However, the TIE offers several advantages as compared to DHM and other interferometric techniques. Rather than using the interferometric combination of multiple beams of light, it relies simply on free-space propagation of a single beam, which is itself a form of self-interference, to render phase measurable. While DHM requires significant spatial stability, i.e. that the interfering beams remain aligned to within fractions of a wavelength (hundreds of nanometers) during the measurement, the TIE requires much less, only that the single beam be held stationary with respect to the camera’s pixels (typically several microns).

For pure phase specimens, in addition to the knowledge of the mean wavelength of the illumination, the camera pixel size and system magnification, the TIE requires only a single defocused, bright-field image acquired at a known defocus position. Since all intensity variations in the defocused image are due to the phase of the specimen, this can be used to reconstruct the specimen’s phase profile. For non-transparent specimens, the TIE requires instead two images with different levels of defocus in order to separate phase- and absorption-induced intensity variations. For robustness, however, three images are typically acquired: one in focus and two defocused symmetrically about the specimen plane [19]. Phase is then retrieved by solving a second order linear elliptic partial differential equation using the acquired images as input. This can be performed in near-real-time on modern computers using fast Fourier transform (FFT) algorithms [20]. The retrieved phase is naturally unwrapped and can readily measure variations of optical thickness greater than one wavelength.

Another advantage of the TIE over interferometric methods is its natural compatibility with commercial bright-field microscopes. Defocus can be implemented rapidly via a motion controller, either utilizing the microscope’s own focus control or by shifting the position of the imaging camera. Alternatively, real-time imaging can be obtained by utilizing beam splitters [21,22], a programmed phase mask [23], or a tunable lens [24] to acquire the defocused images without physical defocusing. The TIE is also significantly more robust than DHM to reduced spatial and temporal coherence of the light source, and is compatible with most sources of illumination including LED and broadband incandescent sources [25–27]. Additionally, since it is compatible with spatially partially coherent illumination, TIE phase microscopy has been shown to produce phase reconstructions with resolution exceeding the coherent diffraction limit [28]. The TIE has been demonstrated to produce useful quantitative phase reconstructions of biological samples in conventional microscopes [29–31].

Since the TIE is a less well-established technique, TIE microscopes are typically validated by using static, known phase targets such as binary phase masks or microlens arrays [21,23–25,29,31]. While TIE is capable of producing accurate reconstructions of such targets, these may not provide an accurate assessment of its capability at retrieving the phase of live cells. As such, having a “gold standard” in the form of the better-established DHM phase image to serve as a reference yields a useful comparison. While earlier studies have provided comparisons of DHM and TIE [32,33], none to our knowledge has attempted to compare the two methods quantitatively in imaging live cells.

2. Digital holographic and transport of intensity equation phase imaging

2.1. Automated Fourier filter selection and curvature correction for digital holographic microscopy

In order to generate an accurate phase profile from the raw data collected from the camera, one needs to numerically compensate a curvature mismatch between the reference and object beams [1,2] that is present in a holographic setup. If the mismatch is not properly compensated, the resulting phase image of a flat surface will be curved. We developed an automated iterative method combining the curvature compensation (discussed in Ref. [2]) with the simultaneous Fourier filter adjustments.

The reconstruction of a hologram by the angular spectrum method [7,8,34] involves the selection of a first order diffraction peak in the Fourier space [see Fig. 1(a)]. The algorithm begins by taking the initial guess of the location of the peak based on the location of the brightest point away from the central 0^th order maximum. It then centers itself around this maximum, and rejects the signals beyond a certain radius [see Fig. 1(b)]. The algorithm then uses the location of this bright point as the center of the Fourier space. The phase reconstruction, shown in Fig. 1(c), is curved due to the curvature mismatch between the reference and object beams. The position of the Fourier filter is adjusted so that the center of curvature is in the center of the phase image [and the center of the phase image is as free from the phase discontinuities as possible – see Fig. 1(d)]. The spherical curvature correction is applied next, resulting in a flatter phase image [Fig. 1(e)]. Finally, adjusting the location of the projection of the center of curvature on the CCD matrix (x_o and y_o in Ref. [2]) produces the image shown in Fig. 1(f), which is free from curvature.

Fig. 1.

The stages of the automatic Fourier filter placement and curvature correction (see Ref. [2] for more detail): (a) the result of the angular spectrum transform applied to the hologram of USAF target, group 6, acquired by camera; (b) filtering of the first diffraction order; (c) phase reconstruction with curvature present; (d) phase reconstruction after the initial filter repositioning; (e) the results of the curvature correction; (f) final curvature adjustment.

While this iterative process may take 30–60 seconds (depending on the image size and initial guesses), it does not require any user input throughout its run. It also only needs to be applied once for a particular setup setting. While the curvature needs to be slightly adjusted for a different microscope objective, the most practical application for this process is to analyze larger images through the tiling of multiple smaller images. In such a case, each region of a larger field of view will have a slightly different curvature mismatch, and the smaller images can be taken sequentially and automatically adjusted for curvature. The results can be compiled into a larger full image and compared to a larger field TIE image.

2.2. Transport of intensity equation phase imaging

The TIE relates the variation of intensity I along the z axis to the gradient of the phase ϕ in the transverse x-y plane through the partial differential equation

$$\frac{\mathrm{\partial }I(\mathbf{\text{x}},z)}{\mathrm{\partial }z}=-\frac{\lambda }{2\pi M}{\mathrm{\nabla }}_{\mathbf{\text{x}}}\cdot [I(\mathbf{\text{x}},z){\mathrm{\nabla }}_{\mathbf{\text{x}}}\varphi (\mathbf{\text{x}},z)],$$ (1)

where x=(x,y) is the coordinate in the transverse (detector) plane, λ is the beam’s wavelength, M is the microscope’s magnification, and ${\mathrm{\nabla }}_{\mathbf{\text{x}}}$ is the gradient operator in the transverse plane.

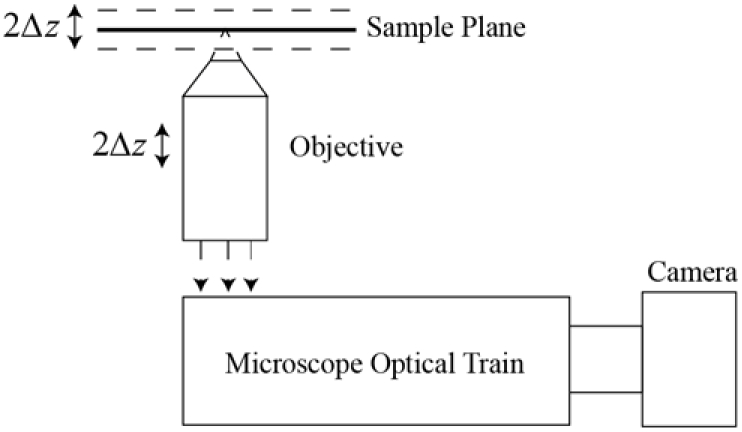
In practice, the derivatives are estimated by finite differences, with transverse derivatives taken between pixels on the camera and the axial derivative being a finite difference of two images acquired with the system focused at axial positions ±Δz, as illustrated in Fig. 2.

Fig. 2.

TIE microscopy performed by defocusing the system about the sample plane.

Additionally, and without loss of generality, if z = 0 is taken to be the central plane about which these images are acquired, the TIE has the finite-difference form

$$\frac{I(\mathbf{\text{x}},\mathrm{\Delta }z)-I(\mathbf{\text{x}},-\mathrm{\Delta }z)}{2\mathrm{\Delta }z}=-\frac{\lambda }{2\pi M}{\mathrm{\nabla }}_{\mathbf{\text{x}}}\cdot [I(\mathbf{\text{x}},0){\mathrm{\nabla }}_{\mathbf{\text{x}}}\varphi (\mathbf{\text{x}},0)].$$ (2)

In this work, this differential equation is solved through defining an auxiliary function [16] whose gradient is assumed to be equal to the product of the in-focus intensity and transverse phase gradient, ${\mathrm{\nabla }}_{\mathbf{\text{x}}}\mathrm{\Theta }=I(\mathbf{\text{x}},0){\mathrm{\nabla }}_{\mathbf{\text{x}}}\varphi (\mathbf{\text{x}},0).$ This leads to a pair of Poisson’s equations

$${{\mathrm{\nabla }}_{\mathbf{\text{x}}}}^2\mathrm{\Theta }=-\frac{2\pi M}{\lambda }\frac{I(\mathbf{\text{x}},\mathrm{\Delta }z)-I(\mathbf{\text{x}},-\mathrm{\Delta }z)}{2\mathrm{\Delta }z},$$ (3)

$${{\mathrm{\nabla }}_{\mathbf{\text{x}}}}^2\varphi (\mathbf{\text{x}},0)={\mathrm{\nabla }}_{\mathbf{\text{x}}}\cdot \left[\frac{{\mathrm{\nabla }}_{\mathbf{\text{x}}}\mathrm{\Theta }}{I(\mathbf{\text{x}},0)}\right].$$ (4)

Phase is retrieved by solving these Poisson’s equations through use of the fast Fourier transform (FFT) [20]. This has the advantage of speed over other numerical methods for directly solving Eq. (2). Note also that solving the TIE requires that the value of the phase or its normal derivative be defined on the boundary of the region of interest, and this is typically not known a priori. The FFT assumes periodic boundary conditions, which will hold in the case of periodic objects and work well in the case of isolated objects. For aperiodic objects with non-trivial phase structure near the edges of the region of interest, the FFT can result in large artifacts near the boundaries. This can be somewhat alleviated by periodic tiling of the measured intensities [35]. Methods have been proposed to measure the boundary values directly by introducing hard-edged apertures in the field of view [20,36,37], but these require precise manufacturing, alignment and measurement.

As mentioned before, TIE is also robust under the conditions of low spatial and temporal coherence of the light source, and is compatible with most sources of illumination including LED and broadband incandescent sources, provided that mean wavelength is used in Eqs. (1) and (2) and the specimen is not strongly dispersive. The use of partially coherent light can essentially eliminate coherent diffraction noise in the reconstructed phase.

The performance of a TIE system depends strongly on the details of the illumination employed [27,38,39]. In a microscope with Kohler illumination, the shape and size of the condenser aperture controls the spatial coherence of the system, and the resolution of TIE is degraded due to blurring of the defocused images by convolution with the scaled condenser aperture function. On the other hand, the in-focus resolution is limited by the maximum spatial frequency of the sample that can be captured by the microscope objective. Larger condenser apertures improve the in-focus resolution by allowing the objective to capture higher spatial frequencies of the specimen. Varying the size of the condenser aperture therefore trades off in-focus versus defocused resolution, and since TIE relies on solving a differential equation using both in- and defocused images, the condenser aperture used must be considered carefully to optimize the reconstructed phase. For example, it has been recently demonstrated that dynamic control of the illumination can be used to combine the strengths of both large and small condenser aperture TIE imaging [28]. By dividing the total exposure time in half and acquiring two images with half of the exposure each, one with a large and one with a small condenser aperture, the reconstruction can produce high resolution phase reconstructions while reducing noise [38]. Additionally, some of the computational steps of the reconstruction can be performed optically, further reducing noise [39]. In order to use a single source to boost the in-focus resolution at all spatial frequencies, while not degrading the defocused resolution due to convolution with a broad condenser aperture, off-axis illumination from a single, annular aperture can be employed [28]. If this annular ring is chosen such that the NA of the condenser illumination is matched to the NA of the objective, the TIE resolution should be approximately twice the resolution of in-focus, coherent imaging, i.e. a minimum resolvable feature size of 0.61λ/NA, as opposed to 1.22λ/NA. Since swapping annuli in the condenser aperture to match each objective is not necessarily practical, similar results can be obtained by replacing the microscope’s illumination system with an LED array, provided an annular set of LEDs is used to illuminate the specimen, and the angle of illumination from each LED through the objective is matched to the NA of the objective.

Finally, it is worth mentioning that the TIE has two drawbacks compared to DHM. The first is that it requires multiple images with axial scanning between the images, which takes time and precise defocus control on the order of the Rayleigh range of the objective, Δz ≈ λ/NA². In principle, if the samples were uniformly attenuating, only a single defocused image would be needed. However, we find that even for weakly attenuating images, the reconstructions are most robust with three acquired images (under-, over- and in-focus). Although not adopted here, this drawback can be overcome with a variety of methods to eliminate mechanical scanning in acquiring defocused images [21–24]. A second drawback is the TIE’s sensitivity to low-spatial-frequency noise [40]. Low spatial frequency noise corresponds to large, slowly varying phase features. Since light is expected to be refracted only weakly by such features in the specimen, only very subtle changes in intensity are expected upon small defocus, and these changes are easily corrupted by noise. Moreover, low-spatial-frequency components of the noise in a measurement are likely to be misinterpreted by the TIE as phase signatures. TIE phase reconstructions are therefore subject to large, slowly-varying background features due to noise. Although a variety of methods have been proposed to alleviate this problem, they either rely on acquiring additional images at more defocus positions [41–45] (and thus longer and more complicated data acquisition), or on computational methods, which use assumptions on the specimen structure to preferentially eliminate noise [46,47] (which limits the class of objects that can be reconstructed). So as not to limit the applicability of our system, and to maintain rapid data acquisition, we do not use any of these noise reduction methods here.

3. Experimental

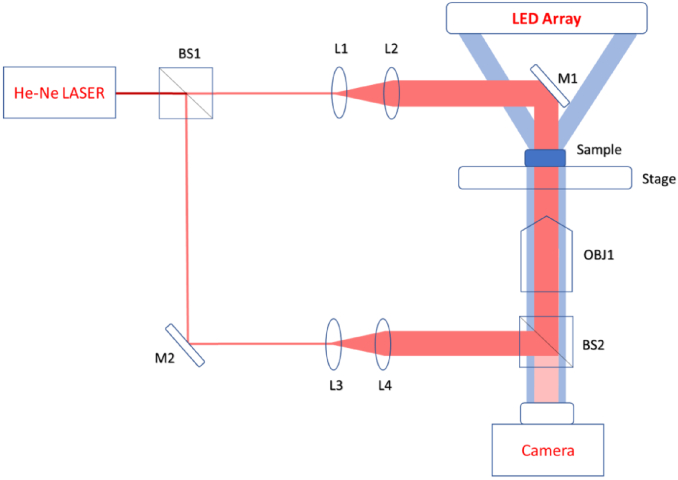
Figure 3 shows the combined DHM and TIE optics setup. A Thorlabs He-Ne Laser (Model HNL008R, λ=633 nm) was used for digital holographic measurements, and a blue LED 2D array (λ=466 nm) was used for TIE. For the DHM measurements, the beam splitter BS1 separated the laser light into the object and reference beams. Plano-convex lenses L1 and L2 expanded the object beam. The object beam was reflected by mirror M1 to pass through the sample. The image was built by the microscope objective OBJ1. The reference beam was reflected by M2, and expanded by L3 and L4. The object and the reference beams were recombined by the beam splitter BS2 and the interference pattern was formed on the camera. The curvature mismatch between the reference and the object beams was compensated numerically using customized in-house software.

Fig. 3.

Combined DHM and TIE setup (see text for details).

To perform TIE measurements, an Adafruit 32 × 32 RGB LED array controlled by Arduino UNO was programmed to project modifiable illumination patterns using the blue LED sources. Light emitted by this array was passed through the sample and focused by objective lens OBJ1 onto the camera. An annular pattern of LEDs was used so that the mirror M1 did not significantly obstruct the illumination; it remained in place during TIE measurements. The objective was focused sequentially on three planes: two on either side of focus, and one in focus. The optical train of the Olympus IX73 inverted microscope and Thorlabs CS505MU CMOS camera were used to capture images. The objective turret was equipped with a motorized motion controller, enabling the precise axial defocus positioning. In-focus, under-focused, and over-focused images were supplied to an FFT-based TIE solver in order to reconstruct the image.

4. Results

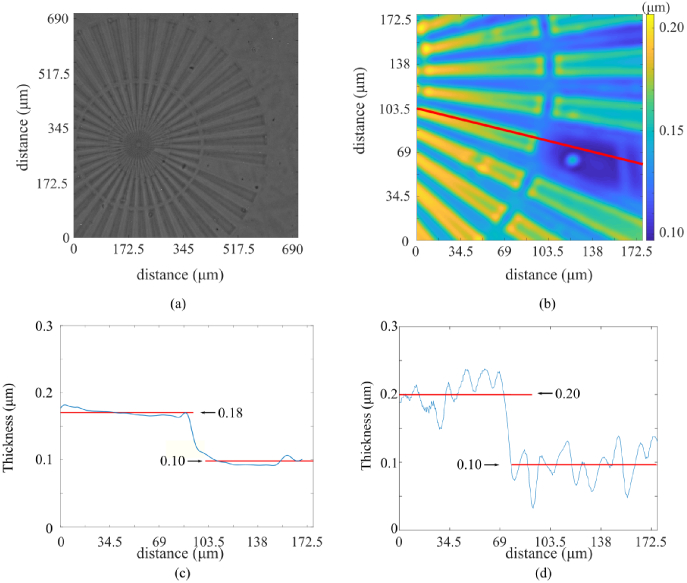
As a test to quantitatively compare both DHM and TIE techniques, a sample with known properties was analyzed. A Benchmark Technologies Quantitative Phase Target (n = 1.52) with an etch depth of 100 nm [see Fig. 4(a)] was imaged, and the phase information was reconstructed by both methods. The results of the 3D reconstruction performed by TIE can be seen in Fig. 4(b). Here, we converted the phase into physical thickness t [see Eq. (5) below].

Fig. 4.

Comparison of a spoke target thickness measurements using DHM and TIE. The bright-field in-focus image of the spoke target is shown in (a), the TIE reconstruction of the optical thickness is shown in (b); (c) and (d) show the cross-section of the same spoke for TIE and DHM respectively.

The phase $\varphi (\mathit{x})$ quantitatively depends on the wavelength of light illuminating the sample. Scaling retrieved phase by a pre-factor dependent on wavelength resulted in a quantity invariant across all wavelengths, as it relies only on the sample thickness t, its index of refraction n_f, and the index of refraction of the surrounding medium n₀. The optical path difference (OPD) is

$$OPD=\frac{\lambda }{2\pi }\varphi (\mathbf{\text{x}})=(n_f-n_o)t.$$ (5)

The cross-section of the reconstructed thickness is shown for TIE in Fig. 4(c) and DHM in Fig. 4(d). It is not clear how uniform the thickness of each step of the phase target actually is, as we could not measure the structure independently from DHM and TIE. The disagreement in the profile step size (0.1 micron for DHM, 0.08 micron for TIE) is well within the range of oscillations seen in DHM and the low-frequency background observed in TIE.

Next, we used DHM and TIE to evaluate the optical thickness profile of a live human epithelial cheek cell (Fig. 5). Our combined DHM/TIE setup allowed the imaging of the same cell without the need to move the sample.

Fig. 5.

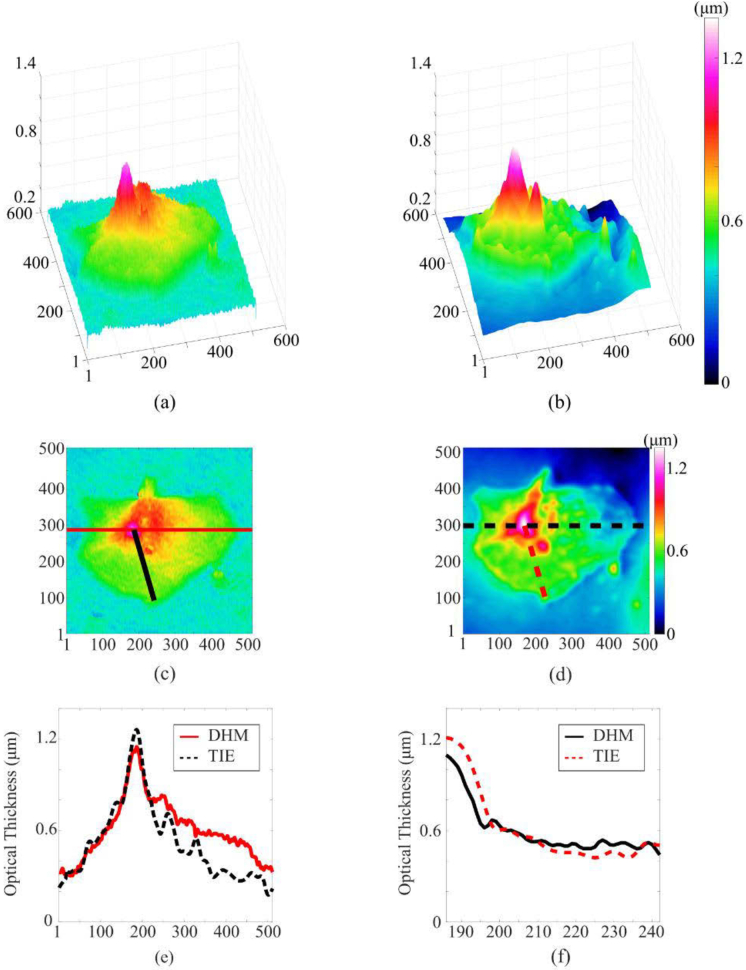
Comparison of a cheek cell optical thickness measurements using DHM (left-hand side) and TIE (right-hand side). The images in (a) and (b) show the off-axis view; (c) and (d) show on-axis view. Vertical axis represents optical thickness. The scale for the horizontal (x and y) axes is in pixels (pixel size is 0.17×0.17 µm²). The cross-section shown as the red solid horizontal line in (c) and the black dashed horizontal line in (d) is plotted in (e), and the cross-section shown as the black solid diagonal line in (c) and the red dashed diagonal line in (d) is plotted in (f).

The results of the single-cell imaging are shown in Fig. 5, where 3D off-axis [Figs. 5(a) and 5(b)] and on-axis [Figs. 5(c) and 5(d)] views of the reconstructed optical thickness are shown.

Figures 5(e) and 5(f) show two cross-sections through the reconstructed optical thickness. As can be seen, the two methods yielded quantitatively similar optical thickness profile for the cell. The observed difference in cell profiles could be due to the fact that the cell has moved between the DHM and TIE measurements (the time to switch between sources, acquire camera frames, move the camera to the new defocus distance, etc.).

Finally, Table 1 shows the RMS error between TIE and DHM phase profiles for each of the line profiles in Figs. 4 and 5. Ongoing improvements to the DHM/TIE system and software will eliminate the time between DHM and TIE acquisitions, so that even measurements of rapid cellular dynamics may be compared between these two techniques.

Table 1. RMS Error between TIE and DHM.

Sample Description	Figure	RMS Error (µm)
Spoke Target	4(c) and 4(f)	0.04
Cheek cell, horizontal line	5(e)	0.14
Cheek cell, vertical line	5(f)	0.09

5. Conclusion

We developed and tested a combination digital holographic microscopy (DHM) and transport of intensity (TIE) microscopic phase imaging system for 3D data acquisition. We performed the comparison between the two techniques. The use of a combined “hybrid” setup allowed the implementation of both methods in rapid succession for static targets and live cells. Quantitative agreement between methods was found in both static and live samples.

Further, we presented a method to automate the selection and positioning of the Fourier domain filter and wavefront curvature correction, simplifying the processing of DHM images. This is particularly important for handling a succession of related images (assembling a larger field of view, or a time series).

Ongoing work includes modifying the experimental setup to perform simultaneous data collection with both the DHM and TIE systems. This can be achieved using dichroic mirrors, taking advantage of the difference in illumination wavelength between the two systems. This combined system will also be used for the analysis of multiple cells and monitoring changes induced by various chemical treatments. Lastly, the availability of simultaneous DHM measurements for validation will enable us to rapidly improve the TIE reconstruction algorithms for live cells by providing an accurate reference phase for comparison.

In the future, we intend to use both DHM and TIE together, and demonstrate that TIE offers a practical tool capable of extracting cell volume from live biological specimen with minimal adjustments. Such a robust system will be used by biological scientists without specialized optical engineering training in a variety of cell imaging applications.

Funding

National Institute on Drug Abuse10.13039/100000026 (RO1 DA047410-01); New York State Department of Health10.13039/100004856 (DOH01-C33920GG-3450000); Peter T. Rowley Breast Cancer Scientific Research Projects (C33920GG).

Disclosures

The authors declare no conflicts of interest.