Abstract
In this paper, a multiple ensemble neural network model with fuzzy response aggregation for the COVID-19 time series is presented. Ensemble neural networks are composed of a set of modules, which are used to produce several predictions under different conditions. The modules are simple neural networks. Fuzzy logic is then used to aggregate the responses of several predictor modules, in this way, improving the final prediction by combining the outputs of the modules in an intelligent way. Fuzzy logic handles the uncertainty in the process of making a final decision about the prediction. The complete model was tested for the case of predicting the COVID-19 time series in Mexico, at the level of the states and the whole country. The simulation results of the multiple ensemble neural network models with fuzzy response integration show very good predicted values in the validation data set. In fact, the prediction errors of the multiple ensemble neural networks are significantly lower than using traditional monolithic neural networks, in this way showing the advantages of the proposed approach.
Keywords: ensembles, neural networks, fuzzy logic, COVID-19 time series
1. Introduction
Recently, we noticed the rapid propagation of the COVID-19 Coronavirus around the world, appearing initially in China and then spreading to neighbor countries, like Thailand, Korea, and Japan, and after that to Europe, America, and later Africa. In particular, Europe, Italy, Spain, France, the United Kingdom, and Germany have been hit hard with the propagation of the COVID-19 virus, having to this moment many confirmed cases and deaths. After that, the virus spread to the American continent, and the United States and Canada which were also hit hard with the spread of the COVID-19 virus. Finally, the virus arrived in Mexico, where it is now becoming a large problem with almost 50,000 confirmed cases as of 18 May 2020.
In relation to COVID-19 prediction, we can mention the following work. In Chen et al. [1], the authors outline the prediction of the SARS-CoV-2 (2019-nCoV) 3C-as a protease structure. In Fan et al. [2], the authors outline an approach for the prediction of the epidemic spread of the coronavirus, driven by the spring festival transportation in China. In Goh et al. [3], the authors discuss the rigidity of the outer shell predicted by a protein intrinsic disorder model with this uncovering COVID-19 infectivity. In Grifoni et al. [4], a bioinformatics approach that can predict candidate targets for immune responses to SARS-CoV-2 was presented. In He [5], the author discusses what could still be done to control COVID-19 outbreaks in addition to the usual measures of isolation and contact tracing that most countries are imposing. In Huang et al. [6], a spatial-temporal distribution of COVID-19 in China and its prediction were described. In Ibrahim et al. [7], the authors describe the prediction of the COVID-19 spike-host cell receptor GRP78 binding site. In Ivanov [8], an approach for predicting the impact of epidemic outbreaks on global supply chains with a simulation-based analysis was presented. In Li et al. [9], the authors described the propagation analysis and prediction of the real COVID-19 time series. In Li et al. [10], the authors describe a forecasting method for the COVID-19 outbreak in China with good results. In Liu et al. [11], the authors report the understanding of unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of appropriate public health interventions. In Roda et al. [12], the authors discussed in detail why it is difficult to accurately predict the COVID-19 epidemic. In Roosa et al. [13], the authors described real-time forecasts of the COVID-19 epidemic in China from February 5, 2020 to February 24, 2020 with good results. In Ton et al. [14], the authors describe the rapid identification of potential inhibitors of SARS-CoV-2 main protease by deep model docking of 1.3 billion compounds. In Wang et al. [15], the authors describe a novel phase-adjusted estimation approach of the number of Coronavirus Disease cases in Wuhan, China. In all this previous related work, we can notice that to date, only simple monolithic neural networks or deep neural models have been used for prediction. However, in this work, we are proposing a new hybrid prediction model that combines ensemble architectures of neural networks with fuzzy logic for response integration, which has not been proposed before. We believe that our model will fill a current gap in existing research, which is the lack of use of multiple ensembles of neural networks in the prediction of complex time series, like the Coronavirus data. In addition, the basic modules are based on nonlinear autoregressive neural networks and function fitting networks. The main idea is that by combining several neural predictors with fuzzy logic, we are able to manage the uncertainty of the individual networks, and the total prediction can have lower uncertainty. This is the main contribution of the paper, the proposed model with ensembles of neural networks and a fuzzy aggregator for combining the predictions of the modules to obtain an improved prediction. The fuzzy aggregator is designed in such a way as to reduce the prediction error by using the information of the individual errors of the neural predictions. The simulation results of the proposed hybrid model are very good when compared with other approaches. In summary, the new prediction model is the main contribution of the paper. However, the resulted predictions are also very important for the Government in making the appropriate decisions to optimally manage the health care system, as in the case of Mexico, but believe that it could be used in other countries as well.
The paper is organized as follows. Section 2 describes the basic concepts about nonlinear autoregressive neural networks. Section 3 outlines the fundamental definitions of function fitting neural networks. Section 4 describes the proposed hybrid method combining ensemble architectures of neural networks with fuzzy logic for response integration. Section 5 shows the knowledge representation for the fuzzy system for response integration. Section 6 shows the simulation results, and finally, Section 7 offers the conclusion.
2. Nonlinear Autoregressive Neural Networks
The NAR (nonlinear autoregressive) neural network uses past values of the time series to estimate predicted future values. The NAR neural network model consists of one input layer, one or more hidden layers, and one output layer. NAR is a dynamic and recurrent network with feedback connections [16]. NAR is used in one-step-ahead or multi-step-ahead time-series forecasting. The NAR model expressed mathematically is presented in the following Equation (1):
| (1) |
where is the value of the considered time series at time , and is the time delay and denotes the transfer function [17]. In this case, two NAR networks are used in the ensemble, one with Levenberg–Marquardt and the other with Bayesian regularization training algorithms.
In Figure 1, the NAR neural network architecture is illustrated in more detail.
Figure 1.
The general architecture of the NAR neural network.
3. Function Fitting Neural Network
The FITNET (function fitting neural network) is another commonly used Multi-Layer Perceptron (MLP) or a class of feedforward artificial neural network (ANN) that contains one hidden layer. A feed-forward network with one hidden layer and enough neurons in the hidden layers can fit any finite input-output mapping problem. The FITNET model uses the process of training a neural network on a set of inputs in order to produce an associate set of target outputs. The FITNET is used for curve-fitting and regression. In Figure 2, is the input neuron, and are the weights, represents the neuron numbers, and is the neuron output [18,19,20].
Figure 2.
The general architecture of an artificial neural network of FITNET type.
In Figure 2, the general architecture of an artificial neural network (ANN) is shown.
The learning or training algorithm used in FITNET is the well-known Levenberg–Marquardt training method and the reason for this is because it is very fast for time-series data.
Neural networks, such as the NAR and the FITNET, and Fuzzy Systems, are commonly used for time-series forecasting. In fact, fuzzy systems, NAR and FITNET have been used in many areas. For example, a model was constructed for both snow-free and snowy areas to forecast monthly and daily albedo [21], wheel-wear prediction models based on NAR demonstrated being useful in predicting dynamic changes of wheel diameters [22], and FITNET was used for atomic coordinate prediction of carbon nanotubes [23]. On the other hand, neuro-fuzzy systems were used for prediction quality of a rubber curing process [24] and cardiovascular disease risk level prediction [25]. However, here the Fuzzy integrator, the NAR, and FITNET neural networks are used to help predict 10 days ahead of 12 states in Mexico and the total of the country using the confirmed and death cases of the COVID-19 using one-hidden layer. The Levenberg–Marquardt backpropagation (trainlm) is used as the training algorithm, the purelin as the transfer function and three feedback delays. The number of epochs is 500, 10 neurons in the hidden layer, and the earning rate is 0.01. The Mexican dataset was obtained from Mexico’s Government website [26].
4. Proposed Method
In Figure 3, the main architecture of the ensemble neural network model is shown. We have a dataset from COVID-19 confirmed and death cases, which consists of 12 states in Mexico and the total data of the country. In modules 1 and 2 of the ensemble, we use the NAR neural network using different parameters, and in module 3 we use the FITNET neural network to train and learn from the given information. The mean square error (MSE) of the training and actual data is normalized using Equation (2):
| (2) |
| (3) |
| (4) |
where the size of the training data, the actual values, and the trained data obtained of the sample [27].
Figure 3.
The main architecture of the system.
Then the normalized mean square errors are used in the fuzzy integrator of Figure 4 to produce the weights w1, w2, w3 and then by using the expression in Equation (5) we combine the predictions to obtain the total prediction PT:
| (5) |
where weight of module 1, the weight of module 2, the weight of module 3, the predicted value of module 1, the predicted value of module 2, and the predicted value of module 3.
Figure 4.
The structure of the fuzzy integrator with Gaussian membership functions.
Regarding the general architecture of Figure 3, the main reasoning behind this is the following. We have one ensemble for each state in Mexico (in the Figure, this is from 1 to N). Then each ensemble has three modules, which consists of the simple neural networks (NAR and FITNET). The reason for using three modules in each ensemble is that in previous work, this architecture has provided good results. Then each ensemble has its own fuzzy aggregator to produce the final prediction of the ensemble.
The structure of the fuzzy integrator system is shown in Figure 4, which is formed by the inputs before fuzzification, the fuzzy inference system (integrator), and the fuzzy outputs after defuzzification. The inputs , , and consist of the normalized mean square errors of the three neural networks that have been used to predict. In this case, e1 is the MSE of module 1, e2 is the NMSE of module 2, and e3 is the NMSE of module 3. The fuzzy inference system consists of three fuzzy rules, and the three outputs are , , and , which are obtained with the weighted mean in the defuzzification process. The main idea of this fuzzy system is to model the process of assigning the weights to the predictions of the modules according to the individual errors of the modules obtained with Equation (1). So basically, for example, if the error of module 1 is low and the errors of the other modules are high, then we assign a high weight to module 1 and low weights to the other ones. The advantage of using a fuzzy approach here with linguistic variables is that the process of assigning the weight has a level of uncertainty, which is modeled with the membership functions and fuzzy reasoning.
Figure 5 illustrates the fuzzy inputs of the membership functions of , , and which is the NMSE of the neural networks in module 1, module 2, and module 3, respectively. The fuzzy values that are considered are low, medium, and large. The inputs , , and have been normalized in the range between 0 and 1.
Figure 5.
The fuzzy input membership functions of , , and with Gaussian functions.
Figure 6 illustrates the fuzzy outputs membership functions of , , and , which are the weighted mean errors of , , and , respectively. The fuzzy values that are considered are low, medium, and high. The outputs , , and have been normalized in a range between 0 and 1.
Figure 6.
The fuzzy output membership function of , , and with Gaussian functions.
The decision to use Gaussian membership functions was done after experimenting with Triangular, Trapezoidal, and Gaussian functions, in which better results were achieved with Gaussians. The results were better in terms of the smoothness of the output prediction results, as well as in terms of accuracy. In the paper, we only report the final design of the Gaussian membership functions that we obtained.
The fuzzy system contains three fuzzy rules, which are the following:
If ( is small) and ( is medium) and ( is large), then ( is high) ( is medium) ( is small).
If ( is large) and ( is small) and ( is medium), then ( is small) ( is high) ( is medium).
If ( is medium) and ( is large) and ( is small), then ( is medium) ( is small) ( is high).
These fuzzy rules express the knowledge of how to combine predictions based on their corresponding errors. Basically, the rules are assigning the weights (outputs) used in performing the average based on the fuzzy values of the errors in the modules. The reason for preferring Mamdani over Sugeno modeling is because a Mamdani fuzzy model is more interpretable in terms of the fuzzy rules (completely linguistic), and also is easier to design. The advantage of using fuzzy logic here is that we are able to handle the uncertainty in making a combined prediction, which is similar to combining the opinions of three experts.
5. Knowledge Representation of the Fuzzy System
In this Section, we show the knowledge representation of the fuzzy system with Gaussian membership functions. The membership values for the Gaussian membership function are defined in the following Equation (6): The membership value is the degree to which a given input belongs to that membership function :
| (6) |
where the center, and the variance are the design parameters.
The Equations (7)–(9) show the membership functions used for the inputs , , and .
| (7) |
| (8) |
| (9) |
The Equations (10)–(12) show the membership functions used for the outputs , , and .
| (10) |
| (11) |
| (12) |
The particular parameter values for the membership functions were defined considering the three possible fuzzy values, which are Low, Medium, and High, assigned and adjusted in a manual way [28,29,30,31,32].
6. Simulation Results
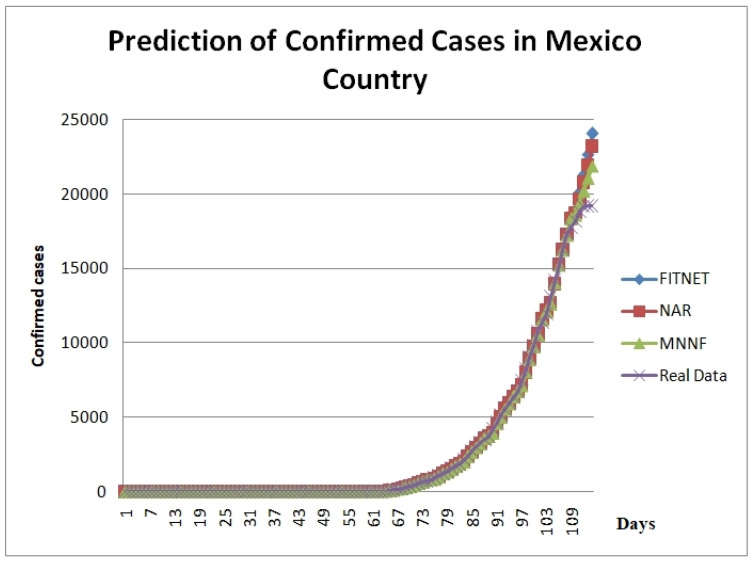
Figure 7 shows the comparison of results of Confirmed Cases Prediction in Mexico using different neural network models; two of them are a monolithic model, FITNET, and NAR versus the Modular Neural Network, which uses a fuzzy logic integrator. Table 1 shows a comparison of the predicted values for confirmed cases of COVID-19 in 10 days ahead for Mexico (whole Country).
Figure 7.
Comparison of the results of confirmed cases predicted in Mexico using different neural network models.
Table 1.
Comparison of predicted values for confirmed cases of Covid-19.
| Predicted Day | Real Data | FITNET | NAR | MNNF |
|---|---|---|---|---|
| 1 | 14,230 | 13,988 | 13,988 | 14,035 |
| 2 | 15,246 | 15,148 | 15,291 | 15,226 |
| 3 | 16,252 | 16,216 | 16,298 | 16,226 |
| 4 | 17,301 | 17,279 | 17,301 | 17,241 |
| 5 | 17,783 | 18,391 | 18,386 | 18,333 |
| 6 | 18,205 | 18,862 | 18,745 | 18,597 |
| 7 | 18,850 | 20,045 | 19,678 | 19,391 |
| 8 | 19,172 | 21,302 | 20,783 | 20,221 |
| 9 | 19,220 | 22,637 | 21,953 | 21,053 |
| 10 | 19,224 | 24,053 | 23,228 | 21,900 |
Figure 8 shows the comparison of the % Root Mean Squared Error (RMSE) in confirmed cases for the different models of ANN for the 12 states and the country of Mexico where the states are indicated as follows: 1 is Baja California, 2 Ciudad de Mexico, 3 Coahuila, 4 Estado de Mexico 5 Jalisco, 6 Nuevo Leon, 7 Puebla, 8 Quintana Roo, 9 Sinaloa, 10 Tabasco, 11 Veracruz, 12 Yucatan and 13 the Country of Mexico. In Figure 8, we can note that the proposed Modular Neural Network with Fuzzy MNNF has lower errors. Table 2 shows the relative errors of prediction for the states and the whole country.
Figure 8.
Comparison of % RMSE in confirmed cases for the different models of ANN for the 12 states.
Table 2.
Example of % RMSE for the different models for the confirmed cases.
| Baja California | Cd. de Mexico | Estado de Mex | Jalisco | Nuevo Leon | Quintana Roo | Sinaloa | Mexico Country | |
|---|---|---|---|---|---|---|---|---|
| MNNF | ||||||||
| MSE | 2529.072 | 1,263,297.767 | 41,570.1111 | 1055.7705 | 131.8613 | 7513.0870 | 74.2234 | 2,415,010.109 |
| RMSE | 50.2898 | 1123.9651 | 203.8874 | 32.4926 | 11.4830 | 86.6780 | 8.6153 | 1554.0302 |
| %RMSE MNNF | 0.0322 | 0.2157 | 0.0651 | 0.0936 | 0.0343 | 0.1099 | 0.0099 | 0.0808 |
| FITNET | ||||||||
| MSE: | 1158.3682 | 1,373,761.46 | 235,501.924 | 1122.0012 | 198.0156 | 8178.0354 | 3994.9508 | 8,280,063.46 |
| RMSE: | 34.0348 | 1172.0757 | 485.2854 | 33.4962 | 14.0718 | 90.4324 | 63.2056 | 2877.5099 |
| %RMSE FITNET | 0.0218 | 0.22500 | 0.1550 | 0.0965 | 0.0421 | 0.1147 | 0.07307008 | 0.14968321 |
| NAR | ||||||||
| MSE | 1463.8333 | 1,318,844.292 | 49,312.6242 | 706.70452 | 117.464185 | 15,407.8063 | 6370.45123 | 5,416,634.47 |
| RMSE | 38.2600 | 1148.4094 | 222.0644 | 26.5839147 | 10.8380895 | 124.128185 | 79.8151065 | 2327.36642 |
| %RMSE NAR | 0.0245 | 0.22046 | 0.0709 | 0.0766 | 0.0324 | 0.1575 | 0.0922 | 0.1210 |
Figure 9 shows the comparison of results of Death Cases Prediction in Mexico using different neural network models, two of them a monolithic model, FITNET, and NAR versus the Modular Neural Network, which uses a fuzzy logic integrator. Table 3 shows a comparison of the predicted values for death cases of Covid-19 in 10 days ahead for Mexico (the whole country). Table 4 shows relative errors of prediction of death cases for the states and the whole country.
Figure 9.
Death cases in Mexico and prediction.
Table 3.
Predicted death cases in 10 days for Mexico.
| Predicted Day | Real Data | FITNET | NAR | MNNF |
|---|---|---|---|---|
| 1 | 1251 | 1256.14422 | 1255.71983 | 1256.63828 |
| 2 | 1347 | 1339.80171 | 1339.88456 | 1340.6627 |
| 3 | 1438 | 1445.1368 | 1442.91771 | 1444.02958 |
| 4 | 1531 | 1533.02409 | 1532.79844 | 1533.68764 |
| 5 | 1625 | 1628.71662 | 1627.20689 | 1628.18016 |
| 6 | 1717 | 1724.59421 | 1722.99607 | 1723.98249 |
| 7 | 1788 | 1829.92399 | 1824.7057 | 1827.52789 |
| 8 | 1837 | 1941.17027 | 1930.41912 | 1935.97883 |
| 9 | 1856 | 2058.54869 | 2040.3259 | 2049.49095 |
| 10 | 1859 | 2182.306 | 2154.63482 | 2168.29111 |
Table 4.
Example of % RMSE for the different models for death cases.
| Baja California | Ciudad de Mex | Estado de Mexico | Jalisco | Nuevo Leon | Quintana Roo | Sinaloa | Mexico Country | |
|---|---|---|---|---|---|---|---|---|
| MNNF | ||||||||
| MSE: | 1119.3858 | 202.0965 | 2578.2210 | 24.9536 | 2.6856 | 254.1817 | 168.0517 | 28,901.5512 |
| RMSE: | 33.4572 | 14.21606 | 50.7761 | 4.9953 | 1.63879 | 15.9430 | 12.9634 | 170.0045 |
| % RMSE | 0.1520 | 0.0421 | 0.2124 | 0.1784 | 0.1092 | 0.1374 | 0.0932 | 0.0914 |
| FITNET | ||||||||
| MSE: | 948.1897 | 35.1181 | 2342.7949 | 17.8936 | 9.8660 | 377.9779 | 283.5697 | 31,643.8956 |
| RMSE: | 30.7926 | 5.9260 | 48.4024 | 4.2300 | 3.1410 | 19.4416 | 16.8395 | 177.8873 |
| %RMSE | 0.1399 | 0.0175 | 0.2025 | 0.1510 | 0.2094 | 0.1676 | 0.1211 | 0.0956 |
| NAR | ||||||||
| MSE: | 780.6350 | 294.4490 | 3664.4998 | 29.1810 | 1.2292 | 146.1051 | 159.1990 | 26,297.2756 |
| RMSE: | 27.9398 | 17.1595 | 60.5351 | 5.4019 | 1.1087 | 12.0873 | 12.61744 | 162.1643 |
| %RMSE | 0.1269 | 0.0509 | 0.2532 | 0.1929 | 0.0739 | 0.1042 | 0.0907 | 0.0872 |
Figure 10 shows the comparison of % RMSE in death cases for the different models of NN for the 12 states and the Country of Mexico where: 1 is Baja California, 2 Ciudad de Mexico, 3 Coahuila, 4 Estado de Mexico 5 Jalisco, 6 Nuevo Leon, 7 Puebla, 8 Quintana Roo, 9 Sinaloa, 10 Tabasco, 11 Veracruz, 12 Yucatan, and 13 the Country of Mexico.
Figure 10.
Comparison of % RMSE in death cases for the different models of NN for the 12 states and the Country of Mexico.
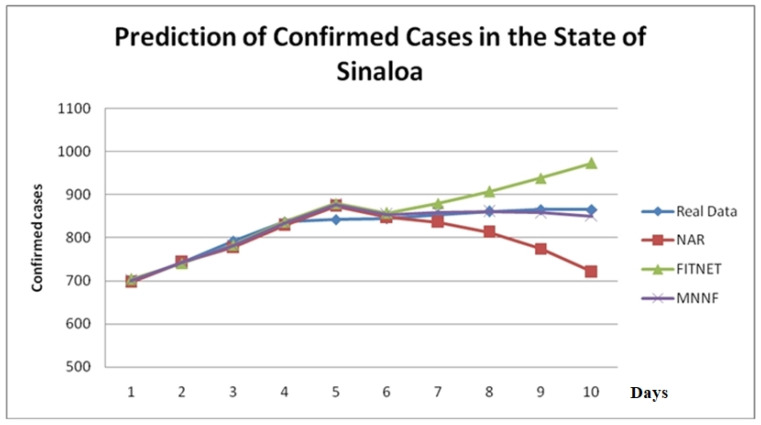
Finally, we show in Figure 11 an example of the prediction in one particular state of Mexico (Sinaloa). We are predicting 10 days ahead (data not previously seen by the model), and in Figure 11 we show the results of the proposed MNNF model when compared to the NAR and FIT models. We can clearly appreciate how the proposed MNNF model is following very closely the real data and the other models after day 5, where they drift apart and loose prediction value. Our explanation of this behavior is that the proposed MNNF is using fuzzy logic for aggregating the results of the modules, and in some way, the uncertainty in making a prediction is being managed appropriately.
Figure 11.
Comparison of prediction of confirmed cases for the state of Sinaloa.
7. Conclusions
In this paper, a new approach with multiple ensemble neural network models and fuzzy response aggregation for the COVID-19 time series was proposed. Ensemble neural networks were used to produce several predictions under different conditions. Fuzzy logic was then used to aggregate the responses of several predictor modules, in this way, improving the final prediction by combining, in a proper way, the outputs of the modules. Fuzzy logic helps in handling the uncertainty in the process of making a final decision about the prediction. The complete model was tested for the case of predicting the COVID-19 time series in Mexico, at the level of the states and the whole country. Simulation results of the multiple ensemble neural network models with fuzzy response integration show very good predicted values in the validation data set. In fact, the prediction errors of the multiple ensemble neural networks were significantly lower than using monolithic neural networks, in this way clearly showing the advantages of the proposed approach. We have to say that the proposed model can be viewed as a general prediction model because it can be applied in other time periods of the COVID-19 time series. For example, in the case of Mexico, right now the time series show an increasing trend, which is presented in this paper, but eventually, there is be a turning point, and the series will decrease, but the model will not have any problem. This is because once we have new data with a decreasing trend, we will train the simple neural networks again and use the same architecture of multiple ensembles and fuzzy aggregators to produce the new predictions in a decreasing fashion.
As future work, we plan to apply the same type of model to other COVID-19 data sets from other countries. In addition, we can also consider other time-series prediction problems, like in finance or economics. Also, regarding the model, we can optimize the structure of the neural networks using meta-heuristics, and we can use type-2 fuzzy logic in the response integration, expecting that results should improve, like in related works [33,34]. Finally, we envision improving the work in this paper by using adaptive fuzzy and neural network techniques, like in [35,36], or applying the proposed models in other kinds of applications [37,38].
Author Contributions
P.M. reviewed the state of the art, proposed the general approach, contributed to the discussion, analysis of the results and improved the final version of the paper; J.C.M. analyzed of the original prediction method and contributed to the simulations; D.S. help design the neural networks and analysis of results; O.C. applied fuzzy logic for response integration of the modules and wrote the initial version of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by TECNM, grant number 7716.20-P.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Chen Y.W., Yiu C.P.B., Wong K.Y. Prediction of the SARS-CoV-2 (2019-nCoV) 3C-like protease (3CLpro) structure: Virtual screening reveals velpatasvir, ledipasvir, and other drug repurposing candidates. F1000Research. 2020;9:129. doi: 10.12688/f1000research.22457.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fan C., Liu L., Guo W., Yang A., Ye C., Jilili M., Ren M., Xu P., Long H., Wang Y. Prediction of Epidemic Spread of the 2019 Novel Coronavirus Driven by Spring Festival Transportation in China: A Population-Based Study. Int. J. Environ. Res. Public Heal. 2020;17:1679. doi: 10.3390/ijerph17051679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Goh G.K.-M., Dunker A.K., Foster J.A., Uversky V.N. Rigidity of the outer shell predicted by a protein intrinsic disorder model sheds light on the COVID-19 (Wuhan-2019-nCoV) infectivity. Biomolecules. 2020;10:331. doi: 10.3390/biom10020331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Grifoni A., Sidney J., Zhang Y., Scheuermann R.H., Peters B., Sette A. A Sequence Homology and Bioinformatic Approach Can Predict Candidate Targets for Immune Responses to SARS-CoV-2. Cell. Host. Microbe. 2020;27:671–680.e2. doi: 10.1016/j.chom.2020.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.He Z. What further should be done to control COVID-19 outbreaks in addition to cases isolation and contact tracing measures? BMC Med. 2020;18:80–83. doi: 10.1186/s12916-020-01551-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huang R., Liu M., Ding Y. Spatial-temporal distribution of COVID-19 in China and its prediction: A data-driven modeling analysis. J. Infect. Dev. Ctries. 2020;14:246–253. doi: 10.3855/jidc.12585. [DOI] [PubMed] [Google Scholar]
- 7.Ibrahim I.M., Abdelmalek D.H., Elshahat M.E., Elfiky A.A. COVID-19 spike-host cell receptor GRP78 binding site prediction. J. Infect. 2020;80:554–562. doi: 10.1016/j.jinf.2020.02.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. Part. E Logist. Transp. Rev. 2020;136:101922. doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li L., Yang Z., Dang Z., Meng C., Huang J., Meng H.T., Wang D., Chen G., Zhang J., Peng H., et al. Propagation analysis and prediction of the COVID-19. Infect. Dis. Model. 2020;5:282–292. doi: 10.1016/j.idm.2020.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li Q., Feng W. Trend and forecasting of the COVID-19 outbreak in China. J. Infect. 2020;80:469–496. doi: 10.1016/j.jinf.2020.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu Z., Magal P., Seydi O., Webb G. Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions. Biology. 2020;9:50. doi: 10.3390/biology9030050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Roda W.C., Varughese M.B., Han D., Li M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020;5:271–281. doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Roosa K., Lee Y., Luo R., Kirpich A., Rothenberg R., Hyman J.M., Yan P., Chowell G. Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect. Dis. Model. 2020;5:256–263. doi: 10.1016/j.idm.2020.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ton A.T., Gentile F., Hsing M., Ban F., Cherkasov A. Rapid Identification of Potential Inhibitors of SARS-CoV-2 Main Protease by Deep Docking of 1.3 Billion Compounds. Mol. Inform. 2020;39:2000028. doi: 10.1002/minf.202000028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang H., Wang Z., Dong Y., Chang R., Xu C., Yu X., Zhang S., Tsamlag L., Shang M., Huang J., et al. Phase-adjusted estimation of the number of Coronavirus Disease 2019 cases in Wuhan, China. Cell Discov. 2020 doi: 10.1038/s41421-020-0148-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sarkar R., Julai S., Hossain S., Chong W.T., Rahman M. A Comparative Study of Activation Functions of NAR and NARX Neural Network for Long-Term Wind Speed Forecasting in Malaysia. Math. Probl. Eng. 2019;2019:1–14. doi: 10.1155/2019/6403081. [DOI] [Google Scholar]
- 17.Le T.-T., Pham B.T., Ly H.-B., Shirzadi A., Le L.M. Lecture Notes in Civil Engineering. Springer; Singapore: 2019. Development of 48-hour Precipitation Forecasting Model using Nonlinear Autoregressive Neural Network; pp. 1191–1196. [Google Scholar]
- 18.Aci M., Avcı M. Artificial neural network approach for atomic coordinate prediction of carbon nanotubes. Appl. Phys. A. 2016;122:631. doi: 10.1007/s00339-016-0153-1. [DOI] [Google Scholar]
- 19.Hoffmann L.F., Parquet Bizarria F.C., Parquet Bizarria J.W. Detection of liner surface defects in solid rocket motors using multilayer perceptron neural networks. Polym. Test. 2020 doi: 10.1016/j.polymertesting.2020.106559. [DOI] [Google Scholar]
- 20.Turabee G., Khowja M.R., Giangrande P., Madonna V., Cosma G., Vakil G., Gerada C., Galea M. The Role of Neural Networks in Predicting the Thermal Life of Electrical Machines. IEEE Access. 2020;8:40283–40297. doi: 10.1109/ACCESS.2020.2975985. [DOI] [Google Scholar]
- 21.Zhang G., Zhou H., Wang C., Xue H., Wang J., Wan H. Forecasting Time Series Albedo Using NARnet Based on EEMD Decomposition. IEEE Trans. Geosci. Remote. Sens. 2020;58:3544–3557. doi: 10.1109/TGRS.2019.2958048. [DOI] [Google Scholar]
- 22.Fan N., Wang S., Liu C., Liu X. Wheel Wear Prediction of High-Speed Train Using NAR and BP Neural Networks; Proceedings of the 2017 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData); Exeter, UK. 21–23 June 2017; pp. 126–130. [Google Scholar]
- 23.Avci M. Neural network-based design approach for submicron MOS integrated circuits. Math. Comput. Simul. 2008;79:1126–1136. doi: 10.1016/j.matcom.2007.10.012. [DOI] [Google Scholar]
- 24.Butdee S., Tangchaidee K. Neuro Fuzzy Based for Prediction Quality of a Rubber Curing Process on a Compression Machine Under Uncertainty Circumstances. Elsevier BV; Amsterdam, The Netherlands: 2020. pp. 2953–2960. [Google Scholar]
- 25.Saxena K., Banodha U. Data Management, Analytics and Innovation. Springer; Singapore: 2020. A Fuzzy Logic Based Cardiovascular Disease Risk Level Prediction System in Correlation to Diabetes and Smoking; pp. 29–40. [Google Scholar]
- 26.Gobierno de Mexico. [(accessed on 9 June 2020)]; Available online: https://coronavirus.gob.mx/datos/#DownZCSV.
- 27.Kumar S.S. Analysis of the Performance Evaluation of Machine Learning Techniques in Business Forecasting. [(accessed on 9 June 2020)];2016 Available online: https://shodhganga.inflibnet.ac.in/handle/10603/109591.
- 28.Guzmán J.C., Miramontes I., Melin P., Prado-Arechiga G. Optimal Genetic Design of Type-1 and Interval Type-2 Fuzzy Systems for Blood Pressure Level Classification. Axioms. 2019;8:8. doi: 10.3390/axioms8010008. [DOI] [Google Scholar]
- 29.Melin P., Miramontes I., Prado-Arechiga G. A hybrid model based on modular neural networks and fuzzy systems for classification of blood pressure and hypertension risk diagnosis. Expert Syst. Appl. 2018;107:146–164. doi: 10.1016/j.eswa.2018.04.023. [DOI] [Google Scholar]
- 30.Cuevas F., Castillo O. Fuzzy Logic Augmentation of Neural and Optimization Algorithms: Theoretical Aspects and Real Applications. Springer; Cham, Switzerland: 2018. Design and implementation of a fuzzy path optimization system for omnidirectional autonomous mobile robot control in real-time; pp. 241–252. [Google Scholar]
- 31.Himavathi S., Umamaheswari B. New membership functions for effective design and implementation of fuzzy systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2001;31:717–723. doi: 10.1109/3468.983428. [DOI] [Google Scholar]
- 32.Franco J.D., Ramirez-Delreal T.A., Villanueva D., Gárate-García A., Armenta-Medina D. Monitoring of Ocimum basilicum seeds growth with image processing and fuzzy logic techniques based on Cloudino-IoT and FIWARE platforms. Comput. Electron. Agric. 2020;173:105389. doi: 10.1016/j.compag.2020.105389. [DOI] [Google Scholar]
- 33.Gonzalez C.I., Melin P., Castro J.R., Mendoza O., Castillo O. An improved sobel edge detection method based on generalized type-2 fuzzy logic. Soft. Comput. 2016;20:773–784. doi: 10.1007/s00500-014-1541-0. [DOI] [Google Scholar]
- 34.Ontiveros E., Melin P., Castillo O. High order α-planes integration: A new approach to computational cost reduction of General Type-2 Fuzzy Systems. Eng. Appl. Artif. Intell. 2018;74:186–197. doi: 10.1016/j.engappai.2018.06.013. [DOI] [Google Scholar]
- 35.Qiu J., Sun K., Rudas I.J., Gao H.-J. Command Filter-Based Adaptive NN Control for MIMO Nonlinear Systems with Full-State Constraints and Actuator Hysteresis. IEEE Trans. Cybern. 2019;PP:1–11. doi: 10.1109/TCYB.2019.2944761. [DOI] [PubMed] [Google Scholar]
- 36.Qiu J., Sun K., Wang T., Gao H.-J. Observer-Based Fuzzy Adaptive Event-Triggered Control for Pure-Feedback Nonlinear Systems with Prescribed Performance. IEEE Trans. Fuzzy Syst. 2019;27:2152–2162. doi: 10.1109/TFUZZ.2019.2895560. [DOI] [Google Scholar]
- 37.Castillo O. Type-2 Fuzzy Logic in Intelligent Control Applications. Springer; Berlin, Germany: 2012. [Google Scholar]
- 38.Ontiveros-Robles E., Melin P., Castillo O. Comparative analysis of noise robustness of type 2 fuzzy logic controllers. Kybernetika. 2018;54:175–201. doi: 10.14736/kyb-2018-1-0175. [DOI] [Google Scholar]