Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 19;20(7):4829–4836. doi: 10.1021/acs.nanolett.0c00756

Correlated Exciton Fluctuations in a Two-Dimensional Semiconductor on a Metal

Rasmus H Godiksen †,‡, Shaojun Wang †,‡,§, T V Raziman †,‡, Marcos H D Guimaraes †,∥, Jaime Gómez Rivas †,‡,§, Alberto G Curto †,‡,*
PMCID: PMC7349615  PMID: 32559090

Abstract

graphic file with name nl0c00756_0006.jpg

Excitons in nanoscale materials can exhibit fluorescence fluctuations. Intermittency is pervasive in zero-dimensional emitters such as single molecules and quantum dots. In contrast, two-dimensional semiconductors are generally regarded as stable light sources. Noise contains, however, valuable information about a material. Here, we demonstrate fluorescence fluctuations in a monolayer semiconductor due to sensitivity to its nanoscopic environment focusing on the case of a metal film. The fluctuations are spatially correlated over tens of micrometers and follow power-law statistics, with simultaneous changes in emission intensity and lifetime. At low temperatures, an additional spectral contribution from interface trap states emerges with fluctuations that are correlated with neutral excitons and anticorrelated with trions. Mastering exciton fluctuations has implications for light-emitting devices such as single-photon sources and could lead to novel excitonic sensors. The quantification of fluorescence fluctuations, including imaging, unlocks a set of promising tools to characterize and exploit two-dimensional semiconductors and their interfaces.

Keywords: tungsten disulfide, fluorescence intermittency, noise, surface traps, trions, charge transfer

Zero-dimensional (0D) systems like semiconductor nanocrystals1,2 and fluorescent dye molecules3 exhibit random jumps between emitting and nonemitting states. As a result, the fluorescence of such quantum emitters fluctuates over time with a telegraphic or flickering signal.4 Such noise in fluorescence is often undesired, as applications include single-photon sources and biological imaging. Extensive efforts in 0D systems have aimed at understanding,5,6 manipulating,4 and suppressing fluctuations.7 Noise contains, however, valuable information about material properties and the interaction with the environment.8 Analyzing noise in fluorescence thus offers an approach for probing local effects such as intrinsic defects, adsorbed molecules, trap states localized near the emitter, the quality of heterostructure interfaces, or changes in the environment. Toward higher dimensionality, although larger semiconductors are expected to be less sensitive to their surroundings, blinking has been reported in perovskites9 and quantum wires.10

In two-dimensional (2D) semiconductors, excitons are confined in the vertical direction, while extending and diffusing along the atomically thin plane.11 Monolayer transition metal dichalcogenides such as MoS2 and WS2 are direct band gap semiconductors.12 As there are no surface dangling bonds, these monolayer semiconductors are generally considered stable light emitters.13 Their integration in devices requires, however, depositing them on metals, insulators, or other semiconductors, where the effects of heterojunctions, strain, or interface imperfections can play a critical role.14 Indeed, the interactions between two monolayers15−17 or between a monolayer and a substrate18 are starting to be exploited to tailor excitons at the nanoscale with unprecedented control. For example, substrates can be used to create localized quantum emitters hosted by the 2D material19−22 or its defects.23 Such 0D-in-2D emitters suffer from fluorescence intermittency.19,23 In stacked bilayer heterostructures, the interlayer charge transfer can result in random oscillations between the emission spectra of two monolayer semiconductors.24 More generally, excitons in a single semiconductor monolayer could be subject to fluctuations reporting on its quality or interfacial disorder, among others.

Here, we demonstrate correlated fluorescence fluctuations over a semiconductor monolayer influenced by its environment. We report strong emission blinking and flickering by placing an atomically thin semiconductor on a metal film, with fluctuations reaching an intensity ratio of 5 between bright and dark events. The fluctuations are temporally synchronized and spatially extended over tens of micrometers. In analogy to blinking in quantum dots, the fluorescence follows power-law statistics and has a frequency spectrum with 1/f noise. We observe a correlation between changes in emission intensity and lifetime, consistent with the existence of trap states at the semiconductor–metal interface. At low temperatures, emission arises from trap states, with fluctuations that are correlated with neutral excitons and anticorrelated with charged excitons (trions). We propose that carrier density fluctuations cause the variations in fluorescence due to a spatial distribution of trap states. Beyond this specific example, our results establish fluorescence fluctuation methods as a framework to characterize the optical and electronic properties of monolayer semiconductors in environments and scales relevant to devices.

Fluorescence Fluctuations: Imaging and Statistics

First, we prepare a monolayer of WS2 with a size of around 50 × 100 μm on a polydimethylsiloxane (PDMS) film and deposit the stack on a gold film with a root-mean-square (RMS) roughness of 4 nm (Figure 1a,b). We record fluorescence microscopy videos under wide-field illumination with a blue lamp using a camera. The resulting fluorescence is also visible by the eye. Compared to the emission of a monolayer on an insulating substrate (SiO2 on Si), the fluorescence intensity displays clearer fluctuations as a function of time for WS2 on Au (Figure 1c and normalized time traces in Supporting Figure 1). We note that fluctuations above noise level are also present for the insulating substrate, although with lower visibility than for the metal film. The emission spectrum remains qualitatively similar during fluctuations (Figure 1d), which occur at room temperature over large areas.

Figure 1.

Figure 1

Open in a new tab

Fluorescence fluctuations of a monolayer semiconductor on a metal film. (a) Illustration of a WS2 monolayer on an Au surface. Roughness results in a spatially varying density of trap states along with the interface. An inhomogeneous band bending facilitates trapping of holes near the contact points. (b) Reflection micrograph highlighting a monolayer region. A few multilayer regions are visible within the monolayer area. (c) Fluorescence time trace showing flickering and blinking for a point of the monolayer on Au (red) compared to a monolayer on a thermally oxidized Si substrate (blue). Time bins are 20 ms. (d) Emission spectrum over time, demonstrating that neutral excitons dominate the emission during fluctuations at room temperature. (e) Fluorescence video snapshots exhibiting fluctuations within monolayer domains. See Video S1.

To investigate the spatial extent of the fluctuations, we refer to each continuous part of a monolayer in fluorescence images as a domain (Figure 1e and Video S1). Most domains appear after transfer from PDMS to Au due to the formation of cracks in the monolayer, but the monolayer properties stay homogeneous (Supporting Figures 2 and 3). Within the same monolayer, some domains fluctuate substantially more than others, as quantified statistically through the values of the mean intensity, the standard deviation, and their ratio as a measure of fluctuation amplitude (Supporting Figure 4). For reference, the same monolayer displays no substantial fluctuations while lying on a polymer stamp before transfer to Au (Video S2). Similarly, the emission of a monolayer lying on both metal and dielectric fluctuates clearly on the metal area (Video S3).

To analyze the synchronous fluctuations within monolayer domains, we select four points and compare their time traces (Figure 2a,b). The time traces are similar for pairs of points within the same domain (AB and CD). In contrast, the traces differ for points in different domains like BC, despite being closer in space than the AB points. To quantify the spatial extension of the fluctuations, we calculate the spatiotemporal correlation function between two points as

graphic file with name nl0c00756_m001.jpg

where Ir1(t) is the intensity time trace at point r1, ΔIr1(t) = Ir1(t) – ⟨Ir1(t)⟩ is the deviation from the mean value calculated over the whole measurement interval, and τ is a delay between both time traces. The correlations are high and long-lasting for pairs of points within the same domain, while they are lower for points in different domains (Figure 2c). The decay of correlation with delay is well described by a double exponential function,24g(2)(τ) = c1e–τ/T1 + c2 e–τ/T2 + c3 (solid lines in Figure 2c, see Supporting Table 1 for fitting parameters), suggesting that two processes such as trapping and detrapping account for the fluctuations.

Figure 2.

Figure 2

Open in a new tab

The fluctuations are spatially correlated within monolayer domains. (a) Fluorescence image indicating selected points for spatial and temporal correlations. (b) The time traces acquired simultaneously at those points show correlated fluctuations for positions inside the same domain (AB and CD). (c) Spatiotemporal correlation function for the same time traces. Points within the same domain (AB and CD) possess high and long-lasting correlations, whereas points in different domains (BC) have almost no correlation. The arrows on the vertical axis indicate the values at zero delay. (d) Spatial correlation function calculated at zero delay for every pixel in the image with respect to the three pixels marked by black crosses. Spatial correlations are homogeneous within the same domain as the cross point, and higher for the most fluctuating domains (1 and 3). Lower correlations with neighboring domains are also present.

Apart from strong intradomain correlations, there are also weaker interdomain spatial correlations. We calculate the correlation function between a pixel inside a given domain (crosses in Figure 2d) and every pixel on the image. The fluctuations show strong spatial correlations within each domain with g(2)(0) ∼ 1. As a general trend, domains with stronger fluctuations have higher spatial correlations (e.g., Domains 1 and 3. See also Supporting Figure 4). Although most domains are uncorrelated with their neighbors (g(2) < 0.1), in a few cases, neighboring domains maintain some degree of spatial correlation (g(2) > 0.5). We attribute the distribution of interdomain spatial correlations to partial electrical connections between domains due to cracks resulting in charge redistribution. On the other hand, spatial correlations are absent in nonfluctuating monolayers on insulating substrates (Supporting Figure 5).

We can draw similarities between our 2D semiconductor and 0D systems. In quantum dots, the distribution of time spent on bright and dark states often follows an inverse power law over several orders of magnitude in on- and off-times. We make a similar analysis for our 2D semiconductor. We define three intensity levels (bright, dark, and neutral) from a typical time trace by setting the threshold values for the bright (dark) events as the average plus (minus) the standard deviation, with neutral states in between (Figure 3a). For a pixel at the center of Domain 2, the number of bright and dark events follows an inverse power law with respect to their duration, P(t) = At–β, where P is the probability density, t is the dwell time, and A and β are retrieved by the fitting. The neutral events are best described instead by an inverse power law with an exponential cutoff, P(t) = At–βe–t/tc, with tc as a fitting parameter. We perform the same analysis at every pixel to represent the power-law exponent β in images (Figure 3b,c and Supporting Section I). The fluctuation statistics are homogeneous within each domain but differ between domains, as expected from the spatial correlation maps (Figure 2d).

Figure 3.

Figure 3

Open in a new tab

Statistical analysis of the fluctuations. (a) The duration of bright and dark events follows a power-law distribution, while neutral events of intermediate brightness follow a truncated power law. Inset: part of a time trace from a pixel in Domain 2 with thresholds defining bright, dark, and neutral events. (b, c) Power-law exponent β for bright and dark events retrieved by fitting the fluorescence image time trace to a power law for each pixel. (d) Power spectral density (for the same point as in panel a) revealing pink noise in the time trace. (e, f) Noise exponent α and noise power At obtained from fitting power spectral density at each pixel.

The inverse power-law behavior suggests a relation between the fluctuation mechanisms in our system and quantum dots. Such dependence is characteristic of an exponential distribution of tunneling distances or depths to trap states near the emitter.25 In our experiments, the spatially correlated fluorescence fluctuations are clearly noticeable for Au films with surface RMS roughness ≥2 nm only (Supporting Figure 8 and Supporting Table 4). The WS2/Au surface inherits roughness from the underlying metal (Supporting Section II, Supporting Figure 9, and Supporting Table 5). Considering the work functions of WS2 (5.01 eV)26 and Au (5.3–5.6 eV)26,27 and previous reports on their contacts,28 we expect upward band bending between n-type WS2 and Au. Roughness causes variations in the distance, creating a distribution of trap states along the interface mediated by local band bending (Figure 1a), resulting in a distribution of tunneling energy and probability. Local changes in roughness and density of trap states under each domain can then be the reason for the observed differences in the power-law exponent β in different domains. Furthermore, previous reports of monolayer WS2/Au junctions pointed out a large number of interface trap states,29,30 which could play a similar role to surface traps in quantum dots proposed as a mechanism for blinking.31 Unlike in quantum dots, fluorescence fluctuations in our system occur in two dimensions.

To shed further light on the origin of the fluctuations, we examine them in the frequency domain using the power spectral density (PSD). For colloidal quantum dots, the PSD takes the form of pink noise.32,33 In semiconductor devices, pink noise generally indicates low-frequency fluctuations in carrier density.34 From a time trace, we calculate the PSD as a function of frequency as PSD(f) = |FFT(ΔI(t))|2, where FFT is the fast Fourier transform. The spectrum can be described as pink noise, as it fits the expression PSD(f) = At/fα with 0.8 < α < 1.2, where At is the noise power (Figure 3d). From the analysis of the PSD (Figure 3e,f), we note that both α and At are generally higher for domains that fluctuate more (Domains 1 and 3). On dielectric substrates, 1/f noise is also present (see a comparison of different Au samples, dielectrics, and a dye film in Supporting Figure 10). In the context of 2D materials, 1/f noise can arise from charge traps at the 2D-material–substrate interface. Electrical 1/f noise has been reported in graphene35 and MoS2 transistors,36 but not in optical measurements of any 2D material to the best of our knowledge.

Fluctuations of Lifetime and Low-Temperature Spectra

In quantum dots, surface-trap-induced or Auger recombinations result in fast nonradiative decay and, hence, a shorter lifetime during dark events.37 Following this analogy, we study the emission lifetime during bright and dark events. We use time-tagged time-resolved measurements to obtain simultaneous time traces of intensity and lifetime. We estimate the average lifetime for each time bin by fitting the fluorescence decay to a biexponential function (see Methods). The measured effective lifetime contains a significant contribution of the slower transition from spin-forbidden exciton states to spin-allowed states.38−40 The measurements reveal that the average lifetime increases when the fluorescence intensity increases (Figure 4a,b). We focus our analysis on a smaller monolayer on Au with strong fluctuations reaching an intensity ratio of 5 between bright and dark events (Figure 4b and Video S5). The fluorescence lifetime-intensity distribution4 provides a statistical overview of the lifetime variations (Figure 4c). The observed linear correlation between intensity and lifetime is a signature of surface-trap-induced nonradiative recombination, as reported for colloidal quantum dots37 and in agreement with the existence of trap states at the WS2/Au interface.

Figure 4.

Figure 4

Open in a new tab

The emission lifetime fluctuates together with the intensity, suggesting surface-trap-induced recombination as the fluctuation mechanism. (a) Fluorescence decay lifetime during dark and bright events retrieved from time-tagged time-resolved traces. (b) Intensity and lifetime traces show a correlation between changes in brightness and the average lifetime. (c) Fluorescence lifetime-intensity distribution histogrammed over 2000 s. The diagonal distribution suggests that the opening and closing of nonradiative channels is responsible for the fluctuations. Data acquired on the WS2 monolayer on Au shown in Video S5 with strong fluorescence fluctuations. (d) Illustration of the dependence of the quantum yield on carrier density. Trapping and detrapping of holes at the WS2/Au interface cause carrier density fluctuations (black arrow), resulting in fluorescence fluctuations. Inset: Fermi level at the limiting regimes of carrier density. Red (white) circles indicate filled (empty) hole states in the semiconductor.

The intensity-lifetime correlation during fluorescence fluctuations corresponds well with recent experiments on electrostatic gating of monolayer WS2,41,42 where an increase of carrier density and Fermi level result in a reduction of both intensity and lifetime. On the basis of these observations, we propose a mechanism for how hole trapping and release events cause fluctuations in carrier density (nd), resulting in fluctuations of intensity and lifetime (Figure 4d). Our monolayers are slightly n-doped (nd ≈ 1012 cm–2)29,43 and have a typical quantum yield of 10–20%40 before transfer to Au. These values set the neutral point for fluctuations due to the dependence of quantum yield on carrier density.41,42 As they occur at the onset of the slope in quantum yield (Figure 4d, black arrow), carrier density fluctuations produce a pronounced change in fluorescence. For comparison, we also placed monolayers of MoS2 and WSe2 on the same Au film. Fluorescence fluctuations are not visible in these cases, in agreement with the carrier densities of MoS2 and WSe2 (highly n-doped and neutral, respectively), for which the quantum yield dependence on carrier density is mostly flat (Figure 4d).42

Next, we demonstrate the existence of trap states at the WS2/Au interface and the dynamic interaction between neutral excitons, trions, and trap states. We conduct spectroscopy at low temperatures on another WS2 monolayer on Au and compare it to a reference one on quartz (Figure 5a). The two fluorescence peaks with the highest energy correspond to neutral excitons (X0) and trions (X–), in agreement with literature38,43,44 and the temperature evolution of the spectrum (Supporting Figure 11). For WS2 on Au, a broad spectral contribution emerges at low temperatures centered around 640 nm (DAu in Figure 5a), which is not present for WS2 on quartz. We assign it to interface trap states.

Figure 5.

Figure 5

Open in a new tab

Spectral correlations at low temperature for neutral exciton, trion, and interface trap states. (a) Low-temperature fluorescence spectra with neutral exciton and trion peaks (X0 and X–). A broad set of peaks appears for WS2 on Au (DAu), whereas it is absent for WS2 on quartz (gray line). (b) Spectral time traces on Au and quartz plotted as the deviation from the mean value at each wavelength, showing that DAu trap states dominate the fluctuations. Trace based on Video S6. (c) Spectral correlation function for the time traces in panel b calculated over 250 s, demonstrating that the fluorescence fluctuations of excitons and trions are anticorrelated on Au. The neutral excitons and trions have mostly positive and negative correlations with DAu, respectively. Both diagonal lines are equal to 1.

The emission from neutral excitons, trions, and trap states fluctuates at low temperatures, but with different amplitudes and not independently. To visualize the relative intensity changes of X0, X–, and DAu, we calculate the spectral time trace as the intensity at each wavelength minus its mean value (Figure 5b). Remarkably, most of the fluctuations now occur in DAu, undergoing internal spectral changes over time (see t = 0–7.5 s in Figure 5b and Video S6). During significant blinking events, all peaks are involved (e.g., t = 7.5–10.0 s in Figure 5b), with X0 increasing together with parts of DAu, and X– decreasing below its mean value. To evaluate such relations between peaks, we calculate the spectral correlation between two wavelengths λ1 and λ2 as a function of time delay:

graphic file with name nl0c00756_m002.jpg

There is an anticorrelation between X0 and X– for a monolayer on Au, while X0 and X– lack correlation on quartz (Figures 5c). The anticorrelation between X0 and X– on Au is in agreement with changes in carrier density during fluorescence fluctuations because the intensity ratio between X0 and X– is inversely proportional to the carrier density via the law of mass action.45 We also observe that X0 and X– correlate and anticorrelate with most of the DAu spectral region, respectively, indicating that the population of trap states controls the carrier density. When the interface traps capture holes, the carrier density increases resulting in a simultaneous increase of the trion and a decrease of the neutral exciton emission (Figure 4d). At room temperature, where trap states are nonradiative, it leads to suppressed excitonic fluorescence.

As confirmation of carrier density fluctuations also at room temperature, we analyze the relative contributions of excitons and trions to the total fluorescence24 in spectral time traces using Gaussian fitting (Supporting Section III and Supporting Figures 12 and 13). Following the law of mass action, we observe an anticorrelation between the total fluorescence and the ratio of the integrated emission of trions and excitons,45,46 confirming that carrier density fluctuations occur during changes in fluorescence. We propose that the spatially correlated fluctuations are due to fast Fermi level equilibration inside each domain. Localized trapping and detrapping events affect the local Fermi level, followed by a quick redistribution of the excess carriers to equilibrate it inside the domain at a much faster rate than the fluorescence fluctuations.

In conclusion, we have reported synchronous fluorescence fluctuations in an atomically thin semiconductor due to the interaction with its environment. We have analyzed a case with strong fluctuations: monolayer WS2 on Au. The fluctuations are spatially extended over micrometer-scale domains and occur at room temperature without major spectral changes. They are thus qualitatively different compared to localized quantum emitters in 2D semiconductors,20,21 which exhibit intermittency with spectral wandering at cryogenic temperatures. The analysis of the fluctuations reveals power-law statistics and pink noise. Together with a correlation between intensity and lifetime, the experimental evidence suggests similarities with blinking in conventional quantum dots. We have drawn several analogies with quantum dots as a starting point for our study. However, in contrast to quantum dots, we measure ensembles of excitons in an extended system. Due to limited spatial and temporal resolutions, fluctuations and additional underlying mechanisms might become evident at smaller and faster scales.

At low temperatures, we observe anticorrelated intensity fluctuations between excitons and trions and the appearance of a broad spectral contribution. On the basis of these observations, we propose a mechanism based on carrier density fluctuations caused by trap states at the semiconductor–metal interface. The fluorescence fluctuations are thus a direct manifestation of charge transfer events. As the Fermi level must be in equilibrium within a monolayer domain, charge transfer at a localized position affects the Fermi level over the entire domain. We anticipate several aspects that may play a role in the magnitude and frequency of the fluctuations: substrate disorder including roughness, domain area, electrical connections between domains, and optical excitation area. These parameters are thus open for future investigations to engineer and exploit exciton fluctuations.

Understanding the mechanisms behind exciton fluctuations is necessary for stable light-emitting devices based on 2D semiconductors, with implications for single-photon sources, lasers, or modulators. Moreover, the observation of fluctuations opens the perspective of exciton-based sensing and imaging using the temporal and spatial changes of their fluorescence to detect the presence of charges or nonfluorescent molecules. Last, we envisage that fluorescence fluctuation methods could lead to a refined understanding and characterization of 2D materials, regarding quality and disorder. In our study, we focused on an example where fluctuations are highly visible. When applied to other van der Waals heterostructures and interfaces with bulk materials, fluctuation analysis tools, including imaging, could retrieve quantitative information buried within apparent noise.

Methods

Sample Preparation

We exfoliated WS2 (bulk crystal from HQ Graphene) using tape (Nitto SPV224PR) onto PDMS (Gel-Pak PF-80-X4) thin-film stamps. We identified the monolayers using fluorescence microscopy and deposited them onto Au films using a soft transfer method that preserves their optical properties.40 Using electron-beam evaporation, we deposited Au films (50–100 nm) on a Ti adhesion layer (1–3 nm) on oxidized silicon substrates (100 nm SiO2 on Si). The PDMS stamp remained on top of the sample to prevent monolayer damage upon its removal. The samples consisted then of PDMS/WS2/Au, unless otherwise indicated. For map analysis (Figures 1–3), we used the same WS2 monolayer shown in Figure 1b and Videos S1 and S2. For the lifetime time trace analysis (Figure 4), we used a smaller monolayer with larger amplitude fluctuations (Video S5). For the low-temperature measurements (Figure 5), we used a different monolayer and removed the PDMS to avoid strain during cooling.

Dynamic Fluorescence Imaging

Fluorescence wide-field imaging was carried out in an inverted microscope using epi-illumination geometry and an objective with adjustable cover-glass correction (60× Nikon S Plan Fluor, NA = 0.7). For excitation, we used a metal halide lamp (EXFO X-Cite 120) with a bandpass filter at 445 nm. After wide-field excitation with a typical power of 0.22 μW/μm2, we detect fluorescence with a 458 nm long-pass filter. For time-resolved wide-field imaging, we used an Andor Neo 5.5 sCMOS camera cooled to −40 °C. For every image time trace and Videos S1 and S4, the time bin per frame is 20 ms. We used a Nikon DS-Fi2 color camera for Videos S2 (15 ms), S3, and S5(60 ms).

Dynamic Fluorescence Lifetime and Spectroscopy

Fluorescence lifetime and spectral time traces were recorded in an upright confocal microscope in epi-illumination geometry through an objective (40× Nikon CFI Plan Fluor ELWD, NA = 0.6) with an adjustable cover-glass correction. A focused laser excites the sample, and detection occurs at the same point through an optical fiber. For time-tagged time-resolved fluorescence measurements, we used a pulsed laser (Fianium SC400 with an acousto-optical filter tuned to 532 nm, 0.13 μW/μm2, pulse duration ∼50 ps), an avalanche photodiode (Micro Photon Devices, 50 μm SPAD, dark counts <25 counts/s), and a PicoHarp 300 time-correlated single-photon counter. For fluorescence spectroscopy, we used a 532 nm continuous-wave laser (14.3 μW/μm2). We recorded spectra with an Andor Shamrock 303 spectrometer and an Andor Newton 970 EMCCD camera cooled to −75 °C and a time bin per spectrum of 25 ms. All fluorescence measurements were carried out at room temperature, except Figure 5 at 35 K using a microscopy cryostat (Oxford Instruments MicrostatHires).

Time-Tagged Time-Resolved Analysis

To analyze the time-tagged time-resolved measurements, we used the SymPhoTime 64 software (Picoquant). First, the time-tagged time-resolved traces were binned to 100 ms. For each time bin, we performed a biexponential reconvolution of each fluorescence decay curve on the form I(t) = A0e–t/τ0 + A1e–t/τ1 with the instrument response function (IRF) measured as the laser reflection. From the fitting, we determined the average lifetime as τavg = (A0 τ02 + A1 τ1)/(A0 τ0 + A1 τ1) and evaluated the goodness of fit 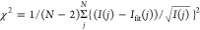Inline graphic per time trace bin, where N is the number of points in the decay curve (Supporting Figure 14).

Acknowledgments

We thank Saravana Balaji Basuvalingam, Shashank Balasubramanyam, and Simone Eizagirre Barker for technical assistance. We thank the anonymous reviewers for their constructive suggestions. This work was financially supported by The Netherlands Organisation for Scientific Research (NWO) through the Gravitation grant “Research Centre for Integrated Nanophotonics” (024.002.033) and an NWO START-UP grant (740.018.009). M.H.D.G. acknowledges support by an NWO VENI grant (15093).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c00756.

  • Thresholds for power-law analysis; quantification of topographical parameters; neutral exciton and trion fluctuations at room temperature; fluorescence comparison of WS2/Au and WS2/SiO2/Si; fluorescence spectra from three different domains of the monolayer WS2 on Au; fluorescence lifetime and intensity imaging before and after transfer to Au; fluctuation statistics for a fluorescence image time trace; WS2 monolayer on an insulating polymer substrate; time trace and noise comparison of WS2 on different substrates; influence of different event thresholds on the power-law analysis; quality of fitting for power-law and noise analysis; atomic force microscopy of different Au substrates; topography comparison of WS2 on Au and Au surfaces; time trace and noise comparison of WS2 on different substrates; fluorescence spectra for WS2/Au at different temperatures; neutral exciton and trion contributions to the total fluorescence in a degraded sample; neutral exciton and trion contributions to the total fluorescence in a fresh sample; evaluation of lifetime data; fitting parameters for the spatiotemporal correlations; power-law exponent for bright events when changing the threshold; power-law exponent for dark events when changing the threshold; roughness parameters for different Au substrates; roughness parameters for WS2/Au (PDF)

  • Video S1 (MP4)

  • Video S2 (MP4)

  • Video S3 (MP4)

  • Video S4 (MP4)

  • Video S5 (MP4)

  • Video S6 (MP4)

The authors declare no competing financial interest.

This paper was published ASAP on June 26, 2020 with an error in the equation in the Fluorescence Fluctuations: Imaging and Statistics. The corrected version reposted on July 8, 2020.

Supplementary Material

nl0c00756_si_001.pdf (14.9MB, pdf)
nl0c00756_si_002.mp4 (28.4MB, mp4)
nl0c00756_si_003.mp4 (4.4MB, mp4)
nl0c00756_si_004.mp4 (6.6MB, mp4)
nl0c00756_si_005.mp4 (9.8MB, mp4)
nl0c00756_si_006.mp4 (5.6MB, mp4)
nl0c00756_si_007.mp4 (6.7MB, mp4)

References

  1. Nirmal M.; et al. Fluorescence intermittency in single cadmium selenide nanocrystals. Nature 1996, 383, 802–804. 10.1038/383802a0. [DOI] [Google Scholar]
  2. Shimizu K. T.; et al. Blinking statistics in single semiconductor nanocrystal quantum dots. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 63, 205316. 10.1103/PhysRevB.63.205316. [DOI] [Google Scholar]
  3. Hoogenboom J. P.; Hernando J.; van Dijk E. M. H. P.; van Hulst N. F.; García-Parajó M. F. Power-law blinking in the fluorescence of single organic molecules. ChemPhysChem 2007, 8, 823–833. 10.1002/cphc.200600783. [DOI] [PubMed] [Google Scholar]
  4. Galland C.; et al. Two types of luminescence blinking revealed by spectroelectrochemistry of single quantum dots. Nature 2011, 479, 203–207. 10.1038/nature10569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Klimov V. I. Optical Nonlinearities and Ultrafast Carrier Dynamics in Semiconductor Nanocrystals. J. Phys. Chem. B 2000, 104, 6112–6123. 10.1021/jp9944132. [DOI] [Google Scholar]
  6. Efros A. L.; Nesbitt D. J. Origin and control of blinking in quantum dots. Nat. Nanotechnol. 2016, 11, 661–671. 10.1038/nnano.2016.140. [DOI] [PubMed] [Google Scholar]
  7. Mahler B.; et al. Towards non-blinking colloidal quantum dots. Nat. Mater. 2008, 7, 659–664. 10.1038/nmat2222. [DOI] [PubMed] [Google Scholar]
  8. Rumyantsev S.; Liu G.; Shur M. S.; Potyrailo R. A.; Balandin A. A. Selective gas sensing with a single pristine graphene transistor. Nano Lett. 2012, 12, 2294–2298. 10.1021/nl3001293. [DOI] [PubMed] [Google Scholar]
  9. Pathoor N.; et al. Fluorescence Blinking Beyond Nanoconfinement: Spatially Synchronous Intermittency of Entire Perovskite Microcrystals. Angew. Chem., Int. Ed. 2018, 57, 11603–11607. 10.1002/anie.201804852. [DOI] [PubMed] [Google Scholar]
  10. Glennon J. J.; Tang R.; Buhro W. E.; Loomis R. A. Synchronous photoluminescence intermittency (blinking) along whole semiconductor quantum wires. Nano Lett. 2007, 7, 3290–3295. 10.1021/nl0714583. [DOI] [PubMed] [Google Scholar]
  11. Kulig M.; et al. Exciton Diffusion and Halo Effects in Monolayer Semiconductors. Phys. Rev. Lett. 2018, 120, 207401. 10.1103/PhysRevLett.120.207401. [DOI] [PubMed] [Google Scholar]
  12. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
  13. Peimyoo N.; et al. Nonblinking, intense two-dimensional light emitter: Monolayer WS2 Triangles. ACS Nano 2013, 7, 10985–10994. 10.1021/nn4046002. [DOI] [PubMed] [Google Scholar]
  14. Raja A.; et al. Dielectric disorder in two-dimensional materials. Nat. Nanotechnol. 2019, 14, 832–837. 10.1038/s41565-019-0520-0. [DOI] [PubMed] [Google Scholar]
  15. Yu H.; Wang Y.; Tong Q.; Xu X.; Yao W. Anomalous Light Cones and Valley Optical Selection Rules of Interlayer Excitons in Twisted Heterobilayers. Phys. Rev. Lett. 2015, 115, 187002. 10.1103/PhysRevLett.115.187002. [DOI] [PubMed] [Google Scholar]
  16. Seyler K. L.; et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 2019, 567, 66–70. 10.1038/s41586-019-0957-1. [DOI] [PubMed] [Google Scholar]
  17. Tran K.; et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 2019, 567, 71–75. 10.1038/s41586-019-0975-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Taniguchi T.; et al. Van der Waals engineering of ferromagnetic semiconductor heterostructures for spin and valleytronics. Sci. Adv. 2017, 3, e1603113 10.1126/sciadv.1603113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Koperski M.; et al. Single photon emitters in exfoliated WSe2 structures. Nat. Nanotechnol. 2015, 10, 503–506. 10.1038/nnano.2015.67. [DOI] [PubMed] [Google Scholar]
  20. Kumar S.; Kaczmarczyk A.; Gerardot B. D. Strain-Induced Spatial and Spectral Isolation of Quantum Emitters in Mono- and Bilayer WSe2. Nano Lett. 2015, 15, 7567–7573. 10.1021/acs.nanolett.5b03312. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Branny A.; Kumar S.; Proux R.; Gerardot B. D. Deterministic strain-induced arrays of quantum emitters in a two-dimensional semiconductor. Nat. Commun. 2017, 8, 15053. 10.1038/ncomms15053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Palacios-Berraquero C.; Kara D. M.; Montblanch A. R.-P.; Barbone M.; Latawiec P.; Yoon D.; Ott A. K.; Loncar M.; Ferrari A. C.; Atature M. Large-scale quantum-emitter arrays in atomically thin semiconductors. Nat. Commun. 2017, 8, 15093. 10.1038/ncomms15093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Martinez L. J.; Pelini T.; Waselowski V.; Maze J. R.; Gil B.; Cassabois G.; Jacques V. Efficient single photon emission from a high-purity hexagonal boron nitride crystal. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 1–5. 10.1103/PhysRevB.94.121405. [DOI] [Google Scholar]
  24. Xu W.; et al. Correlated fluorescence blinking in two-dimensional semiconductor heterostructures. Nature 2017, 541, 62–67. 10.1038/nature20601. [DOI] [PubMed] [Google Scholar]
  25. Kuno M.; Fromm D. P.; Hamann H. F.; Gallagher A.; Nesbitt D. J. Nonexponential “blinking” kinetics of single CdSe quantum dots: A universal power law behavior. J. Chem. Phys. 2000, 112, 3117. 10.1063/1.480896. [DOI] [Google Scholar]
  26. Chanana A.; Mahapatra S. Density functional theory based study of chlorine doped WS2-metal interface. Appl. Phys. Lett. 2016, 108, 103107. 10.1063/1.4943267. [DOI] [Google Scholar]
  27. Sachtler W. M. H.; Dorgelo G. J. H.; Holscher A. A. The work function of gold. Surf. Sci. 1966, 5, 221–229. 10.1016/0039-6028(66)90083-5. [DOI] [Google Scholar]
  28. Somvanshi D.; et al. Nature of carrier injection in metal/2D-semiconductor interface and its implications for the limits of contact resistance. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 205423. 10.1103/PhysRevB.96.205423. [DOI] [Google Scholar]
  29. Fan Y.; et al. Photoinduced Schottky Barrier Lowering in 2D Monolayer WS2 Photodetectors. Adv. Opt. Mater. 2016, 4, 1573–1581. 10.1002/adom.201600221. [DOI] [Google Scholar]
  30. Kim C.; et al. Fermi Level Pinning at Electrical Metal Contacts of Monolayer Molybdenum Dichalcogenides. ACS Nano 2017, 11, 1588–1596. 10.1021/acsnano.6b07159. [DOI] [PubMed] [Google Scholar]
  31. Frantsuzov P.; Kuno M.; Jankó B.; Marcus R. A. Universal emission intermittency in quantum dots, nanorods and nanowires. Nat. Phys. 2008, 4, 519–522. 10.1038/nphys1001. [DOI] [Google Scholar]
  32. Pelton M.; Grier D. G.; Guyot-Sionnest P. Characterizing quantum-dot blinking using noise power spectra. Appl. Phys. Lett. 2004, 85, 819. 10.1063/1.1779356. [DOI] [Google Scholar]
  33. Sadegh S.; Barkai E.; Krapf D. 1/f Noise for Intermittent Quantum Dots Exhibits Non-Stationarity and Critical Exponents. New J. Phys. 2014, 16, 113054. 10.1088/1367-2630/16/11/113054. [DOI] [Google Scholar]
  34. Hooge F. N. Discussion of recent experiments on 1/f noise. Physica 1972, 60, 130–144. 10.1016/0031-8914(72)90226-1. [DOI] [Google Scholar]
  35. Balandin A. A. Low-frequency 1/f noise in graphene devices. Nat. Nanotechnol. 2013, 8, 549–555. 10.1038/nnano.2013.144. [DOI] [PubMed] [Google Scholar]
  36. Sangwan V. K.; et al. Low-frequency electronic noise in single-layer MoS2 transistors. Nano Lett. 2013, 13, 4351–4355. 10.1021/nl402150r. [DOI] [PubMed] [Google Scholar]
  37. Yuan G.; Gómez D. E.; Kirkwood N.; Boldt K.; Mulvaney P. Two Mechanisms Determine Quantum Dot Blinking. ACS Nano 2018, 12, 3397–3405. 10.1021/acsnano.7b09052. [DOI] [PubMed] [Google Scholar]
  38. Wang G.; et al. In-Plane Propagation of Light in Transition Metal Dichalcogenide Monolayers: Optical Selection Rules. Phys. Rev. Lett. 2017, 119, 047401. 10.1103/PhysRevLett.119.047401. [DOI] [PubMed] [Google Scholar]
  39. Palummo M.; Bernardi M.; Grossman J. C. Exciton radiative lifetimes in two-dimensional transition metal dichalcogenides. Nano Lett. 2015, 15, 2794–2800. 10.1021/nl503799t. [DOI] [PubMed] [Google Scholar]
  40. Eizagirre Barker S.; et al. Preserving the Emission Lifetime and Efficiency of a Monolayer Semiconductor upon Transfer. Adv. Opt. Mater. 2019, 7, 1900351. 10.1002/adom.201900351. [DOI] [Google Scholar]
  41. Shang J.; et al. Observation of Excitonic Fine Structure in a 2D Transition-Metal Dichalcogenide Semiconductor. ACS Nano 2015, 9, 647–655. 10.1021/nn5059908. [DOI] [PubMed] [Google Scholar]
  42. Lien D.-H.; et al. Electrical suppression of all nonradiative recombination pathways in monolayer semiconductors. Science 2019, 364, 468–471. 10.1126/science.aaw8053. [DOI] [PubMed] [Google Scholar]
  43. Jadczak J.; et al. Probing of free and localized excitons and trions in atomically thin WSe2, WS2, MoSe2 and MoS2 in photoluminescence and reflectivity experiments. Nanotechnology 2017, 28, 395702. 10.1088/1361-6528/aa87d0. [DOI] [PubMed] [Google Scholar]
  44. Plechinger G.; et al. Identification of excitons, trions and biexcitons in single-layer WS2. Phys. Status Solidi RRL 2015, 9, 457–461. 10.1002/pssr.201510224. [DOI] [Google Scholar]
  45. Ross J. S.; Wu S.; Yu H.; Ghimire N. J.; Jones A. M.; Aivazian G.; Yan J.; Mandrus D. G.; Xiao D.; Yao W.; Xu X. Electrical control of neutral and charged excitons in a monolayer semiconductor. Nat. Commun. 2013, 4, 1474. 10.1038/ncomms2498. [DOI] [PubMed] [Google Scholar]
  46. Siviniant J.; Scalbert D.; Kavokin A. V.; Coquillat D.; Lascaray J.-P. Chemical equilibrium between excitons, electrons, and negatively charged excitons in semiconductor quantum wells. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1602. 10.1103/PhysRevB.59.1602. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c00756_si_001.pdf (14.9MB, pdf)
nl0c00756_si_002.mp4 (28.4MB, mp4)
nl0c00756_si_003.mp4 (4.4MB, mp4)
nl0c00756_si_004.mp4 (6.6MB, mp4)
nl0c00756_si_005.mp4 (9.8MB, mp4)
nl0c00756_si_006.mp4 (5.6MB, mp4)
nl0c00756_si_007.mp4 (6.7MB, mp4)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES