Abstract
Post-translational modifications (PTMs) of proteins are recognized as crucial components of cell signaling pathways through modulating folding, altering stability, changing interactions with ligands, and, therefore, serving multiple regulatory functions. PTMs occur as covalent modifications of the protein’s amino acid side chains or the length and composition of their termini. Here we study the functional consequences of PTMs for α-synuclein (αSyn) interactions with the nanopore of the voltage-dependent anion channel (VDAC) of the outer mitochondrial membrane. PTMs were mimicked by a divalent Alexa Fluor 488 sidechain attached separately at two positions on the αSyn C-terminus. Using single-channel reconstitution into planar lipid membranes, we find that such modifications change interactions drastically in both efficiency of VDAC inhibition by αSyn and its translocation through the VDAC nanopore. Analysis of the on/off kinetics in terms of an interaction “quasipotential” allows the positions of the C-terminal modifications to be determined with an accuracy of about three residues. Moreover, our results uncover a previously unobserved mechanism by which cytosolic proteins control β-barrel channels and thus a new regulatory function for PTMs.
Introduction
The DNA sequencing revolution has yielded a wealth of genomic information, so that that the primary and secondary structure of proteins and polypeptides, if not their final, functional folds, can be predicted. The relationship between the genome and the proteome, i.e. the final protein expression levels in vivo, however, remains an active area of research. Ideal tools for quantitation of the proteome would operate at as granular a level as possible, with the ultimate goal being quantitative measurement of the proteome of a single cell.1, 2
Complicating proteomic measurement is the presence of misfolded and especially post-translationally modified proteins.3, 4 Proteins that have undergone post-translational modifications (PTMs) exhibit functions and structures that are different from unmodified proteins. Quantitation of PTM levels in a population of otherwise identical proteins may be as important for understanding cellular function as the base protein expression levels.
In principle, nanopore-based detection technology is well-suited for comparing small populations of similar biomolecules. As a single-molecule technique, nanopore detection is local and requires extremely small sample volumes. In addition, detection of small chemical modifications such as cytosine methylation has been amply demonstrated.5-7 Unlike the usual polynucleic acid analytes, however, which are uniformly charged, generally without secondary structure, and containing only 4 basic units (excluding cytosine methylation), proteins and polypeptides are heterogeneously charged, have additional structure over a range of length scales, and comprise 22 chemically distinct residues before PTM.
In previous work, we have shown that the motion of a polypeptide in a nanopore can be understood in terms of an energy landscape by constructing an interaction “quasipotential” with contributions from the entropy, membrane association, and voltage-induced electrodynamics.8, 9 This method is very general and can be applied to different nanopore systems and biopolymer analytes.10, 11 Here, we show that a PTM mimic at a single residue affects the quasipotential and consequently the interaction dynamics. As a model system, we choose the well-characterized, intrinsically disordered neuronal protein α-synuclein (αSyn) to explore the effect of PTMs on the dynamics of interaction with a large β-barrel membrane protein of the mitochondrial outer membrane, the voltage-dependent anion channel (VDAC). To chemically model PTM, we use Alexa Fluor 488 (“Alexa”) functionalization. We find that the bulky, divalent Alexa sidechain introduces an additional entropic term to the interaction potential that has a strong effect on the capture and retraction/translocation dynamics through VDAC nanopore. Analysis using energy landscape modeling allows determination of the PTM position to within a few residues. Finally, we discuss the ramifications of PTMs for the function of cytosolic VDAC regulators, including αSyn and its more abundant counterpart, dimeric tubulin.
Results and Modeling
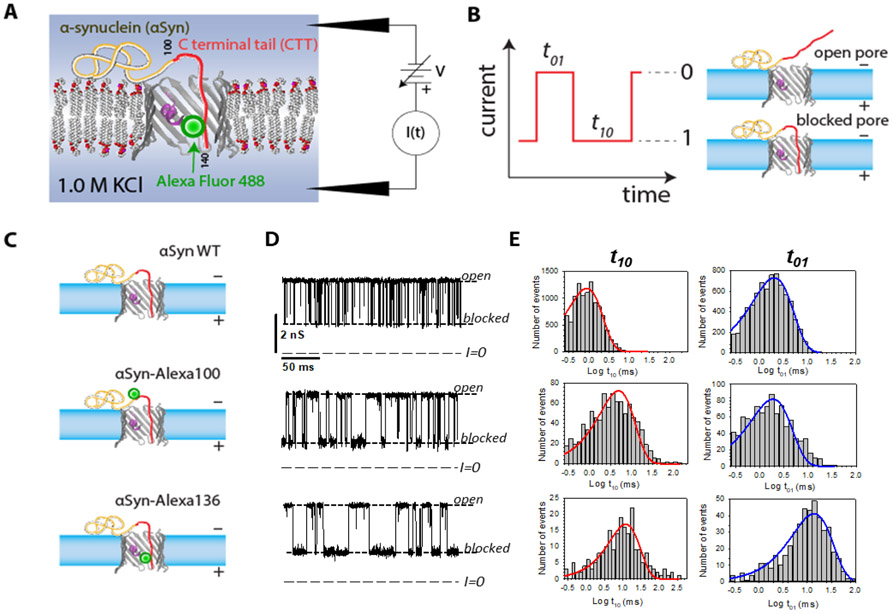
The experimental setup is shown in Figure 1A. The nanopore is a single mitochondrial passive ATP/ADP transport channel VDAC reconstituted into a diphytanoylphosphatidylcholine (DPhPC) lipid bilayer membrane separating 1.0 M aqueous solutions of potassium chloride (M = mol/l) buffered at pH 7.4 by 5 mM HEPES. The VDAC channel is a β barrel with an N-terminal helix forming a narrow constriction at the center of the membrane (PDB ID: 3EMN).12 The analyte protein, αSyn, is a 14.5 kDa intrinsically disordered protein comprising 140 residues that can be roughly divided into a nearly net neutral 95-residue N-terminal lipid-binding domain (shown in yellow) and a polyanionic, 45-residue C-terminal tail (CTT), which carries 15 negative charges on the last 37 amino acids (shown in red).
Figure 1.
Probing αSyn with a VDAC nanopore. (A) Experimental setup (not to scale). The acidic C-terminal tail (CTT) of membrane-bound αSyn is drawn into the nanopore by an externally applied transmembrane voltage. (B) Definitions of open (0) and blocked (1) states. Durations in each state are denoted t01 and t10, respectively. (C) A schematic of three αSyn constructs: the WT, and αSyn labeled with Alexa Fluor 488 at residues 100 and 136, αSyn-Alexa100 and αSyn-Alexa136, respectively. (D) Experimentally observed stochastic fluctuations of nanopore conductance between open and blocked states for three αSyn constructs at −30 mV of applied voltage. Single VDAC channel was reconstituted to the planar membranes formed with DPhPC. The membrane-bathing solutions contained 1 M KCl buffered with 5 mM HEPES at pH 7.4. Dashed lines indicate VDAC open and αSyn-blocked states and zero current. For presentation, all current records were smoothed with a 1 kHz lowpass Bessel digital filter using Clampfit 10.7. (E) Corresponding to the traces in (D), distributions of state t01 and t10 durations show quantitative differences in the kinetics of the αSyn-nanopore interaction introduced by Alexa Fluor 488 functionalization.
When a potential (“voltage”) is externally applied across the membrane (in a voltage-clamp mode), an ionic current through the VDAC nanopore is observed. Subsequent addition of αSyn at a final concentration of 50 nM to either side of the membrane and application of voltage with the appropriate polarity (negative from the side of αSyn addition to drive the negatively charged CTT of αSyn into the pore) leads to fluctuations in the current between two well defined states, an open state (0) and a blocked state (1) with a conductance ≈40% that of the open state (Figure 1B). Transitions between the two states were detected with a simple threshold current level. Transitions to the blocked state were detected when the absolute current level dropped below the threshold; transitions to the open state were recorded when the absolute current level rose above the threshold. For each transition, the time before transitions to the blocked state, t01, and the time spent in the blocked state, t10, were recorded. Sample current time series and log-binned transition time histograms are shown in Figure 1D, E. For presentation, the current traces in Figure 1D are filtered to 1 kHz, but a larger bandwidth was used for analysis (see Methods). The applied voltages are below the threshold for observing frequent voltage-induced gating of VDAC reconstituted in a DPhPC membrane at 1.0 M ionic strength.13
To study the effects of a PTM mimic, we compared the interaction kinetics of αSyn wild type (WT) with two modified constructs, αSyn-Alexa100 and αSyn-Alexa136, in which an Alexa Fluor 488 C5 maleimide sidechain was introduced to cysteine mutants at residues 100 and 136, respectively (see Methods). As shown schematically in Figure 1C, the modification (green circle) at residue 136 is positioned near the C-terminus of the αSyn-Alexa136 construct, while the modification at residue 100 is near the junction between the membrane-binding N-terminal domain (shown in yellow) and the polyanionic C-terminal domain (shown in red). The Alexa side chain adds 720 Da to the modified constructs, as well as 2 anionic charges at the modification position. Sample current time series and log-binned transition time histograms for the modified constructs are also shown in Figures 1D and 1E.
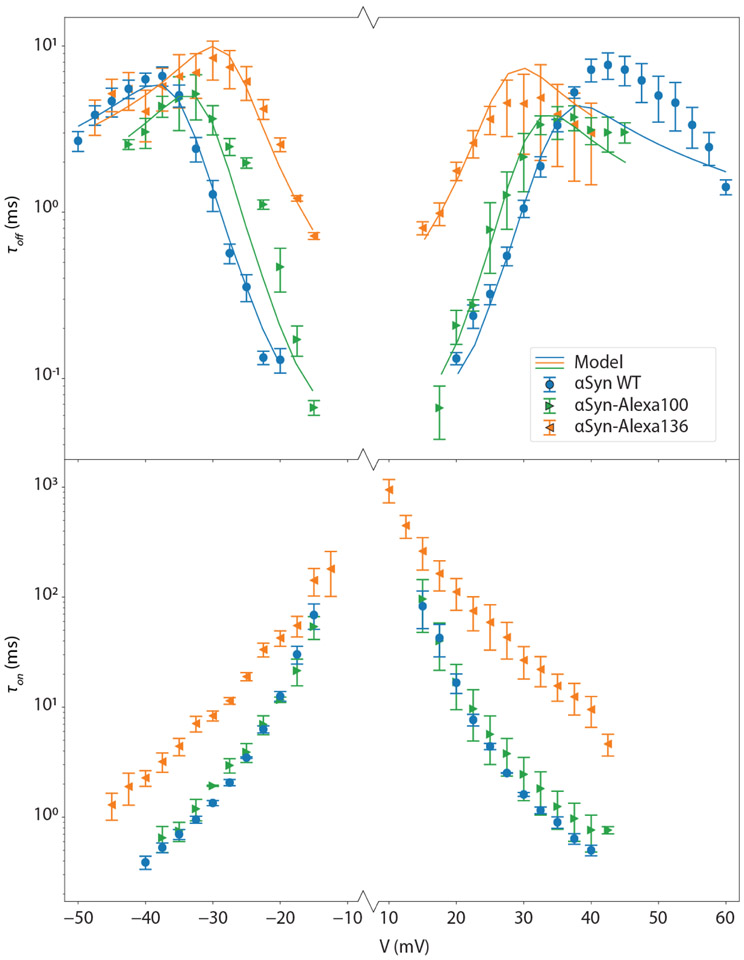
The average times characterizing the kinetics of the stochastic interaction between αSyn and VDAC, are denoted τon(V) = 〈t01〉 and τoff(V) = 〈t10〉, where the brackets stand for averages over all events at each voltage V. Experimental results for τoff (top panel) and τon (bottom panel) as functions of voltage and αSyn construct are shown in Figure 2. Each data point represents the average and standard error from the mean of a minimum of 3 independent experiments (except for αSyn-Alexa136 at positive voltages and the αSyn-Alexa100 τon, each of which comprise 2 experiments). Standard error is used because it is the appropriate statistical measure for the χ2 goodness-of-fit metric used for model optimizations. The top panel shows the voltage dependence of τoff, while the bottom panel shows that of τon. τon decreases exponentially with voltage, indicating an Arrhenius (barrier-limited) process for capture. Quantitative calculation of the energy barrier describing the Arrhenius process from basic physical principles is difficult; thus, empirical Markov modeling has previously been applied to understanding τon.8 For present purposes, visual inspection of the features of τon will suffice.
Figure 2.
Experimental and modeling results. Average kinetic data are shown as discrete points, with error bars representing the standard error of the mean from repeated independent measurements. The average blockage time (τoff, top panel) increases exponentially with absolute voltage at low voltages but decreases at higher voltages. The average time between blockages (τon, bottom panel) decreases monotonically and exponentially with voltage amplitude. Lines denote modeling results using energy landscape modeling.
By contrast, τoff has two regimes, with an exponential increase with absolute voltage at low voltages and a decrease with voltage at higher voltages. These general features of τoff for the αSyn-VDAC interaction have an established physical basis.8, 13 In particular, the exponential increase in τoff at low voltages corresponds to trapping the C-terminus of αSyn in an electrostatic potential well of depth that increases linearly with absolute voltage in this regime; the dominant process by which the αSyn molecule escapes is by retraction of its C-terminus from the nanopore without unbinding the N-terminal domain from the lipid surface (Fig. 1B).9 At higher voltages, τoff decreases with absolute voltage; the electrostatic potential barrier to retraction cannot be readily surmounted within the time scales associated with unbinding the αSyn from the membrane surface, and unbinding followed by translocation is the dominant mechanism by which αSyn exits the VDAC nanopore at the opposite side of the membrane.8, 14
The data in Figure 2 indicate that addition of the Alexa branch has a remarkably strong effect on the kinetics of the αSyn-VDAC interaction. The effect is particularly strong for αSyn-Alexa136, which shows an order of magnitude increase in τoff in the retraction regime and a similar increase in τon. Because residue 136 is close to the C-terminus of αSyn and thus participates in the equilibrium between capture and retraction,8 this observation suggests that the addition of the negatively charged Alexa branch introduces a significant energy barrier to the C-terminal domain either entering or leaving the VDAC nanopore. For αSyn-Alexa100, by contrast, the effect on low-voltage capture and retraction times is negligible. This occurs because the modified residue is located near the end of the C-terminal domain such that the C-terminal domain can be captured (and subsequently retracted) without probing the modified residue; on the other hand, this residue must move through the nanopore for translocation to occur, so its effect on the onset of the translocation regime is significant.
Given that the observed escape times depend on the complex collective motions of the entire αSyn molecule, it is rather remarkable that the modification of a single residue makes such a profound difference in the observed kinetics. To understand the voltage dependence of the off-rate, we adapted the previously described energy landscape modeling for the interaction of αSyn with the VDAC nanopore.8 The energy landscape is described by a one-dimensional “quasipotential,” so called because it usually also represents forces such as hydrodynamic drag arising from electroosmotic flow that are not strictly conservative but can nonetheless be expressed as the gradient of a potential.8, 11 The quasipotential U(x) is constructed from a combination of voltage-dependent potential UE(x), surface binding energy of αSyn UB(x), and the entropic potential US(x). The spatial dimension, x, corresponds to the distance along the contour of an αSyn molecule, or to the number of residues that have passed the center of the VDAC nanopore; thus, at x = 0, the C-terminus at residue 140 is in the center of the pore, while at x = L, where L = 56 nm is the total contour length of αSyn, the N-terminus at residue 1 is in the center of the pore. The voltage-dependent potential is
The effective linear charge density σ(x) encapsulates the combined effects of the applied electrical potential on the native, sequence-dependent charge density of the polypeptide and hydrodynamic drag arising from electroosmotic flow.15 For simplicity, here σ(x) is divided into two regions corresponding to the anionic C-terminal tail and the net neutral N-terminal domain.
The entropic potential is
where ν ≈ 0.59 is the Flory exponent.16, 17 The surface binding energy is modeled as an error function with height Eb, which corresponds to the membrane binding energy, a width wb, and a position xb which corresponds to the extent of the αSyn molecule that has translocated the nanopore before being arrested by the membrane-bound domain:
The total quasipotential for WT αSyn is then U(x) = UWT(x) = UE(x) + US(x) + UB(x).
For Alexa-modified constructs, the theory is modified by adding an additional Gaussian term in the quasipotential representing the entropic penalty of constraining the Alexa “branch” in the VDAC nanopore. This term is parameterized by the height of the entropic barrier, EX; its width, wX, which is expected to correspond to the width of VDAC’s N-terminal α-helix which forms the narrowest constriction in the VDAC pore (Fig. 1A); and the position of the sidechain along the molecule, xX:
The total quasipotential is then
The average escape time τoff corresponds to the calculated mean first passage time τ of a particle diffusing in the potential U(x) with an empirical diffusion constant D. The diffusion constant is related via the fluctuation-dissipation relation to the mobility of the polypeptide in the channel, which is subject to complex hydrodynamic18, 19 and hydration interactions.20 The mean first passage time is the first moment of the first passage time distribution, and for a reduced potential is given by:21
Here x0 is the initial position at which the molecule is first observed, also known as the “injection point.” It has previously been shown that the fast kinetics of the capture process allow this value to be equated with the “equilibrium position” once the molecule has been captured.9 Thus, for this calculation, x0 is calculated separately for each voltage to be the position of the minimum in U(x) in the range between 5 and 13 nm.
Because τoff contains data from multiple independent experiments, the model was optimized only to the average times instead of the full distributions, which would have been computationally expensive. However, using only the average reduces the amount of information in the data, so we fixed several parameters that had been allowed to vary in previous work. In particular, the voltage offset V0 for the independent measurements was assumed to average to zero and its value was fixed accordingly. The diffusion constant D and surface binding energy width wb were also fixed to the previously determined values. All other parameters were allowed to vary. xX was constrained to lie between 0 and 6 nm (residue numbers 140 and 125, respectively) for αSyn-Alexa136, and between 13 and 19 nm (residue numbers 108 and 93, respectively) for αSyn-Alexa100. Furthermore, the two additional acidic charges associated with Alexa functionalization were explicitly included in the calculations for those constructs by adding 0.02 nC/m to σc.
The optimization results are shown in Table 1 and by the solid curves in Figure 2, while quasipotentials corresponding to the optimized values of the model are shown in Figure 3 for αSyn-Alexa136 (dashed lines) and αSyn-Alexa100 (solid lines). The peaks in the quasipotential corresponding to the Alexa moieties are clearly visible. The agreement with the experimental data—except for WT αSyn at positive voltages, where the model underestimates the escape time—and previous results (recalculated from Ref. 8 after correcting an overestimate of the entropy function) using a slightly different αSyn construct, αSyn-Ac with an N-terminal acetate group, is quite good. The best fit position for the residues are found to be nm for αSyn-Alexa136 and for αSyn-Alexa100, thus establishing the modification location to within about 3 residues. The expected values are 1.6 nm and 16 nm, respectively, using a 0.4 nm amino acid separation;22 the deviation for αSyn-Alexa136 could indicate that early in the capture process, the αSyn CTT piles up in the mouth of the nanopore before passing VDAC’s N-terminal constriction. The model may also be sensitive to deviations from physical reality in this regime; at the ends of the polypeptide, the number of correlated polymer segments (“Kuhn lengths”) on either side of the nanopore is no longer large, violating an assumption that enters into the derivation of US(x).
Table 1.
Fit parameters for joint energy landscape modeling of τoff for all data sets. All data sets are described by just 9 fit parameters.
| Parameter | (95% CI) | (68% CI) | ||
|---|---|---|---|---|
| Model parameters | αSyn-Ac | αSyn WT | αSyn-Alexa136 | αSyn-Alexa100 |
| V0 / [mV] | 0 (fixed) | |||
| σC / [nC/m]b | ||||
| σN / [nC/m]b | ||||
| Eb/kBT | ||||
| wb / [nm] | 7.13 (fixed) | |||
| / [nm] | ||||
| / [nm] | ||||
| log10 D / [nm2/s] | 5.491 (fixed) | |||
| xX / [nm] | --- | --- | ||
| wX / [nm] | --- | --- | ||
| EX / kBT | --- | --- | ||
| Derived quantities | ||||
| D / [μm2/s] | 0.309 (fixed) | |||
| QC/e | ||||
| QN/e | ||||
Figure 3.
Results of energy landscape modeling for modified α-synuclein constructs. Energy landscapes are shown for αSyn-Alexa100 (solid curves) and αSyn-Alexa136 (dashed curves) for several transmembrane potentials and polarities. Actual residue positions 100 and 136 are marked with vertical arrows. (Top right) Molecular model of VDAC nanopore. The constriction in the center of the nanopore is formed by its N-terminal helix (shown as spheres sized by the atomic van der Waals radii).
The width of UX, , gives a full width at half maximum of about 1.5 nm. This dimension corresponds to the 1.2 nm diameter of an α-helix, suggesting that the entropy is indeed dominated by the constriction in the center of the VDAC nanopore due to the position of its N-terminal helix (see molecular model in Figure 3).
The height of UX is of most interest due to the implications for inserting additional polypeptide strands into the VDAC nanopore. The value EX = 4.5 kBT is quite large (Table 1). Surprisingly, the magnitude of this energy penalty corresponds closely to that previously observed for insertion of a second αSyn WT molecule into the VDAC channel (≈ 5 kBT).8 This close correspondence is consistent with the narrow width of UX, i.e. the localization to VDAC’s nanopore constriction zone, which is approximately the same size as 1 or 2 residues and therefore is not sensitive to whether the second molecule is a long polypeptide or a short bulky sidechain like Alexa Fluor 488.
Discussion
VDAC efficiently controls metabolite fluxes through mitochondrial outer membranes via its interactions with cytosolic proteins.23 It was shown that αSyn is not the only cytosolic protein to interact with VDAC in vitro13 and in vivo.24 Dimeric tubulin, the abundant cytosolic protein primarily known for its role as building block for microtubules, has also been proven to regulate VDAC in vitro25 and in vivo.26 It was demonstrated that α- and β-tubulin subunits, especially its β3 isoform, associate with VDAC in cells.27, 28 The only structural similarity between αSyn and tubulin is the presence of a polyanionic, disordered CTT which are responsible for the dynamic partial blockage of VDAC.29 As a result, these two physiologically unrelated proteins block the VDAC nanopore in vitro by the same physical mechanism, and their motion in the nanopore can be modeled using a common physical framework.8, 10 The important consequence for mitochondrial physiology is that the VDAC blocked state is essentially impermeable for ATP and ADP, as was shown in channel-based experiments30 and in MD simulations31 for the tubulin-VDAC interaction. Therefore, one of the intriguing implications of VDAC regulation by tubulin is its proposed coupling with the Warburg-type aerobic glycolysis characteristic of many tumor cells, where the VDAC-tubulin complex may play a role of a “glycolytic switch” towards aerobic glycolysis or oxidative phosphorylation.32 As for monomeric αSyn, which accounts for up to 1% of the total protein content of normal neurons, interaction with VDAC is also a mechanism for regulation of metabolite exchange between mitochondria and the cytosol. In diseased states, VDAC may also serve as a pathway for αSyn translocation into the mitochondria, where it targets respiratory complexes at the inner membrane and thus impairs mitochondrial function.24
Although most of the PTM sites of αSyn belong to its N-terminal and NAC domains,33, 34 multiple sites of phosphorylation, nitration, ubiquitination, and sumoylation are found in the C-terminal domain (Table 2). The −2 charge of the Alexa Fluor 488 sidechain mimics phosphorylation of αSyn’s Y136 residue by introducing two negative charges to this residue; however, the phosphate group is much smaller in volume and is likely to contribute only a very small entropic penalty to the free energy profile. For a transmembrane potential of 20 mV, however, an addition of 2 charges gives a factor of exp(2eV/kBT) ≈ 5-fold increase in the blockage time and reduces the potential required for translocation. Therefore, we expect that in vivo, αSyn phosphorylation at the end of the CTT reduces ATP and ADP fluxes through VDAC and promotes αSyn translocation to mitochondria,33 where it disrupts mitochondrial function.35 On the other hand, ubiquitination and sumoylation of αSyn should lead to the opposite outcome, as the attachment of bulky ubiquitin or SUMO proteins to the beginning of the αSyn CTT (Table 2) would prevent αSyn from translocating via the VDAC nanopore, making αSyn behave similarly to tubulin. We thus speculate that a physiological implication of these PTMs is prevention of αSyn translocation to the mitochondrial inner membrane, thereby protecting mitochondrial function.
Table 2.
Post-translational modifications to polyanionic C-terminal domains of αSyn and tubulin.
| PTM | CT residues affected |
Effect on residue charge |
Increase in residue volume |
References | Predicted effects |
|---|---|---|---|---|---|
| α-Synuclein | |||||
| Phosphorylation | 125, 129, 133, 136 | −2 | 54 Å3 | 41 | Higher translocation probability, longer dwell time at low voltages |
| Nitration | 125, 133, 136 | 0 | 53 Å3 | Molecular volume from MW and density of NO2 liquid | Minimal |
| Ubiquitination/Sumoylation | 96 / 96, 102 | 0 / −5 (does not affect CTT properties) | 11130 Å3 / 14890 Å3 | 42 | Eliminates translocation, behaves like tubulin |
| Dopamination | 125-129 | 0 | 150 Å3 | 33, 42 | Smaller capture rate, longer dwell time at low voltages |
| Tubulin | |||||
| Polyglutamylation (N residues) | varies by isotype | −(N + 1) | N × 155 Å3 | 42 | Longer dwell time, stronger dependence on voltage |
| Polyglycylation (N residues) | varies by isotype | −1 | N × 66 Å3 | 42 | Longer dwell time, same voltage dependence |
As for tubulin, considering that the majority of multiple tubulin PTMs occur at its CTTs,36-38 and that glutamylation and glycylation are manifested through formation of linear poly-Glu or poly-Gly branches of variable length, a possible impact of such PTMs on tubulin regulation of VDAC, and consequently mitochondria, should be dramatic. The linear chain of branches could reach up to 21 glutamates and 34 glycines.39 The molecular size of Alexa Fluor 488 is comparable to a branch of about five glutamates or eleven glycines (Table 2). Interestingly, 3-6 glutamates per each branch are typically found in tubulin purified from adult brain tissue.40 The level of polyglutamylation in brain tubulin changes dramatically during development:36 polyglutamylation increases in β-tubulins starting from nonglutamylated β -isoforms in neonatal animals and reaching high level of polyglutamylation in adult brains.
Because polyglutamylation of the tubulin CTT produces a branched structure which can interact with the nanopore in a variety of ways and cannot necessarily be described by a single free energy profile, the extension of this work to polyglutamylated CTTs is not trivial and will be the subject of future investigation. The polyglycylated tubulin CTT, however, which carries 1 negative charge at the terminal glycine and adds 66 Å3 per glycine, is likely to be well modeled by the Alexa Fluor 488 C5 maleimide sidechain, which carries 2 negative charges and has a nominal volume of 720 Å3, based on molecular weight and an assumed specific density of 1. Thus, one expects that the primary effect of polyglycylation is stabilize the tubulin CTT in the VDAC nanopore, increasing its effectiveness in regulation.
Conclusions
Inspired by the importance of post-translational modifications in cell signaling, we imitated PTMs of a 140 amino acid cytosolic protein αSyn by attaching divalent Alexa Fluor 488 to the beginning and end of the C-terminal tail. Each of these modifications increased the total negative charge of the tail by two elementary charges and introduced extra bulkiness at the modification location, significantly changing the dynamics of the αSyn/nanopore interaction. Time-resolved single-molecule events of αSyn capture by the VDAC nanopore were analyzed within a framework of a one-dimensional diffusion model using an interaction “quasipotential” that incorporates mostly electrostatic and entropic components of α-syn interaction with the nanopore. This analysis proved to be an effective means of quantitatively describing the modification effects on the kinetics of the interaction and yielded the positions of the modifications with a precision of about 3 residues. The technique is general and can readily be applied to other nanopores and analytes, suggesting that it could be extended to quantify populations of an analyte that have undergone PTMs. In principle, it can also be used to determine the positions of PTMs in disordered or denatured protein analytes, or to design engineered pores that are sensitive to particular protein features. Finally, in view of the recently established role of disordered charged termini of cytosolic proteins in control of VDAC-facilitated transport, our findings establish a new mechanism of PTM-induced regulation of protein function.
Methods
Protein Purification
VDAC was isolated from the frozen mitochondrial fractions of rat liver that were a generous gift of Dr. Marco Colombini (University of Maryland, College Park, USA) and purified following the standard methods43 on a hydroxiapatite/celite (2:1) column.44 VDAC purified from mitochondrial fraction of rat liver contains all three isoforms with VDAC1 being the predominant one (~ 80% of total VDACs).45 αSyn was expressed, purified, and characterized as previously described.13, 46 The Alexa Fluor 488 modified αSyn constructs were produced as described previously.47 To obtain constructs containing the Alexa Fluor 488 fluorophore at positions 100 and 136, respectively, individual cysteine mutants L100C and Y136C were produced and then derivatized with Alexa Fluor 488 C5 maleimide (Thermo Fisher) following the manufacturer recommended protocol. αSyn WT, αSyn-Alexa100 and αSyn-Alexa136 were generous gifts of Dr. Jennifer Lee (NHLBI, NIH, Bethesda, USA).
Channel Reconstitution
Planar bilayer membranes were formed from diphytanoyl-phosphatidylcholine (DPhPC) (Avanti Polar Lipids, Alabaster, AL) from two opposing lipid monolayers of across ~70 μm aperture in the 15-μm-thick Teflon partition separating two ~1.2-mL compartments as previously described.48 Channel currents were recorded as described previously49, 50 using an Axopatch 200B amplifier (Axon Instruments, Inc., Foster City, CA) in the voltage clamp mode. Data were filtered by a low pass 8-pole Butterworth filter (Model 900, Frequency Devices, Inc., Haverhill, MA) at 15 kHz and a low pass Bessel filter at 10 kHz, and directly saved into computer memory with a sampling frequency of 50 kHz. VDAC insertion was achieved by adding purified VDAC in a 2.5% Triton X-100 solution to the aqueous phase of 1 M (M = mol/L) KCl buffered with 5 mM Hepes at pH 7.4 in the cis compartment while stirring. Potential is defined as positive when it is greater at the side of VDAC addition (cis). αSyn constructs at final concentration of 50 nM were added symmetrically to the membrane-bathing solutions to both sides of the membrane after VDAC channel reconstitution; statistical analysis of the blockage events began 15 min after αSyn addition to ensure a steady state.
Analysis of Open and Blocked Times
For single-channel data analysis by Clampfit 10.7, a digital 8-pole Bessel low pass filter set at 5 kHz was applied to current recordings. Individual events of current blockages were discriminated and kinetic parameters were acquired by fitting single exponentials to logarithmically binned histograms51 as described previously.13, 52 Four different logarithmic probability fits were generated using different fitting algorithms and the mean of the fitted time constants was used as the mean for the characteristic open and blockage times. Each channel experiment was repeated 3-7 times on different membranes.
Modeling and Optimization
The model was implemented using custom Python code. Optimization was performed on the Bridges53, 54 high performance computing system using the DREAM Markov Chain Monte Carlo (MCMC) algorithm55 implemented in the software package Bumps.56 Confidence intervals on parameters and model predictions are calculated from the last 647,040 of at least 14.6 million total DREAM samples.
Visualizations
Molecular visualizations were produced using VMD.57
Acknowledgements
Authors thank Jennifer Lee for providing αSyn WT, αSyn-Alexa100 and αSyn-Alexa136. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575. Specifically, it used the Bridges system, which is supported by NSF award number ACI-1445606, at the Pittsburgh Supercomputing Center (PSC). P. A. G., T. K. R., and S. M. B. were supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH.
Footnotes
Conflicts of interest
The authors declare no competing financial interest. The authors declare that they have no conflicts of interest with the contents of this article. Certain commercial materials, equipment, and instruments are identified in this work to describe the experimental procedure as completely as possible. In no case does such an identification imply a recommendation or endorsement by NIST, nor does it imply that the materials, equipment, or instrument identified are necessarily the best available for the purpose.
References
- 1.Marx V, Nature Methods, 2019, 16, 809–812. [DOI] [PubMed] [Google Scholar]
- 2.Taniguchi Y, Choi PJ, Li G-W, Chen H, Babu M, Hearn J, Emili A and Xie XS, Science, 2010, 329, 533–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bononi A, Agnoletto C, De Marchi E, Marchi S, Patergnani S, Bonora M, Giorgi C, Missiroli S, Poletti F, Rimessi A and Pinton P, Enzyme Research, 2011, 2011, 1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Venne AS, Kollipara L and Zahedi RP, PROTEOMICS, 2014, 14, 513–524. [DOI] [PubMed] [Google Scholar]
- 5.Laszlo AH, Derrington IM, Brinkerhoff H, Langford KW, Nova IC, Samson JM, Bartlett JJ, Pavlenok M and Gundlach JH, Proceedings of the National Academy of Sciences, 2013, 110, 18904–18909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Qiu H, Sarathy A, Schulten K and Leburton J-P, npj 2D Materials and Applications, 2017, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Simpson JT, Workman RE, Zuzarte PC, David M, Dursi LJ and Timp W, Nature Methods, 2017, 14, 407–410. [DOI] [PubMed] [Google Scholar]
- 8.Hoogerheide DP, Gurnev PA, Rostovtseva TK and Bezrukov SM, Nanoscale, 2017, 9, 183–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hoogerheide DP, Gurnev PA, Rostovtseva TK and Bezrukov SM, Biophys J, 2018, 114, 772–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rostovtseva TK, Gurnev PA, Hoogerheide DP, Rovini A, Sirajuddin M and Bezrukov SM, J Biol Chem, 2018, 293, 10949–10962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hoogerheide DP, Albertorio F and Golovchenko JA, Phys Rev Lett, 2013, 111, 248301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ujwal R, Cascio D, Colletier JP, Faham S, Zhang J, Toro L, Ping PP and Abramson J, Proc Natl Acad Sci USA, 2008, 105, 17742–17747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rostovtseva TK, Gurnev PA, Protchenko O, Hoogerheide DP, Yap TL, Philpott CC, Lee JC and Bezrukov SM, J Biol Chem, 2015, 290, 18467–18477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hoogerheide DP, Gurnev PA, Rostovtseva TK and Bezrukov SM, Biophysical journal, 2018, 114, 772–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.van Dorp S, Keyser UF, Dekker NH, Dekker C and Lemay SG, Nature Physics, 2009, 5, 347–351. [Google Scholar]
- 16.Lubensky DK and Nelson DR, Biophys J, 1999, 77, 1824–1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sung W and Park PJ, Phys Rev Lett, 1996, 77, 783–786. [DOI] [PubMed] [Google Scholar]
- 18.Misiunas K, Pagliara S, Lauga E, Lister JR and Keyser UF, Phys Rev Lett, 2015, 115. [DOI] [PubMed] [Google Scholar]
- 19.Pagliara S, Dettmer SL, Misiunas K, Lea L, Tan Y and Keyser UF, Eur. Phys. J. Special Topics, 2014, 223, 3145–3163. [Google Scholar]
- 20.Aguilella-Arzo M, Andrio A, Aguilella VM and Alcaraz A, Phys. Chem. Chem. Phys, 2009, 11, 358–365. [DOI] [PubMed] [Google Scholar]
- 21.van Kampen NG, Stochastic processes in physics and chemistry, Elsevier, Amsterdam ; Boston, 3rd edn., 2007. [Google Scholar]
- 22.Ainavarapu SRK, Brujić J, Huang HH, Wiita AP, Lu H, Li L, Walther KA, Carrion-Vazquez M, Li H and Fernandez JM, Biophys J, 2007, 92, 225–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rostovtseva TK and Bezrukov SM, Journal, 2015, 18, 3–31. [Google Scholar]
- 24.Rovini A, Gurnev PA, Beilina A, Queralt-Martín M, Rosencrans W, Cookson MR, Bezrukov SM and Rostovtseva TK, Cellular and Molecular Life Sciences, 2019, DOI: 10.1007/s00018-019-03386-w, in press. [DOI] [Google Scholar]
- 25.Rostovtseva TK, Sheldon KL, Hassanzadeh E, Monge C, Saks V, Bezrukov SM and Sackett DL, Proc. Natl. Acad. Sci. U S A, 2008, 105, 18746–18751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maldonado EN, Patnaik J, Mullins MR and Lemasters JJ, Cancer Res, 2010, 70, 10192–10201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rostovtseva TK, Gurnev PA, Hoogerheide DP, Rovini A, Sirajuddin M and Bezrukov SM, J Biol Chem, 2018, DOI: 10.1074/jbc.RA117.001569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Carre M, Andre N, Carles G, Borghi H, Brichese L, Briand C and Braguer D, J. Biol. Chem, 2002, 277, 33664–33669. [DOI] [PubMed] [Google Scholar]
- 29.Rostovtseva TK, Hoogerheide DP, Rovini A and Bezrukov SM, Journal, 2017, 185–216. [Google Scholar]
- 30.Gurnev PA, Rostovtseva TK and Bezrukov SM, FEBS Lett, 2011, 585, 2363–2366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Noskov SY, Rostovtseva TK and Bezrukov SM, Biochemistry-Us, 2013, 52, 9246–9256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Maldonado EN and Lemasters JJ, The Journal of pharmacology and experimental therapeutics, 2012, 342, 637–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Barrett PJ and Greenamyre JT, Brain Research, 2015, 1628, 247–253. [DOI] [PubMed] [Google Scholar]
- 34.Zhang J, Li X and Li J-D, Frontiers in Neuroscience, 2019, 13.30760975 [Google Scholar]
- 35.Devi L, Raghavendran V, Prabhu BM, Avadhani NG and Anandatheerthavarada HK, J Biol Chem, 2008, 283, 9089–9100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Redeker V, Methods Cell Biol, 2010, 95, 77–103. [DOI] [PubMed] [Google Scholar]
- 37.Roll-Mecak A, Semin Cell Dev Biol, 2015, 37, 11–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Westermann S and Weber K, Nature reviews. Molecular cell biology, 2003, 4, 938–947. [DOI] [PubMed] [Google Scholar]
- 39.Redeker V, Levilliers N, Schmitter JM, Le Caer JP, Rossier J, Adoutte A and Bre MH, Science, 1994, 266, 1688–1691. [DOI] [PubMed] [Google Scholar]
- 40.Schneider A, Plessmann U, Felleisen R and Weber K, FEBS Lett, 1998, 429, 399–402. [DOI] [PubMed] [Google Scholar]
- 41.Armen RS, Uitto OD and Feller SE, Biophys J, 1998, 75, 734–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chothia C, Nature, 1975, 254, 304–308. [DOI] [PubMed] [Google Scholar]
- 43.Blachly-Dyson E, Peng S, Colombini M and Forte M, Science, 1990, 247, 1233–1236. [DOI] [PubMed] [Google Scholar]
- 44.Palmieri F and De Pinto V, J Bioenerg Biomembr, 1989, 21, 417–425. [DOI] [PubMed] [Google Scholar]
- 45.Yamamoto T, Yamada A, Watanabe M, Yoshimura Y, Yamazaki N, Yoshimura Y, Yamauchi T, Kataoka M, Nagata T, Terada H and Shinohara Y, J Proteome Res, 2006, 5, 3336–3344. [DOI] [PubMed] [Google Scholar]
- 46.Pfefferkorn CM and Lee JC, J Phys Chem B, 2010, 114, 4615–4622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jacobs D, Hoogerheide DP, Rovini A, Jiang Z, Lee JC, Rostovtseva TK and Bezrukov SM, Sci Rep, 2019, 9, 4580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gurnev PA, Martin MQ, Aguilella VM, Rostovtseva TK and Bezrukov SM, Biophys J, 2012, 102, 161a–161a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rostovtseva TK, Kazemi N, Weinrich M and Bezrukov SM, J. Biol. Chem, 2006, 281, 37496–37506. [DOI] [PubMed] [Google Scholar]
- 50.Gurnev PA, Yap TL, Pfefferkorn CM, Rostovtseva TK, Berezhkovskii AM, Lee JC, Parsegian VA and Bezrukov SM, Biophys. J, 2014, 106, 556–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sigworth FJ and Sine SM, Biophys. J, 1987, 52, 1047–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Weinrich M, Worcester DL and Bezrukov SM, Nanoscale, 2017, 9, 13291–13297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Nystrom NA, Levine MJ, Roskies RZ and Scott JR, presented in part at the Proceedings of the 2015 XSEDE Conference: Scientific Advancements Enabled by Enhanced Cyberinfrastructure, St. Louis, Missouri, 2015. [Google Scholar]
- 54.Towns J, Cockerill T, Dahan M, Foster I, Gaither K, Grimshaw A, Hazlewood V, Lathrop S, Lifka D, Peterson GD, Roskies R, Scott JR and Wilkins-Diehr N, Comput Sci Eng, 2014, 16, 62–74. [Google Scholar]
- 55.Vrugt JA, ter Braak CJF, Diks CGH, Robinson BA, Hyman JM and Higdon D, Int J Nonlin Sci Num, 2009, 10, 273–290. [Google Scholar]
- 56.Kienzle PA, Krycka J, Patel N and Sahin Bumps I (Version 0.7.5.4) [Computer Software].College Park, MD: University of Maryland; 2011. [Google Scholar]
- 57.Humphrey W, Dalke A and Schulten K, J Mol Graph, 1996, 14, 33–38, 27–38. [DOI] [PubMed] [Google Scholar]