Abstract
In cluster physics, the determination of the ground-state structure of medium-sized and large-sized clusters is a challenge due to the number of local minimal values on the potential energy surface growing exponentially with cluster size. Although machine learning approaches have had much success in materials sciences, their applications in clusters are often hindered by the geometric complexity clusters. Persistent homology provides a new topological strategy to simplify geometric complexity while retaining important chemical and physical information without having to “downgrade” the original data. We further propose persistent pairwise independence (PPI) to enhance the predictive power of persistent homology. We construct topology-based machine learning models to reveal hidden structure–energy relationships in lithium (Li) clusters. We integrate the topology-based machine learning models, a particle swarm optimization algorithm, and density functional theory calculations to accelerate the search of the globally stable structure of clusters.
Graphical Abstract
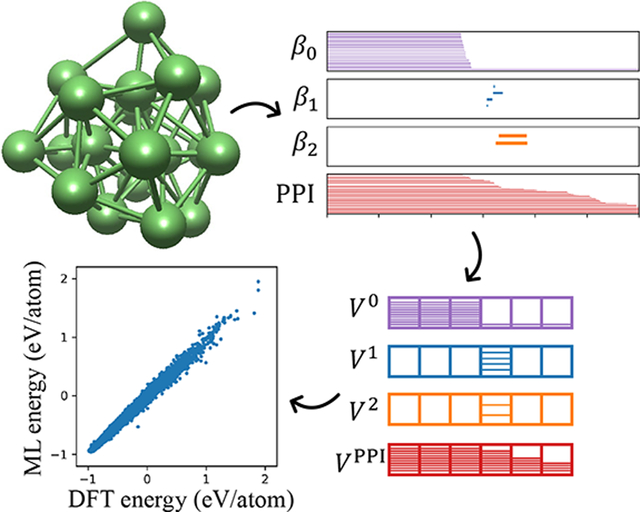
The determination of the topography of the potential energy surfaces of various clusters is a subject of intensive research in cluster physics. One of the most challenging tasks is to determine the ground-state structure of medium and large clusters due to the fact that the number of local minima on the potential energy surface grows exponentially with the increase of cluster size.1 It is commonly believed that the binding energy of a cluster is mainly determined by the geometric structure of the cluster. Therefore, the understanding of the structure-energy relationship of clusters is the holy grail in cluster research. In particular, the prediction of structures with the global minimal energy and near minimal energies is of practical interest.
Several efficient global optimization methods, including random sampling,2 basin hopping,3 minimal hopping,4 simulated annealing,5 genetic algorithm,6–8 and particle swarm optimization (PSO) algorithm,9 have been developed in the past few decades for searching structures with near-global minimal energies. Among them, the PSO algorithm, first proposed by Kennedy and Eberhart,9,10 is a relatively efficient one. Call et al. applied the PSO algorithm to the structure prediction of small clusters or isolated molecules.11 Recently, Ma et al. have developed a PSO-based structure analysis method,12 which is widely applied to structure predictions. However, all the aforementioned methods are computationally expensive due to involved first-principle calculations of numerous local minimum values.1 As shown in a recent review,13 machine learning (ML) has been proven to be an efficient strategy for estimating the density functional theory (DFT) energy of ground states of materials and for the prediction of material properties. It has the potential for material structure prediction as well.
Recently, machine learning has had tremendous success in science, engineering, finance, medicine, and various other industrial sectors. Initial successes of machine learning approaches were limited to image and video processing, computer vision, etc. For relatively simple data sets, such as images, advanced machine learning algorithms, such as a convolutional neural network (CNN), can automatically extract image patterns without handcrafted input features. Such predictive models involve two essential components, namely, data set and learning algorithm. However, for general data sets, particularly data sets with complex geometric structures in material sciences and molecular biology, the internal structural complexity hinders the performance of the aforementioned two-component machine learning approach. A predictive machine learning model for complex data consists of three essential components: the data set, learning algorithm, and data representation. The representations of data, called “descriptors” or “features”, play an essential role in constructing an efficient machine learning model for data sets with complex internal structures.
For complex three-dimensional (3D) cluster data, the representations used in machine learning vary greatly in their nature. Some representations are generated from Cartesian coordinates, geometric properties, electrostatics, atom types, and atomic partial charges.13–30 The most direct and crude representation is Cartesian coordinates, but as regressive neural networks are numerical fitting methods, the output depends on the absolute values of the input coordinates. Since translation and rotation of a cluster should not change cluster intrinsic properties, Cartesian coordinate representation has a major limitation in energy predictions. The conventional solution is to describe cluster structures by using graph theory or symmetric functions that are invariant to translation and rotation. Graph-based representations have been successfully applied to predict molecular properties.31,32 Meanwhile, many symmetric functions based on interatomic distances have been developed,33–37 which are equally applicable to very different systems such as bulk metals, clusters or molecules. However, graph-based representations may neglect some geometric details, such as distortion, whereas symmetric function models often contain too complex structural detail and are frequently computationally intractable, due to its rather complicated conversion formula. Therefore, continuous, complete and simple low-dimensional representations that are invariant to translation and rotation are greatly desired.
Topology, free of metrics or coordinates, offers an entirely different approach and could provide the ultimate simplification of structural complexity. In fact, one only needs qualitative topological information to understand many physical properties. However, traditional topology oversimplifies data structures and leads to too much loss in geometric information. Persistent homology is a relatively new method that bridges geometry and topology. It integrates multiscale geometric analysis and algebraic topology via a filtration process, rendering a low-dimensional representation of complex data.38–40 Persistent homology characterizes the geometric features in data without having to “downgrade” the original data as much as the original topology does. Topological invariants, i.e., the properties of topological spaces that do not vary with certain types of continuous deformations, are used as the key feature of persistent homology. Through filtration and persistence, topological invariants can capture geometric structures continuously over a range of spatial scales. Unlike commonly used computational homology, which results in truly metric free or coordinate-free representations, persistent homology is able to embed geometric information into topological invariants so that the “birth”, “death”, and “persistence” of isolated components, circles, holes, and void at all geometric scales can be monitored by topological measurements. The basic idea of size functions was introduced by Frosini and Landi41 and by Robins.42 Edelsbrunner et al.38 formulated persistent homology, and Zomorodian and Carlsson generalized the mathematical theory.39 Usually, topological persistence over the filtration is represented either in persistent diagrams or in persistent barcodes,43 in which various horizontal line segments or bars indicate homology generators. Persistent homology has been applied to a variety of fields, including image analysis,44–47 image retrieval,48 chaotic dynamics verification,49,50 shape recognition,51 and computational biology.14,52–54 Wei and workers explored the utility of persistent homology for the quantitative analysis of protein54 and fullerene55 and proposed some of the first integrations of persistent homology and machine learning.56 It has been shown that persistent-homology-based machine learning algorithms outperform other methods in D3R Grand Challenges, a worldwide competition series in computer-aided drug design.57
The objective of the present work is to introduce persistent homology as a unique representation of cluster structures. The persistent homology representation of cluster structures is realized using persistent barcodes. To enhance the predictive power of persistent barcode representation, we propose a new concept, persistent pairwise independence (PPI), as an auxiliary feature. The resulting topological fingerprints, including both persistent barcodes and PPI, are employed in a machine learning model to understand the structure–energy relationship of clusters. In a further combination with the PSO algorithm and DFT calculation, a topology-ML-PSO–DFT protocol is developed for the high throughput screen of cluster structures with the global energy minima. Lithium (Li) is the lightest metallic element in the periodic table and Li cLuster is a subject of intense research in Li anode materials in storage battery. So Li cluster were studied by our topology-ML-PSO-DFT protocol as an illustration in this work. In fact, the idea about the combination of ML model with DFT-based structure prediction is not new.58–62 Among them, the Gaussian approximation potential (GAP) method is a relatively efficient one and has been successfully tested on many cases. However, these works focused on the acceleration of crystal structure relaxation with ML model learning and interatomic potential. In contrast, the part of acceleration in our work focused on the combination of ML model and stochastic global optimization algorithm to avoid the expensive DFT calculation on screening local minimum values.
In this work, persistent homology is used to characterize topological invariants, such as isolated components, circles, rings, loops, pockets, voids, and cavities, via topological spaces and algebraic group representations. We associate each atom in a cluster with an ever-increasing diameter to systematically generate a multiscale representation. We use persistent barcodes to represent cluster atomic interactions. Topological invariants are combined with PPIs to describe cluster molecules in our machine learning modeling. The global optimization algorithm and the first principle calculation used in this work are also discussed.
Simplicial Homology.
Let {v0, v1, …, vn} be an affine independent sets in , and a k-simplex, σk, is a k-dimensional polytope that is the convex hull of above k + 1 vertices, expressed as
| (1) |
To combine these geometric components, such as vertices, edges, triangles, and tetrahedrons together under certain rules, a simplicial complex K is constructed, which is a set of simplices that satisfies the following two conditions. The first is that any face of a simplex from K is also in K. The second is that the intersection of any two simplices in K is either empty or a shared face of both simplices.
A k-chain [σk] is a linear combination of k-simplex σk. The coefficients αi can be chosen from rational number field , integers , and prime field with prime number ρ. For simplicity, in this work the coefficients αi is chosen from , for which the addition operation between two chains is the modulo 2 addition for the coefficients of their corresponding simplices. The set of all k-chains of simplicial complex K together with the addition operation forms an Abelian group Ck(K, ). The homology of a topological space is represented by a series of Abelian groups satisfying certain relations.
Let ∂k be a boundary operator ∂k: Ck → Ck−1. The boundary of a k-simplex is given by
| (2) |
where means the elimination of vertex vi from the simplex. The most important topological property is that a boundary has no boundary. In other words, a k-chain will be mapped to an empty set by the twice applications of boundary operations ∂k−1∂k = . The kth cycle group Zk and the kth boundary group Bk are the subgroups of Ck defined respectively as
| (3) |
and
| (4) |
The kth homology group Hk, defined by the kth cycle group Zk and the kth boundary group Bk, is given by the quotient group
| (5) |
The homology group extracts low-dimensional topological invariants from original data, which can lie in a very high dimensional space. In practical applications, it is the Betti number (βk), one of the most important topological invariants, that is employed in our computation. For a given cluster structure, roughly speaking, the number of independent components, rings and cavities are topological invariants and they are referred to as β0, β1, and β2, respectively.20 With the homology group Hk, the kth Betti number is given by
| (6) |
However, as mentioned earlier, the Betti number alone leads to a severe topological abstraction of real-world data.
Persistent Homology, Barcode, and Persistent Pairwise Independence.
Persistent homology addresses the aforementioned oversimplification issue by introducing a multiscale geometric analysis to the original homology. Specifically, it systematically creates a family of inclusive topological spaces from a filtration process and then defines a nested family of homology groups over the filtration. In a filtration process, a chain complex, including a family of ordered subcomplexes, is created from a given simplicial complex K by a parameter ϵ,
| (7) |
In our case, a simple choice of ϵ is the atomic diameter, which goes from 0 to a given maximal length ϵmax. A simplex is a geometric generalization of a triangle to arbitrary dimensions, namely, a 0-simplex is a vertex, a 1-simplex is an edge, a 2-simplex is a triangle, and a 3-simplex represents a tetrahedron. Simplexes can describe very complicated geometric shapes and are much more computationally tractable than the original shapes that they represent. There are actually many different types of simplicial complex constructions that can be used in persistent homology. The Vietoris Rips complex,63 a type of a simplicial complex derived from the connectivity of ϵ-balls in a given metric space, is used in this work as it is fairly easy to describe and reasonably practical for point cloud data. For example, a 1-simplex is formed if two points with diameter ϵ contact with each other. Vietoris Rips complex models the pairwise interaction of atoms. Specifically, for ϵ sufficiently small, one has only isolated points, i.e., 0-simplexes, whereas, for ϵ sufficiently large, one can have high-dimensional simplex. As such, a nested sequence of subcomplexes is defined when we grow diameter ϵ-ball around each atom in a cluster, as shown in eq 7. For each subcomplex in a chain complex, homology groups and the corresponding topological invariants can be computed. The resulting family of topological invariants in terms of persistent Betti numbers record the “birth” and/or “death” of all topological features in data, giving rise to topological fingerprints. Therefore, the evolution of topological invariants over the filtration process can be recorded as a barcode43 or a persistence diagram.
The proposed persistent pairwise independence (PPI) counts the independence of each pair of atoms (or points) over the filtration. Initially, all atoms are not connected. The number of PPI bars is equal to the number of pairs of independent atoms. As the filtration parameter increases, some pairs of atoms become connected and their persistent bars terminate. The proposed PPI barcode is more informative than the β0 persistent barcode. As shown in Figure 1, it can be used together with topological invariants to describe material structures.
Figure 1.
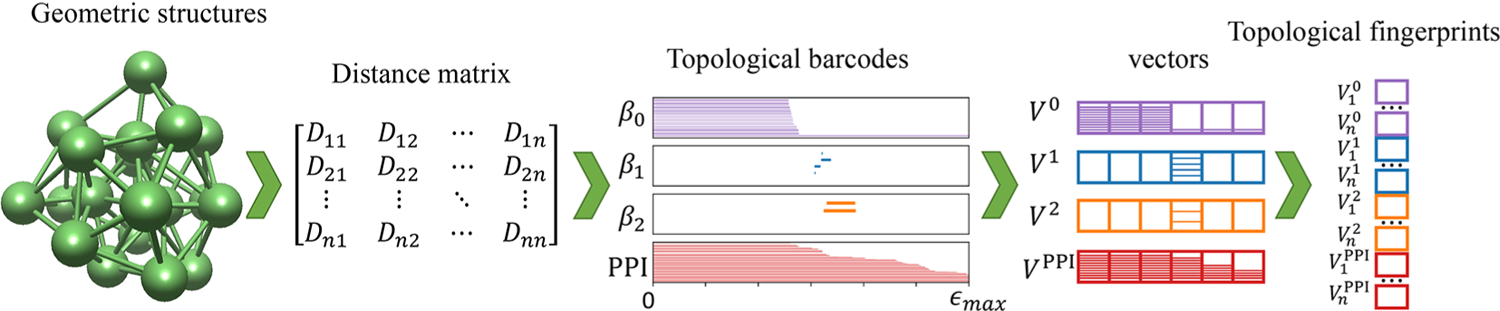
Flowchart illustrating the workflow from a geometric structure, distance matrix, topological barcodes, and vectors of topological invariants (V0, V1, V2) and persistent PPI (VPPI), to final topological fingerprints.
Topological Fingerprints as Machine Learning Features.
A basic assumption of persistent homology as applied to cluster binding energy predictions is that vectors of topological invariants and PPI are able to effectively represent cluster structures. We call such vector topological fingerprints (TFs).14,54,55 To convert barcodes of β0, β1, β2, and PPI to 1D vector applied in machine learning, we combine the birth, death, and persistence patterns of β0, β1, β2, and PPI. In practice, the abscissas of barcodes from 0 to ϵmax are divided into n equal length subintervals. Then, the patterns of topological invariants and PPI are counted and recorded on each subinterval, further transformed to four n-length vectors V0, V1, V2, and VPPI. As shown in Figure 1, on the basis of the point cloud data of a cluster, represented by a distance matrix, we calculate topological invariants and PPI from 0 to ϵmax according to definition mentioned above and present all this information in four barcodes, corresponding to β0, β1, β2, and PPI. With [0, ϵmax] divided evenly into [ϵ1, ϵ2, …, ϵi, ϵi+1, …, ϵmax], represents how many persistent β0 within [ϵi, ϵi+1], represents how many persistent β1 within [ϵi, ϵi+1], represents how many persistent β2 within [ϵi, ϵi+1], and represents how many PPI within range [ϵi, ϵi+1]. Finally, these vectors were combined together as TFs, , a 4n-length vector.
To further demonstrate the advantage and benefit of TFs using the barcode representation, Figure 2 illustrates the structures of a quadrilateral Li4 cluster and an octahedral Li6 cluster at various filtration diameters. The horizontal axis represents the filtration parameter ϵ. From top to bottom, the behaviors of β0, β1, β2, and PPI are depicted in four individual subfigures. It is seen that as ϵ increases, initially isolated atoms will gradually grow into ϵ-balls with increasing diameter. Once two ϵ-ball overlap with each other, one β0 bar is terminated. As shown in Figure 2, at the very beginning, all ϵ-balls do not overlap with one another. There are four purple bars in the first subfigure, meaning that there are four isolated β0 bars. When the filtration parameter reaches 3 Å, each ϵ-ball overlaps with its closest two balls, forming a connected square. Therefore, four bars of β0 (purple bars) turn into one bar and a β1 (blue bars) bar appears, which represents the emergence of an independent noncontractible quadrilateral structure (loops). In the end when the filtration parameter reaches around 4.2 Å, the β1 bar disappears, leaving only a β0 bar persistent in all subfigures. As can be seen from the last subfigure, Li4 cluster has two different kinds of bars of PPI with lengths around 3 and 4.2 Å, respectively, indicating its two types of interatomic distances. Similarly, an octahedral structure is captured by bars β0 and β2 (orange bars) in Figure 2b. First, there are β0 bars at the beginning. As the filtration progress, there are only one β0 bar and one β2 bar, which corresponds to void structure in the center of the cage. The initial six β0 bars imply this void structure having six vertices. It is obvious that polygon and polyhedron structures, even with perturbations, could be described by β0, β1, and β2 bars. More specific examples of barcode representation are shown in the Supporting Information.
Figure 2.
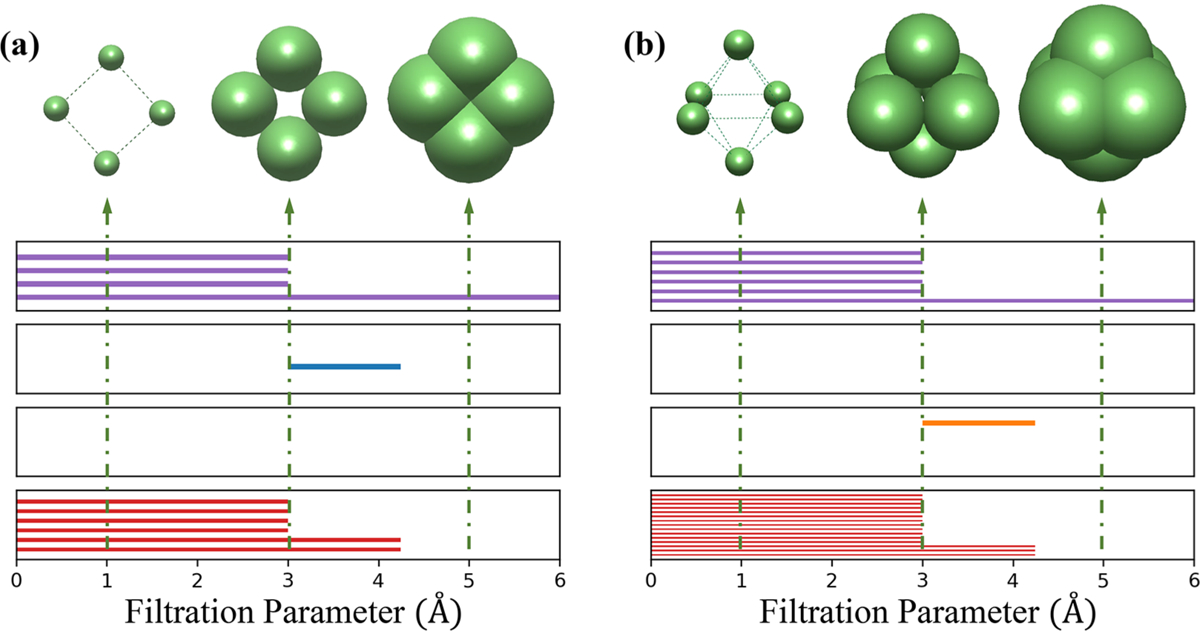
Illustration of barcode changes for two clusters. The diameter-based filtration process and barcodes for (a) Li4 cluster and (b) Li6 cluster. With the increase of their diameter ϵ, the balls connect to form higher-dimensional simplexes. In this manner, the previously formed simplicial complex is included in the latter ones. Four panels from top to bottom are β0, β1, β2, and PPI barcodes, respectively. The horizontal axis is the filtration parameter (Å).
Machine Learning Models.
The success of a machine learning model for material sciences depends not only on the quality of original data, appropriate descriptors but also on learning algorithms. Gradient boosting regression (GBR)64 and neural network (NN)65 have been the methods of choice for modeling atomic interactions. In particular, the GBR is known to be robust to small data sets and less prone to overfitting. Compared with NN, GBR is very easy to train and much more efficient. Essentially, GBR constructs a strong regressor from an ensemble of weak regressors. Here, we choose GBR to optimize feature parameters, including the structure of the TFs, the number of subintervals in each angstrom, and ϵmax.
Once the optimized feature parameters are obtained, we further choose the neural network method for deep learning. Neural networks are modeled after the function of neurons in the brain. A neural network applies activation functions, called perceptrons, to inputs. During the training, weights of the neurons are updated through the backpropagation to minimize a loss function over many epochs, or passes of an entire training data set. The detail of the machine learning models used in this work was listed in the Supporting Information). In this work, to evaluate the performance of our models, mean absolute error (MAE) and Pearson correlation coefficient (PCC) were used. The MAE is given by
| (8) |
where N is the number of samples and fi and yi are the prediction and true value of sample i, respectively. Given a pair of random variables (X, Y), the formula of PCC is
| (9) |
where the cov(X, Y) is the covariance of X and Y and σx and σy are the standard deviations of X and Y, respectively.
Particle Swarm Optimization (PSO).
The next vital ingredient required in the prediction of the global stable structure of a cluster is a stochastic global optimization algorithm. Particle swarm optimization (PSO) strategy is based on behaviors of swarms of flocks of birds, where a displacement velocity updates the position of each candidate particle. In this work, a candidate cluster structure is regarded as a particle. The jth dimension of ith particle is updated over a unit time according to
| (10) |
where t denotes the generation index, is the coordinate of the jth dimension of the ith particle, and is its correspond displacement velocity per unit time. Each velocity is determined according to the formula
| (11) |
where w is the inertia coefficient, is the value of the given coordinate from the best solution seen by the swarm, is the value of the given coordinate from the best solution seen by the ith particle, and c1 and c2 are constants. Here, r1 and r2 are random numbers. The methodology has been demonstrated to be efficient and powerful for global structural convergence.12,66,67 The first generation of clusters are stochastically generated from crystal structures.
Topology-ML-PSO-DFT Protocol.
Our topology-ML-PSO-DFT protocol consists of mainly four steps as depicted in the flowchart of Figure 3. First, the initial structures are randomly generated from crystal structures. Once a new structure generated, the TFs are calculated and used to examine the consistency of this structure with all the previous ones. When the TFs of the two structures are the same, we conclude that they are identical and discard the new structure. In this work, the number of subintervals in each angstrom is the essential parameter of our model and ultimately determines the length of the TFs and the precision for deduplication. The larger the number of subintervals per unit length, the more compatible the deduplication process is. Then, the PSO procedure is applied to generate new structures for the next generation. After all the structures of the final generation have been generated, the three lowest energy structures of every generation determined by the machine learning model were collected in a low-energy set. Eventually, the structures in the low-energy set are further optimized using DFT calculation to obtain more stable structures, among them the structure with the lowest binding energy was picked as the final globally stable structure.
Figure 3.
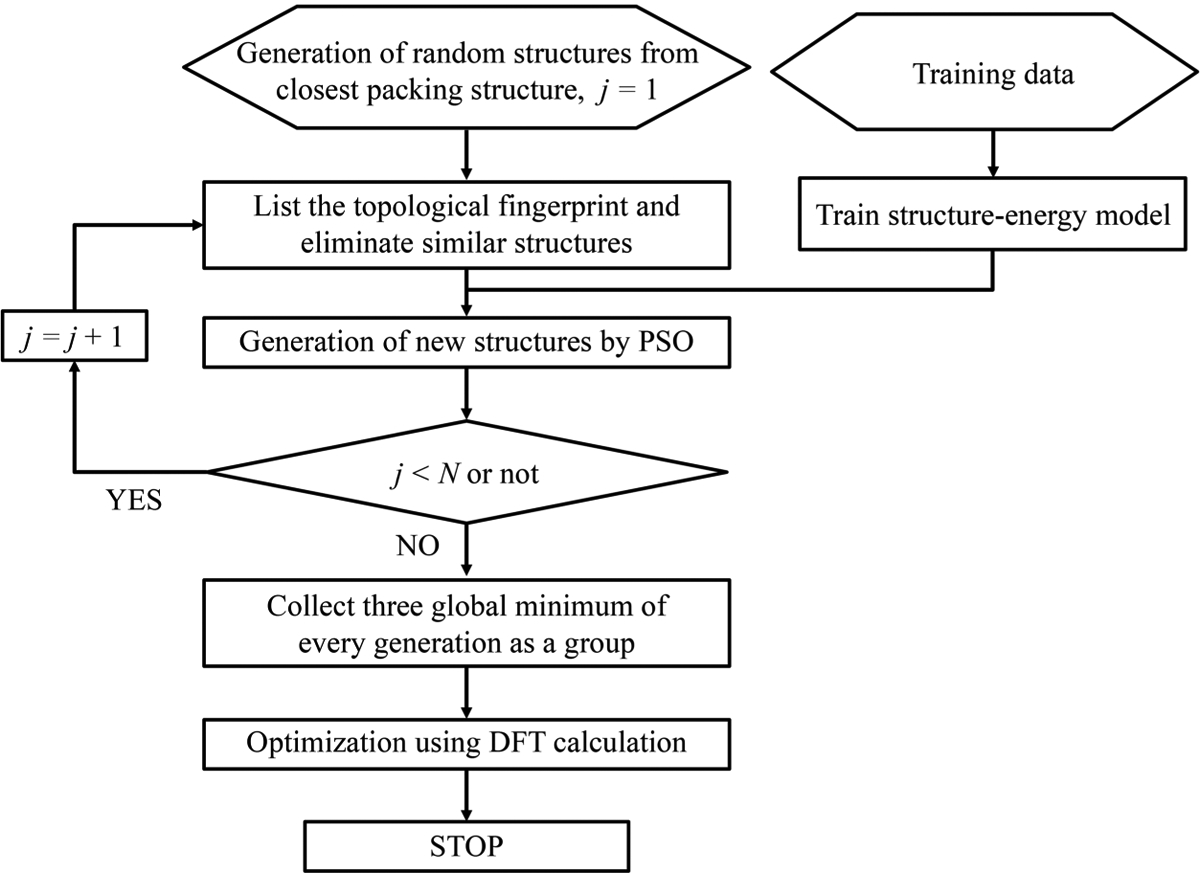
Flowchart of a topology-ML-PSO-DFT protocol
DFT Calculation.
For Lin clusters, to match the results of previous studies,12,67 the DFT calculations were performed using the same method, namely, the plane-wave projector-augmented wave method68,69 implemented in the Vienna ab initio simulation package (VASP)70 with an energy cutoff of 520 eV. The generalized gradient approximation (GGA) with the Perdew–Burke–Enzerhoff parametrization (PBE)71 was chosen as the exchange–correlation potential. The binding energy, the energy to form a cluster with joint atoms from isolated atoms in a vacuum, is defined as
| (12) |
where Ecluster, Eatom, and n is the energy of cluster, the energy of the sole atom, and the numbers of atoms, respectively. The energy was divided by n is to make clusters with a different number of atoms comparable.
Data and Model Availability.
To ensure the reproducibility of the results, the code and data used in this work were uploaded to Github. More details are given in the Supporting Information.
First, we generate some data of small-size clusters for machine learning and optimize essential parameters. With generated data and optimized parameters, the comparisons of the algorithm of GBR and NN were also carried out. Then, we apply the model to predict the most stable isomer for medium-size clusters.
Data Generation.
Li is the lightest metallic element in the periodic table. Li clusters are thus considered to be prototype systems for understanding the various physical properties of simple metal clusters. Numerous theoretical studies have been performed to understand the structures of Li clusters.12,72–78 Here, we use the PSO method to generate the structures of Lin clusters, where n = 3, 4, …, 10, for optimizing the essential parameters and training our machine learning models. For each cluster, a search with a population size of 50 was performed and stopped at the 21st generations. All the above-mentioned DFT calculations were performed with ion step below 20. A total of 136 617 structures was produced. Meanwhile, it has also carried on the processing of duplication removal for similar structures with identical TFs. Finally, 70% of structures are used as the training set, with the other 30% being used as the testing set.
Parameter Optimization.
First, the structure of TFs, i.e., the number of subintervals in each angstrom and ϵmax, should be optimized. The number of subintervals in each angstrom, ns, is an essential parameter of our model and ultimately determines the length of the TFs and the precision for deduplication, which means that the ns affects the number of distinct structures we finally collect. Thus, we first optimize the structure of TFs and ϵmax with ns = 10. Subsequently, ns could be optimized. As for the structure of TFs, the topological invariants and PPI could be described by birth, death, and persistence.
We are interested in examining the utility of the newly proposed PPI. In the comparison of the statistics in the first three lines in Table 1, the MAE of the TFs without PPI is0.039 eV/atom, and with PPI used the MAE is below 0.030 eV/atom. Therefore, it can be concluded that the accuracy of the present model has been significantly improved by the application of PPI as an auxiliary feature. More specifically, the death of PPI is more effective than the persistence of PPI.
Table 1.
List of Mean Absolute Error (MAE), Pearson Correlation Coefficient (PCC), and ϵmax Used in the Present Worka
| structure of TFs | ϵmax | MAE (eV/atom) | PCC |
|---|---|---|---|
| p(β0)+p(β1)+p(β2) | 10 | 0.039 | 0.979 |
| p(β0)+p(β1)+p(β2)+p(PPI) | 10 | 0.028 | 0.986 |
| p(β0)+p(β1)+p(β2)+d(PPI) | 10 | 0.026 | 0.990 |
| p(β1)+p(β2)+d(PPI) | 10 | 0.031 | 0.981 |
| bd(β0)+bd(β1)+bd(β2)+d(PPI) | 10 | 0.030 | 0.983 |
| bpd(β1)+bpd(β1)+bpd(β2)+d(PPI) | 10 | 0.026 | 0.988 |
| p(β0)+p(β1)+p(β2)+d(PPI) | 5 | 0.028 | 0.986 |
| p(β0)+p(β1)+p(β2)+d(PPI) | 15 | 0.026 | 0.989 |
b(*), p(*), and d(*) represent the birth, the persistence, and the death of topological invariant *, respectively. Here, bd(*) represents b(*)+d(*) and bpd(*) represents b(*)+p(*)+d(*).
As shown in Table 1, the combination of the persistence of β0, β1, and β2 and the death of PPI would provide the lowest MAE and the highest PCC when the value of ϵmax was the same. However, it is obvious when the structures of TFs were the same, the PCC would be increased in accordance with the increase of the value of ϵmax, but the increase was not obvious when ϵmax was greater than 10 Å. Thus, we choose the combination of the persistence of β0, β1, and β2 and death of PPI with ϵmax of 10 Å as our TFs. These results are further compared with previous ML model, GAP,60 with GBR as the base ML algorithm. More details are shown in Supporting Information. The PCC of GAP the GAP model is 0.990.
In this work, since the structure of TFs and ϵmax were settled, 119 219, 130 099, and 132 874 distinct structures linked to the binding energy were acquired after deduplication process from initial 136 617 structures with ns of 5, 10, and 20, respectively. We compared the MAE and PCC of the algorithm of the GBR and NN and found the latter algorithm had a better predictive ability. As shown in Figure 4, the MAEs of ns = 10 and ns = 20 by NN were minimal, and their PCCs were higher than others. A higher value of ns indicates a longer time training model needs. Thus, the followed work was all based on the algorithm of NN with ns of 10.
Figure 4.
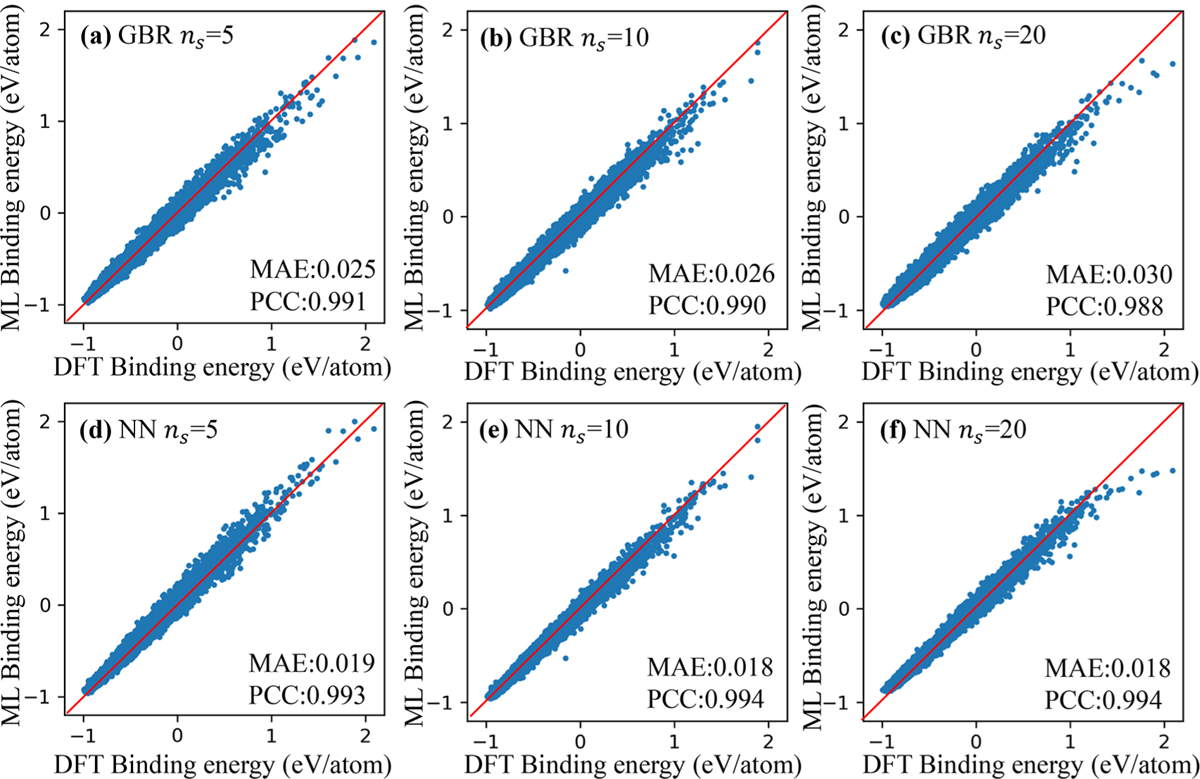
Comparison between persistent homology prediction results and DFT calculation results of the binding energy of Lin (n = 3, 4, …, 10) with the number of subintervals in 1 Å being (a) 5 with GBR, (b) 10 with GBR, (c) 20 with GBR, (d) 5 with NN, (e) 10 with NN, and (f) 20 with NN.
Performance on Lin.
Additionally, we use the same method to generate only two generation of Li20 and Li40 clusters for further testing our model. The learning task is to predict the cluster binding energy of Li20 and Li40 clusters with model learning on Lin (n = 3, 4, …, 10) clusters. As shown in Figure 5, the model trained on Lin (n = 3, 4, …, 10) cluster data performed well on Lin (n = 3, 4, …, 10) (PCC = 0.993) and Li20 clusters (PCC = 0.990) but did not do well on Li40 clusters (PCC = 0.950). The MAEs of both Li20 and Li40 are larger than MAE of Lin (n = 3, 4, …, 10). The larger MAEs were caused by the systematical error (overall migration of prediction compared to true value). Since we only concerned about relative energy values rather than absolute energy values (it has no effect on global stable structure search when all prediction energy values shift to lower or higher values overall), the quality of the model was evaluated by the PCC. The results showed that our model could be applied in a certain range (Li2n, n was the maximum value of number of atoms learned) with wide adaptability and exactitude. The reason for its large deviation on Li40 is that there are some contributions from long-range interactions in large clusters that cannot be learned from small-sized clusters. These results are further compared with GAP, as shown in Figure 5, on Li20, TF model performs better.
Figure 5.
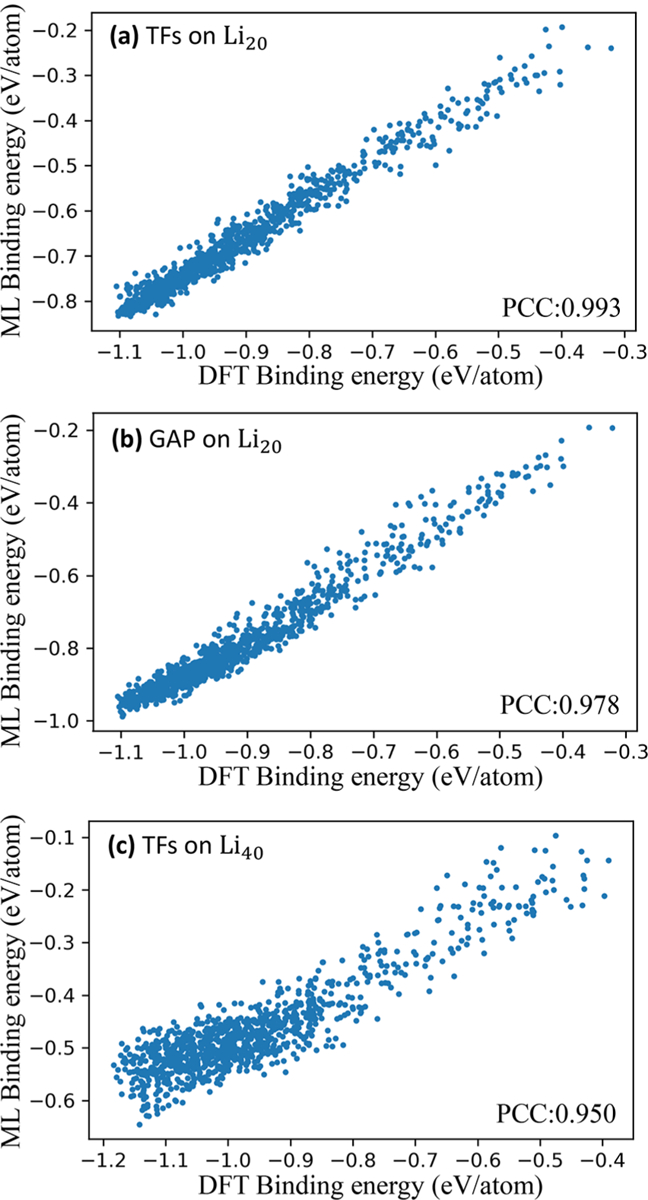
Comparison between persistent homology prediction and DFT calculation of the binding energy of (a) TFs on Li20, (b) GAP on Li40, and (c) TFs on Li40.
Putative Globally Stable Structures of Li20 and Li40.
As a case study, we test our structure prediction protocol on Li20 and Li40 clusters. Our topology-ML-PSO-DFT protocol mainly consists of two steps. First, a search with the population size of 2000 was performed and stopped at the 15th generation through the machine learning model, which avoided the expensive DFT calculation on screening local minimum values. Second, three predicted lowest energy structures (determined by our machine learning model) of every generation were collected for deduplication and optimized through DFT calculations. For each cluster, two independently topology-ML-PSO-DFT structural searchs were performed and both searchs found the same lowest energy structure.
Our predicted lowest energy structures of Li20 is composed of three centered trigonal prisms with five additional capped atoms, as shown in Figure 6a. This is in agreement with the result of Ma et al. obtained by CALYPSO12,67 and Fournier et al. obtained by using the Tabu search in the descriptor space.77 The second and the third lowest energy structures are very similar. The only difference is that the middle layer of the first one is an isosceles trapezoid (Figure 6b) whereas the other is hexagonal (see Figure 6c). Ma et al. found the latter structure but not the former. As shown in Figure 6d, our predicted lowest energy structure of Li40 is a 45-atom polyicosahedron with five missing vertex atoms. This is also in agreement with the previous work,12 more detail of this structure could be found in the Supporting Information. In order to demonstrate the role of the ML model in the structure prediction, three independent topology-ML-PSO-DFT searches of Li20 and three independently PSO-DFT searches of Li20 with a population size of 20 were performed and stopped when the lowest energy structures were found. Since the DFT calculation is far more computationally expensive than the ML model prediction, only the DFT calculation is used to measure the efficiency. The average number of DFT calculations taken of topology-ML-PSO-DFT is 21 and of PSO-DFT is 480. The ratio of average CPU time used of topology-ML-PSO-DFT/PSO-DFT is 1:25. Of course, a large DFT-based data set is required for training the ML model, which is even more computationally expensive than the structure search. However, if we did not carry out just one, but two or more structure searches, the ML-PSO-DFT would reach orders of magnitude speedup compared to PSO-DFT. For example, ML model training on Lin (n = 3, 4, …, 10) could be applied to the structure search of Lin (n = 11, 12, …, 20).
Figure 6.
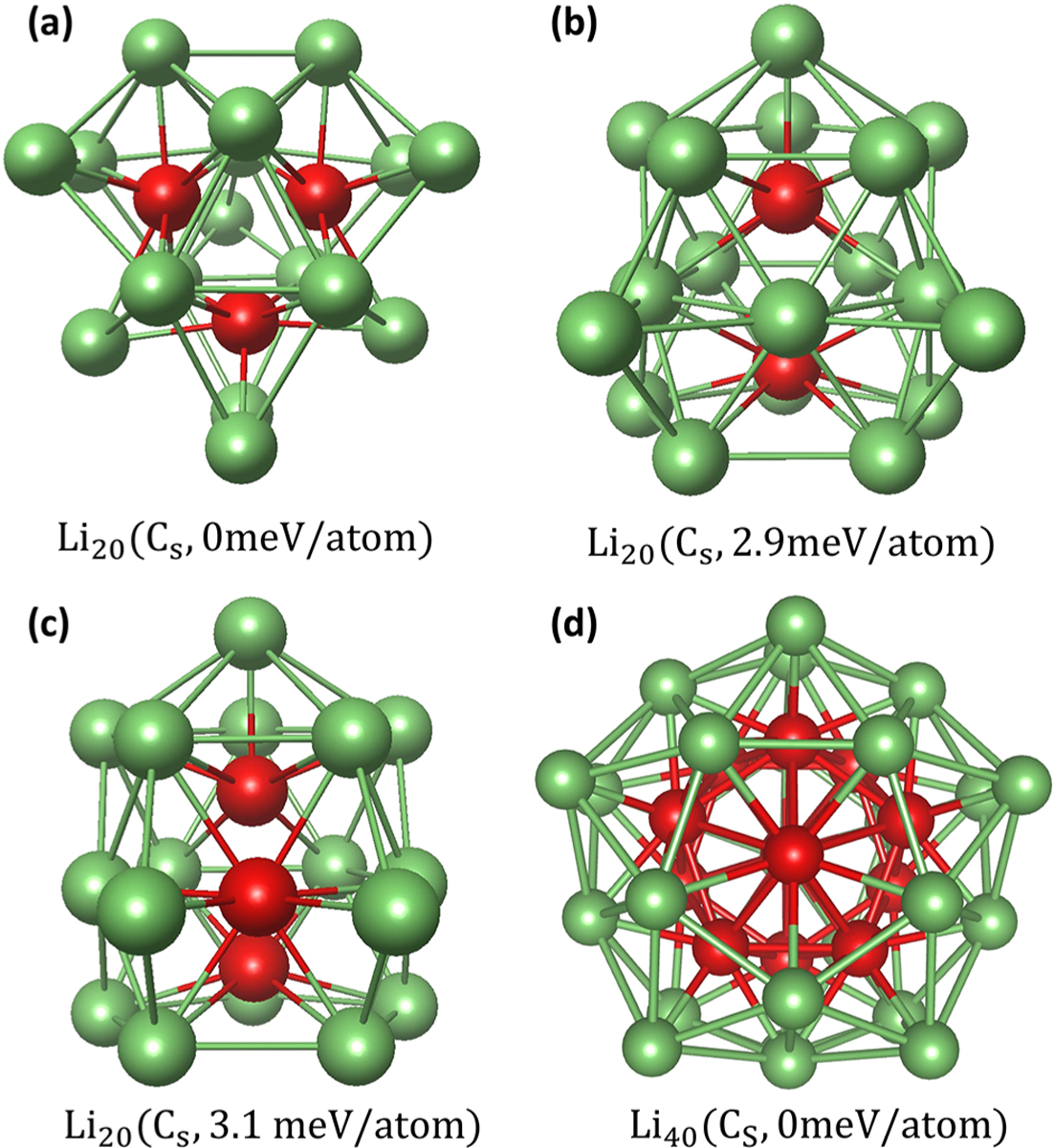
(a) Putative global stable structure of Li20. Two metastable structures of Li20 are depicted in (b), (c). (d) Putative global stable structure of Li40. The internal and external atoms are shown in red and green, respectively.
In conclusion, data representation is one of three major ingredients of machine learning (ML) studies. It becomes more important as the data complexity increases. A wide variety of data representation has been proposed for material sciences. However, topology has been hardly introduced to the field. In this work, we introduce persistent homology, a new branch of algebraic topology, as a new tool for representing metal cluster structures. Unlike conventional topology, persistent homology bridges geometry and topology, achieving an interplay between geometry and topology without downgrading important geometric information of structures. Persistent homology extracts low-dimensional topological invariants from high-dimensional data. It has been successfully applied to various data science problems. To enhance the predictive power of persistent homology, we propose persistent pairwise independence (PPI) as an auxiliary feature. Persistent barcodes of both topological invariants and PPI are utilized as cluster descriptors. Our topology-based ML models are found to offer highly accurate predictions of lithium (Li) cluster binding energies. Then, a systematic predictive protocol for generating the globally stable cluster structure is constructed by integrating a topology-based ML, particle swarm optimization (PSO), and density functional theory (DFT) calculation. The proposed topology-ML-PSO-DFT protocol is validated on medium-sized Lin clusters. The predicted globally stable structure is in agreement with that in the literature. Therefore, the current methodology has been proved to be a reliable approach for cluster structure prediction. It is worthy to mention that this is the first time that topology and ML are applied to avoid the expensive DFT calculation on screening local minimum values. However, there are many aspects to be improved, such as the precision and generalization. Moreover, the method accelerating crystal structure relaxation by ML could be integrated with our method to further accelerate structure prediction in future work. This work is a precursor for the prediction of multielement clusters and the structure prediction of complex crystal surface adsorption.
Supplementary Material
ACKNOWLEDGMENTS
The research was financially supported by Soft Science Research Project of Guangdong Province (2017B030301013), National Key R&D Program of China (2016YFB0700600) and Shenzhen Science and Technology Research Grant (ZDSYS201707281026184). The work of Guo-Wei Wei was supported in partial by NSF Grants DMS1721024, DMS1761320, IIS1900473, NIH grants GM126189 and GM129004, Bristol-Myers Squibb, and Pfizer.
Footnotes
Complete contact information is available at: https://pubs.acs.org/10.1021/acs.jpclett.0c00974
Supporting Information
The Supporting Information is available free of charge on the ACS Publications Web site. The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c00974.
Parameters of machine learning models, more specific examples of barcode representation, putative globally stable structures of Li40 (PDF)
The authors declare no competing financial interest.
Contributor Information
Xin Chen, School of Advanced Materials, Shenzhen Graduate School, Peking University, Shenzhen 518055, People’s Republic of China.
Dong Chen, School of Advanced Materials, Shenzhen Graduate School, Peking University, Shenzhen 518055, People’s Republic of China.
Mouyi Weng, School of Advanced Materials, Shenzhen Graduate School, Peking University, Shenzhen 518055, People’s Republic of China.
Yi Jiang, School of Advanced Materials, Shenzhen Graduate School, Peking University, Shenzhen 518055, People’s Republic of China.
Guo-Wei Wei, Department of Mathematics, Michigan State University, East Lansing, Michigan 48824, United States.
Feng Pan, School of Advanced Materials, Shenzhen Graduate School, Peking University, Shenzhen 518055, People’s Republic of China.
REFERENCES
- (1).Stillinger FH Exponential multiplicity of inherent structures. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top 1999, 59, 48. [DOI] [PubMed] [Google Scholar]
- (2).Pickard CJ; Needs R Ab initio random structure searching. J. Phys.: Condens. Matter 2011, 23, 053201. [DOI] [PubMed] [Google Scholar]
- (3).Wales DJ; Doye JP Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar]
- (4).Goedecker S Minima hopping: An efficient search method for the global minimum of the potential energy surface of complex molecular systems. J. Chem. Phys 2004, 120, 9911–9917. [DOI] [PubMed] [Google Scholar]
- (5).Kirkpatrick S; Gelatt CD; Vecchi MP Optimization by simulated annealing. Science 1983, 220, 671–680. [DOI] [PubMed] [Google Scholar]
- (6).Deaven DM; Ho K-M Molecular geometry optimization with a genetic algorithm. Phys. Rev. Lett 1995, 75, 288. [DOI] [PubMed] [Google Scholar]
- (7).Hartke B Global geometry optimization of clusters using genetic algorithms. J. Phys. Chem 1993, 97, 9973–9976. [Google Scholar]
- (8).Oganov AR; Glass CW Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys 2006, 124, 244704. [DOI] [PubMed] [Google Scholar]
- (9).Eberhart R; Kennedy J A new optimizer using particle swarm theory. MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science; IEEE, 1995; pp 39–43. [Google Scholar]
- (10).Kennedy J Particle swarm optimization. Encyclopedia of machine learning 2010, 760–766. [Google Scholar]
- (11).Call ST; Zubarev DY; Boldyrev AI Global minimum structure searches via particle swarm optimization. J. Comput. Chem 2007, 28, 1177–1186. [DOI] [PubMed] [Google Scholar]
- (12).Lv J; Wang Y; Zhu L; Ma Y Particle-swarm structure prediction on clusters. J. Chem. Phys 2012, 137, 084104. [DOI] [PubMed] [Google Scholar]
- (13).Ward L; Wolverton C Atomistic calculations and materials informatics: A review. Curr. Opin. Solid State Mater. Sci 2017, 21, 167–176. [Google Scholar]
- (14).Cang Z; Wei G-W TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. PLoS Comput. Biol 2017, 13, No. e1005690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Carrete J; Li W; Mingo N; Wang S; Curtarolo S Finding unprecedentedly low-thermal-conductivity half-Heusler semiconductors via high-throughput materials modeling. Phys. Rev. X 2014, 4, 011019. [Google Scholar]
- (16).Curtarolo S; Morgan D; Persson K; Rodgers J; Ceder G Predicting crystal structures with data mining of quantum calculations. Phys. Rev. Lett 2003, 91, 135503. [DOI] [PubMed] [Google Scholar]
- (17).De Jong M; Chen W; Notestine R; Persson K; Ceder G; Jain A; Asta M; Gamst A A statistical learning framework for materials science: application to elastic moduli of k-nary inorganic polycrystalline compounds. Sci. Rep 2016, 6, 34256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Faber FA; Lindmaa A; Von Lilienfeld OA; Armiento R Machine Learning Energies of 2 Million Elpasolite (A B C 2 D 6) Crystals. Phys. Rev. Lett 2016, 117, 135502. [DOI] [PubMed] [Google Scholar]
- (19).Furmanchuk A; Agrawal A; Choudhary A Predictive analytics for crystalline materials: bulk modulus. RSC Adv. 2016, 6, 95246–95251. [Google Scholar]
- (20).Meredig B; Agrawal A; Kirklin S; Saal JE; Doak J; Thompson A; Zhang K; Choudhary A; Wolverton C Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B: Condens. Matter Mater. Phys 2014, 89, 094104. [Google Scholar]
- (21).Moot T; Isayev O; Call RW; McCullough SM; Zemaitis M; Lopez R; Cahoon JF; Tropsha A Material informatics driven design and experimental validation of lead titanate as an aqueous solar photocathode. Materials Discovery 2016, 6, 9–16. [Google Scholar]
- (22).Pilania G; Mannodi-Kanakkithodi A; Uberuaga B; Ramprasad R; Gubernatis J; Lookman T Machine learning bandgaps of double perovskites. Sci. Rep 2016, 6, 19375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Pyzer-Knapp EO; Simm GN; Guzik AA A Bayesian approach to calibrating high-throughput virtual screening results and application to organic photovoltaic materials. Mater. Horiz 2016, 3, 226–233. [Google Scholar]
- (24).Seko A; Hayashi H; Nakayama K; Takahashi A; Tanaka I Representation of compounds for machine-learning prediction of physical properties. Phys. Rev. B: Condens. Matter Mater. Phys 2017, 95, 144110. [Google Scholar]
- (25).Steinhardt PJ; Nelson DR; Ronchetti M Bond-orientational order in liquids and glasses. Phys. Rev. B: Condens. Matter Mater. Phys 1983, 28, 784. [Google Scholar]
- (26).Ward L; Agrawal A; Choudhary A; Wolverton C A general-purpose machine learning framework for predicting properties of inorganic materials. npj Computational Materials 2016, 2, 16028. [Google Scholar]
- (27).Ward L; Liu R; Krishna A; Hegde VI; Agrawal A; Choudhary A; Wolverton C Including crystal structure attributes in machine learning models of formation energies via Voronoi tessellations. Phys. Rev. B: Condens. Matter Mater. Phys 2017, 96, 024104. [Google Scholar]
- (28).Jie J; Hu Z; Qian G; Weng M; Li S; Li S; Hu M; Chen D; Pan F Discovering unusual structures from exception using big data and machine learning techniques. Science Bulletin 2019, 64, 612–616. [DOI] [PubMed] [Google Scholar]
- (29).Chen D; Li S; Jie J; Li S; Zheng S; Weng M; Yu C; Li S; Chen D; Pan F A descriptor of “material genes”: Effective atomic size in structural unit of ionic crystals. Sci. China: Technol. Sci 2019, 62, 849–855. [Google Scholar]
- (30).Jie J; Weng M; Li S; Chen D; Li S; Xiao W; Zhen J; Pan F; Wang L A new MaterialGo database and its comparison with other high-throughput electronic structure databases for their predicted energy band gaps. Sci. China: Technol. Sci 2019, 62, 1423–1430. [Google Scholar]
- (31).Coley CW; Barzilay R; Green WH; Jaakkola TS; Jensen KF Convolutional embedding of attributed molecular graphs for physical property prediction. J. Chem. Inf. Model 2017, 57, 1757–1772. [DOI] [PubMed] [Google Scholar]
- (32).Duvenaud DK; Maclaurin D; Iparraguirre J; Bombarell R; Hirzel T; Aspuru-Guzik A; Adams RP Convolutional networks on graphs for learning molecular fingerprints. Advances in neural information processing systems 2015, 2224–2232. [Google Scholar]
- (33).Behler J Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys 2011, 134, 074106. [DOI] [PubMed] [Google Scholar]
- (34).Gassner H; Probst M; Lauenstein A; Hermansson K Representation of intermolecular potential functions by neural networks. J. Phys. Chem. A 1998, 102, 4596–4605. [Google Scholar]
- (35).Ludwig J; Vlachos DG Ab initio molecular dynamics of hydrogen dissociation on metal surfaces using neural networks and novelty sampling. J. Chem. Phys 2007, 127, 154716. [DOI] [PubMed] [Google Scholar]
- (36).Lorenz S; Groß A; Scheffler M Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem. Phys. Lett 2004, 395, 210–215. [Google Scholar]
- (37).Lorenz S; Scheffler M; Gross A Descriptions of surface chemical reactions using a neural network representation of the potential-energy surface. Phys. Rev. B: Condens. Matter Mater. Phys 2006, 73, 115431. [Google Scholar]
- (38).Edelsbrunner H; Letscher D; Zomorodian A Topological persistence and simplification. Proceedings 41st Annual Symposium on Foundations of Computer Science; IEEE, 2000; pp 454–463. [Google Scholar]
- (39).Zomorodian A; Carlsson G Computing persistent homology. Discrete & Computational Geometry 2005, 33, 249–274. [Google Scholar]
- (40).Zomorodian A; Carlsson G Localized homology. Computational Geometry 2008, 41, 126–148. [Google Scholar]
- (41).Frosini P; Landi C Size theory as a topological tool for computer vision. Pattern Recognition and Image Analysis 1999, 9, 596–603. [Google Scholar]
- (42).Robins V Towards computing homology from finite approximations. Topology proceedings 1999, 503–532. [Google Scholar]
- (43).Ghrist R Barcodes: the persistent topology of data. Bulletin of the American Mathematical Society 2008, 45, 61–75. [Google Scholar]
- (44).Bendich P; Edelsbrunner H; Kerber M Computing robustness and persistence for images. IEEE transactions on visualization and computer graphics 2010, 16, 1251–1260. [DOI] [PubMed] [Google Scholar]
- (45).Carlsson G; Ishkhanov T; De Silva V; Zomorodian A On the local behavior of spaces of natural images. International journal of computer vision 2008, 76, 1–12. [Google Scholar]
- (46).Pachauri D; Hinrichs C; Chung MK; Johnson SC; Singh V Topology-based kernels with application to inference problems in Alzheimer’s disease. IEEE transactions on medical imaging 2011, 30, 1760–1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Singh G; Memoli F; Ishkhanov T; Sapiro G; Carlsson G; Ringach DL Topological analysis of population activity in visual cortex. Journal of vision 2008, 8, 11–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Frosini P; Landi C Persistent betti numbers for a noise tolerant shape-based approach to image retrieval. Pattern Recognition Letters 2013, 34, 863–872. [Google Scholar]
- (49).Kaczynski T; Mischaikow K; Mrozek M Computational homology; Springer Science & Business Media, 2006; Vol. 157. [Google Scholar]
- (50).Mischaikow K; Mrozek M; Reiss J; Szymczak A Construction of symbolic dynamics from experimental time series. Phys. Rev. Lett 1999, 82, 1144. [Google Scholar]
- (51).Di Fabio B; Landi C A Mayer–Vietoris formula for persistent homology with an application to shape recognition in the presence of occlusions. Foundations of Computational Mathematics 2011, 11, 499. [Google Scholar]
- (52).Dabaghian Y; Mémoli F; Frank L; Carlsson G A topological paradigm for hippocampal spatial map formation using persistent homology. PLoS Comput. Biol 2012, 8, No. e1002581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Kasson PM; Zomorodian A; Park S; Singhal N; Guibas LJ; Pande VS Persistent voids: a new structural metric for membrane fusion. Bioinformatics 2007, 23, 1753–1759. [DOI] [PubMed] [Google Scholar]
- (54).Xia K; Wei G-W Persistent homology analysis of protein structure, flexibility, and folding. International journal for numerical methods in biomedical engineering 2014, 30, 814–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Xia K; Feng X; Tong Y; Wei GW Persistent homology for the quantitative prediction of fullerene stability. J. Comput. Chem 2015, 36, 408–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Cang Z; Mu L; Wu K; Opron K; Xia K; Wei G-W A topological approach for protein classification. Computational and Mathematical Biophysics 2015, 3, 140–162. [Google Scholar]
- (57).Nguyen DD; Cang Z; Wu K; Wang M; Cao Y; Wei G-W Mathematical deep learning for pose and binding affinity prediction and ranking in D3R Grand Challenges. J. Comput.-Aided Mol. Des 2019, 33, 71–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Podryabinkin EV; Tikhonov EV; Shapeev AV; Oganov AR Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys. Rev. B: Condens. Matter Mater. Phys 2019, 99, 064114. [Google Scholar]
- (59).Deringer VL; Pickard CJ; Csányi G Data-Driven Learning of Total and Local Energies in Elemental Boron. Phys. Rev. Lett 2018, 120, 156001. [DOI] [PubMed] [Google Scholar]
- (60).Bartók AP; Payne MC; Kondor R; Csányi G Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett 2010, 104, 136403. [DOI] [PubMed] [Google Scholar]
- (61).Deringer VL; Csányi G; Proserpio DM Extracting Crystal Chemistry from Amorphous Carbon Structures. ChemPhysChem 2017, 18, 873–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Hu Q; Weng M; Chen X; Li S; Pan F; Wang L-W Neural Network Force Fields for Metal Growth Based on Energy Decompositions. J. Phys. Chem. Lett 2020, 11, 1364–1369. [DOI] [PubMed] [Google Scholar]
- (63).Edelsbrunner H; Mücke EP Three-dimensional alpha shapes. ACM Transactions on Graphics (TOG) 1994, 13, 43–72. [Google Scholar]
- (64).Zeng Y; Li Q; Bai K Prediction of interstitial diffusion activation energies of nitrogen, oxygen, boron and carbon in bcc, fcc, and hcp metals using machine learning. Comput. Mater. Sci 2018, 144, 232–247. [Google Scholar]
- (65).Behler J Neural network potential-energy surfaces in chemistry: a tool for large-scale simulations. Phys. Chem. Chem. Phys 2011, 13, 17930–17955. [DOI] [PubMed] [Google Scholar]
- (66).Wang Y; Lv J; Zhu L; Ma Y Crystal structure prediction via particle-swarm optimization. Phys. Rev. B: Condens. Matter Mater. Phys 2010, 82, 094116. [Google Scholar]
- (67).Wang Y; Lv J; Zhu L; Ma Y CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun 2012, 183, 2063–2070. [Google Scholar]
- (68).Blöchl PE Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys 1994, 50, 17953. [DOI] [PubMed] [Google Scholar]
- (69).Kresse G; Joubert D From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys 1999, 59, 1758. [Google Scholar]
- (70).Kresse G; Furthmüller J Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys 1996, 54, 11169. [DOI] [PubMed] [Google Scholar]
- (71).Perdew JP; Burke K; Ernzerhof M Generalized gradient approximation made simple. Phys. Rev. Lett 1996, 77, 3865. [DOI] [PubMed] [Google Scholar]
- (72).Centeno J; Fuentealba P Big bang methodology applied to atomic clusters. Int. J. Quantum Chem 2011, 111, 1419–1435. [Google Scholar]
- (73).Gardet G; Rogemond F; Chermette H Density functional theory study of some structural and energetic properties of small lithium clusters. J. Chem. Phys 1996, 105, 9933–9947. [Google Scholar]
- (74).Goel N; Gautam S; Dharamvir K Density functional studies of LiN and LiN+ (N = 2–30) clusters: Structure, binding and charge distribution. Int. J. Quantum Chem 2012, 112, 575–586. [Google Scholar]
- (75).Guo Z; Lu B; Jiang X; Zhao J; Xie R-H Structural, electronic, and optical properties of medium-sized Lin clusters (n = 20, 30, 40, 50) by density functional theory. Phys. E 2010, 42, 1755–1762. [Google Scholar]
- (76).Knight W; Clemenger K; de Heer WA; Saunders WA; Chou M; Cohen ML Electronic shell structure and abundances of sodium clusters. Phys. Rev. Lett 1984, 52, 2141. [Google Scholar]
- (77).Fournier R; Bo Yi Cheng J; Wong A Theoretical study of the structure of lithium clusters. J. Chem. Phys 2003, 119, 9444–9454. [Google Scholar]
- (78).Sung M-W; Kawai R; Weare JH Packing transitions in nanosized Li clusters. Phys. Rev. Lett 1994, 73, 3552. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


