CONSPECTUS:
The oxygen reduction reaction (ORR) is a multiproton/multielectron transformation in which dioxygen (O2) is reduced to water or hydrogen peroxide and serves as the cathode reaction in most fuel cells. The ORR (O2 + 4e− + 4H+ → 2H2O) involves up to nine substrates and thus requires navigating a complicated reaction landscape, typically with several high-energy intermediates. Many catalysts can perform this reaction, though few operate with fast rates and at low overpotentials (close to the thermodynamic potential). Attempts to optimize these parameters, both in homogeneous and heterogeneous electrocatalytic systems, have focused on modifying catalyst design and understanding kinetic/thermodynamic relationships between catalytic intermediates. One such method for analyzing and predicting catalyst reactivity and efficiency has been the development of “molecular scaling relationships”. Here, we share our experience deriving and utilizing molecular scaling relationships for soluble, iron-porphyrin-catalyzed O2 reduction in organic solvents. These relationships correlate turnover frequencies (TOFmax) and effective overpotentials (ηeff), properties uniquely defined for homogeneous catalysts. Following a general introduction of scaling relationships for both homogeneous and heterogeneous electrocatalysis, we describe the components of such scaling relationships: (i) the overall thermochemistry of the reaction and (ii) the rate and rate law of the catalyzed reaction. We then show how connecting these thermodynamic and kinetic parameters reveals multiple molecular scaling relationships for iron-porphyrin-catalyzed O2 reduction. For example, the log(TOFmax) responds steeply to changes in ηeff that result from different catalyst reduction potentials (18.5 decades in TOFmax/V in ηeff) but much less dramatically to changes in ηeff that arise from varying the pKa of the acid buffer (5.1 decades in TOFmax/V in ηeff). Thus, a single scaling relationship is not always sufficient for describing molecular electrocatalysis. This is particularly evident when the catalyst identity and reaction conditions are coupled. Using these multiple scaling relationships, we demonstrate that the metrics of turnover frequency and effective overpotential can be predictably tuned to achieve faster rates at lowered overpotentials. This Account uses a collection of related stories describing our research on soluble iron-porphyrin-catalyzed ORR to show how molecular scaling relationships can be derived and used for any electrocatalytic reaction. Such scaling relationships are powerful tools that connect the thermochemistry, mechanism, and rate law for a catalytic system. We hope that this collection shows the utility and simplicity of the molecular scaling approach for understanding catalysis, for enabling direct comparisons between catalyst systems, and for optimizing catalytic processes.
Graphical Abstract
I. INTRODUCTION
The reduction of dioxygen (O2) to water (H2O) is a critical chemical transformation for many biological and artificial energy systems, such as cellular respiration and fuel cell technologies.1–3 For energy applications, the four-electron/four-proton (4e−/4H+) reduction of O2 to H2O (eq 1) is preferred over the less exoergic 2e−/2H+ reduction of O2 to hydrogen peroxide (H2O2).
| (1) |
Performing the 4e−/4H+ oxygen reduction reaction (ORR) at high rates and close to its thermodynamic potential (e.g., at low overpotentials) is a major challenge.1,4–6 The best systems use platinum-group-metal catalysts, but improved replacements with earth-abundant materials are required for next-generation energy technologies.4 Many of the fundamental aspects of this challenge are more amenable to study with homogeneous molecular ORR electrocatalysts, though soluble catalysts are less likely to be the technological solution.7,8 Research on molecular electrocatalysts provides new strategies for efficient catalysis of the ORR and other proton/electron energy-conversion reactions.
This Account describes how our studies of soluble iron porphyrin ORR catalysts (Fe(por)) in organic solvents led us to develop “molecular scaling relationships”. These relationships reveal how the primary metrics of catalysis (turnover frequency and overpotential) depend on the components of the catalytic system. Using ORR electrocatalysis by iron porphyrins as a case study, we develop the thermodynamic and kinetic parameters relevant to molecular electrocatalysis and then derive the corresponding molecular scaling relationships. We demonstrate how catalysis depends not on only on catalyst identity but also on the buffer and the medium. These quantitative relationships provide a powerful new way to understand, compare, and improve multiproton/multielectron electrocatalytic systems. We hope that this Account will stimulate our readers to use this approach for their catalytic applications.
II. METRICS FOR HOMOGENEOUS MOLECULAR ELECTROCATALYSIS
Molecular electrocatalysis involves soluble catalysts, often in nonaqueous media, that are driven by the exchange of electrons with an electrode. The primary scientific metrics that describe a catalytic system–defined as both the electrocatalyst and its surrounding medium–are rates, over potentials, selectivity, and robustness. Emphasized here are the parameters of maximum turnover frequency (TOFmax), or moles of product per mole of catalyst (in the reaction diffusion layer) per second, and effective overpotential (ηeff, see below).9,10 With this emphasis, the “best” catalyst is the one that attains the highest TOFmax at the lowest ηeff.
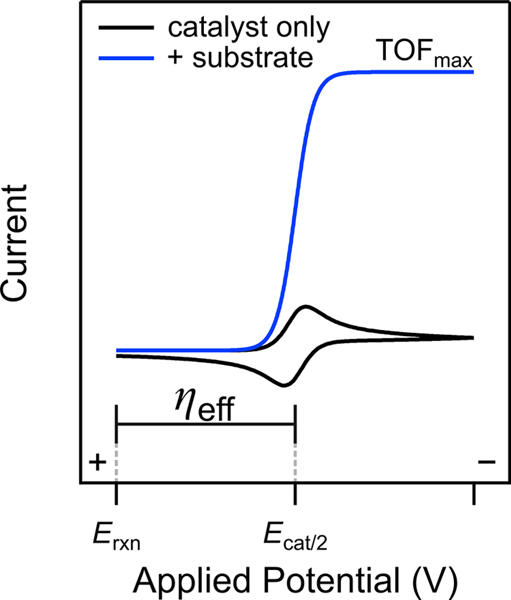
Cyclic voltammetry is the technique most often used to evaluate molecular electrocatalysis, where TOFmax is obtained by analyzing the response of the electrocatalyst in the presence and absence of substrate (blue and black curves in Figure 1).11 In an ideal system, the catalytic current reaches a maximum at potentials beyond Ecat/2,11,12 where it is limited by chemical steps in the solution.13,14 For nonideal voltammograms, foot-of-the-wave analysis (FOWA) is often used to extract TOFmax from the “foot” of the catalytic wave.11,13 The ηeff is defined as the difference between Ecat/2 and the thermodynamic potential of the reaction of interest under catalytic conditions (Erxn; eq 2).9,10 In Fe(por)-catalyzed ORR, Ecat/2 is equivalent to the iron(III)/iron(II) reduction potential, E1/2(FeIII/FeII), and Erxn is the ORR equilibrium potential under the reaction conditions, EO2/H2O (eq 3).10–12,15
| (2) |
| (3) |
Figure 1.
Simulated voltammograms of an electrocatalytic (EC′) reaction driven by a molecular catalyst in the presence (blue) and absence (black) of substrate. Erxn is the equilibrium potential of the catalyzed reaction, and Erxn − Ecat/2 is the reaction overpotential (ηeff). Adapted with permission from ref 7. Copyright 2018 American Chemical Society.
III. STANDARD AND EQUILIBRIUM POTENTIALS
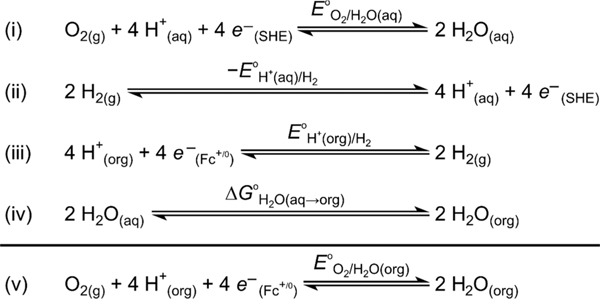
The thermodynamic potential of a catalyzed reaction is needed to determine ηeff.9,10 Until recently, however, the standard potentials were not known for ORR or many other multiproton/multielectron reactions in organic solvents. Building on Roberts and Bullock’s seminal work,16 Roberts, Appel, and our laboratory developed a method to estimate such potentials from the aqueous standard potential and the nonaqueous standard hydrogen potential (E°H+/H2; collected from open-circuit potential measurements in the organic solvent of interest containing an acid/base buffer of known pKa) using a thermochemical cycle (Scheme 1).17 This approach has been used to determine the standard potentials for reductions of O2, CO2, and N2 to various products in acetonitrile (MeCN) and dimethylformamide (DMF).17,18
| (4) |
Scheme 1.
Thermochemical Cycle to Estimate E°O2/H2O in Nonaqueous Solvents from E°H+/H2a
aAdapted from ref 17.
The equilibrium potential under catalytic conditions (Erxn) almost always differs from the standard potential because standard-state conditions (e.g., [H2O] = 1 M) are almost never used. The equilibrium potential is given by the Nernst equation (eq 4 for the ORR), which includes the concentrations or pressures of all species involved and the acid pKa. To determine Erxn, we strongly recommend that catalytic solutions be buffered with 1:1 acid (HA) and conjugate base (A−).12,19,20 If only HA is present, then the [A−] at the electrode is not known, and EO2/H2O is undefined. Additionally, homoconjugation of acids and their conjugate bases in organic media (AH···A−) can strongly affect the [HA]/[A−] ratio unless their concentrations are equal.12,19,20
The methods described in this section allow for straightforward determination of the thermodynamic efficiencies of molecular catalysis for many proton-coupled electron transfer (PCET) reactions. We encourage authors to take advantage of these approaches so that they may report ηeff in addition to TOFmax in their studies.
IV. SCALING RELATIONSHIPS 1: IDENTIFYING CORRELATIONS
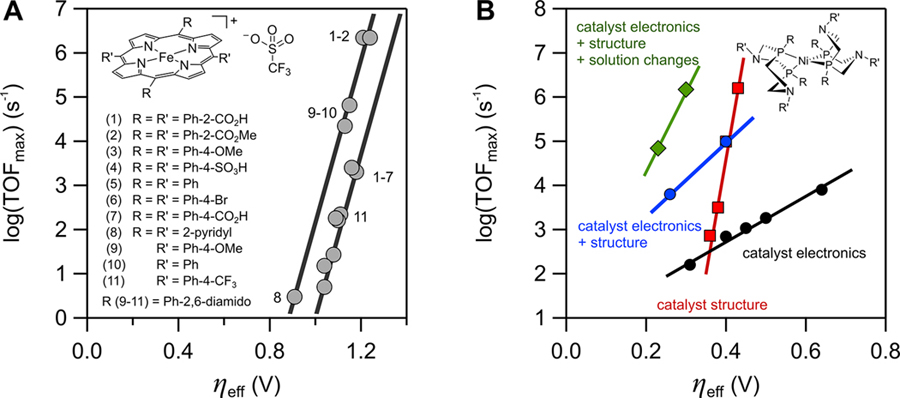
Using the above approaches, we determined kinetic (TOFmax) and thermodynamic (ηeff) values for many Fe(por) ORR catalysts under different conditions. Analysis of these data showed linear correlations between log(TOFmax) and ηeff (eq 5, Figure 2A).10 Such correlations between kinetic and thermodynamic parameters have often been used to derive structure/activity relationships for molecular electrocatalysts.10,21–23 Correlations using TOFmax values are not quite linear free energy relationships (LFERs), because TOFmax values depend on reaction conditions. However, changes in log(TOFmax) are linear with changes in ΔGǂ as long as the reaction conditions do not change (eq 7). Most importantly, normal LFERs correlate a rate parameter with the free energy for that particular step. Thus, TOFmax values generally should not correlate with the overall reaction energetics ηeff, which cover many steps. In fact, there are multiple log(TOFmax)/ηeff correlations, as described below.
Figure 2.
Plots of log(TOFmax) vs ηeff: (A) For the ORR catalyzed by various Fe(por) complexes with DMF–H+ in MeCN and DMF (some catalysts [inset] were studied in both solvents; see ref 10). (Adapted with permission from ref 10. Copyright 2016 American Chemical Society.) (B) For catalytic hydrogen evolution by a series of structurally similar nickel phosphine−amine complexes. The lines describe scaling relationships between TOFmax and ηeff. (Adapted with permission from ref 26. Copyright 2018 American Chemical Society.)
| (5) |
| (6) |
| (7) |
Plotting log(TOFmax) vs ηeff is the simplest way to compare the efficiencies of a set of molecular electrocatalytic systems (Figure 2), where each (ηeff, log(TOFmax)) point describes a catalytic system. The closer these points are to the top-left corner of the plot, the better the system (lower overpotentials, faster rates).21,24,25 For instance, the points at the top right of Figure 2A represent spectacularly rapid ORR catalysts (TOFmax values >106 s−1, the fastest known), yet the high rates come at a cost of high overpotentials (ηeff > 1.2 V)10. Similar trade-offs in log(TOFmax)/ηeff are observed for other electrocatalysts and reactions. For example, the scaling relationships in Figure 2A for 11 different Fe(por) ORR catalysts resemble those in Figure 2B for hydrogen evolution electrocatalysis by nickel phosphine–amine complexes.26 The different slopes of the lines in Figure 2B indicate that the catalytic TOFmax varies in different ways depending on how ηeff is changed (see sections VI–VIII).
The scaling relationships common to heterogeneous electrocatalysis are also kinetic/thermodynamic relationships,5,6 but they are otherwise quite different from the molecular examples above. Heterogeneous scaling relationships typically correlate current density at a given overpotential with a single relevant scaling “descriptor” chosen by the researcher. Thermochemical descriptors such as the surface–H or surface–OH bond strengths are common, because they are both relevant to catalytic steps and relatively easy to compute.5,6 The heterogeneous analysis assumes that the free energies of the important intermediates all scale with the descriptor (the “scaling” relationship). Plots of rate vs descriptor frequently show a “volcano” shape, where the peak position can provide valuable predictions for a particular mechanism (see ref 27 regarding criticisms of this approach)5,28,29
In contrast, the next section shows that molecular electrocatalysts often have more complex mechanisms, in which electrons and protons are often added in separate steps. The subsequent sections (VI–VIII) then bring together these tools and results to understand ORR catalysis by soluble iron porphyrins, and to thereby develop the more complex molecular scaling relationships that correlate TOFmax and ηeff.
V. THE MECHANISM OF O2 REDUCTION BY IRON PORPHYRINS IN NONAQUEOUS SOLVENTS
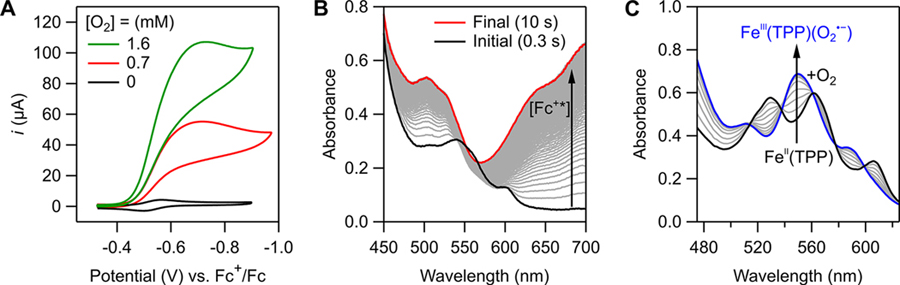
Deriving log(TOFmax)/ηeff relationships for molecular electrocatalysts relies on knowing the catalytic rate law. This section describes our parallel electrochemical and spectroscopic studies of O2 reduction catalyzed by iron tetraphenylporphyrin, Fe(TPP), as a case study.30 In acidified, anaerobic DMF, voltammograms of Fe(TPP) showed a reversible FeIII/FeII redox couple.30,31 Upon saturating the solution with O2, a large, irreversible current appeared, centered over E1/2(FeIII/FeII) (Figure 3A). The shape of the voltammogram suggested an EC′ mechanism, where rapid, reversible ET was followed by irreversible chemical step(s).11 From such voltammograms, TOFmax values were calculated using foot-of-the-wave analysis (FOWA).13,32 The variation of TOFmax with reaction conditions showed that the reaction was first-order in [Fe(TPP)], [O2], and [acid] and yielded the third-order rate constant, kcat (eqs 8 and 9).30,31
| (8) |
| (9) |
Figure 3.
(A) Voltammograms of 0.3 mM [FeIII(TPP)]OTf in the presence of 1 M pTsOH and varying [O2]. (B) Stopped-flow optical spectra for the reaction of O2 (0.33 mM), pTsOH (50 mM), and Fc* (3 mM) catalyzed by [FeIII(TPP)]OTf (30 μM), showing the formation of Fc*+ (arrow). (C) Optical spectra of a titration of O2-saturated DMF into a solution of 50 μM FeII(TPP) and 0.1 M [n-Bu4N][PF6] at 213 K. Figures adapted with permission from ref 30. Copyright 2019 American Chemical Society.
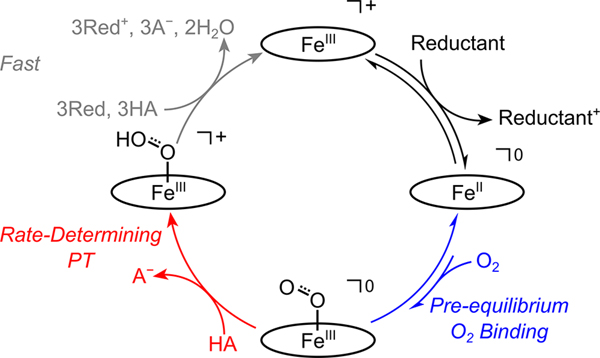
The rate law indicated an ORR mechanism of initial electron transfer (ET) to form FeII(TPP), pre-equilibrium O2-binding to form the iron-superoxo complex, FeIII(TPP)(O2•−), and rate-limiting protonation of FeIII(TPP)(O2•−) (Figure 4).30 To probe the underlying thermochemistry of these intermediates, we examined both equilibrium and catalytic ORR reactions using decamethylferrocene (Fc*) as the terminal reductant and p-toluene sulfonic acid (pTsOH) as the acid.
Figure 4.
General mechanism for O2 reduction catalyzed by Fe(por) in DMF or MeCN, with the porphyrin abbreviated as an oval. “Reductant” can be either a chemical reductant or an electrode. Adapted with permission from ref 30. Copyright 2019 American Chemical Society.
The thermodynamics of the two pre-equilibrium steps–ET and O2 binding–were measured directly using variable-temperature UV–vis spectroscopy. For example, addition of O2 to FeII(TPP) showed reversible formation of FeIII(TPP)(O2•−) (Figure 3C). Van ′t Hoff analyses of the derived equilibrium constants for ET (KET) and O2 binding (KO2) yielded the ΔH° and ΔS° for both steps.30
The catalytic reaction was monitored by variable-temperature optical stopped-flow, combining a solution of [FeIII(TPP)]OTf, O2, and pTsOH with a solution of Fc* (Figure 3B). Globally fitting the kinetic data using COPASI33 gave thermochemical parameters for the ET and O2 pre-equilibria that agreed with the values obtained from the van ′t Hoff analyses, providing strong evidence for the proposed mechanism. The derived rate constants showed a significant activation barrier for proton transfer (PT). Computations revealed that much of this barrier stemmed from the requisite formation of a preassociation complex involving an acid molecule, DMF solvent, and FeIII(TPP)(O2•−). Under conditions where FeII(TPP) is the predominant catalyst resting state, kcat = KO2kPT; thus, changes to either (or both) of these terms will impact TOFmax.30
VI. SCALING RELATIONSHIPS 2: EFFECTS OF CATALYST E1/2 AND BUFFER pKa ON Fe(por)-CATALYZED O2 REDUCTION
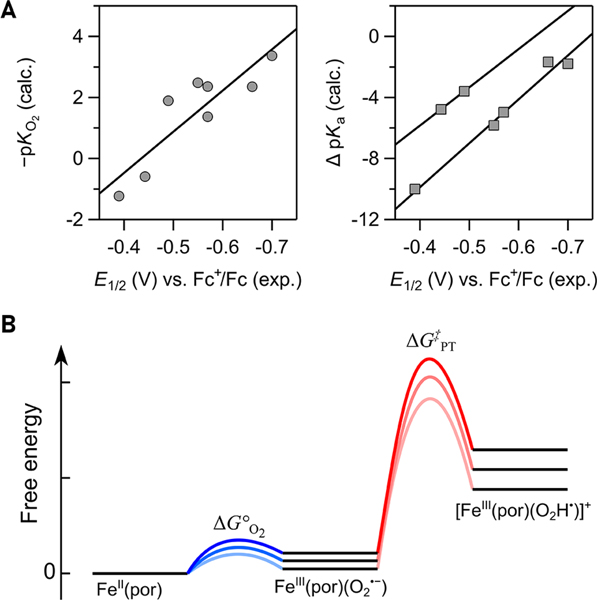
The mechanistic conclusions provided a more quantitative understanding of the relationship between log(TOFmax) and ηeff. The variation in TOFmax is due to changes in ΔGǂ, which is (under most conditions) the sum of the free energy for pre-equilibrium O2 binding and the barrier for protonation (ΔGǂPT) of FeIII(por)(O2•−) by exogenous acid (eq 10, Figure 5).30 depends on the catalyst, and ΔGǂPT is well approximated via the Bronsted law, as a fraction (α) of the PT driving force, ΔG°PT. ΔG°PT is, in turn, given by the difference in pKa between the acid and FeIII(TPP)(O2•−) (eq 11). Values of and ΔG°PT are therefore influenced by intrinsic properties of the catalyst system, namely, the catalyst E1/2 and buffer pKa. Changes in the overpotential are described by eq 3 above, .
Figure 5.
(A) Computed values for O2 binding (pKO2, left) and pKa[FeIII(por)(O2H•)]+ − pKa[DMF–H]+ (right), correlated with E1/2(FeIII/FeII) for some of the Fe(por) in Figure 2A (ref 10). (B) Chemical steps to the rate-determining step and their free energy profile for three different Fe(por) catalysts, equivalent to eq 10. Adapted with permission from ref 10. Copyright 2016 American Chemical Society.
| (10) |
| (11) |
Effect of Catalyst E1/2
The empirical scaling line in Figure 2A corresponds to systemsin which only E1/2 was varied. Changes in E1/2 do not shift the ORR equilibrium potential; thus, . In terms of TOFmax, changes in E1/2 affect both and the pKa of the superoxide complex (eq 12).
A quantitative understanding of the effects of E1/2 on TOF for Fe(por)-catalyzed ORR required computational determination of and pKa([Fe(por)(O2H•)]+) values by our collaborators Dr. Neeraj Kumar and Dr. Simone Raugei. Both alues correlated linearly with the experimental .10 nserting these values and the Brønsted α measured for Fe(por)-catalyzed ORR (0.3) into eq 12 gives eq 13, which predicts a log(TOFmax)/ηeff slope of 19 decades (dec) in TOFmax per V in Δηeff.10,15
| (12) |
| (13) |
This analysis shows how the electronic structure of the catalyst modulates the barrier for catalysis. Catalysts with more negative E1/2 values yield faster TOFmax values because O2 binding is more favorable (larger KO2 and the iron superoxide intermediate is more basic (higher pKa). The combination of experimental and computational results enabled us to quantitatively interpret the slopes of these intrinsic scaling relationships for a series of catalysts with similar electronic structures.
Effect of Buffer pKa
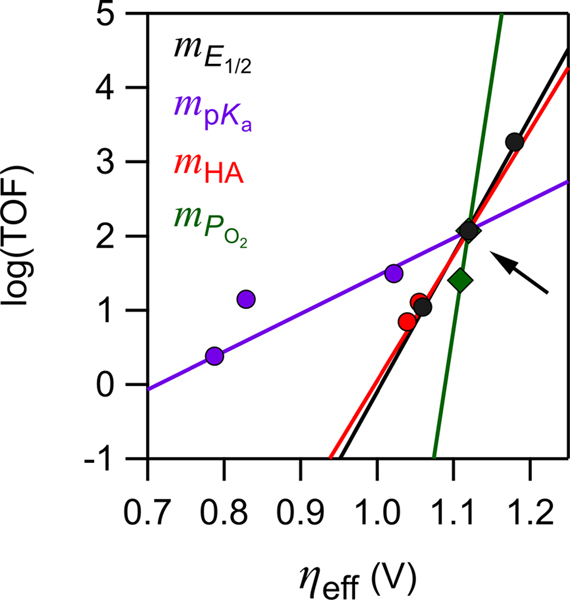
A similar scaling relationship can be derived for a set of catalytic systems in which a single Fe(por) catalyst is evaluated using buffers with different pKa values.15 Changing the buffer identity shifts the ORR equilibrium potential because higher proton activity makes O2 reduction more favorable. From the Nernst equation (eq 4 above), each unit decrease in pKa causes an increase in EORR by 0.0592 V . For the TOFmax, a change in the buffer acidity usually only affects the rate of the PT step via the Br0nsted law (eq 14; exceptions are described below). This leads to a new scaling relationship (eq 15) with a predicted scaling slope m of 5.1 dec/V (α = 0.3, as above). Figure 6 shows this as the purple line, with experimental results (purple points).15
| (14) |
| (15) |
Figure 6.
Scaling relations for Fe(por) ORR catalysis predicted (lines) and measured (points) upon changing the acid concentration (red), partial pressure of O2 (green), acid pKa (purple), and catalyst E1/2 (black; additional data points shown in Figure 2A). The intersection point (arrow) is Fe(TPP)OTf with 100 mM H–DMF+ under 1 atm of O2. Adapted with permission from ref 15. Copyright 2017 American Chemical Society.
Discussion of e1/2 and pKa Scaling Relationships
Equations 13 and 15 show that changes in the two key intrinsic properties of the catalytic system, E1/2 and buffer pKa, have very different effects on the scaling slopes. The log(TOFmax)/ηeff relationship is 3.6 times shallower when pKa is changed rather than E1/2. As a result, can be improved with less penalty to TOFmax by changing the buffer instead of the catalyst identity. For example, replacing [DMF–H]+ with trifluoroacetic acid (ΔpKa = 6.0 in DMF) gave a 104 increase in TOFmax relative to the predicted value for changing ηeff by the same amount via E1/2 (Figure 6).15 The shallow dependence on pKa arises because proton transfer is the rate-limiting step, and thus, the proton transfer barrier (ΔGǂPT) changes by only a fraction (α = 0.3) of the ΔG°PT. In contrast, pre-equilibrium steps will usually be more sensitive to ηeff. For example, Wang and Stahl discovered that cobalt-catalyzed O2 reduction to H2O2 showed a shallow log(TOFmax)/ηeff correlation as the catalyst was varied, 6 dec/V versus the 18.5 dec/V we found for Fe(por).22 The origin of this difference was traced to differences in initial O2 binding. The Fe(por) catalysts have unfavorable KO2 pre-equilibria that are strongly dependent on E1/2. In contrast, O2-binding to the cobalt catalysts is strongly favored regardless of E1/2. These examples show that there are many possible log(TOFmax)/ηeff scaling relationships, depending on the mechanism of catalysis and the property of the catalytic system being varied.
VII. SCALING RELATIONSHIPS 3: EFFECTS OF CONCENTRATIONS
Molecular scaling relationships can also be derived for the effects of experimental or operational conditions on the catalyst system. The simplest operational choice is the concentrations of the reagents, which includes PO2, [HA], [A−], and [H2O] for the ORR. Varying each of these parameters influences the log(TOFmax)/ηeff slopes in unique, predictable ways.15
For changes in concentrations, the slope m of a scaling relationship (eq 5) can be precisely derived from the kinetic and thermodynamic equations (eq 9 and 4, repeated here for ease of presentation).
| (5) |
| (9) |
| (4) |
Since catalysis is first order in [HA] and PO2 (proportional to [O2]), a 10-fold increase in either results in a 10-fold increase in TOF. Changing the [A−] or [H2O], however, does not influence the TOF, since neither appears in the rate law. 10-fold increases in these concentrations all shift ηeff in different ways: +59 mV for [HA], −59 mV for [A−], −30 mV for [H2O], and +15 mV for PO2. Experiments confirm these predictions, as shown by the red and green points (experiments) and lines (theory) in Figure 6.15 The log(TOFmax)/ηeff slopes for [HA] and PO2 differ by a factor of 4 because [HA] and PO2 contribute equally to the kinetics (eq 9) but have different stoichiometries in the ORR, four HA per O2, which set the exponents in the Nernst equation (eq 4).
The ability to predict the relationship between log(TOFmax) and ηeff means that a wide parameter space can be predictably accessed simply by changing the solution conditions for a single catalyst. This conclusion is valuable because most catalysis research involves some searching of parameter space for the best catalytic results (including studies from the authors and those critical of this section34–24). Another important use of this log(TOFmax)/ηeff concentration analysis is to enable quantitative comparisons of catalytic systems that were studied under different conditions.
VIII. SCALING RELATIONSHIPS 4: SUMMATIVE EFFECTS
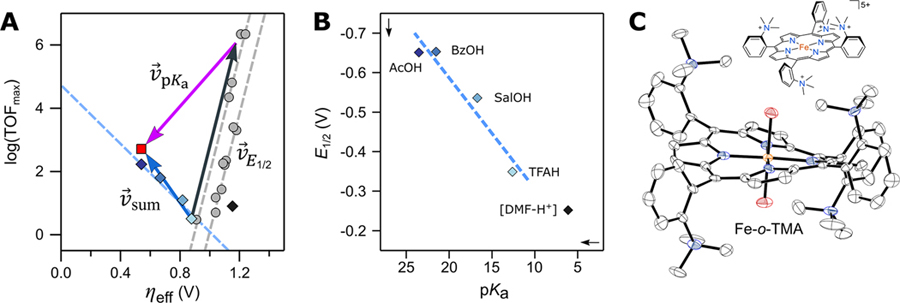
We recently discovered a log(TOFmax)/ηeff scaling relationship with a negative slope, using the polycationic iron αβαβ-trimethylanilinium porphyrin (Fe-o-TMA) and various carboxylic acid buffers (Figure 7).35 The simultaneous improvement in both TOFmax and ηeff was unlike all of the scaling relationships above, which had positive slopes and involved trade-offs between TOFmax and ηeff. However, despite seemingly haven “broken” from the scaling relationships, we demonstrated that this unprecedented result could be predicted by combining the known pKa and E1/2 relationships developed for our Fe(por) systems.
Figure 7.
(A) Plot of log(TOFmax) vs ηeff for catalytic systems of Fe-o-TMA and varying buffers (blue diamonds match buffers in part B). Superimposed vectors show predicted changes from ΔpKa (purple), ΔE1/2 (black), and summative effects (blue). The predicted/observed values for acetic acid buffer are the red square/dark-blue diamond. Prior Fe(por) data and ΔE1/2 scaling relationships included for reference (gray). (B) Plot of E1/2 vs acid pKa at 0.1 M buffer. (C) Drawing of Fe-o-TMA and the solid-state X-ray crystal structure of [Fe-o-TMA·2H2O]OTf5 (H atoms and triflates omitted, thermal ellipsoids at 50% probability). Figures adapted with permission from ref 35. Copyright 2020 American Association for the Advancement of Science.
When studied under conditions identical to those of other Fe(por) ORR catalysts (buffered [DMF–H+]), Fe-o-TMA fell close to one of the original E1/2 scaling relationships.10,35 Thus, the highly cationic ligand did not improve or even affect catalysis, in contrast to what was reported for CO2 electroreduction.25,36 The inverse scaling for Fe-o-TMA with buffered carboxylic acids only occurred because the buffer affected both pKa and E1/2. Buffers with weaker acids (higher pKa) gave much more negative E1/2 values with a roughly linear dependence (Figure 7B). The E1/2 shifts were due to axial ligand binding of the anionic carboxylates,35,37 an electrostatic effect seen only with anionic ligands and only to the pentacationic catalyst.15 Because the buffer identity affected both pKa and E1/2, neither individual scaling relationship predicted the composite changes in the catalytic system. However, by considering changes made to both the pKa and E1/2 components, the individual data points and inverse log(TOFmax)/ηeff correlation could be predicted quantitatively.35
| (16) |
| (17) |
| (18) |
Using the scaling relations specifically derived for Fe(por)-catalyzed ORR, the experimental changes in pKa and E1/2 in this system were mathematically represented as vectors in the log(TOFmax)/ηeff space (eqs 16 and 17). For instance, the vector in eq 16 describes how changes in pKa (ΔpKa) affect both ηeff and log(TOFmax) according to the pKa relationship described in section VI. An analogous vector exists for changes in E1/2 (eq 17). The sum of these two vectors (eq 18) predicts net changes in ηeff and log(TOFmax) using only experimental values for ΔpKa and ΔE1/2.
For example, replacing CF3C(O)OH with CH3C(O)OH gave ΔpKa = 10.9 and ΔE1/2 = −0.302. The sum of these changes (eqs 16–18) predicted both the directionality and distance in the observed data: the black + purple vectors sum to the blue vector in Figure 7. This result is a first-of-a-kind application of molecular scaling relationships, where a tandem, two-scaling relationship approach can be used to simultaneously improve both rates and overpotentials.35
We believe that similar vector analyses could be applied to any multistep molecular electrocatalytic reaction where different properties of the catalyst system show different log(TOFmax)/ηeff relationships. This requirement is typically fulfilled because multistep reactions often have pre-equilibrium and rate-limiting steps with different stoichiometries and free energies. Implementing different combinations of these scaling relationships should allow optimization—in some cases via inverse scaling—to achieve faster rates at lower overpotentials.
IX. COUPLING INTRINSIC AND OPERATIONAL PARAMETERS OF A CATALYTIC SYSTEM
The previous sections show how the efficiency of a catalytic system can be improved by changing the catalyst and solution conditions. In many of these examples, the “intrinsic” properties of the system (e.g., E1/2, pKa, and catalyst identity) are independent of the “operational” conditions like substrate concentrations.15,34 However, the intrinsic and operational parameters cannot always be separated. In the Fe-o-TMA system above, the nature and concentration of the buffer affect E1/2 via carboxylate binding to the catalyst. The change in catalyst speciation with respect to the solution composition is what enables inverse scaling.35
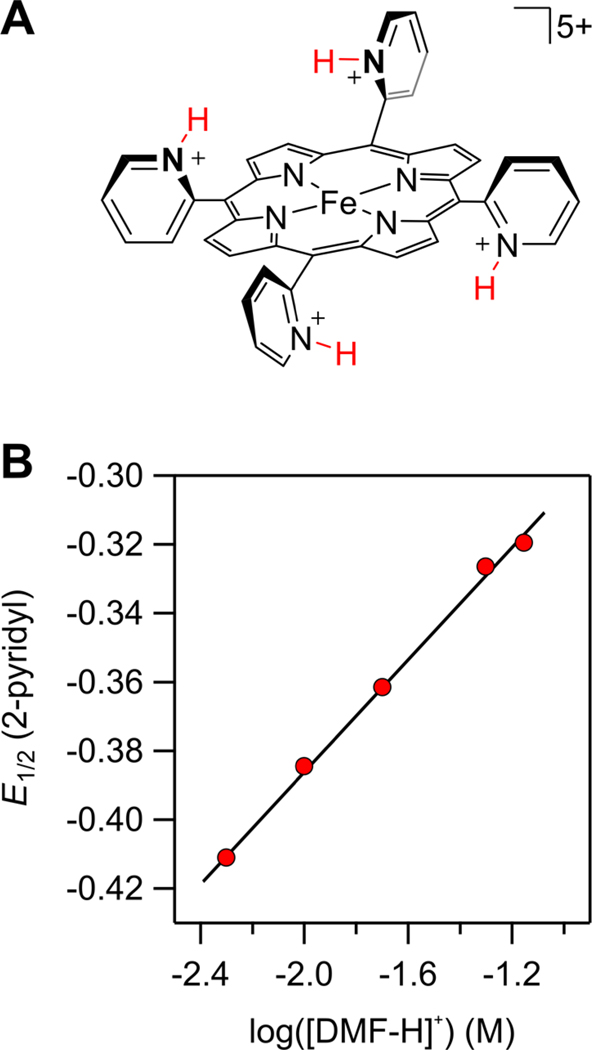
Another example occurs when a catalyst’s ligand contains protonatable functionalities such that changes to acid concentration (an operational parameter) can influence the intrinsic properties of the catalyst. For instance, our studies of the ORR catalyzed by iron tetra-o-pyridylporphyrin showed an unusual, inverse-order dependence on [DMF–H+].10 The decrease in TOFmax occurred in tandem with an 88 mV shift in E1/2 per decade increase in [DMF–H+], which was attributed to protonation equilibria among the many proteomers (Figure 8). The increase in E1/2 caused decreases in both KO2 and the basicity of the superoxide adduct. Because variation in acid concentration, an operational parameter, changes the intrinsic catalyst identity, the two parameters are inherently connected and must be considered together when analyzing log(TOFmax)/ηeff relationships.
Figure 8.
Iron o-pyridylporphyrin, shown as the tetra-protonated complex, and its E1/2 as a function of [HA]. Adapted with permission from ref 10. Copyright 2016 American Chemical Society.
Many other electrocatalytic systems likely exhibit similar complex relationships between intrinsic and operational parameters. It is therefore more valuable to consider globally how all solution components affect catalyst behavior. The alternative approach, which emphasizes only standard state conditions, can miss these cooperative effects. In addition, measurements and extrapolations to standard states are challenging and are in practice almost never done (even by those who advocate for such an approach24,25). We emphasize that the linkage between various parameters of a catalytic system is not a complication but rather an opportunity. Cooperativity between the catalyst active site and surrounding medium is an exciting, underexplored approach to improving catalysis.
X. CONCLUSIONS AND PROSPECTS
This Account surveys our examination of oxygen reduction reaction (ORR) catalysis by soluble iron porphyrins (Fe(por)) in organic solvents, which builds from a fundamental understanding of the reaction thermodynamics, kinetics, and mechanism. We developed procedures to determine nonaqueous standard potentials for the ORR and other PCET half reactions, and we examined the rate law and mechanism of Fe(por)-catalyzed ORR using both electrochemical and spectroscopic techniques. Key reaction intermediates were identified and their thermochemistry measured. Examining our large data set of turnover frequencies and thermochemical overpotentials (ηeff) revealed a number of empirical linear correlations, log(TOFmax) = m(ηeff) + C, when one component of the catalytic system is changed.
Such “molecular scaling relationships” have been found in several reactions, including H2 evolution and O2 reduction to water or hydrogen peroxide,10,14,22,27,35,38 and could be further developed for any multiproton/multielectron catalysis. Deriving relationships between log(TOFmax) and ηeff requires knowing the rate law for catalysis and the thermodynamics of the reaction of interest. For operational parameters like substrate concentration, the reaction order in substrate and the stoichiometry of that substrate in the overall reaction dictate the slope of the scaling line. Molecular scaling relationships based on intrinsic properties like catalyst E1/2 and buffer pKa require additional experimental or computational inputs.
These connections between kinetics and thermodynamics require linear free energy relationships (LFERs). LFERs, while approximate, have been shown experimentally and computationally to hold for many reaction steps and are key to both molecular scaling relationships and heterogeneous analogues. They assume (i) that the free energies of intermediates scale with each other, here the linear scaling of both pKO2 and pKa([Fe(por)(O2H•)]+) with E1/2, and (ii) that ΔGǂ for each step correlates with the ΔG° for that step, here in the Br0nsted catalysis “law” relating kPT to ΔGǂPT.
Electrocatalysis by soluble molecules is often found to follow mechanisms in which PT and ET occur in separate steps of the cycle. Therefore, changing one component of a catalytic system affects the different steps of the cycle in different ways, and a single scaling parameter cannot provide a complete description. The TOFmax for Fe(por)-catalyzed ORR responds very differently when the ηeff is varied via the buffer pKa, which usually affects only the rate-limiting PT step, rather than by changing the catalyst E1/2 which affects that step and the pre-equilibrium ET and O2-binding steps. In contrast, the mechanisms typically used for heterogeneous PCET scaling relationships involve e−/H+ addition together, so that the energetics of each step usually correlate with the overall energetics of the multiproton/multielectron reactions, allowing the use of a single scaling parameter such as a surface–H bond strength. For molecular electrocatalysis, using ηeff is advantageous as the thermochemical parameter because it considers contributions from multiple system components, and because it is a critical parameter to be optimized.
Molecular scaling relationships are powerful tools for understanding and improving molecular electrocatalytic processes. They predict behavior across a wide range of parameter space, thus enabling comparisons of catalytic systems examined under different conditions. The molecular scaling relationships developed here reveal underlying thermochemical insights about a catalytic system under any conditions, even when standard states are challenging to define. These molecular scaling relationships often can predict reactivity under a variety of conditions and with different catalysts. Most notably, these scaling relationships quantitatively explain the dramatic improvement in ORR electrocatalysis when using a highly cationic iron porphyrin with buffers containing carboxylic acid buffers. This improvement results from cooperativity between the nominal catalyst and the other components of the catalytic system, emphasizing that both intrinsic and operational parameters must be included in analyses of electrocatalytic processes.
We hope that this Account will encourage other researchers in the field to use this approach for their systems. Once the thermochemistry and rate law have been established, molecular scaling relationships can be readily derived and used for understanding and improving catalytic performance.
ACKNOWLEDGMENTS
The authors thank all our co-workers, colleagues, and collaborators who contributed to this work. This research was supported as part of the Center for Molecular Electrocatalysis, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences. D.J.M. recognizes support from an NSF GRFP. M.L.P. recognizes current support by a NIH postdoctoral fellowship (F32GM130071).
Biographies
Daniel J. Martin received his B.S. in Chemistry with Highest Honors from The University of North Carolina at Chapel Hill in 2015. He is currently a Ph.D. candidate at Yale University as an NSF Graduate Research Fellow.
Catherine F. Wise received a B.S. in Chemistry from the College of William and Mary in 2015 and is currently a Ph.D. Candidate in the Department of Chemistry at Yale University.
Michael L. Pegis received his B.S. from Western Washington University and his Ph.D. in Chemistry from Yale University. He is currently an NIH postdoctoral fellow in the Surendranath group at MIT.
James M. Mayer did undergraduate research at Hunter College with Edwin Abbott, and with William Klemperer while earning his A.B. at Harvard. He completed a Ph.D. at Caltech under the direction of John Bercaw in 1982, and after two years as a Visiting Scientist at DuPont, he moved to the University of Washington. In 2014, he moved to Yale University.
Footnotes
The authors declare no competing financial interest.
Contributor Information
Daniel J. Martin, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Catherine F. Wise, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Michael L. Pegis, Department of Chemistry, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, United States.
James M. Mayer, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
REFERENCES
- (1).Solomon EI; Stahl SS, Introduction: Oxygen Reduction and Activation in Catalysis. Chem. Rev 2018, 118, 2299–2301. [DOI] [PubMed] [Google Scholar]
- (2).Wikström M; Krab K; Sharma V. Oxygen Activation and Energy Conservation by Cytochrome c Oxidase. Chem. Rev 2018, 118, 2469–2490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Mano N; de Poulpiquet A. O2 Reduction in Enzymatic Biofuel Cells. Chem. Rev 2018, 118, 2392–2468. [DOI] [PubMed] [Google Scholar]
- (4).Gewirth AA; Varnell JA; DiAscro AM Nonprecious Metal Catalysts for Oxygen Reduction in Heterogeneous Aqueous Systems. Chem. Rev 2018, 118, 2313–2339. [DOI] [PubMed] [Google Scholar]
- (5).Kulkarni A; Siahrostami S; Patel A; Nørskov JK, Understanding Catalytic Activity Trends in the Oxygen Reduction Reaction. Chem. Rev 2018, 118, 2302–2312. [DOI] [PubMed] [Google Scholar]
- (6).Montemore MM; van Spronsen MA; Madix RJ; Friend CM O2 Activation by Metal Surfaces: Implications for Bonding and Reactivity on Heterogeneous Catalysts. Chem. Rev 2018, 118, 2816–2862. [DOI] [PubMed] [Google Scholar]
- (7).Pegis ML; Wise CF; Martin DJ; Mayer JM Oxygen Reduction by Homogeneous Molecular Catalysts and Electrocatalysts. Chem. Rev 2018, 118, 2340–2391. [DOI] [PubMed] [Google Scholar]
- (8).Ren S; Joulié D; Salvatore D; Torbensen K; Wang M; Robert M; Berlinguette CP Molecular Electrocatalysts Can Mediate Fast, Selective CO2 Reduction in a Flow Cell. Science 2019, 365, 367–369. [DOI] [PubMed] [Google Scholar]
- (9).Passard G; Ullman AM; Brodsky CN; Nocera DG Oxygen Reduction Catalysis at a Dicobalt Center: The Relationship of Faradaic Efficiency to Overpotential. J. Am. Chem. Soc 2016, 138, 2925–2928. [DOI] [PubMed] [Google Scholar]
- (10).Pegis ML; McKeown BA; Kumar N; Lang K; Wasylenko DJ; Zhang XP; Raugei S; Mayer JM Homogenous Electrocatalytic Oxygen Reduction Rates Correlate with Reaction Overpotential in Acidic Organic Solutions. ACS Cent. Sci 2016, 2, 850–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Rountree ES; McCarthy BD; Eisenhart TT; Dempsey JL Evaluation of Homogeneous Electrocatalysts by Cyclic Voltammetry. Inorg. Chem 2014, 53, 9983–10002. [DOI] [PubMed] [Google Scholar]
- (12).Appel AM; Helm ML Determining the Overpotential for a Molecular Electrocatalyst. ACS Catal. 2014, 4, 630–633. [Google Scholar]
- (13).Costentin C; Drouet S; Robert M; Savéant J-M Turnover Numbers, Turnover Frequencies, and Overpotential in Molecular Catalysis of Electrochemical Reactions. Cyclic Voltammetry and Preparative-Scale Electrolysis. J. Am. Chem. Soc 2012, 134, 11235–11242. [DOI] [PubMed] [Google Scholar]
- (14).Costentin C; Passard G; Savéant J-M Benchmarking of Homogeneous Electrocatalysts: Overpotential, Turnover Frequency, Limiting Turnover Number. J. Am. Chem. Soc 2015, 137, 5461–5467. [DOI] [PubMed] [Google Scholar]
- (15).Pegis ML; Wise CF; Koronkiewicz B; Mayer JM Identifying and Breaking Scaling Relations in Molecular Catalysis of Electrochemical Reactions. J. Am. Chem. Soc 2017, 139, 11000–11003. [DOI] [PubMed] [Google Scholar]
- (16).Roberts JAS; Bullock RM Direct Determination of Equilibrium Potentials for Hydrogen Oxidation/Production by Open Circuit Potential Measurements in Acetonitrile. Inorg. Chem 2013, 52, 3823–3835. [DOI] [PubMed] [Google Scholar]
- (17).Pegis ML; Roberts JAS; Wasylenko DJ; Mader EA; Appel AM; Mayer JM Standard Reduction Potentials for Oxygen and Carbon Dioxide Couples in Acetonitrile and N, N′-Dimethylformamide. Inorg. Chem 2015, 54, 11883–11888. [DOI] [PubMed] [Google Scholar]
- (18).Lindley BM; Appel AM; Krogh-Jespersen K; Mayer JM; Miller AJM Evaluating the Thermodynamics of Electrocatalytic N2 Reduction in Acetonitrile. ACS Energy Lett. 2016, 1, 698–704. [Google Scholar]
- (19).Hooe SL; Rheingold AL; Machan CW Electrocatalytic Reduction of Dioxygen to Hydrogen Peroxide by a Molecular Manganese Complex with a Bipyridine-Containing Schiff Base Ligand. J. Am. Chem. Soc 2018, 140, 3232–3241. [DOI] [PubMed] [Google Scholar]
- (20).Fourmond V; Jacques P-A; Fontecave M; Artero V. H2 Evolution and Molecular Electrocatalysts: Determination of Overpotentials and Effect of Homoconjugation. Inorg. Chem 2010, 49, 10338–10347. [DOI] [PubMed] [Google Scholar]
- (21).Nichols EM; Derrick JS; Nistanaki SK; Smith PT; Chang CJ Positional Effects of Second-Sphere Amide Pendants on Electrochemical CO2 Reduction Catalyzed by Iron Porphyrins. Chem. Sci 2018, 9, 2952–2960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Wang Y-H; Pegis ML; Mayer JM; Stahl SS Molecular Cobalt Catalysts for O2 Reduction: Low-Overpotential Production of H2O2 and Comparison with Iron-Based Catalysts. J. Am. Chem. Soc 2017, 139, 16458–16461. [DOI] [PubMed] [Google Scholar]
- (23).Kilgore UJ; Stewart MP; Helm ML; Dougherty WG; Kassel WS; DuBois MR; DuBois DL; Bullock RM Studies of a Series of [Ni(PR2NPh2)2(CH3CN)]2+ Complexes as Electrocatalysts for H2 Production: Substituent Variation at the Phosphorus Atom of the P2N2 Ligand. Inorg. Chem 2011, 50, 10908–10918. [DOI] [PubMed] [Google Scholar]
- (24).Costentin C; Drouet S; Robert M; Savéant J-M A Local Proton Source Enhances CO2 Electroreduction to CO by a Molecular Fe Catalyst. Science 2012, 338, 90–94. [DOI] [PubMed] [Google Scholar]
- (25).Azcarate I; Costentin C; Robert M; Savéant J-M Through-Space Charge Interaction Substituent Effects in Molecular Catalysis Leading to the Design of the Most Efficient Catalyst of CO2-to-CO Electrochemical Conversion. J. Am. Chem. Soc 2016, 138, 16639–16644. [DOI] [PubMed] [Google Scholar]
- (26).Klug CM; Cardenas AJP; Bullock RM; O’Hagan M; Wiedner ES Reversing the Tradeoff between Rate and Overpotential in Molecular Electrocatalysts for H2 Production. ACS Catal. 2018, 8, 3286–3296. [Google Scholar]
- (27).Quaino P; Juarez F; Santos E; Schmickler W. Volcano Plots in Hydrogen Electrocatalysis - Uses and Abuses. Beilstein J. Nanotechnol 2014, 5, 846–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Greeley J; Jaramillo TF; Bonde J; Chorkendorff I; Nørskov JK Computational High-Throughput Screening of Electrocatalytic Materials for Hydrogen Evolution. Nat. Mater 2006, 5, 909–913. [DOI] [PubMed] [Google Scholar]
- (29).Trasatti S. Work Function, Electronegativity, and Electrochemical Behaviour of Metals. J. Electroanal. Chem. Interfacial Electrochem 1972, 39, 163–184. [Google Scholar]
- (30).Pegis ML; Martin DJ; Wise CF; Brezny AC; Johnson SI; Johnson LE; Kumar N; Raugei S; Mayer JM Mechanism of Catalytic O2 Reduction by Iron Tetraphenylporphyrin. J. Am. Chem. Soc 2019, 141, 8315–8326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Wasylenko DJ; Rodriguez C; Pegis ML; Mayer JM Direct Comparison of Electrochemical and Spectrochemical Kinetics for Catalytic Oxygen Reduction. J. Am. Chem. Soc 2014, 136, 12544–12547. [DOI] [PubMed] [Google Scholar]
- (32).Costentin C; Savéant J-M Multielectron, Multistep Molecular Catalysis of Electrochemical Reactions: Benchmarking of Homogeneous Catalysts. ChemElectroChem 2014, 1, 1226–1236. [Google Scholar]
- (33).Hoops S; Sahle S; Gauges R; Lee C; Pahle J; Simus N; Singhal M; Xu L; Mendes P; Kummer U. COPASI-a COmplex PAthway Simulator. Bioinformatics 2006, 22, 3067–3074. [DOI] [PubMed] [Google Scholar]
- (34).Costentin C; Savéant J-M Homogeneous Molecular Catalysis of Electrochemical Reactions: Manipulating Intrinsic and Operational Factors for Catalyst Improvement. J. Am. Chem. Soc 2018, 140, 16669–16675. [DOI] [PubMed] [Google Scholar]
- (35).Martin DJ; Mercado BQ; Mayer JM Combining Scaling Relationships Overcomes Rate versus Overpotential Trade-Offs in O2 Molecular Electrocatalysis. Sci. Adv 2020, 6, No. eaaz3318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Nichols AW; Machan CW Secondary-Sphere Effects in Molecular Electrocatalytic CO2 Reduction. Front. Chem 2019, 7, 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Lexa D; Rentien P; Savéant JM; Xu F. Methods for Investigating the Mechanistic and Kinetic Role of Ligand Exchange Reactions in Coordination Electrochemistry. J. Electroanal. Chem. Interfacial Electrochem 1985, 191, 253–279. [Google Scholar]
- (38).Wang Y-H; Schneider PE; Goldsmith ZK; Mondal B; Hammes-Schiffer S; Stahl SS Brønsted Acid Scaling Relationships Enable Control Over Product Selectivity from O2 Reduction with a Mononuclear Cobalt Porphyrin Catalyst. ACS Cent. Sci 2019, 5, 1024–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]