CLME: An R Package for Linear Mixed Effects Models under Inequality Constraints

Abstract

In many applications researchers are typically interested in testing for inequality constraints in the context of linear fixed effects and mixed effects models. Although there exists a large body of literature for performing statistical inference under inequality constraints, user friendly statistical software for implementing such methods is lacking, especially in the context of linear fixed and mixed effects models. In this article we introduce CLME, a package in the R language that can be used for testing a broad collection of inequality constraints. It uses residual bootstrap based methodology which is reasonably robust to non-normality as well as heteroscedasticity. The package is illustrated using two data sets. The package also contains a graphical interface built using the shiny package.

1. Introduction

Inequality constraints arise naturally in many applications. For example, to evaluate if a chemical is a toxin, a toxicologist may conduct a dose-response study to determine if the mean response is monotonic in dose. More precisely, suppose θ_i, i ≥ 2, are the mean responses of a chemical corresponding to p dose groups. In this case the null and alternative hypotheses of interest are H₀ : θ₁ = θ₂ = … = θ_p, and H_a : θ₁ ≤ θ₂ ≤ …θ_p, with at least one strict inequality (known as the simple order constraint), respectively. Sometimes, when the doses exceed the maximum tolerated dose (MTD), it may result in a dose-related toxicity and the monotonicity is violated causing down-turn at some (unknown) dose i (Simpson and Margolin 1986). In such cases, researchers are interested in testing for an umbrella alternative H_ai : θ₁ ≤ θ₂ … ≤ θ_i−1 ≤ θ_i ≤ θ_i+1 ≥ … ≥ θ_p, with at least one strict inequality.

In a multi-center rat uterotophic assay conducted by the OECD (Organization for Economic Cooperation and Development), researchers were interested in studying the effect of exposure to estrogen like compounds in the uterine weights of pre-pubertal rats. They were interested in testing if the mean uterine weights of animals exposed to estrogen like compounds increased in comparison to the uterine weights of control animals (Kanno et al. 2003). Thus the alternative hypothesis of interest is H_a : θ₁ ≤ θ_i, i ≥ 2, with at least one strict inequality, known as the simple tree order. Here θ₁ is the mean of the control group and θ_i, i ≥ 2, are the means of the treatment groups.

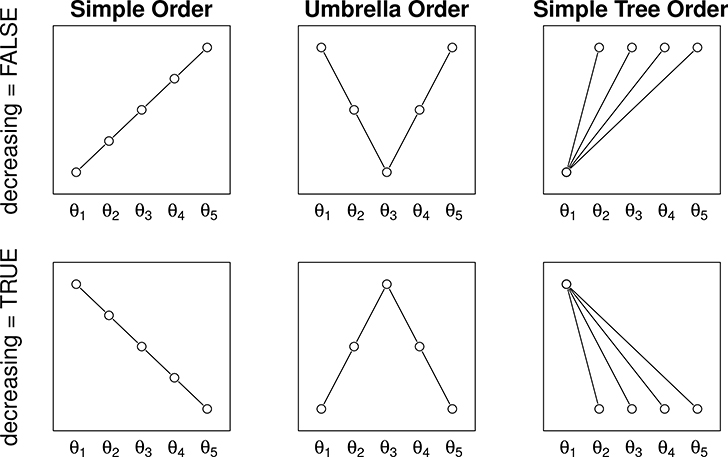
In cancer trials, it is common for researchers to be interested in evaluating a cocktail of two or more experimental drugs in combination, each tried at low, medium and high doses. In such cases, the typical order restriction of interest is the loop order denoted by $\{{\theta }_{control,control}\le {\theta }_{control,low}\le {\theta }_{control,medium}\le {\theta }_{high,high}\}\bigcup \{{\theta }_{control,control}\le {\theta }_{low,control}\le {\theta }_{medium,control}\le {\theta }_{high,high}\}$, where θ_a,b denotes the mean response corresponding to a^th dose of the first treatment and b^th dose of the second treatment. The above null and alternative hypotheses can in general be expressed as $H_0:\mathcal{C}\theta =\mathbf{c}$ and $H_a:\mathcal{C}\theta \ge \mathbf{c}$, respectively, where A is a suitable matrix of zeros, ones and negative ones of appropriate order, θ = (θ₁, θ₂, … , θ_p)^⊤ and c is a suitable vector of known scalars, for example a vector of zero’s. Some examples of $\mathcal{C}$ and c are provided later, and an illustration of some common orders is given in Figure 1.

Figure 1:

Illustration of order restrictions. Each circle represents a parameter of interest. Inequalities between two parameters (i.e., circles) are provided by the lines. The vertical axis denotes relative magnitude of connected parameters. No relationship (either <, =, or >) is known among parameters that are not connected. A nodal parameter is a parameter whose order relationship with every other parameter is known a priori or given by the hypothesis that is is being tested. For example, θ₃ is the nodal parameter in the umbrella orders.

It is of common interest to perform statistical inference under inequality constraints, such as those described above, in a linear mixed effects model setting, especially in the context of repeated measures design where a researcher may be interested in detecting trends. However, despite the existence of a large body of literature on constrained inference spanning over five decades and three books on testing for order restrictions (Barlow et al. 1972; Robertson et al. 1988; Silvapulle and Sen 2005), it was only recently that researchers developed methods for performing constrained inference in linear mixed effects models (Davidov and Rosen 2011; Rosen and Davidov 2011; Farnan et al. 2014). While Davidov and Rosen (2011) and Rosen and Davidov (2011) developed likelihood ratio based methods, Farnan et al. (2014) developed a residual bootstrap based method that is designed to be robust to non-normality as well as to heteroscedasticity. Furthermore, Farnan’s methodology allows for modeling categorical as well as continuous covariates.

Surprisingly, not even the popular statistical analysis program SAS (SAS Institute Inc. 2011) has the capability to perform tests under general inequality constraints in a linear fixed effects model, let alone in the context of mixed effects models. As demonstrated in Farnan et al. (2014), statistical methods that are specifically designed for testing inequality constraints are expected to enjoy substantially higher power than the usual omnibus procedures (e.g., ANOVA) which are designed for two-sided alternatives. This observation, together with the fact that there does not exist a general software for performing statistical tests under linear inequality constraints in linear mixed effects models, motivates the current work. In this paper we introduce an R package, called CLME (‘Constrainted Linear Mixed Effects’) based on the distribution-free residual bootstrap methodology developed in Farnan et al. (2014). There are several packages in R which offer constrained fixed effects models, including glmc (Chaudhuri et al. 2006) and ic.infer (Grömping 2010), but neither of these appear to offer support for mixed models; the present work fills this void. Furthermore, since the methodology is based on residual bootstrap, CLME does not depend on normality or homogeneity of variances for the residuals or random effects.

The rest of the paper is organized as follows: Section 2 provides a brief description of the constrained inference for linear mixed effects (LME) models presented by Farnan et al. (2014). Section 3 describes the contents of the package CLME along with implementation details. Section 4 provides some illustrative examples using the package, and Section 5 concludes the paper with a summary and some comments on planned developments of CLME.

2. Linear mixed effect models under inequality constraints

2.1. Definition of the model

Let

$$Y={\mathbf{X}}_1{\theta }_1+{\mathbf{X}}_2{\theta }_2+\mathbf{U}\xi +ϵ$$ (1)

denote a linear mixed effects (LME) model where Y is the N × 1 response vector, X₁ is a design matrix of order N × p₁ and θ₁ is the corresponding p₁ × 1 vector of coefficients (often treatment effects). X₂ is an N × p₂ a known matrix of covariates, θ₂ is the p₂ × 1 vector of regression coefficients, and U is a N × c matrix of known constants (random effects). For simplicity we write X = (X₁ : X₂) and $\mathbf{U}=\left({\mathbf{U}}_1:{\mathbf{U}}_2:\dots ,:{\mathbf{U}}_{c_q}\right)$, where : denotes column-binding and U_i is an N × c_i matrix, with ${\sum }_{i=1}^q{c}_i=c$. We also denote $\theta ={\left({\theta }_1^{\top },{\theta }_2^{\top }\right)}^{\top }$ and p = p₁ + p₂.

The random vector $\xi ={\left({\xi }_1^{\top },{\xi }_2^{\top },\dots ,{\xi }_q^{\top }\right)}^{\top }$ is c×1, where each ξ_i is a c_i×1 vector corresponding to U_i, for i = 1, … , q. The elements of ξ are independently distributed with mean 0 and covariance matrix $\mathbf{T}=\mathrm{diag}\left({\tau }_1^2{\mathbf{I}}_{c_1},{\tau }_2^2{\mathbf{I}}_{c_2},\dots ,{\tau }_q^2{\mathbf{I}}_{c_q}\right)$. The residual term ϵ is similarly defined with mean 0 and covariance matrix $\mathbf{\Sigma }=\mathrm{diag}\left({\sigma }_1^2{\mathbf{I}}_{n_1},{\sigma }_2^2{\mathbf{I}}_{n_2},\dots ,{\sigma }_k^2{\mathbf{I}}_{n_k}\right)$, where i = 1, … , k and ${\sum }_{i=1}^k{n}_i=N$.

Although the above model description and the methodology implemented in CLME allows for fairly general settings, in many applications one may not require the full available flexibility. For example, in most applications it may be sufficient to assume that T = τ²I, instead of the general heteroscedastic structure for T described above.

Let $\mathcal{C}$ be an r × p matrix so that $\mathcal{C}\theta$ represents the linear combinations which are subject to inequality constraints specified by the alternative hypothesis. Thus the hypotheses of interest are given by:

$$H_o:\mathcal{C}\theta =\mathbf{0}\text{versus}{H}_a:\mathcal{C}\theta \ge \mathbf{0},$$ (2)

such that at least one of the r inequalities is strict. Farnan et al. (2014) suggested the pool adjacent violators algorithm (‘PAVA’) to implement the order constraints (isotonization). We depart from their methodology in that we use the package isotone (de Leeuw et al. 2009) for isotonization, and in particular the function activeSet. In some cases using active set methodology leads to the same results as using PAVA; though using active sets is a more general approach and enables easy specification of complex order restrictions. This also enables access to a number of solvers for activeSet, including least squares, least absolute deviation, and others.

CLME is designed to implement two general classes of statistical tests. The likelihood ratio type (LRT) statistic (Davidov and Rosen 2011) is the default setting, but the user may instead choose the Williams’ type test statistic (Williams 1971, 1977; Peddada et al. 2001; Farnan et al. 2014). In both cases, to keep the methodology robust to non-normality and potential heteroscedasticity, the p values are evaluated using the residual bootstrap methodology developed in Farnan et al. (2014). Thus, although our likelihood ratio type statistic is motivated by the likelihood ratio principle under the normality assumption, it does not use the normal theory based asymptotic distribution for the test statistic. Hence we use the phrase ‘likelihood ratio type test’ rather than ‘likelihood ratio test’, and results from CLME will not always align with those of a direct implementation of (Davidov and Rosen 2011).

2.2. Performance of residual bootstrap methodology

Farnan (2011) and later Farnan et al. (2014) investigated the performance of the residual bootstrap based test using the above defined likelihood ratio type test (LRT) statistic and the following Williams type statistic (W) under a wide range of distributions and variance structures. For example, Farnan (2011) generated data from a wide range of non-normal distributions including, gamma, log-normal and mixture of normals and different patterns of variances to study the Type I error and power of these tests. A subset of these results were reported in Farnan et al. (2014). The residual bootstrap based methodology, using the above test statistics, generally performed well in terms of Type I errors and power. The Type I errors were generally close to nominal levels.

The Williams type statistic is defined in general as:

$$W=\max \left\{\left[\mathcal{B}{\tilde{\theta }}_1\right]\odot {\left[\sqrt{\mathrm{diag}\left\{\mathcal{B}\mathrm{Var}(\widehat{\theta }){\mathcal{B}}^{\top }\right\}}\right]}^{-1}\right\},$$ (3)

where ⨀ denote the Schur-product of vectors, i.e., a ⨀ b = (a₁b₁, a₂b₂, … , a_rb_r)^⊤, ${\tilde{\theta }}_1$ denotes the estimator of θ₁ under the inequality constraint of interest, and ${\widehat{\theta }}_1$ denotes the unconstrained estimator of θ₁ (e.g., the MLE). For a given order restriction specified by $\mathcal{C}$, the contrast matrix $\mathcal{B}$ is derived from the largest hypothesized difference(s); in the simple order this is the difference between θ₁ and θ_p1. The structure of $\mathcal{B}$ is similar to that of $\mathcal{C}$, and is further described in the paragraph titled ‘Constraints’ in Section 3.1.

3. Contents of CLME

In this section we describe the functions included in CLME and some notes on their implementation. We start by describing the main function of the package, clme. Afterwards, we detail some of the secondary functions which users may find useful.

3.1. Main function

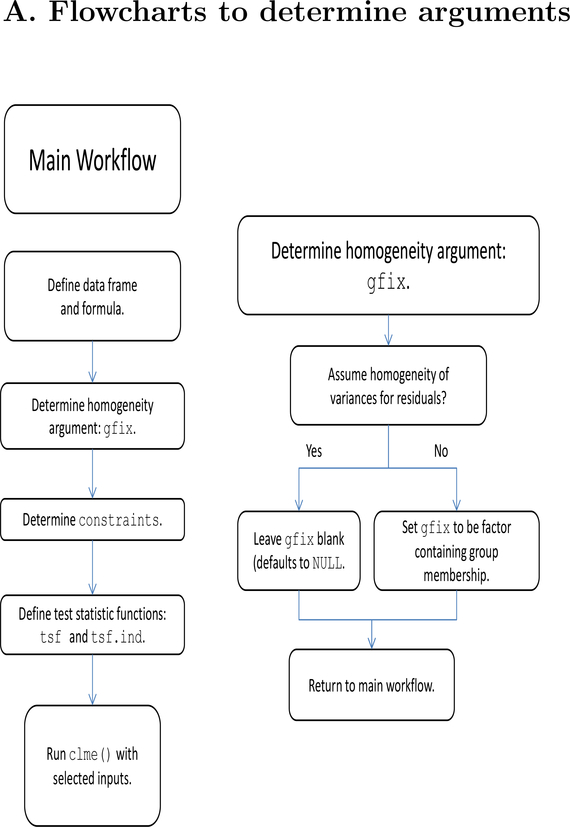
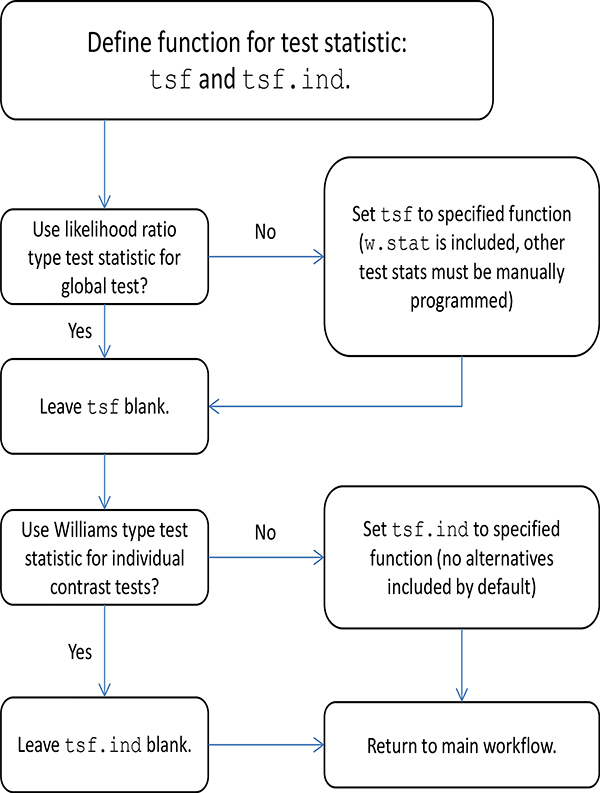
The main function of CLME is clme. This function implements the order restricted residual bootstrap test described in Farnan et al. (2014). Among the arguments listed below, only the formula and the dataset are required for the model to run. A series of flowcharts are provided in the appendix (Figures 8–10) to guide a user through specification of the arguments for clme.

Figure 8:

Main flowchart to determine arguments (left) and flowchart to determine groups for residual variance (right).

Figure 10:

Flowcharts to determine arguments defining the test statistic.

• formula a formula expression; the constrained effect(s) must come before any unconstrained effects.

• data data frame containing the variables in the model.

• gfix optional vector of group levels for residual variances. Data should be sorted by this value.

• constraints list containing the constraints.

• tsf function to calculate the test statistic.

• tsf.ind function to calculate the test statistic for individual contrasts.

• mySolver solver to use in isotonization (passed to activeSet).

• verbose logical, prints iteration step. Argument can be vector of multiple logicals; successive elements are passed to further functions.

• levels list to manually specify labels for constrained coefficients.

• ncon the number of constrained terms in the formula; the first ncon terms are constrained.

• … space for additional arguments.

Several of the arguments to clme require further explanation.

Formula

The formula should be a formula object following typical specification in R. That is, it is a two-sided expression using a tilde operator to separate the dependent variable from the independent variables. For example, the formula y = x1 + x2 is interpreted as modeling y as a linear fucntion of x1 and x2. Random effects are specified in a similar manner as in the popular lme4 package (Bates et al. 2015), using parentheses. For example, the formula y = x1 + x2 + (1|u) is equivalent to the previous formula, but includes u as a random effect.

Note that clme runs a model without the intercept (and removes the intercept if it was requested). This is done so that the parameters are means of interest, rather than the intercept and offsets, thereby simplifing the computations involved.

Constraints

The argument constraints is a list describing the order restrictions using the following elements:

• order text string specifying the type of order. Allowed values are ‘simple’, ‘umbrella’, and ‘simple.tree’.

• node numeric indicating which element of θ₁ is the node.

• decreasing logical indicating decreasing order. For simple orders, a decreasing order implies a downward trend. For umbrella or simple tree orders, a decreasing order implies a decrease from the node. See Figure 1 for an illustration.

• A matrix describing the order restrictions in $\mathcal{C}$.

• B matrix of coefficients defining the Williams type statistic (only necessary if Williams’ type test is desired). This corresponds to $\mathcal{B}$ in Equation (3).

The values of A and B use the same format as the argument isomat from the function activeSet in package isotone: each is a matrix with two columns where the rows define a specific constraints. For example, A and B are shown below for the decreasing umbrella order with p₁ = 5 and a node at θ_1,3 (the third element of θ₁).

$$\mathrm{A}=\left[\begin{array}{ll}1& 2\\ 2& 3\\ 4& 3\\ 5& 4\end{array}\right]$$

and,

$$\mathrm{B}=\left[\begin{array}{cc}1& 3\\ 5& 3\end{array}\right]$$

The alternative hypothesis is H_a : θ₁ ≤ θ₂ ≤ θ₃ ≥ θ₄ ≥ θ₅. The first row of A defines the constraint θ₁ ≤ θ₂, the second row defines the constraint θ₂ ≤ θ₃, and so on. The entries of the rows are the coefficient indices, and the parameter indexed in the left column is hypothesized to be less than or equal to that indexed by the right column. The B matrix is similarly structured, but defines only the contrasts for the largest hypothesized difference(s). Under the umbrella order, this will be the node compared to the first and last values; the specific form of the Williams’ type statistic from Equation 3 is:

$$W=\max \left\{\frac{{\tilde{\theta }}_3-{\tilde{\theta }}_1}{\sqrt{\mathrm{Var}\left({\widehat{\theta }}_3-{\widehat{\theta }}_1\right)}},\frac{{\tilde{\theta }}_3-{\tilde{\theta }}_5}{\sqrt{\mathrm{Var}\left({\widehat{\theta }}_3-{\widehat{\theta }}_5\right)}}\right\},$$

hence the B matrix holds the contrasts ${\tilde{\theta }}_3-{\tilde{\theta }}_1$ and ${\tilde{\theta }}_3-{\tilde{\theta }}_5$.

Not all of the elements of constraints are necessary. There are three general formats by which to pass the constraints to clme.

Specific Defaults

One may specify only the elements order, node, and decreasing. In this case the program will call an internal function to generate the values of A and B. Allowed values for order are ‘simple’, ‘umbrella’, and ‘simple.tree’; also, the node may be omitted for simple orders. Each of the three elements may also be vector-valued (e.g., order=c(‘simple’,’umbrella’)) to test multiple orders.

Custom constraints

Alternatively, the list of constraints may contain A directly. This is particularly useful for specifying custom order restrictions such as loop orders or block orders. When a custom A is passed, the program will ignore any values of order, node, and decreasing. If the Williams’ type test is selected, a custom B is also needed.

Unspecified

Finally, constraints may be left unspecified. In this case the program will search for both simple and umbrella orders with all possible nodes, both increasing and decreasing orders. As with the first case, the program will estimate the order using the maximum test statistic of all the tested orders.

When testing multiple orders the test statistic is taken as the maximum of all the tested orders, and the program will note the order which produced this value as the estimated order. The bootstrap null distribution of the test statistic is constructed from all the order patterns under consideration, not just the estimated order (that is, for each bootstrap sample, the test statistic is computed for all candidate orders, and the maximum is taken). For reproducibility, one may use seed argument to set the seed for the pseudo-random number generator.

Test statistic: tsf and tsf.ind

The argument tsf is a function which computes the desired global test statistic. This defaults to lrt.stat, the LRT statistic. Alternatively one may select the Williams’ type statistic from Equation 3 by setting tsf=w.stat. The related argument tsf.ind computes the test statistic to test the individual constraints. The Williams type test, w.stat.ind, is default. These two arguments are analogous to the global F test and pairwise t tests in the context of analysis of variance. For other test statistics, the user may submit a custom function function for tsf and/or tsf.ind. We refer to the documentation of lrt.stat for more details on the format of custom test statistic functions.

The output from any custom tsf should be numeric. Output with length greater than 1 corresponds to multiple global hypotheses being tested. This should not be used for testing all the individual constraints from the A matrix, as these are calculated separately using the tsf.ind argument. If desired, the test statistic function should also specify the names attribute of the test statistic, for example naming the contrast. An example of testing multiple global hypotheses is shown in Section 4.2, a reanalysis of data from the Fibroid Growth Study (Peddada et al. 2008).

Homogeneity of variances: gfix

The model described in Section 2 permits flexibility. In particular, both ξ (if random effects are included) and ϵ may be modeled under the assumption of homogeneity or heterogeneity of variances. Currently, each random effect term is modeled with a separate variance component. The argument gfix defines groups for the residual variance(s). By default, the data are modeled with a single residual variance. If gfix is supplied, then each group of gfix is modeled with a separate residual variance. For example if the constrained effect is the variable x1, defined as treatment groups, then gfix=x1 will produce a residual variance for each treatment group.

The output of clme is a list with elements:

• theta vector of estimates of fixed-effects coefficients, θ.

• theta.null vector of estimates of θ under the null hypothesis.

• ssq estimate of the residual variance(s), ${\sigma }_i^2$, i = 1, … , k.

• tsq estimate of the random effect variance component(s), ${\tau }_i^2$, i = 1, … , q.

• cov.theta the covariance matrix of the unconstrained estimates of θ.

• ts.glb test statistic for the global hypothesis.

• ts.ind vector of test statistics for each of the constraints (each row of A).

• mySolver the solver used in activeSet.

• constraints List containing the constraints (A) and the contrast for the global test (B).

• dframe data frame containing the variables in the model.

• search.grid matrix containing the orders to perform a search over.

• cust.const logical, whether custom constraints were specified, or constraints were generated.

• ncon the number of constrained effects

• tsf function to calculate the test statistic.

• tsf.ind function to calculate the test statistic for individual contrasts.

• residuals matrix containing residuals. For mixed models three types of residuals are given.

• random.effects predicted values of the random effects.

• gfix group sample sizes for residual variances.

• gfix_group group membership to define residual variances.

• gran group sizes for random effect variance components.

• formula the formula used in the model.

• call the function call.

• P1 the number of constrained parameters.

• mq.phi initial values for the random effect variance componebts.

• order list describing the specified constraints.

The function clme only fits the model. To run the bootstrap test, users should run summary.clme on the fitted object. The summary.clme method accepts arguments object (an object of class clme, the output from function clme) as well as nsim, the number of bootstrap simulations to perform, and for replicability, seed, the seed for the random number generator (RNG). Both nsim and seed can be passed to clme, in which case summary.clme will use those values. The output of summary.clme returns the same fitted object, but appends p-values.

3.2. Secondary function

Typical use of CLME will involve fitting a clme object, and then calling summary.clme to conduct inference. In the course of its evaluation, the summary function calls several other functions, of which the primary one is resid_boot. This performs the integral function of obtaining the bootstrap samples for inference. Some of the arguments for resid_boot are equivalent to those of clme, but some additional arguments are provided to allow users greater flexibility. The arguments to resid_boot are:

• formula a formula expression, the constrained effect should be the first term on the right-hand side.

• data data frame containing the variables in the model.

• gfix optional vector of group levels for residual variances.

• null.resids logical, whether to generate bootstrap samples under the null hypothesis. Defaults to TRUE.

• eps estimates of residuals.

• xi predicted values of the random effects.

• theta vector of fixed-effects coefficients.

• ssq vector of residual variance estimate(s).

• tsq vector of random effect variance component(s).

• cov.theta covariance matrix of the unconstrained fixed effects estimates.

• seed set the seed for the RNG

• nsim number of bootstrap samples to generate (M).

• mySolver the solver to pass to activeSet.

• … space for additional arguments.

CLME constructs a bootstrap sample as follows:

Step 1: Obtain ${\widehat{\theta }}_0$, the estimate of θ under the null hypothesis.

Step 2: Compute the observed values of the random effects and residuals. Denote $\widehat{\mathbf{\Psi }}=\mathbf{U}\widehat{\mathbf{T}}\mathbf{U}+\widehat{\mathbf{\Sigma }}$, where $\widehat{\mathbf{T}}$ and $\widehat{\mathbf{\Sigma }}$ are the estimates of T and Σ described in Section 2. Then compute:

$$\widehat{\mathit{ϵ}}=\left(\mathbf{I}-\mathbf{X}{\left({\mathbf{X}}^{\top }{\widehat{\mathbf{\Psi }}}^{-1}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\top }{\widehat{\mathbf{\Psi }}}^{-1}\right)\mathbf{Y},$$

and

$$\widehat{\mathit{\xi }}=\widehat{\mathbf{T}}{\mathbf{U}}^{\top }{\widehat{\mathbf{\Psi }}}^{-1}\widehat{\mathit{ϵ}}.$$

Step 3: Standardize the observed values of the random effects and residuals. Define ${\widehat{\mathit{\delta }}}_i=\frac{{\widehat{\mathit{\xi }}}_i}{sd\left({\widehat{\mathit{\xi }}}_i\right)}$, i = 1, … , q and ${\widehat{\mathit{\nu }}}_i=\frac{{\widehat{\mathit{ϵ}}}_i}{sd\left({\widehat{\mathit{ϵ}}}_i\right)}$, i = 1, … , k, where sd(·) denotes the standard deviation of the elements in the vector.

Step 4: Obtain the bootstrap samples. Let $\widehat{\mathit{\nu }}*$ denote a bootstrap sample of $\widehat{\mathit{\nu }}$ and let $\widehat{\mathit{\delta }}*$ denote a bootstrap sample of $\widehat{\mathit{\delta }}$. Then define ${\widehat{\mathit{ϵ}}}^{*}={\widehat{\sigma }}_i{\widehat{\mathit{\nu }}}_i^{*}$, i = 1, … , k and ${\widehat{\mathit{\xi }}}^{*}={\widehat{\tau }}_i{\widehat{\mathit{\delta }}}_i^{*}$, i = 1, … , q. Finally, construct the final bootstrap sample as:

$$\mathbf{Y}*=\mathbf{X}{\widehat{\theta }}_0+\mathbf{U}\mathit{\xi }*+\mathit{ϵ}*.$$

In typical use resid_boot will follow the above procedure, and the arguments will be specified appropriately. However, for greater flexibility, the user may submit any numeric vector of the appropriate length for several of the values. In particular:

Fixed effects

The vector of fixed-effects coefficients is represented with theta. By default this will be ${\widehat{\theta }}_0$, the estimate of θ under the null hypothesis. If the user wishes to center the bootstrap samples at a different location, they may submit an alternative vector for theta. For example, one may specify theta to be the fitted estimate of θ rather than the null estimate (a vector of length p). This will cause the bootstraps to be centered at the fitted alternative hypothesis rather than the null hypothesis (these two estimates of θ are availabled in a fitted clme object, elements theta and theta.null). Or the user may wish to center at an unconstrained point estimate, $\widehat{\theta }$. Note that the only effect specifying theta will have is changing the fixed-effects estimate in Step 4 above. In particular, the observed random effects and residuals will not be affected. Also, null.resids must be set to FALSE for the specified value of theta to be used directly. Otherwise, theta will be projected onto the null hypothesis (so that $\mathcal{C}\theta =\mathbf{0}$) using activeSet from package isotone.

Variance estimates

The argument ssq denotes the vector of estimated residual variance terms, $\left({\widehat{\sigma }}_1^2,\dots ,{\widehat{\sigma }}_k^2\right)$. If specified, then these values will be used in place of ${\widehat{\sigma }}_i^2$, i = 1, … , k in Step 4 above. If length(ssq) > 1 then the user should specify gfix as the residual variance groups as with the main function clme. The argument tsq is similarly defined, but containing the random-effect variance components $\left({\widehat{\tau }}_1^2,\dots ,{\widehat{\tau }}_q^2\right)$.

Residuals

The observed residuals are denoted by eps. By default these are calculated as shown for $\widehat{ϵ}$ in Step 2 above, the residuals from an unconstrained point estimate (e.g., generalized least squares). The user may supply an N × 1 vector containing residuals calculated in some other fashion. Similarly, the observed random effects are denoted with xi, and by default are calculated as shown for $\widehat{\mathit{\xi }}$ in Step 2 above. Again, the user may submit a vector with alternative values for the observed random effects.

The only necessary arguments for resid_boot are formula and data, these will be used to obtain the model matrices. If provided, the values of theta, ssq, tsq, eps and xi will be used for bootstrapping. Any of these values that are left unspecified will be computed as described in Steps 1–4 above.

3.3. Other package contents

Shiny application

The shiny package (RStudio and Inc. 2014) offers the ability to develop a graphical user interface (GUI) which implements CLME. A GUI developed in shiny can be run locally or deployed online. This is particularly beneficial to researchers who are not as familiar with R, or programming in general, but wish to use the methods described here. The package CLME includes a shiny application to run clme. After installing the package, a user may run the command shiny_clme() to call the GUI and begin using CLME without any need for further programming.

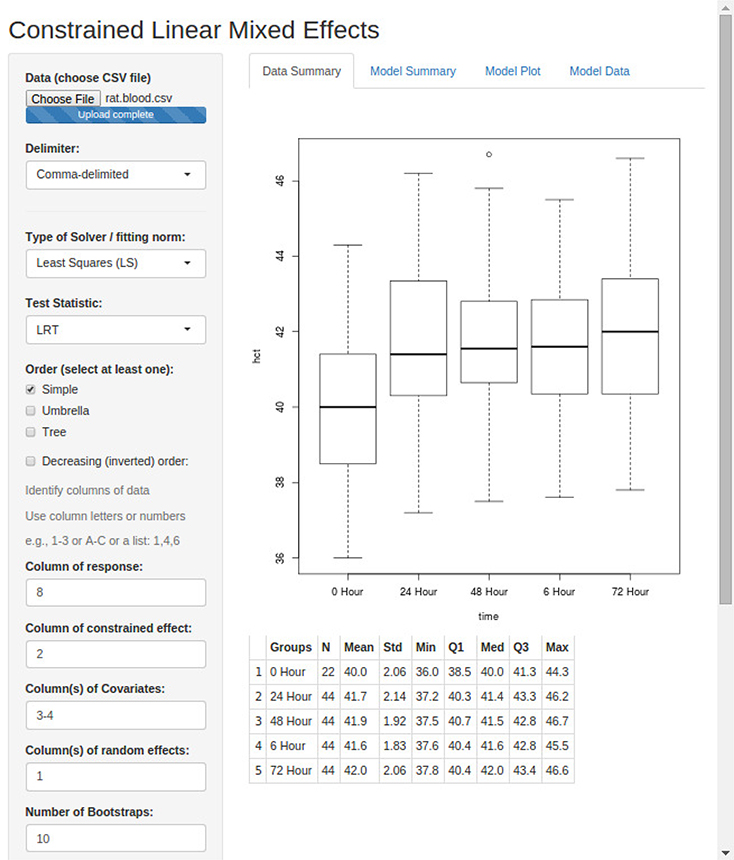
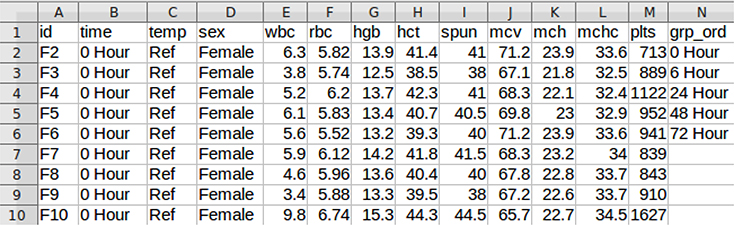
Figure 2 shows the GUI for clme with the arguments filled in. This example uses the rat.blood dataset (which was printed to a comma-delimited file). The column headers are: id, time, temp, sex, wbc, rbc, hgb, hct, spun, mcv, mch, mchc, plts, and grp ord. The final column was added to the dataset, it contains the values ‘0 Hour’, ‘6 Hour’, ‘24 Hour’, ‘48 Hour’, and ‘72 Hour’. This column was added so that the proper order of groups for the constrained effect can be defined. A screenshot of the first 15 rows of this file can be seen in Figure 3.

Figure 2:

Screenshot of the GUI for clme, build in shiny.

Figure 3:

Screenshot of the top several rows of the dataset used in Figure 2.

First the user should browse to the dataset (which should be a CSV file with the first row being a header), and then select the desired function arguments. Some arguments are provided by default (e.g., the global test statistic and the type of solver for isotonization). There are several checkboxes to define the order, and then the user must tell the application which variables to use. The variables are identified using either their column number or column letter (e.g., 1 or A). Multiple variables may be separated by a comma (e.g., 1,2,4 or A,B,D), a range of variables may be defined with a dash (e.g., 1–4 or A-D), or a combination of the two can be used. These values should be set to ‘None’ to indicate no covariates or random effects. Group levels for the constrained effect may not be read into R with the correct order; an extra column may contain the ordered group levels (it may therefore have different length than the rest of the dataset). The user is recommended to inspect the bottom of the summary output to verify the ordering of the group levels.

If we wish to model hct, we specify column 8 for the response variable. Then the constrained effect is time, which is in column 2. The other covariates, temp and sex, are in columns 3 and 4, so we type ‘3–4’ (alternatively, we could have typed ‘3,4’, or ‘C,D’), and finally the random effect, id, is in column 1. Since this is just for illustration, we specified only 10 bootstrap samples. Figure Figure 2 shows the first panel of output, which contains summary information on the dataset: a boxplot of the response variable for each level of the constrained effect (if the constrained effect is a factor), and a table of descriptive statistics. The other three panels are: ‘Model Summary’, which provides the summary printout of the fitted model (several examples are shown in Section 4); ‘Model Plot’, which provides a plot of the fitted means with indication of significance (e.g., Figure 5); and ‘Model Data’ prints the data used for the analysis.

Figure 5:

Plot of estimated coefficients of mean hematocrit (HCT) from Case (A). The model assumed an increasing simple order and homogeneity of variances across treatment groups. Solid lines denote no significant difference, while dashed lines denote statistical significance.

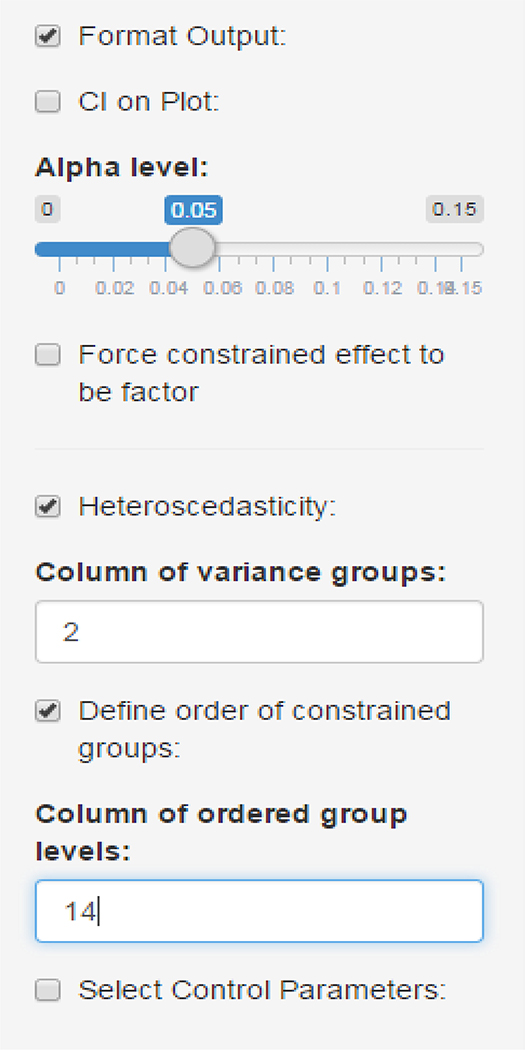
Figure Figure 4 shows several of the optional parameters in the GUI. By clicking the ‘Format Output’ checkbox, one can request a confidence interval to show on the plot, adjust the Type I error rate, and force the constrained effect to be a factor (not all file imports will bring in text variables as a factor). The ‘Heteroscedasticity’ box bring up another input field to select a variable, which allows one to set the gfix parameter of clme. In this case, we have entered ‘2’, which corresponds to the variable time. This has the effect of assuming each time group has a unique variance.

Figure 4:

Some additional control parameters available in the GUI for clme.

The checkbox ‘Define order of constrained groups’ will bring up another input field. Here we enter 14, to select the ‘grp ord’ variable which was discussed above. Note on the boxplot in Figure 2 that the groups are out of order: Without this column, the time periods would be out of order: the ‘6 Hour’ group would be placed between the ‘48 Hour’ and ‘72 Hour’ groups. By specifying this input, we correct the order (output not shown). The checkbox ‘Select Control Parameters’ allows one to set the seed for the RNG, as well as the maximum number of iterations and the convergence threshold for both the EM algorithm and the MINQUE algorithm.

Methods

The function clme outputs an object of the S3 class clme. The methods available for this class are briefly described in Table 1.

Table 1:

List of methods currently defined for objects of class clme. All methods extracting some value (e.g., fixef) will also work on the result of summary results of an object of class clme.

Generic name	Description
AIC	Computes Akaike information criterion.
as	Coerces an object to class clme.
BIC	Computes Bayesian information criterion.
confint	Computes individual confidence intervals for fixed effects parameters. Intervals are centered at the constrained estimates, but use standard errors of the unconstrained estimates.
fixef	Extracts estimates fixed-effects coefficients, θ (also, fixed.effects and coef).
formula	Extracts the formula for the model.
is	Tests if an object is of class clme
logLik	Computes the log-likelihood under the assumption of Normality.
model.frame	Data frame with the variables in the model.
model.matrix	The fixed-effects design matrix.
nobs	Number of observations.
plot	Produces a plot of the constrained coefficients and denotes statistical significance.
print	A basic printout of the model results.
ranef	Extracts predictions of the random effects (also, random.effects).
residuals	Extract various types of residuals.
sigma	The residual variance(s).
summary	Obtains inference (e.g., p-values) for objects of class clme.
VarCorr	Estimates of variance components.
vcov	The variance-covariance matrix of the fixed-effects estimates.

4. Sample implementation

In this section we demonstrate the use of CLME by applying it to two real-world data sets. Some of the analyses mimic those performed in the original papers but in the context of order-restricted inference. Other analyses are intended to exhibit certain features of the package or compare the available options. We emphasize that these analyses are intended not as a scientific reanalysis, but as an illustration. Consequently some modeling choices, the assumption of homogeneity of variances in particular, are not thoroughly investigated. The data analyzed are included in the package as the datasets rat.blood and fibroid.

4.1. Hematologic parameters from Sprague-Dawley rats

In a recent study on the effect the amount of time a sample is stored has on various hematological parameters, Cora et al. (2012) conducted a time course study using blood samples drawn from Sprague-Dawley rats. Blood samples from 11 female and 11 male rats were kept at either room temperature 21 °C (the control group) or refrigerated at 3 °C for 6, 24, 48 or 72 hours (see Cora et al. (2012) for more details). Although the authors obtained data on a variety of hematological variables in this repeated measure time course study, we shall focus on hematocrit (HCT) and the white blood cell (WBC) count over time. In the case of HCT we shall illustrate some of the options of CLME while testing for simple order with an increasing trend in time. In the case of WBC we test for simple tree order the mean WBC count in the freezer group was at least as high as that of the 0 hour.

First, we load the package and the data.

R> library(“CLME”)
R> data(“rat.blood”)

Hematocrit

We illustrate CLME using three different settings. In the first case (Case A) we test the following hypotheses:

$$H_0:{\theta }_1={\theta }_2={\theta }_3={\theta }_4={\theta }_5$$

Vs.

$$H_{aA}:{\theta }_1\le {\theta }_2\le {\theta }_3\le {\theta }_4\le {\theta }_5,$$ (A)

with at least one strict inequality, here θ_i is the mean corresponding to either 0, 6, 24, 48 or 72 hours. In the second case (Case B), we test for a union of umbrella alternatives. If the null hypothesis is rejected then the algorithm selects the pattern that has largest value of test statistic:

$$H_0:{\theta }_1={\theta }_2={\theta }_3={\theta }_4={\theta }_5$$

Vs.

$$H_{aB}:\{\bigcup _{i=1}^5{\theta }_1\le {\theta }_2\le \dots \le {\theta }_i\ge \dots \ge {\theta }_5\cup \bigcup _{i=1}^5{\theta }_1\ge {\theta }_2\ge \dots \ge {\theta }_i\le \dots \le {\theta }_5.\}$$ (B)

Thus in (B) the order is unspecified but limited to either umbrella or inverted umbrella orders. Note that simple orders (increasing or decreasing) are a special case of umbrella orders, where the peak is the first or last parameter. The peak or the trough of each umbrella is specified using the specification of node. Case (C) is a repeat of case (A), but there we will assume heteroscedasticity of variances between the time groups.

We initially use the default arguments as far as possible. We use the gender of the rat and the storage temperature of the sample as covariates. The R code to test case (A) is provided below along with the results.

R> const <- list(order = “simple”, node = 1, decreasing = FALSE)
R> hct1 <- clme(hct ~ time + temp + sex + (1|id), data = rat.blood,
+    constraints = const, levels = list(2, levels(rat.blood$time)))
R> hct1b <- summary(hct1, seed = 42)
R> hct1b

Linear mixed model subject to order restrictions
Formula: hct ~ time + temp + sex + (1 | id) − 1

Order specified: increasing simple order

log-likelihood: −296.6
AIC:             611.3
BIC:             624.3
(log-likelihood, AIC, BIC computed under normality)

Global test:
 Contrast       Statistic p–value
 Bootstrap LRT       0.17  0.0020

Individual Tests (Williams’ type tests):
 Contrast           Estimate  Statistic  p–value
 6 Hour – 0 Hour       1.342      4.862   0.0000
 24 Hour – 6 Hour      0.086      0.399   0.1480
 48 Hour – 24 Hour     0.180      0.829   0.0550
 72 Hour – 48 Hour     0.150      0.693   0.1070

Variance components:
Source            Variance
 id                2.2006
 Residual          1.0314

Fixed effect coefficients (theta):
          Estimate  Std. Err  95% lower  95% upper
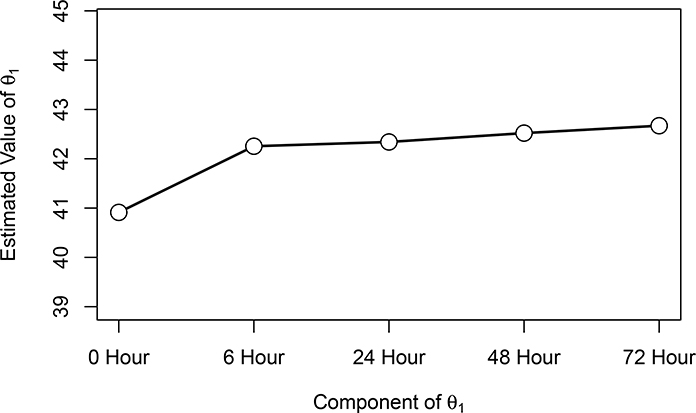
 0 Hour    40.9121    0.5226     39.888     41.936
 6 Hour    42.2542    0.5055     41.263     43.245
 24 Hour   42.3405    0.5055     41.350     43.331
 48 Hour   42.5201    0.5055     41.529     43.511
 72 Hour   42.6701    0.5055     41.679     43.661
 tempRT     0.5023    0.1531      0.202      0.802
 sexMale   −1.8333    0.6804     −3.167     −0.500
Std. Errors and confidence limits based on unconstrained covariance matrix

Parameters are ordered according to the following factor levels:
0 Hour, 6 Hour, 24 Hour, 48 Hour, 72 Hour

Model based on 1000 bootstrap samples

R> plot( hct1b, ci = TRUE, legendx = “bottomright”, inset = 0.08)

We find strong evidence (p = 0.002) of an increasing pattern in mean HCT. The coefficients are plotted in Figure 5 with indications of significance for the individual contrasts.

To test case (B) we simply need to omit the constraints from the call to clme. The code and results are given below.

R> hct2 <- clme(hct ~ time + temp + sex + (1|id), data = rat.blood,
+    levels = list(2, levels(rat.blood$time)))
R> summary(hct2, seed = 42)

Linear mixed model subject to order restrictions
Formula: hct ~ time + temp + sex + (1 | id) − 1

Order estimated: increasing simple order

log-likelihood: −296.6
AIC:             611.3
BIC:             624.3
(log–likelihood, AIC, BIC computed under normality)

Global test:
 Contrast       Statistic  p–value
 Bootstrap LRT       0.17   0.0070
 
Individual Tests (Williams’ type tests):
 Contrast           Estimate  Statistic  p–value
 6 Hour – 0 Hour       1.342      4.862   0.0000
 24 Hour – 6 Hour      0.086      0.399   0.1480
 48 Hour – 24 Hour     0.180      0.829   0.0550
 72 Hour – 48 Hour     0.150      0.693   0.1070

Variance components:
Source            Variance
 id                2.2006
 Residual          1.0314

Fixed effect coefficients (theta):
          Estimate Std. Err 95% lower 95% upper
 0 Hour    40.9121   0.5226    39.888    41.936
 6 Hour    42.2542   0.5055    41.263    43.245
 24 Hour   42.3405   0.5055    41.350    43.331
 48 Hour   42.5201   0.5055    41.529    43.511
 72 Hour   42.6701   0.5055    41.679    43.661
 tempRT     0.5023   0.1531     0.202     0.802
 sexMale   −1.8333   0.6804    −3.167    −0.500
Std. Errors and confidence limits based on unconstrained covariance matrix

Parameters are ordered according to the following factor levels:
0 Hour, 6 Hour, 24 Hour, 48 Hour, 72 Hour

Model based on 1000 bootstrap samples

Observe that the alternative hypothesis in (B) is much larger than the alternative hypothesis in (A). Thus, while the conclusions of tests for (A) and (B) are the same: that the parameters satisfy an increasing simple order, the p value associated with (B) is larger because the alternative hypothesis in (B) is larger than the alternative in (A).

Accounting for heteroscedasticity is simple in CLME. For example, suppose we wish to model each of the time points with a different residual variance. To do this we pass the time groups as the argument gfix, as shown below. We will call this case (C).

R> hct3 <- clme(hct ~ time + temp + sex + (1|id), data = rat.blood,
+    gfix = rat.blood$time, constraints = const,
+    levels = list(2, levels(rat.blood$time)))
R> summary( hct3, seed = 42 )

Linear mixed model subject to order restrictions
Formula: hct ~ time + temp + sex + (1 | id) − 1

Order specified: increasing simple order

log–likelihood: −291.4
AIC:             608.9
BIC:             627.7
(log-likelihood, AIC, BIC computed under normality)

Global test:
 Contrast        Statistic  p–value
 Bootstrap LRT       0.266   0.0010

Individual Tests (Williams’ type tests):
 Contrast           Estimate  Statistic  p–value
 6 Hour – 0 Hour       1.326      4.937   0.0000
 24 Hour – 6 Hour      0.086      0.465   0.1250
 48 Hour – 24 Hour     0.180      0.902   0.0430
 72 Hour – 48 Hour     0.150      0.823   0.0890

Variance components:
Source           Variance
 id               2.13092
 0 Hour           1.22617
 6 Hour           0.54469
 24 Hour          0.97074
 48 Hour          0.77105
 72 Hour          0.69144

Fixed effect coefficients (theta):
          Estimate Std. Err 95% lower 95% upper
 0 Hour    40.9258   0.5032    39.940    41.912
 6 Hour    42.2521   0.4625    41.346    43.159
 24 Hour   42.3385   0.4729    41.412    43.265
 48 Hour   42.5180   0.4681    41.601    43.435
 72 Hour   42.6680   0.4661    41.754    43.582
 tempRT     0.5341   0.1273     0.285     0.784
 sexMale   −1.8511   0.6345    −3.095    −0.608
Std. Errors and confidence limits based on unconstrained covariance matrix

Parameters are ordered according to the following factor levels:
0 Hour, 6 Hour, 24 Hour, 48 Hour, 72 Hour

Model based on 1000 bootstrap samples

White blood cell count

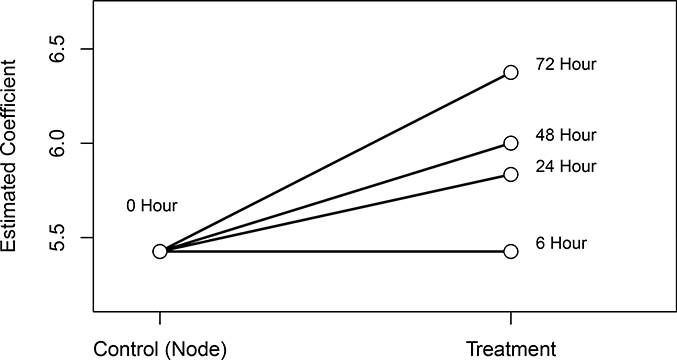
Using the white blood cell count data of Cora et al. (2012), we now illustrate our package for testing a simple tree order. Here the nodal parameter is taken to be the population mean corresponding to the 0 hour group. Since boxplots of the residuals (not shown) suggested the variances were potentially equal across the groups, we assume homogeneity of variances. For illustration, in this example we use the Williams’ type test statistic. The code and results are below, and the coefficients are plotted in Figure 6.

Figure 6:

Plot of estimated coefficients of white blood cell (WBC) count. Solid lines denote no significant difference, while dashed lines denote statistical significance.

R> const <- list( order = “simple.tree” , node = 1 , decreasing = FALSE)
R> wbc <- clme(wbc ~ time + temp + sex + (1|id), data = rat.blood,
+    constraints = const, levels = list(2, levels(rat.blood$time)),
+    tsf = w.stat )
R> summary( wbc, seed = 42)

Linear mixed model subject to order restrictions 
Formula: wbc ~ time + temp + sex + (1 | id) − 1

Order specified: increasing tree order with node at 1

log-likelihood: −236.3
AIC:             490.5
BIC:             503.6
(log–likelihood, AIC, BIC computed under normality)

Global test:
 Contrast          Statistic  p–value
 72 Hour – 0 Hour 5.207  0.0000

Individual Tests (Williams’ type tests):
 Contrast          Estimate  Statistic  p–value
 6 Hour –  0 Hour     0.000      0.000   1.0000
 24 Hour – 0 Hour     0.409      2.240   0.0120
 48 Hour – 0 Hour     0.574      3.150   0.0000
 72 Hour – 0 Hour     0.949      5.207   0.0000

Variance components:
Source            Variance
 id                1.51920
 Residual          0.45017

Fixed effect coefficients (theta):
          Estimate  Std. Err  95% lower  95% upper
 0 Hour     5.4262    0.4007      4.641      6.212
 6 Hour     5.4262    0.3910      4.660      6.193
 24 Hour    5.8348    0.3910      5.068      6.601
 48 Hour    6.0007    0.3910      5.234      6.767
 72 Hour    6.3757    0.3910      5.609      7.142
 tempRT    −0.1947    0.1011     −0.393      0.004
 sexMale    1.8229    0.5336      0.777      2.869
Std. Errors and confidence limits based on unconstrained covariance matrix

Parameters are ordered according to the following factor levels:
0 Hour, 6 Hour, 24 Hour, 48 Hour, 72 Hour

Model based on 1000 bootstrap samples

R> plot(wbc, legend = “topleft”, inset = 0.08)

Our results are consistent with those of Cora et al. (2012), but we have in addition detected the 0 hour - 48 hour and 0 hour - 24 hour contrasts as being significant, which were not identified by Cora et al. (2012). There does appear to be an increasing pattern over time, but the differences from control are not statistically significant until sufficient time has passed.

As an alternative to Williams’ type test, we repeated the analysis using the LRT (results not provided) and discovered that the LRT did not reject the null hypothesis at the 5% level of significance (p = 0.252). This discrepancy between Williams’ type and LRT is not surprising in view of the simulation study reported in Farnan et al. (2014), which indicated that Williams’ type test can be more powerful than LRT in some cases.

4.2. Fibroid growth rates

Peddada et al. (2008) investigated growth rate of of uterine leiomyomata (fibroids) in black and white women. Since fibroids are hormonally mediated and there is a drop in estrogen levels as women age, it may be reasonable to hypothesize a reduction in fibroid growth rates. Interestingly, Peddada et al. (2008) reported that for white women the rate of growth of fibroids decreased with age (i.e., simple order with decreasing pattern), whereas they did not find any reduction in the average growth rate of fibroids with age for black women. They defined the three age groups as follows: Young (< 35), Middle (35 − 44), and Old (≥ 45). We shall now re-analyze their data using the methodology available in our package CLME where the alternative hypothesis for women of each race group is a decreasing simple order. Note that for confidentiality, we use a subset of the data from the Fibroid Growth Study, excluding cases which may be personally identifiable, particularly those with only one fibroid analyzed in the study. This subset of the data represents 240 fibroids on 54 women. The original analysis in Peddada et al. (2008) represented 262 fibroids on 72 women.

The interest in this case is to test for a simple order for each race using a linear mixed effects model. This analysis serves as a useful illustration of customizing the order restrictions, because it cannot be performed with the default settings of CLME. First we load the data and perform some manipulations to get a factor that we can use. We define the variable race.age to encode the interaction of the race and age variables; with six levels ordered as: young black, middle-age black, older black, young white, middle-age white, and older white.

R> data(“fibroid”)
R> race.age <- factor(paste0( fibroid$race, “.”, fibroid$age ) ,
+    levels = c(“Black.Yng”, “Black.Mid”, “Black.Old”,
+    “White.Yng”, “White.Mid”, “White.Old”) )
R> fibroid$race.age <- race.age

We performed our analysis adjusting for the initial fibroid volume as a covariate, which was grouped into three categories: < 14,14−65cm³, ≥ 65cm³ with the < 14 category taken to be the baseline. To deal with repeated measurements, we took subject ID as the random effect.

R> initVol <- rep(“small”, nrow(fibroid))
R> idx1 <- (14000 <= fibroid$vol & fibroid$vol < 65000)
R> idx2 <- (65000 <= fibroid$vol)
R> initVol[idx1] <- “medium”
R> initVol[idx2] <- “large”
R> fibroid$initVol <- factor(initVol, levels = c(“small”, “medium”, “large”))

For the interaction between the Age and Race terms, we require constraints which define a decreasing simple order over age for both blacks and whites, but do not impose any order restriction between blacks and whites. We do this as follows:

R> const <- list()
R> const$A <- cbind( 2:6 , 1:5 )[−3, ]
R> const$B <- rbind( c(3, 1), c(6, 4) )
R> const

$A
      [,1] [,2]
[1,]     2    1
[2,]     3    2
[3,]     5    4
[4,]     6    5

$B

      [,1]  [,2]
[1,]     3     1
[2,]     6     4

To understand the construction of these matrices, recall the parameter vector θ₁ is ordered as: young black, middle-age black, older black, young white, middle-age white, and older white. The groups of the constrained effect are transformed into column indicators, meaning there will be six parameters: (θ_{Y B}, θ_MB, θ_OB, θ_YW, θ_MW, θ_OW), where YB denotes "young black," MB denotes "middle-aged black," and so on. Hence, the first three elements of θ correspond to the blacks, and the last three elements correspond to the whites.

The A matrix must define the proper order restriction on these elements. The first row defines the constraint θ_MB ≤ θ_{Y B}, the first row defines the constraint θ_OB ≤ θ_MB. The second two rows define similar constraints for the white women. None of the rows define a restriction between any of the first three elements (blacks) and any of the last three elements (whites); hence there is no order restriction imposed between the two races.

To test for a decreasing simple order for both blacks and whites, we must also define a function to compute the Williams’ type test statistic of Farnan et al. (2014) for both blacks and whites separately. While the matrix of contrasts is provided above, by default the Williams’ type test will take the maximum and report a single test statistic. We require a test statistic for each of these contrasts. This is similar to the function w.stat.ind which calculates the test statistics for the individual constraints. However, submitting tsf=w.stat.ind will test all of the constraints in the matrix constA instead of the contrasts in constB. To correct this, we make a small modification to w.stat.ind.

R> w.blk.wht <- function (theta, cov.theta, B, A, …) {
+    stats <- vector(“numeric”, length = nrow(B))
+    ctd <- diag(cov.theta)
+    stats <- apply(B, 1, FUN = function(a, theta, cov, ctd) {
+      std <- sqrt(ctd[a[1]] + ctd[a[2]] − 2 * cov.theta[a[1], a[2]])
+      (theta[a[2]] - theta[a[1]])/std
+    }, theta = theta, cov = cov.theta, ctd = ctd)
+    names(stats) <- c(“Black.Yng - Black.Old”, “White.Yng - White.Old” )
+    return(stats)
+ }

All we have done is replace calls to A with calls to B; this will accomplish our goal of producing a global test for both blacks and whites individually.

We are then ready to run the analysis. For simplicity, we assume homogeneity of variances. Results of the analysis are shown in Figure 7. The code for this figure is given below, since it cannot be produced through CLME.

Figure 7:

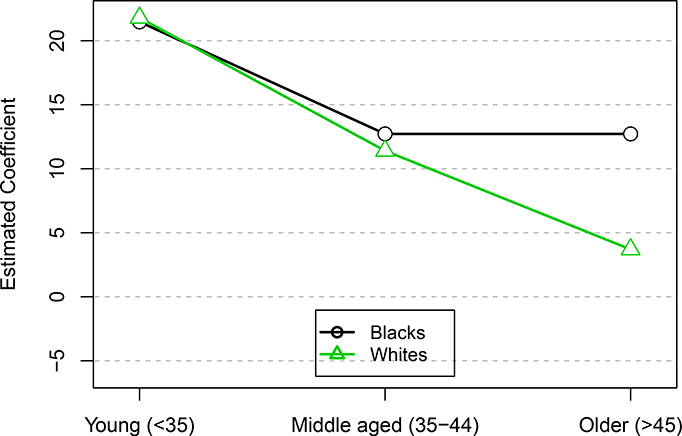
Plot of estimated coefficients of 6-month mean fibroid growth by race and age group. Black lines with circles correspond to Blacks, green lines with triangles correspond to Whites. Growth rates for each fibroid were averaged over the 2–4 time points. None of the individual constraints were significant. The global tests found a significant decreasing trend for white women, but not for black women.

R> fib <- clme(lfgr ~ race.age + initVol + (1|id), data = fibroid,
+    constraints = const, tsf = w.blk.wht, levels = list(10, levels(race.age)))
R> summary( fib, seed = 42 )

Linear mixed model subject to order restrictions
Formula: lfgr ~ race.age + initVol + (1 | id) − 1

Custom order constraints were provided

log-likelihood: −1085
AIC:             2189
BIC:             2206
(log-likelihood, AIC, BIC computed under normality)

Global tests:
 Contrast               Statistic  p-value
 Black.Yng - Black.Old      1.116   0.1880
 White.Yng - White.Old 2.270 0.0150

Individual Tests (Williams' type tests):
 Contrast               Estimate  Statistic  p-value
 Black.Yng - Black.Mid    8.7520      1.454   0.0580
 Black.Mid - Black.Old    0.0000      0.000   1.0000
 White.Yng - White.Mid    10.391      1.217   0.0640
 White.Mid - White.Old    7.7030      1.059   0.0830

Variance components:
Source            Variance
 id                107.58
 Residual          419.15

Fixed effect coefficients (theta):
                Estimate Std. Err 95% lower 95% upper
 Black.Yng        21.471    5.087    11.501    31.441
 Black.Mid        12.719    3.910     5.055    20.383
 Black.Old        12.719    6.277     0.416    25.023
 White.Yng        21.795    6.746     8.573    35.016
 White.Mid        11.403    5.751     0.132    22.674
 White.Old         3.700    4.872    −5.848    13.249
 initVolmedium    −4.720    3.201   −10.995     1.554
 initVollarge     −3.641    3.854   −11.194     3.912
Std. Errors and confidence limits based on unconstrained covariance matrix

Parameters are ordered according to the following factor levels:
Black.Yng, Black.Mid, Black.Old, White.Yng, White.Mid, White.Old

Model based on 1000 bootstrap samples

R> plot(x = 1, y = 0, col = 0, ylim = c(−6, 22), xlim = c(0.9, 3.1),
+    xlab = “”, ylab = “Estimated Coefficient”, xaxt = “n”)
R> axis(side=1, at=1:3,
+    labels = c(“Young (<35)”, “Middle aged (35–44)”, “Older (>45)”) )
R> for( y1 in seq(−15, 25, 5) ){
+    lines( x = c(0, 7), y = c(y1, y1), col = “grey”, lty = 2 )
+ }
R> lty1 <− 1 + (fib$p.value.ind[1]<0.05)
R> lty2 <− 1 + (fib$p.value.ind[2]<0.05)
R> lty3 <− 1 + (fib$p.value.ind[3]<0.05)
R> lty4 <− 1 + (fib$p.value.ind[4]<0.05)
R> points(c(1, 2), fib$theta[1:2], col = 1, type = “l”, lwd = 2 , lty = lty1)
R> points(c(2, 3), fib$theta[2:3], col = 1, type = “l”, lwd = 2 , lty = lty2)
R> points(c(1, 2), fib$theta[4:5], col = 3, type = “l”, lwd = 2 , lty = lty3)
R> points(c(2, 3), fib$theta[5:6], col = 3, type = “l”, lwd = 2 , lty = lty4)
R> points(1:3, fib$theta[1:3], col = 1, cex = 1.5, pch = 21, bg = “white”)
26 CLME: An R package for constrained LME models
R> points(1:3, fib$theta[4:6], col = 3, cex = 1.5, pch = 24, bg = “white”)
R> legend(“bottom”, lty = c(1, 1), pch = c(21, 24), col = c(1, 3), pt.bg = 0,
+    pt.cex = 1.1, lwd = 2, inset = 0.03, cex = 0.9,
+    legend = c(“Blacks    ”,  “Whites”))

The global tests found significant evidence of a decreasing simple order for white women (p = 0.0150) but not for black women (p = 0.1880). In particular, fibroid growth in older white women was found to be less than that of younger women. Neither of the individual constrasts for the white women (Young-Middle and Middle-Old) were significant at the α = 0.05 level. The significant decreasing trend confirms the conclusions of Peddada et al. (2008).

4.3. Comparison with other packages

In this section we provide some comparisons of CLME to lme4, which is a popular package for the analysis of linear mixed models. We will use the rat.blood data, and in particular the response varibale hct. We chose this variable because the observed means at each time point happen to be ordered according to a simple order. Hence, the fitted means will not be changed by clme, so the results between clme and lmer will be more comparable.

R> library(“lme4”)
R> cons  <- list(order = “simple”, decreasing = FALSE, node = 1 )
R> clme_out <- clme( hct ~ time + temp + sex + (1|id),
+               data = rat.blood, constraints = cons )
R> lmer_out1 <- lmer( hct ~ time + temp + sex + (1|id) − 1, data = rat.blood )
R> lmer_out2 <- lmer( hct ~ time + temp + sex + (1|id) − 1,
+               data = rat.blood, REML = FALSE )
R> rbind(fixef(clme_out), fixef(lmer_out1), fixef(lmer_out2))

     time0 Hour time6 Hour time24 Hour time48 Hour time72 Hour    tempRT
[1,]   40.91212   42.25417    42.34053    42.52008    42.67008 0.5022727
[2,]   40.91212   42.25417    42.34053    42.52008    42.67008 0.5022727
[3,]   40.91212   42.25417    42.34053    42.52008    42.67008 0.5022727
       sexMale
[1,] −1.833333
[2,] −1.833333
[3,] −1.833333

R> VarCorr(clme_out)

         Variance
id       2.200622
Residual 1.031353
attr(,“class”)
[1] “varcorr_clme”

R> VarCorr(lmer_out1)

 Groups   Name       Std.Dev.
 id      (Intercept) 1.55933
 Residual            0.90356

R> VarCorr(lmer_out2)

 Groups   Name        Std.Dev.
 id       (Intercept) 1.48486
 Residual             0.89063

R> c( AIC(clme_out), AIC(lmer_out1), AIC(lmer_out2) )

[1] 611.2926 613.7119 605.7245

These results indicate that, when the observed means do not violate the assumed order, clme produces results that are similar to those of lmer. The variance estimates (and hence the log-likelihood and AIC) differ somewhat but, as shown, this is also true when using lmer by specifying a different optimization criterion (REML=FALSE).

Users should be aware that clme is less computationally efficient than lmer. This should not be entirely surprising, as lme4 includes functions written in C++, while CLME is written entirely in R. While computation times depend on computer specifications, we provide some time relative time benchmarks between the packages using rbenchmark (Kusnierczyk 2012). First we compare the relative time for model fitting.

R> library(“rbenchmark”)
R> set.seed( 42 )
R> BMclme <- function(x=0){
+   clme(hct ~ time + temp + sex + (1|id), data = rat.blood,
+        constraints = cons)
+ }
R> BMlmer <- function(x=0){
+   lmer(hct ~ time + temp + sex + (1|id), data = rat.blood )
+ }
R> benchmark(BMlmer(), BMclme(), replications=100 )[,1:4]

      test replications elapsed relative
2 BMclme()          100  89.157   24.083
1 BMlmer()          100  3.702     1.000

As one can see, clme is significantly slower relative to lmer, though note that the elapsed time is over 100 runs of each functions; in this test an average run of clme evaluated in less than 1 second. Additionally, we tested the speed of the bootstrap functions of CLME and lme4. Note that for simplicity we used 100 bootstrap samples for each, and only performed 10 replications for time benchmarks.

R> set.seed( 42 )
R> beta_sum <- function(.) {
+   beta=fixef(.)
+ }
R> BMclme <- function(x=0){
+   summary( clme_out, nsim = 100, seed = 42 )
+ }
R> BMlmer1 <- function(x=0){
+   bootMer(lmer_out1, FUN=beta_sum, nsim = 100, seed = 42, type = “parametric”)
+ }
R> BMlmer2 <- function(x=0){
+   bootMer(lmer_out2, FUN=beta_sum, nsim = 100, seed = 42,
+           use.u=TRUE, type = “semiparametric”)
+ }
R> benchmark( BMclme(), BMlmer1(), BMlmer2(), replications=10 )[,1:4]

       test replications elapsed relative
1  BMclme()           10  64.178    2.830
2 BMlmer1()           10  22.675    1.000
3 BMlmer2()           10  22.809    1.006

While lmer still evaluates much faster than clme, the relative difference is not as extreme as for the model fitting.

5. Summary

In this paper we have introduced the R package CLME for performing statistical tests under linear inequality constraints. It allows the user to choose either the likelihood ratio type statistic or Williams’ type statistic. Since it is based on the residual bootstrap methodology it is not dependant on any Normality assumption. As demonstrated in the paper, the package is simple to implement with default settings (Section 4.1), and more complex hypotheses (Section 4.2) can be accommodated with relatively little effort.

Due to the flexibility and distribution-free nature of the model, as well as the ease of use, we anticipate that many researchers may benefit from using the order-restricted model implemented in CLME instead of standard ANOVA models. Other than this package, there does not appear to be any software which offers constrained inference for linear mixed effects models.

While the current release is stable, the authors have an interest in further developing the functionality of CLME. There are many potential improvements that we foresee. On the methodological side these include: adding more models, such as logistic models; implementing an automated choice of the number of bootstrap samples (see Jiang and Salzman 2012); allowing for correlated random effects; and adding the ability to perform power or sample size calculations. Furthermore, the software does not currently allow for complex covariance structures for the variance components, such as the AR(1) process, although it may be extended to accommodate such structures. Other projected developments include enabling the program to take advantage of parallel processing to speed up the repetitive calculations for each bootstrap sample. Finally, as noted, the shiny offers the ability to create apps, making complex models easily available to researchers without the need to write R codes. The included app can be run locally, but shiny apps can be hosted on a server and deployed online. A well-designed and web-based application could put the power and flexibility of CLME at a researcher’s fingertips. Future developments include improving the app and deploying it online.

Figure 9:

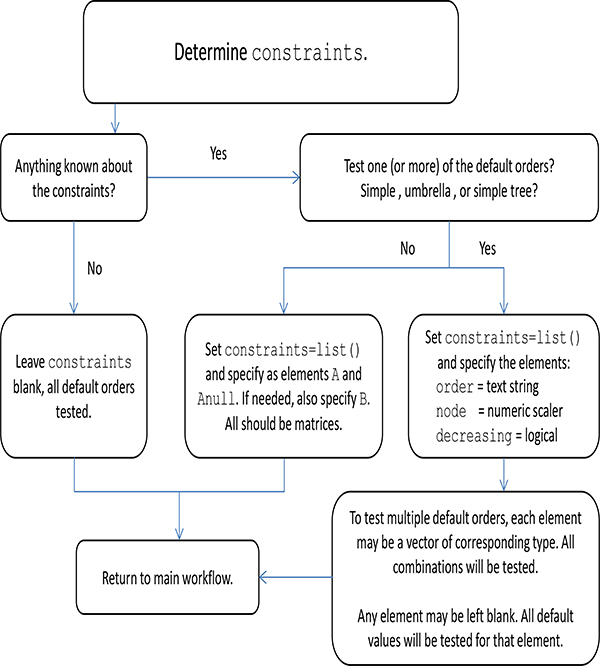
Flowchart to determine constraints.