Highlights
-
•
A new compartmental model, forced-SIR, quantifies COVID-19 pandemics impact.
-
•
Effectiveness of COVID-19 intervention measures is linked to models parameters.
-
•
Application of the model to 10 countries reveals a wide range of COVID-19 impacts.
Keywords: COVID-19, Compartmental model, Modeling pandemic evolution
Abstract
A simple analytical model for modeling the evolution of the 2020 COVID-19 pandemic is presented. The model is based on the numerical solution of the widely used Susceptible-Infectious-Removed (SIR) populations model for describing epidemics. We consider an expanded version of the original Kermack-McKendrick model, which includes a decaying value of the parameter β (the effective contact rate), interpreted as an effect of externally imposed conditions, to which we refer as the forced-SIR (FSIR) model. We introduce an approximate analytical solution to the differential equations that represent the FSIR model which gives very reasonable fits to real data for a number of countries over a period of 100 days (from the first onset of exponential increase, in China). The proposed model contains 3 adjustable parameters which are obtained by fitting actual data (up to April 28, 2020). We analyze these results to infer the physical meaning of the parameters involved. We use the model to make predictions about the total expected number of infections in each country as well as the date when the number of infections will have reached 99% of this total. We also compare key findings of the model with recently reported results on the high contagiousness and rapid spread of the disease.
1. Introduction
The recent pandemic due to the COVID-19 virus has created unprecedented turmoil and changed the daily life of people over the entire planet. It has also yielded a grim toll of victims that succumb to its attack. While there is great expertise in the medical community and the community of statisticians in dealing with epidemics, less is known about this particular disease to make reliable predictions for the evolution of the current pandemic.
In studying past epidemics, scientists have systematically applied “random mixing” models which assume that an infectious individual may spread the disease to any susceptible member of the population, as originally considered by Kermack and McKendrick [1]. More recent modeling approaches considered contact networks in which the epidemic spreads only across the edges of a contact network within a population [2], [3], [4], Bayesian inference models [5], models of spatial contacts in real cities or countries or in large-scale artificial cities and synthetic populations [6], [7], [8], and computational predictions of protein structures [9], to name just a few of the modeling efforts.
In the case of COVID-19, there is considerable uncertainty in the data collected about infected individuals due to the difficulty of testing large numbers of suspected cases. Although an avalanche of research studies are currently investigating the COVID-19 epidemiological characteristics [10], [11], [12], [13], [14], it appears that a simple model which can capture the basic behavior of the pandemic phenomenon, in spite of the large uncertainty in the data, can possibly offer useful guidance for its near-term and longer-term evolution. This paper aims to provide such a simple model with very few adjustable parameters.
2. The model
2.1. Derivation of the model
The original mathematical description of the spread of an infectious disease in a population is the so-called SIR model, due to Kermack and McKendrick [1] which divides the (fixed) population of N individuals into three compartments (groups, classes):
-
•
S(t) the number of individuals susceptible but not yet infected with the disease;
-
•
I(t) the number of infected individuals;
-
•
R(t) the number of individuals removed (recovered) from the infected group, either by becoming healthy again with long-term immunity or by passing away.
Models that involve additional compartments can be constructed by considering more detailed stages of the infection or flows among the various compartments. The choice of the compartments is related to the disease that is being studied. For example, in the SIS model, susceptible individuals can become infected/infectious but when they are recovered/removed they can become susceptible again, that is, no permanent immunity is acquired. In the SEIR model, individuals are grouped in four compartments, one more than in the SIR model: the additional compartment is the group of “Exposed” (E) individuals, who have become infected but not yet infectious themselves. A recent model [15] considers eight stages of infection: susceptible (S), infected (I), diagnosed (D), ailing (A), recognized (R), threatened (T), healed (H) and extinct (E), collectively termed SIDARTHE. In the present study we have chosen to focus on the SIR model, which is the simplest model incorporating the Covid-19 epidemic dynamic. We are thus effectively combining the exposed and the infectious compartments of the SEIR model into one group; I(t) = infected and/or infectious individuals (referred hereafter as infected individuals). Although this combination of compartments misses some details of the disease evolution, in light of the approximate analytical solution we introduce later, it should not substantially affect the conclusions to be drawn from the approximate model.
The SIR model involves two positive parameters, β and γ which have the following meaning: - β describes the effective contact rate of the disease: an infected individual comes into contact with β other individuals per unit time (the fraction that are susceptible to contracting the disease is S/N);
- γ is the mean removal (recovery) rate, that is, is the mean period of time during which an infected individual can pass it on before being removed from the group of the infected individuals.
This model obeys the following differential equations:
| (1a) |
| (1b) |
| (1c) |
Many recent studies (e.g. [16], [17], [18]), have attempted to model the data of the COVID-19 pandemic by imposing time-dependence conditions (or by data assimilation) on the rates β and γ involved in the original SIR model, in order to account for the imposition of social-distancing measures, quarantine of infected individuals, and other interventions designed to slow down the spread of the disease. Motivated by such considerations, we will introduce a variation of the original model in which the parameter β is a time-dependent, monotonically decreasing function. This change can drastically affect the evolution of the populations. We give below a specific example to illustrate this point. Since the presence of time-dependence in β introduces a forcing term, which for reasonable parameter values lowers the number of infected individuals (“flattens the curve”).
The system of equations that describe the SIR, with or without the time-dependence in the parameter β, can be easily solved numerically, as shown in Fig. 1 , giving the three group populations (S, I, R) as a function of time. Kermack and McKendrick pointed out that “it is impossible from these equations to obtain I(t) as an explicit function of t” (p. 713, [1]), but provided approximations valid under certain conditions. Here we aim to give a simple approximate analytical solution inspired by the numerical solution.
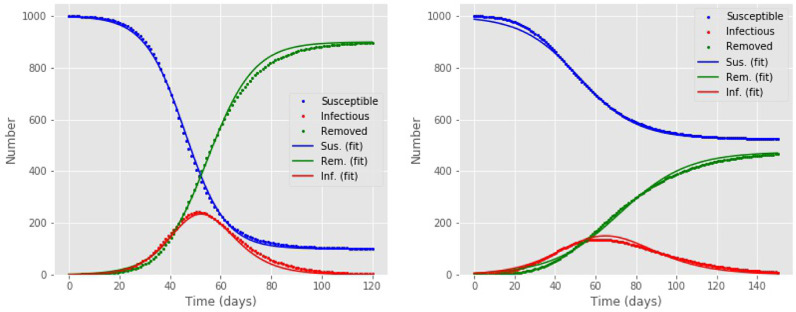
Fig. 1.
Numerical solution of the models, giving the susceptible S(t) (blue points), infected I(t) (red points) and removed R(t) (green points) populations as functions of time t in days; the corresponding colored lines give the approximate solutions obtained by the analytical expressions, Eq. (3). Left: The SIR model, with parameter values and ; the parameter β is constant. Right: The SIR model with a time-dependent parameter β with exponential decay and parameter values (see text for details). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
We observe from the numerical solution of the SIR model, shown in Fig. 1, that both the susceptible and the removed populations (S and R, respectively) behave like sigmoids, which is the typical behavior of solutions to differential equations that involve exponential growth and decay. Moreover, the infected population is always given by the following expression
| (2) |
From these observations, we take the approximate solutions to be given by:
| (3a) |
| (3b) |
| (3c) |
where N′, α 1, α 2, t 1, t 2 are treated as adjustable parameters, with t 1 and t 2 representing the times at which the and populations reach their sigmoid midpoint values, respectively. Interestingly, the analytical expressions introduced above fit even better the numerical solution of the model with a time-dependent β parameter. In Fig. 1 we give examples of how well the approximate analytical expressions fit the “exact” numerical ones. In these examples, for the model with time-dependent β we assumed although we emphasize that this assumption is for illustrative purposes only and does not affect the general behavior of the model. Indeed, as we show below, β(t) takes in our solution the behavior of a sigmoid. For the SIR model in the example of Fig. 1, the fit to the analytical expression of Eq. (3) has an RMSE value of 9.4 and the integral of the I(t) values differs from the exact result by %. For the model with time-dependent β in the example we considered, the fit to the analytical model of Eq. (3) has an RMSE value of 8.3 and the integral of I(t) differs from the exact result by 0.3%.
Since the analytical model of Eq. (3) can capture the behavior of the SIR model including a time-dependent β, which represent the “forcing” or “flattening” of the curve of infected individuals, we refer to it as the “FSIR” model.
2.2. Analysis of the model
Here we derive relations between the parameters used in the model of Eq. (3), and the parameters of the original set of differential equations, Eq. (1). To keep the expressions simple, we will assume and define . By inserting the expressions for and in Eq. (1b) we find:
| (4) |
where we have defined . Similarly, by inserting the expressions for and in Eq. (1c) we obtain:
| (5) |
Thus, in the approximate model described by Eq. (3), the parameters β and γ of the original SIR model become time-dependent, if we treat α as constant to be determined by fitting the data (see next section). In the FSIR model the effect of interventions and measures can be inferred from the values of the adjustable parameters t 1, Δt and N′, as will be explained in the next section, so that there is no need to impose specific time-dependent conditions on the model parameters themselves. It should be noted that the time-dependence of the coefficients β(t) and γ(t) is an inherent property of the proposed analytical model described by Eq. (3); β(t), as a monotonically decreasing function of time, can relate to the populations decreased mobility, lock-downs and other non-pharmaceutical interventions, which decrease the contact rate among susceptible individuals [19], [20].
The quantity we defined in the expression of β(t) is the fraction of the original susceptible population that was infected, and thus does become part of the removed population. There are two possible limiting values for this quantity: n′ → 1, the limit in which the entire susceptible population was exposed and eventually becomes removed population, and n′ → 0, the limit in which only a tiny fraction of the susceptible population was exposed. In the first limit we obtain:
| (6) |
while in the second limit we obtain:
| (7) |
From the first expression we see that for t ≫ t 1 the value of β 1(t) increases exponentially, which is an unphysical result. From the second expression, we see that β is a monotonically decreasing function of time and for t ≫ t 1 tends to the constant value
which is the expected behavior in the FSIR model.
For t ≪ t 1 and assuming that αΔt > 1 we find that
which relates the adjustable parameter α of the analytical model to the value of the parameter β appearing in the original SIR model.
The quantity of the SIR model is used to estimate the value of the basic reproduction number of an epidemic. From our analytical model, in the limit n′ → 0, the quantity β/γ takes the form
| (8) |
For and assuming that αt 1 ≫ 1 (as is the case for the fits to reported data discussed in the next section), this quantity becomes
For t ≫ t 2, the quantity β/γ becomes
The first number is very large for typical values of the parameters in the FSIR model obtained from fits to reported data, while the second value is very small, close to zero. Neither result is realistic. In the important range t 1 < t < t 2, we find from numerical results that this quantity is approximately described by a decaying exponential in time
with λ ≈ 1/2α. This result implies that in this range we would expect (the functional form we assumed for illustrative purposes in Fig. 1), and γ ~ eαt. From this last expression, taking the time average of γ in the range which we call we find
where we have used
from the expression of Eq. (5), a reasonable approximation for t ≳ t 2. The last relation for the average value of γ is obeyed to a good approximation for each case of reported data we examined.
Using the preceding analysis that led to the relations β ≈ α for the initial value of β and for the average value of γ, we suggest that a reasonable representation of the quantity β/γ is given by the value of αΔt. Thus, we will use this value as a proxy for R 0, and will refer to it as . The parameters estimated from the fit of our analytical model to reported data give a value of which is in agreement with the recently reported median value of R 0 for the pandemic.
3. Application to reported data
We use our analytical FSIR model to fit the behavior of infected populations of different countries, as obtained from the European Centre for Disease Prevention and Control (ECDC) [21], for a period ending on April 28, 2020 which corresponds to 100 days from the onset of the exponential growth of reported cases in China.
In order to obtain a meaningful fit, we had to consider data for each country that show a monotonic increase at the beginning. This means that a few data points in each case were excluded, as they corresponded to sporadic reports of very few isolated cases, typically 1 to 10 in a given day, interspersed by several days of zero cases. In practice this means that the fitting begins at a certain cutoff day denoted as t 0. In order to make the fit more robust and simpler, we chose . Moreover, we found by trial-and-error that the value is the optimal choice for all the countries we considered. This leaves three adjustable parameters in the model that can be varied to obtain the best fit to the data, namely t 1, t 2 and N′; instead of t 1 and t 2, we elected to use instead as independent parameters t 1 and . The best fit here is defined in the Root-Mean-Square (RMS) sense.
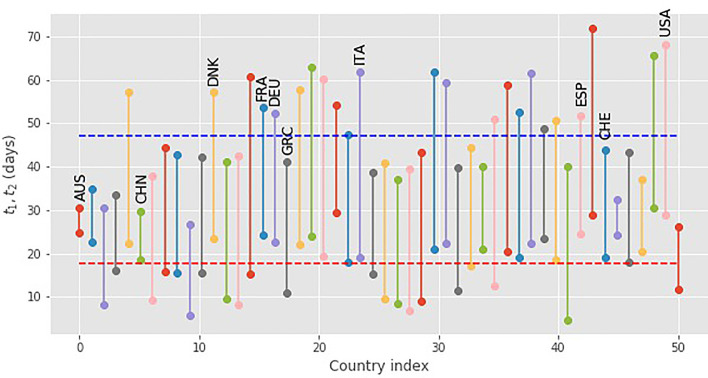
We were able to obtain reasonable fits for 50 countries from the entire database [21]. The resulting values for the parameters t 1, t 2, are shown in Fig. 2 ( is the distance between each pair of values). The averages and standard deviations for this set are giving . The values of the parameters involved span a wide range. For other countries in the database, the data are either too noisy or have not reached the point where the FSIR model can provide a good fit: specifically, the model needs to include data up to the maximum of the curve, otherwise it does not give meaningful values for the fitting parameters.
Fig. 2.
The values of the parameters t1 and for 50 countries, obtained by fitting the FSIR model with data up to 28 April 2020. The dashed lines give the average values of the parameters, ⟨t1⟩ (red) and (blue) of the FSIR model defined by Eq. (3). The countries with labels are used to examine the behavior of the model in more detail. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
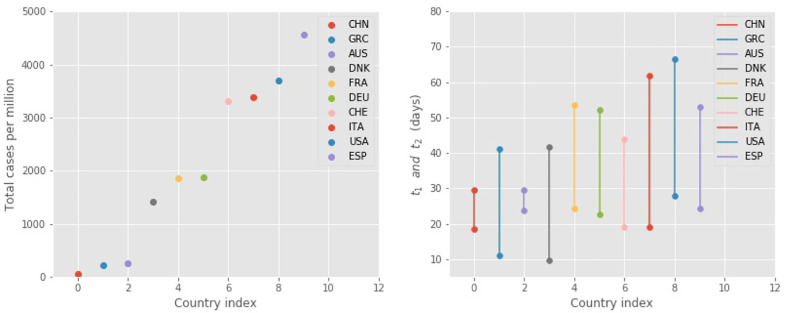
Instead of including all 50 countries in the following discussion, we have chosen to focus on 10 countries that span the whole range of parameter values and could hopefully provide some insight to the behavior of the pandemic. The choice of the 10 countries also aims to represent parts of the world more heavily or less heavily impacted by the disease, as well as more typical cases. Here we defined the impact as the total number NT of infected individuals during the first wave of the pandemic, as predicted by the FSIR model; this number is scaled by the population of the country, NP, in Fig. 3 . In particular, we have included 3 countries in which the impact was small, China, Greece and Australia for which (NT/NP) < 500 infected per million, 3 countries in which the impact was moderate, Denmark, Germany and France for which 1, 000 < (NT/NP) < 2,000 infected per million, and four countries where the impact was large, Switzerland, Italy, USA and Spain for which (NT/NP) > 3, 000 infected per million. The average value for t 1 for this set of 10 countries is and for Δt it is .
Fig. 3.
Left: the estimated total cases (NT) scaled by the population of each country. Right: t1 and t2 values (dots) in 10 countries, as obtained in the FSIR model by fitting the raw data reported in [21], including data up to April 28, 2020 (see also Fig. 4 for specific examples).
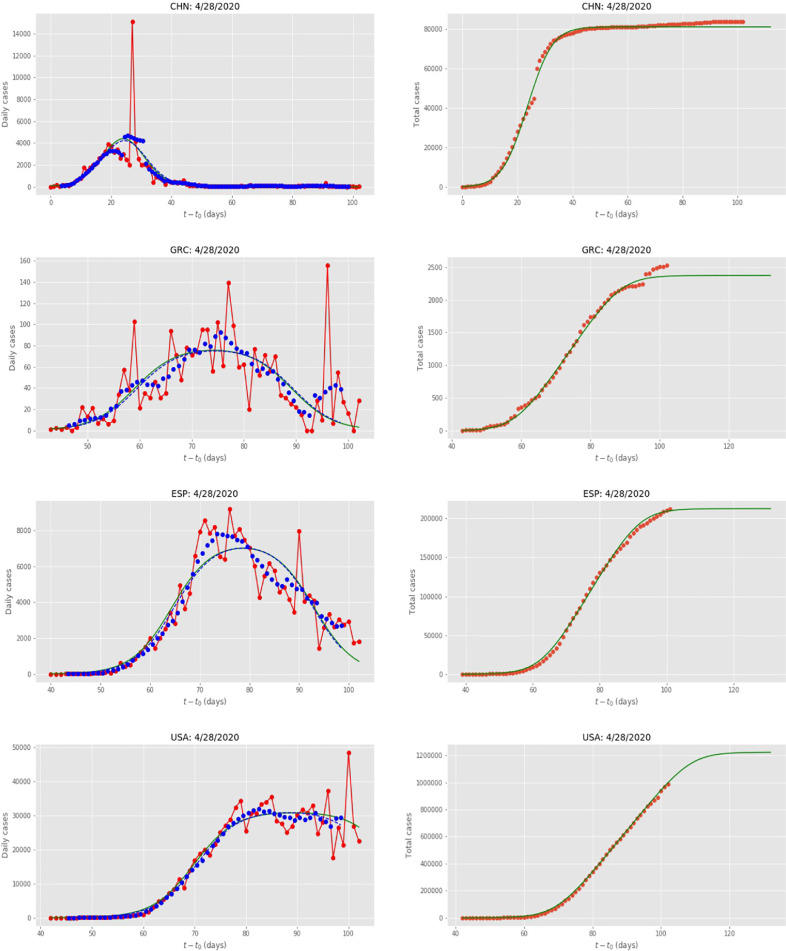
In Fig. 4 we give some examples of the actual fits for the “outlier” countries (China, Greece, USA and Spain). To have a measure of the fit that is comparable between different countries, we defined the “quality of fit” as:
| (9) |
which is expressed as a percentage (multiplied by a factor of 100). The resulting values of the parameters, including our choices of t 0, are given in Table 1 .
Fig. 4.
Data for China (CHN), Greece (GRC), USA and Spain (ESP) and the United States of America (USA). Red dots are the daily data reported in [21], the green lines are the fits by the FSIR model. The blue dots are seven-day running averages and the blue dashed lines are the fits by the FSIR model; in all cases the green and blue-dashed lines are essentially indistinguishable, except for USA near the end of the examined period. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Table 1.
The values of the various parameters that enter in the FSIR model of Eq. (3), for the 10 countries considered (see text for details). The countries have been indexed according to their NT values, scaled by the population of each country. The next-to-last column includes the values for the expected total number of cases NT when the number of infections has dropped to near zero, and is an extrapolated value (rounded to the nearest 100). The last column includes the number of days D (counting from April 28) until the value of NT has reached 99% of its final value; a negative number (for China, Australia, Switzerland, and Greece) indicates that this date has already passed.
| Index | Country | (Symbol) | t0 | t1 | Δt | N′ | Qfit | NT | D |
|---|---|---|---|---|---|---|---|---|---|
| (days) | (days) | (days) | (%) | (days) | |||||
| 0 | China | (CHN) | 17 | 18.5 | 11.1 | 7343 | 16.19 | 81,100 | |
| 1 | Greece | (GRC) | 65 | 11.0 | 30.1 | 79 | 36.91 | 2400 | |
| 2 | Australia | (AUS) | 61 | 23.8 | 5.7 | 1143 | 6.61 | 6500 | |
| 3 | Denmark | (DNK) | 75 | 9.63 | 32.0 | 258 | 21.30 | 8200 | 7 |
| 4 | France | (FRA) | 57 | 24.4 | 29.2 | 4272 | 20.97 | 124,800 | 1 |
| 5 | Germany | (DEU) | 57 | 22.6 | 29.7 | 5246 | 17.22 | 156,000 | 0 |
| 6 | Switzerland | (CHE) | 59 | 19.1 | 24.7 | 1142 | 14.62 | 28,100 | |
| 7 | Italy | (ITA) | 53 | 19.0 | 42.8 | 4774 | 15.13 | 204,000 | 3 |
| 8 | United States | (USA) | 59 | 27.9 | 38.7 | 31,314 | 12.58 | 1,210,300 | 14 |
| 9 | Spain | (ESP) | 56 | 24.3 | 28.7 | 7417 | 14.42 | 212,800 | 0 |
The values of the parameters obtained reveal interesting behavior.
-
•
t 0: The value of this parameter is similar for all countries, except for China with . This simply reflects the fact that the pandemic originated in China and then spread through the rest of the world. The rest of the countries have starting dates of the exponential increase within one week from the earliest, Italy (with ) to the latest, such as Greece and Denmark (with and 75, respectively). The time lag between most countries and China is approximately 6 weeks.
-
•
t 1: This value indicates the position of the mid-point of the sigmoid representing the behavior of the susceptible population, S. The shorter it is, the sooner the country experiences the exponential increase in the infected cases, thus urgently necessitating the introduction of health interventions and measures to limit the spread of the disease. The three countries with the shortest t 1 values are Greece, Denmark and China; unsurprisingly, these countries also have of the lowest number of cases per million, as shown in Fig. 3.
-
•
Δt: This value indicates the lag between the sigmoid that describes the recovered population () and the sigmoid of the susceptible population (). As such, it can be interpreted as the effective rate of removal (γ in the SIR model). In Table 1 we present the values of Δt for each country. The average of Δt is close to 27.5 days ( ~ 4 weeks), a value consistent with a recently reported estimated median time of approximately 2 weeks from onset to clinical recovery for mild cases, and 3–6 weeks for patients with severe or critical disease [22], [23], [24]. Australia and China show an unusual low value, Δt= 5.7, and 11.1 days, respectively. The value of this parameter has a significant effect on the total expected number of cases (see below).
-
•
N′: the value of this parameter is representative of the number of daily cases near the peak of the curve. It is close to reported values for this quantity for all the countries. Interestingly, if we assume that the total number of susceptible individuals is close to the population of each country, which in all cases is in the range of then the ratio as we assumed for the FSIR model earlier.
In Table 1 we also include the values for the quality of the fit, which range from 6.6 (AUS) and 12.6 (USA) to 36.8 (Greece), representing a measure of the relative noise in the data; the noise is largest for Greece because the numbers are rather small. We have also considered fitting the FSIR model to seven-day running averages of the reported cases, and this in general makes almost no difference to the value of the parameters or the quality of the fit (see Fig. 4 for examples).
Using the analytic expression for we can extrapolate to long times and try to obtain an estimate for the total value of cases over a long period, when the number of daily cases of infection have essentially dropped to negligible levels (this corresponds to ). We call this asymptotic value NT and report it in Table 1.
The average (over all countries in the set) of Δt is 27.31 ± 11.35 (median of Δt is 29.48), the average of is 0.058 ± 0.042, and the average of 1/Δt is 0.052 ± 0.047, (all numbers reported to 3 significant digits). It should be noted that the average of Δt over the set of the 50 countries mentioned earlier is 29.20 ± 9.16.
The FSIR-estimated average of Δt = 27.31 ± 11.35 yields an average reproduction number of (7.37, if we consider the median value of Δt). Initial estimates of the early dynamics in Wuhan, China, suggested a value for R 0 in the range 2.2–2.7. For China, the FSIR model estimates . However, the FSIR estimates for the rest of the countries in the set, suggest much higher values of . By conducting an elaborate analysis of datasets and data sources, estimating distributions of epidemiological parameters, and integrating uncertainties in parameters values, Sanche et al.[10] reported a median (95% CI 3.8 – 8.9) for China. The FSIR estimated values of for the countries we study fall almost entirely within this range.
The estimated values correspond to the models fitted parameters for actual data. Since a fixed value as explained above, the adjustable fitted parameter Δt is the one essentially yielding the value of through the relation (with ). Large values of R 0 have been reported in the literature [10], [25]. However, fitting real country data tends to produce higher values of Δt because a seemingly single epidemic wave in a country can be the aggregate result of the superposition of smaller or larger sub-epidemics [26].
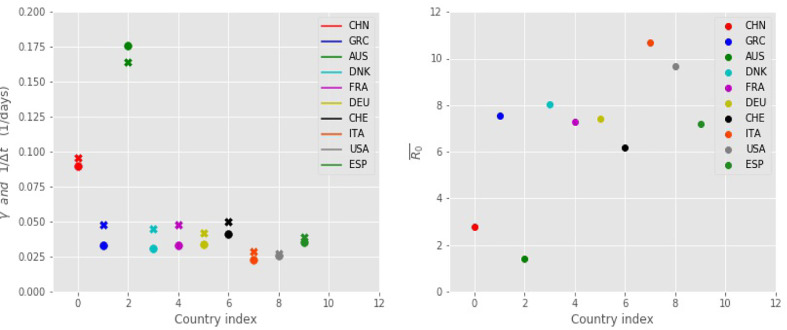
Fig. 5 depicts the FSIR-obtained values of plotted in conjuction with the 1/Δt values, for the 10 countries considered. For each country, the values are very close in magnitude, as was explained in a previous section. It should be noted that is calculated as the time average of the coefficient γ(t), as presented in Eq. (5), over the time period starting from t 0 until the expected total number of infected people, NT, has reached 99% of its final value. Fig. 5 also depicts the values for each country (calculated as where α ≈ 0.25 and the value of each country’s Δt is presented in Table 1).
Fig. 5.
Left: Estimates of (filled x symbols) and 1/Δt (filled circles) for the 10 countries considered in Table 1; these values are useful in estimating the reproduction number . Right: Estimated values for the reproduction number for the 10 countries considered, as obtained from the FSIR model. The larger the value the more adversely affected by the disease the country is.
As measured by the estimate of the basic reproduction number Italy is the country most adversely affected by the disease (), followed by the USA (), Denmark (), Greece (), Germany (), France (), and Spain (). Greece, although it suffered relatively small number of cases, has a large value for the basic reproduction number (). USA, Spain, and Italy suffer the highest numbers of expected total cases (NT), whereas in the case of Greece the expected total number of cases is one of the lowest in the set, presumably due to the fast implementation of measures imposed by the government and followed by the citizens. It should be noted that Greece has one of the smaller t 1 values. Australia, with has the lowest value of .
4. Assessment and conclusions
The model presented here offers several advantages, but also has certain limitations. As a model of the simple SIR type, it restricts the compartmentalization of the population in only 3 classes (S, I, R). It is a simple deterministic model, which does not take into consideration age, gender, spatial position or any other factors. It assumes homogeneous mixing, that is, individuals make contact at random, the transmission and recovery rates are positive and the same for all individuals, there is no vaccine available, the total population size is constant and large, and any recovered person obtains permanent immunity.
Its main strength is the simplicity and the insight it offers to how the pandemic affects large populations such as countries, states, or cities. The model relies on only three parameters all of which are obtained by directly fitting the reported data of daily populations of infected individuals. The effect of interventions and measures can be inferred from the values of the adjustable parameters t 1, Δt, and N′, so there is no need to impose specific time-dependent conditions on the model parameters themselves (it should be noted that the time it takes for infectious individuals to recover is independent of non-pharmaceutical interventions). As such, it is particular useful in obtaining adjustable parameters at the beginning of the an epidemic, but not after different non-pharmaceutical interventions are applied, or if there is a second peak or multiple waves (sub-epidemics) in the number of infectious individuals at later times.
An additional advantage of the model is that the values of the parameters derived from the data for different countries can be used to estimate the quantity a crucial measure of how each country has been affected. This is again in reasonable agreement with the picture described qualitatively in news reports about each country, and offers a quantitative assessment of the severity of the situation. For instance, as Fig. 5 shows, low values of the parameters and 1/Δt, which are directly obtained from the model, are indicative of high values, as in the cases of Italy, USA and Spain, all of which have suffered relatively large effects. In contrast, high values of these parameters are indicative of relatively mild effects, as is the case for China and Australia. Greece seems to be an exception, having average values for these parameters (similar to several other countries), yet suffered relatively mild effects as judged by the total number of infected and the fatalities. In this respect, our model can also offer useful insight: it is not just the value of that matters, but also how soon measures are adopted, as described by the parameter t 1, and how strictly they are enforced, as described by the parameter Δt. Thus, the model can provide some guidance on the relative merits of different approaches.
Finally, the projections of the total amount of infected individuals for the first wave, as predicted by extending the time evolution of the model to the future, are quite sensible. In this sense, the model offers useful estimates of when the total number of infections of the first wave will be reached in each country.
Nevertheless, the model has important limitations.
First, it contains no information on, and therefore can make no predictions about, the case mortality rate. The number of fatalities (case fatality) is roughly proportional to the total number of infected cases, although the constant of proportionality varies in each country, ranging from a high of about 0.15 for Belgium, 0.14 for France, 0.13 for Italy, to a low of about 0.01 for Australia, and about 0.05 for Greece, China, and Denmark [27]. Fig. 6 presents the case fatality ratio and the deaths (COVID-related deaths) per 100K of the population, for each country. The case fatality ratio represents the mortality per absolute number of cases, that is, the total confirmed cases within a country. Greece, Denmark, and China have low values of case fatality ratios and deaths per 100K of the population, and so have Germany and the USA. Australia has the lowest ratio. In the other end, France, Italy, and Spain have the highest ratios. Additional information is ndeed to explain these results, possibly having to do with the capabilities of the health care system in each country, which is not related simply to the dynamics of the disease spread in the population; such factors are not contained in the mathematical model considered here.
Fig. 6.
Left: Case fatality ratios as reported in [27] for 10 countries. Right: Deaths per 100K inhabitants for each country; these values closely follow the trends of the expected total number of infections scaled by the population, see Fig. 3.
Second, the extrapolation to future cases of infection is only a lower limit. This point has been discussed in an elegant mathematical analysis of the data by Fokas et al. [28]. We emphasize here that this shortcoming is not traced to the analytical FSIR model, but rather to the underlying differential equations assumed to describe the phenomenon (the original SIR model). The reason is that any set of linear differential equations that describe exponential decay and growth, as those of Eq. (1) do, will necessarily have exponential (logistic) behavior of the tails; this is captured by our analytical model, but apparently does not represent the actual data for the long-term behavior of the total number of infected individuals. This is evident in Fig. 4: in the countries that have long passed the peak of the reported cases, the tail does not asymptote to a constant value, as the sigmoid (logistic) model predicts, but the number actually keeps growing at a slow rate. To capture this behavior, non-linear terms are needed in the underlying differential equations (see [28]).
We suggest that, despite its limitations, the simple analytical model presented here can be useful for a quantitative evaluation of different efforts to contain the pandemic.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
CRediT authorship contribution statement
Efthimios Kaxiras: Conceptualization, Data curation, Formal analysis, Investigation, Supervision, Writing - original draft, Writing - review & editing. Georgios Neofotistos: Formal analysis, Investigation, Writing - review & editing. Eleni Angelaki: Software, Formal analysis, Investigation, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This work grew out of a lecture and a lab exercise on numerical solutions of ordinary differential equations, presented on April 10, 2020 in the course “APMTH-10: Computing for Science and Engineering”, which the three authors teach. We gratefully acknowledge support from the Computing in Engineering Education (CEE) group of the Active Learning Labs in developing and offering this course.
References
- 1.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc Roy Soc A. 1927;115:772. [Google Scholar]
- 2.Barthélemy M., Barrat A., Pastor-Satorras R., Vespignani A. Dynamical patterns of epidemic outbreaks in complex heterogeneous networks. J Theor Biol. 2005;235(2):275–288. doi: 10.1016/j.jtbi.2005.01.011. [DOI] [PubMed] [Google Scholar]
- 3.Ferrari M.J., Bansal S., Meyers L.A., Bjørnstad O.N. Network frailty and the geometry of herd immunity. Proc Biol Sci. 2006;273(1602):2743–2748. doi: 10.1098/rspb.2006.3636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Volz E. SIR Dynamics in random networks with heterogeneous connectivity. J Math Biol. 2008;56(3):293–310. doi: 10.1007/s00285-007-0116-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Groendyke C., Welch D., Hunter D.R. Bayesian inference for contact networks given epidemic data. Scand J Stat. 2011;38(3):600–616. [Google Scholar]
- 6.Tagliazucchi E., Balenzuela P., Travizano M., Mindlin G.B., Mininni P.D. Lessons from being challenged by COVID-19. Chaos Solitons Fractals. 2020;137:109923. doi: 10.1016/j.chaos.2020.109923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu Q.H., Ajelli M., Aleta A., Merler S., Moreno Y., Vespignani A. Measurability of the epidemic reproduction number in data-driven contact networks. Proc Natl Acad Sci. 2018;115(50):12680–12685. doi: 10.1073/pnas.1811115115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang M., Verbraeck A., Meng R., Chen B., Qiu X. Modeling spatial contacts for epidemic prediction in a large-scale artificial city. Journal of Artificial Societies and SocialSimulation. 2016;19(4):3. doi: 10.18564/jasss-3148-616. [DOI] [Google Scholar]; (downloaded from http://jasss.soc.surrey.ac.uk/19/4/3.html on 4/9/2020).
- 9.Jumper J., Tunyasuvunakool K., Kohli P., Hassabis D., AlphaFold Team. Computational predictions of protein structures associated with COVID-19. 2020. https://deepmind.com/research/open-source/computational-predictions-of-protein-structures-associated-with-COVID-19. AlphaFold Team, Version 2, DeepMind website, 8 April.
- 10.Sanche S., Lin Y.T., Xu C., Romero-Severson E., Hengartner N., Ke R. High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2. Emerg Infect Dis. 2020 doi: 10.3201/eid2607.200282. [DOI] [PMC free article] [PubMed] [Google Scholar]; (accessed on April 15, 2020).
- 11.Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Imai N., Dorigatti I., Cori A., Riley S., Ferguson N.M.. Estimating the potential total number of novel coronavirus cases in Wuhan City, China. [cited 2020 Feb 2]. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/2019-nCoV-outbreak-report-17–01-2020.
- 13.Rothe C., Schunk M., Sothmann P., Bretzel G., Froeschl G., Wallrauch C. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N Engl J Med. 2020;382:970–971. doi: 10.1056/NEJMc2001468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wynants L., Ben B.V.C., Bonten M., Collins G., Debray T., DeVos M. Prediction models for diagnosis, prognosis of COVID-19 infection: systematic review, critical appraisal. BMJ. 2020;369:m1328. doi: 10.1136/bmj.m1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Giordano G., Blanchini F., Bruno R. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med. 2020;26:855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Barmparis G., Tsironis G.. Estimating the infection horizon of COVID-19 in eight countries with a data-driven approach. 2020. ISSN 0960-0779, 10.1016/j.chaos.2020.109842, 109842. [DOI] [PMC free article] [PubMed]
- 17.Franco E.. A feedback SIR (fSIR) model highlights advantages and limitations of infection-based social distancing. 2020. [q-bio.PE], downloaded on April 29, 2020. arXiv: 2004.13216.
- 18.Nadler P., Wang S., Arcucci R., Yang X., Guo Y.. An epidemiological modelling approach for Covid19 via data assimilation. 2020. [stat.AP], downloaded on April 29, 2020. arXiv: 2004.12130. [DOI] [PMC free article] [PubMed]
- 19.Flaxman S. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020 doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- 20.Dehning J., Zierenberg J., Spitzner F.P., Wibral M., Neto J.P., Wilczek M., Priesemann V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science. 2020 doi: 10.1126/science.abb9789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.https://opendata.ecdc.europa.eu/covid19/casedistribution/csv.
- 22.Report of the WHO-China joint mission on coronavirus disease 2019 (COVID-19) 16–24 February 2020 https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf.
- 23.Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. Lancet. 2020;395:1054–1062. doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wölfel R., Corman V.M., Guggemos W. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020;581:465–469. doi: 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
- 25.Liu Y., Gayle A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Travel Med. 2020;27(2):taaa021. doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chowell G., Tariq A., Hyman J.M. A novel sub-epidemic modeling framework for short-term forecasting epidemic waves. BMC Med. 2019 doi: 10.1186/s12916-0191406-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.https://coronavirus.jhu.edu/data/mortality.
- 28.Fokas A., Dikaios N., Kastis G.. Predictive mathematical models for the number of individuals infected with COVID-19. MedRxiv. doi: 10.1101/2020.05.02.20088591. [DOI]