Simulation model of security control lane operation in the state of the COVID-19 epidemic

Abstract

The article presents a discrete event simulation model for the various security control lanes configurations. The aim of the article was to check the impact of social distance on the performance of security control lanes. Different ways of passenger flow across the lane were compared. The model was verified on actual data. The results obtained indicate that it is better to use lanes with a dedicated service area for each passenger on Entry Area than a free flow along the lane. This knowledge is extremely important for security checkpoint designers. It will help ensure proper performance under normal conditions and limit performance losses under epidemic conditions. The results were also divided according to different structure of the passenger stream (percentage share of flags, lowcost and charter operations). The results showed that this has a significant impact on efficiency.

Highlights

• •3 different configurations of the security control lane have been analysed.
• •A simulation model was developed for 3 different passenger flow strategies.
• •The division between lowcost, charter and flag passengers has been applied.
• •The performance losses of lanes during the Covid-19 epidemic were checked.
• •Reconfiguration of the system has been suggested as a corrective action.

1. Introduction

Hardly anyone expected that the COVID-19 epidemic would have such a big impact on the functioning of the air transport system. Preliminary scientific research conducted by virologists (De Vos, 2020) has indicated the need to introduce a distance between people. In March 2020, when large European clusters of COVID-19 cases were identified, first restrictions on crossing borders were introduced, followed by international and intercontinental flights (e.g. Europe – USA). It has become clear that it was only a matter of time before further restrictions would be imposed on air traffic. However, no one expected that air traffic would be virtually stopped as it was reduced by more than 80% (ICAO, 2020). Before the outbreak of the epidemic, about 30,000 aircraft took off daily; this value was only about 2500 daily in March, April and May (ICAO, 2020).

Restoration of air traffic depends on several factors: government restrictions and guidelines on air traffic, demand for air services and ticket prices. However, a key aspect that airport managers and airline managers will have to face is how to ensure the safety of passengers and persuade them to use air transport again in an epidemic situation. There are general regulatory guidelines for airport passenger service (EASA, 2020). Mandatory temperature check for passengers at the entrance of the passenger terminal and appropriate distancing have been introduced.

One of the systems where hygiene and social distance are difficult to meet is security checkpoint. According to the research, this process is one of the more stressful service processes (Bezzerra and Gomes, 2015). In this situation, it is easy for a passenger as well as a security control operator to make a mistake and not meet epidemic requirements and contribute to the transmission of COVID-19. Maintaining proper distancing and hygiene rules (e.g. disinfection of hands as well as X-ray trays) is crucial for the safe implementation of the safety control process.

The infrastructure of the current security control systems (e.g. length of conveyors, number of technical devices) guaranteed adequate performance under the assumptions of no distancing and other epidemic requirements (Li et al., 2018). The application of social distance has resulted in significantly reduced passenger numbers in each area of the security control lane. Kierzkowski and Kisiel (2015a) made an analysis which directly showed that this factor has a key impact on reduction of system performance. Therefore, social distance has a significant impact on reducing the performance of the security control lane and this has also been proven in this article. Corrective actions must be put in place to maintain the high performance of security control lane in epidemic state. Two solutions may be introduced. First of these assumes that passengers will be forced to be at the airport much earlier. Then there is more time to handle them. But then it will not reduce the number of people in the queue, where the COVID-19 transmissions may occur. The second solution is to try to increase the performance of the system in a state of epidemic. And that's what this article deals with.

This article presents a simulation model which has been applied to analyse the impact of the application of social distance on the performance of the security control lane at the airport. This topic was taken up in order to establish a structure of security control lane that will be both efficient during normal operation and efficient in an epidemic. Such an analysis has not yet been done in literature, because there was no such demand. Now this subject is extremely important to the proper functioning of the airport.

Chapter 2 presents an overview of literature related to the subject under consideration. Chapter 3 contains a formal description of the security control lane model. The validation of the model are presented in Chapter 4. Simulation experiments and recommendations on the configuration of an airport security control lane in an epidemic situation were also ultimately presented as a scientific contribution in Chapter 5. The own configuration of the security control lane was developed and its performance was tested by simulation. Chapter 6 contains a summary.

2. State of the art

The literature overview was divided into two groups:

• -general overview of the methods and tools used to model various passenger service systems,
• -overview of the modelling of the security control system.

2.1. General overview

The general overview of the methods was to verify whether research studies were devoted to the analysis of the functioning of systems in a disrupted state. Airport processes modelling has a long history. However, the first models (Chamberlain and Micka, 1969; Smith and Murphy, 1968) were quickly identified as useless (Eilon and Mathewson, 1973). It can be seen that the primary focus was on modelling systems in terms of estimating their performance. An overview of such models was developed by Wu and Mengersen (2013). There, the history of modelling of service processes at airports can be successfully followed. In the aspect of this article it is important whether process disturbances have already been analysed. In particular, it is important to check whether work in epidemic conditions has already been taken into account.

Solak et al. (2009) proposed model that makes it possible to estimate the maximum passenger delay. The authors performed theoretical considerations on a simple model consisting of check-in and security control subsystems in order to verify the proposed method. It was then applied practically at the airport terminal in Atlanta. An analysis was carried out for the profiles of check-in arrivals at the service point and passenger service occurring in the hourly peak. The presented model is based on the performance of paths between successive points of service. In the aspect of an epidemic, it may be useful to estimate this indicator due to system disruption. However, this model did not consider an epidemic condition. Passengers did not keep a sufficient distance from each other.

Kobza and Jacobson (1996) presented An alternative solution suitable for conducting a wider spectrum of analyses. The model concerns arriving passengers' service. The assumptions of the model enable consideration of various scenarios, e.g. allocating appropriate resources to the number of passengers arriving on a given aircraft, dynamic relocation of resources according to specific strategies. This is a quasi-stochastic model. Some of the data is given by probability distributions matched on the basis of actual data from the airport in New York. Some of the processes are described by deterministic transition times between individual service subsystems. This model can therefore be useful in the aspect of epidemics. However, you will need to know how much the efficiency of individual processes will decrease. This data can then be updated in the model and the performance in the disturbed state can be checked.

On the basis of Kobza and Jacobson (1996), a similar model was developed, including check-in of passengers departing from a given airport. It is presented by Jim and Chang (1998). The model was extended with additional graph apexes including additional services, i.e. restaurants, information points, etc. The model implements the characteristics of service times in individual subsystems. Therefore, there are already models available that allow to reproduce the path of passenger movements in a microscopic view. This may enable the estimation of the most vulnerable zones for the spread of epidemic risks.

The dynamic allocation of checkpoints through the use of a stochastic simulation model was considered by Hsu et al. (2012). In this case, the function of the objective was to minimize the resources used, assuming that certain requirements regarding the waiting time of passengers for service were met. The model was used at an airport in Taiwan for China Airline. This model could be used to dynamically change the number of seats in order to minimize queues for flights that have more passengers. This will reduce contact between passengers in long queues. Bruno and Govense (2010) also see the possibility of improving the system in dynamic management. A mathematical model was developed and pre-verified. However, the paper does not provide details that show the scale of benefits obtained.

The work presented above shows that they have some potential to be applied in terms of epidemic condition. However, their aim was mainly to analyse performance in a state of normal system operation.

2.2. Modelling of security control system

Due to the possibility of implementing the security control process according to different procedures, using different control methods, studies on the analysis of the performance of this stage of passenger service mainly focuses on the development of models on a microscopic scale. Van Boekhold et al. (2014) present a simulation model, which was used to analyse the sensitivity of the security control process to changes in personnel performance, initial control, random alarm index, triggered alarm index and the number of luggage items. Leone (2002), on the basis of the completed simulation experiments, presents the relationship between the number of triggered alarms and the performance of the security checkpoint. These models can be useful if the control procedure changes due to an epidemic. If this affects the number of operators or the number of alerts, this model will estimate the change in performance. After all, in the history of aviation, security screening procedures have already been modified. This has also been analysed in scientific work. Leone and Liu (2003) estimated the actual performance of the hand luggage control proces after the introduction of regulations requiring the use of ETD control. The results are compared with the theoretical performance values of the equipment.

Li et al. (2018) used a computer simulation in order to compare six different structures of queuing passengers before security control. The Monte-Carlo analysis was carried out in the aspect of determining the structure with the highest performance. The analysis takes into account the factor whether the passenger has hand luggage determining the passenger service time. In addition, it was assumed that passengers can choose the queue according to three different rules: random, the shortest queue or and the shortest waiting time. As a result of the analysis, it was found that different passenger queuing structures were appropriate for different passenger preferences in terms of queue selection strategies. It is important that in terms of providing distance in a state of epidemic, it can be difficult to apply certain types of queues. This model could be useful to analyse this fact. However, in this case it might be better to use virtual queuing. Then the queuing system will be completely eliminated. De Lange et al. (2013) proposed to assign passengers a selected period of time during which they should report for security control. This allows passengers to stay outside the queue system while waiting for the security control process. A simulation experiment was conducted which, in addition to shortening the waiting time, also showed the possibility of limiting the resources necessary to perform the security control process.

The way passenger flow directly before and in the security control system also has a significant impact on the performance of the system. Kierzkowski and Kisiel (2015a) modelled passenger flow to compare two configuration variants of security lanes – single and double. Subsequently, in Kierzkowski and Kisiel (2015b) a simulation model was used to analyse the sensitivity of the size of passenger preparation and baggage reclaim areas to the performance of the security checkpoint for the double lane and, in Kierzkowski and Kisiel (2015c), for the single lane. These articles indicated that the capacity of individual zones of the security line is crucial. The epidemic, which introduced the need for social distance, reduced the capacity of these zones. This will significantly reduce the capacity of these lines. This is precisely the reason why research in this article has begun.

A complete review of the literature (Chapter 2) has shown that the impact of changes in handling procedures related to the epidemic condition has not been analysed so far. In particular, the impact of social distance on process characteristics has not been studied. In this article, this will be supplemented so that stakeholders can rely on proven knowledge when designing the security control structure. The aim of this article is to enable the planning of a security control structure that will minimize performance losses in an epidemic.

3. Structure of the security control lane simulation model

This chapter presents the structure of the simulation model. In chapter 3.1. general assumptions are presented, which relate to the parameters adopted to describe the capacity of the individual lane areas. In this article, a single lane of security control is considered. This means that this line consists of one WTMD (passenger screening) and one X-ray device (baggage screening). In addition, 2 ETDs (explosive trace detection) are used for passenger and baggage screening. However, for a single security control lane it is possible to organise the flow of passengers in different ways. Therefore Chapters 3.2 to 3.4 show which are analysed in this article.

3.1. General assumptions

Screening of passengers, at European airports, shall be carried out in accordance with EU legislation EC (2008), EU (2015). It may be carried out, inter alia, by a manual check, a metal detection device or a security scanner. However, baggage may be checked using a manual check or X-ray machine. In addition, the passenger and luggage are checked at random for traces of explosives. The screening lane that will be analysed in this article is in line with Fig. 1 . This structure of the system can be found at most European airports as it meets the requirements of EC (2008), EU (2015).

Fig. 1.

Structure of the analysed security control lane.

It is assumed that the structure of security control lines consists of 3 main areas:

• •Entry area (EA), in which the passenger prepares for the security check. The number of passengers that may simultaneously be in the zone is marked as EA _c,
• •inspection area (ozn. IA), where basic baggage inspection (x-ray screening) as well as basic (metal detection) and extended (manual and ETD)inspection) of the passenger is performed. The number of passengers that may simultaneously be in the area is indicated as IA _c,
• •exit area (ozn. EXA), where the passenger picks up the baggage after inspection or where an expanded baggage inspection (manual or ETD) is carried out. The number of passengers that may simultaneously be in the area is indicated as EXA _c,

Fig. 1 also indicates those indicators which represent similarly the physical size (length) of the lane. This is only to suggest that it is related to the capacity of these areas. In a state of epidemics, the capacity of individual areas is limited due to the need for adequate distance (D) between passengers. The greater the distance between the passengers, the larger the station must be to accommodate the same number of passengers. In this article the focus will be on the opposite situation. Specifically, for a given structure without a social distance, a distance (D) will be introduced and this will reduce the number of passengers in the areas. Therefore, at a later stage, the parametrisation of the lane through its capacity will be applied.

When the passenger is placed in the Entry Area, begins to count the baggage preparation time, which is described by the probability density function f (tEA). Only when this time has passed and the conditions described in chapters 3.2 to 3.4 are fulfilled does the passenger move to the Inspection Area. There, with probability pmcont the passenger is directed to an expanded inspection. The time for this inspection is tmcont and is defined by the probability density function f (tmcont). After completing the passenger inspection process, the passenger goes to the Collection Area, where can pick up his baggage after successfully completing baggage x-ray inspection. Baggage pick-up time is tEXA and is defined by the probability density function f (tEXA). The basic baggage inspection (x-ray) process is tcontBag and is defined by the probability density function f (tcontBag). However, if the baggage was assigned to secondary inspection with pmcontBag probability, then the extended control time tmcontBag is defined by the probability density function f (tmcontBag). And the passenger moves to the Secondary Inspection Area to collect baggage after the expanded inspection. After collecting the luggage, the passenger leaves the simulation model. The actual values of the described probability density functions will be described in chapter 4. Detailed model algorithms for different lane structures are described in chapter 3.2. - 3.4.

3.2. Queue-Queue based security control lane

The first and at the same time the basic structure of the security control line is Queue-Queue based security control lane (QQ lane). This structure has been named as the basic one because it is the main reference. The actual process characteristics for this structure are known and it will be the basis for the verification of the simulation model. The flow of passengers at this lane is shown in Fig. 2 .

Fig. 2.

Flow structure for QQ lane.

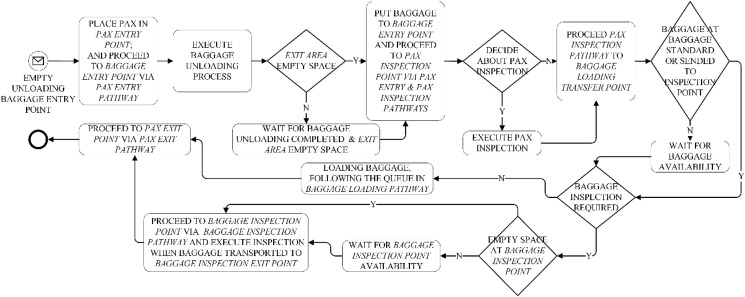
The process of passenger (PAX) and baggage control on QQ lane begins in the Entry Area. PAX is generated at Pax Entry Point when the current Entry Area capacity has not been reached. PAX takes the last available place in the PAX Entry Pathway. PAX moves towards the Pax Entry Pathway, depending on the process performed by the passengers who are ahead. It can therefore be said that PAX is in queue in the Entry Area. If PAX is ready for inspection, is in the first in queue (Baggage Unloading Transfer Point) and the capacity of the Exit Area is not currently reached, then PAX moves to the PAX Inspection Point. At the same time, the passenger's baggage is generated at Baggage Entry Point, where it begins its service process. The baggage handling process will be described further. The passenger path will now be continued.

At PAX Inspection Point it is decided whether an extended passenger inspection is necessary. If it is necessary, it is carried out there and only then the passenger moves on to the Baggage Loading Transfer Point. If not, the passenger is immediately moving to Baggage Loading Transfer Point. This is where the dependent event occurs. If the baggage has completed the basic inspection and is located in the Baggage Standard Exit Point, PAX begins to collect the baggage. PAX follows the Baggage Loading Pathway towards the queue of passengers who are served before him. Here, however, at any time (when PAX finishes picking up his baggage) he leaves the queue and via PAX Exit Pathway moves to PAX Exit Point, where he is removed from the model.

However, if the passenger's baggage has been placed in the Baggage Inspection Exit Point, then an extended baggage Inspection is required. Then PAX from Baggage Loading Transfer Point moves to Baggage Inspection Transfer Point via Baggage Inspection Pathway. Additional inspection and baggage collection is carried out there. After this process, the passenger moves through the PAX Exit Pathway to Pax Exit Point and is removed from the model.

Fig. 3 shows the process execution algorithm for a single PAX. The BPMN notation was used to show this algorithm.

Fig. 3.

Passenger movement algorithm for QQ lane.

The baggage check in this model structure starts when the passenger's baggage is queued at Baggage Entry Point. Then, depending on the previous baggage, it moves to X-Ray Inspection Point. There the basic inspection is carried out and it is decided whether an extended inspection is required. If so, your baggage will pass through Baggage Pathway to Baggage Inspection Exit Point. If not, the baggage will pass through the Baggage Pathway to Baggage Standard Exit Point. Baggage is transferred to the Baggage Loading Transfer Point or Baggage Inspection Transfer Point, as appropriate, in accordance with the Baggage Loading Transfer Point or Baggage Inspection Exit Point, in accordance with the Baggage Pathway's previously stated terms and conditions. The algorithm (in BPMN notation) of handling a single baggage is shown in Fig. 4 .

Fig. 4.

Baggage movement algorithm for QQ lane.

3.3. Dedicated Stand - queue based security control lane

Dedicated Stand - Queue based security control lane (DSQ lane) differs in passenger flow only in the Entry Area. The flow structure is shown in Fig. 5 . This is a structure that is also found at some airports. Passengers in Entry Area are preparing for control in dedicated, one-passenger stands. These stands are parallel. In the structure of QQ lane, the passengers have moved in Entry Area in FIFO strategy (first in first out). In the DSQ lane, the passenger who first completed the preparation process for control goes first out to the Inspection Area. This structure allows to overtake in the order of service.

Fig. 5.

Flow structure for DSQ lane.

When the current value of the entrance area capacity is not reached, a new passenger is generated at PAX Entry Point. The passenger moves through the PAX Entry Pathway to the first free Baggage Unloading Transfer Point. At this point the passenger prepares the baggage for control. Once the preparation is complete, when a seat is available at Exit Area and Pax Inspection Point, the passenger moves to it. The process continues according to QQ lane. Fig. 6 shows the process execution algorithm for a single PAX. The BPMN notation was used to show this algorithm.

Fig. 6.

Passenger movement algorithm for DSQ lane.

In the DSQ lane there is also a difference in baggage handling in the Entry Area. The baggage must be collected by the Operator and then moved by the Operator through the Baggage Pathway from Baggage Unloading Transfer Point to X-Ray Inspection Point. The baggage processing algorithm in the BPMN notation is shown in Fig. 7 .

Fig. 7.

Baggage movement algorithm for DSQ lane.

3.4. Dedicated Stand – Dedicated Stand based security control lane

When QQ and DSQ lane are compared, it is easier to maintain the required distance between passengers in the Entry Area for DSQ lane. This is simply the result of the structure of the technical system of the position. Each separate passenger preparation station may have a certain distance from each other. Therefore, this article proposes Dedicated Stand - Dedicated Stand based security control lane (DDS lane). This is a response to the demand arising from regulations that require a distance for the entire flow of passengers through the security control lane. It's hard to force passengers to keep their distance when they walk freely along the queue at the entrance and exit in QQ lane or at the exit in DSQ lane.

DDS lane is the same as DSQ in the Entry Area. However, it differs in Exit Area compared to DDS lane. The flow structure is shown in Fig. 8 . However, the passenger flow method in Exit Area DDS lane is similar to the passenger flow in Entry Area DSQ lane. After leaving Pax Inspection Point, PAX moves to Baggage Loading Transfer Point. There PAX is awaiting information on whether the baggage needs extended inspection. If so, PAX travels along the Baggage Inspection Pathway to the Baggage Inspection Transfer Point and there is an extended inspection with baggage claim.

Fig. 8.

Flow structure for DDS lane.

If extended baggage inspection is not required, the passenger awaits the baggage to arrive at the appropriate Baggage Standard Exit Point. Then the baggage claim process is carried out and the passenger leaves the model via PAX Exit Pathway.

The algorithm of the passenger flow path is presented in Fig. 9 . In turn, Fig. 10 presents the algorithm of baggage flow. Here, too, the baggage inspection process is different. An Exit Area should involve an operator who transfers luggage from X-Ray Inspection Point to the appropriate Baggage Standard Exit Point or Baggage Inspection Exit Point. The rest of the assumptions are the same as for DSQ lane.

Fig. 9.

Passenger movement algorithm for DDS lane.

Fig. 10.

Baggage movement algorithm for DDS lane.

4. Model validation

The model was validated on a sample of over 10,000 data collected as part of research conducted at Wrocław airport since 2013. As part of the study, all necessary data was collected that enabled the development of the input data presented in chapter 3.1. The data concerned the implementation times of individual activities as part of passenger service in the security control system. Table 1 presents data on the implementation of individual activities in the security control system.

Table 1.

Adapted probability density functions for the simulation model.

Activity	Probability density function	Validation (λ)
Baggage unloading, flag carrier	$f\left(t_{EA}^{FC}\right)=\sqrt{\frac{\mathrm{356,4}}{2\pi \cdot t_{EA}^{F{C}^3}}}\cdot exp\left(-\frac{\mathrm{356,4}\cdot {\left(t_{EA}^{FC}-\mathrm{32,3}\right)}^2}{2\cdot 32,3^2\cdot t_{EA}^{FC}}\right)$	0,67
Baggage unloading, lowcost carrier	$f\left(t_{EA}^{LC}\right)=\frac{\mathrm{1,27}}{\mathrm{38,3}}{\left(\frac{t_{EA}^{LC}-\mathrm{45,56}}{\mathrm{38,3}}\right)}^{\mathrm{0,27}}\cdot \text{exp}(-{\left(\frac{t_{EA}^{LC}-\mathrm{45,56}}{\mathrm{38,3}}\right)}^{\mathrm{1,27}})$	0,42
Baggage unloading, charter carrier	$f\left(t_{EA}^{FC}\right)=\frac{\text{exp}\left(-\mathrm{0,5}\cdot {\left(\frac{\ln \left(t_{EA}^{FC}-\mathrm{34,5}\right)-\mathrm{3,6}}{\mathrm{0,58}}\right)}^2\right)}{(t_{EA}^{FC}-\mathrm{3,6})\cdot \mathrm{0,58}\cdot \sqrt{2\pi }}$	0,37
Baggage collection, flag carrier	$f\left(t_{EXA}^{FC}\right)=\frac{\mathrm{2,79}}{\mathrm{26,9}}{\left(\frac{t_{EXA}^{FC}-\mathrm{14,54}}{\mathrm{26,9}}\right)}^{\mathrm{1,79}}\cdot \text{exp}(-{\left(\frac{t_{EXA}^{FC}-\mathrm{14,54}}{\mathrm{26,9}}\right)}^{\mathrm{2,79}})$	0,56
Baggage collection, lowcost carrier	$f\left(t_{EXA}^{LC}\right)=\sqrt{\frac{875}{2\pi \cdot t_{EXA}^{F{C}^3}}}\cdot exp\left(-\frac{875\cdot {\left(t_{EA}^{LC}-108\right)}^2}{2\cdot {108}^2\cdot t_{EA}^{FC}}\right)$	0,34
Baggage collection, charter carrier	$f\left(t_{EXA}^{CC}\right)=\frac{\mathrm{1,31}}{\mathrm{52,6}}{\left(\frac{t_{EXA}^{CC}-\mathrm{63,9}}{\mathrm{52,6}}\right)}^{\mathrm{0,31}}\cdot \text{exp}(-{\left(\frac{t_{EXA}^{CC}-\mathrm{63,9}}{\mathrm{52,6}}\right)}^{\mathrm{1,31}})$	0,62
Passenger inspection	$f\left(t_{mcontr}\right)=\frac{\text{exp}\left(-\mathrm{0,5}\cdot {\left(\frac{\ln \left(t_{EA}^{FC}-\mathrm{11,8}\right)-\mathrm{2,96}}{\mathrm{0,27}}\right)}^2\right)}{(t_{EA}^{FC}-\mathrm{2,96})\cdot \mathrm{0,27}\cdot \sqrt{2\pi }}$	0,23
Baggage x-ray inspection	$f\left(t_{contBag}\right)=\frac{\mathrm{1,62}}{\mathrm{14,08}}{\left(\frac{t_{contBag}}{\mathrm{14,08}}\right)}^{\mathrm{0,62}}\cdot \text{exp}(-{\left(\frac{t_{contBag}}{\mathrm{14,08}}\right)}^{\mathrm{1,62}})$	0,44
Baggage extended inspection	$f\left(t_{mcontBAG}\right)=\frac{\text{exp}(-\mathrm{0,5}\cdot {\left(\frac{t_{mcontBAG}-\mathrm{22,62}}{\mathrm{3,11}}\right)}^2)}{\mathrm{3,11}\cdot \sqrt{2\pi }}$	0,47

Model validation was carried out in two ways. First, the correctness of matching of individual probability density functions was checked. Then this data was entered into the simulation model. 100 simulations were carried out for QQ lane, because such lane is just at Airport Wroclaw. Area capacities are 6 PAX in the Entry Area and 4 PAX in the Exit Area. The distribution for passengers' leaving Pax Inspection Point times was compared from simulation data and real data. The Kolmogorov-Smirnov test was used here, which is suitable for simulation models that are based on discrete events (Belli et al., 2012). The critical value was 1.17 and was less than the critical value 1.36. This confirms that the model is working properly for significance level 0.05. Also, all probability density functions have a lower critical value (Table 1). There also the same test was used.

During the analysis of the data, it was noted that functions are significantly different for different air carriers. As each airport may have a different structure of air operations, it was decided to make the resulting data dependent also on the structure of the passenger stream. Therefore, the data in Table 1 presents the functions for flags, lowcost and charter carriers. The likelihood that a passenger pmcont and baggage pmcontBAG will be referred to an extended inspection has been deliberately concealed. This is sensitive safety data and it is preferable not to make it publicly available.

5. Simulation experiments

In the simulation model, the effect of applying the distance between passengers to the actual position was checked. Experiment 1 is a real QQ lane with capacities of 6 EA and 4 EXA. Subsequently, the passengers distance introduced (D = 2m) resulted in a loss of 5 EA and 3 EXA (Experiment 2), while the lane is still the same size. Then, in Experiment 3, it was checked what would happen if the airport changed its flow structure to DSQ lane during the epidemic. It was then also checked whether the DSQ lane configuration proposed by the authors will maintain performance (Experiment 4). Because it makes it possible to manage the distance between passengers better.

For each experiment, it was tested what would happen if it turned out that after the epidemic only flags or lowcost or charter carriers would resume operations. It also checked what would happen if the streams were to mix. Several different passenger stream structures were selected and divided into 7 different scenarios (Table 2 ). The overall results are presented in Table 3 . The minimum, maximum, average, quartile 1 and quartile 3 for the hourly performance of the lane were collected from the simulation model.

Table 2.

Percentages of the different passengers groups in the passenger flow.

Scenario No.	Flag pax	Low cost pax	Charter pax
1	100%	0%	0%
2	0%	100%	0%
3	0%	0%	100%
4	50%	50%	0%
5	0%	50%	50%
6	50%	0%	50%
7	33%	34%	33%

Table 3.

Performance results of the security control station depending on the experiment and scenario.

Experiment	Scenario	EAc	EXAc	Configuration	Średnia [pax/h]	Max [pax/h]	Min [pax/h]	Q1 [pax/h]	Q3 [pax/h]
1	1	6	4	QQ lane	285	270	300	281	289
	2				132	118	140	128	135
	3				127	115	137	124	130
	4				175	158	190	169	180
	5				129	121	140	126	133
	6				171	150	192	167	176
	7				155	139	169	151	160
2	1	5	3	QQ lane	222	213	234	219	226
	2				100	87	114	97	102
	3				97	87	106	95	100
	4				134	120	148	130	139
	5				98	90	109	96	101
	6				133	115	151	128	136
	7				119	106	137	115	123
3	1	5	3	DSQ lane	226	215	237	222	228
	2				103	92	116	99	105
	3				99	89	112	96	103
	4				140	125	162	134	145
	5				101	92	113	98	104
	6				138	123	153	135	141
	7				123	106	136	119	127
4	1	5	3	DDS lane	173	163	186	170	176
	2				88	80	99	86	91
	3				86	79	98	83	89
	4				118	104	131	115	121
	5				88	78	100	85	91
	6				114	99	125	111	118
	7				104	92	115	101	107

In this chapter, a sensitivity analysis was later carried out to see if the extension of the lane will significantly affect process performance. In Scenario 5, the capacity was increased by 1 passenger in the exit area. QQ, DSQ and DDS lane configurations were re-analysed. In scenario 6, capacity was increased by 1 passenger in the entry area. QQ, DSQ and DDS lane configurations were re-analysed. The results are in Table 4 .

Table 4.

Sensitivity analysis of security control lane on areas capacity change.

Experiment	Scenario	EAc	EXAc	Model stanowiska	Średnia [pax/h]	Max [pax/h]	Min [pax/h]	Q1 [pax/h]	Q3 [pax/h]
5	1	5	4	QQ lane	284	274	296	281	288
	2				129	120	140	127	132
	3				126	114	137	124	129
	4				167	154	184	163	172
	5				127	117	136	124	131
	6				165	143	179	162	170
	7				150	139	164	147	155
	1	5	4	DSQ lane	272	263	284	269	276
	2				131	119	146	128	135
	3				128	117	141	125	133
	4				175	158	189	171	180
	5				129	118	140	126	133
	6				174	156	194	169	179
	7				155	138	172	152	160
	1	5	4	DDS lane	228	217	240	225	232
	2				119	108	132	116	123
	3				114	105	128	112	118
	4				156	141	170	153	160
	5				117	105	129	114	120
	6				153	141	172	150	158
	7				138	124	153	135	142
6	1	6	3	QQ lane	222	212	233	219	226
	2				100	89	115	97	104
	3				97	87	108	94	101
	4				136	120	151	132	141
	5				98	88	109	96	102
	6				132	112	147	127	137
	7				119	108	134	115	123
	1	6	3	DSQ lane	227	215	238	224	231
	2				101	87	112	99	105
	3				98	90	115	95	102
	4				140	127	155	135	144
	5				100	89	111	98	103
	6				138	123	153	134	143
	7				122	110	142	119	126
	1	6	3	DDS lane	173	163	180	170	176
	2				89	78	100	86	92
	3				85	73	96	83	88
	4				117	105	139	114	121
	5				87	78	97	85	91
	6				115	103	137	112	118
	7				104	95	117	101	109

As shown by the studies carried out (Table 3), the application of the restrictions on the operation of the screening station related to passenger distance has a significant impact on performance. QQ, DSQ and DDS lied through the distance between passengers give significantly different results. The differences between the minimum and maximum values and the average value are similar in all cases. QQ lane and DSQ lane give significantly better results than DDS lane. It should be noted that in the case of distance requirements, the performance of the actual system (Experiment 1) decreases by about 20% (Experiment 2, 3). The airport's passenger service manager should take this aspect into account as a decrease in capacity may cause the queues to get longer. The consequence of this phenomenon may be that passengers are late at the gate. From the conducted research it is recommended to use the system configuration according to the DSQ model in the compromise between system performance and meeting the requirements of social distance at Entry Area. However, passengers should be instructed to avoid contact in the Exit Area as well.

To make contact between passengers more impossible, DDS configuration is recommended. This, however, will limit the performance of the system and stakeholders need to have a performance reserve or expand areas of security control lanes. It is then important to know which zone needs to be extended in order to achieve greater efficiency gains. Therefore, a sensitivity analysis was performed and one place each in the Entry Area (Experiment 5) and Exit Area (Experiment 6) was increased. The results are presented in Table 4.

As shown by the studies carried out (Table 4), if there is a possibility to increase one of the areas, it is more beneficial to increase the Exit Area. Introducing a QQ lane and increasing the Exit Area capacity to 4 (Experiment 5) results in a similar performance with the original system (Experiment 1). Experiment 6 results in a 5% lower performance than the Experiment 1. As can be seen, the minimum and maximum values in relation to the average value are outliers. Processes can therefore be qualified as stable with a small standard deviation. It should also be noted that the performance of traditional carrier passenger stations is twice as high as that of lowcost and chartered passenger flow. As can also be seen, passengers of low-cost and traditional carriers behave similarly in the screening system. The performance of the stations for any configuration is similar.

It should also be noted, for the whole, that the performance of the lanes varies according to the type of passenger stream. It is important to note that the stakeholders cannot rely on someone else's research work, if there is a different passenger flow in stakeholders system. Otherwise, it may turn out that stakeholder will build a system that does not achieve the appropriate performance. The research has shown that each case can be individual and it is necessary to do a dedicated analysis, for a given stream of passengers. For example, the performance for Scenario 1 is twice as high as for Scenario 2 or 3. This shows that passengers who travel with flag carrier go much faster. On the other hand, passengers of lowcost and charter carriers behave similarly in the security control system.

6. Summary

It is unquestionable that the state of the COVID-19 epidemic is creating a significant mess in the management of the security control system. It results directly in a very high loss of performance. This is obviously influenced by the need to ensure a distance between passengers. This reduces the capacity of individual areas of the security control lane. And when the number of passengers using the lane at the same time is reduced, its performance drops dramatically. In order to minimize the impact or to prevent such a deterioration of the system, different configurations of passenger flow through security control lane were analysed.

The advantages and disadvantages of the different configurations of the lanes were indicated and their performance was determined. The results are very interesting as two pieces of advice can be suggested. If the stakeholder does not have space in his system to expand the lanes, he should use the DSQ lane configuration. Then the expected performance will be achieved, but this will only improve the distance in the Entry Area. In the Exit Area stakeholder will have to constantly supervise the movement of the passengers and give them tips for keeping a distance. However, if the stakeholder has space to expand the system, it is advisable to focus on expanding the Exit Area and adapting system to DDS lane. The results also showed the importance of taking into account the structure of the passenger stream. Each airport should conduct an analysis based on its own flight schedule. This will ensure the best results from the simulation model.

Further work will be aimed at developing an even more accurate model and at checking whether the behavior of passengers during an epidemic affects the duration of individual operations. In addition, consideration will be given to the extension of passenger inspection to include the possibility of using passenger neutralization devices (disinfection gates) to propose more comprehensive conditions for handling epidemics. An analysis of the risk of passengers passing through the security control lane depending on the configuration will be carried out taking into account the epidemic conditions.

CRediT authorship contribution statement

Artur Kierzkowski: Conceptualization, Methodology, Validation, Writing - original draft, Writing - review & editing. Tomasz Kisiel: Software, Formal analysis, Writing - original draft, Writing - review & editing.