Global stability and cost-effectiveness analysis of COVID-19 considering the impact of the environment: using data from Ghana

Highlights

• •COVID-19 spread dynamics with environmental compartment is proposed.
• •Global stability of the disease-free and endemic equilibria was obtain using Lyapunov’s function.
• •Global sensitivity analysis was studied.
• •A cost-effectiveness analysis presented.

Abstract

COVID-19 potentially threatens the lives and livelihood of people all over the world. The disease is presently a major health concern in Ghana and the rest of the world. Although, human to human transmission dynamics has been established, not much research is done on the dynamics of the virus in the environment and the role human play by releasing the virus into the environment. Therefore, investigating the human-environment-human by use of mathematical analysis and optimal control theory is relatively necessary. The dynamics of COVID-19 for this study is segregated into compartments as: Susceptible (S), Exposed (E), Asymptomatic (A), Symptomatic (I), Recovered (R) and the Virus in the environment/surfaces (V). The basic reproduction number ${\mathcal{R}}_0$ without controls is computed. The application of Lyapunov’s function is used to analyse the global stability of the proposed model. We fit the model to real data from Ghana in the time window 12th March 2020 to 7th May 2020, with the aid of python programming language using the least-squares method. The average basic reproduction number without controls, ${\mathcal{R}}_0^a,$ is approximately 2.68. An optimal control is formulated based on the sensitivity analysis. Numerical simulation of the model is also done to verify the analytic results. The admissible control set such as: effective testing and quarantine when boarders are opened, the usage of masks and face shields through media education, cleaning of surfaces with home-based detergents, practising proper cough etiquette and fumigating commercial areas; health centers is simulated in MATLAB. We used forward-backward sweep Runge-Kutta scheme which gave interesting results in the main text, for example, the cost-effectiveness analysis shows that, Strategy 4 (safety measures adopted by the asymptomatic and symptomatic individuals such as practicing proper coughing etiquette by maintaining a distance, covering coughs and sneezes with disposable tissues or clothing and washing of hands after coughing or sneezing) is the most cost-effective strategy among all the six control intervention strategies under consideration.

1. Introduction

The COVID-19 is a communicable disease which is caused by coronavirus of a new kind. As of 21st January 2020, only 4 countries namely: China (278 cases), Republic of Korea (1 case), Thailand (2 cases) and Japan (1 case) were affected with a total of 282 confirmed cases including 6 deaths [1]. The United States recorded its first case on 23rd January 2020 as a result of an exported case from China [2]. This amounted to a total of 581 confirmed cases. France and Australia also reported 3 confirmed cases each while China’s confirmed cases were exponentially increasing summing the total confirmed cases to 1320 as of 25th January [3]. Germany joined the race on 28th January with reported case of 1 [4]. Italy also reported its first 2 confirmed cases on 31st January 2020 contributing to 9826 globally confirmed cases [5]. The first-time a Health Care Worker was diagnosed with coronavirus happened in France on 1st February 2020. Spain and the United Kingdom reported their first confirmed cases on the same day each with 1 and 2 cases respectively [6]. Philippines recorded the first death outside China on 1st February 2020 [7]. The first African country to report a confirmed case was Egypt on 14th February 2020 [8]. The statistics as of 19th June, 2020, 06:25 GMT showed that, there were 8,586,115 confirmed cases, 456,458 confirmed deaths and 4,535,245, recovered cases globally [9]. Ghana recorded its first confirmed cases on 12th March, 2020 [10]. These were 2 imported cases from Norway and Turkey. Prior to the identification of these cases, effective measures such as testing and public education had been put in place to create awareness which demonstrated the country’s preparedness to face this pandemic [11]. Earlier measures after the first incidence included; a ban on individuals from countries which had recorded over 200 cases and 14 days mandatory quarantine for all persons who were allowed to enter its territory. Also, as part of the early measures against the spread, schools, conferences, social gatherings, sporting activities and political rallies were all halted as enhanced measures against the spread of COVID-19 [12]. On 30th March 2020, Accra and Kumasi which are the major cities in the country experienced lockdown together with some internal travel restrictions. Ghana had recorded 12,929, confirmed cases including 66 deaths and 4,468 recovered with 8,395 active individuals as of 18th June, 2020 [11]. It is important to note that these deaths were also attributed to risk factors such as hypertension, diabetes and other cardiovascular diseases [11]. In Fig. 1 a and 1b we show the daily reported cases per day as of 18th June 2020. Since the outbreak of COVID-19, many mathematical models have provided some insightful ideas to health authorities on how best to control the disease spread. For example, see the works of [13], [14], [15], [16], [17], [18], [19], [20], [21]. Asamoah et al. [22] studied an (SEAQI_sHRRADS_p) model to describe COVID-19 human-human transmission dynamics for Ghana and Egypt; and obtained various epidemiological parameter values. They suggested that: a continuous increase in the rate of diagnoses, the rate of quarantine through doubling enhanced contact tracing, and stringent safety measures in hospitals (and/or isolation centres); with a constant supply of effective personal protective equipment’s (PPEs) will help reduce the control reproduction number ${\mathcal{R}}_c,$ to less than unity as the lockdown measures are been lifted. Adding natural recovery to their model, they showed that an increase in natural recovery from the asymptomatic stage reduces the control reproduction number. They also noticed that the choice of a force of infection influences the control reproduction number. Although, human to human mathematical analysis has been established, not much mathematical analysis is done on the dynamics of the virus in the environment and the role human play by releasing the viruses into the environment. The mathematical model that studied the role of the environment focused on the seafood market in Wuhan and used Atangana-Bleanu-Caputo operators for their investigation without the use of optimal control model [23] (see also [24]). The work by Zhang et al. [25] discussed the airborne transmission as the main route for the spread of COVID-19. Ferretti et al. [26], also quantified SARS-CoV-2 transmission dynamics and noticed that, 6% of the secondary outcomes can be linked to environmental transmission. They also noted that, presymptomatic transmissions can sufficiently maintain the epidemic growth. Hence, we want to study the mathematical dynamics of viral load in the environment and the use of non-pharmaceutical measures together with cost-effectiveness analysis. Thus, by developing a mathematical and optimal control model for human-environment-human transmission dynamics. Despite that other optimal control model on COVID-19 have been studied (see for example [27], [28], [29], [30], [31], [32]). But, to the best of our knowledge, there exists no compartmental model which focuses on environment to human dynamics of COVID-19 in Ghana together with cost-effectiveness analysis. Hence, this paper will contribute to the existing knowledge on the spread of COVID-19 and the dynamical influence of the virus in the environment through human activities in Ghana. It will also assist health care authorities and the government to see the optimal trajectory of the implementation of non-pharmaceutical interventions.

Fig. 1.

Daily Infected trend and bar plot for confirmed cases for Ghana.

The rest of this paper is partition as follows: Section 2 contains the model formulation, definition of model parameters, invariant region, boundedness, equilibrium points and stability analysis. Section 3 contains the model fit, parameter estimation, and sensitivity analysis. Section 4 contains optimal control problem and cost-effectiveness analysis. In Section 5, we give concluding remarks and recommendations.

2. Model formulation and analysis

This section discusses the transmission dynamics of COVID-19, model analysis, properties and the equilibrium points, computation for the basic reproductive number and the stability analysis. In dealing with the dynamics of COVID-19 so as to implement the necessary control measures, we consider the compartments; Susceptible (S), Exposed/pre asymptomatic (E), Asymptomatic (A), Symptomatic (I), Recovery (R) and the Virus in the Environment, thus, on surfaces (V). As a deterministic model, we suppose that, the compartments depend on time. The total population of individuals, N(t) at time t is given as; $N\left(t\right)=S\left(t\right)+E\left(t\right)+A\left(t\right)+I\left(t\right)+R\left(t\right)$. We also consider that all parameters are positive and it is only the I compartment which experiences disease induced death at a rate, α. The overall force of infection is given as $\lambda =S[\beta (\eta A+I)+{\beta }_{1}V]$. The model further assumes that, no exposed individual transmits the disease. The proportion of those in E class into both A and I classes is given as $k_2(1-\gamma )E$ and k ₁ γE respectively. Similarly, individuals recovering from the A class is $v_2(1-\varphi )A$ and those joining the I class from the A compartment is v ₁ ϕA. Though, not much had been said with regards to the possibility of the recovered individuals joining the susceptible population. All the same we included it so to ascertain the impact of short and long-term immunity on the dynamics of COVID-19, denoted as ρ, where ρ ≥ 0. Table 1 further explains the individual parameters.

Table 1.

Parameters with their interpretation for model (1).

Parameter	Description
Λ	Recruitment rate
λ	Force of infection
ω	Natural death rate
β	Transmission rate
β1	Transmission rate from the environment
η	Relative transmissibility of asymptomatic individuals
γ	Proportion of individuals who are timely diagnosis
k1	Progression rate from exposed to the symptomatic (severely infected) class
k2	Progression rate from exposed to the asymptomatic class
α	Disease induced death rate
ϕ	Proportion of asymptomatic patients who later move to the symptomatic (severely infected) class
v1	Progression from asymptomatic to the symptomatic (severely infected) class
v2	Progression from asymptomatic to the recovered class
ϵ	The rate at which symptomatic (severely infected) patients recovers
ρ	The rate at which the recovered individuals join the susceptible class
τ1	Natural decay rate of virus from the environment (Surfaces)
m1	The rate of viral release into the environment by asymptomatic patients
m2	The rate at which symptomatic patients release virus into the environment

The differential equations of the COVID-19 model in Fig. 2 are given below as;

$$\begin{array}{cc}\hfill \frac{dS}{dt}& =\Lambda -\omega S-\beta (IS+\eta AS)-{\beta }_{1}VS+\rho R,\hfill \\ \hfill \frac{dE}{dt}& =\beta (IS+\eta AS)+{\beta }_{1}VS-k_2(1-\gamma )E-k_1\gamma E-\omega E,\hfill \\ \hfill \frac{dA}{dt}& =k_2(1-\gamma )E-\omega A-v_1\varphi A-v_2(1-\varphi )A,\hfill \\ \hfill \frac{dI}{dt}& =k_1\gamma E+v_1\varphi A-ϵI-(\omega +\alpha )I,\hfill \\ \hfill \frac{dR}{dt}& =v_2(1-\varphi )A+ϵI-\rho R-\omega R,\hfill \\ \hfill \frac{dV}{dt}& =m_{1}A+m_{2}I-{\tau }_{1}V,\hfill \end{array}$$ (1)

given that S ≥ 0, E ≥ 0, A ≥ 0, I ≥ 0, R ≥ 0 and V ≥ 0.

Fig. 2.

A model diagram of COVID-19 Dynamics.

2.1. Analysis on the model

We simplify Eq. (1) to get the total differential equation as;

$$\begin{array}{c}\hfill \{\begin{array}{cc}\frac{dN}{dt}\hfill & =\Lambda -\omega N-\alpha I,\hfill \\ \frac{dV}{dt}\hfill & =m_{1}A+m_{2}I-{\tau }_{1}V,\hfill \end{array}\end{array}$$ (2)

where $N=S+E+A+I+R$.

Theorem 1

The solution set {S(t), E(t), A(t), I(t), R(t), V(t)} is positive whenever the parameters are non-negative such that the initial conditions are also given as

$$\left\{S\right(0)\ge 0,E(0)\ge 0,A(0)\ge 0,I(0)\ge 0,R(0)\ge 0,V(0)\ge 0\},$$

The proof of Theorem 1 can be obtained using the procedures presented in [33] , as shown below.

Proof

We let $Y={(S,E,A,I,R,V)}^{\mathcal{T}}$ and $K_0=\beta I,K_1=\beta A,K_2={\beta }_{1}V$ where $\mathcal{T}$ is transposition, then our differential Eq. (1) can be rewritten in a matrix form as $\frac{dY}{dt}=MY+M_1,$ where

$$\begin{array}{cc}& M=\left(\begin{array}{cccccc}-(\omega +K_0+\eta K_1+K_2)& 0& 0& 0& \rho & 0\\ (K_0+\eta K_1+K_2)& -(K_2(1-\gamma )+k_1\gamma +\omega )& 0& 0& 0& 0\\ 0& k_2(1-\gamma )& -(\omega +v_1\varphi +v_2(1-\gamma ))& 0& 0& 0\\ 0& k_1\gamma & v_1\varphi & -(ϵ+\omega +\alpha )& 0& 0\\ 0& 0& v_2(1-\varphi )& ϵ& -(\rho +\omega )& 0\\ 0& 0& m_1& m_2& 0& -{\tau }_1\end{array}\right),\hfill \\ & M_1=\left(\begin{array}{c}\Lambda \\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right).\hfill \end{array}$$

Now, using the third equation in model (1), thus

$$\frac{dA}{dt}=k_2(1-\gamma )E-\omega A-v_1\varphi A-v_2(1-\varphi )A,$$

and deploying the method of integration factor and change of variables [33], yields

$$\begin{array}{ccc}\hfill A\left(t\right)& =& A\left(0\right)e^{-(\omega +v_1\varphi +v_2(1-\varphi ))t}+e^{-(\omega +v_1\varphi +v_2(1-\varphi ))t}{k}_2(1-\gamma )\hfill \\ & & \times {\int }_0^{t}E\left(s\right)e^{-(\omega +v_1\varphi +v_2(1-\varphi ))s}ds,\hfill \\ & =& e^{-(\omega +v_1\varphi +v_2(1-\varphi ))t}[A\left(0\right)+k_2(1-\gamma ){\int }_0^{t}E\left(s\right)e^{-(\omega +v_1\varphi +v_2(1-\varphi ))s}ds].\hfill \end{array}$$

Next, we consider the fourth, fifth, sixth equation of model (1) and using the same above process, we have

$$I\left(t\right)=e^{-(ϵ+\omega +\alpha )t}[I\left(0\right)+v_1\varphi {\int }_0^{t}A\left(s\right)e^{-(ϵ+\omega +\alpha )s}ds+k_1\gamma {\int }_0^{t}E\left(s\right)e^{-(ϵ+\omega +\alpha )s}ds].$$

$$R\left(t\right)=e^{-(\rho +\omega )t}[R\left(0\right)+v_2(1-\varphi ){\int }_0^{t}A\left(s\right)e^{-(\rho +\omega )s}ds+ϵ{\int }_0^{t}I\left(s\right)e^{-(\rho +\omega )s}ds].$$

$$V\left(t\right)=e^{-\left({\tau }_1\right)t}[V\left(0\right)+m_1{\int }_0^{t}A\left(s\right)e^{-\left({\tau }_1\right)s}ds+m_2{\int }_0^{t}I\left(s\right)e^{-\left({\tau }_1\right)s}ds].$$

Hence, from [34] and [35], we see that $\frac{dA}{dt}{|}_{t=t_0}\ge 0,$ $\frac{dI}{dt}{|}_{t=t_0}\ge 0,$ $\frac{dR}{dt}{|}_{t=t_0}\ge 0,$ $\frac{dV}{dt}{|}_{t=t_0}\ge 0,$ and $\frac{dE}{dt}{|}_{t=t_0}\ge 0,$ provided $E\left(t_0\right)=0,$ with same ideas being valid for S(t), this guarantees that the state variable remain positive during the entire scope of the study [33]. Grounded on this, we can say that matrix M has all its off diagonal entries to be non-negative and that matrix M ₁ ≥ 0, which proves the properties of Metzler matrix [33], [36]. Therefore it implies that model (1) is positively invariant in ${\mathbb{R}}_{+}^6$ [33]. For alternative proof to the above assertion see Atangana et al. [37]. □

2.2. Boundedness

Theorem 2

The model of the system in Eq. (1) has solutions bounded within invariant region, $\Omega \in {\mathbb{R}}^6$ written as

$$\Omega =\{(S,E,A,I,R,V)\in {\mathbb{R}}_{+}^6:N\left(t\right)\le \frac{\Lambda }{\omega },V\left(t\right)\le \frac{\Lambda m}{\omega {\tau }_1}\}.$$

where $m=(m_1+m_2).$

Proof

From the first equation of (2) we have

$$\frac{dN}{dt}\le -\omega N+\Lambda .$$ (3)

Now, take M ₂ to be a solution which is unique to the initial value problem

$$\{\begin{array}{c}\frac{d}{dt}{M}_2\left(t\right)=\Lambda -\omega M_2\left(t\right)\text{for}t>0,\hfill \\ M_2\left(0\right)=N\left(0\right).\hfill \end{array}$$ (4)

Which when solved gives

$$M_2\left(t\right)=\frac{\Lambda }{\omega }(1-e^{(-\omega t)})+N\left(0\right)e^{(-\omega t)}.$$

Hence, by the comparison principle (see for instant Theorem 5 of [38]), it accompanies that

$$N\left(t\right)\le \frac{\Lambda }{\omega }(1-e^{(-\omega t)})+N\left(0\right)e^{(-\omega t)}.$$ (5)

Also from the second equation of (2), we let $m=(m_1+m_2)$ with the assumption that $0<A+I\le \frac{\Lambda }{\omega }$. Then,

$$\frac{\mathit{dV}}{\mathit{dt}}\le \frac{m\Lambda }{\omega }-{\tau }_{1}V.$$ (6)

Now, let M ₃ to be a solution which is unique to the initial value problem

$$\{\begin{array}{c}\frac{d}{dt}{M}_3\left(t\right)=\frac{m\Lambda }{\omega }-{\tau }_{1}V\text{for}t>0,\hfill \\ M_3\left(0\right)=V\left(0\right).\hfill \end{array}$$ (7)

Which when solved gives

$$M_3\left(t\right)=\frac{m\Lambda }{\omega }(1-e^{(-{\tau }_{1}t)})+V\left(0\right)e^{(-\tau t)},$$

and, by the comparison principle (see for instant Theorem 5 of [38]), it accompanies that

$$V\left(t\right)\le \frac{m\Lambda }{\omega }(1-e^{(-\tau t)})+V\left(0\right)e^{(-\tau t)}.$$ (8)

From (5) and (8) it connotes that, all the possible solution sets of the state variables S, E, A, I, R, V is bounded and, by the blow-up phenomena, hence the solutions exist and is defined for all t ≥ 0 [38]. Furthermore, for $t\to +\infty ,$ we get

$$\begin{array}{cc}\hfill 0& \le N\left(t\right)\le \frac{\Lambda }{\omega },\hfill \\ \hfill 0& \le V\left(t\right)\le \frac{m\Lambda }{\omega {\tau }_1}.\hfill \end{array}$$

This guarantees that, all the possible solution sets of the state variables S, E, A, I, R, V are contained in Ω making the model both mathematically and epidemiologically well posed (thus, model (1) is positively invariant). □

2.3. Disease free equilibrium point, $\mathcal{E}$

Here, we first focus on equilibrium points when there is no disease in the system. Considering Eq. (1), we put $E=A=I=R=V=0$. This indicates that, there is no disease in the system at this stage. Therefore, solving for the stationary points, we have $\mathcal{E}=(S^{*},0,0,0,0,0)$ where $S^{*}=\frac{\Lambda }{\omega }.$

2.4. Basic reproductive number, ${\mathcal{R}}_0$

For the ${\mathcal{R}}_0$, we use the concept of the next generation approach. Here, we seek to find the average number of new infections given that an infected individual is introduced into the population under study [39]. We let G be the next generation matrix which consists of f_i(x), $v_i^{+}\left(x\right)$ and $v_i^{-}\left(x\right),$ $i=1,2,\dots ,n\in \mathbb{N}$; where f_i(x) is the rate at which a new infection occurs in compartment i. Also, $v_i^{+}$ and $v_i^{-}$ are the rate of immigration into compartment i and the rate at which new individuals are transferred from compartment i respectively. We note that, all the functions are continuously differentiable at least twice [39]. Let

$$F=\left[\frac{\partial f_i\left(x_0\right)}{\partial x_i}\right]\text{and}V=\left[\frac{\partial V_i\left(x_0\right)}{\partial x_i\left(x_0\right)}\right],$$

where $V_i=v_i^{-}\left(x\right)-v_i^{+}\left(x\right)$.

Now the next generation matrix is defined as;

$$G=F{V}^{-1}.$$

Hence, the ${\mathcal{R}}_0$ is given as the maximum absolute eigenvalue of the next generation matrix (G) given that, σ contains all the eigenvalues of G. This eigenvalue is known as the spectral radius (ρ). This is represented as

$$\rho \left(G\right)=\text{sup}\left\{\right|\lambda |:\lambda \in \sigma (G\left)\right\}.$$

Among the infected classes (E, A, I, V), we have f_i as

$$\begin{array}{c}\hfill f_i=\left[\begin{array}{c}\beta (AS+IS)+{\beta }_{1}VS\\ 0\\ 0\\ 0\end{array}\right].\end{array}$$

Finding the Jacobian of the matrix f_i gives

$$\begin{array}{cc}\hfill F=\left[\begin{array}{cccc}0& \eta \beta S& \beta S& {\beta }_{1}S\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]& =\left[\begin{array}{cccc}0& \eta \beta \frac{\Lambda }{\omega }& \beta \frac{\Lambda }{\omega }& {\beta }_1\frac{\Lambda }{\omega }\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right].\hfill \end{array}$$

Considering the same compartments $(E,A,I,V)$, we get the matrix V as

$$\begin{array}{c}\hfill V_i=\left[\begin{array}{c}{k}_2(1-\gamma )E+k_1\gamma E+\omega E\\ -k_2(1-\gamma )E+\omega A+v_1\varphi A+v_2(1-\varphi )A\\ -k_1\gamma E-v_1\varphi A+ϵI+(\omega +\alpha )I\\ -m_{1}A-m_{2}I+{\tau }_{1}V\end{array}\right].\end{array}$$

Finding the Jacobian matrix of V_i gives

$$\begin{array}{c}\hfill {\displaystyle V=\left[\begin{array}{cccc}\gamma k_1+k_2(1-\gamma )+\omega & 0& 0& 0\\ -k_2(1-\gamma )& \omega +\varphi v_1+v_2(1-\varphi )& 0& 0\\ -\gamma k_1& -\varphi v_1& \alpha +ϵ+\omega & 0\\ 0& -m_1& -m_2& {\tau }_1\end{array}\right].}\end{array}$$

After computing for the eigenvalues of the matrix G, we have that the maximum absolute eigenvalue, ${\mathcal{R}}_0$ is given as;

$$\begin{array}{cc}\hfill {\mathcal{R}}_0& =\underset{\text{secondary}\text{infection}\text{seeded}\text{by}\text{A}\text{state}\text{through}\text{direct}\text{contact}}{\underbrace{\frac{\beta \eta \Lambda {\kappa }_2(1-\gamma )}{\omega ({\kappa }_2(1-\gamma )+{\kappa }_1\gamma +\omega )(\omega +{\nu }_1\varphi +{\nu }_2(1-\varphi ))}}}\hfill \\ & +\underset{\text{secondary}\text{infection}\text{seeded}\text{by}\text{I}\text{state}\text{through}\text{direct}\text{contact}}{\underbrace{\frac{\beta \Lambda [(\omega +{\nu }_1\varphi +{\nu }_2(1-\varphi )){\kappa }_1\gamma +{\kappa }_2{\nu }_1(1-\gamma )\varphi ]}{\omega ({\kappa }_2(1-\gamma )+{\kappa }_1\gamma +\omega )(\omega +{\nu }_1\varphi +{\nu }_2(1-\varphi ))(\epsilon +\omega +\alpha )}}}\hfill \\ & +\underset{\text{secondary}\text{infection}\text{seeded}\text{by}\text{A}\text{state}\text{through}\text{the}\text{environment}}{\underbrace{\frac{{\beta }_1{m}_1\Lambda {\kappa }_2(1-\gamma )}{\omega ({\kappa }_2(1-\gamma )+{\kappa }_1\gamma +\omega )(\omega +{\nu }_1\varphi +{\nu }_2(1-\varphi )){\tau }_1}}}\hfill \\ & +\underset{\text{secondary}\text{infection}\text{seeded}\text{by}\text{I}\text{state}\text{through}\text{the}\text{environment}}{\underbrace{\frac{{\beta }_1{m}_2\Lambda [(\omega +{\nu }_1\varphi +{\nu }_2(1-\varphi )){\kappa }_1\gamma +{\kappa }_2{\nu }_1(1-\gamma )\varphi ]}{\omega ({\kappa }_2(1-\gamma )+{\kappa }_1\gamma +\omega )(\omega +{\nu }_1\varphi +{\nu }_2(1-\varphi ))(\epsilon +\omega +\alpha ){\tau }_1},}}\hfill \end{array}$$ (9)

which can be written as

$${\mathcal{R}}_0={\mathcal{R}}_A+{\mathcal{R}}_I+{\mathcal{R}}_{Ae}+{\mathcal{R}}_{Ie},$$ (10)

where ${\mathcal{R}}_A$ is the secondary infections generated by asymptomatic persons through direct contact; ${\mathcal{R}}_I$ is the secondary infections generated by symptomatic persons through direct contact; ${\mathcal{R}}_{Ae}$ is the secondary infection seeded by asymptomatic persons through the environment; and ${\mathcal{R}}_{Ie}$ is the secondary infection seeded by symptomatic persons through the environment. We can also express ${\mathcal{R}}_0$ in terms of (T ₁, C ₁, Q ₁, Y ₁, X ₁) as;

$${\mathcal{R}}_0=\frac{\Lambda }{\omega T_1}\left[\begin{array}{c}\beta \left(\frac{C_1{k}_1\gamma {\tau }_1+X_1{Y}_1\eta {\tau }_1+X_1{v}_1\rho {\tau }_1}{{\tau }_1{C}_1{Y}_1}\right)+{\beta }_1\left(\frac{m_1{Q}_1+C_1{k}_1\gamma m_2+X_1{m}_2{v}_1\varphi }{{\tau }_1{C}_1{Y}_1}\right)\end{array}\right].$$ (11)

where $T_1=\gamma k_1+k_2(1-\gamma )+\omega ,C_1=\omega +\varphi v_1+v_2(1-\varphi ),Q_1=k_2\varphi v_1(1-\gamma ),Y_1=\alpha +ϵ+\omega ,X_1=k_2(1-\gamma ).$

2.5. Endemic equilibrium point, ${\mathcal{E}}^{**}$

We let, ${\mathcal{E}}^{**},$ be the endemic equilibrium points. Considering Eq. (1), we solve for the endemic equilibrium points ${\mathcal{E}}^{**}=\{S^{**},E^{**},A^{**},I^{**},R^{**},V^{**}\}$ with an assumption that; at the endemic state, E ≠ 0, A ≠ 0, I ≠ 0, R ≠ 0, V ≠ 0. Hence, equating the derivatives of Eq. (1) to zero, yields

$$\begin{array}{cc}\hfill \Lambda -\omega S-\beta (IS+\eta AS)-{\beta }_{1}VS+\rho R& =0,\hfill \\ \hfill \beta (IS+\eta AS)+{\beta }_{1}VS-k_2(1-\gamma )E-k_1\gamma E-\omega E& =0,\hfill \\ \hfill k_2(1-\gamma )E-\omega A-v_1\varphi A-v_2(1-\varphi )A& =0,\hfill \\ \hfill k_1\gamma E+v_1\varphi A-ϵI-(\omega +\alpha )I& =0,\hfill \\ \hfill v_2(1-\varphi )A+ϵI-\rho R-\omega R& =0,\hfill \\ \hfill m_{1}A+m_{2}I-{\tau }_{1}V& =0.\hfill \end{array}$$ (12)

Now, expressing the other state variables in terms of E, it implies that

$$\begin{array}{cc}& A=\frac{X_{1}E}{C_1},\hfill \\ & I=\frac{k_1\gamma E}{Y_1}+\frac{v_1{Q}_{1}E}{Y_1{C}_1},\hfill \\ & R=\frac{v_2(1-\varphi )X_{1}E}{(\rho +\omega )C_1}+\frac{ϵk_1\gamma E}{(\rho +\omega )Y_1}+\frac{Q_{1}E}{Y_1{C}_1},\hfill \\ & V=\frac{m_1{X}_{1}E}{{\tau }_1{C}_1}+m_2\left[\begin{array}{c}\frac{k_1\gamma E}{Y_1{\tau }_1}+\frac{Q_{1}E}{Y_1{C}_1{\tau }_1}\end{array}\right].\hfill \end{array}$$

We now substitute A, I and V into second Eq. (12) and factorizing E out gives

$$\left[\begin{array}{c}\beta S\left[\begin{array}{c}\frac{k_1\gamma }{Y_1}+\frac{Q_1}{Y_1{C}_1}+\frac{\eta X_1}{C_1}\end{array}\right]+{\beta }_{1}S\left[\begin{array}{c}\frac{m_1{X}_1}{{\tau }_1{C}_1}+m_2\left(\begin{array}{c}\frac{k_1\gamma }{Y_1{\tau }_1}+\frac{Q_1}{Y_1{C}_1{\tau }_1}\end{array}\right)\end{array}\right]-T_1\end{array}\right]E=0.$$ (13)

From the initial hypothesis, E ≠ 0 and this implies that,

$$\beta S^{*}\left[\begin{array}{c}\frac{k_1\gamma }{Y_1}+\frac{Q_1}{Y_1{C}_1}+\frac{\eta X_1}{C_1}\end{array}\right]+{\beta }_1{S}^{*}\left[\begin{array}{c}\frac{m_1{X}_1}{{\tau }_1{C}_1}+m_2\left(\begin{array}{c}\frac{k_1\gamma }{Y_1{\tau }_1}+\frac{Q_1}{Y_1{C}_1{\tau }_1}\end{array}\right)\end{array}\right]-T_1=0.$$ (14)

Making S* in Eq. (14) the subject gives

$$S^{*}=\frac{T_1}{\beta \left[\begin{array}{c}\frac{k_1\gamma }{Y_1}+\frac{Q_1}{Y_1{C}_1}+\frac{\eta X_1}{C_1}\end{array}\right]+{\beta }_1\left[\begin{array}{c}\frac{m_1{X}_1}{{\tau }_1{C}_1}+m_2\left(\begin{array}{c}\frac{k_1\gamma }{Y_1{\tau }_1}+\frac{Q_1}{Y_1{C}_1{\tau }_1}\end{array}\right)\end{array}\right]}.$$ (15)

Now, adding first equation and second equation of (12), we substitute S* from Eq. (15) and simplify E* we get

$$E^{*}=\frac{T_1}{HL}-\frac{\Lambda }{L},$$ (16)

where

$$\begin{array}{cc}\hfill H& =\beta \left[\begin{array}{c}{\displaystyle \frac{k_1\gamma }{Y_1}+\frac{Q_1}{Y_1{C}_1}+\frac{\eta X_1}{C_1}}\end{array}\right]+{\beta }_1\left[\begin{array}{c}\frac{m_1{X}_1}{{\tau }_1{C}_1}+m_2\left(\begin{array}{c}\frac{k_1\gamma }{Y_1{\tau }_1}+\frac{Q_1}{Y_1{C}_1{\tau }_1}\end{array}\right)\end{array}\right],\hfill \\ \hfill L& =\left[\begin{array}{c}{\displaystyle \frac{\rho v_2(1-\varphi )X_1}{(\rho +\omega )C_1}+\frac{\rho k_1\gamma ϵ}{(\rho +\omega )Y_1}+\frac{\rho Q_1ϵ}{(\rho +\omega )Y_1{C}_1}-T_1}\end{array}\right].\hfill \end{array}$$

But, we know that the basic reproduction number is expressed as

$$\begin{array}{c}\hfill {\mathcal{R}}_0=\frac{\Lambda }{\omega T_1}\left[\begin{array}{c}{\displaystyle \beta \left(\frac{C_1{k}_1\gamma {\tau }_1+X_1{Y}_1\eta {\tau }_1+X_1{v}_1\rho {\tau }_1}{{\tau }_1{C}_1{Y}_1}\right)}\hfill \\ {\displaystyle +{\beta }_1\left(\frac{m_1{Q}_1+C_1{k}_1\gamma m_2+X_1{m}_2{v}_1\varphi }{{\tau }_1{C}_1{Y}_1}\right)}\hfill \end{array}\right].\end{array}$$ (17)

Therefore, we express the endemic equilibrium points, (S*, E*, A*, I*, R*, V*) in terms of ${\mathcal{R}}_0$ as;

$$\begin{array}{ccc}& & {\displaystyle S^{**}=\frac{\Lambda }{{\mathcal{R}}_0\omega },A^{**}=g_1{E}^{**},I^{**}=g_2{E}^{**},}\hfill \\ & & {\displaystyle R^{**}=g_3{E}^{**},V^{**}=(\frac{m_1{X}_1}{{\tau }_1{C}_1}+m_2(\frac{k_1\gamma }{Y_1{\tau }_1}+\frac{Q_1}{Y_1{C}_1{\tau }_1}))E^{**},}\hfill \\ & & {\displaystyle E^{**}=\frac{\Lambda }{\omega (g_1+(1-\alpha )g_2+g_3+1)}(1-\frac{1}{{\mathcal{R}}_0}).}\hfill \end{array}$$

where $g_1=\frac{X_1}{C_1},g_2=(\frac{k_1\gamma }{Y_1}+\frac{v_1{Q}_1}{Y_1{C}_1}),g_3=(\frac{v_2(1-\varphi )X_1}{(\rho +\omega )C_1}+\frac{ϵk_1\gamma }{(\rho +\omega )Y_1}+\frac{Q_1}{Y_1{C}_1})$. Therefore, the endemic equilibrium for the COVID-19 model remains positive if and only if ${\mathcal{R}}_0>1,$ since at the endemic equilibrium, E > 0, R > 0, I > 0, A > 0. Fulfilling, that we have a unique endemic equilibrium point ${\mathcal{E}}^{**},$ when ${\mathcal{R}}_0>1$. (see [40] for an alternative prove on unique endemic equilibrium point.

2.6. Global stability

We focus on the application of Lyapunov’s function in this area. Lyapunov function is a scalar function which may be employed to ascertain global stability [41].

Definition 1

Let the equilibrium of $y^{\prime }=f\left(y\right)$ be y* such that $f:{\mathbb{R}}^n\mapsto {\mathbb{R}}^n$. We define L to be a continuous scalar function, implying; $L:{\mathbb{R}}^n\mapsto \mathbb{R}$. If the conditions

$$L\left(y^{*}\right)=0,L\left(y\right)>0\forall y\ne y^{*},$$

are satisfied, then the function L is said to be positive definite. Also, a scalar function L(y) such that $L:{\mathbb{R}}^n\mapsto \mathbb{R}$ is called radially unbounded if L(y)↦∞ as ||y||↦∞ [41].

Based on the preliminary notes above, we now state the Lyapunov stability theorem.

Theorem 3 Lyapunov Stability Theorem —

The equilibrium, y* is globally stable if the function, L(y) is radially unbounded and positive definite globally such that it has globally negative time derivative,

$$\dot{L}\left(y\right)<0\forall y\ne y^{*}.$$

We say that; the function L(y) is a Lyapunov function if it satisfies the above theorem, the proof can be found in [41] .

Another important theorem which also plays a key role here is the Kransovkii-LaSalle theorem. This is an extension of Lyapunov function. In summary, this theorem puts forward that; considering an autonomous system, $y^{\prime }=f\left(y\right)$ which has equilibrium, y* and that $f\left(y^{*}\right)=0,$ we assume there is a continuously differentiable positive definite and radially unbounded function $L:{\mathbb{R}}^n\mapsto \mathbb{R}$ which meets the condition $\dot{L}\left(y\right)\le 0\forall t,$ $y\in {\mathbb{R}}^n$. We then define the invariant set as

$$\zeta =\{y\in {\mathbb{R}}^n|\dot{L}\left(y\right)=0\}.$$

From the set above, the equilibrium y* is globally stable if ζ constitutes only the equilibrium y* [41](a fractional prove of stability can be extracted from [42]).

Theorem 4

The disease-free equilibrium point of the COVID-19 model is globally stable if ${\mathcal{R}}_0<1$ .

Proof

We employ the approach in [43] to analyze both the stability at disease free and endemic equilibrium. We define a Lyapunov, L for the disease-free equilibrium point as follows;

$$\begin{array}{ccc}\hfill L& =& E+(\frac{\beta \eta }{C_1}+\frac{\beta v_1\varphi }{Y_1{C}_1}+\frac{{\beta }_1{m}_2{v}_1\varphi }{Y_1{\tau }_1{C}_1}+\frac{{\beta }_1{m}_1}{C_1{\tau }_1})A\hfill \\ & & +(\frac{\beta }{Y_1}+\frac{{\beta }_1{m}_2}{Y_1{\tau }_1})I+\frac{{\beta }_1}{{\tau }_1}V.\hfill \end{array}$$

Differentiating L with respect to t gives;

$$\dot{L}=\dot{E}+(\frac{\beta \eta }{C_1}+\frac{\beta v_1\varphi }{Y_1{C}_1}+\frac{{\beta }_1{m}_2{v}_1\varphi }{Y_1{\tau }_1{C}_1}+\frac{{\beta }_1{m}_1}{C_1{\tau }_1})\dot{A}+\left(\frac{{\beta }_1{m}_2}{Y_1{\tau }_1}\right)\dot{I}+\frac{{\beta }_1}{{\tau }_1}\dot{V}.$$

We substitute $\dot{E},$ $\dot{A},$ $\dot{I},$ $\dot{V}$ from Eq. (1) into $\dot{L}$ gives;

$$\begin{array}{ccc}\hfill \dot{L}& =& \beta (IS+\eta AS)+{\beta }_{1}VS-k_2(1-\gamma )E-k_1\gamma E-\omega E\hfill \\ & & +(\frac{\beta \eta }{C_1}+\frac{\beta v_1\varphi }{Y_1{C}_1}+\frac{{\beta }_1{m}_2{v}_1\varphi }{Y_1{\tau }_1{C}_1}+\frac{{\beta }_1{m}_1}{C_1{\tau }_1})\hfill \\ & & \times (k_2(1-\gamma )E-\omega A-v_1\varphi A-v_2(1-\varphi )A)\hfill \\ & & +(\frac{\beta }{Y_1}+\frac{{\beta }_1{m}_2}{Y_1{\tau }_1})(k_1\gamma E+v_1\varphi A-ϵI-(\omega +\alpha )I)\hfill \\ & & +\frac{{\beta }_1}{{\tau }_1}(m_{1}A+m_{2}I-{\tau }_{1}V).\hfill \end{array}$$

After further simplification we have

$$\begin{array}{cc}\hfill \dot{L}& =T_1\left[\begin{array}{c}\frac{\Lambda }{\omega T_1}\left[\begin{array}{c}\beta (\frac{\eta X_1}{C_1}+\frac{\gamma k_1}{Y_1}+\frac{Q_1}{Y_1{C}_1})+{\beta }_1(\frac{m_1{X}_1}{{\tau }_1{C}_1}+\frac{m_2\gamma k_1}{{\tau }_1{Y}_1}+\frac{m_2{Q}_1}{{\tau }_1{Y}_1{C}_1})\end{array}\right]-1\end{array}\right]\hfill \\ & =T_1({\mathcal{R}}_0-1)E\hfill \end{array}$$

Therefore, $\dot{L}\le 0$ whenever ${\mathcal{R}}_0<1$. Also, $\dot{L}=0$ if and only if $E=A=I=V=0$. We then define the invariant set as

$$\zeta =\{(E,A,I,V)\in {\mathbb{R}}^n:\dot{L}\left(y\right)=0\}.$$

Hence, by the Krasovkii-LaSalle theorem, it follows that since ζ houses only the equilibrium ${\mathcal{E}}^{*},$ the ${\mathcal{E}}^{*}$ is said to be globally stable whenever ${\mathcal{R}}_0<1$ [41]. □

Theorem 5

If ${\mathcal{R}}_0>1,$ the endemic equilibrium point of the COVID-19 model is globally asymptotically stable in $\Omega$ [44] .

Proof

Similarly, to check for the global stability for the endemic equilibrium point, we define a Lyapunov function, L ₁;

$$\begin{array}{ccc}\hfill L_1& =& (S-S^{**}-S^{**}\ln \frac{S}{S^{**}})+h_1(E-E^{*}-E^{**}\ln \frac{E}{E^{**}})\hfill \\ & & +h_2(A-A^{**}-A^{**}\ln \frac{A}{A^{**}})+h_3(I-I^{**}-I^{*}\ln \frac{I}{I^{*}})\hfill \\ & & +h_4(R-R^{**}-R^{**}\ln \frac{R}{R^{**}})+h_5(V-V^{**}-V^{**}\ln \frac{V}{V^{**}}).\hfill \end{array}$$

Differentiating the function above gives;

$$\begin{array}{cc}\hfill {\dot{L}}_1& =(1-\frac{S^{**}}{S})\dot{S}+h_1(1-\frac{E^{**}}{E})\dot{E}+h_2(1-\frac{A^{**}}{A})\dot{A}+h_3(1-\frac{I^{**}}{I})\dot{I}\hfill \\ & +h_4(1-\frac{R^{**}}{R})\dot{R}+h_5(1-\frac{V^{**}}{V})\dot{V}.\hfill \end{array}$$ (18)

Substituting Eq. (1) into Eq. (18) with further simplification gives;

$$\begin{array}{ccc}\hfill \dot{L_1}& =& -\omega (1-\frac{1}{x_1}){}^{2}S+(1-\frac{1}{x_1}+x_4-x_4{x}_1)\beta I^{**}{S}^{**}\hfill \\ & & +(1-\frac{1}{x_1}+x_3-x_3{x}_1)\beta \eta A^{**}{S}^{**}\hfill \\ & & +(1-\frac{1}{x_1}+x_6-x_6{x}_1){\beta }_1{V}^{**}{S}^{**}+(1-\frac{1}{x_1}+x_5-\frac{x_5}{x_1})\rho R^{**}\hfill \\ & & +(x_1{x}_4-x_2-\frac{x_1{x}_4}{x_2}+1)\beta I^{**}{S}^{**}{h}_1\hfill \\ & & +(x_1{x}_3-x_2-\frac{x_1{x}_3}{x_2}+1)\beta \eta A^{**}{S}^{**}{h}_1\hfill \\ & & +(x_1{x}_6-x_2-\frac{x_1{x}_6}{x_2}+1){\beta }_1{V}^{**}{S}^{**}{h}_1\hfill \\ & & +(1+x_2-x_3-\frac{x_2}{x_3})h_2{k}_2(1-\gamma )E^{**}\hfill \\ & & +(1+x_2-x_4-\frac{x_2}{x_4})h_3{k}_1\gamma E^{**}+(1+x_3-x_4-\frac{x_3}{x_4})h_3{v}_1\varphi A^{**}\hfill \\ & & +(1+x_3-x_5-\frac{x_3}{x_5})h_4{v}_2(1-\varphi )A^{**}\hfill \\ & & +(1+x_4-x_5-\frac{x_4}{x_5})ϵI^{**}{h}_4\hfill \\ & & +(1+x_3-x_6-\frac{x_3}{x_6})h_5{m}_1{A}^{**}+(1+x_4-x_6-\frac{x_4}{x_6})h_5{m}_2{I}^{**}\hfill \end{array}$$

where $x_1=\frac{S}{S^{**}},$ $x_2=\frac{E}{E^{**}},$ $x_3=\frac{A}{A^{**}},$ $x_4=\frac{I}{I^{**}},$ $x_5=\frac{R}{R^{**}}$ and $x_6=\frac{V}{V^{**}}$. We let

$${\dot{L}}_1=-\omega (1-\frac{1}{x_1}){}^{2}S+T(x_1,x_2,x_3,x_4,x_5,x_6),$$

where

$$\begin{array}{ccc}\hfill T& =& \beta I^{**}{S}^{**}+\beta \eta A^{**}{S}^{**}+{\beta }_1{V}^{**}{S}^{**}+\rho R^{**}+\beta I^{**}{S}^{**}{h}_1\hfill \\ & & +\beta \eta A^{**}{S}^{**}{h}_1+h_2{k}_2(1-\gamma )E^{**}+h_3{k}_1\gamma E^{**}\hfill \\ & & +h_3{v}_1\varphi A^{**}+{\beta }_1{V}^{**}{S}^{**}{h}_1+h_4{v}_2(1-\varphi )A^{**}+ϵI^{*}{h}_4\hfill \\ & & +h_5{m}_1{A}^{**}+h_5{m}_2{I}^{**}\hfill \\ & & +(-\beta I^{**}{S}^{**}-\beta \eta A^{**}{S}^{**}-{\beta }_1{V}^{**}{S}^{**}-\rho R^{**})\frac{1}{x_1}\hfill \\ & & +(-\beta I^{**}{S}^{**}{h}_1-\beta \eta A^{**}{S}^{**}{h}_1-{\beta }_1{V}^{**}{S}^{**}{h}_1+h_3{k}_1\gamma E^{*})x_2\hfill \\ & & +(\beta \eta A^{**}{S}^{**}-h_2{k}_2(1-\gamma )E^{**}+h_3{v}_1\varphi A^{*}+h_4{v}_2(1-\varphi )A^{**}\hfill \\ & & +h_5{m}_1{A}^{**})x_3\hfill \\ & & +(\beta I^{**}{S}^{**}-h_3{k}_1\gamma E^{**}-h_3{v}_1\varphi A^{**}+ϵI^{*}{h}_4+h_5{m}_2{I}^{*})x_4\hfill \\ & & +(\rho R^{**}-h_4{v}_2(1-\varphi )A^{**}-ϵI^{**}{h}_4)x_5\hfill \\ & & +(-h_5{m}_1{A}^{**}-h_5{m}_2{I}^{**}+{\beta }_1{V}^{**}{S}^{**})x_6\hfill \\ & & +(-\beta I^{**}{S}^{**}+\beta I^{**}{S}^{**}{h}_1)x_4{x}_1\hfill \\ & & +(-\beta \eta A^{**}{S}^{**}+\beta \eta A^{**}{S}^{**}{h}_1)x_3{x}_1\hfill \\ & & +(-{\beta }_1{V}^{**}{S}^{**}+{\beta }_1{V}^{**}{S}^{**}{h}_1)x_6{x}_1\hfill \\ & & -\rho R^{**}\frac{x_5}{x_1}-\beta I^{**}{S}^{**}{h}_1\frac{x_1{x}_4}{x_2}-\beta \eta A^{**}{S}^{**}{h}_1\frac{x_3{x}_1}{x_2}\hfill \\ & & -{\beta }_1{V}^{**}{S}^{**}{h}_1\frac{x_6{x}_1}{x_2}-h_2{k}_2(1-\gamma )E^{*}\frac{x_2}{x_3}\hfill \\ & & -h_3{k}_1\gamma E^{**}\frac{x_2}{x_4}-h_3{v}_1\varphi A^{**}\frac{x_3}{x_4}-h_4{v}_2(1-\varphi )A^{**}\frac{x_3}{x_5}\hfill \\ & & -ϵI^{**}{h}_4\frac{x_4}{x_5}-h_5{m}_1{A}^{**}\frac{x_3}{x_6}-h_5{m}_2{I}^{**}\frac{x_4}{x_6}.\hfill \end{array}$$

Considering the expression

$$\beta I^{**}{S}^{**}{h}_1=\beta I^{**}{S}^{**},$$

we have that, $h_1=1$. This implies that the coefficients of x ₁ x ₄, x ₃ x ₁ and x ₆ x ₁ are all 0. Equating the coefficients of x ₂, x ₃, x ₄, x ₅ and x ₆ to 0 and solving for h ₂, h ₃, h ₄ and h ₅ gives;

$$\begin{array}{cc}\hfill h_2& =\frac{\beta \eta A^{**}{S}^{**}}{k_2(1-\gamma )E^{**}}+\frac{(\beta I^{**}{S}^{**}+\beta \eta A^{**}{S}^{**}+{\beta }_1{V}^{**}{S}^{**})v_1\varphi A^{**}}{k_1\gamma E^{**}{k}_2(1-\gamma )E^{**}}\hfill \\ & +\frac{v_2(1-\varphi )A^{*}\rho R^{**}}{(v_2(1-\varphi )A^{**}+ϵI^{**})k_2(1-\gamma )E^{**}}+\frac{m_1{A}^{**}{\beta }_1{V}^{**}{S}^{**}}{(m_1{A}^{**}+m_2{I}^{**})k_2(1-\gamma )E^{**}},\hfill \\ \hfill h_3& =\frac{\beta I^{**}{S}^{**}+\beta \eta A^{**}{S}^{**}+{\beta }_1{V}^{**}{S}^{**}}{k_1\gamma E^{**}},\hfill \\ \hfill h_4& =\frac{\rho R^{**}}{v_2(1-\varphi )A^{**}+ϵI^{**}},\hfill \\ \hfill h_5& =\frac{{\beta }_1{V}^{**}{S}^{**}}{m_1{A}^{**}+m_2{I}^{**}}.\hfill \end{array}$$

Therefore, T can be rewritten as

$$\begin{array}{ccc}\hfill T& =& -\beta I^{**}{S}^{**}(x_2-x_4+\frac{1}{x_1}+\frac{x_1{x}_4}{x_2}-2)\hfill \\ & & -\beta \eta A^{**}{S}^{**}(x_2-x_3+\frac{1}{x_1}+\frac{x_3{x}_1}{x_2}-2)\hfill \\ & & -{\beta }_1{V}^{**}{S}^{**}(x_2-x_6+\frac{1}{x_1}+\frac{x_1{x}_6}{x_2}-2)-\rho R^{**}(-1+\frac{1}{x_1}-x_5+\frac{x_5}{x_1}-2)\hfill \\ & & -h_2{k}_2(1-\gamma )E^{**}(x_3-1-x_2+\frac{x_2}{x_3})-h_3{k}_1\gamma E^{**}(x_4-1-x_2+\frac{x_2}{x_4})\hfill \\ & & -h_3{v}_1\varphi A^{**}(x_4-1-x_3+\frac{x_3}{x_4})-h_4{v}_2(1-\varphi )A^{**}(x_5-1-x_3+\frac{x_3}{x_5})\hfill \\ & & -ϵI^{**}{h}_4(x_5-1-x_4+\frac{x_4}{x_5})-h_5{m}_1{A}^{**}(x_6-1-x_3+\frac{x_3}{x_6})\hfill \\ & & -h_5{m}_2{I}^{**}(x_6-1-x_4+\frac{x_4}{x_6}).\hfill \end{array}$$

It then follows that, T ≤ 0 if $x_1=1,$ $x_2=1,$ $x_3=1,$ $x_4=1,$ $x_5=1$ and $x_6=1$. Hence we may conclude that;

$${\dot{L}}_1=-\omega (1-\frac{1}{x_1}){}^{2}S+T(x_1,x_2,x_3,x_4,x_5,x_6)\le 0.$$

By LaSalle theorem, the invariant set is defined as

$${\zeta }_1=\{(S,E,A,I,R,V)\in D:L_1=0\}.$$

Since the invariant set, ζ ₁ only contains the endemic equilibrium (S ^⁎⁎, E ^⁎⁎, A ^⁎⁎, I ^⁎⁎, R ^⁎⁎, V ^⁎⁎), then the endemic equilibrium is said to be globally asymptotically stable under the given region $\Omega$. □

3. Parameter estimation and numerical simulations

In this section, our focus is to verify the validity of the model. This is achieved by fitting and comparing the proposed model with a real data to know its degree of accuracy. This will justify the model’s competency on predicting for a realistic outcome. Considering Ghana as a case study, the cumulative daily reported cases of COVID-19 were extracted from the situation reports of the WHO and the Ministry of Health, Ghana [11]. The collected data ranges from the onset of the pandemic in Ghana; that is from 12th March to 7th May, 2020. As of 7th May, 2020, 4012 cases were confirmed with 18 deaths and 323 recovered individuals. No clear detail was given with respect to the relapse of the recovered individuals into the susceptible class though this study factored. Estimating parameter values is very key as far as epidemiological study is concerned. We utilize the least squares method in this context since it is very efficient and reliable [41]. This method seeks to fit the observed data sets, Y_i, with the estimated values, X_i, such that; the sum of squares of errors between the observed and fitted curve is minimal [41]. The sum of squares error, SSE, is illustrated mathematically as;

$$SSE=\sum _{i=1}^k{(Y_i-X_i)}^2.$$

Table Appendix A account for the daily recorded cases and daily percentage change in the number of recorded cases.

The estimated parameter values and the fitted model using Python programming language are shown in Table 2 and Fig. 3 respectively. The blue points in Fig. 3 represent the cumulative number of daily confirmed cases while the red line designates the fitted model. From the estimated parameter values in Table 2, it is clear that; even if all the infected individuals are treated, the susceptible class is still vulnerable to be infected since the rate at which the environment contribute to infection, β ₁, is significant, thus 4.00199$\times {10}^{-8}$. Based on the estimated value for γ, only 1% of the exposed individuals join the infected compartment without passing through the asymptomatic state. Again, only 0.5% of the individuals in the asymptomatic class join the symptomatic class at the rate of 0.2 per day while the rest of the asymptomatic populace recover at the rate of 0.799994 per day.

Table 2.

Estimated parameter values for the COVID-19 model (1).

Parameter	Range	Baseline value	Reference
η	$0.62811041-0.6366{\text{day}}^{-1}$	0.6323	Estimated
ω	$0.000042578{\text{day}}^{-1}$	0.000042578	[11]
ρ	$0.41138431{\text{day}}^{-1}$	0.41138431	Estimated
β	$6.038\times {10}^{-8}-0.8038$	$6.038\times {10}^{-8}$	Estimated
γ	$0.01000-0.0648$	0.0374	Estimated
β1	$4.00199\times {10}^{-8}$	$4.00199\times {10}^{-8}$	Estimated
Λ	$1319.294{\text{day}}^{-1}$	1319.294	[45], [46]
k1	$0.1923000-0.07142238{\text{day}}^{-1}$	0.1318	Estimated
k2	$0.176300-0.14285824{\text{day}}^{-1}$	0.1596	Estimated
α	$0.0044-0.0099{\text{day}}^{-1}$	0.0072	Estimated
ϕ	0.00500005	0.0050	Estimated
v1	$0.1929-0.2000{\text{day}}^{-1}$	0.1965	Estimated
v2	$0.79999398{\text{day}}^{-1}$	0.8000	Estimated
ϵ	$0.0805084-0.098026529{\text{day}}^{-1}$	0.0893	[11]
τ1	$0.29000-0.3333{\text{day}}^{-1}$	0.3117	[47]
m1	$0.01780400{\text{day}}^{-1}$	0.0178	Estimated
m2	$0.92152716{\text{day}}^{-1}$	0.9215	Estimated

Fig. 3.

Fitted diagram of confirmed cases in Ghana and the proposed model.

3.1. Basic reproduction number, ${\mathcal{R}}_0$ with no control

Our main objective here is to compute the basic reproduction number of the model (1). Using the values $\eta =0.62811041,\omega =0.000042578,\rho =0.41138431,\beta =6.038\times {10}^{-8},{\beta }_1=4.00199\times {10}^{-8},\gamma =0.01000001,\Lambda =1319.294,k_1=0.07142238,k_2=0.14285824,\alpha =0.00440000,\varphi =0.00500005,v_1=0.20005051,v_2=0.79999398,ϵ=0.0805840,{\tau }_1=0.2900000,m_1=0.01780400,m_2=0.92152716,$ and substituting it into the ${\mathcal{R}}_0$ expression result in;

$$\begin{array}{cc}\hfill {\mathcal{R}}_0& =\frac{\Lambda }{\omega T_1}\left[\begin{array}{c}\beta \left(\frac{C_1{k}_1\gamma {\tau }_1+X_1{Y}_1\eta {\tau }_1+X_1{v}_1\rho {\tau }_1}{{\tau }_1{C}_1{Y}_1}\right)+{\beta }_1\left(\frac{m_1{Q}_1+C_1{k}_1\gamma m_2+X_1{m}_2{v}_1\varphi }{{\tau }_1{C}_1{Y}_1}\right)\end{array}\right]\hfill \\ & =\frac{1319.294}{4.2578\times {10}^{-5}\times \left(0.1421865\right)}(7.3634285\times {10}^{-9}+1.7708567\times {10}^{-9})\hfill \\ & =1.99,\hfill \end{array}$$

where $T_1=0.14218646,$ $C_1=0.7970368,$ $Q_1=0.0001415,$ $Y_1=0.0849510,$ $X_1=0.1414297$. However, using the baseline values in Table 2 and substituting it into the ${\mathcal{R}}_0$ expression result in;

$$\begin{array}{cc}\hfill {\mathcal{R}}_0& =\frac{1319.294}{4.2578\times {10}^{-5}\times \left(0.15860\right)}(1.05604\times {10}^{-8}+6.71352\times {10}^{-9})\hfill \\ & =3.37,\hfill \end{array}$$

where $T_1=0.15860,$ $C_1=0.79703,$ $Q_1=0.00015,$ $Y_1=0.09654,$ $X_1=0.15363$. Therefore, the average basic reproduction number, ${\mathcal{R}}_0^a,$ without control strategies in Ghana is approximately 2.68. This indicates that on average a single infected individual can spread the disease to 2 to 3 susceptible individuals. Hence, strengthening prophylaxis such as social distancing, wearing of nose masks, regular hand washing with soap and contact tracing, will highly perturb the key parameters aiding the spread of the disease. Suppose that, the implementation of these measures decreases the estimated values of η, β and β ₁ to 0.32811041, $4.038\times {10}^{-8}$ and $2.00199\times {10}^{-8}$ respectively, then the basic reproduction number with these control outcomes will be given as 0.79774. This shows how effective these control measures are in COVID-19 battle field.

3.2. Sensitivity analysis

Varying estimated parameter values might give different output as seen in 3.1 and it is on this note that, we want to explore parameters which significantly influence the end results of the model under study. This concept is very important since it discusses and informs us about the most relevant factors to deal with so as to minimize the spread of COVID-19.

Definition 2

The parameter, p is said to be sensitive if any small alteration on p causes a significant change in the solution. It is worthy to note that, the parameter p is termed to be locally sensitive if the change in the value of parameter p influences the output of the model. In the same way, global sensitivity takes into account the overall change in the model output as a result of the change in all parameter values within their respective range [41].

In computing for the normalized sensitivity index (${ϵ}_{{\mathcal{R}}_0}^p$) on the ${\mathcal{R}}_0$ for each of the parameters p, we use the formulae below [41];

$${ϵ}_{{\mathcal{R}}_0}^p=\frac{\partial {\mathcal{R}}_0}{\partial p}\frac{p}{{\mathcal{R}}_0}.$$

Applying the formula above gives the parameters with their sensitivity index in the Table 3 .

Table 3.

Normalized sensitivity index for each parameter for the COVID-19 model (1).

Parameter	Description	Sensitivity Index
η	Relative transmissibility by asymptomatic individuals	$+0.7367$
ω	Natural death rate	-1.0005
β	Transmission rate by asymptomatic and symptomatic individuals	$+0.8060$
β1	Environmental transmission	$+0.1939$
γ	Proportion of individuals who are timely diagnosis	$+0.1693$
Λ	Recruitment rate	$+1.0000$
k1	Progression rate from exposed to the symptomatic class	$+0.1676$
k2	Progression rate from exposed to the asymptomatic class	$-0.1673$
α	Disease induced death rate	$-0.0112$
ϕ	Proportion of A patients who later move to the I class	$+0.0460$
v1	Progression from asymptomatic to the symptomatic class	$+0.0419$
v2	Progression from asymptomatic to the recovered class	$-0.8263$
ϵ	The rate at which symptomatic patients are recovered	$-0.2043$
τ1	Natural decay rate of virus from the environment (Surfaces)	$-0.1939$
m1	The rate of viral release into the environment by asymptomatic patients	$+0.0477$
m2	The rate at which I patients release virus into the environment	$+0.1461$

From Table 3, all parameters with positive values, η, β, β ₁, γ, Λ, k ₁, ϕ, v ₁, m ₁ and m ₂ indicate the increase in transmission of COVID-19 in the population in accordance to an increase in these parameter values. Prominent among these are Λ, β and η. On the other hand, parameters with negative sensitivity index, ω, k ₂, α, v ₂, ϵ and τ ₁ indicate the decrease in the spread of COVID-19 for each unit increase in these parameters. Exploiting sensitivity analysis on this study enlightens policy makers on where to put more efforts in the fight against COVID-19. For example, the sensitivity index of Λ on ${\mathcal{R}}_0$ is 1. This implies that, a 1% change in the value of Λ will cause a corresponding increase in ${\mathcal{R}}_0$ by 1%. In the same manner, a 1% change in β increases the number of secondary infections by 0.8%. From the global sensitivity analysis as shown in Fig. 4 , it is clear that, fortifying measures which will aid in accelerating ϵ, γ and τ ₁ will reduce the ${\mathcal{R}}_0$. These measures may include fumigating the environment (surfaces) especially in crowded areas such as markets and essential service providing institutions like banks, police stations and hospitals. Regular disinfecting of the transport systems would also increase the virus diminishing rate from the system, enhancing the outcome of the control reproductive number. Though, ω contributes significantly towards the reduction in the ${\mathcal{R}}_0,$ but it is not considered as good candidate to be used as a control variable. This is grounded on the fact that, ω, is the natural death rate of the population of which we do not have much dominance.

Fig. 4.

Global sensitivity plot .

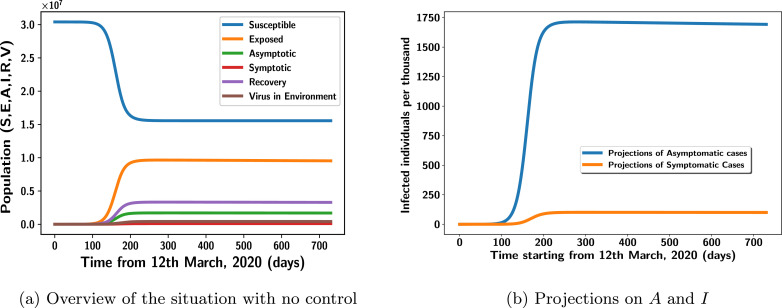
In the same setting as illustrated in Fig. 4, the parameters m ₂, m ₁, k ₂, Λ, β ₁, β, η prove to be more influential in increasing the reproduction number after performing the global sensitivity analysis. This is backed by the results in Figs. 5 , 6 , 7 and Fig. 8 where the effects of β, β ₁, m ₁, m ₂, η and ρ on the infected population are explored. From the Fig. 5a, 5 b, 6 a, 6 b, 7 a, 7 b, 8 a, 8 b, we have a confirmation that, the number of the infected individuals increase as the parameters, β, β ₁, m ₁, m ₂, η and ρ increase. So, does the recruitment rate, Λ. Therefore, the government’s decision on travel restriction has really been of help to the country against the spread of the disease since this contributed massively to reduce the secondary infections which might have been contracted as a result of individuals from highly infected countries. Also, the analysis figures out that, mass testing and proper observance of social distancing with its complementary measures would far help in this fight. This analysis also establishes the fact that; adapting to healthy living/lifestyle which seek to boost the immune system such as proper dietary habit and abstinence from alcohol would significantly increase the number of individuals in the recovery compartment. One key feature which needs much attention is the rate at which viruses are released into the environment. This rate is very high among the asymptomatic patients, see Fig. 4. This can be attributed to the fact that; since individuals in this class are mostly unaware about their contraction of COVID-19, strict measures against the virus’ propagation is not properly observed among individuals in this class contributing to this effect. Fig. 5a, is the simulation of the situation as of 7th May, 2020. Here, the basic reproduction number, ${\mathcal{R}}_0$ is 1.99. The graph confirms this figure that, if no effective control measures are employed, then this disease would continue to be experienced in the population for all time until the population gets diminished. Fig. 5b describes the projections of the infected and asymptomatic individuals with no control measure for about two years period. It clearly depicts that, the number of individuals in the asymptomatic compartment far exceeds that of the infected class even as time transcends. This confirms the results of the parameter estimates that, only 1% of all the exposed individuals branch into the symptomatic class at the rate of 0.1676 while the rest move to the asymptomatic class. The model shows that, asymptomatic individuals can join the severely infected class. However, the estimated parameter value shows that, only few people experience such situation, that is, 0.5%.

Fig. 5.

The dynamics of COVID-19 in Ghana considering the impact of the environment.

Fig. 6.

The effects of varying β, β₁ on the infected population.

Fig. 7.

The effects of varying m₁ and m₂ on the infected population.

Fig. 8.

The effects of η and ρ on the infected population.

Though, not much had been said with regards to the possibility of the recovered individuals joining the susceptible population. Notwithstanding, after our model’s fitting, it was shown that, this situation might be possible at the rate of $0.41138{\text{day}}^{-1}$ as shown in Fig. 8b. This calls attention that, treatment must be geared towards provision of long term or permanent immunity so as to break the path between the recovered class and reinfection.

4. Optimal control on the model

Considering the system $x^{\prime }\left(t\right)=f\left(x\left(t\right)\right)$ with $x\left(0\right)=x_0,$ such that $x_0\in {\mathbb{R}}^n$ where $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ and $x:[0,\infty )\to {\mathbb{R}}^n$. We introduce variables responsible for the control u_i, $i=1,2,3\dots n\in \mathbb{N}$. We then have;

$$x^{\prime }\left(t\right)=f(x\left(t\right),u\left(t\right)),x\left(0\right)=x_0,$$

with $u:[0,\infty )\to A\subset {\mathbb{R}}^n$. The admissible control set is given as; $U^{*}=\{u\left(t\right)\in L^{\prime }(t_0,t_f)|u\left(t\right)\in A\}.$ The aim here is to target the best control variables, u_i, which can efficiently reduce the rate of secondary transmission at a minimum cost of their implementation at any time t ₍₀₎ ≤ t ≤ t _(f) [41]. That is, we seek to achieve a reduction in the number of individuals in the susceptible, exposed, asymptomatic, severely infected classes and also reduce the content of the virus in the system at a minimum cost simultaneously. To achieve the above objective demands a lot of constructive considerations. For example, implementing total lock down for about two months as a control strategy in this context might highly prove not to be feasible. The loop hole here is; is the country adequately prepared both financially and technically to provide to the satisfaction of its inhabitants the basic needs such as food, water and others throughout the whole period assigned for this measure? It is highly probable the answer might be a big no. It is an undeniable fact that, this measure might prove impractical in controlling the spread in this country. This is why there is a need to objectively sort for more dense restrictive measures with flexible and feasible approaches to be employed in this setting so as to control the disease. We rely on the Pontryagin’s maximum principle as applied in [48] for this analysis. We base on the premises above to set below likely control strategies:

• 1. $u_1=$ The effective testing and quarantine when boarders are opened.
• 2. $u_2=$ Intensifying the usage of nose masks and face shields through education.
• 3. $u_3=$ Cleaning of surfaces with home-based detergents.
• 4. $u_4=$ Safety measures adopted by the asymptomatic and symptomatic individuals such as; practising proper cough etiquette (maintaining a distance, cover coughs and sneezes with disposable tissues or clothing and wash hands after cough or sneezes).
• 5. $u_5=$ Fumigating commercial areas such as markets.

The objective functional under discussion, Q, which is to be minimized is given as;

$$\begin{array}{ccc}& & Q(u_1,u_2,u_3,u_4,u_5)=\text{min}{\int }_{t_0}^{t_f}\hfill \\ & & \times [E+A+I+V+\frac{b_1}{2}{u}_1^2+\frac{b_2}{2}{u}_2^2+\frac{b_3}{2}{u}_3^2+\frac{b_4}{2}{u}_4^2+\frac{b_5}{2}{u}_5^2]dt;\hfill \end{array}$$ (19)

subject to the constraints;

$$\begin{array}{ccc}\hfill \frac{dS}{dt}& =& (1-u_1)\Lambda -\omega S-(1-u_2)\beta (IS+\eta AS)-(1-u_2-u_3){\beta }_{1}VS,\hfill \\ \hfill \frac{dE}{dt}& =& (1-u_2)\beta (IS+\eta AS)+(1-u_2-u_3){\beta }_{1}VS-k_1\gamma E\hfill \\ & & -k_2(1-\gamma )E-\omega E,\hfill \\ \hfill \frac{dA}{dt}& =& k_2(1-\gamma )E-\omega A-v_1\varphi A-v_2(1-\varphi )A,\hfill \\ \hfill \frac{dI}{dt}& =& k_1\gamma E+v_1\varphi A-ϵI-(\omega +\alpha )I,\hfill \\ \hfill \frac{dR}{dt}& =& v_2(1-\varphi )A+ϵI-\omega R,\hfill \\ \hfill \frac{dV}{dt}& =& (1-u_4)m_{1}A+(1-u_4)m_{2}I-(u_5+{\tau }_1)V.\hfill \end{array}$$ (20)

Where, S > 0, E ≥ 0, A ≥ 0, I ≥ 0, R ≥ 0, V ≥ 0. From Eq. (19), we assume that, the weight constant of the exposed, infected (A and I classes) and the virus in the system is 1. Also, to better observe and understand the influence of these control strategies on the model, we assumed that; no recovered individual is vulnerable to be reinfected in Eq. (20). We accounted for the respective affiliated costs, $b_1{u}_1^2,$ $b_2{u}_2^2,$ $b_3{u}_3^2,$ $b_4{u}_4^2,$ $b_5{u}_5^2,$ which are possible to be incurred during implementation where the square denotes their severity.

It is very necessary to ensure that, the proposed optimal solution exists. For this reason, we employ Filippove-Cesari theorem as used in [37]. In this case, we show that, the existence of the optimal control solution is guaranteed if the following conditions are satisfied;

• 1.The admissible control set is compact and bounded.
• 2.The control sets together with the state variables is non-empty.
• 3.A linear function in the state and control variables bound the state systems of differential equations.
• 4.The convexity of the integrand of cost functional with respect to u on the set A [37].

We now have the Hessian matrix of the given cost functional as;

$$\begin{array}{c}\hfill \left[\begin{array}{ccccc}{b}_1& 0& 0& 0& 0\\ 0& b_2& 0& 0& 0\\ 0& 0& b_3& 0& 0\\ 0& 0& 0& b_4& 0\\ 0& 0& 0& 0& b_5\end{array}\right]\end{array}$$

Since the computed Hessian matrix above is everywhere positive definite, it follows that, the objective functional, Q(u ₁, u ₂, u ₃, u ₄, u ₅) is strictly convex [37]. We also have that, $\exists b=min\{b_1,b_2,b_3,b_4,b_5\}>0$ given that the integrand of the objective functional,

$$\begin{array}{cc}\hfill Q& =E+A+I+V+\frac{b_1}{2}{u}_1^2+\frac{b_2}{2}{u}_2^2+\frac{b_3}{2}{u}_3^2+\frac{b_4}{2}{u}_4^2+\frac{b_5}{2}{u}_5^2,\hfill \\ & \ge \frac{b_1}{2}{u}_1^2+\frac{b_2}{2}{u}_2^2+\frac{b_3}{2}{u}_3^2+\frac{b_4}{2}{u}_4^2+\frac{b_5}{2}{u}_5^2,\hfill \\ & \ge b(u_1^2+u_2^2+u_3^2+u_4^2+u_5^2),\hfill \end{array}$$

holds under the condition $E+A+I+V\ge 0.$ Applying Pontryagin’s maximum principle where we have the state variables as $S=S^{{}^{★}},$ $E=E^{{}^{★}},$ $A=A^{{}^{★}},$ $I=I^{{}^{★}},$ $R=R^{{}^{★}}$ and $V=V^{{}^{★}}$ gives the Hamiltonian function;

$$\begin{array}{ccc}\hfill H& =& E^{★}+A^{★}+I^{★}+V^{★}+\frac{b_1}{2}{u}_1^2+\frac{b_2}{2}{u}_2^2+\frac{b_3}{2}{u}_3^2+\frac{b_4}{2}{u}_4^2+\frac{b_5}{2}{u}_5^2\hfill \\ & & {\displaystyle +{\lambda }_1[(1-u_1)\Lambda -\omega S^{★}-(1-u_2)\beta (I^{★}{S}^{★}+\eta A^{★}{S}^{★})}\hfill \\ & & -(1-u_2-u_3){\beta }_1{V}^{★}{S}^{★}]\hfill \\ & & {\displaystyle +{\lambda }_2[(1-u_2)\beta (I^{★}{S}^{★}+\eta A^{★}{S}^{★})+(1-u_2-u_3){\beta }_1{V}^{★}{S}^{★}}\hfill \\ & & -k_1\gamma E^{★}-k_2(1-\lambda )E^{★}-\omega E^{★}]\hfill \\ & & {\displaystyle +{\lambda }_3[k_2(1-\gamma )E^{★}-\omega A^{★}-v_1\varphi A^{★}-v_2(1-\varphi )A^{★}]}\hfill \\ & & +{\lambda }_4[k_1\gamma E^{★}+v_1\varphi A^{★}-ϵI^{★}-(\omega +\alpha )I^{★}]\hfill \\ & & {\displaystyle +{\lambda }_5[v_2(1-\varphi )A^{★}+ϵI^{★}-\omega R^{★}]+{\lambda }_6[(1-u_4)m_1{A}^{★}}\hfill \\ & & +(1-u_4)m_2{I}^{★}-(u_5+{\tau }_1)V^{★}].\hfill \end{array}$$

We now take into accounts the existence of the adjoint function λ_i, $i=1,2,3\dots 6,$ such that they satisfy the equations;

$$\begin{array}{ccc}\hfill \frac{d{\lambda }_1}{\mathit{dt}}& =& -\frac{\partial H}{\partial S^{★}},\hfill \\ \hfill {\displaystyle }& =& {\lambda }_1[\omega +(1-u_2)\beta (I^{★}+\eta A^{★})+(1-u_2-u_3){\beta }_1{V}^{★}]\hfill \\ & & {\displaystyle -{\lambda }_2[\omega +(1-u_2)\beta (I^{★}+\eta A^{★})+(1-u_2-u_3){\beta }_1{V}^{★}];}\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_2}{\mathit{dt}}}& =& -\frac{\partial H}{\partial E^{★}},\hfill \\ & =& -1+{\lambda }_2[k_1\gamma +k_2(1-\gamma )+\omega ]-{\lambda }_3{k}_2(1-\gamma )-{\lambda }_4{k}_1\gamma ;\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_3}{\mathit{dt}}}& =& -\frac{\partial H}{\partial A^{★}},\hfill \\ & =& -1+{\lambda }_1(1-u_2)\beta \eta S^{★}-{\lambda }_2(1-u_2)\beta \eta S^{★}\hfill \\ & & +{\lambda }_3[\omega +v_1\varphi +v_2(1-\varphi )]-{\lambda }_4{v}_1\varphi \hfill \\ & & {\displaystyle -{\lambda }_5{v}_2(1-\varphi )-{\lambda }_6(1-u_4)m_1;}\hfill \\ \hfill {\displaystyle \frac{d{\lambda }_4}{\mathit{dt}}}& =& -\frac{\partial H}{\partial I^{★}},\hfill \\ & =& -1+{\lambda }_1(1-u_2)\beta S^{★}-{\lambda }_2(1-u_2)\beta S^{★}\hfill \\ & & +{\lambda }_4[ϵ+\omega +\alpha ]-{\lambda }_5ϵ-{\lambda }_6(1-u_4)m_2;\hfill \\ \hfill \frac{d{\lambda }_5}{\mathit{dt}}& =& -\frac{\partial H}{\partial R^{★}},\hfill \\ & =& {\lambda }_5\omega ;\hfill \\ \hfill \frac{d{\lambda }_6}{\mathit{dt}}& =& -\frac{\partial H}{\partial V^{★}},\hfill \\ & =& -1+{\lambda }_1(1-u_2-u_3){\beta }_1{S}^{★}-{\lambda }_2(1-u_2-u_3){\beta }_1{S}^{★}\hfill \\ & & +{\lambda }_6(u_5+{\tau }_1);\hfill \end{array}$$

with the transversality condition ${\lambda }_i\left(t_f\right)=0$ given that ∀u_i where $i=1,2,\dots ,5,$ we have

$$\frac{\partial H}{\partial u_i}=0.$$

The optimal control strategies with respect to the befitting variation argument is given as;

$$\begin{array}{ccc}\hfill u_1^{★}& =& \text{min}\{\text{max}(0,\frac{{\lambda }_1\Lambda }{b_1}),u_{1\text{max}}\};\hfill \\ \hfill {\displaystyle u_2^{★}}& =& \text{min}\{\text{max}(0,\frac{(-{\lambda }_1+{\lambda }_2)[\beta (I^{★}{S}^{★}+n{A}^{★}{S}^{★})+{\beta }_1{V}^{★}{S}^{★}]}{b_2}),u_{2\text{max}}\};\hfill \\ \hfill {\displaystyle u_3^{★}}& =& \text{min}\{\text{max}(0,\frac{(-{\lambda }_1+{\lambda }_2){\beta }_1{V}^{★}{S}^{★}}{b_3}),u_{3\text{max}}\};\hfill \\ \hfill {\displaystyle u_4^{★}}& =& \text{min}\{\text{max}(0,\frac{{\lambda }_6[m_1{A}^{★}+m_2{I}^{★}]}{b_4}),u_{4\text{max}}\};\hfill \\ \hfill {\displaystyle u_5^{★}}& =& \text{min}\{\text{max}(0,\frac{{\lambda }_6{V}^{★}}{b_5}),u_{5\text{max}}\}.\hfill \end{array}$$

We progress with the numerical simulations on the optimal control by using the estimated parameters in Table 2.

4.1. Numerical results of the optimal control analysis

Using the forward-backward sweep method as introduced by Lenhart and Workman [49]; and extensively explored by [28], [50], [51], [52] and the references therein. We considered the following equal weight factors, initial data for the state variables along with the parameter values, thus $b_1=10,b_2=10,b_3=10,b_4=10,b_5=10$; $S\left(0\right)=30416000,E\left(0\right)=5,A\left(0\right)=5,I\left(0\right)=2,R\left(0\right)=0,V\left(0\right)=0$; $\Lambda =1319.294,\omega =0.10142578,\beta =0.0001,\eta =0.62811041,{\beta }_1=0.0001,k_1=0.07142238,k_2=0.014285824,\gamma ,=0.0374,v_1=0.20005051,v_2=0.79999398,\varphi =0.10500005,ϵ=0.0805840,\alpha =0.00440000,m_1=0.71780400,m_2=0.52152716,{\tau }_1=0.2900000$ for the numerical simulations of the optimal control problem. From Figs. 9 a–9 d, the solution trajectories which considers the individual effects of each of the control variables, $u_i,i=1,2,\dots ,5$ on the E, A, I and V population were figured out respectively. The red lines depict the uncontrolled population while the blue lines show the controlled population. These control measures were all highly significant in reducing the asymptomatic and the virus in the populations as compared to the exposed and severely infected populations. It can be inferred here that, adapting to these measures effectively minimize the rate of virus into the environment decreasing the rate of transmission through the environment which was very sensitive in the previous analysis, see Fig. 4. More to this, Fig. 10 demonstrates the solution trajectories by implementing all the control variables on the E, A, I and V populations with increase in time. Similarly, the red line represents the uncontrolled case while the blue line illustrates the collective controlled state.

Fig. 9.

Solution trajectories showing the effects of the combined efforts of optimal control strategies $u_i(i=1,2,\dots ,5)$ on the E, A, I and V populations for 90 days.

Fig. 10.

Solution trajectories showing the effects of the combined efforts of optimal control strategies $u_i(i=1,2,\dots ,5)$ on the E, A, I and V populations for 300 days.

Figs. 9e, f, 10e and f illustrate the optimal profile effects of respective controls u ₁, u ₂, u ₃, u ₄ and u ₅ on COVID-19 transmission dynamics in the population and the environment. Fig. 11 represents the effect of control u ₁ on COVID-19 transmission dynamics in the population and the environment. Comparisons of the dynamics of the subpopulations of exposed, asymptomatic, and symptomatic individuals and the number of virus with control u ₂ and without any control implementation is demonstrated by Fig. 12 . Fig. 13, Fig. 14, Fig. 15 shows the respective dynamics when control u ₃, u ₄ and u ₅ is used separately. It is revealed that the application of the control delayed the COVID-19 virus to peak, and significantly reduces the virus prevalence in the population and the size of the virus present in the community. It is observed that the numbers of exposed, asymptomatic, severely infected individuals, as well as the number of virus with control diminish more rapidly than when there is no control. It is seen that the separate use of any of the three controls causes a sharp decrease in the number of human infections as well as the number of virus presents in the community. To achieve an optimal control of COVID-19 at a minimized cost, then the following ideas deduced from numerical simulation’s results in Figs. 9e, f, 10 e and f can be adhered to: Considering the trajectory of the control measure u ₁, it can be seen that, u ₁ should be maintained at 0.5005 for the whole period until the 90th day then maintained at 0.499 after day 90 as shown in Fig. 10e. For the control measure u ₂, efforts must be implemented around 0.5005. Similarly, efforts on u ₃ also behave like u ₂. The major differences are that; the maximum effort which can be applied on u ₃ is around 0.50046 as compared to 0.5005 in u ₂ as shown in Fig. 10e and f. Given that the disease continues to persist within the 90 days, then the regulation on u ₄ is that, efforts must start from 0.4996 after day 90 as shown in Fig. 10f. Lastly, efforts on u ₅ must start around 0.4998 and gradually increased to around 0.5008. This effort has to be also maintained until the 90th day and maintained at 0.4998 after day 90 as shown in Fig. 10f. In a nut shell, the results of our optimal control analysis guarantee that, ensuring the effective utilization of the above-mentioned optimal control strategies will significantly contribute to the reduction in the spread within the susceptible population. This will far help to minimize the numerous effects which might have been experienced in the days ahead as far as the pandemic is concerned.

Fig. 11.

The optimal effect of applying only control u₁.

Fig. 12.

The optimal effect of applying only control u₂.

Fig. 13.

The optimal effect of applying only control u₃.

Fig. 14.

The optimal effect of applying only control u₄.

Fig. 15.

The optimal effect of applying only control u₅.

4.2. Cost-effectiveness analysis

Here, cost-effectiveness analysis is carried out based on the numerical implementation of the optimality system conducted in Section 4. The cost benefits associated with the implementation of the control strategies can be compared through cost-effectiveness analysis. Thus, following the approach used in several previous studies [53], [54], [55], [56], the incremental cost-effectiveness ratio (ICER) is calculated to determine the most cost-effective strategy of all the different control intervention strategies considered in this work. Most often, ICER is employed to measure up the changes between the costs and the health benefits of any two different control intervention strategies i and j competing for the same limited resources. ICER is defined mathematically as

$$\text{ICER}=\frac{\text{Difference}\text{in}\text{costs}\text{of}\text{control}\text{strategies}i\text{and}j}{\text{Difference}\text{in}\text{infections}\text{averted}\text{by}\text{control}\text{strategies}i\text{and}j}.$$ (21)

The numerator of ICER in Eq. (21) consists of the differences in intervention costs, averted disease costs and costs of prevented cases among others. While the ICER denominator measures the difference in health outcome, which includes the total population of infection averted or total number of cases of susceptibility prevented as the case may be.

Owing to the simulation results of the optimality system, the six control strategies, namely, Strategy 1 (u₁ only), Strategy 2 (u₂ only), Strategy 3 (u₃ only), Strategy 4 (u₄ only), Strategy 5 (u₅ only) and Strategy 6 (which combines the use of controls ui, i = 1, 2, … , 5) are ranked in increasing order of total number of infections averted as presented in Table 4 .

Table 4.

Strategies 1–6 in increasing order of the number of infections averted.

Strategy	Total infections averted	Total cost ($)	ICER
Strategy 6	4.4136 × 109	3.35	$7.5902\times {10}^{-10}$
Strategy 4	7.0065 × 109	0.05	$-1.2727\times {10}^{-9}$
Strategy 3	7.0550 × 109	0.80	$1.5464\times {10}^{-8}$
Strategy 5	1.0748 × 1010	0.45	$9.4774\times {10}^{-11}$
Strategy 1	1.1681 × 1010	1.25	$8.5745\times {10}^{-10}$
Strategy 2	1.7117 × 1010	0.80	$-8.2781\times {10}^{-11}$

Now, ICER is calculated for the intervention Strategies 6 and 4 in order to compare the two competing strategies incrementally as follows:

$$\begin{array}{cc}\hfill \text{ICER}\left(6\right)& =\frac{3.35}{4.4136\times {10}^9}=7.5902\times {10}^{-10},\hfill \\ \hfill \text{ICER}\left(4\right)& =\frac{0.05-3.35}{7.0065\times {10}^9-4.4136\times {10}^9}=-1.2727\times {10}^{-9},\hfill \\ \hfill \text{ICER}\left(3\right)& =\frac{0.80-0.05}{7.0550\times {10}^9-7.0065\times {10}^9}=1.5464\times {10}^{-8},\hfill \\ \hfill \text{ICER}\left(5\right)& =\frac{0.45-0.80}{1.0748\times {10}^{10}-7.0550\times {10}^9}=-9.4774\times {10}^{-11},\hfill \\ \hfill \text{ICER}\left(1\right)& =\frac{1.25-0.45}{1.1681\times {10}^{10}-1.0748\times {10}^{10}}=8.5745\times {10}^{-10},\hfill \\ \hfill \text{ICER}\left(2\right)& =\frac{0.80-1.25}{1.7117\times {10}^{10}-1.1681\times {10}^{10}}=-8.2781\times {10}^{-11}.\hfill \end{array}$$

From Table 4, it is observed that the value of ICER(6) is greater than that of ICER(4). This indicates that Strategy 6 is more costly and less effective than Strategy 4. For this reason, Strategy 6 is excluded from the list of alternative control interventions competing for the same limited resources and ICER is recalculated for Strategies 4 and 3 as illustrated by Table 5 .

Table 5.

Comparison between control intervention Strategies 4 and 3.

Strategy	Total infections averted	Total cost ($)	ICER
Strategy 4	7.0065 × 109	0.05	$7.1362\times {10}^{-12}$
Strategy 3	7.0550 × 109	0.80	$1.5464\times {10}^{-8}$
Strategy 5	1.0748 × 1010	0.45	$9.4774\times {10}^{-11}$
Strategy 1	1.1681 × 1010	1.25	$8.5745\times {10}^{-10}$
Strategy 2	1.7117 × 1010	0.80	$-8.2781\times {10}^{-11}$

It is seen from Table 5 that the value of ICER(3) is more than the ICER(4) value. The implication of this is that Strategy 3 is strongly dominated, more costly and less effective when compared with Strategy 4. Therefore, Strategy 3 is excluded from the list of alternative interventions and ICER is recalculated for Strategies 4 and 5. The results of the new computation is presented by Table 6 .

Table 6.

Comparison between control intervention Strategies 4 and 5.

Strategy	Total infections averted	Total cost ($)	ICER
Strategy 4	7.0065 × 109	0.05	$7.1362\times {10}^{-12}$
Strategy 5	1.0748 × 1010	0.45	$1.0691\times {10}^{-10}$
Strategy 1	1.1681 × 1010	1.25	$8.5745\times {10}^{-10}$
Strategy 2	1.7117 × 1010	0.80	$-8.2781\times {10}^{-11}$

Table 6 shows that the ICER(4) is lower than ICER(5). Then, it follows that Strategy 5 is more costly and less effective than Strategy 4. Hence, Strategy 5 is excluded from the list of alternative interventions and ICER is recalculated for Strategies 4 and 1 as shown in Table 7 .

Table 7.

Comparison between control intervention Strategies 4 and 1.

Strategy	Total infections averted	Total cost ($)	ICER
Strategy 4	7.0065 × 109	0.05	$7.1362\times {10}^{-12}$
Strategy 1	1.1681 × 1010	1.25	$2.5671\times {10}^{-10}$
Strategy 2	1.7117 × 1010	0.80	$-8.2781\times {10}^{-11}$

It can be seen in Table 7 that ICER(1) is greater than ICER(4). This implies that the implementation of Strategy 1 is more costly and less effective than the implementation of Strategy 4. Hence, Strategy 1 is discarded from the list of alternative control intervention strategies competing for the same limited resources. Now, the ICER is finally recalculated for Strategies 4 and 2 as shown in Table 8 .

Table 8.

Comparison between control intervention Strategies 4 and 2.

Strategy	Total infections averted	Total cost ($)	ICER
Strategy 4	7.0065 × 109	0.05	$7.1362\times {10}^{-12}$
Strategy 2	1.7117 × 1010	0.80	$7.4180\times {10}^{-11}$

Table 8 reveals that ICER(2) is greater than ICER(4). Hence, Strategy 2 is considered to be strongly dominated, more costly and less effective than Strategy 4. Consequently, Strategy 4 (cleaning of surfaces with home based detergents) is the most cost-effective strategy among all the six control intervention strategies under consideration in this work.

5. Concluding remarks

With reference to the recent travel restrictions in Ghana and other parts of the world, we formulated COVID-19 dynamics in Ghana as a deterministic model. The purpose of the study was to consider humans as key players in the transmission of this virus. The disease-free equilibrium and endemic equilibrium points were found to be globally asymptotically stable. We found that, the major transmission parameters β, β ₁, m ₁ and m ₂ contributing to the basic reproduction number of $1.99-3.37$ were all attributed to humans through personal contact with the susceptible class or activities with the environs. It is further inferred from this study that; applying optimal control strategy on the rate at which the virus is released into the system, m ₁ and m ₂, and also on the relative transmission rate due to human behavior will considerably strike down COVID-19 pandemic.

It was also found that, it might be possible the recovered individuals can be reinfected, see Fig. 8b. When this happens, then the number of the infected individuals will also increase. Therefore, we highly recommend that, drug manufacturers should aim at drug samples which will induce permanent immunity in the recovered individuals so as to reduce the susceptible population. Cost-effectiveness analysis was carried out based on the numerical implementation of the optimality system conducted in Section 4. This showed that, safety adopted by the asymptomatic and symptomatic individuals such as practicing proper cough etiquette by maintaining a distance, covering coughs and sneezes with disposable tissues or clothing and washing of hands after coughing or sneezing is the most cost-effective strategy, followed by intensifying the usage of nose mask and face shields through education, then the effective testing and quarantine when boarders are opened, fumigating the commercial areas such as markets, cleaning of surfaces with home-based detergents, and lastly, thecombination of all the control interventions analysed in this study. It is highly guaranteed that, this study will help policy makers in the control of the pandemic in Ghana. Further research on this subject and other epidemiological study can be investigated, such as

• 1.The impact of religious activities on the spread and control of the disease;
• 2.Optimal control model which seeks to reduce the disease induced death rate.

Data availability statement

The parameter values (data) used to support the findings of this study have been described in Section 3 and Appendix A.

Disclosure

The authors fully acknowledge that this paper was developed as a result of the first and second author’s thesis and project work.

CRediT authorship contribution statement

Joshua Kiddy K. Asamoah: Conceptualization, Supervision, Investigation, Cost-effectiveness analysis, Writing - review & editing. Mark A. Owusu: Investigation, Validation. Zhen Jin: Funding acquisition, Supervision, Review & editing. F.T. Oduro: Supervision. Afeez Abidemi: Cost-effectiveness analysis. Esther Opoku Gyasi: Review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Confirmed cases for Ghana as of 7th May 2020.

Table A.9.

Cumulative daily confirmed cases of COVID-19 as of 7th May, 2020 in Ghana.

Day	12th Mar	13th Mar	14th Mar	15th Mar	16th Mar	17th Mar	18th Mar
Cases	2	2	2	2	6	6	6
% Change	-	0	0	0	200	0	0
Day	19th Mar	20th Mar	21st Mar	22nd Mar	23rd Mar	24th Mar	25th Mar
Cases	11	16	21	24	27	51	66
% Change	83.3	45.5	31.3	14.3	12.5	88.9	29.4
Day	26th Mar	27th	28th Mar	29th Mar	30th Mar	31st Mar	1st April
Cases	68	132	137	137	152	161	195
% Change	3.0	94.0	3.8	0	10.9	5.9	21.1
Day	2nd April	3rd April	4th April	5th April	6th April	7th April	8th April
Cases	204	205	214	214	287	313	313
% Change	4.6	0.5	4.4	0	34.1	9.1	0
Day	9th April	10th April	11th April	12th April	13th April	14th April	15th April
Cases	378	408	566	566	566	566	641
% Change	20.7	7.9	38.7	0	0	0	13.3
Day	16th April	17th April	18th April	19th April	20th April	21st April	22nd April
Cases	641	641	834	1042	1042	1042	1279
% Change	0	0	30.1	17.0	0	0	22.7
Day	23rd April	24th April	25th April	26th April	27th April	28th April	29th April
Cases	1279	1279	1550	1550	1671	2074	2074
% Change	0	0	21.2	0	7.8	24.1	0
Day	30th April	1st May	2nd May	3rd May	4th May	5th May	6th May
Cases	2074	2169	2719	2719	3091	3091	3091
% Change	0	4.6	25.4	0	12.0	0	0
Day	7th May
Cases	4012
% Change	12.0

Supplementary material

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.chaos.2020.110103.

Appendix B. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/