Tabular Potentials for Monte Carlo Simulation of Supertoroids with Short-Range Interactions

Abstract

We describe a methodology for constructing tabular potentials of supertoroids with short-range interactions, which requires the calculation of the volume of overlap of these shapes for many relative positions and orientations. Recent advances in the synthesis of anisotropic colloids have made experimental realizations of such particles feasible and have increased the practical impact of fundamental simulation studies of these families of shapes. This extends our recent work on superquadric potentials to now include a family of ring-like shapes with a hole in the middle. Along with the addition of supertoroids, the ability to make tables for nonidentical particles and particle pairs with multiple, disconnected overlap volumes was added. Using newly developed extensions to a previously published algorithm, we produced tabular potentials for all of these new cases. The algorithmic developments in this work will enable Monte Carlo simulations of a wider variety of shapes to predict thermodynamic properties over a range of conditions.

1. Introduction

Due to the development of new techniques for nanoparticle construction [1–5], recent years have seen rapid growth in the use of anisotropic colloids [6, 7]. Colloids have become an appealing base for self-assembly studies because the interaction, both attractive and repulsive, between particles can be controlled by manipulating the properties of the individual particles, such as the particle anisotropy [8–11]. This push for the development of more exotic types of colloids has caused an increased demand for simulations that accurately and efficiently predict the system behavior over a range of thermodynamic conditions. Many studies have presented models that describe the behavior of systems of convex, solid particles [10, 12–14]. Expansion of the model to include porous, concave [15–18] shapes would allow the examination of systems relevant for drug delivery [17, 19–21], optics [17, 19], catalysis [22], and photonics [20, 21]. Existing models also focus on single-component systems [9, 18], rather than multicomponent systems. While existing algorithms aim to efficiently compute the overlap of hard superquadrics during the many-particle simulation [23], computational time may be further reduced by use of tabular potentials. This work outlines a modification to the methodology presented in Ref. [10], which was previously used to create tabular potentials for simulation of superquadrics, so that the method is now also capable of simulating supertoroids.

Supertoroids and superquadrics are both sets of geometric primitives that can have their curvature and spatial dimensions easily manipulated to model a wide variety of shapes [24]. However, supertoroids are challenging to simulate due to the hole in the middle. In some special cases, when another particle of similar size approaches the surface of the toroid, but it is too large to pass through the hole, there is effectively a concave curvature to the surface. This effective concave curvature due to the presence of the hole must be handled with the specialized algorithms discussed in this work due to the possibility that the excluded volume overlap of two particles contains multiple regions that are not connected. If another particle is small enough to pass through the hole in the toroid, then inner and outer surfaces must be distinguished, which is beyond the scope of this work. Other factors included in this work are modifications to the algorithm such that tables were generated for nonidentical particles. The methodology described within this manuscript was implemented in the FEASST simulation package and is planned for eventual public release [25]. The methods for the modifications are outlined in Sec. 2, and the results for specific cases are given in Sec. 3.

Specifically, the following four different pair interactions were considered: toroid-toroid, supertoroid-supertoroid, cube-sphere, and toroid-sphere. These cases were divided into the following two categories: interactions between identical particles (Sec. 3.1), and interactions between nonidentical particles (Sec. 3.2). Finally, conclusions and future work are discussed in Sec. 4.

2. Methods

2.1. Supertoroids and the Depletant Potential

Particles were modeled using the supertoroid equation given by the following parametric equation [24].

$$r(\eta ,\omega )=\left[\begin{array}{c}{a}_4+{\text{cos}}^{{\epsilon }_1}\eta \\ a_3{\text{sin}}^{{\epsilon }_1}\eta \end{array}\right]\otimes \left[\begin{array}{c}{a}_1{\text{cos}}^{{\epsilon }_2}\omega \\ a_2{\text{sin}}^{{\epsilon }_2}\omega \end{array}\right]=\left[\begin{array}{c}{a}_1\left(a_4+{\text{cos}}^{{\epsilon }_1}\eta \right){\text{cos}}^{{\epsilon }_2}\omega \\ a_2\left(a_4+{\text{cos}}^{{\epsilon }_1}\eta \right){\text{sin}}^{{\epsilon }_2}\omega \\ a_3{\text{sin}}^{{\epsilon }_1}\eta \end{array}\right]\begin{array}{l}-\mathit{\pi }\le \eta \le \mathit{\pi }\hfill \\ -\mathit{\pi }\le \omega \le \mathit{\pi }\hfill \end{array}$$ (1)

The ε₁ and ε₂ parameters define the curvature of the particle. The a₁, a₂, and a₃ parameters are scaling factors that determine the extents of the particle along the axis in the x, y, and z dimensions, respectively. In the z dimension, the particle extends up to values of ±a₃, but the maximum extents of the particles in the x and y dimensions also depend upon the a₄ parameter, which is directly related to the size of the hole. Note that Eq. (1) reduces to the superquadric equation when a₄ = 0. Figure 1 shows the relationship between a₄ and the size of the hole in the supertoroid.

Fig. 1.

The cross section of a toroid in the x-y plane, where ε₁ = ε₂ = 1 and a₁ = a₂. The outer and inner surfaces intersect the x and y axes at a_i(a₄ + 1) and a_i(a₄ − 1), respectively (i.e., i = 1, 2 for x, y).

In order to specify the relative position and orientation of two particles, one particle is used as a reference. Specifically, the center of the reference particle is on the origin, as described by Eq. (1). In addition, the orientation of the reference particle is also as described in Eq. (1). The relative position of the center of the second particle with respect to the center of the reference particle is defined by spherical coordinates (r_S, θ_S, ϕ_S) using the mathematical convention of radial, azimuthal, and polar angles, respectively. The orientation of the second particle relative to the reference particle is defined using Euler angles (ϕ_E, θ_E, ψ_E), which represent a rotation with respect to the orientation of the reference particle. These Euler angles are defined via the so-called “x-convention,” which is given by a rotation by ϕ_E about the z-axis, θ_E about the new x-axis, and then ψ_E about the new z-axis. With these six degrees of freedom, we are able to describe any spatial configuration of two particles. All angles are defined in radians in this work, and the ranges of each of these angles are considered from 0 to π/2, using 51 evenly-spaced points between and inclusive to these bounds for the calculations in the following results section.

The following anisotropic model is similar to that described in Ref. [10]. In particular, the shapes are modeled as hard particles with short-range attractions given by an implicit depletant potential. The total potential energy between two particles, U, is given by

$$U=U_h+U_d$$ (2)

where U_h is the potential energy due to hard sphere interactions, and U_d is the short-range attraction. The hard potential is simply given by

$$U_h=\{\begin{array}{ll}\infty \hfill & \text{ if }r<r_h\hfill \\ 0\hfill & \text{ if }r\ge r_h\hfill \end{array}$$ (3)

where r_h is the hard contact distance, which is a function of orientation and is computed numerically [10]. This numerical calculation utilizes a grid of surface points, as described in Ref. [10], using the parameter n_s = 50 in this work.

A short-range depletant potential, U_d, is described by

$$U_d=-\frac{\Delta V_{ex}}{\frac{4}{3}\pi R_d^3}\varphi k_{B}T$$ (4)

where R_d = 0:04 is the radius of a depletant particle, k_B is the Boltzmann constant, T is the temperature, ϕ is a depletant number density, and ΔV_ex is the excluded volume overlap between two supertoroid particles, which is computed numerically. This excluded volume calculation represents an implicit model of an ideal gas of noninteracting solvent. The use of these pairwise interactions in Monte Carlo simulations also assumes that many-body effects are minimal. This many-body assumption increases in validity as the ratio of R_d to the particle size [e.g., max(a₁, a₂, a₃)] decreases to values much less than one. A visualization of the depletant system is shown by Fig. 2, where the explicit version shows the depletant particles along with the larger supertoroids, and the implicit version shows the excluded volume around the supertoroids that the depletant is unable to occupy. The overlap of these excluded volumes represents the extra space that is freed up in the bulk, which the depletant molecules can sample relative to the infinite separation case. Thus, there is an entropic driving force for the excluded volumes to overlap, and this effect may be calculated analytically as in Eq. (4), by assuming the depletants are noninteracting point particles. The excluded volume was approximated by increasing the size of the shape with the following transformations, similar to the method described in Ref. [10]. The first three size parameters were transformed as a_i → a_i + R_d for i = 1,2,3. The particle center to ring center distance, a₄a₁, as shown in Fig. 1, remains constant. Thus, the parameter for the size of the hole was transformed as $a_4\to \frac{a_1}{a_1+R_d}{a}_4$ for the case of a₁ = a₂. This transformed shape represented the approximate excluded volume and was centered and oriented the same as the hard particle shape. The potential at contact, U(r_H), was then computed based on the overlap volume of these transformed shapes. For the remainder of this manuscript, we normalize the potential energy, U, by the arbitrary energy scale ϕk_BT. Thus, the normalized potential energy is simply the negative ratio of the overlap of the excluded volumes to the volume of a spherical depletant. The overlap of the excluded volumes was computed as described in Ref. [10], using voxels of size 0:05 and 128 test points per voxel.

Fig. 2.

The depletant system using two different visualizations. Explicit shows depletant particles surrounding larger colloids, while implicit shows the excluded volume around each colloid.

The hard contact distance, r_H, and the excluded volume, ΔV_ex, are computationally expensive to calculate. Thus, values of the potential for various orientations of two particles were calculated and stored in a table, referred to as the tabular potential, for use during the simulation of the particles. The focus of this work is the optimization of the calculation of the tabular potential [10] for use with supertoroids.

2.2. Algorithm

To compute ΔV_ex, the methods outlined in Appendixes B and C of Ref. [10] were utilized, with two optimizations that made the algorithm capable of handling the special cases presented by supertoroids. First, an initial estimate of the region of overlap of the two shapes was obtained as described in Fig. 3. We could encapsulate each toroid in a sphere that contained all possible orientations of each individual supertoroid. While it would be more efficient to consider only the overlap of the sphere, it was computationally more simple to consider the overlap of two cuboids or boxes that contained these spheres. The overlap of the two boxes provided a maximum possible volume of overlap for the two shapes, based solely on the relative distance between the particle centers and the maximal extent of the particle surface from the center in any direction. This method reduced the volume necessary for the Monte Carlo integration and thus reduced the time required to compute the overlap volume, depending on the shape.

Fig. 3.

A two-dimensional cross section of the concept used to estimate the finite region which contains the entirety of the overlap of the shapes. The maximum bounds of the shape from the center to each dimension are illustrated as a bounding box for each particle. The overlap of these bounding boxes then becomes the region in which Monte Carlo integration is performed.

In the previous study [10], concave shapes were not used due to the possibility that two separate regions of excluded volume overlap could be created along a concave surface. Due to the hole of the supertoroid, the possibility of distinct and separate excluded volume regions could not be avoided. The method described in Ref. [10] uses the most recent point of contact from the hard surface calculation to initialize the flood fill algorithm for Monte Carlo volume integration of voxels. With the possibility of two distinct volumes of overlap that do not touch, the previous method would only find one of these overlap volumes. Thus, for the supertoroid overlap volume calculation, all of the points that define the hard surface were then used to initialize voxel searches, also taking into account the previous search so as to not overcount. This resulted in a slight decrease in efficiency, but it enabled the calculation of multiple regions of ΔV_ex.

3. Results

In the following subsections, four different pairs of shapes were considered with reported values for the hard contact distance, r_h, and the energy at contact, U(r_h). In the remainder of this section, we simply refer to U(r_h) as the potential energy. Thus, the potential energy is always reported as that at contact in the remainder of this work and is normalized by ϕk_BT. The four pairs of shapes include toroid-toroid, supertoroid-supertoroid, cube-sphere, and toroid-sphere. These test cases were chosen for a broad array of shapes, and were divided into two categories. First, we consider the interaction between two identical toroids and supertoroids in Sec. 3.1. Then, we consider the interaction between nonidentical particles, specifically for cube-sphere and toroid-sphere interactions in Sec. 3.2. This broad range of particle pair interactions demonstrates the range of types of shapes that may be considered within the methodology described in this manuscript. However, we do not consider any case where the toroid is large enough that another particle may fit inside the hole, which is beyond the scope of this work. All shapes were normalized such that their maximum extents in the largest dimension is unity.

3.1. Identical Supertoroids

Here, we consider the interaction between two identical toroids and supertoroids. Toroids are distinguished from supertoroids as the shape that is formed when a circle or ellipse is rotated about a point outside of the circle or ellipse but along one of the two principal axes. Thus, toroids have the parameters ε₁ = ε₂ = 1, while supertoroids are not subject to this constraint.

The first test case is that of toroid-toroid interactions. The toroids are described by the following parameters: a₁ = a₂ = a₃ = 0.2, a₄ = 1.5, and ε₁ = ε₂ = 1. This shape is the solid of revolution that would result from rotating a circle of radius 0.2 about the z-axis, where the circle is centered on the x-axis at a point of a₁ a₄ = 0.3. Figure 4 shows a plot of the calculated hard contact distance for identical round supertoroids over a range of $0\le {\varphi }_S\le \frac{\pi }{2}$ while all other angles are held constant at 0. When ϕ_S = 0, the two toroids stack on top of each other and are separated by a distance of 2a₃ = 0.4. As ϕ_S increases, the orientations of the toroids remain fixed, but the relative position of the toroids changes as the center of the top toroid is rotated along the x-axis. When ϕ_S reaches a value of π/2, the toroids are touching on the sides with a center separation distance of 2a₁ (a₄ + 1) = 1.

Fig. 4.

Hard contact distance, r_H (center to center distance between particles when particle surfaces touch), for identical, round supertoroids (a₁ = a₂ = a₃ = 0.2, a₄ = 1.5 and ε₁ = ε₂ = 1) as a function of the polar spherical coordinate, ϕ_S. Visualizations of ϕ_S = 0 and π/2 are shown on the left and right, respectively. All other spherical coordinate angles and Euler angles are 0. Note that all distances were dimensionless by normalization with their maximum extents in the largest dimension.

The potential energy at contact is shown in Fig. 5 for the toroid-toroid interaction as a function of the two spherical coordinate angles when Euler angles are zero. When the Euler angles are 0, the z-axis is the axis of revolution of both particles. Thus, there is no dependence on the azimuthal angle, θ_S. The potential decreases with increasing polar angle, ϕ_S, because the most contact between the toroids is possible when this angle is zero, and there is a circular contact line. As ϕ_S increases, the particles move toward a side-by-side relative orientation and there is only a point of contact instead of a line. This leads to a decrease in the overlap of the excluded volumes of the two shapes. Figure 5 also shows the dependence on the Euler angles. The potential is independent of the first rotation about the z-axis, ϕ_E, because the toroids are solids of revolution oriented about the z-axis. As θ_E, the second rotation about the new x-axis, increases to a value of π/2, the toroids become perpendicular. This perpendicular configuration does not have as large of an excluded volume overlap. Note that special symmetry for ε₁ = ε₂ = 1 allows for a reduced table size, as utilized in Ref. [10] for cylinders.

Fig. 5.

The toroid-toroid potential energy at hard contact for the shapes described in Fig. 4 as a function of (left) two spherical coordinates, the azimuthal θ_S and polar ϕ_S, while Euler angles are zero, and (right) two Euler angles while the spherical coordinate angles are zero.

The next test case is for supertoroids. Supertoroids have ε₁ ≠ 1 or ε₂ ≠ 1. The supertoroids are described by the following parameters: a₁ = a₂ = a₃ = 0.1, a₄ = 4, and ε₁ = ε₂ = 0.01. The small ε parameters lead to sharp edges and vertices. The supertoroid extends 2a₁ (a₄ + 1) = 1 in the x and y coordinates and 0.2 in the z coordinate. The square hole in the toroid is of size 2a₁ (a₄ − 1) = 0.6 in the x and y dimensions (i.e., i = 1, 2) and 2a₃ = 0.2 in the z dimension. Figure 6 shows a plot of the calculated hard contact distance for identical square supertoroids over a range of $0\le {\varphi }_S\le \frac{\pi }{2}$ while all other angles are held constant at zero. When ϕ_S = 0, the two supertoroids stack on top of one another and are separated by a distance of 2a₃ = 0.2. As ϕ_S increases, the orientations of the toroids remain fixed, but the relative position of the toroids changes. When ϕ_S reaches a value of ϕ/2, the toroids are touching on the flat sides with the centers separated by a distance of unity. There is a peak in r_H just before ϕ/2 is reached, which corresponds with the configuration where the top edge of the bottom toroid is touching the bottom edge of the top toroid. This behavior is not observed in the round toroids and is due to the sharp edges determined by the small ε parameter values.

Fig. 6.

Hard contact distance, r_H, for identical, square supertoroids (a₁ = a₂ = a₃ = 0.1, a₄ = 4, and ε₁ = ε₂ = 0.01) as a function of the polar spherical coordinate, ϕ_S. Visualizations of ϕ_S = 0 and π/2 are shown on the left and right, respectively. All other spherical coordinate angles and Euler angles are zero.

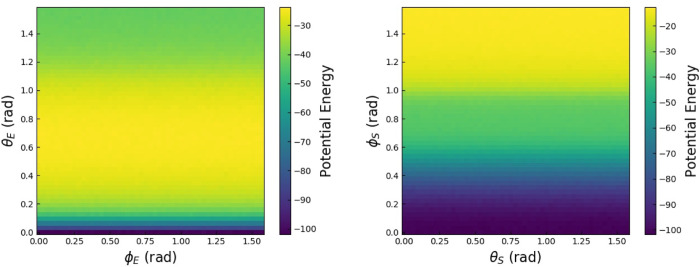
The potential energy at contact is shown in Fig. 7 for the supertoroid-supertoroid interaction as a function of the two spherical coordinate angles when Euler angles are zero. In this case, the supertoroids are not solids of revolution along the z-axis as was the case for the toroids. Thus, there is a dependence on the azimuthal angle, θ_S, as well as the polar angle, ϕ_S. In this case, the most excluded volume overlap is seen for low values of ϕS, when the entire face is in contact on the plane perpendicular to the z-axis. When ϕ_S = 0, there is no θ_S dependence by definition. However, as the polar angle increases, the overlap decreases until the edges touch as described for the peak in Fig. 6. The potential then decreases slightly as the skinny sides of the supertoroids contact. Figure 7 also shows the dependence on Euler angles. As opposed to the round toroid case, there is no axis of symmetry, and thus a nontrivial dependence on both Euler angles. As θ_E increases to π/2, the toroid rotates such that the skinny side of the top supertoroid contacts two separate ends of the ring of the reference toroid, as shown in the image at the top left corner in the right image of Fig. 7. In this case, there are two separate regions of excluded volume overlap that must both be computed. The previous algorithm as described in Ref. [10] would not properly account for both of these overlaps, but the algorithm as described in this paper does. The most excluded volume overlap occurs when the supertoroids are stacked vertically on top of one another.

Fig. 7.

The supertoroid-supertoroid potential energy at hard contact for the shapes described in Fig. 6 as a function of (left) two spherical coordinates, the azimuthal θ_S and the polar ϕ_S, while Euler angles are zero, and (right) two Euler angles while the spherical coordinate angles are zero.

3.2. Nonidentical Particles

In the previous section and Ref. [10], only the interactions of two identical particles were considered. In this section, the pair of particles are not identical. In particular, we consider the interactions between a cube and a sphere first, and then a toroid and a sphere. For the cube-sphere interaction, the cube is defined by the following parameters: a₁ = a₂ = a₃ = 0.5, a₄ = 0, and ε₁ = ε₂ = 0.01. The cube has unit side lengths and relatively sharp edges due to the small ε parameters. The cube was defined as the reference particle on the origin, and the orientation is given by Eq. (1), while the sphere has a center position specified by the spherical coordinates. The sphere has the same parameters as the cube, except ε₁ = ε₂ = 1. Thus, the sphere has a diameter of unity. The sphere also has no dependence on Euler angles because of its isotropy.

The left image in Fig. 8 shows the calculated hard contact distance over the polar spherical coordinate, ϕ_S, from 0 to π/2. To begin, at ϕ_S = 0, the sphere is on top of the cube. As ϕ_S increases, the sphere rolls along the side of the cube and contacts with the edge of the cube at an angle of ϕ_S = π/4. At this point, the center of the sphere is as far as possible from the center of the cube while the objects are still in contact, at a value of $r_H=\sqrt{\left(2\right)}/2+1/2$. However, there is some noise in the computed contact distance in Fig. 8. This is due to the discrete nature of the algorithms used, where a grid with a finer mesh would smooth out this discrepancy. The ε parameters lead to this sharp edge, which is more difficult for the method to model precisely as opposed to more smooth surfaces. While the n_s parameter described below Eq. (3) may be increased to minimize this effect, n_s = 50 is still used in this work to demonstrate and warn the reader that certain shape combinations may require careful selection of these parameters.

Fig. 8.

(Left) Hard contact distance, r_H, for a cube centered on the origin and a sphere with center point given by the polar spherical coordinate, ϕ_S. The side lengths of the cube and the diameter of the sphere are both unity. All other spherical coordinate angles and Euler angles are zero. (Right) The cube-sphere potential energy at hard contact as a function of the two spherical coordinates, the azimuthal angle, θ_S, and the polar angle, ϕ_S.

The potential energy at contact, U(r_H), for the cube-sphere pair and both the azimuthal, θ_S, and polar, ϕ_S, spherical coordinates are shown in the right image of Fig. 8. The potential energy at contact is greatest when the sphere contacts the middle of the flat face of the cube. This is because the excluded volume overlap is the largest. This occurs when values of the spherical coordinates are either 0 or π/2. When both spherical coordinates are π/4, the sphere is in contact with a vertex or corner of the cube. The excluded volume overlap is thus minimum at this position, which is shown in the middle of the right image in Fig. 8.

Finally, we consider the interaction between a toroid and a sphere. In this case, the toroid is round as in the very first test case, with the following parameters: a₁ = a₂ = a₃ = 0.2, a₄ = 1.5, and ε₁ = ε₂ = 1. Thus, the toroid is 0.4 high in the z-dimension, with its axis of symmetry along the z-axis. The toroid is used as the reference particle, and it also has a cross section with unit diameter for the outer surface in the x-y plane. The left image in Fig. 9 shows the distance between the centers of the two particles as a function of the polar spherical coordinate, ϕ_S. When ϕ_S = 0, the sphere sits slightly inside of the hole of the toroid, at a value that is less than half of the sum of the z-dimension parameters, a₃, of both shapes (e.g., a little less than 0.7). As ϕ_S increases, the sphere rolls outside of this hole, and the distance between the centers increases nearly linearly, until it eventually plateaus at a distance of 1 when ϕ_S = π/2.

Fig. 9.

(Left) Hard contact distance, r_H, for a toroid centered on the origin and a sphere with center point given by the polar spherical coordinate, ϕ_S. The sphere has a diameter of 1, and the toroid has the following parameters: a₁ = a₂ = a₃ = 0.2, a₄ = 1.5, and ε₁ = ε₂ = 1. (Right) The toroid-sphere potential energy at hard contact as a function of the azimuthal, θ_S, and polar, ϕ_S, spherical coordinates.

The right image in Fig. 9 shows the potential energy at contact as a function of the spherical coordinates. There is no dependence on the azimuthal spherical coordinate, θ_S, because of the rotational symmetry of the toroid about the z-axis and the isotropy of the sphere. Note that the algorithm uses random numbers to compute the excluded volume overlap, and thus there is some noise associated with this procedure. In particular, the volume of overlap of the two shapes is determined by the ratio of randomly selected points within the voxel that are inside of both shapes. Thus, even when the overlap volumes should be exactly the same, a different series of random numbers may yield a slight variation in the volume calculation; this is the source of the slight differences in color that may be observed for different values of θ_S, and it may be diminished by increasing the number of test points per voxel, or decreasing the voxel size. The most favorable configuration by far is when the sphere sits slightly inside of the hole of the toroid at ϕ_S = 0. This leads to a large overlap of excluded volume when compared to any other configuration.

4. Conclusion

This work demonstrated an algorithm for computing a tabular potential of supertoroids, nonidentical particles, and shapes with the possibility of disconnected excluded overlap values. By adding these cases to the existing FEASST [25] software, the breadth of the algorithm is now greatly increased. However, the table generation is still limited by computation time. This time could be reduced by implementing rotational symmetry for the supertoroids to limit the number of angles for which the potential needs to be explicitly calculated. Further improvement could be obtained by minimizing the size of the initial overlap volume bound as described in Fig. 3. Future work includes using the tabular potential to conduct Monte Carlo simulations of supertoroids, but this is beyond the scope of this work. Similarly, more work needs to be done to include nonidentical particles in simulations, as these would currently require more than one tabular potential to simulate. Furthermore, particles that fit inside the hole of a supertoroid may require separate inner and outer tabular potentials.

About the authors:

Harold Hatch is a chemical engineer in the Chemical Sciences Division in the Material Measurement Laboratory of the National Institute of Standards and Technology. Gordon McCann conducted this work as a summer undergraduate research fellow at the National Institute of Standards and Technology while completing his degree in the Physics Department at Gettysburg College. Gordon McCann is now a graduate student in the Physics Department at Florida State University. The National Institute of Standards and Technology is an agency of the U.S. Department of Commerce.