Navigating Through Time: A Spatial Navigation Perspective on How the Brain May Encode Time

Abstract

Interval timing, which operates on timescales of seconds to minutes, is distributed across multiple brain regions and may use distinct circuit mechanisms as compared to millisecond timing and circadian rhythms. However, its study has proven difficult as timing on this scale is deeply entangled with other behaviors. Several circuit and cellular mechanisms could generate sequential or ramping activity patterns that carry timing information. Here we propose that a productive approach is to draw parallels between interval timing and spatial navigation, where direct analogies can be made between the variables of interest and the mathematical operations necessitated. Along with designing experiments that isolate or disambiguate timing behavior from other variables, new techniques will facilitate studies that directly address the neural mechanisms that are responsible for interval timing.

INTRODUCTION

Perhaps no concept is simultaneously as permeant and as elusive as time. It pervades our behaviors and is ingrained in our language and interactions, yet it is unclear if time is a real physical quantity (Rovelli 2018). No sensory organ is dedicated to the detection of time, indicating that our percept and concept of time are internally generated, maintained, and understood. As humans, our devotion to clocks, schedules, and “ETAs” has clouded our ability to describe what is a natural timing behavior in the animal kingdom, and thus we may overestimate the importance of timing.

But consider the alternative, that timing is so innate and natural that we take it for granted. Imagine a foraging animal who detects a nearby predator (Figure 1a). To avoid capture, she freezes and stops foraging until she thinks the danger has passed (Dill & Fraser 1997; Koivula et al. 1995). An optimal strategy would be to have an internal model of how long the predator typically stays in a given area (Cooper & Frederick 2007; Martín & López 1999) and to wait at least that long before venturing onward. Using an internal measure of time, she compares between the current duration and the estimated typical duration. Likewise, timing is important for the predator (Hugie 2003), as she can maximize her chances of catching dinner by waiting for the prey to emerge in an open field and then estimating how long it will take to intercept her expected trajectory. But this example illustrates a pitfall in studying time. Rather than measure how long it takes for the prey to reach safety, the predator can optimize her pursuit based upon relative distance (Jennions et al. 2003). This entanglement of time with variables such as distance and velocity often confound the study of timing. While one approach is to dedicate separate circuits to encoding pure timing and pure spatial information, an alternative implementation is for time to be embedded in an all-inclusive spatial-temporal framework, where a more general process generates behaviorally-relevant sequences (Buzsáki & Llinás 2017). The hippocampus has been proposed as the region where these variables are integrated (Eichenbaum 2017; Hasselmo 2012; Hasselmo et al. 2010; Meck et al. 1984, 2013).

Figure 1: Scales of neural timing and analogy to spatial navigation.

(a) An animal is foraging for food when a predator is detected. The animal can choose to wait for a given amount of time (top) or risk continuing without waiting (bottom). (b) Diversity of timescales, brain regions, and neural circuits involved in the encoding of time from milliseconds to days. (far left) Neurons in auditory cortex tuned to msec inter-click intervals (Sadagopan & Wang 2009). (middle left) In eyeblink conditioning, a conditioned stimulus (tone) precedes an unconditioned stimulus (air puff) by a fixed interval, and animals learn to blink and cerebellar neurons respond just before the air puff (Berthier & Moore 1986; Kotani et al. 2003). (near left) Two odors are presented with a delay, and the animal licks to receive a reward only when the odors are identical. Pyramidal cells of hippocampus fire sequentially during the delay period (MacDonald et al. 2013). (near right) Animals press a lever after a delay period to receive a reward. Neurons in cortex and striatum encode the delay period with a variety of patterns including tuning to various times or ramping activity (Matell et al. 2003). (middle right) Neurons in the LEC encode the cumulative duration of traversals in alternating black and white rooms over the course of tens of minutes (Tsao et al. 2018). (far right) A transcription-translation feedback loop in neurons of the suprachiasmatic nucleus results in 24-hour rhythms (Takahashi 2017; Welsh et al. 1995). Illustrations inspired by data from the cited studies. (c) Spatial path integration in 2-D (left half). At ‘start,’ position is known exactly. As the animal moves towards target ‘end’ or goal, actual position x(t) is shown in black and internal estimate of position x’(t) in gray. Integration of a velocity signal (yellow region, inferred from self-motion cues) updates position but accumulates error until landmark or border that allows for error correction is reached (‘reset’ or ‘end’, gray arrow). Cells in spatial navigation (right half), from left to right: velocity cells and head direction cells encode speed and orientation of the animal with uncertainty indicated in yellow; grid cells encode periodic representation of position; place cells encode current position; border cells indicate proximity to borders or objects. Grid cells integrate incoming speed and orientation signals and are summed to produce single-peaked place cells. Border cells can reset or correct these position signals. (d) Interval timing through time-integration in 1-D (left half). Elapsed time is measured after a start signal. External time t shown in black while internal estimate of time t’, in gray, indicates perception that more time (gray line above black line) or less time (gray line below black line) has elapsed relative to external time. Estimate of time is informed by a moment-by-moment temporal derivative that represents the animal’s ongoing passage of time signal and runs until a ‘reset’ (correction cue) or ‘stop’ is encountered. Cells of interval timing (right half): temporal derivative cell encodes internal representation of the passage of time, represented here as a pacemaker (left) whose inter-spike-interval dt’ approximates discrete time steps dt. Continuous-time version of this process is represented by temporal derivative cell whose deviation from true time (black line) is shown by the gray trace. Output of temporal derivative cell is integrated by hypothesized periodically firing temporal cells. These are summed to produce well-tuned time cells. Border cells fire at start or stop positions and reset or correct encoding of time in temporal periodic cells and in time cells.

While timing is fundamental, it is unclear how explicit or conscious its representation is, whether neural circuits precisely encode time, or how many neural clocks reside in the brain (Howard et al. 2014; Karmarkar & Buonomano 2007; Lusk et al. 2016; Meck 1996). In this review, to frame the discussion in a manner amenable to achieving mechanistic insight, we focus on pure timing in the brain that operates on the range of seconds to minutes. First, we discuss the brain regions and behaviors associated with the encoding of time across a broad range of timescales. Next, we draw an analogy to spatial navigation, as the seconds-minutes scale can be considered as navigating an abstract time dimension as opposed to space, and thus similar mechanisms and circuitry may underlie both. Within this framework we then explore cellular and circuit mechanisms capable of computing seconds-minutes timing. Finally, we propose experiments that could help uncover the neural circuitry responsible for these computations.

TIMESCALES OF NEURAL TIMING CIRCUITS AND BEHAVIORS

Organisms can accurately track temporal information across many timescales, from milliseconds to days. The circuits must be diverse enough to cover these timescales and also to match a wide range of desired behaviors (Figure 1b). Previous research has sought to establish whether the brain uses a single clock or many independent clocks in order to encode time across scales and modalities and whether different clocks might time using distinct or common neural mechanisms (Ivry & Schlerf 2008; Karmarkar & Buonomano 2007; Lusk et al. 2016; Merchant et al. 2013; Paton & Buonomano 2018). As evidence that the brain appears to use multiple independent clocks across different time scales, duration judgments at one interval are not disrupted by a distractor at a different timescale (Spencer et al. 2009).

Specialized circuits can operate with millisecond precision, especially for coordinating motor movements (Sober et al. 2018). The cerebellum has been implicated in a number of timing behaviors on this timescale (Ivry 1997; Mauk & Buonomano 2004), such as for eyeblink conditioning (Figure 1b, middle left). The auditory system is also specialized to operate with high temporal precision, with neurons detecting sub-millisecond interaural time differences (Carr & Konishi 1990) or others tuned to interval~10 ms (Sadagopan & Wang 2009) (Figure 1b, far left). On the other end of the timescale are the circuits involved in 24-hour circadian rhythms, particularly neurons of the suprachiasmatic nucleus (Takahashi 2017) (Figure 1b, far right).

Between these two extremes, many behaviors require tracking time at the intermediate scale of seconds-minutes (Figure 1b, middle panels). While our conscious perception of these timescales is well-ingrained in our lexicon (“just a sec,” “in a minute”), the neural mechanisms responsible are not well-understood. Nonetheless, the neocortex, basal ganglia, and cerebellum have been implicated in interval timing (Akhlaghpour et al. 2016; Bakhurin et al. 2017; Howard et al. 2014; Jin et al. 2009; Leon & Shadlen 2003; Lusk et al. 2016; Matell et al. 2003; Mello et al. 2015; Mita et al. 2009; Soares et al. 2016; Tiganj et al. 2018).

The hippocampus is also involved in interval timing as temporal information is crucial to memory and the hippocampus is heavily involved in episodic memory formation (Squire 1992; Tulving 2002). Following upon early efforts (Meck et al. 1984), numerous recent studies have expanded upon the role of the hippocampal formation in the encoding of time. For example, neurons in CA1 fire sequentially during a delay period between the presentation of two odors when animals are immobile (MacDonald et al. 2013) (Figure 1b, near left). Neurons in the rodent hippocampus and medial entorhinal cortex (MEC) represent elapsed time during treadmill running (Kraus et al. 2013, 2015; Mau et al. 2018; Pastalkova et al. 2008). In freely foraging rats, neurons in the lateral entorhinal cortex (LEC) ramp their activity over the course of seconds to minutes such that time intervals can be decoded from their population activity (Tsao et al. 2018) (Figure 1b, middle right). And in one final example, MEC neurons fire sequentially and tile the wait period in mice trained to stop at a door in virtual reality for 6 seconds (Heys & Dombeck 2018).

Given the vast difference in timing mechanisms at the ends of the spectrum (milliseconds: synaptic mechanisms; 24-hours: genetic mechanisms), discovery of the mechanisms responsible for the seconds-minutes scale should prove informative on their own and may also shed light on general mechanisms of neural circuits (Howard et al. 2014; Karmarkar & Buonomano 2007; Tiganj et al. 2015). Different mechanistic frameworks will be useful to guide interpretation of neural data and to design future experiments. In this context, we propose that a way forward for understanding this intermediate seconds-minutes timescale is to draw an analogy to spatial navigation.

DEFINITION OF VARIABLES IN INTERVAL TIMING BY ANALOGY TO SPATIAL NAVIGATION

Why Compare Seconds-Minutes Timing to Spatial Navigation?

The brain regions and neural mechanisms responsible for seconds-minutes time encoding may parallel that of spatial navigation. Many commonalities are shared between the two systems and in the encoded parameters. The timescale for activity patterns in spatially active cells in the rodent hippocampus, for example, spans periods of sub-second to tens of seconds (Bittner et al. 2017; Kjelstrup et al. 2008; Mau et al. 2018; Stensola et al. 2012). The resolution of time and space encoding appears to be similar; for example, the statistics of neural activity in hippocampal neurons during track navigation and duration-specific treadmill running are highly similar as quantified by field width, peak firing rates, and measures of population activity (Kraus et al. 2013; Pastalkova et al. 2008). Lesion studies also show parallels in the types of tasks that are dependent on the hippocampus. In spatial tasks, navigation based on cues is not hippocampus dependent, but navigation reliant on an allocentric map is hippocampus dependent (Maguire et al. 2006; Morris et al. 1982; O’Keefe & Nadel 1978). Similarly for timing tasks, delay classical conditioning is not hippocampus dependent but trace conditioning is hippocampus dependent (Bangasser et al. 2006; McEchron et al. 2003). These parallels indicate that the hippocampus is differentially necessary for aspects of spatial and temporal tasks.

Moreover, many brain regions with spatial representations also engage in seconds-minutes timing, and thus similar computational strategies and circuit motifs may be responsible in both cases. For example, alongside place cells in dorsal CA1 in the hippocampus, studies have found cells that encode temporal information or combined spatial and temporal information (Kraus et al. 2013; MacDonald et al. 2011). In MEC, spatially periodic grid cells coexist with time-encoding cells, while some grid cells can also encode temporal information (Heys & Dombeck 2018; Kraus et al. 2015). Thus, the study of time encoding may be able to follow the successful strategies used in the navigation field, where the tight interplay between theoretical models and experiments has yielded a rich understanding of the circuits involved in spatial navigation. Just as the brain uses idiothetic cues for path integration and sensory landmark cues for error correction through updates of current position during spatial navigation (Bush & Burgess 2014; Jayakumar et al. 2019; Savelli & Knierim 2019; Zhang et al. 2014), we reason that an internal sense of the passage of time may analogously be integrated to compute elapsed time while external sensory cues correct for errors (Figure 1c–d). Our main contention is that the neural computations underlying both systems share the same canonical form with two main components: integration and updates to correct for accumulated errors.

Defining the Variables and Concepts

Each key variable of spatial navigation has a complementary variable in seconds-minutes timing (Figure 1c–d): position in space x(t) (a 2-dimensional vector of spatial coordinates) to position in a time interval t, spatial velocity v = dx/dt to the passage of time γ = dt’/dt, physical boundaries or landmarks in space to sensory cues indicating the start, end, or intermediate position in a time interval. We distinguish actual position x(t) and the internal representation of position x’(t). Differences between these quantities indicate an error in the internal representation. Likewise, the internal representation of time t’ may deviate from t (e.g. t’ ≠ t).

In both cases, two key processes are necessitated: a moment-by-moment integration of a velocity signal (‘path integration’ or ‘time integration’) and the update of the representation based on sensory cues. The first process (‘time integration’) is useful in timing for the same reason path integration is used in spatial navigation: sensory cues may provide accurate locations in time or space, but they can be infrequent. To attain a continuous sense of time, an integration process is needed to bridge the gap. However, integration suffers from an accumulation of errors, and thus sensory cues can reset or correct the internal representations of time and space positions (Campbell et al. 2018; Jayakumar et al. 2019).

In seconds-minutes timing, the organism begins with a start point. Next, the duration of the timing period must be tracked in the absence of external cues using some internally generated representation of time and using ‘time integration’. This internal time t’ typically approximates an absolute (external) time t and its passage is denoted by what we term the temporal derivative defined as γ = dt’/dt, where the choice of γ is inspired by the use of the Lorentz factor in physics to relate the change in time between two reference frames (Lorentz 1903) and can be thought of as the perceived passage of time for an observer relative to absolute time (Figure 1d). At any point, sensory cues carrying information about external (absolute) time can adjust or reset the internal representation. These resets can be thought of as a new start point when the internal time t’ is synchronized to absolute time t. Similarly, in spatial navigation, after a start point, the internal spatial representation of position x’(t) is continuously updated by an estimate of distance travelled based on idiothetic cues used to estimate heading direction and speed, a process termed ‘path integration’ (McNaughton et al. 2006) or ‘dead reckoning’ (Figure 1c). At any point, sensory landmark cues can provide information to reset the internal representation of spatial position (x’(t) is synchronized to actual position x(t)).

A pure integrator of an uncorrelated random signal, such as we propose for path integration or time integration in the absence of external cues, accumulates error proportional to the square root of the distance or the time interval. This relation represents a lower bound. Observed error rates in interval timing are typically described as linear in accordance with Weber’s Law and scalar expectancy timing (Gibbon 1977), although error rates in time intervals inferred from population neural activity in at least one study appear to follow a square root relationship (Itskov et al. 2011). In practice, error rates can grow linearly with the time interval through simple changes in the statistics of the temporal derivative signal, such as correlated errors across time or a bias that shifts the signal up or down as exemplified by neuropharmacological manipulations that increase or decrease one’s perception of the passage of time (Meck 1996; Soares et al. 2016). External cues play a large role in error correction. In spatial navigation, even in the dark, the animal can use odors and somatosensory cues to guide navigation (Save et al. 2000). For example, interacting with the border of an open field can reset some of the errors accumulated by grid cells (Hardcastle et al. 2015). Thus, it is important to compare spatial path integration and seconds-minutes timing across conditions under which the presence and reliability of external cues or resets are similar.

Comparison to Cells of the Spatial Navigation System

Given these parallels, it is reasonable to hypothesize that similar cell types and encoding strategies may be encountered across the two systems and be found in similar brain regions (Figure 1c–d, lower panels). For example, many hippocampal place cells have single-peaked, well-tuned, and sparse firing fields (O’Keefe & Dostrovsky 1971) that are highly context-dependent and flexible (Anderson & Jeffery 2003). Time cells in the hippocampus with similarly single-peaked, well-tuned, and sparse fields have already been described (see below). Grid cells in the MEC are coherent over different contexts, and their multi-peaked firing fields appear unstructured over small environments (Fyhn et al. 2004), but the hexagonal structure is more apparent over larger environments (Hafting et al. 2005). These properties are consistent with specialized circuitry that yields a metric for space (Moser & Moser 2008). We expect that time encoding cells in the MEC similarly form a metric for timing, with periodically active multi-peaked time cells emerging for longer time intervals (Kraus et al. 2015). Place cells can also show multi-peaked firing in larger environments (Fenton et al. 2008), so multiple fields may also be expected for hippocampal time cells over longer times. We also expect start and stop cells that are similar to border cells in the spatial navigation system (Solstad et al. 2008). Lastly, analogous to head direction cells of the postsubiculum (Ranck 1984; Taube et al. 1990) and speed cells within MEC (Kropff et al. 2015), the input to the timing system should be a temporal derivative cell whose moment-by-moment firing rate represents the temporal derivative γ and can account for changes in the perception of the speed of time, a phenomenon dependent on emotional state (Schirmer 2011) or disease state (Densen 1977) and modifiable with certain drugs (Meck 1996) or optogenetic manipulations (Soares et al. 2016). Note however some nuances. Since time is one-dimensional and unidirectional, a ‘direction of time’ cell is not needed, so there is no analogy to head direction cells. Also, certain network architectures such as attractor networks could “move” neural activity at a constant velocity using asymmetric connectivity and thus avoid the need for a temporal derivative input. Lastly, the spatial encoding system stops updating when the animal stops as velocity inputs drop to zero, but in time encoding the temporal derivative input is presumably constant and will persist. An explicit stop or reset signal is required to halt time encoding.

Experimental evidence for many of these cell types already exists. Timing cells have been observed in the hippocampus over the 10–20 second timescale (Kraus et al. 2013; MacDonald et al. 2011) and in the MEC over the 6–8 second timescale (Heys & Dombeck 2018; Kraus et al. 2015). Temporal periodic cells with multiple activity peaks might be expected in MEC over longer timescales, which has been observed in grid cells during treadmill running (Kraus et al. 2015) and rest active cells during periods of immobility (Authors unpublished). Cells with ramping activity over timescales ranging from seconds to hours have been observed in the LEC (Tahvildari et al. 2007; Tsao et al. 2018), the hippocampus (Hampson et al. 1993) and other cortical structures (Quintana & Fuster 1999). An interoceptive signal that provides the temporal derivative signal would imply the presence of parallel mechanisms between time and space; for example, time cells in the MEC might be expected to perform integration of a temporal derivative signal using a similar circuit to grid cells integrating velocity and head direction signals. This signal could arise in the LEC or other regions such as the insula (Craig 2009; Wittmann 2009).

COMPUTATIONAL MODELS OF TIME REPRESENTATION

Various patterns of activity have been described by which neurons can encode time. These include cells that fire sequentially during a time interval, especially in the hippocampus and the MEC (Heys & Dombeck 2018; Kraus et al. 2013, 2015; MacDonald et al. 2011; Pastalkova et al. 2008; Salz et al. 2016) and cells that monotonically increase or decrease their firing rate during a time interval (Hampson et al. 1993; Tahvildari et al. 2007; Tsao et al. 2018). Why does the brain encode time in so different ways? Do the different activity patterns implement the same algorithm? Are the algorithms biologically plausible? Computational models that explain mechanisms underlying various patterns of time encoding could help provide answers.

Here, we focus on models of sequentially active cells and of ramping cells (Figure 2). A ramping code allows for any given individual cell to carry information about elapsed time throughout the entire interval and therefore fewer cells are needed. On the other hand, each moment in the ramping code is highly correlated to other moments, making it difficult to associate one moment with a memory of an item or an object. In contrast, with sequential activity, each cell is active at one specific moment, allowing association of this specific moment with an item and or an object by associative plasticity (Rolls & Mills 2019). Further, the code is energetically efficient as only one cell needs to be active at any given time point (Barlow 1972), but such a sparse code demands a larger population of cells for long intervals. Thus, each code may be better suited for given demands of the neural computation. Conversely, the biology of a given network or neuron may determine which coding strategy it can support.

Figure 2: Models for time cells.

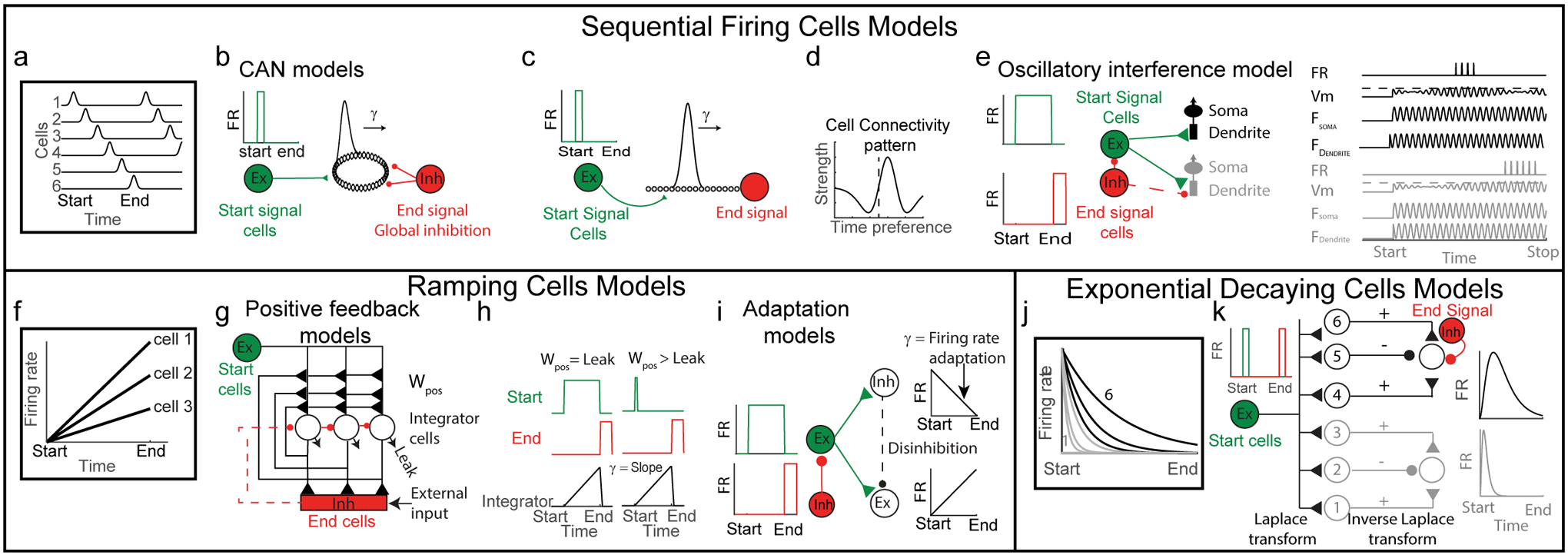
(a) Sequential firing of time cells. Each row represents firing rate (FR) of one cell. Each cell is active at a specific moment within the time interval, and together the sequence of firing cells tiles the entire interval. (b) Ring attractor CAN model. Start population of cells fire a burst at the beginning of the time interval (left, green) and input to a ring attractor (middle, black). Global inhibition provides end signal (right, red). (c) Line attractor CAN model. Start population fire a burst at the beginning of the time interval (left, green) and input to a line attractor (middle, black). End signal is simply cells at the end of the sequence (right, red). (d) Mean connectivity pattern of cells in the CAN model. y-axis represents strength of outgoing weights. x-axis represents time preference of cells that receive the inputs (aligned to the time preference of the output cell at 0, dashed line). (e) Sequence of 2 time cells created by the oscillatory interference model. Start cell fires during the entire interval (top left, green). End signal cell inhibits start cell or integrator cells at the end of the interval (left bottom). On the right a scheme of 2 cells (one in black and one in grey). Each cell excited by a start cell. The dendritic frequency oscillation of each cell (F_dendrite) is different than its somatic frequency oscillation (F_soma, which differs in the 2 cells) and results in an interference pattern (Vm). The membrane potential crosses the firing threshold every beat oscillation. (f) Scheme of 3 ramping cells. Each cell has a different slope. (g) A network model that uses a positive feedback mechanism to integrate inputs over time and generate ramping cells. All integrator cells receive feedforward input from start cells (green). Output integrator cells (black) are connected by recurrent excitation and also send excitation to end neurons. End cells (red) inhibit integrator cells once the rate of inputs they receive crosses a threshold or by external input. Adapted from (Seung et al. 2000). (h) Activity of each cell type (start cells: green; end cells: red; integrator cells: black) when recurrent excitation is equal to the leak current (left, W_pos > Leak). or when recurrent excitation is slightly higher than the leak current (right, W_pos > Leak). (i) A model network generating ramping activity by an adaptation process. A population of excitatory persistent firing cells (fire at a constant rate during the time interval) excite a population of inhibitory (Inh) and excitatory (Ex) neurons. Due to adaptation of the firing rate in the inhibitory neurons, their firing rate decreases. This disinhibits the excitatory population, which in turn increases their firing rate, which creates a ramping firing pattern. Adapted from (Reutimann et al. 2004). (j) Exponentially decaying firing rates of 6 cells with different time constants in response to a start burst, analogous to the Laplace transform of a delta function (a start burst). (k) Start cells (green) give a pulse input to a cell population with exponentially decaying firing rates, each with different time constants (the cells arranged according to their time constants in increasing order bottom to top). The exponentially decaying cell population projects to the output layer cells (on the right) through center-off surround-on connectivity pattern. Thus, each cell in the output layer receives a weighted sum of several exponential decaying cells, implementing an inverse Laplace transform, which in turn produces time cells in the output layer (Howard et al. 2014; Liu et al. 2019).

Models for Sequential Firing of Cells

In sequential firing of timing cells, each cell fires at a specific moment in time (time field) and together the population tiles the entire interval (Figure 2a). What network or cellular mechanisms could generate such a code? Several theoretical models of spatial path integration have suggested means through which grid and place fields could be formed. In many of these models, neurons path-integrate speed and direction of movement to form fields (Burak & Fiete 2009; Burgess et al. 2007; Fuhs & Touretzky 2006; McNaughton et al. 2006; O’Keefe & Recce 1993; Samsonovich & McNaughton 1997; Zhang 1996). These models can be modified for ‘time integration’, resulting in the formation of time fields instead of place fields and, at the population level, in the formation of sequences of firing fields.

Continuous attractor network models

In continuous attractor network (CAN) models (Burak & Fiete 2009; Couey et al. 2013; Fuhs & Touretzky 2006; Guanella et al. 2007; McNaughton et al. 2006; Samsonovich & McNaughton 1997), a population of neurons is arranged on a 2-dimensional sheet and connected using “Mexican hat” connectivity (Figure 2d). Excitation of this network generates a regular pattern of activity bumps. Inputs reflecting the animal’s velocity cause this pattern to move on the sheet, creating a place or grid firing pattern in single neurons. For time encoding, speed and direction input is not needed, and only a 1-D network and excitatory input supporting 1-D bump generation is needed. Cells at opposite ends of the 1-D network can be connected to form a periodic boundary condition, resulting in a ring attractor (Figure 2b) as in models of head direction (Blair et al. 2014; Sharp et al. 2001; Skaggs et al. 1995; Zhang 1996). Alternatively, the cells need not be connected at the ends, resulting in a line attractor (Figure 2c). One mechanism to generate movement of the bump at a constant speed is to use asymmetric connectivity (e.g. Mexican hat offset in one direction) (Figure 2d) or by threshold adaptation that creates effective connection asymmetry (Itskov et al. 2011). The temporal derivative (γ) in such a model is defined by the speed of the sequential firing of the cells (Figure 2b–c) and is controlled by the level of asymmetry (Figure 2d). Ideally these connections, and therefore the bump speed, would remain constant to represent external time consistently; however, this speed could be modified through plasticity or via external inputs. The speed of the sequential firing could also be used to encode different time intervals: longer intervals could be encoded by a slower moving bump and shorter intervals by a faster moving bump. Alternately, the bump could move at a constant speed for all time intervals and the number of cells participating in the sequence could change.

How and where could an activity bump be initiated? A start signal could be generated by a population of neurons that are driven by an external cue, which in turn excite a specific location on the 1-D network (Figure 2b–c), from which point time integration begins. Different contexts could be encoded by starting the bump at different locations on the 1-D network (Figure 2b–c). For time encoding, as opposed to space encoding, since the temporal derivative signal is internally generated, a distinct stop signal would likely need to act directly on the integrator. For a ring attractor, global (rather than focal) inhibition would be needed to suppress the bump(s) and prevent more from emerging (Figure 2b). Ambiguity in the amount of time encoded will arise if the duration of the interval is longer than the duration of one period around a ring attractor. This ambiguity could be solved using multiple modules, each with different periods. Interestingly, a modular grid code was found to be more efficient than a place cell code for encoding space (Burak et al. 2006; Mathis et al. 2012; Mosheiff et al. 2017; Sreenivasan & Fiete 2011). It remains to be seen whether time encoding is governed by similar rules.

Other similar models can also generate sequential activity for time encoding. For example, chaotic networks can generate sequential firing of cells similar to those found in the posterior parietal cortex (PPC) (Rajan et al. 2016). Time-dependent changes in the state of a complex neural network can also provide a reliable read-out of elapsed time (Karmarkar & Buonomano 2007; Laje & Buonomano 2013; Sussillo & Abbott 2009).

Oscillatory interference models

Oscillatory interference models (Burgess et al. 2007; O’Keefe & Recce 1993) could also generate sequential firing of time-selective cells. Each cell receives two oscillatory input signals, either through oscillating inputs, or by different cell compartments possessing different resonant frequencies that oscillate when depolarized (Giocomo et al. 2007) (Figure 2e). These signals interfere with each other, creating beat oscillations in the membrane potential. By modulating the frequency of one oscillator proportional to running speed, these models can generate 1-D place fields (O’Keefe & Recce 1993) and, with proper modifications, also 2-D grid firing fields (Burgess et al. 2007). A simple version of this model could generate time cells (Hasselmo 2008). For a constant temporal derivative, the two oscillatory signal frequencies should be fixed, resulting in temporal beat oscillations of the membrane potential and firing at every beat, creating time fields (Figure 2e). This model also resembles the use of multiple oscillators for encoding the order of words in serial recall (Brown et al. 2000) and temporal intervals in the timing of behavioral responses (Matell & Meck 2004; Miall 1989).

To generate a sequence of firing cells, various mechanisms could be used. Multiple cells could fire at the same beat frequency but with different phases. This is similar to gird cell networks, where grid cells belonging to the same module share the same spatial frequencies but differ in their phases (Barry et al. 2007; Stensola et al. 2012). This could be implemented by presynaptic cells triggering oscillations in time cells with different delays. The problem, however, is that these time delays must be on the order of the sequences they are meant to generate. Thus, the task of generating a time sequence is passed to the input layer, making such a scheme implausible. Alternatively, sequence generation could be implemented by different time cells oscillating at a range of different baseline frequencies (Hasselmo 2014) so that a single input frequency would result in different phases of firing across the population. In this model, if time cells fire periodically in time, the population firing sequence would not repeat and instead the cell firing order would change at each repetition. This contrasts with CAN models, which predict the preservation of the order of cells’ firing in each repetition. To circumvent these issues, combining CAN and oscillatory interference models has been used to model robust grid cell firing (Bush & Burgess 2014) and could also be useful for time encoding.

The start signal could be provided by cells that fire following certain internal or external cues and persist during the time interval (Figure 2e). Such persistent firing has been observed in entorhinal cortex (Tahvildari et al. 2007; Yoshida et al. 2008). Like CAN models, the temporal derivative (γ) in oscillatory interference models is defined by the speed of sequential firing. Encoding different time intervals could be implemented either by changing the speed of sequential firing (changing the frequency of one of the oscillators) or by using a constant speed of sequential firing, but recruiting a different number of cells according to the interval. Time integration could be terminated by inhibiting the start population or the integrator (time cells) directly (Figure 2e).

Models for Ramping Cells

Recordings in several brain areas have revealed cells that monotonically increase or decrease in firing rate during task time intervals (Hampson et al. 1993; Quintana & Fuster 1999; Tsao et al. 2018) (Figure 2f). This change in firing rate can appear linear or exponential and therefore elapsed time is encoded by instantaneous firing rate (Figure 2f). Though there are no clear analogies to ramping cells in spatial navigation, we consider ramping models since these cells have been widely described in the timing literature.

Temporal integrators

Cellular (Durstewitz 2003) and network (Shankar & Howard 2012) models have been proposed to explain ramping cell activity. In some models (Balcı & Simen 2016; Lim & Goldman 2013; Simen et al. 2011), the cells act as temporal integrators of their inputs. Leak currents counteract the input-driven depolarization. To counterbalance the leak current and effectively integrate and store inputs over time, cells require either a precise positive feedback mechanism (Seung et al. 2000; Simen et al. 2011) or a negative derivative feedback mechanism (Lim & Goldman 2013). In both cases, input depolarization is preserved over time through stable firing (Figure 2g, h). To generate ramping activity, an excitatory step input, which defines the temporal derivative (γ), could serve as the start signal (Figure 2h). Timing cells integrate this input by using positive feedback to generate a linear increase in firing rate (Figure 2h). The temporal derivative (γ) is represented by the slope of the ramp (Figure 2h). To terminate integration, inhibitory cells that are activated once the ramping cells reach a certain threshold could send negative feedback (Figure 2g, h), or the stop or reset signal could be provided by internal or external cues to drive inhibition of the timing cells (Figure 2g) (Durstewitz 2003; Grossberg & Merrill 1992; Grossberg & Schmajuk 1991).

Alternatively, the positive feedback could be larger than the leak currents (Durstewitz 2003), making the cells no longer perfect integrators. A start signal to such cells simply requires an excitatory burst to begin the positive feedback loop and time integration (Figure 2h), resulting in a gradual increase in firing rate during the interval (Figure 2h). The temporal derivative (γ) is defined by the increasing slope of the ramp, which is determined by the excess of positive feedback over the leak currents. The end mechanism could be the same as in the preceding section. Once the cells stop firing, inhibition at rest would be required to prevent spurious integration.

Adaptation models

Another model (Reutimann et al. 2004) makes use of adaptation to generate ramping. This entails three populations of cells. The first is composed of cells that fire at a constant rate from the beginning to end of the interval. During the interval, these cells excite a second population of inhibitory neurons and a third population of excitatory neurons (Figure 2i). The excitatory cells are also inhibited by the inhibitory cells. Adaptation in the inhibitory cells leads to a gradual decrease in their firing rate during the interval. This leads to disinhibition of the excitatory cells, which then gradually increase their firing rate, creating a ramping pattern. Thus, the time interval is encoded by both increasing (ramping) and decreasing (ramping) firing rates. The first population of persistent activity cells defines the start signal and the temporal derivative (γ) is defined by the firing rate adaptation (firing rate slope).

Using exponential firing rate or ramping cells to generate sequential firing

Another class of models uses exponential decay of firing rate, rather than linear changes in rate, with a range of decay rates across cells (Howard et al. 2014; Liu et al. 2019; Tiganj et al. 2015). A first population of cells performs a Laplace transform on a start input burst to generate different timescales of exponentially decaying firing rates across the population. A second layer of cells then performs an inverse Laplace transform to generate timing fields in sequentially activated cells. This model allows for coding time over a wide range of timescales (Figure 2j–k) and accounts for the decrease in numerical density and increase in variance often observed in time cell responses over longer intervals (Mau et al. 2018; Tiganj et al. 2018). Similarly, it is also possible to generate sequential firing by adjusting ramping cell input through a Hebbian learning rule together with mutual inhibition between cells to ensure sparse activity (Rolls & Mills 2019).

PROPOSED EXPERIMENTS

Behavioral design to isolate timing and perturbations to test causality

As time is entangled in most behaviors in one way or another, studying timing circuitry during immobility helps isolate time from other variables. Interestingly, in the hippocampal-entorhinal region, different circuits appear to be recruited depending on whether animals are mobile or immobile (Arriaga & Han 2017; Heys & Dombeck 2018; Kay et al. 2016). Recent studies in rodent LEC found that neural activity patterns recorded during open field foraging could be used to decode time during the experience (Tsao et al. 2018). However, it is unclear if the neural representations indeed relate to the animal’s perception or memory of time or whether the neural representation serves to encode other sensory stimuli or motor patterns that were systematically changing. Similarly, hippocampal sequences recorded during wheel running (Pastalkova et al. 2008) can carry temporal information; however, with animals running at a fairly constant pace it is difficult to distinguish time from distance. Treadmill running with variations in speed were later used to distinguish these possibilities and demonstrate time encoding during locomotion in MEC (Kraus et al. 2015), demonstrating the importance of experimental design when investigating time encoding.

Engaging animals in timing tasks in which temporally informative sensory and motor cues are kept to a minimum, and thus the passage of time is the dominant variable, could alleviate some of these issues (Heys & Dombeck 2018; Leon & Shadlen 2003; M. Bright et al. 2019; MacDonald et al. 2013). However, even for immobile animals in a static environment, internally generated cues, such as heartbeat and breathing, could still provide temporal information. Further, such tasks limit the study of many natural timing behaviors. Even using tasks in which time is the dominant variable, the question remains as to whether changing neural activity patterns over time relate to the animal’s representation, perception, or memory of time. Here, neural perturbation experiments provide an excellent means to test for causality. For example, by inactivating a brain region or circuit thought to contain a time representation using optogenetic or chemogenetic methods (Armbruster et al. 2007; Boyden et al. 2005) and then testing for altered timing behavior or learning, it should be possible to determine the necessity of a region or circuit for the perception or learning of different time intervals (Soares et al. 2016). Optogenetics and chemogenetics may have advantages over lesions. For example, recent seemingly contradictory reports about whether sequential time cell activity in MEC is necessary for downstream time cell activity in the hippocampus (Robinson et al. 2017; Sabariego et al. 2019) may be explained by compensatory mechanisms allowing for hippocampal activity pattern recovery after MEC lesions, while such recovery does not take place during transient optogenetic MEC inactivation.

External cues

Similar to the representation of space with path integration, the brain’s representation of time is predicted to drift with respect to external time (non-unitary temporal derivative, Figure 1d), but this drift can be corrected by using external cues. This process could be investigated by adding temporally informative cues to the delay period of a long timing task. For example, animals could first be trained on an instrumental task to wait after a cue (light flash) and then report when an amount of time had elapsed (say 20 seconds) by licking for reward. On probe trials, a “metronome-like” sound cue (i.e. “temporal landmark” every few seconds) could be added. Behaviorally, the error in lick times would be expected to decrease if the external sensory cues are used to correct for integration errors. Imaging (Harvey et al. 2012; Heys & Dombeck 2018; Mau et al. 2018) or electrophysiology (Jun et al. 2017; Tiganj et al. 2018) methods could be used to identify differences in representations from large populations of time encoding neurons. For example, in the case of sequential firing representations, time tuning curves would be expected to narrow near the sound cues (Mau et al. 2018; Tiganj et al. 2018) and in the case of ramping representations, slope (trial-trial) variability would be expected to be reduced near the cues (Howard et al. 2014; Liu et al. 2019).

Timescales

Models for sequential firing networks make several testable predictions about repeating firing fields over long intervals. For example, ring attractors are expected to produce repeating sequences when the encoding time exceeds the ring period, while line attractors would not generate repeating sequences and instead recruit more neurons to the end of the sequence to encode longer intervals. For oscillatory interference models, different beat frequencies across the population are needed to generate sequences and therefore, while individual cells will display repetitive firing fields over long intervals, population sequences would become incoherent over repeated cycles. Differentiating between these predictions could then be accomplished by engaging an animal in a timing task in which the timing period exceeds the duration of sequences that have been previously described (>20 seconds) (Cameron et al. 2019; Heys & Dombeck 2018; Kraus et al. 2013, 2015; MacDonald et al. 2013; Pastalkova et al. 2008; Salz et al. 2016).

Circuit structures

Finally, next-generation circuit cracking techniques should prove useful in distinguishing between the models and determining the exact mechanisms underlying time-integration. Influence mapping, for example, uses single cell optogenetic activation along with population Ca²⁺ imaging to determine the (direct or indirect) circuit connectivity between neurons in vivo (Chettih & Harvey 2019). This approach could be used to unveil the predicted “Mexican hat” connectivity between sequential firing cells in CAN models, the predicted connectivity between cells with exponentially decaying firing rates and sequential firing cells in the Laplace transform model (Liu et al. 2019), or the predicted inhibitory connectivity between negative and positive ramping cells in ramping cell models. Dendritic synaptic input mapping might also be useful to establish mechanisms of time encoding and integration (Marvin et al. 2018; Wilson et al. 2018). These methods involve using dendritic imaging of functional fluorescence indicators, such as GCaMP (Dana et al. 2019) or iGluSNFr (Marvin et al. 2013, 2018), in vivo to record synaptic input patterns. This method could be used to discover the asymmetric excitatory tuning curve inputs (with respect to somatic tuning) predicted for CAN models, the exponentially decaying inputs predicted by the Laplace transform model, the pulse of excitatory input predicted for the positive feedback ramping integrator, or the persistent excitatory input predicted for the perfect integrator ramping model. Lastly, retrograde circuit tracing techniques (Tervo et al. 2016) could be used to hunt down the source and nature of the temporal derivative (γ) signal.

CONCLUSIONS

Time is as abstract as it is pervasive in animal behavior and neural circuits. For the same reasons it is elusive and difficult to study, it may serve as a powerful window into general mechanisms of cognition and neural computations. The study of spatial navigation was once viewed similarly, but the unraveling of the place code has opened the door to a goldmine of insights into how the brain works. Understanding the time code for interval timing likewise carries great potential; by leveraging what we already know about spatial navigation, perhaps we are not too far from realizing it.