Robust classification of cell cycle phase and biological feature extraction by image-based deep learning

Abstract

Across the cell cycle, the subcellular organization undergoes major spatiotemporal changes that could in principle contain biological features that could potentially represent cell cycle phase. We applied convolutional neural network-based classifiers to extract such putative features from the fluorescence microscope images of cells stained for the nucleus, the Golgi apparatus, and the microtubule cytoskeleton. We demonstrate that cell images can be robustly classified according to G1/S and G2 cell cycle phases without the need for specific cell cycle markers. Grad-CAM analysis of the classification models enabled us to extract several pairs of quantitative parameters of specific subcellular features as good classifiers for the cell cycle phase. These results collectively demonstrate that machine learning-based image processing is useful to extract biological features underlying cellular phenomena of interest in an unbiased and data-driven manner.

INTRODUCTION

Proliferating cells undergo dynamic changes in subcellular organization during the cell cycle. While the dramatic structural rearrangements in mitosis are most prominent, subcellular components are also extensively reorganized during interphase. For example, DNA is replicated during S phase, resulting in a doubling of chromatin content and the concordant regulation of nuclear size (Webster et al., 2009; Mukherjee et al., 2016). Organelles such as the Golgi apparatus and endoplasmic reticulum also have cell cycle-dependent dynamics in number or size to align with mitotic distribution and inheritance (Lowe and Barr, 2007; Mascanzoni et al., 2019). At the molecular level, the architecture of cytoskeletal components such as microtubule and actin filaments has marked cell cycle phase dynamics (Champion et al., 2017; Jones et al., 2019). Although these dynamic changes are empirically known, the development of advances in reference-free, image-based quantitative analyses of cell morphology have been limited because of the lack of information on which subcellular features and components selectively align with specific cell cycle phases.

Traditionally, cellular imaging approaches employ cell cycle markers to monitor cell cycle phase. These markers localize to the nucleus and change their expression levels depending on cell cycle phase (Sakaue-Sawano et al., 2008; Gookin et al., 2017). While such markers are practically useful for many types of experiments, they are also biased to the conditions of their experimental expression and distribution (Sobecki et al., 2017; Miller et al., 2018). For many types of biological or clinical samples, a less invasive and more unbiased approach to subcellular component classification would be useful. For example, it would be helpful to identify subcellular components that change their localization or spatial organization across cell cycle phases. In addition, if such commonly observed components could be directly used as reference-free cell cycle markers, it would enable simple, unbiased quantitative methods for cell classification based on intrinsic cell cycle components.

Machine learning is a proven computational approach that may be useful to extract cell cycle-dependent features without knowing a priori which parameters to focus on. A growing literature indicates the potential utility of machine learning in unbiased image analyses for cell biological applications. For example, machine learning-based segmentation and classification were performed on various cell types including yeast and mammalian cultured cells (Boland and Murphy, 2001; Conrad et al., 2004; Nanni and Lumini, 2008; Chong et al., 2015; Xu et al., 2015, 2019; Pärnamaa and Parts, 2017; Zhang et al., 2020). Also, image-based classification can be combined with flow cytometry to achieve single-cell imaging cytometry (Eulenberg et al., 2017; Fang et al., 2019; Gupta et al., 2019; Meng et al., 2019), although classification within interphase, that is, G1, S, and G2 phases based on cell images is difficult (Eulenberg et al., 2017). Finally, machine learning classification of subcellular protein localization patterns using large image datasets is a promising trend (Sullivan et al., 2018; Schormann et al., 2020). Therefore, the use of a machine learning in image-based classification of cell cycle phase would be a useful advance.

In this study, we sought two main goals: 1) to employ machine learning to construct an image-based cell cycle classification and 2) to quantitatively identify classifiers for cell cycle phase based on key features that are different from current cell cycle markers. We applied a convolutional neural network (CNN) that is known to be effective for image classification in cell biology (Dürr and Sick, 2016; Xu et al., 2017; Rodrigues et al., 2019) and then established a computational pipeline where 1) microscopic images of fluorescently labeled cells are classified according to their cell cycle phase, 2) candidate features are selected by model interpretation, and 3) identification of key features that represent cell cycle phase. We focus on Hoechst (DNA), GM130 (Golgi), and EB1 (microtubule plus-ends) and show that combinations of features from these subcellular components quantitatively represent G1/S and G2 phases of human cultured cells. The approach only requires conventional microscope equipment and regular cell preparations, making it easy to apply to a wide range of studies using biological and medical images.

RESULTS

Classification by CNN models of cellular morphology

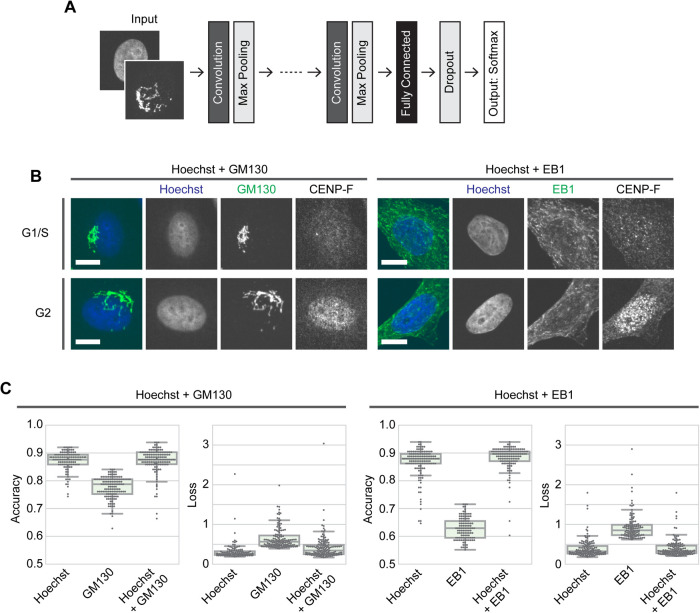
We constructed several CNN-based deep learning models to objectively classify fluorescence images of cells according to classification parameters of interest such as cell cycle phase. The architecture of the CNN models is schematically shown in Figure 1A (see Materials and Methods for details). The models contain two to seven convolutional and max pooling layers followed by a set of fully connected and dropout layers. The output layer returns the probability distributions of two classes by Softmax. We comprehensively searched for optimal parameter sets including the number of convolutional layers and the dropout rate by using a Bayesian optimization algorithm. Then we constructed specific models by fitting the parameters through learning. Optimized hyperparameter sets used in the models are listed in Supplemental File S1. The results of the Bayesian optimization were also used to verify and compare the overall accuracy of the models, and only data with an accuracy greater than 0.55 were counted.

FIGURE 1:

CNN-based classification of cell cycle phase. (A) Schematic of the CNN architecture used in this study. See Materials and Methods for details. (B) Representative images of HeLa cells stained with Hoechst and antibodies to GM130 or EB1 and CENP-F. Scale bar, 10 μm. (C) Results of Bayesian optimization for CNN models. Test accuracies (left) and absolute values of the loss function (right) are shown for each condition. The accuracies of GM130 and EB1 were significantly different from those of the other categories by Steel–Dwass test (p < 0.0001); n = 115–142 trials each.

We first evaluated the performance of our CNN models by the classification of ciliated and nonciliated NIH3T3 cells. Cilia are microtubule-based cellular projections that have important roles in cellular functions (Anvarian et al., 2019). In NIH3T3 cells, cilia formation can be induced by serum starvation and a single cell typically has only one cilium. Immunostaining with antibodies to acetylated tubulin or to the peripheral membrane protein Arl13b can clearly mark cilia. We prepared a dataset of ciliated and nonciliated cell images that consisted of 2104 and 130 images for training and test, respectively (see Materials and Methods for details). Cells were stained with Hoechst as well as antibodies to acetylated tubulin and Arl13b (Supplemental Figure S1A). Hoechst staining was used to locate each cell for cropping regions of interest. Arl13b staining was used only to ensure the annotation quality of the dataset where cells that were positive for both acetylated tubulin and Arl13b were annotated as cilium-positive. After this annotation, acetylated tubulin staining alone was used for the deep learning analyses. CNN model learning worked well for this classification task. The models tended to overfit on prolonged epochs (Supplemental Figure S1B, bottom), so limiting epochs to around 10 was optimal for this task. Successful models achieved more than 95% accuracy for the test data (Supplemental Figure S1B). We thus concluded that our CNN models were effective for the fluorescence image-based classification of cells.

Classification by CNN models of cell cycle phase

We then applied our CNN to the classification of cell cycle phase. Cell cycle markers such as CENP-F and Cyclin E have generally been used to distinguish phases of the cell cycle. However, the usage of a cell cycle marker fills a slot for subsequent multicolor immunostaining, while a CNN-based marker-free classification could remove this restriction. In addition, CNN models could be used to identify new features of cell cycle-dependent morphological and structural pattern shifts that might be overlooked by conventional analyses. For example, the pattern of Hoechst staining can dynamically shift as the DNA content doubles during S phase, given that flow cytometry can distinguish between cell cycle phases based on the staining of DNA. Furthermore, Hoechst staining patterns may reflect dynamic changes in chromatin structure during the cell cycle. Other interesting targets include organelles such as the Golgi apparatus and endoplasmic reticulum as well as molecular components such as the microtubule and actin cytoskeletons. Given that these subcellular structures are reorganized to enable cell division, they can exhibit dynamic spatial pattern shifts during interphase. The Golgi apparatus, for example, must double in quantity to be properly distributed in G2 phase toward mitosis, while microtubules become more dynamic in the G2 phase to prepare for mitotic spindle formation, which may be evident by changes in spatial patterning. Therefore, we tested whether our CNN models could detect cell cycle-specific features of subcellular structural patterns from cellular fluorescence images. Hereafter, HeLa cells were used unless otherwise stated. Cells were stained with Hoechst and an antibody to either the cis-Golgi matrix protein GM130 or the microtubule plus end-binding protein EB1, as well as an antibody to the G2 marker protein CENP-F (Figure 1B). Although CENP-F can be detected in the nucleus at late S phase (Landberg et al., 1996), for simplicity, CENP-F-positive and -negative cells in interphase are hereafter defined as cells at G2 and G1/S phases, respectively. Mitotic cells were morphologically identified and excluded from the dataset. CENP-F staining was used only for annotation purposes and not for subsequent deep learning processes. For the Hoechst + GM130 dataset, 1848 and 113 images were prepared for training and test, respectively, and for the Hoechst + EB1 dataset, 1884 and 116 images were prepared for training and test, respectively (see Materials and Methods for details).

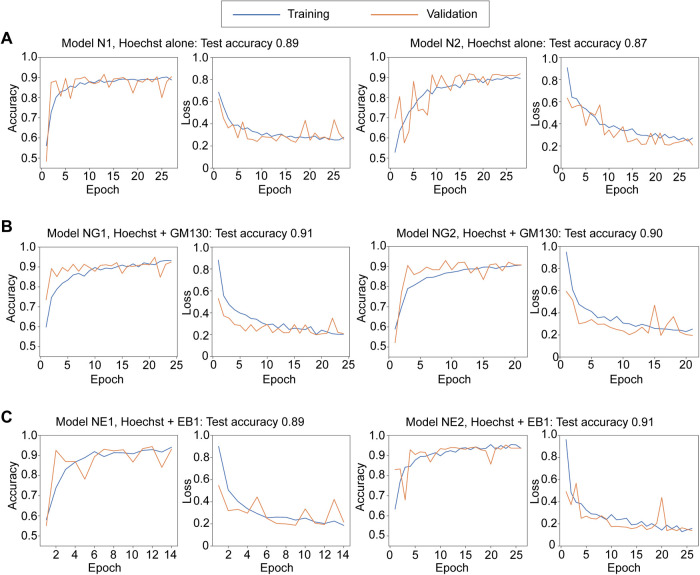
We first tested whether the CNN models could distinguish G1/S and G2 phases based on Hoechst staining alone. When Hoechst staining channels of the Hoechst + GM130 images (Figure 1B) were used, tuned models with Bayesian optimization achieved around 90% accuracy for classification of G1/S and G2 phases based solely on Hoechst-stained images (Figure 1C). Learning with epochs of around 10–25 worked well with little to no overfitting (Figure 2A and Supplemental Figure S2A). We similarly classified the cell cycle phases using RPE1 cells stained with Hoechst and the antibody to CENP-F (Supplemental Figure S4A) to examine if our deep learning approach can be also applied to other cell types. As in the case of HeLa cells, tuned CNN models classified Hoechst-stained images according to G1/S and G2 phases with an accuracy of around 90% (Supplemental Figure S4B). Together, our CNN models could learn to distinguish between G1/S and G2 phases of HeLa and RPE1 cells based on Hoechst-stained images.

FIGURE 2:

Learning curves of CNN models. Learning curves of two representative models in each condition are shown. The accuracies for the test data are shown above each graph. See also Supplemental Figure S2.

Effect of cytoplasmic structural patterns in CNN classification

Next, we tested if CNN models could classify cell cycle phases based on cellular features other than the patterns from Hoechst staining. We focused on spatial patterns in the Golgi apparatus and microtubule plus-ends represented by GM130 and EB1, respectively (Figure 1B). In Bayesian optimization, the learning of CNN models based on the GM130 channel alone was less successful (up to ∼80% accuracy) compared with the ∼90% accuracy of Hoechst-based models (Figure 1C). EB1 channel-based learning resulted in ∼60% accuracy, indicating that the EB1 channel alone is not sufficient to classify G1/S and G2 phases by our CNN models (Figure 1C).

We then tested if combinations of two channels, that is, Hoechst + GM130 or EB1, would have additive effects. Bayesian optimization with two channel images resulted in a ∼90% accuracy for either combination, which is comparable to the accuracy achieved with the Hoechst channel alone (Figure 1C). Consistently, successful models for both Hoechst + GM130 and Hoechst + EB1 images showed similar learning curves to those for Hoechst alone (Figure 2, B and C, and Supplemental Figure S2, B and C). No obvious tendencies or characteristics were found among correctly and incorrectly classified images (Supplemental Figure S3). The expression level of CENP-F that was used for annotation gradually increases during the S-G2 transition (not in an all-or-none manner), which may limit the accuracy of classification as discussed later (Figure 4). Taken together, the classification of cell cycle phases with our CNN models based on GM130 or EB1 staining patterns worked, but only when combined with the information of Hoechst staining patterns.

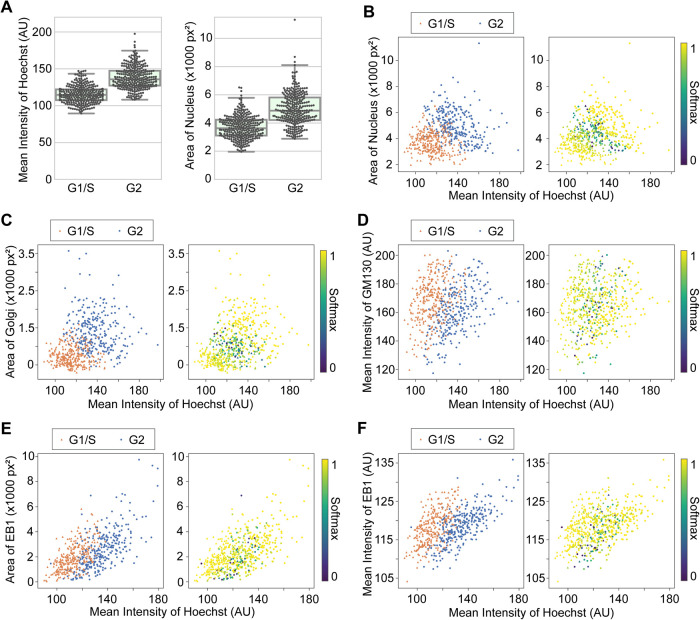
FIGURE 4:

Class separation by image quantification of selected features. Quantification was performed with original (annotated, but not classified with CNN) images. (A) Comparison of the mean intensities of Hoechst and the areas of nuclei between G1/S and G2 phases. p < 0.0001 by Mann–Whitney U test for both of the pairs. (B–F) 2D plots of indicated pairs of the features. In each panel, the same dataset was color coded in different ways; (left) by classes, G1/S (orange) and G2 (blue); (right) by Softmax values.

Extraction of cellular features used in CNN classification

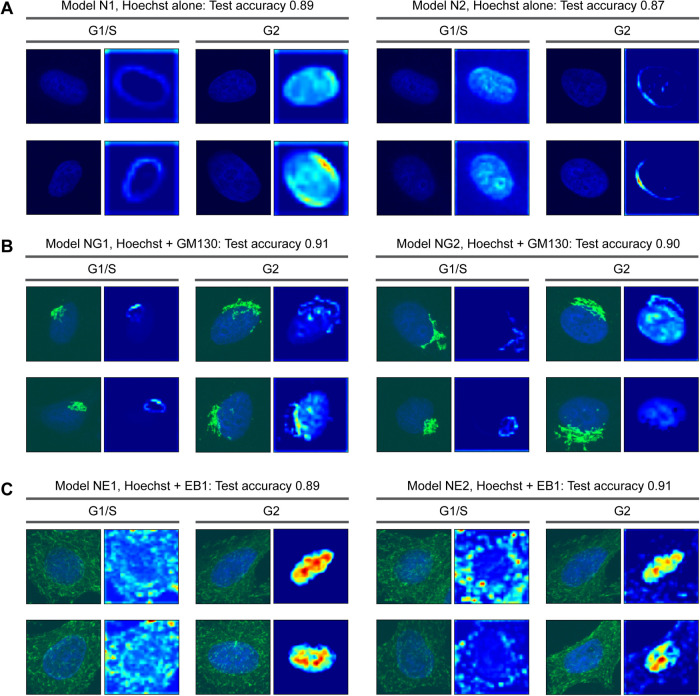
What specific features do the CNN models employ for image classification? We verified the models using Grad-CAM, which generates heat maps representing regions that have a greater weight in CNN classification (Selvaraju et al., 2020). First, we analyzed models based on the Hoechst channel alone. Grad-CAM showed that the CNN models focused on two features of nuclei, the outlines and entire regions (Figure 3A). Interestingly, two distinct models used opposite combinations of these features; Model N1 focused on outlines for the assessment of G1/S and whole regions for G2, while Model N2 focused on whole regions for G1/S and outlines for G2 (Figure 3A). In either case, the results suggest that the shape and area features that representing the nuclei, along with the DNA content (the intensity of Hoechst staining), are important parameters for the CNN models to classify cell cycle phases.

FIGURE 3:

Grad-CAM analysis to visualize where in images the CNN models focused on. Representative Grad-CAM heat maps with input images for correctly classified images are shown. The model numbers correspond to those in Figure 2.

It remains unclear whether the CNN models use intranuclear patterns of Hoechst staining in classification. The Grad-CAM data indicate that CNN models appear to focus on fine structures, or ring-like patterns, inside nuclei (Figure 3A). We therefore tested if CNN models require information from intranuclear patterns for the classification of cell cycle phase. We prepared a dataset of binary images where the nuclei were filled with their mean intensity values while the backgrounds were zero-filled (Supplemental Figure S5A). The dataset was derived from the one used in the Hoechst-based classification. Bayesian optimization resulted in ∼90% accuracy with the dataset of binary images, which is comparable to the results from the original images (Supplemental Figure S5A). Also, we experimentally prepared a similar dataset using the histone deacetylase inhibitor Trichostatin A (TSA). The addition of TSA to the cell culture medium induces the hyperacetylation of histones and modification of chromatin structures, resulting in a homogenization of Hoechst staining patterns (Tóth et al., 2004; Bártová et al., 2005). While TSA treatment indeed made Hoechst staining more uniform, CNN models based on both TSA-treated and dimethyl sulfoxide (DMSO) control images achieved ∼90% accuracy (Supplemental Figure S5B). This is consistent with the result from the binary images (Supplemental Figure S5A). Together, these results indicate that, for accurate cell cycle classification, CNN models do not necessarily require structural patterns inside the nuclei.

Although the information from GM130 or EB1, alongside that of Hoechst, did not increase the accuracy of CNN models compared with Hoechst alone (Figure 1C), it remains important to understand what features CNN models focus on in the two channel images. Analysis of the models using Grad-CAM showed that, when using two channel images, the CNN models frequently focused on the Golgi apparatus or microtubule plus-ends in addition to the nuclei. For example, two models based on the Hoechst-GM130 dataset focused on the outlines of the Golgi apparatus for the classification of G1/S, while the whole nuclear region in combination with the Golgi outline were used for the assessment of G2 (Figure 3B). In the case of the Hoechst-EB1 dataset, EB1 distributions and whole nuclear regions were preferentially used for the identification of G1/S and G2, respectively (Figure 3C). These results suggest that despite little improvement of accuracy, CNN models tend to use multiple features in the classification, if they are available, by incorporating additional information of GM130 or EB1.

Biological interpretation of the CNN-based classification

The Grad-CAM results suggest that cellular images can be classified into G1/S and G2 phases according to the spatial patterns and/or the intensities of Hoechst, GM130, and EB1. Therefore, by focusing on these parameters, conventional image quantification could classify the images similar to the CNN models, providing a more explicit interpretation to the classification, such as the classification of cell cycle phase based on changes in nuclear size. In effect, the CNN models can use discrete features for quantitative image analyses. We measured the mean intensities and areas of Hoechst (nuclei), GM130 (Golgi), and EB1 of the images used in the construction of CNN models and the training and test datasets were pooled.

Quantitative analyses demonstrated that the mean intensities of Hoechst and the areas of nuclei were significantly greater in G2 compared with G1/S (Figure 4A). Despite these statistically clear tendencies in the overall populations, however, individual G1/S and G2 phase populations were unable to be fully clustered. We then combined the mean intensities and areas to make a 2D plot that was able to cluster the G1/S and G2 populations (Figure 4B, left). Moreover, when the information of the classification probabilities (Softmax) provided by a CNN model were added to the plot, the data in the border region tended to exhibit smaller Softmax values (Figure 4B, right). We similarly tested the mean intensities and areas for GM130 and EB1. Given that the GM130 or EB1 channel alone was not sufficient for cell cycle classification, but worked in combination with the Hoechst channel, we generated 2D plots using the mean intensities of Hoechst for one of the two axes. Consequently, 2D plotting of the areas or the mean intensities of Golgi or EB1 against the mean intensities of Hoechst resulted in well-clustered populations of G1/S and G2 phases, with smaller Softmax values at the border regions (Figure 4, C–F). These results demonstrate that the image quantification based on combinations of two distinct features, but not single features alone, can separate cellular populations according to their cell cycle phase. The results also demonstrate that cell cycle phase can be classified by parameters with biological significance, such as nuclear size.

We further investigated whether and how combinations of quantitative measurements efficiently enable cell cycle classification. Multivariate analyses for the Hoechst-GM130 image data were performed with six parameters consisting of mean intensities, area, and SDs of intensities for the Hoechst and GM130 channels, respectively. A principal component analysis (PCA) resulted in good separation of the G1/S and G2 clusters with the first two principal components, PC1 and PC2 (Supplemental Figure S6A). The cumulative proportion of the variance exceeded 75% with the two principal components (data not shown). In a loading plot, the mean intensities and SDs showed similar distributions both for Hoechst and GM130, and interestingly, the areas of nuclei and Golgi were located close to each other (Supplemental Figure S6B). The loading plot suggests that PC1 and PC2 are related to intensities and areas, respectively. Given the results of the quantification in Figure 4, B–D, for example, the area and mean intensity of Hoechst increase in G2 compared with G1/S and may result in greater scores of PC1 and PC2, while an increased area of Golgi at G2 could result in a diluted protein level of GM130, which may explain the opposite PC2 loadings of the mean intensity and area of GM130 (Supplemental Figure S6B). In addition, given that the quantification in Figure 4, B–D is based on the Grad-CAM results, the results from PCA may further support our interpretation that the CNN models focus on intracellular parameters related to subcellular organization such as DNA content and organelle size. The loading plot also suggests that the SDs have a high correlation to the mean intensities for both Hoechst and GM130 and are thus reducible (Supplemental Figure S6B). Indeed, a correlation coefficient matrix showed relatively higher correlation coefficients between the mean and SD of intensities (Supplemental Figure S6C). Logistic regression analysis with six parameters also well classified the cell cycle phases (Supplemental Figure S6D). To test which parameters are essential, we performed a logistic regression analysis with some of the parameters dropped out. Consistent with the results in Figures 4, B and C, combinations of two parameters, namely, the mean intensity of Hoechst and the area of Hoechst or GM130, were sufficient for logistic regression models to classify the cell cycle phase (Supplemental Figure S6D). In sum, the results of the multivariate analyses are consistent with and further support the conclusions of the quantitative analyses on cell cycle phase classification shown in Figure 4.

DISCUSSION

In this study, we investigated whether machine learning approaches could enable the classification of cell cycle phase. We constructed CNN models and used them to classify fluorescence images of cells according to categories of interest. Remarkably, our models could robustly classify G1/S and G2 phases of HeLa and RPE1 cells without cell cycle markers (Figures 1 and 2 and Supplemental Figures S2 and S3). While usage of a cell cycle marker fills a slot to limit multicolor immunostaining, our CNN-based classification only requires Hoechst staining that is frequently used in cellular experiments for cell cycle phase classification. Thus, conventional image datasets can be used for cell cycle classification. Learning with combinations of multiple cell cycle markers will further expand the scope of the application for the classification of G1, S, and G2 phase with applications in live cell imaging and mitotic phases.

While providing an efficient tool for cell phase classification, our CNN-based approach also provided several biological insights. Grad-CAM analyses showed that CNN models focused on distinct cellular features for their assessment of G1/S and G2 phases (Figure 3), specifically, the area and intensity of staining. Indeed, by plotting two of these features together, cell cycle phases were computationally well separated (Figure 4, B–F). Since DNA content doubles during S phase and nuclear size increases accordingly, it is therefore reasonable that the mean intensities and areas of cells under Hoechst staining were greater at G2 than G1/S phases (Figure 4, A and B). Consistent with our finding that the differences in each parameter alone is not clear enough for clustering entire populations (Figure 4A), the Grad-CAM results suggest that CNN models may seek to use combinations of features (Figure 3A). The results of the image quantification are also consistent with the idea that a combination of parameters including the nuclear size and DNA content can be effective for separating cell cycle phase in a multivariate feature space (Gut et al., 2015). While the selection of nucleus-related parameters is straightforward as flow cytometry already commonly uses DNA content for cell cycle classification, the advantage of our approach is that it allows the extraction of features from cell images without prior knowledge, reference, or bias.

For classification based on the combination of Hoechst and GM130 images at G2, Golgi area tended to be greater, while mean intensities of GM130 tended to smaller (Figure 4, C and D). Taking a closer look, the Golgi apparatus is densely packed at G1/S and spreads over the nuclei (Figures 1B and 3B). This is presumably due to mechanisms coupled with cell cycle progression compaction toward mitosis (Tang and Wang, 2013; Wei and Seemann, 2017). It is therefore likely that the spreading of the Golgi apparatus at G2 results in an increased area and a decreased intensity of GM130 staining at G2 compared with G1/S. Importantly, the results in this study provide quantitative evidence for the dynamic remodeling of the Golgi organization coupled with the cell cycle during interphase. On the other hand, contrary to expectations, the results for EB1 indicate that both the areas (i.e., the numbers) and the mean intensities of EB1 foci distributed similarly between G1/S and G2 phases (Figure 4, E and F). Contrary to expectations, the results showed no detectable changes in microtubule elongation dynamics during interphase. This is consistent with the result that EB1 images alone were unable to be classified by cell cycle phase by our CNN models (Figure 1C). Interestingly, both the areas and the mean intensities of EB1 correlated with the mean intensities of Hoechst (Figure 4, E and F). Such alignments in 2D feature space may help to keep the G1/S and G2 populations separated. Given that, based on the Grad-CAM results, the CNN models likely use salient information from the EB1 images (Figure 3C), there could be EB1-related biological features yet to be uncovered and explained.

In conclusion, this study demonstrates that quantitative image analyses based on CNN classification can provide insights into the computational and biological significance of cellular images. As a proof of principle, we extracted biologically significant features that represent spatial and temporal classes of cells such as cell cycle phases. Our results confirm that CNN models are a powerful classification tool for biological imaging, but in a more novel context can also serve as an unbiased experimental tool to extract previously unknown biological features that might otherwise be overlooked by researcher inspection of the micrographs. In other words, CNN models can provide guidance on what features may be interesting or important to focus on. The approach developed in this study requires no special equipment or sample preparations except conventional microscopes and regular cellular immunofluorescence protocols. Our approach can be thus easily translated to other studies that use primary biological materials. While we used fixed cells in this study, the application to live cell imaging will be a feasible future option. Furthermore, higher resolution images will enable researchers to focus on the finer structures of subcellular components. For example, despite being dispensable in formal cell cycle classification (Figure 4B and Supplemental Figure S5), under certain conditions, CNN models may be able to interrogate intranuclear structures such as the chromatin to reveal novel structural systems dynamics orthogonal or parallel to cell cycle phases. It will be thus interesting to combine our approach with superresolution microscopy, which may reveal cell cycle-dependent structural dynamics in the subnuclear space. Such refined applications of machine learning for the classification of subtle differences in organelle and cytoskeletal dynamics with biological explainability may provide new insights to the fields of cell and developmental biology and the medical and pharmaceutical sciences.

MATERIALS AND METHODS

Antibodies and chemicals

Chemicals were from Fujifilm Wako Pure Chemical Corporation, unless otherwise noted. Primary antibodies used were acetylated tubulin (1:10,000; 6-11B-1; Sigma), Arl13b (1:500; 17711-1-AP; Proteintech), GM130 (1:1,000; 610822; BD Biosciences), EB1 (1:1,000; 610534; BD Biosciences), and CENP-F (1:500; ab108483; Abcam). Alexa Fluor–conjugated secondary antibodies (1:500) were purchased from Thermo Fisher Scientific. Hoechst 33258 and TSA were purchased from Thermo Fisher Scientific and Alomone Labs, respectively.

Cell lines and immunofluorescence

Cell culturing and immunofluorescence were previously described (Takao et al., 2017, 2019) and the details are as follows. NIH3T3 cells (ATCC) were cultured in DMEM supplied with 10% Fetal Clone III (Hyclone, GE Healthcare) and 1% penicillin/stereptomycin (Life Technologies, Thermo Fisher Scientific). HeLa and RPE1 cells (ECACC) were cultured in DMEM supplied with 10% fetal bovine serum (Life Technologies, Thermo Fisher Scientific) and 1% penicillin/streptomycin.

NIH3T3 cells cultured on coverslips were serum starved with DMEM containing 0.5% Fetal Clone III to induce cilium formation for 24 h before fixation. The cells were then fixed with 3.7% paraformaldehyde in phosphate-buffered saline (PBS) for 10 min and incubated in blocking buffer (0.05% Triton X-100 and 1% bovine serum albumin in PBS) for 20 min to permeabilize and block at RT. The cells were then incubated with primary antibodies in blocking buffer for 1 h at RT, washed three times, and incubated with secondary antibodies for 1 h at RT. The cells were subsequently stained with 1 μg/ml Hoechst in PBS for 5 min, washed three times, and mounted with ProlongGold (Thermo Fisher Scientific).

HeLa and RPE1 cells cultured on coverslips were fixed with cold methanol at –20°C for 5 min. For the experiments with TSA treatment, 1 μM TSA or 0.1% DMSO (control) was added to the culturing medium 6 h before fixation. The procedures after fixation were same as those described above for NIH3T3 cells.

Microscopy

A spinning disk-based confocal microscope (IXplore SpinSR; Olympus; Hayashi and Okada, 2015) equipped with a 60× oil-immersion objective (PLAPON60×OSC2/NA 1.4, Olympus) was used for image acquisition. The 3D cell images were recorded by using a complementary metal–oxide–semiconductor (CMOS) camera (ORCA-Flash4.0 V3, Hamamatsu Photonics) with 2 × 2 digital binning resulting in a pixel size of 0.2167 μm and Z-interval of 1 μm.

Image processing, quantification, and construction of CNN models

Original 16-bit z-stack images were maximum intensity projected with ImageJ. The rest of the processes were performed with our Python (version 3.7.4) codes on the JupyterLab (version 1.2.3) platform unless otherwise stated. The images were standardized with conversion into 8-bit and cropped to designated sizes (∼130 × 130 pixels) covering most of single cell areas by centering the centroids of nuclei (Hoechst staining). The images were annotated by manually sorting the cropped images into the class folders (e.g., “ciliated and nonciliated” and “G1/S and G2”), split into training and test data with the ratio 8:2, and converted into NumPy matrices with class labels to construct the datasets for the subsequent CNN modeling. The training data were augmented by rotation and parallel translation to increase the number of data by four times and 20% of the training data were further split into the validation data in the learning processes. CNN models were constructed using the Keras package that was also used for Bayesian optimization. The size of convolution kernels and max pooling were fixed to 3 × 3 and 2 × 2, respectively. Maximum pooling is a pooling operation for downsampling by extracting the maximum value from each 2 × 2 window. One or two of the channels (e.g., Hoechst and/or GM130) were selected as the input; note that the marker channel (e.g., CENP-F) was removed from the datasets and never used in the learning processes. ReLU (rectified linear unit; also known as ramp function) was used as the activation function, except the output layer that used Softmax. The Softmax function turns the probability distributions of potential outcomes. Binary cross-entropy loss was used as the loss function. Above operations and functions are commonly used in neural networks. For Bayesian optimization, hyperparameters were searched with the following settings of the parameter ranges (minimum, maximum): the number of hidden convolution and max pooling layers (0, 6), the number of convolution kernels (2, 50), the rate of dropout (0, 0.9), and the number of batches (4, 100). GPU provided by Google Colaboratory was used for Bayesian optimization and in part for other calculations. The Grad-CAM codes were from previous work (Selvaraju et al., 2020). In this study, the results from the last maximum pooling layer (immediately before the fully connected layer) were focused in all Grad-CAM analyses. See Supplemental File S1 for details such as the Python package versions and information for the CNN models. The Python code is available via GitHub (https://github.com/dtakao-lab/Nagao2020). The image datasets and tuned models are available via Zenodo (10.5281/zenodo.3745864).

For the image quantification in Figure 4, we used our Python codes. The areas of Hoechst, GM130, and EB1 were extracted by using clipping binary masks with given thresholds. The training and test datasets were pooled and the results from Model N1, NG1, or NE1 were used for the Softmax values. The statistical tests were performed with Python and R (version 3.6.1).

Abbreviations used:

CNN

convolutional neural network

DMSO

dimethyl sulfoxide

PBS

phosphate-buffered saline

PCA

principal component analysis

TSA

Trichostatin A.