Cell-type-specific mechanical response and myosin dynamics during retinal lens development in Drosophila

Abstract

During organogenesis, different cell types need to work together to generate functional multicellular structures. To study this process, we made use of the genetically tractable fly retina, with a focus on the mechanisms that coordinate morphogenesis between the different epithelial cell types that make up the optical lens. Our work shows that these epithelial cells present contractile apical-medial MyosinII meshworks, which control the apical area and junctional geometry of these cells during lens development. Our study also suggests that these MyosinII meshworks drive cell shape changes in response to external forces, and thus they mediate part of the biomechanical coupling that takes place between these cells. Importantly, our work, including mathematical modeling of forces and material stiffness during lens development, raises the possibility that increased cell stiffness acts as a mechanism for limiting this mechanical coupling. We propose this might be required in complex tissues, where different cell types undergo concurrent morphogenesis and where averaging out of forces across cells could compromise individual cell apical geometry and thereby organ function.

INTRODUCTION

Many of our organs consist of different polarized cell types, including epithelial cells, which adhere to one another through lateral adherens junctions (AJ) to form tissues. How different cell types work together to induce a complex tissue to generate a functional organ is not fully understood. To a large extent, epithelial tissue patterning has mostly been studied in relatively simple, homogeneous epithelia that consist of one cell type, with a focus on specific instances of cell shape change such as during apical constriction (Martin et al., 2009a), cell intercalation in the fly embryo (Bertet et al., 2004; Blankenship et al., 2006), or cell spreading during zebrafish gastrulation (Lavoie et al., 2017). In these simple epithelia, cell and tissue shape depends in part on the balance of contractile forces generated by the actomyosin cytoskeleton and intercellular adhesion through Cadherins (Heisenberg and Bellaiche, 2013; Munjal and Lecuit, 2014; Lecuit and Yap, 2015). In this balance, adhesion promotes AJ extension while Myosin-II (MyoII) contractility antagonizes this process.

An essential regulator of cell and tissue shape is the contractile actomyosin cytoskeleton, which consists of at least two pools—a medial meshwork that runs below the apical membrane and actomyosin filaments that localize at the AJ. These two pools are linked, as the medial meshwork is anchored to the AJ through discrete points of contact (Roh-Johnson et al., 2012; Heisenberg and Bellaiche, 2013). The medial meshwork is pulsatile, with cycles of discrete node contraction and relaxation that occur over tens of seconds and that can promote apical area fluctuations and AJ remodeling over similar time scales (Coravos et al., 2017). Contractile pulses appear to be self-organizing and associated with cycles of phosphorylation and dephosphorylation of the MyoII regulatory light chain and thus cycles of assembly/disassembly of the meshworks (Kasza et al., 2014; Vasquez et al., 2014; Munjal et al., 2015; Mason et al., 2016). The AJ pool of actomyosin is linked to the Cadherin system and is thought to function as part of a ratchet mechanism that can harness the contractile forces applied onto the AJ by the medial meshwork to promote AJ remodeling (Coravos et al., 2017). As morphogenesis proceeds in a simple epithelium, individual cell heterogeneities tend to be “averaged out” to produce a homogenous tissue, consisting of cells with very similar apical geometries (Gibson et al., 2006; Farhadifar et al., 2007).

However, most organs consist of complex tissues where different cell types adopt distinct apical geometries that best suit their function. How different cell apical geometries and areas are generated within a group of cells and what mechanisms mediate their persistence despite exposure to forces arising from concurrent cell morphogenetic programs remain poorly understood. Recent studies have begun to investigate these questions by studying the mechanical properties of different tissues undergoing concurrent morphogenesis and how cell packing is organized in 3D. These studies have revealed key features of epithelial morphogenesis. In the fly wing, for example, the actomyosin cytoskeleton can reorganize to increase tissue stiffness in response to extrinsic tensile forces (Duda et al., 2019). Similarly, different mechanical properties correlate with different tissue behaviors in the fly embryo (Rauzi et al., 2015). Cell shape and packing have also been shown to be constrained in a curved environment and when tissues are bent (Rupprecht et al., 2017; Gomez-Galvez et al., 2018). All these studies point to an important role for mechanical forces during tissue morphogenesis.

Here we made use of the Drosophila retina to study the mechanical properties of different cell types as they undergo distinct, concurrent morphogenesis programs to assemble into a functional multicellular unit. All retinal cells are genetically tractable and can be imaged at high spatial-temporal resolution intravitally (Fichelson et al., 2012). The fly retina consists of approximately 750 identical physiological units called ommatidia. Each ommatidium comprises different epithelial cell types: four cone cells, surrounded by two primary pigment cells, themselves surrounded by a ring of interommatidial cells (Ready, 1989) (Figure 1A). During ommatidium morphogenesis, these epithelial cells acquire distinct apical geometries and areas. Similar to simple epithelia, the apical geometry of retinal cells is regulated by a combination of adhesion and actomyosin contractility at the AJ (Del Signore et al., 2018). In particular, the interplay between E/Ncadherin expression in the cone cells controls their apical geometry and topology in the plane of the epithelium (Hayashi and Carthew, 2004; Kafer et al., 2007; Chan et al., 2017). This function for NCadherin has been linked to the down-regulation of MyoII accumulation at the AJ shared between the cone cells and increased MyoII levels at the AJ these cells share with the surrounding pigment cells (Chan et al., 2017). While adhesion and actomyosin at the AJ work together to pattern the optical lens, the medial/cytoplasmic actomyosin cytoskeleton of the corresponding retinal cells has not been investigated in detail. In addition, it is not clear how forces are balanced across the ommatidium as the lens cells undergo morphogenesis. Here we combined molecular genetics, light-induced perturbation experiments, and computational modeling to describe the actomyosin cytoskeleton in retinal epithelial cells that make up the optical lens and to probe the balance of forces that are at play during eye development. Our work shows that all lens cell types present medial MyoII meshworks. These are contractile but do not show any particular persistent polarization in the way they contract. Our results indicate that they contribute to controlling the shape and size of the apical area of retinal cells. They also drive cell shape changes in response to force perturbation in all cell types except: the lens secreting cone cells, which keep their apical areas and shapes largely unchanged when challenged by extrinsic forces. Generation of a 2D mechanical model of forces in the developing lens and genetic perturbation of the contractile actomyosin cytoskeleton suggest that this is because cone cells are stiffer than the other retinal cell types. Our work thus reveals that cell stiffness is an important parameter of tissue morphogenesis that modulates the ability of cells to respond to mechanical forces.

FIGURE 1:

Retinal cells expand their apical area during lens development. (A) The arrangement of cells in the ommatidium. A, anterior; P, posterior; Eq, equatorial; Pl, Polar. (B–B’’) Snapshots taken from a time-lapse movie of ommatidium development, with AJs labeled with endogenous Ecad::GFP. Scale bar = 5 μm. (C) Total apical area of each of the three cell layers over time (n = 13 ommatidia from 2 pupae). Table indicates rates of apical area change over time. Error bars = SD. (D) Cummings estimation plot with upper axis showing distribution of apical area of individual primary pigment cells, cone cells, and interommatidial cells at three different stages of morphogenesis (n = 9 ommatidia from 5 pupae). On the lower axis, mean differences for comparisons to the cell apical area at 20 h are plotted as bootstrap sampling distributions; dot = mean difference; error bars = 95% CI. Unpaired mean difference of MidPPC (n = 6) minus EarlyPPC (n = 6): 9.14 (95CI 4.94; 12.9); LatePPC (n = 6) minus EarlyPPC (n = 6): 28.8 (95CI 19.1; 37.3); MidCC (n = 12) minus EarlyCC (n = 12): 0.616 (95CI –0.141; 1.43); LateCC (n = 12) minus EarlyCC (n = 12): 5.47 (95CI 3.93; 6.84); MidIOC (n = 33) minus EarlyIOC (n = 33): 0.667 (95CI –0.0907; 1.42); LateIOC (n = 25) minus EarlyIOC (n = 33): 1.31 (95CI 0.38; 2.22). (E) Percentage apical area of each of the three cell layers relative to the apical area of the whole ommatidium over time (n = 13 ommatidia from 2 pupae). Table indicates rates of percentage apical area change over time. Error bars = S.D.

RESULTS

Retinal cells increase their apical area during ommatidium morphogenesis

First, we sought to examine the dynamics of apical area changes in retinal cells that make up the lens as they acquire their position and apical geometry during ommatidium development (Figure 1B; Supplemental Movie S1). During ommatidium morphogenesis, the total apical area of the ommatidial core cells, defined as the cone and primary pigment cells, increases over time (Larson et al., 2010). We examined 13 ommatidia using time-lapse imaging, ensuring they were of similar developmental stage. These quantifications confirmed a previous report that the total apical area of the core cells increases through time (Figure 1C) (Larson et al., 2010). It also showed that the combined apical area of the interommatidial cells increases transiently, then decreases as these cells thin and some are eliminated through apoptosis (Brachmann and Cagan, 2003) (Figure 1C). Additionally, we found that as retinal cells gradually remodeled their apical area and shape, they did so at different, cell-type-specific rates (Figure 1C). The primary pigment cells had an average rate of area change of 8.9 ± 0.5 μm²/h (mean ± SD). The cone cells and interommatidial cells had two phases of apical area change. For the cone cells, we found that there was an initial slow expansion phase of 1.0 ± 0.4 μm²/h, followed by a faster phase of 3.0 ± 0.6 μm²/h. Interommatidial cells had an initial fast expansion rate of 8.2 ± 5.2 μm²/h on average, followed by a slower average rate of area decrease of –6.0 ± 3.8 μm²/h. Thus, the rate of the initial phase of area expansion in the interommatidial cells is very similar to that of the primary pigment cells. Examining the changes in area of individual cells over time (Figure 1D) showed that they follow a similar trend to that of the respective cell type groups. Consistent with these results, analysis of the relative contributions of the cone cells, primary pigment cells, and interommatidial cells to total ommatidial lens area demonstrated that the contribution of the cone and primary pigment cells increases over time while that of the interommatidial cells decreased (Figure 1E; Supplemental Movie S1).

Movie S1.

Download video file ^{(10MB, mp4)}

Retinal cell apical area change over time. ;Ecad::GFP; pupal retina with AJs labelled in grey by Ecad::GFP. Imaging initiated from 15hrs APF for ∼12hrs showing how ommatidial cells change shape and size during development. 5min frame interval. Movie post‐processed by bleach correction and filtering with a Gaussian blur in FIJI. Scale bar = 5μm

Apical area fluctuations correlate with apical expansion rates

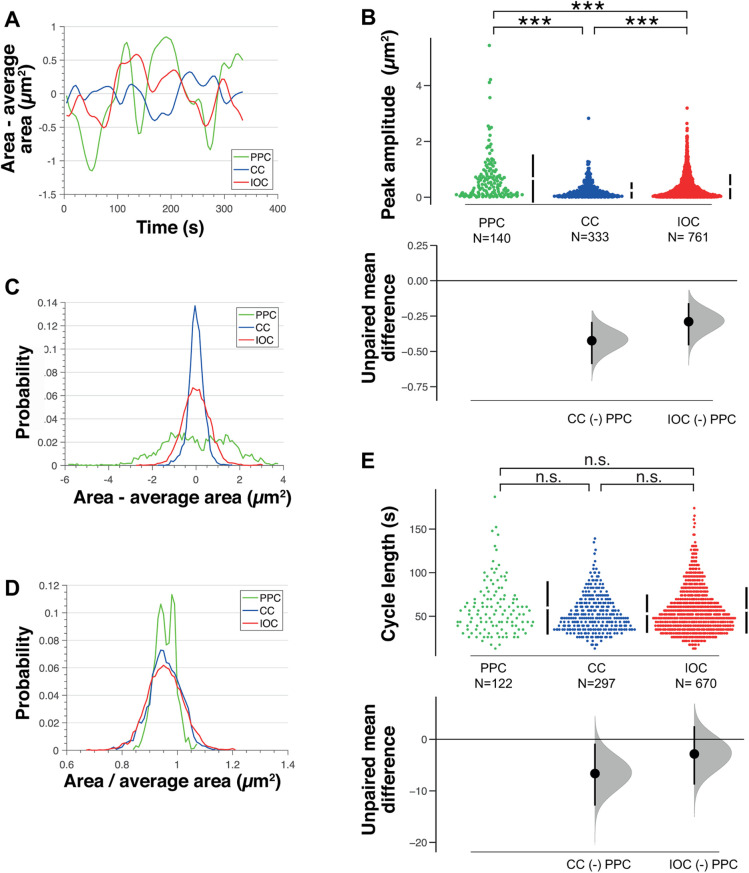
In simple epithelia, changes in apical area have been shown to occur through small fluctuations over short time scales that are stabilized incrementally (Martin et al., 2009a; Fernandez-Gonzalez and Zallen, 2011; Sawyer et al., 2011). Here, we tested whether this is the case in the retina. We found that in the lens, all cell types undergo fluctuations in apical area over a few minutes (Figure 2A). However, the amplitude of area fluctuations was different for each cell type (Figure 2B). The primary pigment cells exhibited the largest fluctuations followed by the interommatidial and cone cells (Figure 2, B and C). As cell surface stiffness is inversely proportional to shape fluctuations (Turlier and Betz, 2019), our results suggest that the cone cells are the stiffest ommatidial cell type. Normalizing the area of individual cells by their average revealed that these differences in fluctuation between cell types are linked to their area (Figure 2D). Thus, the primary pigment cells, which have the largest apical area also have the highest median area fluctuation amplitudes. To complement this analysis, we also quantified the cycle length of fluctuations (defined as the time between subsequent peaks). We found that these cycle lengths were similar between retinal cell types (Figure 2E). Altogether, these quantifications suggest the cells that have the largest apical area and highest fluctuations over short time scales undergo the fastest expansion of their apical area through long time scales.

FIGURE 2:

Highest apical area fluctuations correlate with fastest apical expansion rates. (A) Apical area minus average apical area for each cell type over time for one representative primary pigment, cone, and interommatidial cell. (B) Cummings estimation plot with upper axis showing distribution of amplitude of peaks in area fluctuations for primary pigment, cone, and interommatidial cells (n = 9 ommatidia from 5 pupae, Kruskal–Wallis test, p < 0.0001, post-hoc Dunn’s multiple comparisons tests: primary pigment-cone cells p < 0.0001, primary pigment-primary pigment p < 0.0001, cone-primary pigment p = 0.0004). On the lower axis, mean differences for comparisons to PPC are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: CC (n = 333) minus PPC (n = 140): –0.424 (95CI –0.589; –0.291); IOC (n = 761) minus PPC (n = 140): –0.29 (95CI –0.457; –0.159) (C) Probability distribution of apical area minus average apical area for primary pigment, cone, and interommatidial cells (n = 9 ommatidia). (D) Probability distribution of apical area normalized by average apical area for primary pigment, cone, and interommatidial cells (n = 9 ommatidia). (E) Cummings estimation plot with upper axis showing distribution of cycle lengths of area fluctuations for primary pigment, cone, and interommatidial cells (n = 9 ommatidia from 5 pupae, Kruskal–Wallis test, p = 0.1708). On the lower axis, mean differences for comparisons to PPC are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: CC (n = 297) minus PPC (n = 122): –6.64 (95CI –12.8; –0.846); IOC (n = 670) minus PPC (n = 122): –2.84 (95CI –8.78; 2.55).

Myosin pulse contractions correlate with fluctuations in cell area

During cell apical constriction, the medial actomyosin meshworks associated with the apical surface of the cell drive the cell’s area fluctuation (Martin et al., 2009b; Fernandez-Gonzalez and Zallen, 2011; Sawyer et al., 2011). To determine whether this is also the case when considering fluctuations of the retinal cell area, we examined the localization and dynamics of MyoII using a GFP-tagged version of the regulatory light chain, Sqh::GFP (Royou et al., 2002). We found that Sqh::GFP localized to the cell contacts and to a medial meshwork in all retinal lens cells (Figure 3A; Supplemental Movie S2). Multiple nodes of high Sqh::GFP intensity could arise simultaneously at different locations in the cytosol of retinal cells (Figure 3B). Further, the percentage of cell area occupied by MyoII nodes and the number of nodes were highest in the interommatidial cells, which undergo apical area thinning compared with the primary pigment or cone cells (Figure 3, C and C’).

FIGURE 3:

Myosin pulse contraction correlates with cell area fluctuation. (A) sqh^AX3; sqhGFP; ommatidium showing that MyoII localizes to an extensive medial meshwork across all cell types. Interommatidial cells are outlined in black, the primary pigment cells are outlined in green, and the cone cells cells are outlined in turquoise. High-intensity MyoII meshworks are outlined by a dashed line in the primary pigment cells. Intensity of MyoII ranges from low (black) to high (white). (B) Kymographs showing MyoII intensity along a line through the center of each cell, indicated by red line in the diagram, for each cell type over time along the x-axis. Red outlines show examples of two nodes occurring concurrently in the same cell. (C, C’) Density of high-intensity MyoII nodes measured by (C) percentage of cell area covered by MyoII nodes and by (C’) count of number of MyoII nodes per μm² of cell area. (C) Cummings estimation plot with upper axis showing distribution of percentages of cell area covered by MyoII nodes. On the lower axis, mean differences for comparisons to PPC are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: CC (n = 20) minus PPC (n = 10): 0.771 (95CI –3.2; 5.48); IOC (n = 46) minus PPC (n = 10): 24.1 (95CI 19.7; 28.8). (C’) Cummings estimation plot with upper axis showing distribution of counts of MyoII nodes per cell area. On the lower axis, mean differences for comparisons to PPC are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of CC (n = 20) minus PPC (n = 10): 1.07 (95CI 0.397; 1.74); IOC (n = 46) minus PPC (n = 10): 1.35 (95CI 1.12; 1.59). (D) Cummings estimation plot with upper axis showing distribution of velocities of MyoII medial meshwork at each stage of morphogenesis for primary pigment, cone, and interommatidial cells (n = 9 ommatidia from 5 pupae, Kruskal–Wallis and Dunn’s post-hoc tests, p < 0.0001 for all tests except primary pigment-primary pigment at 20 h APF where p = 0.5545). On the lower axis, mean differences for comparisons to PPC at each stage of morphogenesis are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: CCearly (n = 1108) minus PPCearly (n = 554): –0.00215 (95CI –0.00241; –0.00189); IOCearly (n = 3001) minus PPCearly (n = 554): 9.96e–05 (95CI –0.000123; 0.000323); CCmid (n = 1600) minus PPCmid (n = 800): –0.00309 (95CI –0.00337; –0.00282); IOCmid (n = 4500) minus PPCmid (n = 800): –0.000648 (95CI –0.00089; –0.000407); CClate (n = 1600) minus PPClate (n = 800): –0.00112 (95CI –0.00126; –0.000984); IOClate (n = 3300) minus PPClate (n = 800): –0.000758 (95CI –0.000882; –0.000636), using 10000 bootstrap resamples. (E) Contractility (mean divergence) over time for one representative primary pigment, cone, and interommatidial cell. (F) Cummings estimation plot with upper axis showing distribution of cycle lengths of peaks in contractility fluctuations for primary pigment, cone, and interommatidial cells (n = 9 ommatidia from 5 pupae, Kruskal–Wallis test, p = 0.053). On the lower axis, mean differences for comparisons to primary pigment cell are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: CC (n = 329) minus PPC (n = 147): –4.63 (95CI –8.95; –0.36); IOC (n = 773) minus PPC (n = 147): –2.43 (95CI –6.42; 1.54]. (G) High magnification images of a pulse of MyoII assembling and disassembling in a primary pigment cell. MyoII is labeled with Sqh::GFP (green) and AJs are labeled with Ecad::Tomato (red). The AJ of the primary pigment cell is outlined with a dashed line. A turquoise line outlines the AJ at the onset of contraction and is used for reference in the subsequent panels. A white dashed line is then used to outline the AJ as the cell undergo local pulsed contraction. Note how primary pigment cell contracts as a MyoII pulse assembles and then relaxes as the pulse disassembles. (H) Fluctuations of MyoII contractility and apical area for one representative interommatidial cell. Note that the peak in MyoII contractility precedes the peak of apical area. Frame interval in the corresponding time lapse was 4.34 s. (I) Heatmap showing temporal cross-correlation for multiple primary pigment, cone and interommatidial cells. This analysis was performed using calculated mean divergence for each cell type, averaged across the apical area of the cell. Each row represents an individual cell (n = 9 ommatidia).

Movie S2.

Download video file ^{(9.4MB, mp4)}

MyoII dynamics in retinal cells. Airyscan processed time‐lapse of sqh^AX3;sqh::GFP/Ecad::Tomato; pupal retina at 30hrs APF. Sqh::GFP in green and AJs in red marked by Ecad::Tomato. Example of movie used for PIV analysis. 4.35sec frame interval. Scale bar = 5μm

Next, to examine the dynamics of the MyoII meshworks in each cell type, we used particle image velocimetry (PIV) (Tseng et al., 2012). First, we calculated the average advection speed of Sqh::GFP particles within the medial meshwork, excluding the pool of Sqh::GFP at the AJ. We found that the velocity of Sqh::GFP motion varies between cell types and between developmental stages (Figure 3D). At early stages, Sqh::GFP particles had similar median velocity in the primary and interommatidial cells, which was greater than that estimated in the cone cells. At mid- and late stages, the primary pigment cells presented the highest median velocity followed by the interommatidial and then the cone cells. Therefore, as lens development proceeds, cells with highest average area fluctuation amplitudes over short time scales (Figure 2B) also present the highest median velocity of Sqh::GFP particle displacement. In addition, the median velocity of Sqh::GFP particle displacement increased for all cells up to when they have acquired their mature geometry (20–25 h after pupal formation [APF]), at which point they slowed down (at 30 h APF) (Figure 3D).

We then used these PIV analyses to estimate the contractility of the actomyosin networks. This was done by calculating the divergence of the corresponding vector fields. Retinal cells present large distributed meshworks (Figure 3A and Supplemental Movie S2). To extract trends at the cell level, we spatially averaged the calculated divergences for each cell type, excluding the junctional MyoII. This approach revealed that the estimated contractility of the cell medial meshworks fluctuates in all cell types with cyclical periods of contraction (pulse assembly: mean divergence < 0) and relaxation (pulse disassembly: mean divergence > 0) (Figure 3E). We found that median cycle length of fluctuations in MyoII contractility was in the range of that calculated for the area fluctuation observed on short time scales (Figures 2E and 3F). This observation is in good agreement with the notion that pulse contractions of the medial myosin meshwork can drive apical area fluctuations over short time scales. Further analysis comparing time spent contracting versus relaxing showed that on these short timescales, there was no net contraction or relaxation (Supplemental Figure S1, A and B).

To further assess whether MyoII pulse contraction is linked to cell area fluctuation, we analyzed ommatidia expressing Sqh::GFP and Ecad::Tomato to label the AJ perimeters. Focusing on the primary pigment cells revealed that localized contraction of the MyoII meshwork occurred in tandem with changes in cell apical area (Figure 3G; Supplemental Movie S3). Further, apical area fluctuation and MyoII contractility fluctuation were strongly cross-correlated for the primary pigment cells and interommatidial cells (Figure 3, H and I). Each peak of MyoII contractility preceded a peak in apical area fluctuation (Figure 3H). The strongest correlation occurred at an average time lag of –31.0 ± 9.7 s (mean ± SEM) for the primary pigment cells and –28.4 ± 3.3 s for the interommatidial cells (Figure 3I). The correlation between peaks of MyoII contractility and apical area fluctuations was not as strong for the cone cells. Altogether, these results are consistent with the hypothesis that the contractile medial MyoII meshwork induces area fluctuation over short time scales in retinal cells, and that on the longer term, these fluctuations drive apical area changes to shape cells during lens formation.

Movie S3.

Download video file ^{(341.5KB, mp4)}

MyoII dynamics in retinal cells. Airyscan processed time‐lapse of sqh^AX3;sqh::GFP/Ecad::Tomato; pupal retina at 30hrs APF showing example region of the primary pigment cell. Sqh::GFP in green and AJs in red marked by Ecad::Tomato. Note that area constrictions occur in tandem with Sqh::GFP pulses. Scale bar = 5μm

Medial MyoII meshworks control the apical geometry of retinal cells

Next, to more directly assess the role of MyoII contractility in controlling the apical geometry and area of the lens cells, we turned to laser ablation. We focused our work on the medial MyoII meshworks in the primary pigment cells because these cells are large and readily accessible (Figure 4A). First, we set up an ablation protocol where we could trigger a destabilization of the entire medial MyoII meshwork, without affecting the AJ pool or cell viability (Figure 4B and Supplemental Movies S4 and S5). Under these conditions, we observed a change in apical geometry and a significant increase in the apical area of the targeted cell (Figure 4, C and D, Supplemental Figure S2A, and Supplemental Movies S4–S6). To ensure that our light-induced perturbations were specific and that the targeted cells were not irreparably damaged, we only considered experiments where the medial meshwork was repaired and reestablished. Reestablishment of the medial meshwork was accompanied by a recovery in the apical geometry and area of the ablated cell (Figure 4B; Supplemental Movie S4).

FIGURE 4:

The contractile medial actomyosin meshwork controls cell shape. (A) Diagram of position of quantified cells relative to medial meshwork ablation (red asterisk). (B) Time-course showing response of cells after medial meshwork ablation in left primary pigment cell. MyoII is labeled by Sqh::GFP. Red star indicates point of laser ablation; 6 pixels is 245 nm. Ablated primary pigment cell is outlined in red. Note how cell area increases as medial meshwork is disrupted and then area is recovered as the meshwork reestablishes. (C) Time-course showing AJs labeled with Ecad::GFP after ablation of the medial meshwork in left primary pigment cell. Region of ablation marked with magenta asterisk. Cell outlines before ablation superimposed on each image with green dotted line. Interommatidial cell is outlined in magenta. (D) Change in apical area over time after ablation, A_(T)/A₍₀₎, A = apical area (n = 14 ommatidia). Inset panel shows y-axis at higher resolution. (E) Cell shape index (perimeter/√area) relative to initial shape parameter over time after ablation (n = 14 ommatidia). (F) Apical area changes over time after ablation of the shared primary pigment cell AJ, A_(T)/A₍₀₎, A = apical area (n = 5 ommatidia from 5 pupae). (G) Changes in apical area for two sequential ablations. The first ablation destabilizes the medial meshwork in primary pigment cell 1 (PPC1, shown in blue on the graph [G’]). The second ablation destabilizes the medial meshwork in primary pigment cell 2 (PPC2 is shown in orange on the graph [G’]). (H) Cummings estimation plot with upper axis showing distribution of lengths of the first MyoII contraction pulse after ablation (n = 5 ommatidia from 4 pupae, one-way ANOVA, p = 0.0005, primary pigment cell compared with cone neighboring interommatidial cell and control interommatidial cell: p < 0.05; other comparisons: n.s.). On the lower axis, mean differences for comparisons to primary pigment cell are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: CC (n = 20) minus PPC (n = 5): –28.9 (95CI –40; –12.9); near IOC (n = 11) minus PPC (n = 5): –21.5 (95CI –37; –4.06); far IOC (n = 6) minus PPC (n = 5): –39.2 (95CI –51.9; –23.2). Error bars: D, E, F) = SEM. All scale bars = 5 μm.

Movie S4.

Download video file ^{(5.5MB, mp4)}

Medial meshwork recovers after ablation and restores cell area. Airyscan processed time lapse of sqh^AX3;sqh::GFP; pupal retina with Sqh::GFP in grey, showing MyoII dynamics after ablation of the medial meshwork in the left‐hand primary pigment cell in frame 3 and then subsequent repair of the meshwork. Note how the cell relaxes area and loses shape but that this is regained as the meshwork repairs. 3.55sec frame interval. Scale bar = 5μm

Movie S5.

Download video file ^{(5.6MB, mp4)}

MyoII medial meshwork ablation in primary pigment cell. Airyscan processed timelapse of sqh^AX3;sqh::GFP; pupal retina with Sqh::GFP in grey, showing MyoII dynamics after ablation of the MyoII medial meshwork in the left‐hand primary pigment cell. Ablation occurs at frame 3 (3.45sec). 1.15sec frame interval. Scale bar = 5μm

Movie S6.

Download video file ^{(5.4MB, mp4)}

Cell shape changes after MyoII medial meshwork external force perturbation. Time‐lapse of ;Ecad::GFP; pupal retina at 30hrs APF with AJs in grey marked with Ecad::GFP. Ablation of medial meshwork in left primary pigment cell occurs at frame 5 (5.08sec). 1.27sec frame interval. Note how neighbouring cell types vary in their response to ablation in terms of area and shape changes. Movie post‐processed by filtering with a Gaussian blur in FIJI. Scale bar = 5μm

Lens cells mount cell-type-specific responses to mechanical perturbation

To investigate mechanical coupling between retinal cells in these experiments, we next quantified the apical deformation of retinal cells. To this end, we measured apical area and quantified apical geometry by calculating the shape index , which indicates the degree of shape anisotropy (Bi et al., 2015). For a regular hexagon, p = 3.72 and increases in magnitude as the shape becomes more elongated. Ablation led to an increase in the area of the targeted cell (Figure 4, B–D) and also affected the shape of its apical area (Figure 4E). In addition, the apical area of the adjacent interommatidial cells and that of the nontargeted primary pigment cell were affected (Figure 4, B–D). The area of the nontargeted primary pigment decreased, and this cell adopted a more elongated apical geometry (Figure 4, D and E). This deformation, which amounted to a 10% decrease in apical area (Figure 4D), was never observed in control animals when monitoring the naturally occurring fluctuation of apical area in these cells (Supplemental Figure S2B). It is specific to the medial meshwork because ablating the AJ shared by the two primary pigment cells did not lead to significant deformation in primary pigment cell area (Figure 4F; Supplemental Movie S7). Thus, medial MyoII meshworks have a greater influence on the control of apical retinal cell area than individual junctions. Interestingly, the neighboring cone cells did not show any change in apical area or geometry even though they share extensive AJs with the targeted cell (Figure 4, D and E). Altogether, these results show that different cell types respond differently to mechanical perturbation.

Movie S7.

Download video file ^{(17.7MB, mp4)}

Laser cutting of one of the AJ shared by the two primary pigment cells. Representative laser ablation of a primary‐primary pigment cell AJ in an ommatidium at 20hrs AFP. Cell outlines are labelled with ECad::GFP. Note how junction repairs by end of movie. Frame interval: 0.93sec. Scale bar = 5μm.

Shrinkage of the nontargeted primary pigment cell could be active via contractile forces intrinsic to the cell or passive as a response to the expansion in apical area of the laser-targeted cell. To decipher between these two possibilities, we destabilized the medial MyoII meshworks in both primary pigment cells sequentially. In this case, no decrease in apical area was observed after the second ablation (Figure 4, G and G’), and both targeted cells increased their area. This confirms that apical MyoII meshworks are required to define the apical area and geometry of pigment cells. It also shows that primary pigment cell contraction in response to laser ablation requires an intact medial MyoII meshwork. Further supporting this idea, quantification of how long the first fluctuation of MyoII contraction after ablation lasts in the nontargeted primary pigment and the near interommatidial cell revealed an increase in duration when compared with wild-type ommatidia (Compare Figure 3F with Figure 4H). The primary pigment cell, which deforms the most in response to ablation, presented the highest average length of the first fluctuation of MyoII contraction after ablation (Figure 4H). Altogether, these experiments indicate that while all retinal cells are mechanically coupled though their AJ, the cone cells deform less than the other retinal cell types in response to external perturbation. Among the lens cells, the primary pigment cells are the most deformable in response to mechanical perturbation.

Computational model of the ommatidium predicts that differences in cell mechanical properties coordinate cell-type-specific shape dynamics

To better understand the physical origin of the cell-type-specific mechanical response to actomyosin perturbations, we developed a 2D tension-elasticity model of the ommatidium. The model construction is inspired by vertex models for epithelial morphogenesis (Fletcher et al., 2014), where each cell is treated as a mechanical medium, carrying edge tensions at the cell–cell interfaces, a bulk tension arising from a contractile medial actomyosin meshwork, and area elasticity penalizing changes in the cell apical area (see Materials and Methods; Figure 5A). Competition between tension and elasticity gives rise to specific cell shapes determined by parameters characterizing edge tension, bulk tension, and area elastic modulus (Figure 5A). Since we are interested in the overall morphology of the ommatidium and its relationship to cell-type-specific properties, we treated the cone cell quartet as one mechanical object, each primary pigment cell as separate entities, and the left and right interommatidial cells as individual mechanical objects. Starting with an initial circular configuration for the ommatidial cluster, we dynamically evolved the points on the cell contours based on their resultant forces in order to obtain the steady-state morphology of the ommatidium (Figure 5B). The forces evolving ommatidium morphology result from minimizing the mechanical energy of the cluster (see Materials and Methods). We benchmarked the model parameters (tension parameters, elastic moduli) to recapitulate the experimentally measured shapes and sizes of the control cone, interommatidial and primary pigment cells (Figure 1D).

FIGURE 5:

Computational model of the ommatidium predicts cell-type-specific mechanical response. (A) Schematic of the tension-elasticity model of the ommatidial cluster showing the edge tensions, bulk elasticity parameters in the cone cell cluster (blue), primary pigment cell (green), and the interommatidial cell clusters (red). (B) Simulations of ablation experiments by reducing bulk tension in one of the primary pigment cells (marked by a star). Left to right: evolution of colony morphology on ablation. (C) Model prediction for the dynamics of the apical area (normalized) for the different cell clusters in the ommatidia, on ablation at t = 0. (D) Model prediction for the dynamics of the cell shape index (perimeter/√area, normalized) for the different cell clusters in the ommatidia, on ablation at t = 0. (E) Simulation of ablation experiments for a softer cone cell (CC) cluster. (F, G) Dynamics of cell area (F) and cell shape index (G) in the ablation simulation showing significant deformation of the cone cell cluster, inconsistent with experimental data. (H) Simulation of the hypercontraction in the right primary pigment cell (marked by red arrows). (I) Model prediction for the dynamics of the apical area (normalized) for the different cell clusters in the ommatidia, on the induction of hypercontraction in the right primary pigment cell at t = 0. (J) Model prediction for the dynamics of the cell shape index (perimeter/√area, normalized) for the different cell clusters in the ommatidia on the induction of hypercontraction in the right primary pigment cell at t = 0.

As our model accurately captured ommatidial cell morphologies, we then sought to test if it could capture the results of the laser ablation experiments (Figure 4). To simulate medial meshwork ablation in the primary pigment cells, we reduced the bulk tension in the left primary pigment cell and allowed the cell cluster to dynamically evolve to a new morphology (Figure 5B). Our model quantitatively captured the experimentally measured morphological transformations, provided that the elastic modulus of the cone cell cluster (k_c) is much higher than that of the interommatidial cell cluster (k_i) and the primary pigment cells (k_pp), i.e. . On reduction in bulk contractility, the area of the targeted primary pigment cell expanded (Figure 5C) while decreasing its shape index (lower aspect ratio) (Figure 5D). In agreement with experimental data (Figure 4, D and E), the shape and area of the cone cell cluster remained unchanged. The interommatidial cell cluster adjacent to the targeted primary pigment cell initially decreased in area, but then recovered over time (Figure 5C) and also thinned in shape (Figure 5D). The inclusion of a rigid cone cell cluster enabled mechanical communication between the primary pigment cells, such that the untargeted primary pigment cell shrunk in area while increasing its shape index (higher aspect ratio) (Figure 5, C and D). These results agree with our experiments (Figure 4, D and E) and suggest that different retinal cell types have different mechanical properties. Simulations with a softer cone cell cluster, whose elasticity was comparable to primary pigment and interommatidial cells, led to significant deformations of the cone cells during ablation (Figure 5, E–G), which was not observed in our experimental perturbations (Figure 4, D and E). Therefore, these simulations suggest that the cone cells are stiffer than their neighbors, and that this stiffness limits their mechanical coupling.

To further test the predictive power of the model, we studied how cell shape might respond to an increase in contractility (higher bulk tension) in the right primary pigment cell (Figure 5H). One strong prediction from the model is that increasing the tension in one primary pigment cell will cause the paired primary pigment cell to increase its apical area (Figure 5I). Furthermore, our model predicted that the shape index should decrease for the paired primary pigment cell and the interommatidial cells while increasing for the constricted primary pigment cell (Figure 5J).

Experimental testing of computational model predictions

To experimentally test the predictions arising from our model, we used genetics to perturb the actomyosin cytoskeleton. First, to induce hypercontraction in one primary pigment cell (simulation in Figure 5H), we inhibited the expression of sds22 (Figure 6A), which encodes for the regulatory subunit of MyoII phosphatase PP1A (Grusche et al., 2009). This did not have any significant effect of the Sqh::GFP intensity within the AJs of the cell when compared with wild type, suggesting this perturbation is relatively specific to the medial meshwork (Supplemental Figure S3). PIV analysis performed on Sqh::GFP demonstrated that this led to a significant decrease in medial meshwork velocity (Figure 6, B and B’). This genetic perturbation resulted in a reduction in apical area and a change in geometry, whereby the targeted cell became more elongated (Figure 6, A, C, and D). As predicted by our computational model, this was accompanied by an increase in average apical area of the nontargeted primary pigment cell (Figure 6C). It also led to a slight decrease in the shape index for the paired cell (Figure 6D).

FIGURE 6:

Myosin regulation and mechanical coupling between retinal cells. (A) Single primary pigment cell expressing sds22^IR. Clone marked by the presence of mCherry. (B) Gardner–Altman estimation plot with left axis showing distribution of velocities of MyoII of wild type and sds22^IR expressing cells. On the right axis, mean difference is plotted as a bootstrap sampling distribution; dot = mean difference, error bars = 95% CI. Unpaired mean difference between WT (n = 628) and sds22^IR (n = 628) is –0.108 (95CI –0.128; –0.0877]. (B’) Velocity distribution for MyoII in wild type vs. sds22^IR expressing primary pigment cells (Kolmogorov–Smirnov test, p < 0.0001). (C) Cummings estimation plot with upper axis showing distribution of areas of primary pigment cells expressing sds22^IR, wild type primary pigment cell in the same ommatidia (paired), and wild-type primary pigment cell in unaffected ommatidia (n = 176, 176, and 254 ommatidia, respectively, one-way ANOVA, p < 0.0001). On the lower axis, mean differences for comparisons to sds22^IR expressing cells are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: paired (n = 176) minus sds22^IR (n = 176): 46.7 (95CI 42.4; 50.9]; wild type (n = 254) minus sds22^IR (n = 176) 29.7 (95CI 26.7; 32.7]. (D) Cummings estimation plot with upper axis showing distribution of cell shape index (perimeter/√area) of primary pigment cells expressing sds22^IR, wild-type primary pigment cell in the same ommatidia (paired) and wild-type primary pigment cell in unaffected ommatidia (n = 40, 40, and 90 ommatidia, respectively, one-way ANOVA, p < 0.0001, sds22^IR-paired p < 0.0001, sds22^IR-wild-type p < 0.001, paired-wild-type p = 0.1585). On the lower axis, mean differences for comparisons to sds22^IR expressing cells are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of: paired (n = 40) minus sds22^IR (n = 40): –0.538 (95CI –0.678; –0.396]; PPC (n = 90) minus sds22^IR (n = 40): –0.436 (95CI –0.557; –0.315]. (E) Ommatidium from a sqh^AX3;sqh::GFP; retina stained for Arm (red) showing actomyosin cable around the perimeter of the cone cell cluster. (F) Single cone cell expressing Rho^N19 marked by the presence of mCherry. (G, H’) Cummings plots with upper axis showing distribution of (G) apical area and (H, H’) cell shape index (perimeter/√area) of (G, H) cone cell clusters, individual cone cells, and (G, H’) primary pigment cells in ommatidia with one cone cell expressing Rho^N19 compared with wild type control ommatidia in the same retinas. For area, one sample T test: cone cluster p = 0.008, cone cell p < 0.0001, and primary pigment cell n.s. p = 0.8728. For shape index, one sample T test: cone cluster p = 0.0129, cone cell p = 0.0465, primary pigment cell p = 0.0003. On the lower axes, mean differences for comparisons of cells in Rho^N19 expressing ommatidia to controls are plotted as bootstrap sampling distributions; dot = mean difference, error bars = 95% CI. Unpaired mean difference of Rho^N19 expressing minus control for area: cone cell cluster (n = 20): 8.74 (95CI 3.06; 15.3]; individual cone cell (n = 20): 8.79 (95CI 6.39; 11.7]; primary pigment cell (n = 40) minus Control PPC (n = 40): –0.397 (95CI –4.93; 4.64]; and for shape index: cone cell cluster (n = 20): 0.0894 (95CI 0.0243; 0.161]; individual cone cell (n = 20): –0.0974 (95CI –0.184; –0.000475]; primary pigment cell (n = 40) minus Control PPC (n = 40): 0.338 (95CI 0.158; 0.508]. (I) Time-course showing AJs labeled with Arm::GFP after ablation of the medial meshwork in left primary pigment cell in an ommatidium where one cone cell expresses Rho^N19 (marked by mCherry, red). Region of ablation marked with a white star. Cell outlines before ablation are superimposed on each image with dotted lines. (J) Apical area changes over time after ablation, A_(T)/A₍₀₎; A, apical area (n = 9 ommatidia). (J’) Magnified panel showing y-axis at higher resolution. (K) Cell shape index (perimeter/√area) relative to initial shape parameter over time after ablation (n = 9 ommatidia). All scale bars = 5 μm.

Second, we aimed to test the prediction that the pattern of force propagation in the ommatidium can be explained if the core cone cells are stiffer than the other cell types. Compatible with this idea, the cone cells contain a cortical actomyosin cable that delineates their AJ with the surrounding primary pigment cells (Figure 6E). This could increase cortical tension and thus make their perimeter stiffer. To test this idea, we sought to inhibit actomyosin in the cone cells and assess the impact of this perturbation on force distribution between each lens cell of the ommatidium. To inhibit actomyosin, we expressed dominant-negative RhoA (Rho^N19) in cone cells. This led to an expansion of the cell apical area (Figure 6, F and G) and to a distortion of their geometry (Figure 6, F and H). This shows that actomyosin is required to shape the cone cells. Consistent with our computational model that cone cell stiffness is a parameter that influences the shape of their neighbors, we found that expression of Rho^N19 in a cone cell induced an elongation of the flanking PPCs (Figure 6H’) without affecting the area of the cell (Figure 6G).

Third, to assess how inhibiting myosin contractility in the cone cells affects mechanical coupling between the remaining cells, we performed laser ablation experiments. Ablating the MyoII meshworks in one primary pigment cell in ommatidia, in which one or two cone cells express Rho^N19, did not lead to change in area and geometry of the cone cell clusters (Figure 6, I–K and Supplemental Movie S8). However, quantifying the area of only the Rho^N19 expressing cone cells showed their area decreased (Figure 6, J and J’). Quantification of the paired pigment cell showed that it was not significantly changed in area (Figure 6J-J’ and Supplemental Figure S4) or when considering its shape index (Figure 6K). Thus, as predicted by our model, altering the mechanical properties of cone cells to render them softer makes them more prone to area change in response to perturbation of the MyoII meshworks in a flanking primary pigment cell. This also impacts mechanical coupling between the two primary pigment cells.

Movie S8.

Download video file ^{(10.5MB, mp4)}

MyoII medial meshwork ablation in primary pigment cell containing a Rho^N19 cone cells. Airyscan processed time‐lapse of ArmGFP pupal retina. The cone cells expressing Rho^N19 is labelled using mCherryFP. The ablation occurs at frame 3 (6.87sec). 2.29 sec frame interval. Scale bar = 5μm

DISCUSSION

How different cells work together to generate a complex tissue organization is not well understood. Here, we studied tissue organization in the fly retina, which is made up of different epithelial cell types that organize with crystal-like precision during lens morphogenesis. Our work reveals a preeminent role for the contractile medial MyoII meshworks in regulating the apical area and geometry of the retinal cells. In addition, our results indicate that these contractile meshworks are required for mechanical coupling and communication between cells.

Mechanical coupling between cells has been studied in simple epithelia, where cell packing tends toward regular hexagonal arrays (Gibson et al., 2006; Farhadifar et al., 2007). In these simple tissues, cells maintain similar mechanical properties. Our work shows this is not the case in a more complex epithelium, where cells need to acquire different morphologies. In the eye, our computational model and experimental observations indicate that different cell types have different mechanical properties. The central cone cells do not deform in response to extrinsic forces. Yet by being stiffer than the surrounding cells, they play a role in distributing forces to the neighboring primary pigment cells. Both our computational model and genetic manipulations suggest this is because the cone cells are stiffer than their neighbors.

In most instances of cell shape changes studied so far, medial MyoII meshworks have been shown to be polarized. In the fly mesoderm, apical constriction is powered by radially polarized contractile meshworks (Martin et al., 2009a). In the germband, pulsatile flows of contractile actomyosin that are polarized along the anterior–posterior axis drive AJ remodeling to promote cell intercalation (Rauzi et al., 2010). In these tissues, where cells are relatively small and present limited numbers of discrete MyoII structures, the calculated time lag between peak contractility and cell apical area fluctuation has been reported to be ∼15 s (Fernandez-Gonzalez and Zallen, 2011; Collinet et al., 2015). In retinal cells, these contractile MyoII meshworks do not appear to be polarized. They exhibit a continuous, distributed, fluctuating mesh through time and space, with multiple contraction nodes that are asynchronous. In these cells, we estimate the time lag between peak contractility and cell apical area fluctuation to be ∼30 s. Further, in contrast to the germband, where intercalating cells maintain their area (Fernandez-Gonzalez and Zallen, 2011; Sawyer et al., 2011) or shrink as they constrict in the mesoderm (Martin et al., 2009a), we find that retinal cells gradually increase their area over time. Therefore, these contractile meshworks can specifically regulate the geometry of apical-junctional cell profile while allowing for area increase. We speculate that other mechanisms are at play that oppose MyoII contractility. These could include osmotic pressure, for example, or preferential adhesion between cells, as demonstrated between the primary pigment and interommatidial cells (Bao et al., 2010; Larson et al., 2010). Finally, we show that in a complex tissue, mechanisms exist that enable cell types to be more resilient to extrinsic forces. This is the case for the cone cells, which show little deformation when challenged with extrinsic mechanical perturbation. Therefore, mechanisms must exist that limit deformation in these cells. One possibility suggested by our model and genetic experiments is that this can be achieved through increased stiffness.

MATERIAL AND METHODS

Fly strains

Flies were raised on standard food at 25°C. Crosses were performed at 25°C. The following fly strains were used:

• ; Ecad::GFP; (Huang et al., 2009)

• sqh^AX3; sqh>sqhGFP; (BL #57144, Royou et al., 2002)

• ; Ecad::Tomato; (Huang et al., 2009).

• ; hsflp;;act>CD2>Gal4,UAS-RFP; (BL #30558).

• ; UAS-sds22-RNAi; (VDRC, 11788).

• ; UAS-Rho^N19; (BL #58818).

• ;; arm - Arm::GFP (BL #8555, Orsulic and Peifer, 1996)

To generate single cells deficient for sds22, hs-flp;;actin>CD2>gal4,UAS-RFP was crossed to UAS-sds22-RNAi. Flies were heat shocked at third instar larval stage at 37°C for 10–15 min and dissected 4 d later. To generate ommatidia expressing Rho^N19, hs-flp;;actin>CD2>gal4,UAS-RFP was crossed to UAS-Rho^N19. Flies were heat shocked at third instar larval stage at 37°C for 10-15 min and staged for laser ablation 2 d later.

Time-lapse imaging

;Ecad::GFP; flies were staged and examined at 15 h APF at 25°C and the pupal case was removed to expose the retina. Pupae were mounted on blue-tac with the retina facing upward and covered with a coverslip as described in Fichelson et al. (2012). Time-lapse imaging was performed on a Zeiss inverted microscope with an Andor spinning disk using a Plan Neofluar 100×/1.3 Ph3 oil immersion objective. Images were acquired using ImageJ Micromanager software (Edelstein et al., 2014). Retinas were imaged for a minimum of 12 h acquiring a Z-series in 1-μm sections every 5 min. Drift in XY and Z was corrected manually. Images were postprocessed in Fiji using the Stack-reg plugin (Thevenaz et al., 1998) to further correct for drift. For imaging of medial meshwork dynamics, sqh^AX3/Y;sqhGFP/EcadTomato; flies were staged to 20, 25, or 30 h APF at 25°C and mounted as described above. Retinas were imaged on a Zeiss LSM880 microscope with a Plan Apochromat 63×/NA 1.4 oil objective using airyscan detectors. Images were acquired at a 40–45 nm pixel size with a speed of 4.35 s/frame. Airyscan processing was performed with the Zen software package to increase resolution.

Measurements of apical area over time

For measurements of the total apical area for each cell type, the outside perimeter of the cone cell cluster, primary pigment cells, and interommatidial cells were traced manually using the Freehand selection tool in Fiji on every 20th frame (100 min) of the time lapse of; Ecad::GFP; retinas. Areas enclosed by each perimeter were measured in Fiji and subtracted from each other to generate areas for each cell layer (e.g., area of interommatidial cell outline minus area of primary pigment cell outline gives the area for the interommatidial cell layer). These areas were then expressed as a percentage of the total ommatidium area. Thirteen ommatidia from the center of the field of view of two independent retinas were registered in time by aligning the midpoint of the four-way vertex stage of the cone cell T1 transition and measurements were averaged for each time point.

PIV

Time-lapse movies of sqh^AX3/Y;sqhGFP/EcadTomato; ommatidia were processed in Fiji with Bleach correction and Gaussian blur and registered with the Stack-reg plugin (Thevenaz et al., 1998) to correct for lateral drift. PIV analysis was performed using the Fiji PIV plugin (Tseng et al., 2012) by choosing an 8 × 8 pixel window with a time lag 4.34 s. Cell contours were tracked using the Tissue Analyzer plugin (Aigouy and Le Bivic, 2016) using Fiji, or manually in Fiji to segment the primary pigment, interommatidial, and cone cells to measure cell apical areas. For calculation of the advection velocities of medial MyoII, the norms of the PIV vectors were averaged within each cell for each frame and divided by the frame rate in MATLAB. Advection speeds of each cell were then averaged in time for the ommatidia at 20, 25, and 30 h APF. Mean divergence of velocity vectors within each cell was calculated in MATLAB for each frame. Mean divergence, apical area, and apical perimeter measurements over time were processed by Gaussian smoothing with a window of 43 s to improve the signal-to-noise ratio in MATLAB. Cycle lengths and peak amplitude were calculated in MATLAB using the “findpeaks” command. Cross-correlation of the rate of area change and the rate of mean divergence change was performed in MATLAB for each cell and plotted as a heatmap.

Kymographs

Kymographs were generated using the Reslice plugin in Fiji along a 1 pixel-wide segmented line that was drawn through the center of the cell and did not overlap with the AJ-associated MyoII in any frame. The movie presented in Figure 3 is of a sqh^AX3; sqhGFP; retina at 30 h APF imaged with a Zeiss LSM880 confocal with a Plan Apochromat 63×/NA 1.4 oil objective using airyscan detectors drift corrected using the Stackreg plugin (Thévenaz et al., 1998) in Fiji.

Node density calculation

Sqh::GFP intensity was thresholded on time-lapse movies of sqh^AX3/Y;sqh::GFP/Ecad::Tomato; in Fiji to select the nodes of high intensity. The number of nodes per cell and the percentage of cell area covered by MyoII nodes were measured using the “Analyze particles” tool in Fiji and averaged over 50 time frames for each cell. Multiple retinal cells from five independent retinas were analyzed.

Laser ablation

Ablations of MyoII medial meshworks were performed using a Zeiss LSM880 microscope with a Plan Apochromat 63×/NA 1.4 oil objective using 740 nm multiphoton excitation from a Ti-sapphire laser. An ROI of 6 × 1 pixels (245 nm) for 30–40 h APF retinas and 4 × 1 pixels (163 nm) for 20 h APF retinas was drawn in the center of the apical region of the cell and targeted with a laser power of 10–20% at the slowest scan speed for one iteration. For monitoring of the MyoII medial meshwork during ablation, sqh^AX3/Y;sqh::GFP/Ecad::Tomato; or sqh^AX3/Y;sqh::GFP; flies were imaged using airyscan detectors. Images were acquired every 3.1–3.6 s and processed with the Zen software. For quantification of area change after ablation, Ecad::GFP flies were used to visualize AJs and images were acquired every 1.27 s before and after ablation. Laser ablations in ommatidia expressing dominant-negative Rho (Rho^N19) were performed following the same protocol, except that images were acquired every 2.29 s before and after ablation.

Cell deformation after ablation

Cell deformations after ablation were analyzed on movies of ;Ecad::GFP or sqh^AX3; SqhGFP retinas where the primary pigment cell’s medial meshwork was targeted. Each cell type of interest was segmented manually using the Freehand Selection tool in Fiji on the initial frame before ablation and then every 10 frames (12.7 s) until the maximum change in area was reached (normally about 200–250 s). Area and perimeter/√area were measured and the ratio before and after ablation over time was calculated and averaged across 14 ommatidia. Analysis of cell deformation following laser ablation in ommatidia expressing dominant-negative Rho (Rho^N19) was performed using the same protocol, except that manual segmentation was performed on every fifth frame (11.5 s), and measurements were performed on nine ommatidia.

Statistical tests

Statistical tests were performed in GraphPad Prism 7. Data were compared using one sample T test, Kruskal–Wallis test, or one-way ANOVA with Tukey’s post-hoc tests. For graphical analysis, data were plotted on a Gardner–Altman or Cummings estimation plot using the DABEST package in R with 5000 bootstrap resamples unless otherwise stated. All confidence intervals (CIs) are bias-corrected and accelerated (Ho et al., 2019)

Mechanical model for ommatidial morphology

The apical surface of the ommatidial cell cluster is modeled as a composite mechanical medium consisting of an inner cone cell cluster of area A_c, a medial concentric layer of two adjacent primary pigment cells of areas A_p1 and A_p2, and an outer layer of two interommatidial cell clusters of areas A_i1 and A_i2 (Figure 5A). In the spirit of vertex models (Farhadifar et al., 2007; Fletcher et al., 2014), each cellular unit (cones, primary or interommatidial) is characterized by a line tension, γ, at cell–cell interfaces; a surface tension, Γ, at their interiors; an elastic modulus, k, penalizing changes in cell apical area. The edge tension arises from a competition between intercellular adhesion and cortical actomyosin contractility, and the bulk tension arises from contractility in the medial actomyosin meshwork. The total mechanical energy of the cell colony is given by

where k_c, k_p, and k_i define the area elastic moduli of the cone, primary pigment, and interommatidial clusters; , , and are the respective surface tensions; and , , and are the respective preferred areas of the three cell types. Intercellular interactions at cell–cell interfaces are given by the term :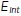

where is the line tension at the interface between cell α and β ( cone cell, primary pigment cell, interommatidial cell) and is the length of the interface. Each point, , on the cone, primary pigment, and interommatidial cell contour evolves in time according to the equation of motion where μ is a friction coefficient.

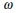To account for pulsatile actomyosin fluctuations, we assume that the cell surface tension fluctuates in time according to , where α labels the cell type, is the base tension, is the frequency of fluctuation, and is a phase-shift calibrated from experimental data. The model is simulated using a custom code implemented using the Surface Evolver program (Brakke, 1992) starting with an initial circular morphology, consisting of an inner circular cone cell cluster and surrounded by concentric rings of primary pigment and interommatidial cells. The model parameters are chosen to reproduce the experimentally measured geometry of the wild-type ommatidia (Table 1). To simulate medial meshwork ablation of cell α, we let Γ_α→Γ_α − ΔΓ after relaxing the cell system to their mechanical equilibrium state. Similarly, to induce hypercontractility we let Γ_α →Γ_α + ΔΓ after mechanical relaxation.

TABLE 1:

Model parameters.

Cell type	Preferred area	Surface tension Γ	Elastic modulus k
Primary pigment (left/right)	1.75	1.0	2.5
Cone cell cluster	1.0	1.0	14.0
Interommatidial cell cluster (left/right)	1.5	1.0	6.0

Interface type	Edge tension γ
Cone-primary pigment	2.5
Primary pigment-primary pigment	0.5
Primary pigment-interommatidial cells	2.0
Interommatidial cells-interommatidial cells	0.5
Interommatidial cells-outside	2.0

Immunofluorescence

Whole mount retinas at 40 h APF were prepared as previously described (Walther and Pichaud, 2006) The following antibodies were used for indirect immunofluorescence: mouse anti-Arm 1/200 (N27-A1, Developmental Studies Hybridoma Bank [DSHB]) and rabbit anti-P-Myosin Light Chain 2 (S19) 1/50 (3671S, Cell Signaling Technology). Mouse or rabbit secondary antibodies conjugated to Alexa 488 or Cy5 (as appropriate) were used at 1/200 each (Jackson ImmunoResearch). Samples were mounted in VectaShield and imaging was performed using a Leica SP5 or SP8 confocal microscope. Images were edited using Fiji and Adobe Photoshop 7.0.

Abbreviations used:

AJ

adherens junction

APF

after pupal formation

CI

confidence interval

MyoII

Myosin-II

PIV

particle image velocimetry.