Multiscale Finite Element Modeling of Mechanical Strains and Fluid Flow in Osteocyte Lacunocanalicular System

Abstract

Osteocytes form over ninety percent of the bone cells and are postulated to be mechanosensors responsible for regulating the function of osteoclasts and osteoblasts in bone modeling and remodeling. Physical activity results in mechanical loading on the bones. Osteocytes are thought to be the main mechanosensory cells in bone. Upon load osteocytes secrete key factors initiating downstream signaling pathways that regulate skeletal metabolism including the Wnt/β-catenin signaling pathway. Osteocytes have dendritic structures and are housed in the lacunae and canaliculi within the bone matrix. Mechanical loading is known to have two primary effects, namely a mechanical strain (membrane disruption by stretching) on the lacunae/cells, and fluid flow, in the form of fluid flow shear stress (FFSS), in the space between the cell membranes and the lacuna-canalicular walls. In response, osteocytes get activated via a process called mechanotransduction in which mechanical signals are transduced to biological responses. The study of mechanotransduction is a complex subject involving principles of engineering mechanics as well as biological signaling pathway studies. Several length scales are involved as the mechanical loading on macro sized bones are converted to strain and FFSS responses at the micro-cellular level. Experimental measurements of strain and FFSS at the cellular level are very difficult and correlating them to specific biological activity makes this a very challenging task. One of the methods commonly adopted is a multi-scale approach that combines biological and mechanical experimentation with in silico numerical modeling of the engineering aspects of the problem. Finite element analysis along with fluid-structure interaction methodologies are used to compute the mechanical strain and FFSS. These types of analyses often involve a multi-length scale approach where models of both the macro bone structure and micro structure at the cellular length scale are used. Imaging modalities play a crucial role in the development of the models and present their own challenges. This paper reviews the efforts of various research groups in addressing this problem and presents the work in our research group. A clear understanding of how mechanical stimuli affect the lacunae and perilacunar tissue strains and shear stresses on the cellular membranes may ultimately lead to a better understanding of the process of osteocyte activation.

INTRODUCTION

Bone undergoes modeling and remodeling. These processes occur with the coordinated activities of three types of cells, namely osteocytes, osteoclasts and osteoblasts. . Osteoblasts are bone forming cells derived from mesenchymal stem cells and some of the osteoblasts get embedded in bone and differentiate into osteocyteswhich are to be the mechanical sensors of the bone [1, 2]. Osteoclasts are multi-nucleated bone resorbing cells forming by a fusion of precursor cells of hematopoietic origin. In modeling, bone grows and/or is reshaped by osteoblasts and osteoclasts which act independently [3]. In remodeling, bone adapts its composition and structural properties in response to its loading environment in a dynamic manner [4, 5]. During remodeling, osteoclast activity occurs first to remove existing bone followed by osteoblasts laying down new bone [3]. Wolff’s theory [6] postulates that bones adapt their structure and mass to mechanical stimuli to optimize their load bearing capacity [7].

Osteocytes make up to ninety percent of the cells in bone. They reside in cavities called lacunae and are connected to each other by dendritic processes, which extend through tunnels called canaliculi. Using microXCT based imaging modality on transiliac biopsies the lacunar density has been shown to be in the range of 18-22,000 per mm³[8]. The spaces between the osteocytes/lacuna and the dendrites/canaliculi are filled with fluid, small molecules and tethering proteins. Osteocytes are considered to be sensors of mechanical loading in bone and transduce stimuli into biological signals in the cell. They subsequently communicate to cells on the bone surface – such as osteoclasts and osteoblasts – through the dendritic processes [9-13]. Mechanotransduction is the process through which the physical/mechanical forces are transformed into biological responses. The process of mechanotransduction, as is currently known, includes the response of the osteocyte to both mechanical deformation/strain as well as the fluid flow in the space between the osteocyte and the lacuna in which it resides.

Loading and Mechanotransduction

Dynamic (or intermittent) loading is known to have a more significant effect than static (continuous) loading in the remodeling process [14]. Factors that affect the response include the magnitude of load, the frequency, and the number of cycles [4, 15]. Short durations of load with a recovery period are more effective than static loads [16]. Burr et al. [17] demonstrated on rat tibia that a recovery period of 4-8 hours is required to reestablish the mechanosensitivity of the cells.

Factors affecting Mechanosensation by Osteocytes

It has been shown that initiation of mechanotransduction varies in bone depending on the bone site. Hsieh et al [18] showed that in rats the strain threshold varied from 1343 microstrains (με) proximally to 2284 με at the midshaft and 3074 με distally. Robling and Turner [16] demonstrated that the mechanical strain required for mechanotransduction was also dependent on mouse strain (C3H/He, C57BL/6, and DBA/2) and ranged from 1000-5000 με.

During physical activities, the whole bone undergoes damage at strains with the magnitude of 3500με. However, the minimum strain needed to initiate an osteogenic response at the cellular level is of the order of 10,000 με [19, 20]. This suggests that at the microscopic scale, bone matrix has several structural components such as the tortuous lacuna-canalicular network (LCN), tethering elements, extra-cellular matrix (ECM) projections, primary cilia and perilacunar matrix regions, which result in increased strain magnitude at the microstructural level compared to global strain.[21-24]. Local microstructural strains in the perilacunar region in cortical bone are five to six times the global bone strains [25, 26]. Nicolella et al [27] showed that in cortical bone of bovine tibia the average strain magnification around the osteocyte lacunae, resulting from macroscopic bone strains of 2000 με, ranged from 1.1 to 3.8 while some lacunae showed a decrease in perilacunar strain due to increased loading. The study suggested that the perilacunar strain was non-monotonic with respect to loading and micro damage present could play a part in local redistribution of bone matrix strains [28]. Verbruggen et al. using a digital image correlation technique showed that the osteocyte experiences much higher strains (about 31000 με) due to physical activity strains of the order of 3000 με on the bone [29].

Morphological Effects:

Currey [30] indicated that lacunar shape, size and orientation contribute to the variation in the strain magnification. The shape of the cells also plays a part in mechanosensation. Flat MLO-Y4 cells were shown to have a higher stiffness compared to round cells in vitro implying that ellipsoidal shaped osteocytes take advantage of their shape to sense lower strain values for mechanotransduction [31]. Kamioka et al. investigated the important influence of osteocyte shape on cell process fluid velocities [32].The number of lacunae and hence the heterogeneity of tissue i.e. perilacunar bone-vs bone matrix adds complexity to models of strain fields not usually incorporated into current numerical FE models.

Fluid Flow and Mechanotransduction

As mentioned before, bone also has interstitial fluid surrounding the cells and their dendrites in the lacunae and canaliculi. Mechanical loading on the bone matrix generates a pressure gradient, which initiates interstitial fluid flow around the osteocyte. The load-induced fluid flow in the lacuna-canalicular network (LCN) creates fluid flow shear stress (FFSS) around the osteocyte cell membrane. Mathematical models showed the transmission of the FFSS on the osteocyte and dendrites causing deformation of the cell membrane and these deformations and shear stress forces result in biochemical signaling [21, 33, 34].

Fluid flows in this space either due to pressures in the circulatory system or due to mechanical loading [35]. Due to the oscillatory nature of forces in cyclic loading, fluids are flushed from the compressive region and osteocytes experience FFSS on the cell membranes up to 3.0 Pa (30 dynes/cm²). FFSS, but not mechanical strain, has been shown to elicit nitric oxide (NO) and prostaglandin (PGE₂) secretion in cell culture models [36]. Thresholds for mechanical strain and FFSS to stimulate the release of NO and PGE₂ have been demonstrated [37, 38]. FFSS of 0.6 Pa on primary human bone cell culture was shown to result in a ~7 fold increase in release in NO and a ~3 fold increase in release of PGE₂ while a substrate stretch of 1000 με resulted in an increase of only 1.65 and 1.3 fold increase in NO and PGE₂ respectively. Mechanical strain in cells due to fluid flow are shown to be much higher compared to substrate stretch. While no direct equivalent shear stress to strain match tests are known to be performed, it was shown that FFSS of 1.6 Pa results in osteocyte cell strains ranging from 8000-23000 με which was time dependent [26]. FFSS in the range of 0.2-2.3 kPa was shown to cause β-catenin nuclear translocation in MLOY-4 osteocyte cells [39].This again substantiates that FFSS results in larger strains in cells compared to mechanical strain. Anderson et al. developed a computational fluid dynamics model of an osteocyte in the micro/nano-scale and predicted the highest fluid shear stress occurs inside the canaliculi rather than lacuna [40].

Diseased Condition and Mechanotransduction

Disease conditions in bone have also been shown to respond to FFSS differentially; it has been hypothesized that the fluid space is larger in osteopenic bones which results in lower FFSS and consequently lower mechanotransduction, while the smaller fluid spaces in osteopetrotic bones could result in higher stimulation[41]. Other factors to consider include local microstructural responses at the lacunar/cellular level. For instance, the Wnt/β-catenin pathway has been shown to be triggered by crosstalk with the prostaglandin pathway in response to loading which then leads to a decrease in expression of negative regulators of the pathway such as Sost and Dkk1 [42, 43]. Osteocytes are known to propagate signals through the dendritic network toward the bone surface. However, it has been observed that regions in the bone that experience similar mechanical strains do not uniformly activate all osteocytes. Our group has shown that in response to in vivo mechanical loading, activation of the Wnt/β-catenin pathway occurs within sub-populations of osteocytes [43]. From some of these observations it is evident that not only is there a complex loading environment in the bone but also the wide variety of architectural features and biological responses of the cell make the study of the mechanotransduction a very challenging and exciting study.

Finite Element Methods to Study Mechanical Strain and Fluid Flow

Finite element (FE) models are often used in situations where it is very difficult to conduct experimental studies to simulate mechanical loading effects on structures. FE models are used to estimate the mechanical strain and fluid flow responses at both the macro, micro and nano structural levels in silico [9]. Critical considerations in the development of FE models are: a) imaging modalities of sufficient resolution to obtain image stacks to be used by segmentation software for 3D model development, b) careful segmentation of the image stack to develop a 3D model – often in the form of surface mesh based STL files, using smoothing and other morphological operations, c) assembly of the different parts of the 3D model into a single unit, d) creation of 3D solid FE meshes from the 3D STL files with sufficiently small size in order to obviate mesh size effects, e) representation of proper boundary conditions and loads on the model to represent physiological conditions accurately, f) running FE analysis in a suitable and well established software, and g) post processing the results to give metrics that would be suitable to interpret the biological phenomena being observed. In this paper we present a review of the various aspects that are involved in the mechanotransduction process: the processes involved in FE modeling and validation of the models; work done in the areas of effects of mechanical strain and fluid flow on the biological response of osteocytes; and imaging modalities and methods used in these studies. We finally describe the ongoing current research in this area.

Macro models of various murine long bones have been developed for studying the strain distribution in the bone and linking it to either biomechanical experiments such as three-point bending tests or other biological phenomena. The strain environment throughout the tibia of mice subjected to three point bending was studied [44]. Other studies using FEA include the determination of strain distributions on rat tibia [45], load strain distribution in mouse ulna [46], dynamic loading on mouse ulna [47], age related distribution of strains in tibia [48]. Strain gages are commonly used to find experimental strain data. However, the gages are often difficult to place in a small bone since they are almost the size of the bone itself and secondly it is possible that the bone could become stiffer due to the application of the gage. Non-contact forms of strain measure such as the digital image correlation technique using cameras and speckled bone are also becoming popular [49, 50]. A comparison of strains between FEA and experimental data from strain gages and digital image correlation technique used to determine strains in a non-contact manner has been conducted [51].

Voxel based FE:

MicroCT based FE models were first introduced to consider the trabecular structures of bone and its heterogeneous properties by converting voxels to elements [52]. Material properties, such as the elastic modulus, can be assigned based on the voxel Hounsfield Unit (HU) intensity being correlated to the material density, using a phantom material, which is then mapped to the elastic modulus [53]. It was also found that increasing the complexity does not necessarily improve the accuracy of results. Voxel specific X-ray attenuation properties were considered in developing micromechanical theory based elastic properties of collagen, hydroxyapatite and water in the voxel [54]. The authors found that using homogeneous properties of bone tends to overestimate the stiffness of bone in mouse femurs. Characterization of cancellous and cortical bone using microCT based FE methods on mouse tibia subjected to in vivo loading was performed to characterize localized patterns of strain in order to correlate them to protein and gene expression [55]. Virtual testing of mouse femurs subjected to three point bending using microCT based FE methods and experiments have been used to predict global elastic-plastic properties [56] and also predict of strain adaptive modeling of bone adaptation [57, 58].

Micro/Nano Level FE Modeling:

A multilevel FE model was developed to determine the strains at the osteocyte microenvironment in a femur during the stance phase of a gait cycle. A macro model was used for the whole bone and a micro model for a single osteocyte was considered. It was determined numerically that the lacunar strains were approximately six times the macro strains [59]. FE model validation using experimental tests on caudal vertebra of mice were done with good correlation [60]. However, predictions of bone adaptation using models followed by experiments was successful for cortical bone but not the trabecular compartment [61]. Strain amplification in actual osteocytes in bone subjected to physiological loading was numerically studied using a complex three dimensional FE model where the cell body, the pericellular matrix (PCM) and extra cellular matrix (ECM) including dendrites was investigated [62]. Confocal microscopy was used to get the image stack of the bone with the lacuna-canalicular network. Results showed that confocal image-based models experienced 350-400% greater strains compared to idealized models. Four lacunae were considered for modeling. This was the first confocal image derived computational model [62]. A 3-D single idealized ellipsoidal shaped osteocyte model with several dendrites was modeled with elastic isotropic properties for materials. Strain amplification was determined for a variety of bone macro strain values and several loading frequencies. Maximum strain amplification increased with the magnitude of matrix bone strain as well as the frequency of load [63].

Fluid-Structure Interaction Modeling of Osteocytes:

Idealized osteocyte lacunocanalicular network(LCN) system fluid-structure interaction (FSI) models have been developed and it is seen that the strains, shear stresses and fluid velocities are lower than those from a realistic osteocyte model [22, 64, 65]. Verbruggen et al. generated an FSI model to investigate the mechanical environment of the osteocyte and confirmed that the extracellular environment of the osteocyte including canalicular tortuosity results in increasing osteogenic strain stimulation [66]. Rad et al. showed that the stress concentration at cilium is a significant factor in cell mechanotransduction [67]. Vaughan et al. developed an FSI model to study the significance of integrin attachments and primary cilia in bone cells under load-induced fluid flow. The results showed that both primary cilia and integrin play a key role in bone mechanotransduction. Furthermore, the configuration of the primary cilium affects its stimulation function [68]. Joukar et al. investigated the effect of osteocyte morphology by including ECM projections using a 3D FSI model. They have also shown the correlation of osteocyte stimulation with the shear stress, calcium, and NO concentration [69]. Exercise stimulates FFSS on osteocytes which is related to the rate of nitric oxide (NO) released by bone cells [70, 71].

With advancing age, bone morphology, and mechanical properties change, which results in the loss of bone density and, eventually, some diseases such as osteoporosis [72]. Tiede-Lewis et al. reviewed and examined the degenerative changes in osteocyte morphology, including the lacuna-canalicular network with aging using different imaging techniques. It was mentioned that gradual deterioration of the dendritic system leads to loss of physical bone condition [73]. It has not been established how the number of dendrites is correlated to osteocyte signaling at a microscale.

To examine the role of bone tissue architectural deterioration on the mechanical environment of the osteocytes during aging, an osteocyte model with several dendrites was simulated and briefly presented here. These models will further our understanding of the osteocyte signaling that can help to prevent bone loss with aging.

Mechanical Strain and Mechanotransduction

Imaging Modalities and Protocols

Three-dimensional Imaging of Bone Samples:

Producing three-dimensional FE models of bone that are realistic is particularly challenging. The minerals in the tissue obstruct the view of internal structures like the LCN and osteocytes. Conventional sectioning and imaging techniques cannot offer adequate resolution in the z-direction, but confocal microscopy and high resolution micro-computed tomography (Micro-CT) systems are making imaging of bone tissue possible at sub-micron resolutions [74].

Micro Computed Tomography (Micro-CT/XCT) or Microtomography:

Micro-CT is a non-destructive form of 3D x-ray imaging. Samples are placed on a rotating stage. X-rays are transmitted and recorded as 2D projections while the sample is rotated in small increments through 180 or 360 degrees. The resultant 2D images are computationally reconstructed to form a 3D representation of the sample [75]. The non-destructive nature of Micro-CT imaging allows visualization of undisturbed bone samples [75]. Micro-XCT is used to image the bone at much higher resolutions.

Scanners typically accommodate samples with up to 300 mm in diameter, although larger sample diameters reduce the resolution of the images. The highest resolution images can resolve features as small as 0.1 μm [75], but a range of 5-150 μm is more typical [76]. However, canalicular diameters in mice average about 0.26 μm, and dendrites are about 0.1 μm in diameter [77], and hence the Micro-XCT is useful for observing the distribution of lacunae, but canaliculi and dendrites are difficult to resolve with most scanners. Furthermore, it can be difficult to classify structures in Micro-CT scans if their optical densities are similar.

Confocal Laser Fluorescence Microscopy:

Confocal microscopy offers better resolution and allows the use of fluorescent dyes for labeling of structures. Fluorescent dyes emit light over a specific emission wavelength range when excited by a laser in their excitation wavelength range. By attaching fluorescent dyes to structures within the bone matrix, different features can be identified in the same sample based on excitation and emission criteria. Dichroic mirrors in the light path filter the emissions, allowing the selection of light from specific dyes and therefore specific structures in the bone. Out of focus light is filtered out using a pinhole significantly reducing the signal-to-noise ratio. While much of the sample is illuminated by the excitation laser, only light that is focused in a particular location will reach the detector. To make a complete image, the microscope scans the sample collecting light for one pixel at a time, producing a series of 2D images that can be easily assembled into a 3D image. Use of multiple fluorophores in the same sample can indicate the relative positions of the structures, and colocalization of structures within the sample. The theoretical resolution limit for confocal microscopy is 0.2 μm due to the wavelength of visible light [78].

The depth of light penetration into the sample limits 3D confocal imaging, particularly in bone, so samples are typically sectioned to allow imaging in deeper tissue [79]. Bones can be demineralized using EDTA, formic acid, or other agents, to allow for thinner sectioning [78, 80], or mineralized tissue can be cleared with a fructose solution that matches the refractive index of the tissue to increase light penetration [81].

Staining Procedures:

Labeling the lacunocanalicular network:

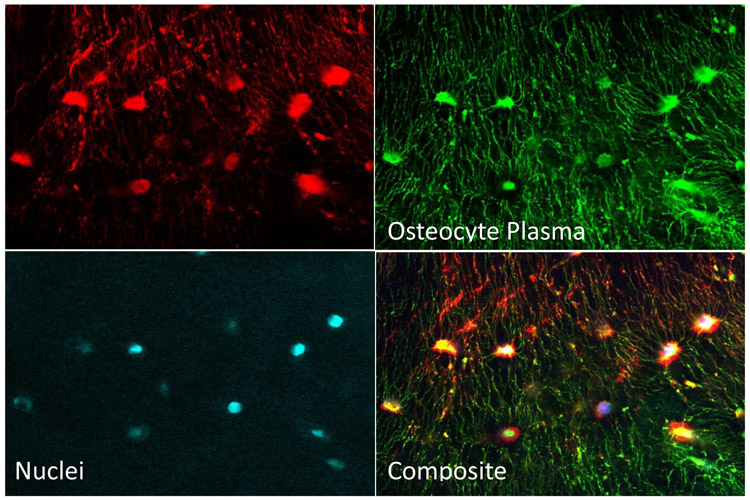
To identify the lacunar cavities and canaliculi within the bone matrix for confocal imaging, the fluid space in these regions is loaded with a fluorescent dye. Different processes are used for decalcified and non-decalcified bones. Decalcification allows easier sample preparation, but the molecular size of the dyes can result in poor penetration into the fluid spaces. Dyes that more easily penetrate the fluid spaces are also easily washed out in the decalcification process, and therefore are only used in non-decalcified bone samples. Sectioning and polishing of the samples make preparation more arduous, but the result can produce more detailed images of the canaliculi. Figure 1 shows a set of confocal microscope images of osteocytes, their nuclei, and the LCN in a bone sample used for modeling purposes.

Figure 1:

Confocal fluorescence microscope false-color images of a single 3D ROI in a bone sample from a 16 wo male C57Bl6 mouse ulna taken at 40x. The lacunocanalicular fluid space was labeled by injection with lysine-fixable dextran-conjugated Texas Red dye, revealing lacunae and canaliculi. Osteocytes were labeled with DiO (green) which identifies plasma membranes in cell bodies and dendrites. Nuclei were labeled with DAPI (cyan).

Lacunocanalicular staining in decalcified bone:

Dextran conjugated dyes with covalently bound lysine residues will bind to nearby biomaterials when fixed with aldehydes. This allows the dye to stay in place while the bone is decalcified. Mice are intravenously injected with 32 mg/kg body weight, lysine fixable, 10 kDa Dextran conjugated Texas Red (DexTR), under anesthesia. Five minutes later the mice are humanely sacrificed. The bones are harvested and fixed for at least one hour in 4% PFA [82]. Following fixation, the bones are incubated in Immunocal bone decalcifier for up to 72 hours to remove minerals from the tissue. The decalcified bones are sectioned with a cryo-stat and cover-slipped in a mounting solution.

Lacunocanalicular staining in non-decalcified bone:

After the bones are fixed, they are sectioned, polished with sandpaper (600, 800, and 1200 grits), and rinsed in EtOH (70%, 95%, and 100% for 5 minutes each). They are incubated in a fluorescent dye such as Fluorescein Isothiocyanate Isomer I (FITC) (4 hrs. at RT) that will fill the lacunocanalicular network. The samples are washed for 30 minutes in 100% EtOH, and cover-slipped without medium.

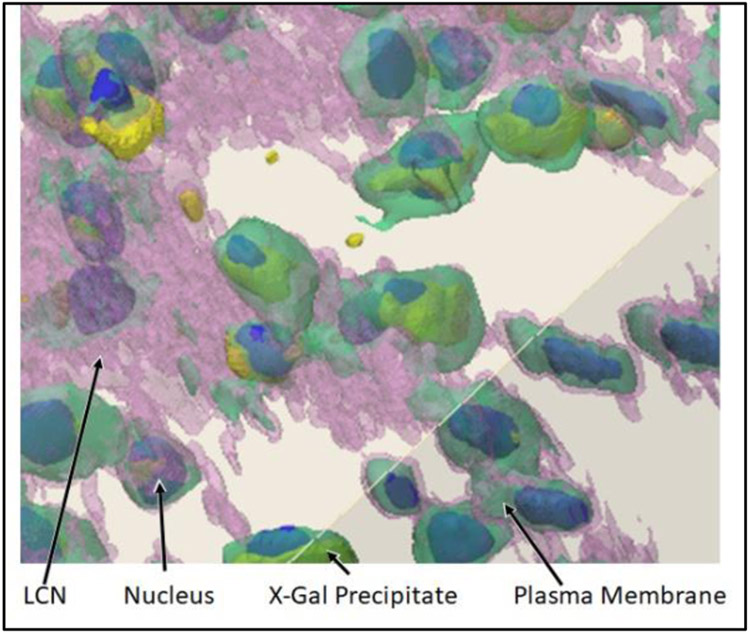
Figure 2 shows a multiplexed image derived from the images in Figure 1. Using this technique, different features of a single sample, e.g. LCN and osteocytes, can be separated into different images for each feature. As described later, each image will be used to create part of an FE model, and allow each tissue type in the model to be assigned appropriate properties for strain analyses.

Figure 2:

3D confocal images were taken at a magnification of 40x. The ivory color represents bone. The bone, LCN, and osteocyte membranes are semi-transparent in this image. The nuclei were labeled with DAPI, shown in blue, and X-Gal precipitate, which indicates activation of the osteocytes) is depicted in yellow. The nuclei and precipitate are opaque in this image, and typically appear tinted by the pink (LCN) and green (osteocyte) colors that surround them.

Finite Element Modeling Methods

Previous FE studies of lacunae in bone have utilized simplified ball-and-stick structures representing single lacunae. Such models have not explained the heterogeneous activation of osteocytes seen by Lara-Castillo, et al. [83]. New software systems, such as the Materialise Innovation Suite^® (www.materialise.com), are designed to automate the process of converting images into FE models, allowing production of more realistic models. Micro-CT and confocal microscope images of the LCN, in bone samples, may be used to generate realistic models for FE solvers, such as FEBio^® (www.febio.org) and ANSYS^®. Analysis using these FE solvers can provide insight into the strain distribution across the LCN, and its effect on the activation of individual osteocytes.

The process of creating FE models from images begins with image segmentation to distinguish different tissue types. Threshold selection is important as it will affect the volumes of the different tissue types [84]. Automated segmentation software with edge detection filters can be utilized in creating the model. In addition, some interpolation of the image is required to reduce pixilation effects and smooth the model for a more accurate representation. Results can vary significantly between software systems, so segmentation should be supported by manual corrections from an experienced operator. [85].

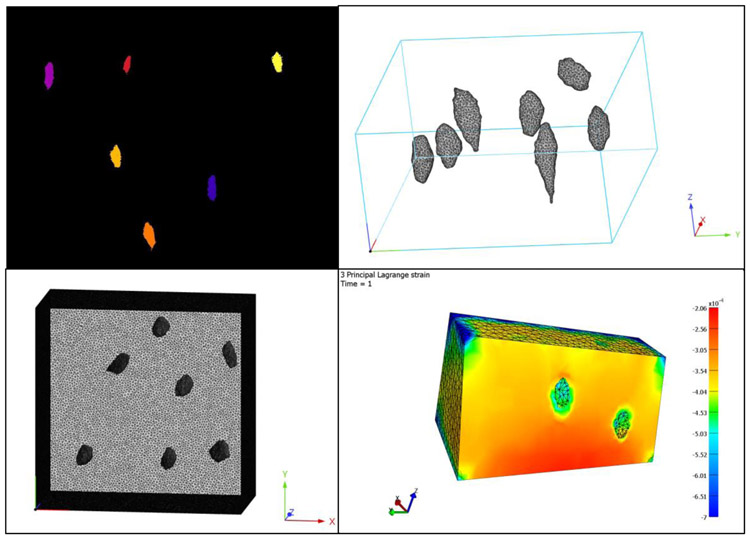
Following image segmentation, mesh generation creates the model to be analyzed. Mesh generation can quickly become time-consuming as models increase in size and complexity. Surface meshes must be generated for each part of interest in the image. Automated meshing generators may produce mesh anomalies that would prevent analysis, particularly overlapping and intersecting elements. Re-meshing procedures and manual adjustments must be made to remove the anomalies. The surface mesh can then be converted into a volumetric mesh. The aspect ratio and size of the mesh elements can affect the accuracy of the results, so it is essential to conduct convergence studies and optimize the mesh density for the model. The volumetric mesh can then be imported into FE analysis solvers which apply specified parameters to the model and calculate the physical properties of the system in response to a given load. Figure 3 shows a sample FE model of bone with lacunae from a stack of images from confocal microscopy.

Figure 3:

FE modeling and analysis begins with defining a mask of a 3D image (top left), followed by generating a surface mesh to fit the mask. The surface mesh is converted to a volume mesh (top right panel shows the volumes of the lacunae and bottom left shows the volume mesh of the bone), which can be processed and analyzed to compute displacements, strains, and other data of interest while simulating application of a load on the model (bottom right).

Consideration of available computational resources may require that some accuracy be sacrificed to reduce processing time or memory requirements. In the study of mechanotransduction, the load applied to the bone occurs at a much larger scale than the microscopic scale of the LCN. Modeling even a small mouse bone with the resolution required for examining strains in the LCN would require enormous computational resources. Therefore, multi-scale modeling in which a large-scale model calculates boundary conditions for a smaller scale model are better suited for the study of mechanotransduction.

Methods of FSI Analysis:

Briefly presented here are two idealized models with eighteen dendrites. The geometry consisting of an osteocyte cell body, interstitial fluid, and bone matrix was sketched in 3D SpaceClaim. The cells were placed inside the lacuna with fluid flow between the cell membrane and bone matrix (inside the pericellular space). The major and minor axes of the cells are 13.5 μm and 7.5 μm while the major and minor axes of the lacuna are 15 μm and 9 μm. The osteocytes are connected through tiny extensions called dendrites. The dendrites reside inside the canaliculi, and the fluid flows around the dendrites through the canaliculi. The dendrites and canaliculi were plotted with diameters of 0.44 μm and 0.6 μm, respectively. The dendrites were assigned as described in experimental data [35]. The cell was placed in the middle of the bone model, and each dendrite and canaliculus was extended to the model faces or edges. Lastly, both the cell and fluid were surrounded by the bone matrix with a side length of 21 μm [7]. These models were meshed using ANSYS software using linear tetrahedral elements for the solid and fluid domains. Given that the fluid flows between two solid domains in a narrow path, a fine mesh is needed. The mesh for the fluid part has 345098 nodes and 1392413 elements and the solid parts have 1116606 nodes and 682235 elements. The solid domains, including cell and bone tissue, were modeled as linearly elastic, isotropic materials. Bone was assigned an elastic modulus of 16 GPa, and Poisson's ratio of 0.38. The cell was assigned a modulus of 4.47 KPa and Poisson's ratio of 0.3. The interstitial fluid has a density of 997 kg/m³ and dynamic viscosity of 0.000855 kg/m³s [7].

A compressive strain of 3000 με and a fluid inlet pressure of 300 Pa was applied to the left side of the model as boundary conditions to mimic the physiological activity. Two-way coupling of solid and fluid domains was used. The solid and fluid domains are analyzed in Structural and CFX modules of ANSYS, respectively. Pressure from the CFX is input to the structural module in which displacements are computed and the fluid and solid domains consistently update their information. Finally, FFSS, velocities, and cell strains were noted.

Results and Discussions

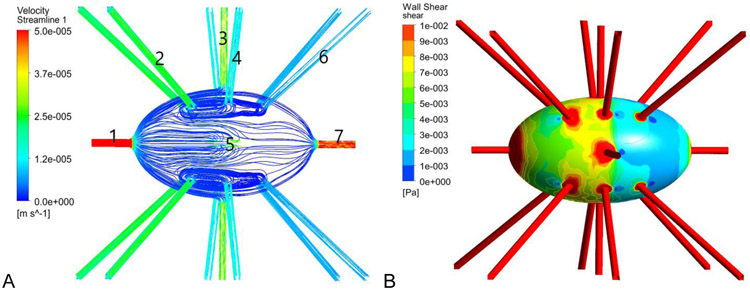
Figures 4 (left panel) shows the velocity distribution on the surface of the osteocytes and dendrites. Regions within the canaliculi undergo greater velocities than the fluid in the lacuna, with a maximum velocity of 235.5 μm/s. Our results are consistent with the previous work of Verbruggen et al. [64]. It is noticeable that the flow is laminar, and velocity streamlines follow the pericellular space region. The figure also shows that fluid velocities are higher in areas in which the pericellular space is relatively small. Figure 4 (right panel) shows wall shear stress distribution on the osteocytes and dendrites resulting from induced fluid flow. The highest shear stresses occur in the osteocyte canaliculi with a maximum shear stress of 4.5 Pa. Average shear stress on the osteocyte cell membranes was observed to be 0.06 Pa.

Figure 4:

A) Velocity streamlines in the fluid in the space between the osteocyte and the lacunar wall and B) the FFSS on the osteocyte cell membranes and dendrite surfaces

CONCLUDING COMMENTS

In silico modeling of the bone along with its various cellular and morphological features is a complex process and is critical to understanding the mechanical response such as mechanical strains and fluid flow velocities and shear stresses. These quantities are difficult to measure in situ. In addition, the mechanical response must be correlated to the biological response of the cells. Complexity of modeling comes from various sources as outlined in this paper. There is still much work to be done in accurately capturing the osteocyte-dendritic structures in its native bone environment and comprehending the mechanobiological response of bone to mechanical loading. Understanding this response and correlating to the biological pathway responses is needed to answer the questions of how bone grows in response to mechanical loading and how various diseases conditions affect this response.