Computational Analysis of Third-Grade Liquid Flow with Cross Diffusion Effects: Application to Entropy Modeling

Abstract

The key goal of this current study is to analyze the entropy generation with cross diffusion effects. The third-grade type non-Newtonian fluid model is used in this study. The current flow problem is modelled with stretching plate. Modified Fourier heat flux is replaced the classical heat flux. The appropriate transformation is availed to convert the basic boundary layers equations into ODEs and then verified by homotopy algorithm. The consequences of various physical quantities on temperature, velocity, entropy and concentration profile are illustrated graphically.

Introduction

Third grade fluid is one of the notable sub kinds of non-Newtonian fluids. The non-Newtonian fluid flow due to the stretching surface is the important area of research due to its broad applications in many industrial and production domains such as, rolling of polymer films, extrusion of metallic sheets, etc. The study on 2nd grade fluid which passed through the stretching sheet is numerically discussed including the variations in thermophysical properties like thermal conductivity, viscosity [1]. It is shown that Eckert number increases the heat transport rate. Hydromagnetic mixed convective heat transfer of 3rd-grade fluid with gyrotactic microorganism is examined [2]. Unsteady flow of power law fluid with uniform velocity is evaluated [3]. With the consideration of heat source and heat sink of MHD flow over a oscillatory stretching sheet is numerically studied [4]. With the impact of chemical reaction, the fourth grade fluid through porous plate of MHD radiative fluid is investigated [5]. In addition to MHD nanofluid, the electrically conductive fluid that of second grade with suction parameter is developed [6]. For the application of bio magnetic the third grade fluid is correlated numerically [7]. The modified Fourier heat flux model for the study of carreau fluid is explored numerically [8]. The various features and applications of non-Newtonian fluids are studied in ref’s [9–15].

There are several techniques available to solve nonlinear problems. The homotopy analysis method (HAM) is initially constructed by Liao [16] in 1992. Moreover, he altered with a non-zero auxiliary parameter [17] . This parameter shows the way to calculate the convergence rate. It also offers great independence to choose the base functions of the solutions. A few more studies about this technique was seen in previous works [18, 19].

Inspired by the above literature surveys, we are constructing a steady 3rd-grade liquid flow with considering radiation, and convective heating effects. Dufour and Soret effects are examined. The system of entropy is discussed briefly for various parameters.

Mathematical Formation

The steady third grade incompressible two dimensional chemically reactive fluid flow due to stretchy surface is considered. The sheet to be stretchy by the pair of same and inverse forces with velocity ($u_w=ax),a>0$, a is known as stretchy rate. The free stream velocity is $u_{\infty }$. ($C_{\infty }$) and ($T_{\infty }$) are the free stream concentration and temperature and in order. The governing equations with boundary conditions are listed below

$$\begin{array}{c}\hfill \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\end{array}$$ 1

$$\begin{array}{cc}\hfill u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=& \mu \frac{{\partial }^{2}x}{\partial y^2}+\frac{{\alpha }_1^{\ast }}{\rho }\left(u\frac{{\partial }^{3}u}{\partial y^2\partial x}+v\frac{{\partial }^{3}u}{\partial y^3}+\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial y^2}+3\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial y^2}\right)\hfill \\ \hfill & +2\frac{{\partial }_2^{\ast }}{\rho }\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial x\partial y}+6\frac{{\beta }^{\ast }}{\rho }{\left(\frac{\partial u}{\partial y}\right)}^2\frac{{\partial }^{2}u}{\partial y^2}+g[{\beta }_T(T-T_{\infty })\hfill \\ \hfill & +{\beta }_C(C-C_{\infty })]\hfill \end{array}$$ 2

$$\begin{array}{c}\hfill \frac{\partial T}{\partial x}u+\frac{\partial T}{\partial y}v=\frac{Q}{\rho c_p}(T-T_{\infty })+\frac{k}{\rho c_p}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{\rho c_p}\frac{\partial q_r}{\partial y}+\frac{D_m{k}_m}{c_s{c}_p}\frac{{\partial }^{2}C}{\partial y^2}\end{array}$$ 3

$$\begin{array}{c}\hfill \frac{\partial u}{\partial x}u+\frac{\partial C}{\partial y}v=D_m\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_m{k}_m}{T_m}\frac{{\partial }^{2}T}{\partial y^2}-k_m(C-C_{\infty })\end{array}$$ 4

The boundary points stated as $u=(u_w(x)=ax),(v=0),(-k\frac{\partial T}{\partial y}=h_f(T_f-T_w)),(C=C_w$) at ($y=0$),

$$\begin{array}{c}\hfill u(\to 0),T(\to T_{\infty }),(C\to C_{\infty })\text{as}y(\to \infty )\end{array}$$ 5

where u & v($=$velocity components along the x & y-direction), $\mu$ ($=$kinematic viscosity), (${\alpha }_1^{\ast }$,${\alpha }_2^{\ast }$ & ${\beta }_1^{\ast }$)($=$material parameters), $\rho$ ($=$fluid density), $({\beta }_T$, ${\beta }_C$) ($=$coefficient of thermal and concentration expansions), $c_p$ ($=$specific heat), $c_s$ ($=$concentration susceptibility), Q ($=$heat capacity of ordinary fluid), $q_r$ ($=$ radiative heat flux), C ($=$concentration), $C_w$ ($=$ fluid wall concentration), $D_m$ ($=$mass diffusion coefficient), $k_m$ ($=$first order chemical reaction parameter).

Incorporating the Cattaneo-Christov heat flux into energy equation, we get

$$\begin{array}{c}\hfill u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+2uv\frac{{\partial }^{2}T}{\partial x\partial y}+\lambda (u^2\frac{{\partial }^{2}T}{\partial x^2}+v^2\frac{{\partial }^{2}T}{\partial y^2}+\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)\frac{\partial T}{\partial x}\\ \hfill +\left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)\frac{\partial T}{\partial y})=\frac{k}{\rho c_p}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{\rho c_p}\frac{\partial q_r}{\partial y}+\frac{D_m{k}_T}{c_s{c}_p}\frac{{\partial }^{2}C}{\partial y^2}+\frac{Q}{\rho c_p}(T-T_{\infty }).\end{array}$$ 6

Consider the transformations given below

$$\begin{array}{c}\hfill \eta =\sqrt{\frac{a}{\mu }}y,v=-\sqrt{a\mu }F(\eta ),u=ax{F}^{{}^{\prime }}(\eta ),\varphi (\eta )=\frac{C-C_{\infty }}{C_w-C_{\infty }},\theta (\eta )=\frac{T-T_{\infty }}{T_f-T_{\infty }}\end{array}$$ 7

Using the above mentioned transformations we retrive the ODE system as follows

$$\begin{array}{cc}\hfill -{F^{{}^{\prime }}}^2+F{F}^{{}^{\prime \prime }}+(3{\alpha }_1+2{\alpha }_2){F^{{}^{\prime \prime }}}^2+6\beta Re{F}^{{}^{\prime \prime \prime }}{F^{{}^{\prime \prime }}}^2+F^{{}^{\prime \prime \prime }}& +{\alpha }_1(2F^{{}^{\prime }}{F}^{{}^{\prime \prime \prime }}-F{F}^{\mathit{iv}})\hfill \\ \hfill & +{\lambda }_1(\theta +N\varphi )=0\hfill \end{array}$$ 8

$$\begin{array}{c}\hfill \left(1+\frac{4}{3}Rd\right){\theta }^{{}^{\prime \prime }}+Prf{\theta }^{{}^{\prime }}+Q_H\theta -\gamma (F{F}^{{}^{\prime }}{\theta }^{{}^{\prime }}+F^2{\theta }^{{}^{\prime \prime }})+Pr{D}_F{\varphi }^{{}^{\prime \prime }}=0\end{array}$$ 9

$$\begin{array}{c}\hfill \frac{1}{\mathit{Sc}}{\varphi }^{{}^{\prime \prime }}+F{\varphi }^{{}^{\prime }}-C_r\varphi +Sr{\theta }^{{}^{\prime \prime }}=0\end{array}$$ 10

Boundary conditions are

$$\begin{array}{c}\hfill F^{{}^{\prime }}(\eta )=1,F(\eta )=0,{\theta }^{{}^{\prime }}(\eta )=-Bi(1-\theta (\eta )),\varphi (\eta )=1\text{at}\eta =0\\ \hfill F^{{}^{\prime }}(\eta )\to 0,\theta (\eta )\to 0,\varphi (\eta )\to 0\text{as}\eta \to \infty \end{array}$$ 11

where ${\alpha }_1={\alpha }_1^{\ast }a/\rho \mu$,${\alpha }_2={\alpha }_2^{\ast }a/\rho \mu$ and $\beta ={\beta }^{\ast }{a}^2/\rho \mu$ ($=$fluid parameters), $Re=a{x}^2/\mu$ ($=$Reynolds number), $Pr=\rho \mu c_p/k$ ($=$ Prandtl number), $Q_H=Q/a\rho c_p$ ($=$Heat generation), $\gamma =\lambda a$ ($=$thermal relaxation), $Sc=\mu /D_B$ ($=$Schmidt number), $C_r=k_m/a$($=$Chemical reaction), $\lambda 1=Gr/R{e}^2$ ($=$local buoyancy parameter), $Gr=g{\beta }_T(T_w-T_{\infty })x^3/{\mu }^2$ ($=$Grashof number), $N={\beta }_C(C_w-C_{\infty })/{\beta }_T(T_w-T_{\infty })$($=$buoyancy ratio parameter), $Rd=4{\sigma }_1{T}_{\infty }^3/k{k}_{\ast }$ ($=$Radiation parameter), $D_F=D_m{k}_T/\mu c_s{c}_p\frac{C_w-C_{\infty }}{T_w-T_{\infty }}$ ($=$ Dufour number), $Sr=\frac{D_m{k}_T}{\mu T_m}\frac{(T_w-T_{\infty })}{(C_w-C_{\infty })}$ ($=$ Soret number).

Heat and mass transfer rate in dimensionless forms are

$$R{e}^{\frac{-1}{2}}N{u}_x=-\left(1+\frac{4}{3}Rd\right){\theta }^{{}^{\prime }}(0),R{e}^{\frac{-1}{2}}S{h}_x=-{\varphi }^{{}^{\prime }}(0).$$

Analytical Procedure and Convergence Study

HAM has been used last twenty years to solve the non-linear system of ODE occurring in various fields. The nonlinear ODE are solved with the aid of HAM algorithm. This algorithm is computed through MATHEMATICA software in our personal computer with 8 GB RAM and 2.30 GHz Processor.

Based on the Fig. 1, the auxiliary parameters have the range $-1.2\le h_F\le 0.3,-1.3\le h_{\theta }\le 0.1,-1.3\le h_{\varphi }\le 0.3$. Approximatley we fixed the h values as $h_F=h_{\theta }=h_{\varphi }=-0.7$ (Table 1).

Fig. 1.

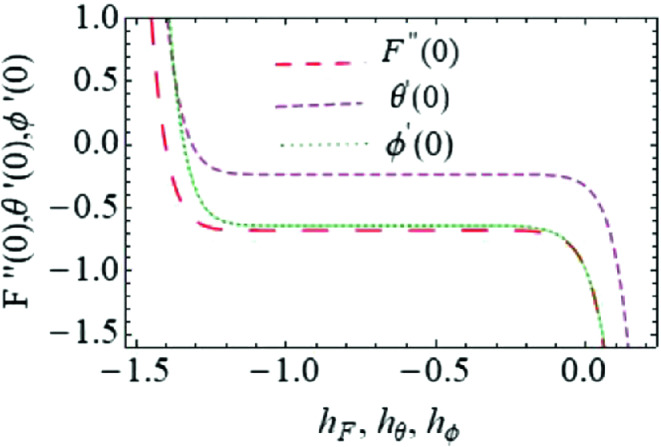
h-curves for $h_{F,\theta ,\varphi }$.

Table 1.

Displays the convergence solutions of HAM in order of approximation when $Pr=0.9,{\alpha }_1=0.1,Sc=0.9,D_F=0.5,Re=0.1,\beta =0.1,{\alpha }_2=0.1,\gamma =0.1,Bi=0.5,Rd=0.3,{\lambda }_1=0.2,N=0.1,Sr=0.3,Q_H=-0.3,h=-0.7,C_r=0.1.$

Order	$-F^{\prime \prime }(0)$	${\theta }^{\prime }(0)$	$-{\varphi }^{\prime }(0)$
1	0.72116	0.23913	0.72777
5	0.67605	0.23555	0.63669
10	0.67817	0.23648	0.63945
15	0.67803	0.23643	0.63897
20	0.67801	0.23644	0.63901
25	0.67803	0.23644	0.63903
30	0.67803	0.23644	0.63903
40	0.67803	0.23644	0.63903
50	0.67803	0.23644	0.63903

Entropy Optimization

The entropy minimization optimization for fluid friction, heat and mass transfer irreversibility’s are given below:

$$\begin{array}{c}\hfill S_{\mathit{gen}}^{\prime \prime \prime }=\frac{K_1}{T_{\infty }^2}[(\frac{\partial T}{\partial y}{)}^2+\frac{16{\sigma }^{}\ast T_{\infty }^3}{3k{k}^{\ast }}(\frac{\partial T}{\partial y}{)}^2+\frac{\mu }{T_{\infty }}+[(\frac{\partial u}{\partial y}{)}^2+\frac{\mathit{RD}}{C_{\infty }}(\frac{\partial c}{\partial y}{)}^2+\frac{\mathit{RD}}{T_{\infty }}(\frac{\partial T}{\partial y})(\frac{\partial c}{\partial y})\end{array}$$

Dimensionless system of entropy generation is defined as:

$$\begin{array}{c}\hfill E_G=Re(1+\frac{4}{3}Rd){\theta }^{\prime 2}+Re(\frac{\mathit{Br}}{\Omega })f^{\prime \prime 2}+Re(\frac{\zeta }{\Omega }{)}^2\lambda {\varphi }^{\prime 2}+Re\frac{\zeta }{\Omega }\lambda {\varphi }^{\prime }{\theta }^{\prime }\end{array}$$

Validation

In order to validate our numerical procedure, the results are validated with earlier report of Maria et al. [10]. The comparison results are given in Table 2.

Table 2.

Comparison in absence of $D_F=0,SR=0,\omega =0,Rd=0,C_r=0,{\lambda }_1=0,N=0,Q_H=0.$

Order	$-f^{\prime \prime }(0)$		$-{\theta }^{\prime }(0)$		$-{\varphi }^{\prime }(0)$
	Ref.  [10]	Current	Ref.  [10]	Current	Ref.  [10]	Current
1	0.81450	0.81450	0.72778	0.72778	0.72778	0.72778
5	0.81221	0.81221	0.58070	0.58070	0.64933	0.64933
8	0.81235	0.81235	0.57779	0.57779	0.64835	0.64835
14	0.81235	0.81235	0.57871	0.57871	0.64873	0.64873
17	0.81235	0.81235	0.57878	0.57878	0.64873	0.64873
25	0.81235	0.81235	0.57878	0.57878	0.64873	0.64873
30	0.81235	0.81235	0.57878	0.57878	0.64873	0.64873
35	0.81235	0.81235	0.57878	0.57878	0.64873	0.64873

Fig. 7.

Effect of $S{h}_x$ for values of Cr and Sr.

Results and Discussion

In this section, we examine the impacts of physical quantities on temperature($\theta (\eta )$), velocity ($F^{{}^{\prime }}(\eta )$), entropy($E_G$) and concentration profiles($\Phi (\eta )$) with the fixed values $Pr=0.9$, $Sc=0.9$, $Re=0.14$, ${\alpha }_1=0.1$, ${\alpha }_2=0.1$, $\beta =0.1$, $\gamma =0.1$, $D_F=0.5$, $Sr=0.3$, $Bi=0.5$, $Rd=0.3$, ${\lambda }_1=0.2$, $N=0.1$,$Q_H=-0.3$, $h=-0.7$ and $Cr=0.1$.

Figure 1 describes the effect of velocity profile ($F^{{}^{\prime }}(\eta )$) on material fluid parameter $({\alpha }_1)$ and mixed convection parameter $({\lambda }_1)$. From Fig. 1(a & b), we have seen an increase in ${\alpha }_1$ and ${\lambda }_1$ the velocity profile ($F^{{}^{\prime }}(\eta )$) rises. Figure 2 revels the temperature profile ($\theta (\eta )$) for different parameters. In Fig. 2(a, b, d), we note that, the ($\theta (\eta )$) enhances for the augmentation in Rd, Bi and $D_F$ and it diminishes for the higher values of Prandtl number Pr as shown in Fig. 2c. Figure 3 depicts the different effects of Cr, Sr, and Sc on concentration profile. From Fig. 3(a) and Fig. 3(c) concentration profile ($\Phi (\eta )$) is inversely proportional to the higher Cr and Sc. Whereas in Fig. 3(b), it is found that ($\Phi (\eta )$) increases with augments in Sr. Figures 4(a–c) shows the effects of $D_F$, Sr and Rd on $E_G$ (entropy generation profile). From these plots we obtain that the system of entropy enhances for the larger values of $D_F$, Sr and Rd.

Fig. 2.

Variation in ($F^{{}^{\prime }}(\eta )$) for ${\alpha }_1$ & ${\lambda }_1$.

Fig. 3.

Variation in ($\theta (\eta )$) for Rd, Bi, Pr and $D_F$.

Fig. 4.

Variation in ($\varphi (\eta )$) for Cr, Sr and Sc.

From Fig. 5(a) we note that the Nusselt number $(N{u}_x)$ decreases with increases in $D_F$. Also, in Fig. 5(b) and Fig. 5(c), it is noted that $N{u}_x$ decrease with upsurge in Rd and $\gamma$. By increasing the $D_F$, fluid resits to move the hotter side of the sheet that subsequently $N{u}_x$ decreases. In addition, it is noted that as we increase the Rd and $\gamma$ the $N{u}_x$ enhances. Figure 6 exposes the mass transfer rate for the combined parameters Sr and Cr. We noted that decreasing trend in mass transfer for larger Sr and mass transfer rate enhance for Cr.

Fig. 5.

Variation in ($E_G$) for $D_F$, Sr and Rd.

Fig. 6.

Effect of $N{u}_x$ for values of $D_F$, Rd and ${\lambda }_1$.

Conclusion

The salient outcomes of $3^{\mathit{rd}}$-grade fluid flow with Soret and Dufour effects along with entropy calculation is stated as follows:

1. Higher range of mixed convection parameter$({\lambda }_1)$ and fluid parameter$({\alpha }_1)$ intensifying the velocity profile.

2. Entropy of the system enhances with radiation, Sored and Dufour numbers.

3. Mass transfer rate rises with chemical reaction and reduces with Soret number.