A Parallel Evolutionary Algorithm with Value Decomposition for Multi-agent Problems

Abstract

Many real-world problems involve cooperation and/or competition among multiple agents. These problems often can be formulated as multi-agent problems. Recently, Reinforcement Learning (RL) has made significant progress on single-agent problems. However, multi-agent problems still cannot be easily solved by traditional RL algorithms. First, the multi-agent environment is considered as a non-stationary system. Second, most multi-agent environments only provide a shared team reward as feedback. As a result, agents may not be able to learn proper cooperative or competitive behaviors by traditional RL. Our algorithm adopts Evolution Strategies (ES) for optimizing policy which is used to control agents and a value decomposition method for estimating proper fitness for each policy. Evolutionary Algorithm is considered as a promising alternative for signal-agent problems. Owing to its simplicity, scalability, and efficiency on zeroth-order optimization, EAs can even outperform RLs on some tasks. In order to solve multi-agent problems by EA, a value decomposition method is used to decompose the team reward. Our method is parallel on multiple cores, which can speed up our algorithm significantly. We test our algorithm on two benchmarking environments, and the experiment results show that our algorithm is better than traditional RL and other representative gradient-free methods.

Introduction

Cooperative and competitive behavior is a common intelligent phenomenon that has been discovered in many domains, such as ant colony [1] and human social behavior [2]. There is a lot of research inspired by such phenomenon [3, 4]. Nowadays, people are becoming more interested in the research of how these behaviors emerge, and some works try to reproduce such phenomena through algorithms directly [5, 6]. This type of research problem can be formally defined as multi-agent tasks. Research on multi-agent problems can help us better understand our social behavior, design better traffic controlling system and so on. In this paper, we focus on cooperative behavior of multi-agent problems.

Recently, RL algorithms have made significant progress on single-agent problems [7, 8]. However, these traditional RL algorithms are not very effective for multi-agent problems, because the multi-agent problem is much more complicated than the single-agent problem. First, the environments of most single-agent problems are stationary. But, in the multi-agent problem setting, the policy of each agent changes over time, the environment would be non-stationary for an agent if it regards other agents as a part of the environment [9]. However, the stationary environment is one of prerequisites for traditional RL convergence [19]. So, the multi-agent problem is non-trivial to be solved by traditional RL algorithms.

Very recently, some research shows that Evolutionary Algorithms (EAs), also makes a competitive performance on single-agent problems [11, 12]. The performance of EA even outperforms RL in several single-agent control tasks. Compared to RL, EA is simple and easier to implement. Also, because EA is a gradient-free method, it is known as a better solution for non-convex optimization problems whose gradient is difficult to obtain. What is more, EA has better parallelization capability. EA is easier to be scaled on multi-core computers compare to some traditional RLs [22].

However, there are some difficulties for traditional EA to solve multi-agent problems. In the multi-agent environment, agents often only receive a shared reward of the whole team [13]. For example, a group of football players receives a reward only after they lost or win that match. If we directly use the team reward to optimize the independent policy through EA, it would be difficult for agents to learn proper cooperative behaviors.

In this paper, we propose an approach, named Parallel Evolution Strategies with Value Decomposition (PES-VD), for cooperative multi-agent problems. PES-VD is a hybrid method, combining with EA and RL. First, we extended the Parallelized Evolution Strategies [11] and designed a variant named Parallelized Evolution Strategies for direct policy search. Second, we take advantage of RL and developed a value decomposition approach to estimate fitness for policy evaluation. Third, in order to improve the efficiency of our approach, we parallel our algorithm in multiple cores.

Related Work

In recent years, several significant progresses have been made in the field of multi-agent problems. Multi-agent reinforcement learning [9, 10] is one of the most popular methods for multi-agent problems.

Similar to the traditional RL, there are two types of multi-agent reinforcement learning: value-based and policy-based. The first type of multi-agent reinforcement learning is always used for solving the multi-agent problem with discrete action-space. One of the most commonly applied methods for multi-agent problems is Independent Q-learning (IQL) [14]. IQL is extended directly from Q-learning, and train each agent through a separated Q-learning. However, this method does not work well for multi-agent problems. Because of the restriction of the tabular manner, IQL only could be used for low-dimension problems. Tampuu et al. replace the tabular manner by deep neural network [15]. With deep neural network, the approach has better generalization ability. Benefits from the decentralized training procedure, these approaches are easy to scale. But these methods are also unstable because of the decentralized training in the non-stationary environment where agents learn simultaneously.

In order to reduce the effect of the non-stationary in the environment, a set of works adopt centralized training and decentralized execution manners. Value Decomposition Network (VDN) [16] acquires the idea from independent deep Q-learning. During the centralized training process, VDN sum up the Q-value of each agent for estimating a team reward. QMIX [17] is another value-based approach, which estimates total Q-value through a monotonic function of each agent’s Q-value. It shows that monotonic function can guarantee consistency between centralized and decentralized policies. However, these value-based methods are not good solutions for multi-agent problems with continue or high-dimensional action space.

Policy-based RL approach is another type of algorithms for multi-agent problems. Counterfactual Multi-Agent Policy Gradients (COMA) [18] is based on the framework of actor-critic reinforcement learning. It needs to train a fully centralized critic in COMA, which will be impractical as the number of agents increasing. Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [19] achieves great performance in a set of simple multi-agent problem environments. Although MADDPG only needs the combination of observations and actions of all agents as training data, the dimension of input space still will grow dramatically as the number of agents increasing.

Evolutionary algorithm (EA) as a type of gradient-free approaches also shows promising performance in agent controlling problems. From the perspective of RL, EAs also can be considered as policy-based algorithms [26]. NeuroEvolution of Augmenting Topologies (NEAT) [20] evolves both the structure and parameters of a neural network. But NEAT is a time-consuming approach, and it is not suitable for optimizing deep neural network. In recent years, researchers also adopt Random Search [21], Evolution Strategies [11] and Genetic Algorithm [12] for optimizing parameters of neural network. Benefit from the rapid development of parallelization technology, these traditional algorithms can gain competitive performance as state-of-the-art RL in some challenging single-agent problem. However, it is difficult for EA to be deployed in multi-agent problems directly, especially for the tasks which only provide a shared team reword. Agents might unable to learn proper behaviors by EA if we directly use the team reward as fitness.

Problem Description

Generally, the multi-agent problem can be formalized as a Markov Game [10] with a tuple $\text{G}=\left\{S,U,O,P,r,N,\gamma ,T\right\}$. It defines an environment with a global state S, where there are N agents. Each agent $i\in \left\{1,\dots N\right\}$ has its observations $O_i$ and actions $A_i$. The state of the environment is initialized randomly by a distribution unavailable to all agents $\rho :S\to \left[0,1\right]$. At each time step, agents carry out actions based on their observations. Typically, these actions are chosen through a policy ${\pi }_i:O_i\times A_i\to \left[0,1\right]$, and form a joint action $U=A_1\times \dots \times A_N$. Then, the environment turns into a new state $s^{\prime }$ according to a transition function $P\left(s^{\prime }|s,\mathit{a}\right):S\times U\times S\to \left[0,1\right]$. For agent $i$, it receives new observations ${\mathit{o}}_i:S\to O_i$ and a reward $r_i:S\times U\to \mathbb{R}$ in this new environment state. $\gamma$ is the reward discount factor and the time horizon $T$ can be a finite or infinite.

In this paper, we consider the cooperation setting. All agents receive a shared team reward $r$ from the environment with discrete time-space and partial observation. Each episode has finite time steps T. Agents choose actions through their deterministic policies $\mathit{\pi }$. So in this cooperation Markov Game setting, the goal of the task is to maximize the expectation of team rewards (1).

$$\underset{\mathit{\pi }}{\text{max}}R\left(\mathit{\pi }\right)=\mathbb{E}\left(\sum _{t=0}^{T}r\left({\mathit{o}}^t,{\mathit{a}}^t\right)\right)$$ 1

Proposed Method

Our method consists of two parts, value decomposition and policies. The value decomposition network can be considered as a coach for guiding the training of agents and is only used while training. A variant named Parallelized Evolution Strategies is designed for the training of independent policies. The overview of our algorithm is shown in Fig. 1. Our method is implemented in parallel. Workers are used to evaluate the policies and calculate the gradient of value decomposition network. Then, the master process collects data from workers to update policies and value decomposition network.

Fig. 1.

The overview of our algorithm

Value decomposition network and policy networks learn simultaneously during the training process, while only policy networks are required during execution. Agents choose actions through their policies independently and interact with the environment. The input data of the policy network is the partial observation of the related agent. Value decomposition estimates fitness for the policies. The input data of the value decomposition network consists of whole observations and the team reward.

Parallelized Evolution Strategies

We employ an artificial neural network which is parameterized by $\mathit{\theta }$ to represents the policy of one agent. Different from gradient-based methods for neural network training, we train these policies through Evolution Strategies. Algorithm 1 illustrates the detail of the variant Parallelized Evolution Strategies used in our algorithm. M workers are used to evaluate the policies in multiple processes, and a master collects the data from workers to update policies.

PES can work well on single-agent problems, even if we simply sum up the rewards of an episode as fitness 11. However, we found this fitness evaluation manner is not suited for cooperative multi-agent problems. So, a predicted state value $v_i$ which is estimated by value decomposition (describe at Sect. 4.2) based on the observations of agent $i$ is used for calculating the fitness $f_i$ of a T steps episode (2).

$$f_i=\sum _{t=1}^T{v}_i^t$$ 2

We extend our method directly from Parallelized Evolutionary Strategies and use a random noise to represent the variance added to the network parameters [11]. So, even each agent has its independent policy network, the overall data transmitted between processes is still acceptable.

Value Decomposition Network

For cooperative multi-agent problems, we found EA always does not work well if we simply regard the team reward as its fitness, because the team reward cannot effectively reflect the contribution of each agent for the whole group. For this reason, we developed a value decomposition network, for evaluating the proper contribution of each agent during the training process.

For the value decomposition network, each value network is parameterized by ${\mathit{\theta }}_{\mathit{i}}^{\mathit{v}}$. At each step, value decomposition takes the observations of all agents as input data for calculating a join value $v^t$ and individual values $v_i$ of each agent. Taking all observations as input can significantly alleviate the effect of non-stationary problems in the multi-agent environment [19]. Inspired by [16], we also assume that the joint value function can be decomposed into value function across agents. So, we have the Eq. (3), and the team reward received from the environment can be used for the training of value decomposition network directly.

$$v^t\approx \sum _{i=1}^N{v}_i$$ 3

We adopt Temporal Differences (TD) error as a loss function for the network updating (4).

$$TD=r^t+\mathrm{\lambda }v\left({\mathit{o}}^{t+1};{\mathit{\theta }}^v\right)-v\left({\mathit{o}}^t;{\mathit{\theta }}^v\right)$$ 4

Because $Q\left({\mathit{o}}^t,{\mathit{a}}^t\right)=\mathbb{E}\left(r^t+\mathrm{\lambda }v\left({\mathit{o}}^{t+1};{\mathit{\theta }}^v\right)\right)$ is not directly equal to $v\left({\mathit{o}}^t;{\mathit{\theta }}^v\right)$, loss function (4) might cannot accurately estimate the actual loss. However, the experiments from Asynchronous Advantage Actor-Critic (A3C) [22] show that this estimation manner can reduce the complexity of the neural network architecture and is more conducive to obtaining stable results.

Different from the critic network in A3C, we implement a separate network for estimating the target state value $v\left({\mathit{o}}^{t+1};{\mathit{\theta }}^{v\prime }\right)$ similar to DQN [8]. The experiment results (Sect. 5.3) show that the separate network can significantly improve the efficiency and stability of our algorithm.

Parallelization

Our algorithm consists of two parts: policies and value decomposition. In order to accelerate the training efficiency and better use computer resources, we implement the policies and the value decomposition algorithm in parallel.

The parallelization of the policy has been introduced in Sect. 4.1. The parallel realization of the value decomposition is inspected by the idea of Parallel Reinforcement Learning in [22]. However, instead of running in multiple threads, we implement our algorithm in multiple cores. Although it will cost more communication resources, running in multiple cores can have better use of CPU resources [22].

Figure 2 illustrates the working flow of the value decomposition network in multiple processes.

Fig. 2.

Parallelization structure of value decomposition network

The master process maintains a global value decomposition network parameterized by ${\mathit{\theta }}_{\mathit{vd}}$ and each worker process has a local value decomposition network parameterized by ${\mathit{\theta }}_{\mathit{vd}}^j$ and a local target value decomposition network. The local value decomposition initializes its parameters from global value decomposition at the beginning. Then, at each generation of PES, the local value decomposition network calculates its gradients and uploads them to the master. Master updates the global value decomposition parameters based on the Eq. (5) and then synchronizes them to the local value decomposition at the beginning of the next generation.

$${\mathit{\theta }}_{\mathit{vd}}\leftarrow {\mathit{\theta }}_{\mathit{vd}}+{\alpha }_{\mathit{vd}}\sum _j^M\partial \left(\mathit{TD}\right)/\partial {\mathit{\theta }}_{\mathit{vd}}^j$$ 5

For the local target value decomposition network, we update its parameters every $\beta >1$ generations. The training process will be more stable and efficient by using a separate network for estimating the target value [8].

Experiment Results

We compare our algorithm with both gradient-based and gradient-free methods in two different multi-agent environments: Multi-Agent Particle Environment (MAPE) [23] and StarCraft Multi-Agent Challenge (SMAC) [13]. For gradient-based methods, we compare with REINFORCE [24], Actor-Critic [25], DQN [8], VDN [16]. Particularly, VDN is a state-of-the-art value-based approach for multi-agent problems. For gradient-free methods, we also compare our method with Random Search (RS) [21] and Evolution Strategies (ES) [11].

We adopt the same network architecture for our algorithm in those two environments. For the Policy network, we use two tanh MLP with 256 units per layer. At each time step, each Policy network takes observations of the related agent as input and outputs actions.

The value network of value decomposition also has two hidden layers. The first layer is a MLP with 256 units, and the second layer is a LSTM with 256 units. The value network takes observations of the related agent as input and outputs a state value. The Mixer layer of value decomposition sums up the values output by each value network. We share the parameters of each value network, which can improve the convergence efficiency of the network in these cooperative multi-agent problems [16]. We run our algorithm on a server with 72 CPU cores.

Experiment on MAPE

Multi-Agent Particle Environment (MAPE) is a 2D simple world with N agents and L landmarks. Action-space is continuous and time is discrete in this environment. At each time step, agents carry out a discrete action. We evaluated our algorithm in the Cooperative Navigation task of MAPE

We compare our algorithm with RS, ES, REINFORCE, Actor-Critic, DQN, VDN in this environment. Each algorithm that we evaluate in this environment had been trained to converge. The max episode steps are 25 in this task.

We evaluate 100 episodes for each method and use the average distance from landmarks (Dist.), the number of collisions (Collisions), and the number of occupied landmarks (Occupied Landmarks) for comparison.

It can be seen from the results in Table 1 that both gradient-based methods (REINFORCE, Actor-Critic, DQN, and VDN) and gradient-free methods (RS and ES) cannot solve the Cooperative Navigation task properly. Those approaches only consider how to maximize the expected reward of the agent itself and ignore the whole team reward. Under this mechanism, agents would lose sign of which behaviors are more beneficial for their team.

Table 1.

The results of cooperative navigation task

Algorithm	Dist.	Collisions	Occupied landmarks
RS	1.92	25.52	0.04
ES	1.37	26.69	0.11
REINFORCE	8.01	25.21	0.01
Actor-critic	1.36	25.73	0.13
DQN	1.56	26.31	0.09
VDN	2.21	25.12	0.5
CAES	0.31	27.11	1.6

However, for this task, we found our method causes more collisions than other approaches among agents while navigation. Because the Evolutionary Algorithm is more concerned about long-term rewards and ignores some short-term conditions. What is more, as agents approaching the landmarks simultaneously, it will be more prone to collisions between agents.

Experiment on SMAC

The StarCraft Multi-Agent Challenge (SMAC), focuses on micromanagement challenges where units are controlled by separated agents. The observations of this environment for each agent are partial. Agents only receive the information around them at a certain distance. There are two groups of units that fight with each other at the tasks of SMAC. One group is controlled by training agents, and the other is controlled by pre-designed rules. The goal of each group is to destroy the opposed one. Agents will receive positive collective rewards depending on how much harm they have made to the opposed group.

We test our algorithm in 3s_vs_4z and 2c_vs_64zg tasks of SMAC. The 3s_vs_4z and 2c_vs_64zg tasks both are homogeneous and asymmetric type missions. It evaluates kiting ability in the 3s_vs_4z task with 3 Stalker ally units and 4 Zealot enemy units. Besides, the 2c_vs_64zg task is a harder one which needs more positioning strategy for agents to win the competition. There are 2 Colossi allay units and 64 Zergling enemy units in the 2c_vs_64zg task. We compare our algorithm with gradient-free methods (RS, ES) in these two tasks.

We train these three algorithms for 1500 generations and evaluate the average episode team reward received at each generation.

As the results shown in Fig. 3 and Fig. 4, in these two SMAC tasks, our method can receive higher average episode rewards than RS and ES. We also found that the performances of RS and ES do not change too much even if been trained longer. On the contrary, our method has the ability to learn different cooperation strategies in different environments.

Fig. 3.

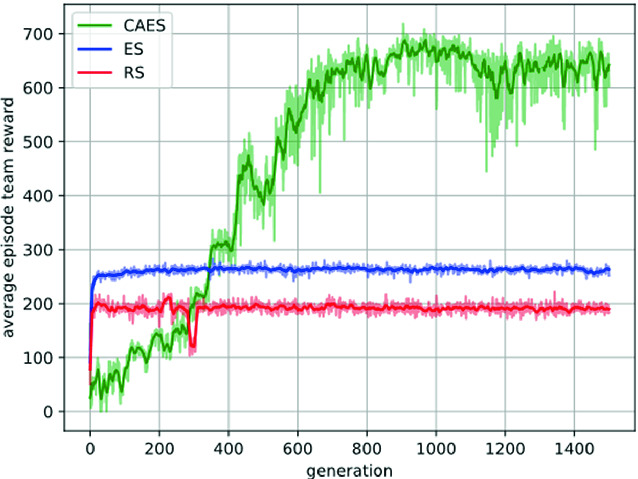
Results in the 3s_vs_4z task

Fig. 4.

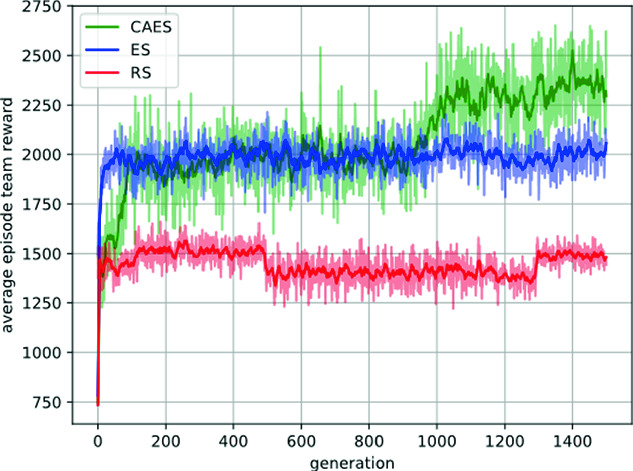
Results in the 2c_vs_64zg task

Separate Network Ablation Experiment

Although A3C does not adopt a separate network for target value prediction, we found using a separate network can improve convergent efficiency and stability for our algorithm. Actually, the complex of our algorithm does not change too much while parallels in multiple processes with a separate network.

We both test our original algorithm and the one without a separate network in the Cooperative Navigation task of MAPE. The results are shown in Fig. 5.

Fig. 5.

Results of without a separated network and with a separated network in Cooperative Navigation task

The results show the average episode team rewards received by agents within 3000 generations of training. The agent trained by the algorithm with a separate network can reach a higher reward faster. However, without separate network one is less efficient, and the episode reward has not been enhanced much even if it has been trained for 6000 generations.

Conclusion and Future Work

Our approach is based on Evolutionary Algorithm which is used for the training of the policy networks. A value decomposition network is adopted for decomposing team reward. Policy networks and value decomposition network are trained simultaneously during the learning process. While only policy networks are needed in the execution phase. We test our algorithm in two different environments and compare it with REINFORCE, Actor-critic, DQN, VDN, RS, ES.

In both environments, our method achieves promising results. For the Cooperative Navigation task in MAPE, CAES is much better than both traditional RLs and gradient-free approaches.

For the other two tasks in SMAC, the experiment results also show that our method is applicable for different cooperative strategies. EA is considered to be not suitable for Multi-Agent problems if it directly using the team reward as fitness. There is a great improvement for EA by using the value decomposition network to predict fitness in Multi-Agent problems.

We also found that, during the training process, the prediction ability of the value decomposition network improves over time. As the predicted fitness estimated by value decomposition in the Cooperative Navigation task shown in Fig. 6, the output of value decomposition is not stable before the 600th generation where the predicted fitness decreases. This means the fitness function of policy also changes gradually. So, it can be seen as a dynamic problem from the perspective of optimization. We should design an algorithm which more suitable for this dynamic problem in our future work.

Fig. 6.

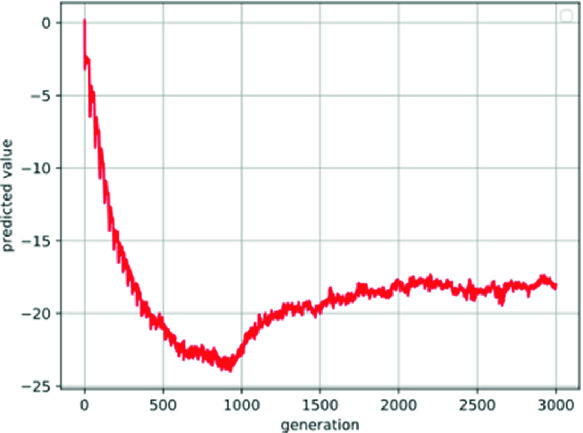
Predicted fitness estimated by value decomposition