Environmental Effects on Guanine-Thymine Mispair Tautomerization Explored with Quantum Mechanical/Molecular Mechanical Free Energy Simulations

Abstract

DNA bases can adopt energetically unfavorable tautomeric forms that enable the formation of Watson-Crick-like (WC-like) mispairs, which have been proposed to give rise to spontaneous mutations in DNA and misincorporation errors in DNA replication and translation. Previous NMR and computational studies have indicated that the population of WC-like guanine-thymine (G-T) mispairs depends on the environment, such as the local nucleic acid sequence and solvation. To investigate these environmental effects, herein G-T mispair tautomerization processes are studied computationally in aqueous solution, in A-form and B-form DNA duplexes, and within the active site of a DNA polymerase λ variant. The wobble G-T (wG-T), WC-like G-T*, and WC-like G*-T forms are considered, where * indicates the enol tautomer of the base. The minimum free energy paths for the tautomerization from the wG-T to the WC-like G-T* and from the WC-like G-T* to the WC-like G*-T are computed with mixed quantum mechanical/molecular mechanical (QM/MM) free energy simulations. The reaction free energies and free energy barriers are found to be significantly influenced by the environment. The wG-T→G-T* tautomerization is predicted to be endoergic in aqueous solution and the DNA duplexes but slightly exoergic in the polymerase, with Arg517 and Asn513 providing electrostatic stabilization of G-T*. The G-T*→G*-T tautomerization is also predicted to be slightly more thermodynamically favorable in the polymerase relative to a DNA duplex. These simulations are consistent with an experimentally driven kinetic misincorporation model suggesting that G-T mispair tautomerization occurs in the ajar polymerase conformation or concertedly with the transition from the ajar to the closed polymerase conformation. Furthermore, the order of the associated two proton transfer reactions is predicted to be different in the polymerase than in aqueous solution and the duplexes. These studies highlight the impact of the environment on the thermodynamics, kinetics, and fundamental mechanisms of G-T mispair tautomerization, which plays a role in a wide range of biochemically important processes.

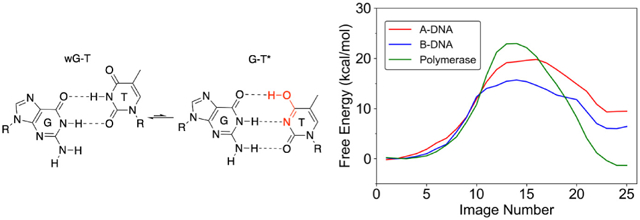
Graphical Abstract

Introduction

In DNA, typically the bases G, C, A, and T, which correspond to guanine, cytosine, adenine, and thymine, respectively, form the canonical Watson-Crick (WC) base pairs G-C and A-T. In some cases, however, the bases can adopt energetically less favorable tautomeric forms, enabling the formation of WC-like mispairs, such as G*-T, G-T*, A*-C, and A-C*, where * denotes the energetically unfavorable enolic (for G and T) or imino (for A and C) tautomeric forms of the bases. By mimicking the canonical Watson-Crick geometry,¹ these mispairs could potentially evade fidelity checkpoints and lead to spontaneous mutations and misincorporation errors in DNA replication and translation.^2-5 Misincorporation can also arise through WC-like anionic G-T⁻ mispairs that form through ionization of T,⁶ although this pathway is thought to play a minor role at physiological pH.⁷ Indeed, WC-like mispairs have been observed in the active sites of DNA polymerases^8-10 and ribosomes^11-13 in catalytically competent conformations. Mutations from replicative errors are proposed to account for a large fraction of mutations that contribute to various forms of cancer.¹⁴ Moreover, the tautomeric forms of bases are proposed to play important roles in DNA damage and repair,^15-16 as well as nucleic acid recognition,^17-18 chemical modifications,^19-22 and catalysis.²³ Thus, understanding the mechanism and thermodynamics of tautomerization is important for a wide range of biomedical applications.

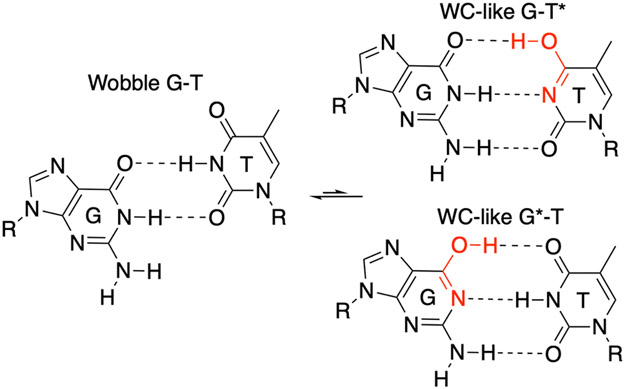
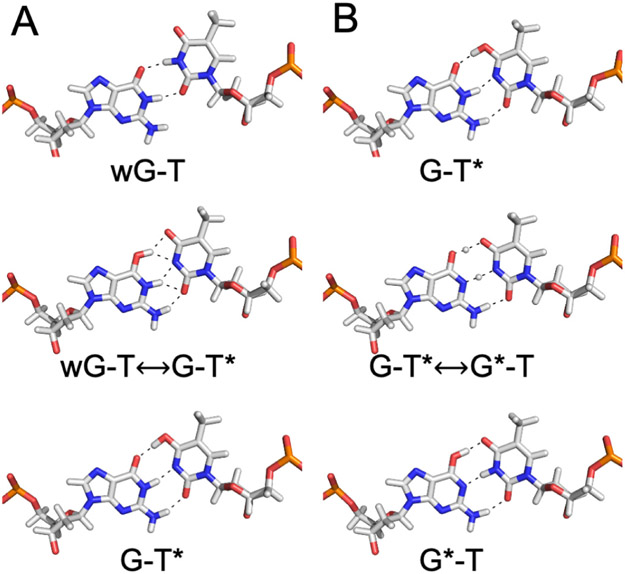
Characterizing the tautomeric forms of the bases experimentally is challenging because of the low abundance of these species.^24-25 Recently, Al-Hashimi and co-workers studied the shortlived, low abundance WC-like G-T and G-U mispairs in B-DNA and A-RNA duplexes using NMR relaxation dispersion.^{7, 15, 26} Their results indicated that at near neutral pH, wobble G-T mispairs (wG-T) are in equilibrium with a low population (~10⁻³) of tautomeric WC-like G-T mispairs composed of the G*-T and G-T* forms in rapid exchange with each other (Figure 1).⁷ They also found evidence suggesting that the frequencies of replication and translational errors are influenced by the free energy associated with forming the tautomeric WC-like mispairs.⁷

Figure 1.

Tautomerization of the wobble G-T mispair into WC-like structures. The asterisk denotes the enol tautomeric form of G or T.

The tautomerization process of G-T mispairs has been shown to depend significantly on the environment. NMR studies indicated that the prevalence of the wobble and WC-like structures for G-T mispairs in B-DNA duplexes is sequence dependent, which could potentially translate into certain sequences being more prone to replicative errors than others.⁷ In addition, no evidence for exchange to a WC-like mispair was found in G-U mispairs when placed next to flexible non-duplex like environments such as bulges and apical loops.⁷ X-ray crystallographic studies illustrated that the G-T mispair adopts a wobble structure in the context of A-DNA²⁷ and B-DNA.²⁸ Furthermore, crystal structures show that the G-T mispair can adopt different configurations depending on polymerase conformation (Table S2).^{9-10, 29-31} For example, the nascent G-T mispair adopts the WC-like structure in a human DNA polymerase λ variant⁹ and in DNA polymerase β¹⁰ when it is in the closed state. In contrast, the nascent G-T mispair adopts a wobble structure in a DNA polymerase BF1 variant when it is in the ajar state,²⁹ in variants of the RB69 polymerase,^32-33 and in Y-family DNA polymerases η³⁰ and DPO4.³⁴ In addition, a systematic crystallographic study of a DNA polymerase RB69 variant illustrated that the local microenvironment plays a significant role in modulating the equilibrium between wobble and WC-like G-T mispairs following incorporation into the DNA.³¹ Computational studies have also indicated that the kinetics and thermodynamics of tautomerization of isolated G-T mispairs can be influenced by different dielectric continuum solvent environments.^35-36 In addition, recently the G-T mispair tautomerization has been studied in a DNA polymerase λ variant using the free energy perturbation (FEP) approach, suggesting that the G*-T form is the most prevalent form of the mispair in this polymerase.³⁷

Despite these earlier studies, a complete understanding of the environmental effects on G-T mispair tautomerization has still not been established. Calculations of the tautomerization free energies have not yet been performed in the context of DNA/RNA duplexes, for which experimental data are available, to serve as a benchmark for the calculations. Furthermore, although it has been proposed that polymerases can greatly alter tautomerization thermodynamics relative to DNA,⁸ quantitative estimates of this effect remain elusive. To further elucidate these environmental effects, we examined the tautomerization process of G-T mispairs in aqueous solution, an A-DNA duplex, a B-DNA duplex, and a DNA polymerase λ variant using mixed quantum mechanical/molecular mechanical (QM/MM) free energy simulations based on the finite-temperature string method with umbrella sampling.^38-39 The free energy profiles corresponding to the G-T tautomerization process were generated for each of these systems, and the impact of electrostatic interactions, duplex geometry, and polymerase environment was analyzed. This work highlights the significance of the environmental effects on the G-T mispair tautomerization process and provides fundamental insights into this critical biochemical reaction.

Methods

We performed QM/MM free energy simulations of G-T mispairs in aqueous solution, A-form and B-form DNA duplexes, and a DNA polymerase λ variant. The crystal structure associated with PDB entry 1D92²⁷ corresponds to an A-DNA duplex composed of eight base pairs with two G-T mispairs occurring between residues 3 and 14 and between residues 6 and 11. After mutating residue 6 from T to C to retain only a single G-T mispair, this structure served as the initial structure for the G-T mispair in an A-DNA duplex. Moreover, residues 3 and 14 of this structure were used to generate an initial structure for the G-T mispair in aqueous solution. The initial structure of the G-T mispair in a B-DNA duplex, which was chosen to have the same sequence as the A-DNA duplex, was generated using the nucleic acid builder (NAB) program in AmberTools⁴⁰ because a crystal structure was not available. The initial structure for the G-T mispair in the DNA polymerase λ variant was obtained from PDB entry 3PML.⁹ Each system was solvated in a cuboid water box with ~0.15 M NaCl after neutralizing with Mg²⁺ ions for the DNA duplexes and Na⁺ for the polymerase. PDB files of the equilibrated systems are provided in the Supporting Information (SI).

A QM/MM approach with QM regions illustrated in Figure 2 and Figure S1 was employed to model all of these systems. The hydrogen link atom approach⁴¹ was used to treat the QM/MM interface. The QM region, which contained 50–61 atoms, was described by the ωB97X-D3 functional⁴² and the 6-311G** basis set.^43-44 Benchmarking of different levels of theory is provided in Table S3. For the MM region, the nucleosides and nucleotides were represented by the OL15 force field,⁴⁵ and the TIP3P water model⁴⁶ was utilized to model the solvent. The van der Waals parameters of the Na⁺ and Cl⁻ ions were obtained from the hydration free energy (HFE) parameter set for the TIP3P water model.⁴⁷ For the polymerase λ variant system, the protein was described by the AMBER ff14SB force field,⁴⁸ and additional polyphosphate parameters⁴⁹ were used to model the bound GTP ligand. Following a full equilibration procedure, the protein residues, water molecules, and ions with no atoms within 18 Å of the N1 atom of the guanine base in the G-T mispair were frozen during the QM/MM free energy simulations. The Q-Chem program⁵⁰ was used to perform the QM calculations. The QM/MM minimizations were performed using the AMBER software package⁴⁰ with the Q-Chem/AMBER interface,⁵¹ while the QM/MM molecular dynamics (MD) simulations were performed using the CHARMM program⁵² with the Q-Chem/CHARMM interface.⁵³

Figure 2.

Illustration of the QM region for the QM/MM simulations of the G-T mispair in the DNA duplexes. The atoms depicted in red are in the QM region, and the cut bonds are indicated by wavy curves. Illustration of the QM regions for the G-T mispair in aqueous solution and the DNA polymerase λ variant are shown in Figure S1.

The finite temperature string method with umbrella sampling^38-39 was utilized to conduct the QM/MM free energy simulations. In this approach, the string is defined in terms of reaction coordinates that are typically inter-atomic distances relevant to the reaction studied. The string is composed of a series of images connecting the reactant and product, where each image is associated with specified values of the reaction coordinates. For each iteration, an umbrella sampling simulation is performed for each image with harmonic restraints on the reaction coordinates. The average values of the reaction coordinates for each image are used to determine the restraints for the next iteration. This process is continued until the string is determined to be converged, as described in more detail below.

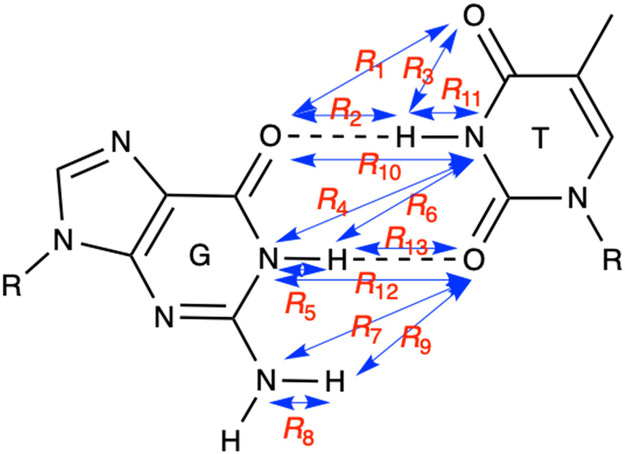
For each system, the string corresponding to the tautomerization from the wobble G-T (wG-T) structure to the WC-like G-T* structure, denoted the wG-T→G-T* string, and the string corresponding to the tautomerization from the WC-like G-T* structure to the WC-like G*-T structure, denoted the G-T*→G*-T string, were calculated (Figure S2). The 13 reaction coordinates used to describe the tautomerization process include all interatomic distances at the interface, as depicted in Figure 3. In each case, the initial string was generated by quadratic interpolation of structures generated for the reactant state, an approximate transition state, and the product state using QM/MM energy minimization in which only the QM region was allowed to move in a fixed MM environment.

Figure 3.

Depiction of the 13 reaction coordinates used to describe the tautomerization process in the QM/MM finite temperature string simulations with umbrella sampling.

The wG-T→G-T* and G-T*→G*-T strings were represented by 25 and 15 images, respectively, and each image was defined in terms of the values of the 13 reaction coordinates used for the umbrella sampling restraints. For a given iteration, a 100 fs MD trajectory was propagated for each image while imposing the associated harmonic restraints on the reaction coordinates. Prior to the subsequent iteration, the string images were redistributed evenly along the updated string that was fitted to the average values of the reaction coordinates sampled in the latest iteration. This cycle continued until the string was converged. Each string was computed with 24 or 25 iterations, producing a total of 397.5 ps of QM/MM MD sampling (Table S4). Convergence of the computed strings is illustrated in Figures S3 and S4. For each string, the combined data for all iterations were analyzed using the binless weighted histogram analysis method (WHAM) approach.⁵⁴ The final string represents the minimum free energy path (MFEP), and the free energy along the MFEP was generated for each string using the combined data from all iterations. Further details about the simulations are provided in the Supporting Information (SI).

These simulations did not consider the direct conversion from wG-T→G*-T but rather assumed a stepwise process involving the G-T* intermediate, as supported by prior calculations.^35-36 Moreover, these simulations do not address the possibility of ionized G-T mispairs because NMR experiments have suggested that under physiological conditions, misincorporation proceeds primarily via the tautomeric and not the anionic species.⁷ The anionic mispairs were also found to be thermodynamically unfavorable in a theoretical study of a DNA polymerase λ variant.³⁷ The main goal of the present work is to compute the relative free energies of the wG-T, G-T*, and G*T tautomers, which do not depend on the reaction paths. The free energy barriers should be interpreted within the limitations of the mechanistic assumptions.

The statistical uncertainties associated with the free energy calculations were analyzed using a bootstrapping error analysis (see Figure S5). However, this analysis does not account for the errors arising from the level of theory used to generate the potential energy surface and the limitations in the conformational sampling. In particular, the functional and basis set used in the DFT calculations are associated with errors in the relative free energies of at least 1 kcal/mol, and the molecular mechanical force field describing the environment increases this error. The errors introduced by the limited conformational sampling are more difficult to estimate because they depend on the accuracy of the starting structure and the conformational flexibility of the system. Altogether, the uncertainties in the relative free energies are estimated to be at least 3 kcal/mol. As discussed below, the consistency of our results with previous calculations and with experimental data provide validation for the qualitative conclusions emerging from this study.

Results and Discussion

Tautomerization from the wG-T state to the G-T* state

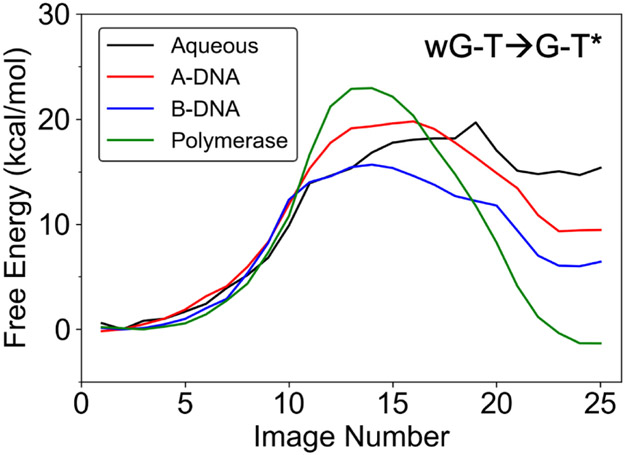
The free energy profiles along the MFEP for the wG-T→G-T* tautomerization in the four different environments studied are depicted in Figure 4. The free energies of tautomerization, ΔG(wG-T→G-T*), and the free energy barriers, ΔG^‡(wG-T→G-T*), computed in aqueous solution, the A-DNA duplex, the B-DNA duplex, and the DNA polymerase λ variant in the closed conformation are given in Table 1. The uncertainty analysis of these free energy profiles is given in Figure S5. Our computed ΔG(wG-T→G-T*) of 6.0 kcal/mol for the B-DNA duplex is qualitatively consistent with previous NMR studies on B-DNA duplexes indicating that the ΔG(wG-T→G-T*) is 4.3–4.7 kcal/mol at 298 K.^{7, 15} In addition, our computed free energy barrier of 15.7 kcal/mol for the B-DNA duplex is consistent with the barrier of 16.0 – 17.0 kcal/mol at room temperature estimated from NMR measurements for the wG-T→G-T* transition in B-DNA duplexes.⁷ The slightly negative free energy change of −1.3 kcal/mol associated with the wG-T→G-T* tautomerization in the DNA polymerase λ variant is also consistent with the observation of the WC-like G-T configuration in the X-ray structure of this system in the same closed conformation⁹, the observation of WC-like mispairs in structures of other DNA polymerases in the closed conformation^8-10 and the tendency of the polymerase active site to be tuned to the WC shape.¹ Furthermore, the “transition state” (wG-T↔G-T*) structures in Figure 5 are consistent with previous computational studies on isolated base pairs indicating that the transition state structure is the zwitterion (G⁺-T⁻) formed after proton transfer from T to G.^{35, 55}

Figure 4.

Free energy profiles along the MFEPs computed from the strings corresponding to the wG-T→G-T* tautomerization for the four systems investigated. The images correspond to equally spaced points along the MFEP. The aqueous system is less well-defined because of the flexibility of the DNA base pair.

Table 1.

Calculated Free Energy Barriers and Reaction Free Energies for G-T Mispair Tautomerization in Aqueous Solution, the A-DNA Duplex, the B-DNA Duplex, and the DNA Polymerase λ Variant.^a

	ΔG‡ (wG-T→G-T*)	ΔG (wG-T→G-T*)	ΔG‡ (G-T*→G*-T)	ΔG (G-T*→G*-T)
Aqueous	19.7	14.7	7.2	0.3
A-DNA	20.0	9.5	7.3	1.4
B-DNA	15.7	6.0	5.7	−0.2
DNA polymerase λ variant	23.0	−1.3	5.4	−2.4

^aEnergies given in kcal/mol, and the temperature is 300 K.

Figure 5.

(A) Representative configurations along the wG-T→G-T* tautomerization process in the A-DNA duplex. These structures are the last configurations of the last iteration of each string simulation for the images corresponding to the reactant state, the “transition state” (i.e., top of the free energy barrier), and the product state in Figure 4. Specifically, these configurations were obtained from images 1, 16, and 23 of the wG-T→G-T* string for the A-DNA duplex. (B) Analogous representative configurations along the G-T*→G*-T tautomerization process in the A-DNA duplex. These configurations were obtained from images 2, 9, and 14 of the G-T*→G*-T string for the A-DNA duplex. Analogous configurations along the wG-T→G-T* tautomerization process for the other systems are given in Figure S6.

To identify the factors determining the different free energy profiles, we examined the structures associated with the reactant state (wG-T), the “transition state” (wG-T↔G-T*) and the product state (G-T*) for the wG-T→G-T* tautomerization in the four systems (Figure 5 and Figure S6). Note that these structures are not stationary points on the free energy surfaces and therefore should be viewed as representative configurations rather than true minima or transition states. Although the wG-T structures are similar for the four different systems, the G-T* structures exhibit more significant differences. In particular, the N1-H1-N3, N2-H21-O2, and O6-H3-O4 hydrogen bonds are more linear in the polymerase variant than in aqueous solution (Table S5). Similarly, the hydrogen bond donor-acceptor distances associated with these two hydrogen bonds are significantly shorter in the polymerase variant than in aqueous solution (Table S5). These trends are consistent with the trends in ΔG(wG-T→G-T*), which indicate that the G-T* tautomer is the most stable in the polymerase variant and the least stable in aqueous solution compared to its wG-T analog. Note that these trends are followed for some but not all of these hydrogen-bonding parameters for the A-DNA and B-DNA systems, which exhibit reaction free energies in between those of the polymerase and the aqueous systems. Thus, these reaction free energy differences are explained in part by differences in hydrogen-bonding interactions between the base pairs.

We also analyzed the steric and electrostatic impact of the A-DNA, B-DNA, and polymerase environments on the G-T mispair tautomerization process. This analysis entailed the calculation of the average energies of the G-T mispair, denoted E_G-T, and the average electrostatic interaction energy between the G-T mispair and the environment, denoted E_elec, during the tautomerization. Specifically, these energies were obtained by averaging the energy of the QM region and the QM/MM electrostatic interaction energy over the last iteration of the string calculation for specific images associated with the wG-T, wG-T↔G-T*, and G-T* states. All of the configurations were weighted to account for the umbrella sampling restraints, and the average energies of the wG-T↔G-T* and G-T* states were computed relative to the average energy of the wG-T state for each system to enable comparisons across systems of different sizes (Table S6). The qualitative trends were reproducible when the same analysis was performed for the second-to-last iteration of the string calculations (Table S6). Differences in E_G-T primarily reflect the impact of environmental restraints on hydrogen-bonding and other internal interactions within the G-T mispair (Figure 5A and Table S5), while differences in E_elec account for the distinct electrostatic environments. Interestingly, the ordering of E_G-T + E_elec for wG-T↔G-T* and G-T* among the DNA duplexes and the polymerase are consistent with the ordering of ΔG^‡(wG-T→-G-T*) and ΔG(wG-T→G-T*), respectively (Table 1). Nevertheless, given the sampling limitations, this analysis should be viewed as providing only qualitative rather than quantitative information.

Although the sequences are identical, the A-DNA and B-DNA duplex structures are different, leading to different interactions of the G-T mispair with the neighboring nucleotides and thus differences in the reaction free energies and free energy barriers associated with tautomerization (Figure 4 and Figure S7). These differences are quantified by analysis of the energies E_G-T and E_elec defined above (Table S6). E_G-T for G-T* is positive for A-DNA and negative for B-DNA, suggesting significant differences in the hydrogen-bonding and other internal interactions within the G-T mispair for these two environments. The positive value of E_elec for the wG-T↔G-T* and G-T* states for both the A-DNA and B-DNA duplexes indicates that the electrostatic environment stabilizes the wG-T state more than the wG-T↔G-T* and G-T* states for both duplexes, although their magnitudes are different. As mentioned above, E_G-T + E_elec is consistent with the higher free energy barrier and more endoergic tautomerization for A-DNA compared to B-DNA. This analysis illustrates that a combination of environmental constraints and electrostatic interactions with the duplex environments, which are structurally distinct, is most likely responsible for the differences in the free energy profiles for tautomerization.

The DNA polymerase λ variant has the largest ΔG^‡(wG-T→G-T*) and has the only negative ΔG(wG-T→G-T*) among the four systems. The P–P distances in the polymerase variant are ~2 Å smaller than those in the DNA duplexes, indicating a more compact structure in the polymerase variant (Table S7). More important are the interactions of the G-T mispair with the protein environment. Analysis of E_G-T and E_elec indicates that a combination of environmental constraints and electrostatic effects results in a more energetically unfavorable wG-T↔G-T* state for the DNA polymerase λ variant compared to the DNA duplexes (Table S6). This analysis is consistent with the observation that the free energy barrier for wG-T→G-T* tautomerization is higher in the DNA polymerase λ variant than in the DNA duplexes (Figure 4). Moreover, analysis of E_elec illustrates that the electrostatic environment of the polymerase stabilizes the G-T* state relative to the wG-T state, in contrast to the DNA duplex environments, which destabilize the G-T* state relative to the wG-T state. This analysis is consistent with the observation that ΔG(wG-T→G-T*) is negative for the DNA polymerase λ variant and positive for the DNA duplexes. This analysis illustrates that the polymerase environment plays an important role in determining the thermodynamics and kinetics for the wG-T→G-T* tautomerization. The computed free energy barrier of ~23 kcal/mol (Table 1) in this closed conformation of the polymerase is much higher than expected based on the rate of misincorporation. This finding is consistent with our experimental studies⁷ implying that tautomerization most likely occurs in an ajar conformation of the polymerase or in a manner that may be coupled to closing of the polymerase. This issue will be discussed further below.

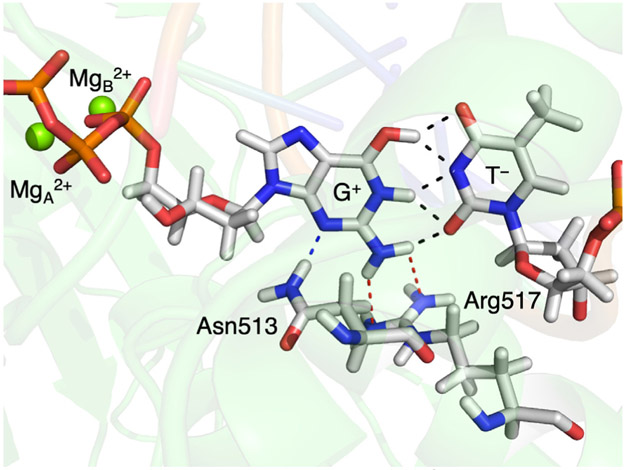
We further examined the polymerase environment to identify the key residues that impact the reaction free energy and free energy barrier. Asn513 and Arg517 exhibit hydrogen-bonding interactions with the guanine base (Figure 6). To elucidate the electrostatic effects, we estimated the electrostatic contributions from these two residues and the two Mg²⁺ ions coordinated to the GTP ligand (Table S8). These calculations indicate that Arg517 significantly stabilizes the G-T* state relative to the wG-T state by ~10 kcal/mol and that Asn513 and the two Mg²⁺ ions also contribute to this stabilization by a smaller amount. This observation is consistent with a previous study in which mutation of Asn279 of DNA polymerase β, which is analogous to Asn513 in the DNA polymerase λ variant, was found to destabilize the WC-like structure of the G-T mispair, converting it to a wobble mispair instead.⁵⁶ In addition, these observations are also consistent with kinetic studies showing that mutation of Arg283 in DNA polymerase β, which is analogous to Arg517 in the DNA polymerase λ variant, reduces the rate of G-T misincorporation by ~10 fold,⁵⁷ presumably by destabilizing the WC-like G-T mispair. This analysis also indicates that the two Mg²⁺ ions destablize the wG-T↔G-T* state, while Arg517 stabilizes the wG-T↔G-T* state (Table S8), leading to an overall destabilization of the wG-T↔G-T* state relative to the wG-T state. These electrostatic effects of the Mg²⁺ ions are consistent with the proximity of these positively charged ions to the slightly positive charge on the G in the zwitterionic G⁺-T⁻ “transition state” (Figure 6). Overall, the electrostatic interactions of Arg517, Asn513 and the two Mg²⁺ ions significantly impact the thermodynamics and kinetics of the wG-T→G-T* tautomerization in the DNA polymerase variant.

Figure 6.

Interactions of Asn513, Arg517, and the two Mg²⁺ ions with the G-T mispair in the DNA polymerase λ variant. This structure is the last configuration of the last iteration for image 14 of the DNA polymerase variant, corresponding to the wG-T↔G-T* state in Figure 4. The hydrogen bonds within the G-T mispair are indicated with black dashed lines, the hydrogen bond between Asn513 and G is indicated with a blue dashed line, and the hydrogen bonds between Arg517 and G are indicated with red dashed lines. The analogous configurations corresponding to the wG-T and G-T* states are shown in Figure S8.

Tautomerization from the G-T* mispair to the G*-T mispair

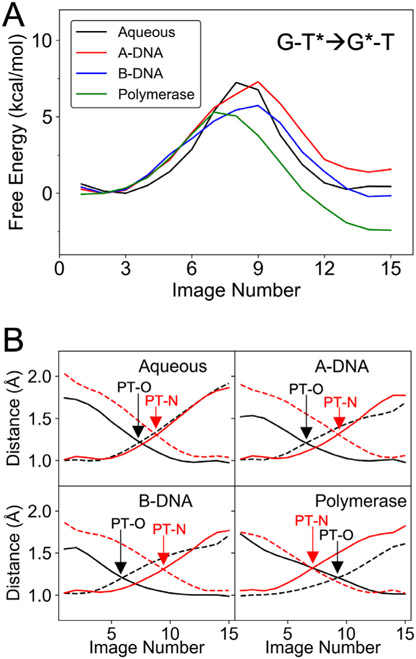
The G-T*→G*-T tautomerization involves two proton transfer (PT) reactions (Figure 5B): the PT reaction between two oxygen atoms, denoted as PT-O, and the PT reaction between two nitrogen atoms, denoted as PT-N. These two reactions were found to be concerted in that a single barrier connects the reactant and product without a stable intermediate (Figure 7A), consistent with previous studies of the double proton transfer in A-T and G-C tautomerization^58-60 and prior studies on G-T mispairs.^35-36 Moreover, our results also indicate that the two PT reactions occurring in the G-T*→G*-T tautomerization process are asynchronous, consistent with a previous computational study.³⁶ However, further analysis indicates that the environment can alter the order of the two proton transfer reactions. Specifically, PT-O occurs first in the aqueous and DNA duplex environments, whereas PT-N occurs first in the DNA polymerase λ variant (Figure 7B). Thus, the polymerase environment alters the fundamental mechanism of this tautomerization process. Moreover, we examined the structures associated with the reactant state (G-T*), “transition state” (G-T*↔G*-T), and product state (G*-T) along the G-T*→G*-T tautomerization process in the four systems (Figure S9) and performed a hydrogen-bonding analysis (Table S5). Our analysis indicates that the G-T*→G*-T tautomerization exhibits smaller differences among the four systems compared to the differences observed for the wG-T→G-T* tautomerization.

Figure 7.

(A) Free energy profiles along the MFEPs computed from the strings corresponding to the G-T*→G*-T tautomerization for the four systems investigated. The images correspond to equally spaced points along the MFEP. (B) The key reaction coordinates associated with the G-T*→G*-T tautomerization along the MFEP, where R2, R3, R5, and R6 are represented by black solid, black dashed, red solid, and red dashed curves, respectively. Note that R2 and R3 are associated with PT-O (i.e., proton transfer between the two oxygen atoms), and R5 and R6 are associated with PT-N (i.e., proton transfer between the two nitrogen atoms).

The computed free energy profiles for the G-T*→G*-T conversion indicate that the environment has a relatively modest influence on ΔG(G-T*→G*-T) and the associated free energy barrier ΔG^‡(G-T*→G*-T) (Table 1 and Figure 7A). In particular, the ΔG(G-T*→G*-T) values in aqueous solution and both DNA duplexes are small, suggesting that this tautomerization is nearly isoergic in these environments, consistent with previous QM calculations using an implicit solvent model^{35, 55} and NMR measurements on G-T mispairs.⁷ In contrast, this tautomerization is slightly exoergic for the DNA polymerase λ variant (Figure 7A and Table 1). The free energy barriers in all four environments are 5 – 7 kcal/mol.

Our results are qualitatively consistent with a previous FEP study³⁷ of tautomerization in the same polymerase variant. In this previous study, the free energy change for the wG-T→G-T* tautomerization was computed to be 1.8 kcal/mol, and the free energy change for the wG-T→G*-T tautomerization was computed to be −0.2 kcal/mol, in contrast to the values of −1.3 and −3.7 kcal/mol, respectively, obtained in the present work. In both studies, the G*-T form was found to be the most stable form in this polymerase variant and was more stable than the G-T* form by ~2 kcal/mol. The quantitative differences for the free energies of the enol tautomers relative to the wG-T form are most likely due to limitations in conformational sampling and differences in the potential energy surfaces. Specifically, the previous FEP study³⁷ used a reparameterized force field to describe the mispairs, whereas the present work uses DFT within a QM/MM framework. Despite these differences in methodology, however, the qualitative results are consistent.

Thermodynamics of conformational transitions in polymerase

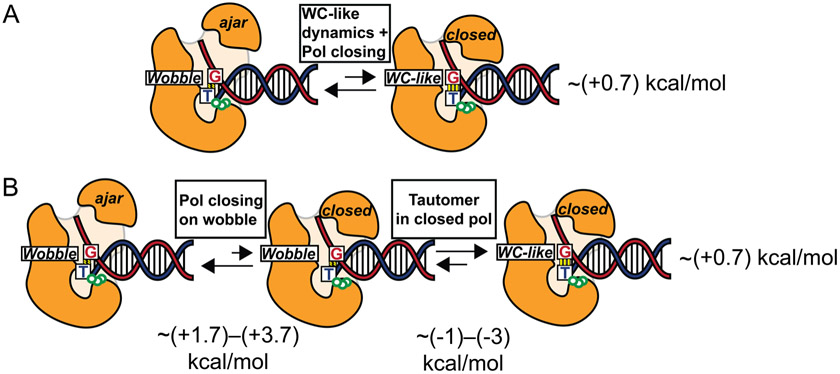
Based on kinetic modeling, the equilibrium between wobble G-T mispairs in an ajar polymerase conformation and WC-like G-T mispairs in a closed polymerase conformation has been proposed to be disfavored by ~0.7 kcal/mol (Figure 8A).⁷ The results obtained in this study indicate that the closed polymerase favors the WC-like G-T mispair by ~1–3 kcal/mol relative to the wobble G-T mispair (Figures 4 and 7A). Since the overall reaction between ajar wobble and closed WC-like mispair is disfavored by ~0.7 kcal/mol, the transition between ajar and closed polymerase with a wobble G-T mispair is deduced to be disfavored by ~1.7–3.7 kcal/mol (Figure 8B), consistent with the crystal structure of DNA polymerase BF1 variant in the ajar state with a wobble G-T mispair.²⁹ Compared to a preformed DNA duplex, which favors the Watson-Crick geometry, the replicating polymerase expends energy (~2–4 kcal/mol) to create an environment that favors the WC-like shape by closing on the wobble. This expense of energy is compensated by more strongly favoring the WC-like tautomer relative to the wobble in the closed state as compared to the duplex, leading to a net +0.7 kcal/mol destabilization in both cases.

Figure 8.

(A) Equilibrium between DNA polymerase in an ajar conformation with a wobble G-T mispair and DNA polymerase in a closed conformation with a WC-like G-T mispair. A value of ~(+0.7) kcal/mol is deduced based on kinetic studies of misincorporation of DNA polyemrase β at 37 °C.⁷ (B) Decomposition of the equilibrium process in A into two steps involving closing of the polymerase on a wobble G-T mispair and subsequent conversion of the wobble mispair into a WC-like conformation within the closed polymerase, as computed in this work. The overall change in free energy is independent of path and therefore is the same for the paths depicted in parts A and B, allowing the deduction of the free energy associated with the first step in part B.

Conclusions

We investigated the environmental effects on G-T mispair tautomerization by studying this process in aqueous solution, an A-DNA duplex, a B-DNA duplex, and a DNA polymerase λ variant using QM/MM free energy simulations. We found that the environment can significantly influence the thermodynamics, kinetics, and reaction mechanisms. The wG-T→G-T* tautomerization is predicted to be endoergic for the aqueous and duplex systems and to be slightly exoergic in the DNA polymerase λ variant. The associated free energy barrier is relatively high for the tautomerization in the closed conformation of the polymerase, supporting prior kinetic models⁷ implying that tautomerization occurs in the ajar conformation or in a concerted manner coupled to the transition from the ajar to the closed conformation. The free energy profiles for the G-T*→G*-T tautomerization are not as sensitive to the environment, although again the tautomerization is most thermodynamically favorable in the DNA polymerase λ variant. Furthermore, we found that the order of the two proton transfer reactions associated with the G-T*→G*-T tautomerization is different in the polymerase environment than in the aqueous and duplex environments, illustrating that the environment can change the fundamental mechanism as well as the thermodynamics and kinetics of tautomerization.

The differences among the reaction free energies and free energy barriers for the G-T tautomerization processes can be explained in terms of hydrogen-bonding interactions between the G-T mispairs and electrostatic interactions between the G-T mispairs and the environment. Analysis of the process in the DNA polymerase λ variant identified specific residues and metal ions that influence the free energy profiles. For the wG-T→G-T* tautomerization, electrostatic stabilization of G-T* relative to wG-T by Arg517 provides an explanation for the thermodynamic favorability of this reaction in the polymerase environment. Arg517 also stabilizes the “transition state” relative to wG-T, but the more dominant electrostatic destabilization by the two Mg²⁺ ions coordinated to the GTP ligand leads to a higher free energy barrier in the polymerase environment. These analyses suggest that mutating Arg517 could impact the probability of G-T mispair tautomerization in the polymerase variant. Moreover, our results also suggest that Asn513 can slightly stablize the G-T* state relative to the wG-T state, consistent with a previous study regarding the analogous Asn279 in DNA polymerase β.⁵⁶ Moreover, the free energy barrier may be lower for the wG-T→G-T* tautomerization when a TTP fragment rather than a GTP fragment is inserted during the polymerization process because of favorable electrostatic interactions of T⁻ in the zwitterionic G⁺-T⁻ transition state with the two Mg²⁺ ions.

Overall, this computational study highlights the significant effects of the environment on G-T mispair tautomerization. The methods outlined in this study can also be applied to the study of G-U mispair tautomerization in the context of A-RNA, for which Watson-Crick like mispairs have also been observed experimentally.⁷ In addition, they can be used to explore other proposed WC-like mispairs^{3, 61} that have proven elusive to study experimentally, to understand the mechanism associated with chemical modifications that are proposed to enhance miscoding via altered tautomerization propensities,^{19-22, 62} and to examine the role of mutagenic metals such as Mn²⁺ in enhancing tautomerization.⁶³ The insights provided by this work could enhance fundamental understanding of biologically important processes such as spontaneous mutations and therapeutic design of nucleic acid base analogues.⁶⁴ This enhanced understanding could also have broader implications for the design of more effective nucleic acid catalysts and nucleic acid base analogues, as well as strategies to prevent spontaneous mutations that may cause certain types of cancer.¹⁴ Similar computational approaches could be used to study other types of DNA mispairs in a variety of environments. Furthermore, these methods could be used to study RNA-ligand recognition^17-18 and catalysis,²³ where the involvement of tautomers has been well-characterized experimentally.