The mechanochemistry of the kinesin-2 KIF3AC heterodimer is related to strain-dependent kinetic properties of KIF3A and KIF3C

Significance

Kinesins are cytoskeletal motors responsible for long-range intracellular transport along microtubules. The mammalian kinesin-2, KIF3AC, is a neuronal heterodimer of fast and slow motor polypeptides. Our results show that KIF3AC has a single observed stepping rate in the presence and absence of load and detaches from the microtubule rapidly under load. Interestingly, both KIF3A and assisting loads accelerate the stepping kinetics of KIF3C. These results suggest that KIF3AC is an unconventional cargo transporter and its motile properties do not represent a combination of alternating fast and slow step kinetics. We demonstrate that the motile properties of KIF3AC represent a mechanochemistry that is specific to KIF3AC and may provide functional advantages in neurons.

Abstract

KIF3AC is a mammalian neuron-specific kinesin-2 implicated in intracellular cargo transport. It is a heterodimer of KIF3A and KIF3C motor polypeptides which have distinct biochemical and motile properties as engineered homodimers. Single-molecule motility assays show that KIF3AC moves processively along microtubules at a rate faster than expected given the motility rates of the KIF3AA and much slower KIF3CC homodimers. To resolve the stepping kinetics of KIF3A and KIF3C motors in homo- and heterodimeric constructs and determine their transport potential under load, we assayed motor activity using interferometric scattering microscopy and optical trapping. The distribution of stepping durations of KIF3AC molecules is described by a rate (k₁ = 11 s⁻¹) without apparent kinetic asymmetry. Asymmetry was also not apparent under hindering or assisting mechanical loads in the optical trap. KIF3AC shows increased force sensitivity relative to KIF3AA yet is more capable of stepping against mechanical load than KIF3CC. Interestingly, the behavior of KIF3C mirrors prior studies of kinesins with increased interhead compliance. Microtubule gliding assays containing 1:1 mixtures of KIF3AA and KIF3CC result in speeds similar to KIF3AC, suggesting the homodimers mechanically impact each other’s motility to reproduce the behavior of the heterodimer. Our observations are consistent with a mechanism in which the stepping of KIF3C can be activated by KIF3A in a strain-dependent manner, similar to application of an assisting load. These results suggest that the mechanochemical properties of KIF3AC can be explained by the strain-dependent kinetics of KIF3A and KIF3C.

Kinesin-2 is a distinctive subfamily of processive kinesins that contains both homodimeric and heterodimeric motors involved in microtubule (MT) plus-end directed cargo transport (1–4). The mammalian heterodimeric kinesin-2s result from three genes: kif3a, kif3b, and kif3c to form heterodimeric motors KIF3AB and KIF3AC (5–9) while expression of the kif17 gene product results in homodimeric kinesin-2, KIF17 (10–12). Moreover, KIF3A and KIF3B do not form homodimers, and KIF3B does not heterodimerize with KIF3C, suggesting distinct transport functions of KIF3AB, KIF3AC, and KIF17. While these studies show that KIF3AB and KIF3AC heterodimerization is preferred over homodimerization, there is evidence for an injury-specific homodimer of KIF3CC in neurons (13). KIF3C also contains a signature 25-residue insert of glycines and serines in loop L11 of the catalytic motor domain, which has been shown to regulate KIF3AC processivity (14) and MT catastrophe promoted by KIF3CC in vitro (15). The structural diversity within the kinesin-2 subfamily suggests that heterodimerization of kinesin-2 motors may be a mechanism to optimize the mechanochemistry of the motors for specific tasks (16).

Motility and biochemical experiments indicate that the activities of KIF3A and KIF3C depend on the motors with which they are partnered. KIF3AC and the engineered homodimers, KIF3AA and KIF3CC, move processively in single-molecule motility assays. KIF3AC has longer run lengths than either of the homodimers (14), and its speed is substantially faster than expected given the very slow rate of the KIF3CC homodimer (Discussion). Additionally, comparison of the presteady-state kinetics of KIF3AC, KIF3AA, and KIF3CC indicates that the rates of association of the motors with MTs and adenosine 5′-diphosphate release depend on the motor’s partner head. These kinetic and motile properties suggest that interhead communication within the heterodimer tunes the mechanochemical properties of KIF3A and KIF3C (4, 14, 17, 18).

While previous studies have described the single-molecule stepping properties of KIF3A, KIF3B, and KIF3AB in substantial detail (16, 19), there have been no comparable studies of heterodimeric KIF3AC. We sought to resolve the stepping kinetics of individual KIF3A and KIF3C motor domains in homo- and heterodimeric motors and to determine the transport potential of the dimers under mechanical load. To accomplish this, we assayed motor activity using interferometric scattering (iSCAT) microscopy, a recent advance in light microscopy which has sufficient spatiotemporal precision to resolve single steps of a kinesin motor during processive runs (20–24), and optical trapping, which reveals the motor performance under forces hindering and assisting plus-end directed motility (25–30). We observed that the step dwell time distribution of KIF3AC is not a combination of the dwell time distributions observed for KIF3AA and KIF3CC and is adequately fit by a single exponential rate. The symmetric stepping of KIF3AC persists under hindering or assisting mechanical load. We show that the kinetics of KIF3C are accelerated by assisting load, and an equal mixture of KIF3AA and KIF3CC promotes MT gliding at the same rate as KIF3AC. Therefore, our results favor a model of KIF3AC motility in which the strain-dependent kinetics of KIF3A and KIF3C give rise to the velocity of KIF3AC. KIF3AC shows decreased stall and detachment forces relative to KIF3AA and detaches from the MT rapidly under hindering or assisting mechanical load. We argue that the mechanochemical properties of KIF3AC observed here and previously may be adaptations for cargo transport in large ensembles.

Results

KIF3AA, KIF3AC, and KIF3CC Step Dwell Times and Backstepping Frequencies Are Distinct in Unloaded Conditions.

We resolved the stepping displacements and kinetics of KIF3AA, KIF3CC, and KIF3AC using iSCAT microscopy. Streptavidin-coated gold nanoparticles (50 nm) were attached to the C-terminal His-tags of kinesin dimers via a biotinylated anti-His antibody to measure the movement of single motors as the alternating heads interacted with a surface-attached MT (SI Appendix, Fig. S1A).

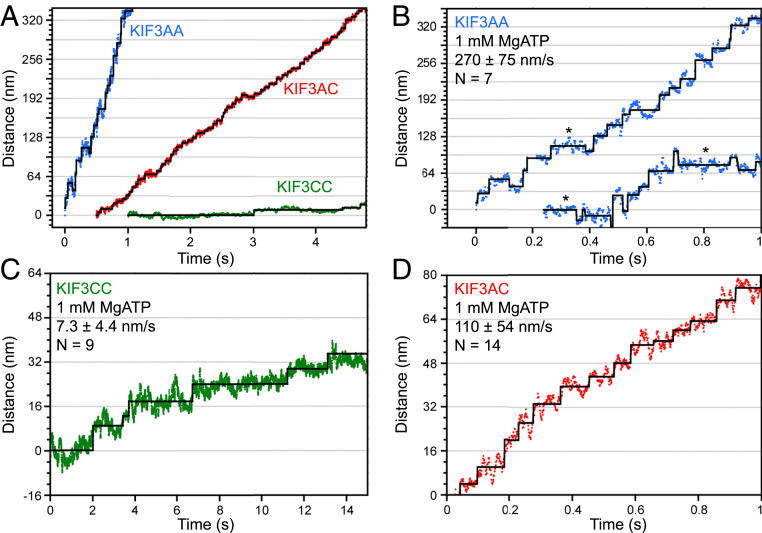
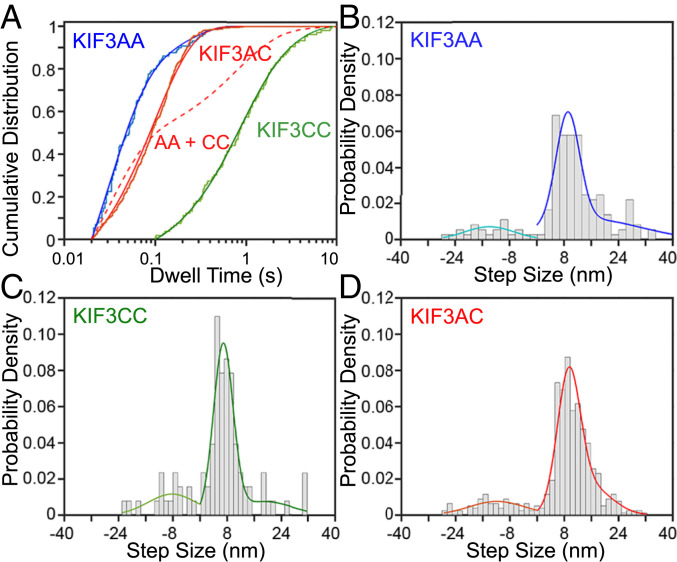
In the presence of 1 mM magnesium adenosine 5′-triphosphate (MgATP), KIF3AA moves processively at a rate of 270 ± 75 nm/s (Fig. 1 A and B), which is similar to the velocity measured previously with the same protein construct in single-molecule Qdot motility assays (14) but slightly slower than observed in optical trapping assays that used a construct with a different dimerization motif (16). Individual steps are clearly resolved in the iSCAT traces (Fig. 1B). After filtering by a Chung–Kennedy filter (31) with an 11-ms width, traces are fit using a step-finding algorithm (ref. 32 and Fig. 1B) to extract the distribution of dwell times and step sizes (Fig. 2 A and B). A double Gaussian distribution is fit to the forward step sizes, and single Gaussian distribution was fit to the backward steps. The most prominent component is centered near 8 nm (9.1 ± 3.5 nm; Fig. 2B and Table 1) with a smaller population (16 ± 15 nm), likely representing two steps that occurred rapidly in sequence and could not be resolved by the step-fitting algorithm. Infrequent backward steps are also resolved (−14 ± 7.2 nm; A_back = 0.12). The dwell times, plotted as cumulative distribution functions (CDFs) (Fig. 2A), are best fit by the sum of two exponential functions (Fig. 2A and Table 1). The fit reveals a predominant fast component (A₁ = 0.83) with a rate of k₁ = 34 s⁻¹. The slower, minor component, k₂ = 6.1 s⁻¹ (A₂ = 0.17), is most likely due to infrequent pauses in stepping (Fig. 1B, asterisks).

Fig. 1.

Nanometric tracking of KIF3AC and engineered homodimers by iSCAT microscopy. (A) Sample traces of KIF3AA (blue), KIF3AC (red), and KIF3CC (green) tracked by iSCAT microscopy shown on the same time and length scales for comparison. Sample traces (B–D) of expanded views of the position along path of travel at 1 mM MgATP for KIF3AA (B), KIF3CC (C), and KIF3AC (D). An asterisk is used to denote instances of pausing for >150 ms in traces of KIF3AA motility. Velocity is reported as the mean ± SD for each motor. N values reflect the number of molecules tracked for iSCAT analysis. Black overlay, Kerssemakers’ algorithm fit (32).

Fig. 2.

KIF3AC steps by a single rate at 1 mM MgATP with 8-nm steps. Step sizes and kinetics measured by iSCAT microscopy for KIF3AC and engineered homodimers. (A) CDF plots and accompanying fits of dwell-time data at 1 mM MgATP for KIF3AA (blue), KIF3AC (red), and KIF3CC (green). Dwell-time data are fit to a single exponential function (KIF3AA) or the sum of two exponential functions as justified by the log-likelihood ratio test (KIF3CC, KIF3AC). Hypothetical curve of the sum of the KIF3AA and KIF3CC fits is plotted (red dashed line). Data are plotted with a logarithmic x axis. (B–D) Histograms of step sizes observed for KIF3AA (B), KIF3CC (C), and KIF3AC (D). Negative step sizes refer to backward steps. Forward and backward step size distributions were fit independently, and fits are shown in different colors. Fit parameters are given in Table 1. For KIF3AA N_steps = 168, for KIF3CC N_steps = 93, and for KIF3AC N_steps = 516.

Table 1.

iSCAT step kinetics and displacement fit parameters

		Step kinetics				Step sizes
Motor	[MgATP], mM	A1	k1, s−1	A2	k2, s−1	Aback	μback, nm	Aforward1	μforward1 (nm)	Aforward2	μforward2, nm
KIF3AA	1	0.83	34	0.17	6.1	0.12	−14 ± 7.2	0.49	9.1 ± 3.5	0.39	16 ± 15
KIF3CC	1	0.68	1.3	0.32	0.44	0.18	−8.2 ± 7.2	0.66	6.9 ± 2.9	0.16	19 ± 8.2
KIF3AC	1	1.0	11	—	—	0.15	−12 ± 8.2	0.60	9.3 ± 3.4	0.25	16 ± 6.4

The relative amplitudes and rates of each exponential fit are shown. Single exponential fit equation: $y=k_{\mathit{1}}{e}^{-k_{\mathit{1}}t}$ and sum of two exponential functions fit equation: $y=A{k}_{\mathit{1}}{e}^{-k_{\mathit{1}}t}+\left(1-A\right)k_{\mathit{2}}{e}^{-k_{\mathit{2}}t}$ where the amplitude A is reported as A₁ and (1 – A) is reported as A₂. For step displacements, A_back and μ_back describe backstepping, A_forward1 and μ_forward1 the dominant forward step size peak near 8 nm, and A_forward2 and μ_forward2 the additional forward peak near 16 nm. Backward and forward step-size distributions were fit independently. For the KIF3AA dwell time fit, the log-likelihood test gives P = 1.4 × 10⁻⁷, justifying a double exponential fit, and for the KIF3CC dwell-time fit the log-likelihood ratio test gives P = 0.036. Means are shown ± σ of the fit curve where σ indicates the width of the Gaussian peak and not the uncertainty in peak position. Dashes, not applicable.

KIF3CC homodimers moved much slower than KIF3AA under identical conditions with an average velocity (7.3 ± 4.4 nm/s; Fig. 1 A and C), similar to values measured previously (14). Step fitting to the KIF3CC traces reveals a step size distribution (Fig. 2C and Table 1) with a prominent component (A_forward1 = 0.66) centered at 6.9 ± 2.9 nm. Backward steps (−8.2 ± 7.2 nm, A_back = 0.18; Table 1) occur more frequently than observed for KIF3AA as isolated steps and not backward runs. There are fewer steps detected near 16 nm, consistent with fewer unresolved fast steps. The distribution of observed dwell times for KIF3CC is best fit by the sum of two exponential functions (green, Fig. 2A) with rates k₁ = 1.3 s⁻¹ and k₂ = 0.44 s⁻¹ (A₁ = 0.68, A₂ = 0.32; Table 1). The ∼30-fold difference in stepping rates between KIF3AA and KIF3CC is consistent with previous single-molecule velocity reports (4, 14).

KIF3AC heterodimers moved processively at a velocity of 110 ± 54 nm/s (Fig. 1D). As observed for KIF3AA and KIF3CC, the most prominent distribution of step sizes for KIF3AC is centered near 8 nm (9.3 ± 3.4 nm; Fig. 2D and Table 1). Backsteps (−12 ± 8.2 nm, A_back = 0.15) are also observed for KIF3AC, as single isolated steps and not processive backward runs. Notably, the cumulative distribution of dwell times for KIF3AC (red, Fig. 2A) is best fit by a single-exponential function (k₁ = 11 s⁻¹; ref. 33) rather than the sum of two exponentials, which may have been expected given the ∼30-fold difference in the unloaded stepping rates of KIF3A and KIF3C homodimers. We confirmed this result was not unique to a single step-finding algorithm by fitting the iSCAT traces of KIF3AC motility using a different program (34) and found similar distributions of dwell times and step sizes (SI Appendix, Fig. S6).

Mathematical modeling was used to determine the conditions under which a single exponential fit could result from two independent rates. We found that at least a twofold difference in rates is necessary to statistically justify fitting the sum of two exponential components (SI Appendix, Fig. S4). The difference between observed and predicted dwell time distributions is illustrated by plotting a hypothetical CDF that is the normalized sum of KIF3AA and KIF3CC dwell times (Fig. 2A, red dashed curve). The data are clearly different from such a model. To further test for asymmetric stepping times, we performed a limping analysis (35). For KIF3AC trajectories of sufficient length (>80 steps), the mean lifetimes of even and odd indexed steps were calculated and found not to be significantly different. On average, the slower steps had a lifetime of 0.14 ± 0.01 s, while the faster steps had a lifetime of 0.13 ± 0.01 s. The average limping factor, the ratio of the mean long and short dwells during a trace, was 1.1 ± 0.1 (SI Appendix, Table S1), which is consistent with symmetric step kinetics.

KIF3AC Detaches from MTs at Lower Forces than Kinesin-2 KIF3AB or Kinesin-1 KIF5B.

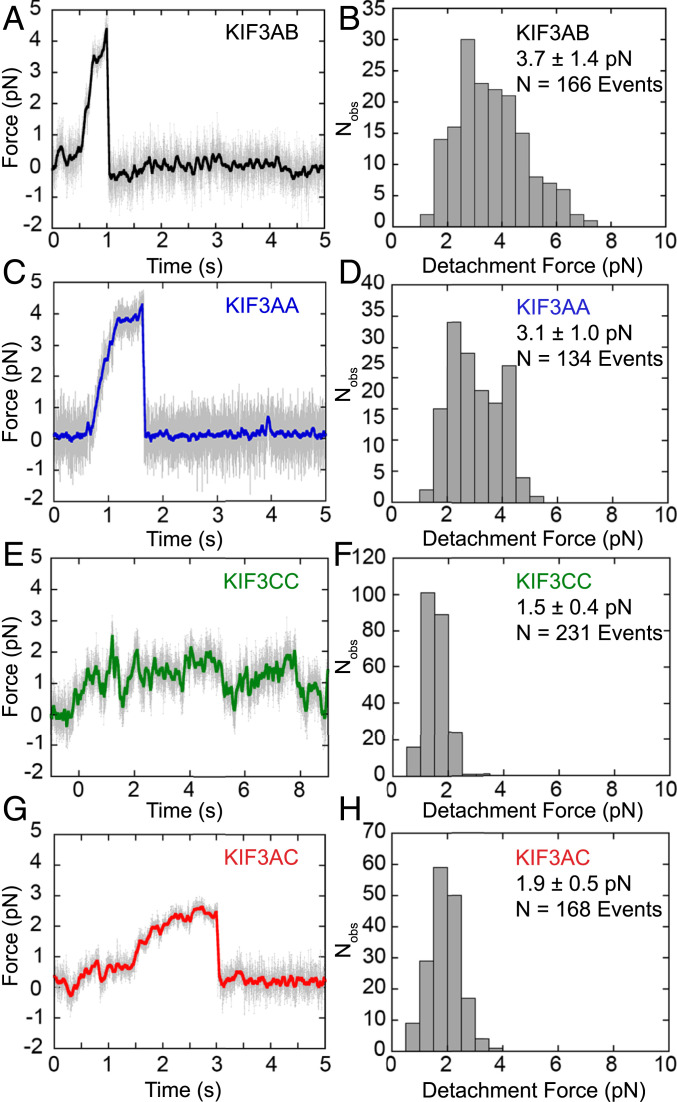
We used a stationary, single-beam, optical trap to determine the ability of heterodimeric KIF3AC and the engineered KIF3AA and KIF3CC homodimers to move and remain attached to the MT in the presence of hindering loads. The unitary detachment, maximum, and stall forces of KIF3AC, KIF3AA, and KIF3CC bound to 0.82-μm streptavidin-coated beads via a biotinylated anti-His antibody were measured (SI Appendix, Supplementary Methods and Fig. S1 B and C). We also determined the same parameters for KIF3AB using this experimental geometry to compare with other published results (16, 36, 37).

The detachment and stall forces of KIF3AA (3.1 to 3.3 pN) are slightly lower than those of KIF3AB (Fig. 3 A–D and Table 2), which are similar to values reported previously (16, 36, 37). KIF3CC and KIF3AC have substantially lower detachment forces than KIF3AA (Fig. 3 C–H and Table 2) at F_detach = 1.5 ± 0.4 pN for KIF3CC and F_detach = 1.9 ± 0.5 pN for KIF3AC. The maximum force and stall force measured for KIF3AA are greater than those for KIF3AC, which are in turn greater than those for KIF3CC. A small percentage of events terminate in a stall (10 to 14%) for KIF3AB, KIF3AA, and KIF3AC, and no stall plateaus are observed for KIF3CC (Table 2). KIF3 motors are more likely to detach under hindering load rather than to become stalled. Previous work shows that a unique insert in loop L11 of KIF3C plays a role in regulating the run length of KIF3AC such that KIF3AC with the KIF3C loop L11 truncated to the length observed in KIF3B (KIF3ACΔL11) is more processive than native KIF3AC (14). However, no significant differences in the detachment, maximum, and stall forces or stall percentage between KIF3AC and KIF3ACΔL11 are observed (Table 2 and SI Appendix, Fig. S2). This result suggests that force sensitivity, as measured in this experimental geometry, is not modulated by loop L11.

Fig. 3.

Force traces and detachment forces measured for KIF3 motor dimers. (A, C, E, and G) Sample force ramps produced by each KIF3 dimer stepping against a stationary trap. Force increases as the distance between the bead center and trap center increases. Raw data are plotted in gray and colored overlaid data are filtered with an 11-ms mean filter for visualization. (B, D, F, and H) Respective histograms of detachment forces. Detachment force is defined as the amount of force on the bead immediately prior to detachment, shown as mean ± SD. N values reflect number of force ramps analyzed. (A and B) KIF3AB, (C and D) KIF3AA, (E and F) KIF3CC, and (G and H) KIF3AC.

Table 2.

Measured ramp force parameters for KIF3 motors

Motor	FDetachment, pN	FMaximum, pN	FStall, pN	Stall, %
KIF3AB	3.7 ± 1.4	4.2 ± 1.4	5.2 ± 0.2	10
KIF3AA	3.1 ± 1.0	3.3 ± 1.1	3.8 ± 0.1	13
KIF3CC	1.5 ± 0.4	1.6 ± 0.4	—	—
KIF3AC	1.9 ± 0.5	2.3 ± 0.6	2.6 ± 0.5	14
KIF3ACΔ11	1.9 ± 0.7	2.4 ± 1.2	2.3 ± 0.3	13

Table of detachment, maximum, and stall force and stall percentage for KIF3AB, KIF3AA, KIF3CC, KIF3AC, and KIF3ACΔL11. Displayed values are means ± SD. Maximum force is defined as the largest force value over baseline that occurs between the beginning of the force ramp and the detachment event. The stall force is defined as the mean force over the final 70 ms of an event that comes to a stall, where a stall is defined as a force plateau in which the SD of the force is less than or equal to 5% of the mean force over that window (37). Dashes represent parameters that were not observed. Measured parameters for KIF3AC and KIF3ACΔL11 were compared through an unpaired student’s t test with an α-reliability level of 0.05, and the differences between KIF3AC and KIF3ACΔL11 for F_detach, F_max, and F_stall were not significant (P = 1, 0.36, and 0.10 respectively). Measured detachment forces of KIF3AB, KIF3AA, KIF3AC, and KIF3CC were compared through an unpaired Student’s t test with an α-reliability level of 0.05, and all differences were highly significant (P < 0.0001). Stall % was compared for KIF3AC and KIF3ACΔL11 using the “N − 1” χ² test, and no significant difference was observed (P = 0.81).

KIF3AC Motility Parameters Are Highly Sensitive to Hindering and Assisting External Loads.

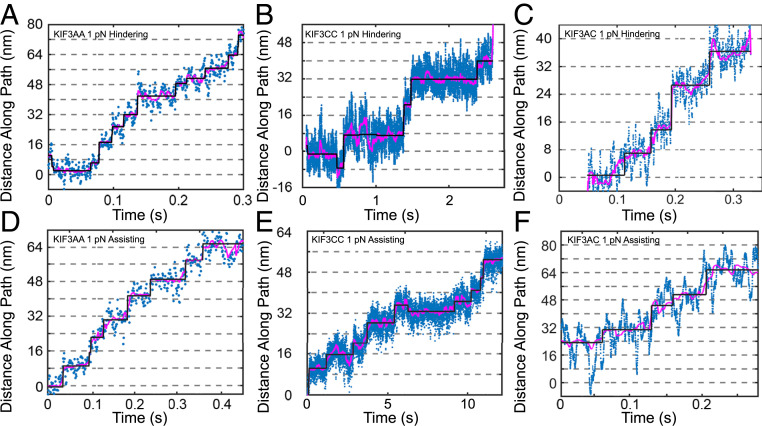
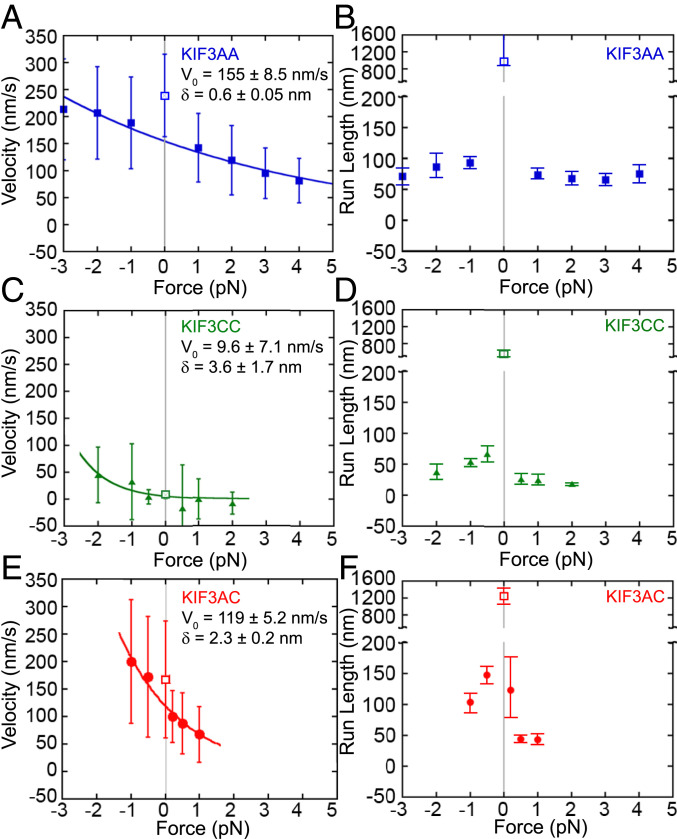
We determined the effect of constant hindering or assisting loads on the velocity, run length, and stepping kinetics of KIF3AA, KIF3CC, and KIF3AC using force feedback in the optical trap (Figs. 4 and 5 and Table 3). KIF3AA steps at an average velocity of 140 ± 64 nm/s under 1-pN hindering load and 190 ± 85 nm/s under 1-pN assisting load (Figs. 4A and 5A and Table 3). It is possible that the difference in velocity observed for KIF3AA under small loads versus in the unloaded iSCAT assays (Fig. 1 A and B) is due to either the difference in attachment strategy or vertical forces developed by contact of the bead with the underlying surface in the optical trap assay (38–40). KIF3AA motility was observed over the range of 2-pN assisting loads to 4-pN hindering external loads, and the change in velocity with force was approximately twofold over this range. This force sensitivity is reflected by the effective distance parameter derived from the fit of the Bell equation $\left(V\left(F\right)=V_0{e}^{\left(\frac{-F\delta }{k_{b}T}\right)}\right)$ (41) to the data, δ = 0.59 ± 0.05 nm (Fig. 5A). The effective distance parameter of KIF3AA represents a relatively weak force dependence for velocity compared to conventional kinesin-1, δ = 3.58 nm, as was reported previously (16). Externally applied 1-pN assisting or hindering loads markedly decrease the average run length of KIF3AA relative to the run length in the absence of external load measured with Qdots (ref. 14, Fig. 5B, and Table 3). In contrast to KIF3AA, KIF3CC motility is nearly stalled under all hindering loads tested (0.5 to 2 pN; Figs. 4B and 5C and Table 3). Assisting loads >1 pN result in faster motility by KIF3CC (Fig. 5C and Table 3). Much like KIF3AA, the KIF3CC run length is decreased >10-fold under both assisting and hindering loads compared to unloaded Qdot results (ref. 14 and unfilled square, Fig. 5D).

Fig. 4.

Stepping traces with constant assisting and hindering loads. Sample traces of the position of the optical trap as it maintained constant 1-pN hindering force on KIF3AA (A), KIF3CC (B), and KIF3AC (C) and as it maintained constant 1-pN assisting force on KIF3AA (D), KIF3CC(E), and KIF3AC (F). The blue points represent the raw data, the magenta line represents filtered data (Methods) and the black line represents the fit of the Kerssemakers’ algorithm to the data (32).

Fig. 5.

Force dependence of velocity and run length measured for KIF3 motors. (A, C, and E) Velocities ± SD versus load for KIF3AA (A), KIF3CC (C), and KIF3AC (E). Negative values on the x axis indicate assisting load, and positive values indicate hindering load. The Bell equation (41) fit to the trapping data are shown by a solid line on each plot: $V\left(F\right)=V_0{e}^{\left(\frac{-F\delta }{k_{b}T}\right)}$, where F is the applied force in piconewtons, V is the velocity, V₀ is the velocity at zero load, δ is the effective distance parameter in nm, and k_bT is the Boltzmann constant times the absolute temperature. A larger distance parameter indicates higher load sensitivity. Parameters in the absence of force, 0 on the x axis, are included from previous Qdot single-molecule studies (14) and shown by an unfilled square with 0 on the x axis highlighted by gray vertical lines. (B, D, and F) Run lengths ± 95% CI versus load for KIF3AA (B), KIF3CC (D), and KIF3AC (F). Negative values on the x axis indicate assisting load, and positive values indicate hindering load.

Table 3.

Measured velocity (Vel) and run length (RL) of KIF3 motors

	1-pN Assisting		Unloaded		1-pN Hindering
Motor	Vel, nm/s	RL, nm	Vel, nm/s	RL, nm	Vel, nm/s	RL, nm
KIF3AA	190 ± 85	93 ± 68	240 ± 76	980 ± 910	140 ± 64	73 ± 62
KIF3CC	41 ± 22	54 ± 54	7.5 ± 6.3	570 ± 470	4.8 ± 16	25 ± 48
KIF3AC	170 ± 110	100 ± 57	170 ± 67	1300 ± 1700	68 ± 50	43 ± 48

Table of measured run lengths and velocities under 1-pN assisting load, unloaded, and 1-pN hindering load conditions at 1 mM MgATP. Displayed values are means ± SD. Unloaded values are included from previous Qdot single-molecule studies at 1 mM MgATP (14).

The KIF3AC velocity load dependence (δ = 1.9 ± 0.4 nm; Fig. 5E) is larger than that of KIF3AA. Under a 1-pN hindering load, KIF3AC moved at a mean velocity of 68 ± 50 nm/s, yet application of a 1-pN assisting load results in an increased mean velocity of 170 ± 110 nm/s (Fig. 4C and Table 3). Similar to KIF3AA and KIF3CC, the run length of KIF3AC is dramatically altered by external loads and decreased ∼10-fold relative to the run length determined in unloaded conditions of the Qdot single-molecule motility assay (ref. 14 and Fig. 5F). While we attempted to observe KIF3AC and KIF3CC motility at higher forces, the data could not be analyzed due to the very short lifetime of motor–MT interaction at high force. Our results show that KIF3AC, KIF3AA, and KIF3CC show similar run length decrease under load (Fig. 5F and Table 3). In contrast, the force dependence of velocity varies significantly among these three motors.

KIF3AC, KIF3AA, and KIF3CC Stepping Kinetics and Step Size Distributions Are Distinct under Hindering or Assisting Loads.

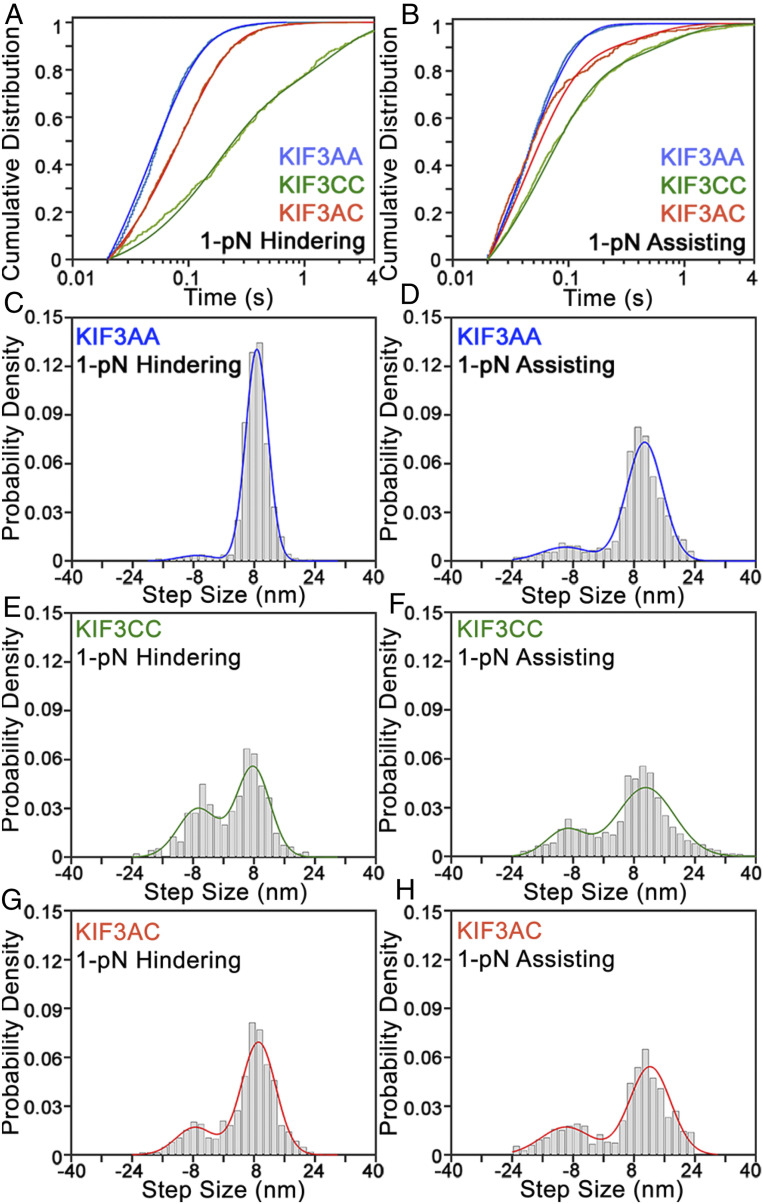
To determine how step sizes and step kinetics are affected by mechanical loads, we performed step-finding analysis on the traces of KIF3AA, KIF3CC, and KIF3AC motility under 1-pN constant hindering or assisting load at 1 mM MgATP (Fig. 4, black overlays). For KIF3AA under a 1-pN hindering load, very few backsteps (A_back = 0.04; Table 4) are observed. Slightly more occur with a 1-pN assisting load (A_back = 0.12; Fig. 6 C and D and Table 4). The distribution of dwell times observed for KIF3AA under 1-pN hindering load was fit by a single exponential function with k₁ = 18 s⁻¹ (Fig. 6A, blue and Table 4). With a 1-pN assisting load, the dwell time distribution of KIF3AA shown in Fig. 6B (blue) was fit by a single exponential function with k₁ = 24 s⁻¹ (Table 4). Given the average step size of KIF3AA near 8 nm, the rates derived from each dwell time distribution for KIF3AA are in agreement with the measured velocities.

Table 4.

Optical trap step kinetics and step displacement fit parameters

			Step kinetics				Step sizes
Motor	[MgATP]	Load, pN	A1	k1, s−1	A2	k2, s−1	Aback	μback, nm	Aforward	μforward, nm
KIF3AA	1 mM	1 pN hindering	1.0	18	—	—	0.04	−7.1 ± 4.8	0.96	8.7 ± 2.9
KIF3AA	1 mM	1 pN assisting	1.0	24	—	—	0.12	−11 ± 6.4	0.88	11 ± 5.5
KIF3CC	1 mM	1 pN hindering	0.61	6.6	0.39	0.6	0.39	−6.7 ± 5.2	0.61	7.8 ± 4.4
KIF3CC	1 mM	1 pN assisting	0.78	18	0.22	2.2	0.20	−9.8 ± 5.1	0.80	11 ± 7.5
KIF3AC	10 μM	1 pN hindering	1.0	5.9	—	—	0.35	−5.0 ± 7.2	0.65	7.8 ± 2.9
KIF3AC	1 mM	1 pN hindering	0.96	11	0.04	2.4	0.21	−7.4 ± 5.0	0.79	9.2 ± 4.5
KIF3AC	1 mM	1 pN assisting	0.88	24	0.12	2.7	0.27	−9.4 ± 7.4	0.73	11 ± 7.3

Dwell time distributions were fit by either a single exponential function or the sum of two exponential functions to determine step kinetics. Single exponential fit equation: $y=k_{\mathit{1}}{e}^{-k_{\mathit{1}}t}$ and sum of two exponential functions fit equation: $y=A{k}_{\mathit{1}}{e}^{-k_{\mathit{1}}t}+\left(1-A\right)k_{\mathit{2}}{e}^{-k_{\mathit{2}}t}$, where the amplitude A is reported as A₁ and (1 – A) is reported as A₂. Amplitude and rate parameters are shown. Justification of a second exponential was determined by the log-likelihood ratio test. For KIF3CC, P < 1 × 10⁻¹⁶ at 1-pN hindering load, and P < 1 × 10⁻¹⁶ at 1-pN assisting load. For KIF3AC, P < 1 × 10⁻¹⁶ at 1-pN hindering load, and P < 1 × 10⁻¹⁶ at 1-pN assisting load. Step-size distributions were fit by the sum of two Gaussian distributions. Relative amplitudes are reported; step sizes are reported as means ± σ of the fit curve, where σ indicates the width of Gaussian peak and not uncertainty in peak position.

Fig. 6.

Step sizes and dwell time distributions derived from constant force stepping traces. (A) CDF plot of dwell times for KIF3AA (blue, N_steps = 1,783), KIF3CC (green, N_steps = 502), and KIF3AC (red, N_steps = 1,271) measured under a 1-pN hindering load. Lighter-colored data are plotted with a darker fit line. (B) CDF plot of dwell times for KIF3AA (blue, N_steps = 2,820), KIF3CC (green, N_steps = 1,480), and KIF3AC (red, N_steps = 845) measured under a 1-pN assisting load. Dwell time distributions are fitted to a single exponential function (KIF3AA) or the sum of two exponential functions (KIF3CC, KIF3AC) as justified by the log-likelihood ratio test. Step-size histograms are shown for 1-pN hindering or assisting load for KIF3AA (C and D), KIF3CC (E and F), and KIF3AC (G and H). Negative step sizes indicate backsteps toward the MT-minus end, and positive step sizes indicate forward steps toward the MT-plus end. Step size distributions are fit by the sum of two Gaussian distributions.

In contrast to KIF3AA, KIF3CC at 1-pN hindering load exhibits many backward steps. The step size distribution has peaks centered at both 7.8 ± 4.4 nm (A_forward = 0.61) and −6.7 ± 5.2 nm (A_back = 0.39) (Fig. 6 E and F and Table 4). The proportion of backsteps taken by KIF3CC under hindering load (A_back = 0.39) is greater than that observed under assisting load (A_back = 0.20) or in the absence of load (A_back = 0.18; Table 1). The sum of two exponential functions provides the best fit to the cumulative distribution of dwell times observed for KIF3CC under 1-pN hindering and assisting load (Fig. 6 A and B). Under hindering load, the KIF3CC dwell time distribution shows a fast rate k₁ = 6.6 s⁻¹ (A₁ = 0.61), and a second slow rate, k₂ = 0.6 s⁻¹ (A₂ = 0.39). In contrast, at 1-pN assisting load, these rates accelerate to k₁ = 18 s⁻¹ (A₁ = 0.78) and k₂ = 2.2 s⁻¹ (A₂ = 0.22). In both cases, these rates are much slower than those observed for KIF3AA.

The step size distribution observed for KIF3AC at 1 mM MgATP (Fig. 6 G and H) reveals a prominent component centered near 8 nm (9.2 ± 4.5 nm, A_forward = 0.79) under 1-pN hindering load and more abundant backsteps than observed in the absence of load (A_back = 0.21; Fig. 6 G and H and Table 4). Step sizes observed for KIF3AC are similar under 1-pN assisting load and 1-pN hindering load. The cumulative distribution of dwell times for KIF3AC under 1-pN hindering and assisting loads are shown in red (Fig. 6 A and B, respectively). Under a 1-pN hindering or assisting load, the dwell time distribution for KIF3AC is best fit by the sum of two exponential functions, based on the log-likelihood ratio test (33), with the majority of the dwell times associated with the faster rate. A rate of k₁ = 11 s⁻¹ (A₁ = 0.96; Table 4 and SI Appendix) describes KIF3AC stepping under a 1-pN hindering load, and k₁ = 24 s⁻¹ (A₁ = 0.88) describes KIF3AC stepping with a 1-pN assisting load. To confirm these results, we performed step-finding analysis on these data using a different step detection algorithm (34) and observed similar results (SI Appendix, Fig. S6). As was observed in the absence of load, KIF3AA steps with the fastest kinetics while KIF3CC steps more slowly, and KIF3AC is intermediate to KIF3AA and KIF3CC.

KIF3AC motility at 10 μM MgATP under a 1-pN hindering load was also observed (SI Appendix, Fig. S3A). The step size distribution reveals primarily 8-nm forward steps (7.8 ± 2.9 nm, A_forward = 0.65) with an additional population of backsteps (−5.0 ± 7.2 nm, A_back = 0.35) which is more prominent than that observed at 1 mM MgATP or in the absence of load (SI Appendix, Fig. S3B and Tables 1 and 4). As was observed in zero-load experiments, backsteps under load are typically single isolated step events. The cumulative distribution of dwell times at 10 μM MgATP is adequately fit by a single exponential function with a rate constant k₁ = 5.9 s⁻¹ (SI Appendix, Fig. S3C), which is consistent with the expected rate of ATP binding based on transient kinetic experiments (17). KIF3AC does not show evidence for asymmetric stepping kinetics as would be expected from alternating fast and slow steps by the KIF3A and KIF3C heads. The relative frequency of backsteps varies between different motors at the MgATP concentrations tested.

Mixed Motor MT Gliding Assays Recapitulate Unloaded KIF3AC Velocity.

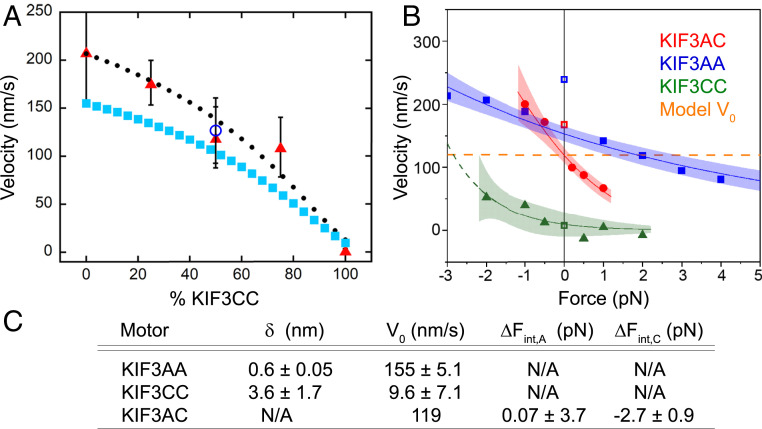
To determine if KIF3A and KIF3C motors can impact each other’s motility independently of heterodimerization, we performed MT gliding assays with mixtures of KIF3AA and KIF3CC. Assays were performed with combinations of motors that ranged between 100% KIF3AA and 100% KIF3CC, keeping total motor concentration constant (Fig. 7A). KIF3AA alone propels MTs at a velocity of 210 ± 55 nm/s, and KIF3CC supports gliding at 1.9 ± 1.6 nm/s (Fig. 7A and SI Appendix, Fig. S5). Strikingly, the speed of MT gliding powered by an equal mixture of KIF3AA and KIF3CC is 120 ± 2.0 nm/s (Fig. 7A and SI Appendix, Fig. S5C), which is not significantly different from the gliding velocity of KIF3AC (126.4 ± 34.3 nm/s; P = 0.2037, unpaired Student’s t test). An equal mixture of KIF3AA and KIF3CC in the gliding filament assay might simulate the internal strains in KIF3AC to some extent. This is borne out by considering the strain-dependent acceleration of KIF3CC and the strain-dependent slowing of KIF3AA (Fig. 5 A and C). Strikingly, the optical trap data for KIF3AC intersect the zero-force axis at the very similar velocity of 119 nm/s (Fig. 5E). These results strongly suggest that mixtures of KIF3AA and KIF3CC homodimers mechanically impact each other’s motility in a way that reproduces the motile behavior of the KIF3AC heterodimer. The faster KIF3AA motor slows due to a hindering load imposed by the slower KIF3CC motor, while the velocity of KIF3CC increases due to the assisting load of KIF3AA. Strikingly, the relationship between MT gliding rate and motor ratio can be modeled directly (Fig. 7A) using the force-dependent parameters obtained from optical trapping results (Fig. 5 and SI Appendix). Thus, the intramolecular strain and the force dependence of the two motors may explain the motile behavior of the KIF3AC heterodimer.

Fig. 7.

The unloaded velocity of KIF3AC is predicted by the force dependence of KIF3AA and KIF3CC velocities and recapitulated by MT gliding by mixtures of KIF3AA and KIF3CC. (A) Plot of MT velocity in a gliding filament assay versus percentage of KIF3CC observed for mixtures of KIF3AA and KIF3CC (red triangles) ± SD. The gliding velocity observed for KIF3AC alone is shown (unfilled blue circle) ± SD. The solid cyan squares represent the hypothetical predicted MT gliding velocity of any mixture of KIF3AA and KIF3CC based on the measured force dependence of the KIF3AA and KIF3CC homodimers in single-bead optical trapping assays (SI Appendix, Eq. S5), and the solid black circles show the predicted line multiplied by 1.3 to better align with the data. (B) Plot of velocity versus force with overlaid Bell equation fits for KIF3AA (blue) and KIF3CC (green). The red curve represents the fit of Eq. 1 to the KIF3AC data and the horizontal line (orange, dashed) intersects with the KIF3AC curve at zero force and crosses the KIF3AA and KIF3CC curves at ∼ ΔF_{A int} and ΔF_{C int} within the corresponding error, respectively. Shaded areas represent the 95% CI of the fits. (C) Parameters derived from the fit of the force dependence of velocity data for KIF3AC, KIF3AA, and KIF3CC.

Force Dependence of KIF3AC Velocity Can Be Modeled from the Force Dependence of KIF3AA and KIF3CC Velocity.

To test if the force velocity of KIF3AC can be inferred from the Bell equation fit parameters for the force velocity of KIF3AA and KIF3CC (Fig. 5 A and C) we derived an equation to predict the force-velocity data for KIF3AC. In the absence of external force, the two heads of a kinesin dimer experience internal strain during stepping. We propose that the A and C heads experience different internal strains within a dimer depending on their dimerization partner. If ΔF_{A int} represents the change in internal strain that KIF3A experiences within KIF3AC relative to KIF3AA and ΔF_{C int} represents the change in internal strain that KIF3C experiences within KIF3AC relative to KIF3CC, the force dependence of the velocity of KIF3AC is expected to be (for derivation see SI Appendix, Supplementary Methods)

$$V_{AC}\left(F\right)=2/\left\{{\left(V_{0A}\right)}^{-1}\exp \left[\frac{\left(F+\mathrm{\Delta }{F}_{Aint}\right){\delta }_A}{k_{b}T}\right]+{\left(V_{0C}\right)}^{-1}\text{exp}\left[\frac{\left(F+\mathrm{\Delta }{F}_{Cint}\right){\delta }_C}{k_{b}T}\right]\right\}.$$ [1]

The unloaded velocities V_0A and V_0C as well as the corresponding distance parameters δ_A and δ_C of KIF3AA and KIF3CC, respectively, are obtained from the Bell equation fits to the KIF3AA and KIF3CC data (Fig. 5 A and C). The two free parameters, ΔF_{A int} and ΔF_{C int} (SI Appendix), represent the predicted change in internal strain experienced by KIF3A and KIF3C in KIF3AC relative to their respective homodimers. The positive ΔF_{A int} indicates that KIF3A experiences a hindering change in strain, while the negative ΔF_{C int} indicates that KIF3C experiences an assisting change in strain. The modeled zero-force velocity of KIF3AC (V = V_0AC = 119 nm/s; orange line in Fig. 7B) crosses the force–velocity curves of KIF3AA and KIF3CC, at ∼1.7 pN (ΔF_{A int}) and ∼ −2.8 pN (ΔF_{C int}), respectively, within the error of the predicted change in internal strain experienced by KIF3A and KIF3C in KIF3AC.

Furthermore, one can estimate the predicted step kinetics of the individual heads under load by solving for the expected velocity and dividing by the step size, d, of each at any given load, (SI Appendix, Eqs. S10 and S11) and the fitted values of ΔF_{A int} and ΔF_{C int}. Assuming a constant step size of d = 8 nm, under a 1-pN assisting load we expect steps by KIF3A to occur at 22 ± 12 s⁻¹ and steps by KIF3C at 30 ± 22 s⁻¹. Under a 1-pN hindering load, our model predicts steps by KIF3A at 17 ± 9.0 s⁻¹ and steps by KIF3C at 5.4 ± 4.0 s⁻¹. Accounting for the uncertainty in these predictions, we would not expect to resolve the different stepping rates of KIF3A and KIF3C in KIF3AC under a 1-pN hindering load. However, it is possible that asymmetric stepping might be resolved if there was less experimental noise.

Discussion

KIF3AC Steps at a Rate that Is Distinct from KIF3AA or KIF3CC.

How fast would KIFAC be expected to move if the two heads operated with the kinetics of their respective homodimers? With velocities of 270 and 7.3 nm/s for KIF3AA and KIF3CC, respectfully, the average dwell times between 8-nm steps are (d/v =) 0.029 s and 1.1 s. The KIF3AC velocity predicted by the simplest scheme of half slow and half fast steps would be v = 2*(d nm)/(0.029 s + 1.1 s) = 15 nm/s. At 110 nm/s, KIF3AC clearly processively steps much faster than this predicted rate. Therefore, we argue that the unloaded kinetic properties of KIF3AC are the result of heterodimerization, which appears to impact the properties of the motor domains in a way that is different from homodimerization.

A key finding of this study is that a dominant stepping rate (11 s⁻¹) was observed for KIF3AC at 1 mM MgATP that is distinct from the stepping of KIF3AA (>30 s⁻¹) and KIF3CC (<1.5 s⁻¹) under identical conditions. The distribution of KIF3AC step durations is not a linear combination of fast KIF3AA and slow KIF3CC step durations, which would be clearly resolved in our experiments (Fig. 2A). Previous work in which dimers were constructed with nonidentical motors showed the alternating stepping rates expected from the alternating head kinetics (42). Even homodimeric kinesins have been reported to limp with alternating long and short dwell times before each step (43, 44). Thus, it was surprising that we did not observe alternating dwell times with KIF3AC. The high acceleration of the KIF3C head and only moderate deceleration of the KIF3A head in the KIF3AC dimer suggests kinetic tuning of the two heads, which we argue is explained by the strain dependence of velocity of the individual heads. We favor a model in which, when the KIF3C head is in the lead position, the rear KIF3A head feels a decreased forward strain and thus detaches from the MT more slowly than in KIF3AA. Conversely, when the KIF3C head is in the rear position, it feels an increased forward strain and detaches from the MT more rapidly than in KIF3CC.

KIF3C Can Be Activated by an Assisting Load or KIF3A.

Although KIF3CC is an exceptionally slow motor in the absence of external force with little net plus-end movement under hindering loads, its stepping rate increases substantially with assisting loads (Fig. 6B). Notably, MT gliding in the presence of KIFCC is activated by the faster motor, KIF3AA (Fig. 7A), such that equal densities of KIF3CC and KIF3AA power gliding at a rate similar to KIF3AC. This result is similar to the intermediate speed observed with half-and-half mixtures of two Caenorhabditis elegans intraflagellar transport kinesins with threefold different velocities (45). In contrast, gliding filament assays with mixtures of various combinations of myosin-II molecules with different velocities tended to be dominated by slower myosins (46, 47).

The shape of the MT gliding velocity curve as a function of the percent of KIF3CC is well modeled by assuming that forces proportional to the respective motor densities are assisting and hindering KIF3CC and KIF3AA, respectively, and the kinetics of the motors are affected with the force-dependent parameters determined by optical trapping (Fig. 7A and Methods). The rates predicted from the trap data are slightly slower than experimentally observed in gliding assays, which may be due to geometric differences between the two studies (40). Notably, based on the force-dependent fits from the optical trapping experiments, an assisting load of ∼2.8 pN on KIF3CC is predicted to have the same speed as unloaded KIF3AC (119 nm/s), which is the same speed as KIF3AA under ∼1.7 pN hindering load (Fig. 7B). While the Bell equation fit to the KIF3AC data predicts that KIF3AC can be accelerated beyond the observed stepping rates of even KIF3AA with a large assisting load, this could not be confirmed experimentally. Thus, our favored model is that the major effect of heterodimerization is the acceleration of KIF3C and slowing of KIF3A resulting in the observed speed. In support of this argument, the KIF3AC force–velocity curve is well fit by a model which uses the V_o and δ of KIF3AA and KIF3CC and only two free parameters which describe the change in interhead strain experienced by KIF3A and KIF3C in KIF3AC relative to KIF3AA and KIF3CC (Fig. 7 B and C). Based on these results, we argue that the properties of KIF3AC are not likely due to “emergent” properties of the individual motor domains upon dimerization but can be explained by differential mechanical constraints on the heads in the homo- and heterodimers.

KIF3CC May Have Insufficient Internal Strain to Activate Efficient Stepping.

Intramolecular strain is a key component of motor–motor communication which enables high processivity and rapid stepping in kinesin dimers (48–52). Thus, we propose that intramolecular strain in the KIF3CC homodimer is insufficient to fully activate the stepping rate, and inclusion of KIF3A in the dimer generates the strain necessary to activate KIF3C to step more quickly. Indeed, the observed stepping kinetics of KIF3CC relative to KIF3AC mirror previous work showing that lengthening the neck linker of kinesin-1 reduced the stepping velocity, yet assisting load could recover the velocity to the wild-type value (48). Furthermore, the force–velocity curve of KIF3AC is well fit by a model in which KIF3C experiences a large increase in interhead strain relative to that experienced in KIF3CC relative to that experienced in KIF3AC (Fig. 7 B and C). Higher interhead compliance also increased the probability of backstepping of kinesin-1 (48), which is observed with our motor dimers that contain KIF3C (Figs. 2C and 6 E and F and Tables 1 and 4).

Intramolecular strain is transmitted via the neck linkers in kinesin motors, yet the neck-linker domains of KIF3A and KIF3C are the same length (53). However, differences in the interactions between the neck linker and the motor domains, possibly via differences in their cover-strand sequences (54, 55), result in stronger or weaker head–head coupling and ultimately affect ATPase kinetics (48–50, 56). When stepping against a stationary trap, KIF3CC detached at the lowest average force, KIF3AC detached at a higher average force while KIF3AA maintained the highest average force of the three. A previous study showed that decreasing intramolecular strain also caused kinesin-1 to detach or stall at lower forces than wild type (48). This observation supports the argument that low interhead strain can explain the relatively low detachment force and velocity of KIF3CC. The apparent higher level of noise in stepping traces recorded for KIF3CC may also reflect the higher compliance of this molecule during stepping. Reduced intramolecular strain may result in ungated detachment of the rearward head from the two-head-bound state. Such a motor would then be highly prone to detachment or stalling under hindering load.

Biological Advantage of Heterodimerization.

Mechanically, our results suggest that heterodimerization is a way to tune the performance of these molecular motors such that they are suited to a specific cellular task. A recent study suggested that scaling of total force generation with the number of motors may happen more efficiently for kinesin-2 motors than in other kinesin subfamilies, suggesting that these motors may be adapted to drive transport in larger teams (57). The high probability of KIF3AC detachment from the MT under load along with the fast MT association kinetics of KIF3AC (4, 17, 18) would enable KIF3AC to navigate obstacles on the MT effectively (58) or transport cargo more efficiently in larger ensembles (59–61). Alternatively, the high probability of KIF3AC detachment from the MT under load may be an adaptation for cooperative transport with other faster motors as observed for KIF3AB-KAP and KIF17 (19). It is also possible that heterodimerization of tail domains is important for recruitment of specific cellular cargos. However, further cell biological experiments are required to resolve this issue.

Methods

KIF3 motor constructs were expressed and purified as published previously (14). iSCAT, MT gliding (14), and optical trap motility assays were performed using standard motility assay conditions (see SI Appendix for details regarding assay conditions, instrumentation, and data collection). Kerssemakers’ algorithm was used to identify and fit steps in the data traces (32) as well as the tDetector algorithm to confirm results for KIF3AC (34). Dwell time data were fit using maximum likelihood estimation in MEMLET (33) either to a single exponential function,

$$y=k_{\mathit{1}}{e}^{\left(-k_{\mathit{1}}t\right)},$$ [2]

or to the sum of two exponential functions:

$$y=A{k}_{\mathit{1}}{e}^{\left(-k_{\mathit{1}}t\right)}+\left(1-A\right)k_{\mathit{2}}{e}^{\left(-k_{\mathit{2}}t\right)},$$ [3]

where A is the relative amplitude of the first component and (1 – A) is reported in the text as A₂ but is not an independently fit variable. The dead time function in MEMLET was used to account for events that may not have been observed due to instrumental limitations. The hypothetical KIF3AA + KIF3CC dwell time CDF (Fig. 2A) was calculated by taking 0.5 times the fit to the KIF3AA dwell time cumulative distribution function plus 0.5 times the fit to the KIF3CC dwell time CDF. Step size data were fit using maximum likelihood estimation in the MEMLET software (33). Step size distributions derived from iSCAT experiments were fit as follows. Forward and backward steps were fit independently. A single Gaussian distribution was fit to the backward steps, and the sum of two Gaussian distributions to the forward steps, as justified by the log-likelihood ratio test. Step size distributions from optical trapping assays were fit by the sum of two Gaussian distributions. Step size data are reported as the mean ± σ of the fit curve, and σ describes the width of the Gaussian peak and not uncertainty in the peak position. Normalized step size histograms were plotted as probability density, and dwell time data were plotted as cumulative distributions (see SI Appendix for details). The Bell equation was fit to velocity versus force data (41):

$$V\left(F\right)=V_0{e}^{\left(\frac{-F\delta }{k_{b}T}\right)},$$ [4]

with T based on the assay temperature, 20 ± 1 °C, V₀ is the unloaded velocity based on the fit, and the effective distance parameter δ defines the force sensitivity. In order for this form of the Bell equation to be valid, a constant average step size is assumed. The StatPlus plugin for Microsoft Excel (AnalystSoft Inc.) was used for statistical analysis for detachment, maximum, and comparison of stall forces was performed using an unpaired Student’s t test with an α-reliability level of 0.05, and statistical analysis of stall percentage was performed using the “N − 1” χ² test with an α-reliability level of 0.05 (Table 2). Nonlinear curve fitting and the corresponding 95% confidence intervals in Fig. 7B were calculated using OriginPro 2018b (OriginLab Corp.).

Data Availability Statement.

Readers will be able to access the data, associated protocols, code, and materials in the paper by contacting the corresponding authors.