Population inversion X-ray laser oscillator

Significance

An X-ray oscillator generating fully coherent pulses at the characteristic length and time scale of atomic and molecular phenomena, angstrom wavelength, and femtosecond time duration has been a dream of laser physics from the 1960s. The paper presents a study of an X-ray oscillator based on population inversion of $K\alpha$ electrons in a transition-metal compound, generating fully coherent, transform-limited, high-power radiation pulses, in the 3- to <1-Å wavelength region, with a high-energy resolution, about 0.05 eV, showing that the dream can now become a reality. The X-ray laser oscillator will open experimental possibilities and research areas in quantum optics, chemical dynamics, imaging, spectroscopy, and interferometric measurements.

Abstract

Oscillators are at the heart of optical lasers, providing stable, transform-limited pulses. Until now, laser oscillators have been available only in the infrared to visible and near-ultraviolet (UV) spectral region. In this paper, we present a study of an oscillator operating in the 5- to 12-keV photon-energy range. We show that, using the $K{\alpha }_1$ line of transition metal compounds as the gain medium, an X-ray free-electron laser as a periodic pump, and a Bragg crystal optical cavity, it is possible to build X-ray oscillators producing intense, fully coherent, transform-limited pulses. As an example, we consider the case of a copper nitrate gain medium generating $\sim$ 5 × ${\mathrm{10}}^{10}$ photons per pulse with 37-fs pulse length and 48-meV spectral resolution at 8-keV photon energy. Our theoretical study and simulation of this system show that, because of the very large gain per pass, the oscillator saturates and reaches full coherence in four to six optical-cavity transits. We discuss the feasibility and design of the X-ray optical cavity and other parts of the oscillator needed for its realization, opening the way to extend X-ray–based research beyond current capabilities.

Since the time Maiman built the first ruby laser in 1960, developing an X-ray laser has been a major goal in laser physics. A laser generating high-intensity, coherent X-ray pulses at angstrom wavelength and femtosecond pulse duration—the characteristic time and length scale for atomic and molecular phenomena—allows imaging of periodic and nonperiodic systems, noncrystalline states, studies of dynamical processes in systems far from equilibrium, nonlinear interactions, and X-ray quantum optics, opening a window into electronic, atomic, and molecular phenomena of interest to biology, chemistry, materials science, and physics (1).

In the atom-based population-inversion laser approach, this task was extremely difficult, because of the very short lifetime of excited atom-core quantum-energy levels, as pointed out initially by Schawlow and Townes (2). Chapline and Wood of Lawrence Livermore National Laboratory (LLNL) estimated that the radiative lifetime of an X-ray laser transition would be about 1 fs times the square of the wavelength in angstroms (3). The short lifetime and large energy needed to excite inner-shell atomic levels, 1 to 10 keV compared to about 1 eV for visible lasers, requires very large pumping power to attain population inversion. No pump available at that time could generate the required power. It has been reported that LLNL scientists used a nuclear device to pump an X-ray laser in the 1980s (4). The development of high-peak-power, short-pulse, visible-light lasers made possible another approach: pumping cylindrical plasmas, in some cases also confining the plasma with magnetic fields. X-rays from the hot plasma pumped the laser. These experiments led to X-ray lasing around 18 nm with gain of about 100 in 1985 (5, 6). More work has been done from that time, and lasing has been demonstrated at several wavelengths in the soft X-ray region, however, with limited peak power and tunability. A review of the most recent work and developments with this approach is given in ref. 7.

X-ray free-electron lasers (XFELs), first proposed in 1992 (8, 9) and developed from the late 1990s to today (10), are a revolutionary tool to explore matter at the atomic length and time scale, with high peak power, transverse coherence, femtosecond pulse duration, and nanometer to angstrom wavelength range, but with limited longitudinal coherence and a photon energy spread of the order of 0.1% (11). They have also been shown to be a very effective pump for creating population inversion in an atomic gain medium, because of the high peak power at the required photon energy. This capability has been demonstrated in experiments of amplified spontaneous emission (ASE) in a Ne gas (12), Cu metal foils (13), and, recently, Mn solutions (14). An intense pump pulse creates a 1-s core hole, and spontaneously emitted $K{\alpha }_1$ fluorescence photons along the direction of the population inversion are amplified. Large values of gain (up to $2\times 10^6$) were observed, and $K{\alpha }_1$ ASE pulses of up to $8\times 10^7$ photons per pulse were generated starting from noise (14). However, ASE pulses typically have a large energy bandwidth and are not transform limited.

Most XFELs operate also in ASE, or self-amplified spontaneous emission (SASE), as it is called in the XFEL community. In SASE mode (15, 16), the X-ray pulse starts from electron shot noise. To improve longitudinal coherence and fluctuations, seeding with external lasers has been successfully implemented for wavelengths larger than a few nanometers (17–22). For harder X-rays, self-seeding systems have been employed to reduce the energy bandwidth by an order of magnitude, e.g., at Linac Coherent Light Source (LCLS) from about $10^{-3}$ to $10^{-4}$, but the pulses are not transform limited and suffer from large intensity fluctuations (23–31). To produce transform-limited free-electron laser (FEL) pulses, one can reduce the pulse duration down to a single coherent SASE spike, making the electron bunch length shorter than the cooperation length (32). The use of emittance spoilers (33–35), the combination of fresh-slice, cascaded amplification (36, 37), nonlinear compression schemes (38), and recently enhanced SASE (39) have succeeded in producing such pulses. However, in these schemes, the coherence is achieved by decreasing the pulse duration below 1 fs, resulting in a large bandwidth and lower photon flux compared to self-seeded modes, as well as large shot-to-shot fluctuation. To drastically increase the photon flux, a double-bunch FEL scheme at LCLS has been investigated (40–42). To generate fully coherent hard X-ray pulses, an X-ray FEL oscillator (XFELO) (43–48) has been proposed. Since the lasing medium is an electron bunch in a typically 100-m-long undulator, XFELO requires a few-hundred-meters-long diamond Bragg crystal cavity wrapped around the undulator. Mechanical stability, radiation focusing, temporal-transverse beam overlap in the cavity, and crystal alignment angular tolerances, of the order of 10 nrad, are important technical issues. If these technical challenges are met, XFELO could operate with a high-repetition-rate, temporally equispaced set of long electron bunches, achieving ultra-narrow bandwidth and very large average brightness at hard X-rays. In this paper, we investigate and propose an alternative route to generate fully coherent transform-limited X-ray pulses.

X-Ray Laser Oscillator

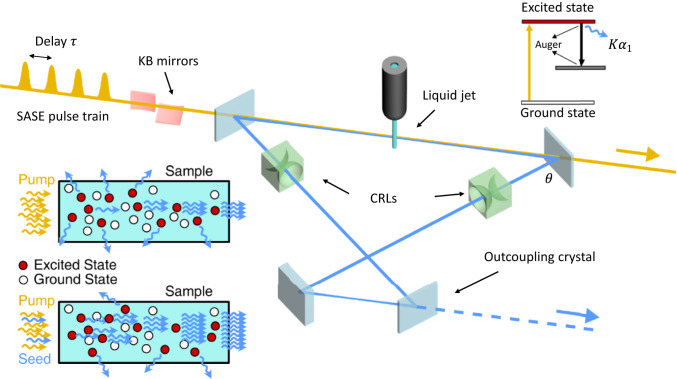
The X-ray laser oscillator (XLO) system described here and shown in Fig. 1 starts with a SASE pump pulse that creates a 1-s core hole population inversion followed by ASE in a liquid jet. To study the physics of the system, we consider, as an example, a lasing medium formed by a jet of concentrated cupric nitrate [Cu(${\mathrm{N}\mathrm{O}}_3$${)}_2$] solution, with 4.2 Cu atoms per cubic nanometer. We have chosen a cupric nitrate solution as a gain medium because the copper $K{\alpha }_1$ photon energy at 8 keV is widely used in X-ray science. Furthermore, cupric nitrate is soluble in high concentrations, does not contain any heavy elements that would reduce the gain by absorbing 8-keV photons, and is straightforward to handle. It is important to note that our results for copper apply, with only minor changes, to other elements, providing a lasing range of 5 to 12 keV. After the ASE gain in the first pass, the $K{\alpha }_1$ signal was recirculated through the cavity and matched with the arrival of subsequent XFEL pulses. This created seeded stimulated emission in each subsequent pass, including losses in the cavity.

Fig. 1.

XLO schematics. A train of SASE pump pulses with spacing $\tau$ passes through a semitransparent crystal and impinges on a liquid jet sample, creating population inversion. The first pulse generates ASE of the $K{\alpha }_1$ line, which is recirculated through a cavity with a roundtrip time that matches $\tau$, seeding the stimulated emission in the subsequent passes. When saturation is reached after four to eight passes, the XLO pulse is outcoupled by rapidly switching the outcoupling crystal into an off-Bragg condition. Note that in the figure, the separation between X-ray pump pulses and the cavity size is not to scale. The energy diagram for population inversion (top right) and principles of ASE (middle left) and seeded stimulated emission (bottom left) are shown.

To analyze the XLO performance, we first considered the amplification process in the lasing medium. The emission from the population-inverted medium was calculated by using a correlation-function approach (49, 50). We used the XATOM software (51–54) to evaluate the photoionization cross-section of the copper atom 1-s level and the Auger decay time to be 0.0324 Mb and 0.823 fs. The evolution of atomic populations was computed, in a one-dimensional (1D) model approximation, via a two-point correlation function of the atomic coherence and two-time correlation function of fields. At the initial stage of emission, the spontaneously emitted radiation triggered the amplification process. During the propagation through the population-inverted medium, radiation was amplified, and the contribution of spontaneous emission became negligible compared to amplified stimulated emission. At this point, the field correlation function can be factorized into classical field amplitudes. Corresponding equations (after neglecting contributions of spontaneous emission) became equivalent to well-known Maxwell–Bloch equations. We then propagated the obtained field through the Bragg crystal-cavity elements and used it as a seed for the following rounds of amplification. We used the same approach for solving the Maxwell–Bloch equations in the subsequent cavity passes. Starting from the second pass, the spontaneous $K{\alpha }_1$ emission along the gain medium was much weaker than the stimulated emission. This approach has been used to simulate the experimentally observed ASE in Ne and Mn (12, 14).

The calculation of the X-ray pulse evolution during the multiple cavity transits requires choosing and optimizing a number of parameters: 1) pumping-pulse power density, duration, and focusing; and 2) lasing-medium geometry. The pumping-radiation Rayleigh length must be larger than the lasing-medium length to obtain a uniform pumping power through the medium. The pulse duration must be near to the value defined by the time-bandwidth product for a transform-limited pulse. It is important to realize that in a system like XLO, the pumping pulse is traveling through the gain medium at the speed of light, and the population-inversion decay time, about 1 fs, is much shorter than the pump-pulse duration. Hence, the population inversion changes as a function of time and position along the lasing medium. Following the pump pulse, as it travels through the gain medium, the stimulated emission of photons is almost instantaneous, and the amplified pulse length is mostly defined by the pump-pulse duration. In our studies, we have optimized the choice of parameters to obtain the largest possible population inversion and number of photons in the output X-ray pulse. Once saturation was achieved after four to eight round trips, the pulse was outcoupled from the cavity. The numerical results will be discussed in a later section.

X-Ray Cavity Design.

The XLO Bragg cavity length $C_l$ can range from 50 cm to a few meters, to match the value of SASE train separation $\tau$ from 1.7 to 10 ns. The cavity length $C_l$ and lateral size $h$ are related to the upper and lower crystals separation $L$, $M$, and Bragg angle $\theta$ by: $\left(L+M\right)=C_l/\left(1-1/\cos 2\theta \right)$ and $h=-\frac{1}{2}\left(L+M\right)\tan 2\theta$, where $C_l=c\tau$. The optimal size is a compromise between ensuring sufficient time to replace the lasing medium between subsequent pulses in the train and guaranteeing sufficient mechanical/temperature stability of the cavity. The resulting X-ray laser pulses were highly monochromatic (as defined by the Bragg optics in the cavity) and transform-limited and provided one-order-of-magnitude higher pulse energy with significantly enhanced stability compared to monochromatized SASE pulses. While the tunability is limited to the width of the emission line (3 to 5 eV for $K{\alpha }_1$ lines in the 5- to 12-keV range), such XLOs can be built for various discrete energies by using different emission lines that match the desired experimental parameters. The unprecedented pulse quality resulting from this approach will improve many X-ray experiments (46).

Kirkpatrick–Baez (KB) mirrors, upstream of the XLO, can be used to effectively pump the lasing medium, as employed in the LCLS Mn ASE experiments (14). Such a setup exists at the LCLS coherent X-ray imaging instrument, and similar systems are available at the SPring-8 Angstrom Compact Free-Electron Laser BL3 and European XFEL Serial Femtosecond Crystallography beamlines. For the wavelength considered in this study, silicon and diamond are optimal choices for the cavity optics. The characteristics of these two crystals for various diffraction planes, matching the Cu $K{\alpha }_1$ emission line, are given in Table 1 and were calculated with dynamical diffraction code XOP (55). The ASE beam divergence depends on the aspect ratio of beam size and gain length and is of order 1 mrad, well above the Si crystal angular acceptance for good reflectivity. The cavity losses are determined by the ratio of crystal angular and energy acceptance versus beam divergence and energy spread exiting the gain medium. Hence, on the first pass, the cavity losses were large, about 99.7%, and needed to be overcompensated by a large XLO laser gain ($10^4$). In the following passes, the losses will be much smaller since the angular spread of the amplified photons matches the crystal acceptance.

Table 1.

Silicon and diamond crystal parameters for 8,048-eV photons in different Bragg reflection geometries

(hkl)	${\theta }_B$, deg	$\mathrm{\Delta }\theta$, $\mu$rad	$\mathrm{\Delta }\omega$, meV	$\mathrm{\Delta }\omega /\omega \times 10^{-6}$	$\tau$, fs
Silicon
333	47.5	10.3	76.0	9.4	23.7
533	68.5	12.5	39.6	5.0	45.5
444	79.3	31.6	48.1	6.0	37.4
Diamond
311	45.7	9.6	75.4	9.4	23.9
400	59.8	14.0	65.6	8.1	27.4
331	70.3	13.0	37.4	4.7	48.1

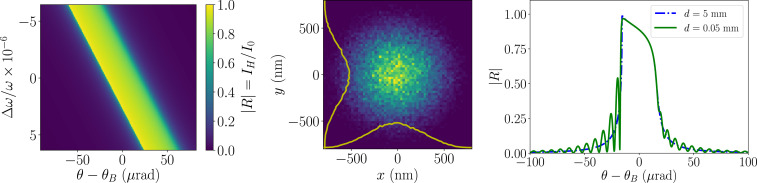
Photons were recirculated by using a tunable four-bounce bowtie $\left(+--+\right)$ Bragg crystal cavity (56), as shown in Fig. 1. Its optical properties are graphed in Fig. 2. The bowtie cavity was tuned to ensure the exact spectral alignment of the Cu $K{\alpha }_1$ peak wavelength with the Bragg reflection angle and temporal alignment with the pulse-train separation $\tau$. The first crystal (upper left) is thin and highly transparent for the incident pump pulse at 9 keV, yet highly reflective at the Bragg angle of the Cu $K{\alpha }_1$ peak. One of the other three crystals (e.g., lower right in Fig. 1) is also thin, but highly reflective at the chosen wavelength. It was used to outcouple the X-ray pulse when it has reached saturation after several amplification cycles. Outcoupling was done by switching to a status with large transmission and near-zero reflection. Several techniques for radiation outcoupling, including a small fast rotation or heating with a laser pulse, can be employed and are currently being studied (57–59). We chose the backscattering Bragg geometry, as it provides a large angular acceptance while reducing the bandwidth (Table 1 and Fig. 2). The Darwin width of the Bragg reflection defines the spectral-angular acceptance and the corresponding X-ray pulse length and lasing medium radius. Using the Si(444) reflection gave a 48-meV bandwidth, while the diamond C*(400) reflection gave a 65-meV bandwidth with a more-than-two-times-smaller angular acceptance. The cavity tolerances in the crystal angle and position have been estimated to be of the order of 1 $\mathrm{\mu }$m and 1 $\mu$rad, well within the capability of present-day crystal support and alignment systems.

Fig. 2.

(Left) DuMond diagram of Si(444) crystal at 8,048 eV. (Center) Refocused ASE radiation at the jet location after two sets of Be lenses with state-of-the-art shape profiles. (Right) Darwin curve for Bragg reflection of 8,048-eV photons, corrected for refraction for the cases of thick ($d$ = 5 mm) and thin ($d$ = 50 $\mathrm{\mu }$m) flat Si(444) crystals at room temperature.

To understand the salient features of the XLO cavity, we used the formalism of Fourier optics and dynamic diffraction theory in perfect crystals (60–62). We selected flat, symmetric crystals to alleviate any additional azimuthal angle effects on the Bragg diffraction (60). We evaluated the crystals’ Darwin reflectivity curves for given thickness and Miller indices using the XOP code (55). The curves obtained were then convoluted with the spectral content of the electromagnetic field. The correction to the Bragg angle ${\theta }_B$ for a Gaussian photon beam is given by a simple geometric relation $\sin {\theta }_B\approx \sin {\theta }_{B_0}\left(1-\mathrm{\Delta }{\varphi }^2/2\right)$, where ${\theta }_{B_0}$ is the Bragg angle for a nondivergent beam, and $\varphi$ is the vertical angle with respect to the plane perpendicular to the crystal surface. The effect of vertical divergence is of a second order for $\left|\mathrm{\Delta }\varphi \right|<10^{-3}$ rad and will leave the radiation field mostly intact in $\varphi$, while selecting in $\theta$.

The crystal reflectivity curve $\left|R\right|$ presented in Fig. 2, Right, where $\left|R\right|=I_H/I_0$, for the initial radiation intensity $I_0$ and diffracted intensity $I_H$. We used a set of two compound refractive lens (CRL) assemblies of $f=$ 52 cm and a collimator in a 4-m cavity to refocus the amplified signal on the jet after four reflections (Fig. 1). Fourier optics simulation results corroborated this requirement (Fig. 2). After the first pass, the cavity efficiency is given by the crystal reflectivity and the losses in the focusing lenses. We estimated the total efficiency in second and later passes to be about 41%. The CRL focusing optics can be adjusted to longer/shorter cavity roundtrips, to minimize liquid jet disturbance. Based on Mn ASE results (14), we can obtain up to almost $10^8\hspace{0.17em}K{\alpha }_1$ photons in the initial pass, providing more than enough signal to overcome the first-pass large cavity losses.

While we focused on the Cu $K{\alpha }_1$ line and a Si(444) crystal Bragg cavity geometry that matches its wavelength, other choices of the lasing medium and matching cavity configurations are possible for the XLO, and switching between different lasing media requires only slight changes in the cavity geometry. For example, the Fe $K{\alpha }_1$ line at 6.4 keV using a Si(333) Bragg reflection with 67.9° Bragg angle can be easily realigned to match the Zn $K{\alpha }_1$ line at 8.6 keV switching to the Si(444) reflection with a small realignment to a 66.3° Bragg angle.

Numerical Simulations

We performed numerical simulations for cupric nitrate as a gain medium using the 1D code (49) with different values of the pumping power and number of passes in the XLO cavity. The parameters for the simulations were determined by the LCLS pump power and pulse duration, by the optical cavity properties, and by the gain medium geometry. The simulations included absorption of the 9-keV pump pulse and 8-keV Cu $K{\alpha }_1$ photons in the cupric nitrate gain medium. For 9-keV LCLS SASE X-ray pulses, we can assume a peak power of 30 to 50 GW with a pulse-duration variable between 20 and 60 fs. Using a 60-fs pulse with 33.6-GW power, the corresponding pulse energy is 2 mJ, which is well within LCLS capabilities. The cavity crystals define a horizontal angular acceptance of 31.6 $\mu$rad (Table 1). To alleviate the effect of diffraction, one must satisfy $d\mathrm{\Delta }\theta \ge \lambda /4\pi$, which yields $d\ge 390$ nm. The gain medium can be described as a thin cylinder of length 300 $\mathrm{\mu }$m, defined by the jet diameter, along the pump-pulse direction of propagation and an effective radius defined by the KB focusing properties for a 9-keV X-ray pump pulse. In our calculation, we assumed a gain medium diameter of 800 nm, satisfying the above condition and justifying the use of a 1D simulation code. At this spot size, the Rayleigh length is $z_R=3.65$ mm, i.e., much longer than the jet size. The vertical angular acceptance is much larger than horizontal, and, hence, we could optimize the system by having an elliptically shaped pump pulse. While in principle, this solution can yield a better XLO performance, for the sake of simplicity, we considered only the case of a gain medium with a circular cross-section, with the radius defined by the horizontal acceptance. In addition to varying the pump-pulse intensity, the gain can also be controlled by the focusing KB optics, albeit with slightly larger cavity losses.

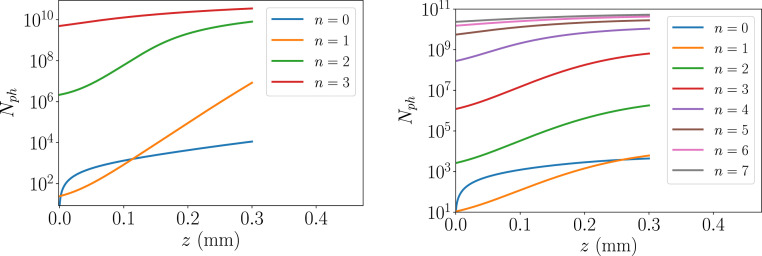
Another important quantity is the number of Cu atoms in the gain medium. Assuming 300-$\mathrm{\mu }$m length and a 800-nm diameter, there are 6.3 $\times$ 10¹¹ Cu atoms in the lasing volume of the (Cu(${\mathrm{N}\mathrm{O}}_3$${)}_2$) solution. This sets the upper limit for the number of XLO photons at saturation. We denote the initial pass as $n=0$ and following passes as $n=\overline{1,N}$, where $N\le 7$. Depending on the pump-pulse parameters, in the initial pass, the ASE process generates about 10³ to 10⁴ photons starting from fluorescence. After seven additional passes, the total number of XLO photons in saturation reaches up to $\ge 5\cdot 10^{10}$, as shown in Fig. 3.

Fig. 3.

XLO gain curves in high-gain (Left) and low-gain (Right) regimes.

We first considered a high-gain XLO case with a SASE train of four pump pulses of 2-mJ and 60-fs duration. In this case, rapid saturation occurred as early as in the third pass, yielding $10^{10}$ photons in 48-meV bandwidth. The XLO brightness is comparable with existing hard X-ray self-seeding XFEL, while offering an order-of-magnitude reduction in bandwidth and much better stability.

We then considered the low-gain case with a SASE train of eight pump pulses of 1-mJ and 60-fs duration. Under these conditions, the gain is reduced, and the cavity power builds up more gradually and radiation supermodes start to form, similarly to refs. 63 and 64. The mode shape is determined by the nonlinear gain, pictured in Fig. 3, and the crystal reflectivity shown in Fig. 2.

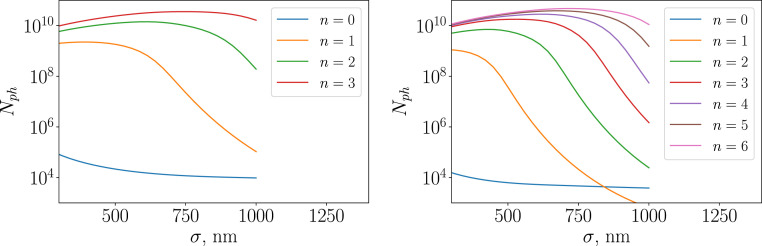
Due to a high degree of nonlinearity in the ASE process, it is important to optimize the gain in XLO, e.g., by using SASE pump size as a tuning knob. While in a single-pass system, increasing pump-photon energy density gives higher photon yield, in the XLO configuration, one has an advantage when gradually increasing the number of photons. Fig. 4 shows a dependence of total number of XLO photons $N_{ph}$ as a function of pump-spot size $\sigma$. One can infer that the gain medium diameter of 800 nm provides the best performance. Fig. 4 also demonstrates the importance of running XLO in saturation, where the $N_{ph}\left(\sigma \right)$ curve becomes relatively flat.

Fig. 4.

The dependence of $N_{ph}$ as a function of SASE pump size $\sigma$ in high-gain (Right) and low-gain (Left) regimes.

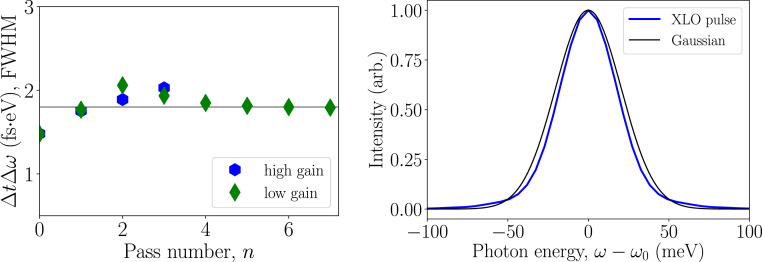
After four passes in both high-/low-gain cases, the resulting XLO radiation time-bandwidth product is essentially transform-limited and is equal to 1.8 fs$\cdot$eV, as shown in Fig. 5. A fully saturated, low-gain XLO produces up to $5\times 10^{10}$ photons. The degeneracy parameter is about $10^{10}$. The constant phase and high-order coherence of the X-ray pulse is the property of XLO and will open experimental possibilities, for instance, in X-ray quantum optics experiments (19, 65).

Fig. 5.

(Left) Resulting time-bandwidth products. The solid black line corresponds to $\mathrm{\Delta }t\mathrm{\Delta }\omega =1.8$ fs$\cdot$eV. (Right) XLO pulse spectrum in high gain regime. Arb., arbitrary units.

LCLS Copper Linac and Liquid Jet Performance.

Multibunch capability at the LCLS Cu linac has been demonstrated with two and four bunches and various time separations from 10 to 200 ns (66–68). Two pulses with variable separation are obtained by using two lasers, both locked to linac radiofrequency (RF), to generate two pulses with variable separation. For the low-gain regime, we plan to raise the number of linac pulses to eight with fixed separation using the two available lasers and an infrared pulse stacker for each laser.

When the SASE pump impinges on the gain medium, it creates a high-temperature plasma channel and generates a shock wave (rarefaction wave). The lasing medium must be replenished, and a fresh gain medium must be provided before the next pump pulse arrives. Recent experiments with slow water jets ($\le$30 m/s) and LCLS Cu linac two-bunch mode (69) showed the shock-wave travel time to be of the order of tens of nanoseconds. The explosion of a liquid jet is a complicated process that involves different mechanisms at different time scales. The experiment reported in ref. 69 focused mainly on the hydrodynamic flow stage, whereas in our case, at 1.7- to 10-ns bunch separation, the hydrodynamic flow is only about to start. We therefore need to perform more experiments to establish the best jet parameters, noticing that it is possible to use higher-speed jets, with velocity up to 200 m/s. This is critical, as the minimal replenishing time $T_{medium}$ will ultimately define the smallest realistic cavity size for XLO operation (69–71). The chosen cavity transit time, $T_{CAV}$, must be a multiple of the linac RF period $T_{RF}$ = 350 ps: $\tau =T_{CAV}=n{T}_{RF}>T_{medium}$. The advantages when using a small $\tau$ are reduced time jitter in the SASE pump pulses and more stability due to a compact cavity size.

To assess the future applications, we provide a comparison of projected parameters of XLO operating at 8 keV and XFELO at 9.8 keV at LCLS-II (47, 48) in Table 2. Note that XFELO would be driven by a superconducting linac with up to a 1-MHz repetition rate and would have a new superconducting gun, while XLO would operate on the LCLS copper linac at a 120-Hz repetition rate. Its operation using the superconducting linac will be studied in the future.

Table 2.

Comparison of some XLO and XFELO parameters at LCLS-II

Parameter	XLO	XFELO
Gain per pass	Up to ${\mathrm{10}}^6$	1.2 to 1.5
Cavity length, m	$\sim$10	$>$260
Lasing medium size, m	$3\times 10^{-4}$	$\sim$100
Angular tolerance, $\mu$rad	1	$\sim$0.01
Number of photons (max)	$5\times 10^{10}$	$10^{10}$
Peak power, MW	$\sim$270	$\sim$4.7
Pulse length, fs	37.4	530
FWHM $\mathrm{\Delta }t\mathrm{\Delta }\omega$, fs$\cdot$eV	1.8	4.4

FWHM, full-width at half-maximum.

Summary

In conclusion, we describe a population-inversion XLO operating in the 5- to 12-keV photon-energy range using an XFEL pulse train as a periodic pump and a liquid jet gain medium. We explore the performance of a cupric nitrate lasing medium in various gain regimes, showing that we can reach saturation in four to eight passes and obtain transform-limited pulses with small linewidth and a large number of photons. We discuss the oscillator’s cavity based on Bragg reflection optics in a bowtie configuration, the lasing medium replenishment using a fast jet, and the multibunch operation of the LCLS copper linac. The potential scientific applications of this X-ray source are extensive and include coherent imaging, inelastic scattering, X-ray quantum optics, multiphoton phenomena, and high-precision interferometry.

Data Availability.

The results of the simulations used to evaluate the oscillator performance are available from A.B. and A.H.