Snapping mechanics of the Venus flytrap (Dionaea muscipula)

Significance

The rapid closure of the carnivorous Venus flytrap (Dionaea muscipula) snap-trap incorporates snap-buckling instability as a speed boost. The trap actuation principles required to overcome the involved energy barrier, as determined by the double-lobe curvature, have remained speculative until now. Here we used 3D digital image correlation for the analysis of trap deformation during closure for both the outer and the inner trap surfaces. Accompanying biomechanical and physiological experiments revealed that successful snapping relies on full trap hydration. In combination with FEM simulations elucidating the mechanical contribution of the various trap tissues to the motion, we show that the trapping mechanics incorporate an elaborate interplay between swelling/shrinking processes of the various tissue layers and the release of trap-internal prestress.

Abstract

The mechanical principles for fast snapping in the iconic Venus flytrap are not yet fully understood. In this study, we obtained time-resolved strain distributions via three-dimensional digital image correlation (DIC) for the outer and inner trap-lobe surfaces throughout the closing motion. In combination with finite element models, the various possible contributions of the trap tissue layers were investigated with respect to the trap’s movement behavior and the amount of strain required for snapping. Supported by in vivo experiments, we show that full trap turgescence is a mechanical–physiological prerequisite for successful (fast and geometrically correct) snapping, driven by differential tissue changes (swelling, shrinking, or no contribution). These are probably the result of the previous accumulation of internal hydrostatic pressure (prestress), which is released after trap triggering. Our research leads to an in-depth mechanical understanding of a complex plant movement incorporating various actuation principles.

Despite a good understanding of the carnivorous Venus flytrap (Dionaea muscipula, Droseraceae) with regard to the physiology of the snap-trap triggering mechanism, the hunting cycle, and the related prey digestion (1–4), mechanistic explanations of the trap movement principles remain incomplete.

The triggering of the trap initiates an active, hydraulically driven lobe deformation (2, 3, 5), which, in combination with the doubly curved lobe geometry, creates a buckling instability. Elastic energy is accumulated, stored, and released during a movement lasting 100 to 300 ms (6): the initially concave trap lobes (open state) begin to move toward each other and eventually change to a convex (closed) state. Each lobe can be considered a curved elastic shell performing snap-buckling. Hydraulic actuation alone cannot account for the fast motion (7, 8). Nevertheless, water displacement processes play a crucial role in the initial active-nastic deformation, with the underlying biochemical mechanisms being little understood (5, 9).

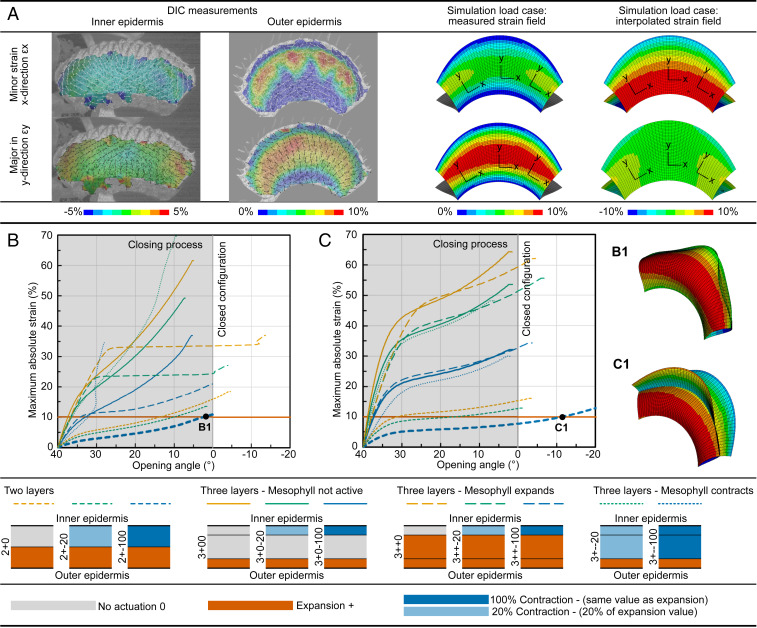
Forterre et al. (10) calculated the three-dimensional (3D) lobe shape change by triangulation of fluorescent dots on its outer surface. They quantified the strain distribution on the inner and outer surfaces before and after closure from molds. For the outer surface, the maximum strain develops perpendicular to the midrib (up to +9%) and is six times the maximum strain parallel to it (Fig. 1A, interpolated load case). Strains on the inner surface are almost undetectable (≤1%). Accordingly, closure is described as being primarily driven by cellular expansions perpendicular to the midrib.

Fig. 1.

Computed trap models with various strain distributions and layer setups without prestress. (A) Measured strain distributions and various load cases for simulations with transformation of coordinate systems. Relationships between opening angle and maximum absolute strain (B) for measured strain distributions and (C) for interpolated strain distributions in all layer setups. The abbreviations correspond to the number of tissue layers (three or two), the behavior of these layers during closure (expansion, +; contraction, −; no actuation, 0), and the extent of expansion or contraction (in %). Moreover, the relative thicknesses of the tissue layers are depicted (see SI Appendix for more details). The only models performing snap-through are the bilayered 2+−100 (inner epidermis contracts as much as the outer epidermis expands) measured load case (B1) and interpolated load case (C1), which, however, do not fit the observed geometrical behavior of the real trap (Movies S7 and S8). Details for all models can be extracted from SI Appendix, Fig. S2.

However, the prepost comparison carried out by Forterre et al. (10) cannot explain the evolution of strains through the entire snapping motion. Moreover, to calculate the global strain distribution of the trap surface, Forterre et al. (10) divided it into local strain fields, assuming that the strain field is homogeneous in the selected 2 mm × 2 mm windows. Consequently, the strain distribution appears to be approximately linear, which is, as explained below, too coarse to produce finite element (FE) models behaving like the snap-through structures resembling a Venus flytrap. Such sudden change from one stable geometric configuration to another can be best understood by the analysis of equilibrium paths, which are essential for the analysis of the nonlinear deformation behavior of structures, as they allow the interpretation of any point or deformation condition for which equilibrium is fulfilled (SI Appendix, Text 1).

By using a reverse biomimetic approach including mechanical modeling via FE simulations and physiological–biomechanical experiments on the real plant (11), we have addressed the following two questions with regard to Dionaea trap actuation: 1) Is prestress required for trap closure? Some authors (12–15) consider hydrostatic pressure (turgor) differences in the tissue layers of the thus prestressed trap lobes as being responsible for maintaining its open position. To evaluate the possible effect of prestress on trap movement behavior, we have investigated the relationship between hydration state (turgescent vs. dehydrated), trap opening angle (geometric state), and triggering response/closure duration and have further evaluated the obtained geometric states regarding the natural trap closing behavior by means of FE models. 2) What are the mechanical contributions of the individual lobe tissue layers to the global trap motion? To determine the types of mechanical behavior (expansion, shrinkage, and neutral behavior) and combinations thereof that can be attributed to the three lobe tissue layers (inner and outer epidermis and mesophyll), strain evolution parameters resulting from 3D digital image correlation (DIC) measurements (16, 17) were investigated in a meta study with FE models. These analyses were substantiated by findings from dehydration experiments carried out to evaluate the hypothetical influence of turgescence/hydraulic prestress. These computer models enable single and combined effects to be investigated that are otherwise not possible in vivo.

Results

DIC Analyses of Dionaea Snap-Trap Surfaces.

Strain distributions in the direction with both higher deformation (denoted as major strain, ε_y) and lower deformation (minor strain, ε_x) were analyzed via DIC throughout the fast snap-trapping motion for both the outer and the inner trap surfaces (Movies S1 and S2). As can be seen in Movie S1, the greatest strain during closure occurs centrally with ε_y perpendicular to the midrib and values of approximately 8 to 10% for the outer surface (Fig. 1). Although possible artifacts attributable to signal loss and imperfect computation (the underlying algorithms require adjoining pixel windows) have to be considered, the margins and the midrib apparently remain undeformed. Additionally, strain in the x direction ε_x parallel to the midrib of approximately 3 to 5% is observable centrally, where the curvature of the trap lobe changes the most. Neither the midrib nor the upper margin deforms, as shown in our recordings. The strain evolution appears to increase evenly with time. For the inner surface, the signal losses and misrepresentations at the upper trap margin seem to be more prominent, possibly because of the teeth-like protrusions (cilia), and these results have consequently been excluded from the interpretation. The strain distribution on the inner surface is more complex than that on the outer surface (Movie S2). Contraction parallel to the midrib is observable centrally (major strain circa 0%, minor strain circa −1.0 to 2.5%). Closer to the margins, the strain field becomes more erroneous, although a major strain of circa +1.0 to 2.5% and a minor strain of circa 0 to −1.5% parallel to the midrib can be detected.

Initial FEM Case Study Regarding Strain Distribution and Snap-Buckling Behavior.

To evaluate the measured strain fields and their correlation with the snap-buckling behavior further, we modeled an open trap loaded by a temperature load case with two different strain distributions (model 1; see Fig. 4). First, a load case was defined based on data from experimental measurements. This measured load case correctly reproduced the distribution obtained from DIC measurements (Fig. 1A). Second, this was compared with an estimation of a possible strain distribution given in Forterre et al. (10) referred to as “interpolated load case” since the values were interpolated over the lobe for loading (Fig. 1A). Additionally, various tissue layer setups with the individual layers exhibiting varying levels of either contraction or expansion (or neither) were investigated (see Fig. 4). We either used three-layered models (inner epidermis, middle layer mesophyll, and outer epidermis), which represent the trap’s real anatomy, or highly simplified bilayered models (13, 14). For any combination of properties, no model exhibited the expected dynamic snap-through behavior, but rather a continuous closing, for both the measured and the interpolated load case (Movies S3–S24). This can be identified in the diagrams in Fig. 1 B and C. A detailed description and interpretation regarding snap-through behavior is explained in SI Appendix, Text 1 and Fig. S2. Snap-through was observable only in the models in which high strain values exceeding those from the experiments were present (Fig. 1). Only the two-layered model in which the inner epidermis contributed with the same absolute strain value as the outer epidermis (but with contraction instead of expansion, designated as 2+−100; see Fig. 1 for details) roughly performed trap closure with the measured 8 to 10% maximum strain for both load cases (Movies S7 and S8). The deformation process (no snap-through) and the deformation figures (Fig. 1 B1 and C1), on the other hand, did not fit the observed geometrical behavior of the real trap. As none of the models and load cases fully qualitatively and quantitatively represented the measured behavior and values, we hypothesized that an additional mechanical effect that had not yet been considered in the simulations supported the snapping mechanism. As suggested by Markin et al. (13), the open trap possibly incorporates an internal pressure difference. This, and the resulting change in curvature, will be treated as prestress in the following, will be included in the future models, and is further referred to as the “ready-to-snap state.”

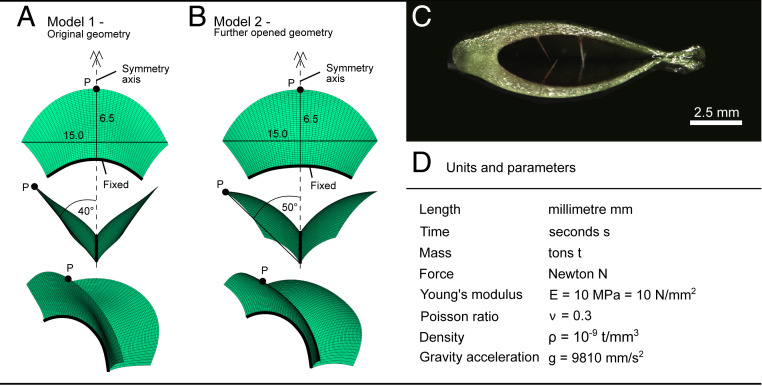
Fig. 4.

FE model basics. FE model (A) of original geometry and (B) of further opened geometry of D. muscipula with dimensions according to the biological specimen. (C) Cross-section of a typical D. muscipula trap showing a linear tapering from base to top. (D) Overview of used units and model parameters according to literature.

Simulation Analysis of Dionaea Snap-Trap Mechanics including a Preceding Prestressing Process.

The non-Venus flytrap-like behavior of the initial models suggests the open geometry of a trap can no longer be interpreted as the initial zero-stress state. Therefore, this geometry should not be taken as the starting point for the simulations as in model 1 (see Fig. 4A). Consequently, a further opened trap was taken as a starting point for the simulations (model 2; see Fig. 4B), reflecting the zero-stress state. As the tangent of the lobe at the midrib remains the same, this wide-angled geometric state of the model gives a higher curvature. To regain the geometry of the open trap, this additional curvature first has to be compensated, leading to a buildup of stress, which is the prerequisite for eventually causing and enabling the observed snap-through behavior of the Venus flytrap. The ready-to-snap configuration is reached by continuous loading until the approximate geometry of fully turgescent traps is obtained, i.e., by changing the opening angle from 50° (zero-stress state) to 40° (ready-to-snap state). Therefore, the required strain is defined as “prestress strain” with the prestress strain distribution assumed to be the same as for opening. The ready-to-snap condition is located before the critical threshold on the equilibrium path as seen in the strain–opening angle relationship (Fig. 2). It can be regarded as the equilibrium configuration for the open state.

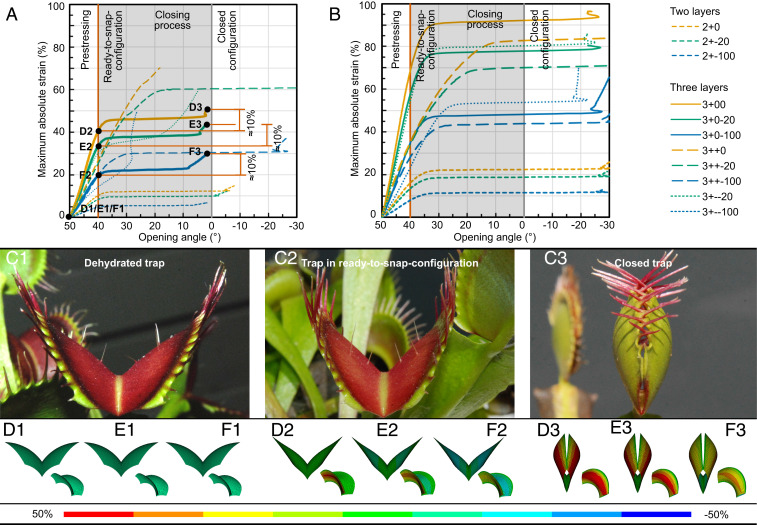
Fig. 2.

Computed trap models with various strain distributions and layer setups including prestress. Relationship between opening angle and maximum applied strain (A) for measured strain distribution and (B) for interpolated strain distribution for all layer setups including a prestress process as predicted by model 2. The abbreviations correspond to the number of tissue layers (three or two), the behavior of these layers during closure (expansion, +; contraction, −; no actuation, 0), and the extent of expansion or contraction (in %) (see SI Appendix for more details). (C1) Dehydrated trap with larger opening angle. (C2) Trap in ready-to-snap configuration with smaller opening angle. (C3) Closed trap. Deformation states of model 2 for models most closely resembling the snap-trapping: (D1) With layer setup 3+00 (outer epidermis expands, and middle and inner layers remain neutral) in zero-stress state. (D2) After loading with the prestress strain, in ready-to-snap configuration, and (D3) after loading with the closing strain (representing the quantitative strain value measured in the DIC experiments; Fig. 1), in closed configuration. Deformation states for layer setup (E1–E3) 3+0−20 (outer epidermis expands, middle layer remains neutral, and inner epidermis contracts by 20% relative to outer epidermal expansion) and (F1–F3) 3+0−100 (outer epidermis expands, middle layer remains neutral, and inner epidermis contracts as much as outer epidermis). Details for all models can be extracted from SI Appendix, Fig. S3.

For final closure, the models were further loaded by the closing strain, which is the strain difference between the total strain for closure and the prestress strain. This represents the quantitative strain value measured in the DIC experiments. In contrast to the models without preceding loading (prestress), snap-through behavior can be observed for almost all layer setups and contributions and for both strain distributions (Fig. 2; more in SI Appendix, Fig. S3 and Movies S3–S24). Strikingly, traps with an interpolated load case application overacted (Movies S3, S5, S7, S9, S11, S13, S15, S17, S19, S21, and S23): the movement of the models was not interrupted when the trap lobes touched but penetrated each other. This is because once the snap-through process is set to work, it cannot be stopped before the next stable state is reached. This artificial penetration arises because contact is not considered in the simulation. This is also the case for models with measured strain distributions in which the mesophyll also expands while the inner epidermis shrinks (3++−20, 3++−100) (SI Appendix, Fig. S4 and Movies S18 and S20). Other layer setups loaded with the measured strain distribution show the expected snap-through behavior. Interestingly, the highly simplified bilayered models (2+0, 2+−20, 2+−100) exhibit full closure while requiring relatively low strains (Fig. 2 A and B and SI Appendix, Fig. S3 and Movies S4, S6, and S8). The models that resembled the snap-trapping including the morphological conditions and the measured values most were calculated with the measured load case, three tissue layers, and a neutral mesophyll (3+00, 3+0−20, 3+0−100) (Fig. 2A and SI Appendix, Fig. S3 and Movies S10, S12, and S14). In all three models, the values for the resulting closing strains in the simulations corresponded well to the measured strains via DIC of ∼10% of the outer epidermis. The difference between the models lies in the contribution of the inner epidermis via shrinking, resulting in a difference in the value of the prestress strain. Without any contribution (3+00), a prestress strain of 40% of the outer epidermis is required (Fig. 2A). An increase of the inner epidermis strain contribution (up to 100% of the value on the outer epidermis) accompanies a decrease of the prestress strain value to 20% cell expansion (3+0−100) (Fig. 2A). With optimization of energy use being one of the most important evolutionary driving factors, low strain should subsequently be favorable. As a result, from the motion behavior and the strain–opening angle relationship, the 3+0−20 with the measured strain field, out of all load cases, was preferred for several reasons: not only is it closer to the finding for the inner epidermis (shrinkage), but it is also congruent with the measured values in the DIC experiments of the outer and the inner epidermis.

Dehydration Experiments.

Assuming that this incorporated prestress state in the open, ready-to-snap trap is the consequence of internal hydrostatic pressure (12), trap snapping and geometrical behavior was tested by decreasing turgor through dehydration that would reduce the stress.

Among traps of the same plant, the relative water content (RWC) was not found to vary significantly, independently of predehydration or postdehydration (predehydration mean 84.3 ± 10.9%, Shapiro–Wilk test for normality p = 0.69, Bartlett test for homogeneity of variances p = 0.41; postdehydration full plant [10 traps], RWC mean 76.4 ± 19.1%, Shapiro–Wilk test for normality p = 0.71, unpaired t test p = 0.0002). This allowed the investigation of possible effects of dehydration on trap-opening angle and trap-closure time of specific individual traps by using various plants in which RWC was measured within one removed trap each. During the dehydration process, the opening angle between the lobes increased (Fig. 3).

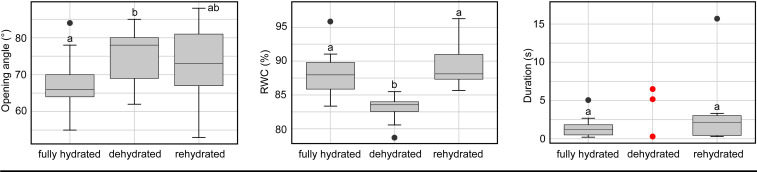
Fig. 3.

Effect of various hydration states (fully hydrated, dehydrated, rehydrated) on D. muscipula traps (n = 9) with regard to opening angle (Left), RWC (Middle), and snapping duration (Right). For trapping duration, only three traps (red dots) responded to triggering in the dehydrated state.

With regard to trap behavior and closure duration, the effect of water loss was striking. Only three out of nine traps closed upon triggering in the dehydrated state; none of the others showed any apparent reaction. After rehydration, the traps regained their initial closure durations but with more scattering. With respect to the trap-opening angle among the selected specimen from randomization, the ezAnova Mauchly’s test indicated that the assumption of sphericity had been met for the different hydration states [F(2,16) = 3.078, p = 0.39, η² = 0.102]. The subsequent post hoc pairwise t test with the Bonferroni correction only showed statistical differences between the fully hydrated and dehydrated state (p = 0.039). In the ezANOVA on RWC levels, Mauchly’s test indicated that sphericity was not violated [F(2,16) = 20.226, p = 0.64, η² = 0.494]. The post hoc pairwise t test with the Bonferroni correction between fully hydrated and dehydrated plants was statistically highly different (p = 0.0065), as was the difference between the dehydrated and rehydrated states (p = 0.0012). The fully hydrated and rehydrated states showed no statistical difference (p > 0.05). Trap angles changed between the fully hydrated and dehydrated states between 0° and 16° in our set of traps. When conditions were much drier, traps were able to open even further, but this was accompanied by irreversible wilting. The increased trap opening was independent of gravity as dehydrated upside-down plants also exhibited the same increased opening angles in their traps (before dehydration mean 69°, after dehydration mean 83° opening angle, five traps in total). This indicates that the turgescent trap incorporates a means to uphold a specific open/ready-to-snap configuration, which cannot be maintained without water supply.

The ready-to-snap configuration of the computer models in which the opening angle is changed from 50° (zero-stress state) to 40° (ready-to-snap state) corresponds well to the maximal change of the opening angle (10°) observed during dehydration. This larger opening angle is regarded to be approximately the zero-stress state.

Discussion

By performing parametric studies on different strain fields, layer setups, and tissue contributions, we gained further insights into Dionaea snapping mechanics. In the following, we discuss the current hypotheses on the basis of our results and propose the most plausible mechanical closure scenario based on our assessment.

The strain values obtained from noncontact full-field 3D surface deformation corroborate previous measurements (10, 18). Nevertheless, our DIC measurements show larger values regarding the continuous evolution of expansion perpendicular to the midrib (10%) on the outer surface: the perpendicular expansion is twice the parallel expansion. Furthermore, we measured 2% shrinkage parallel to the midrib on the inner surface. This discrepancy could have several causes. First, biological specimens can be highly variable. For example, age, hydration status, and cultivation conditions are likely to influence trap shape and behavior. As Forterre et al. (10) have stated, trap architecture is an important factor with regard to fast closure. The interrelationship between trap-lobe thickness, size, and curvature determines the nature of snapping and, as such, the strain distribution. Second, our DIC approach provides highly detailed information depending on the camera resolution (among other factors). As a consequence, facet analysis might have resulted in a more probable strain distribution pattern than the local strain field obtained from microscopic hairs and glands (10) or ink dots (18). Admittedly, the stochastic pattern coating might have added a (small) resistive force to the surface that the trap is required to overcome to close. From the apical movies, however, we have not observed any difference in the behavior of the two trap lobes, which would have been the case if the coating had impeded the motion substantially, as trap lobes can show highly individual closing modes (19, 20).

The strain distributions measured in this study and those reported by Forterre et al. (10) were both applied to FE models of the open trap with variable layer setups and tissue contributions and zero prestress (Fig. 1 C and D and SI Appendix, Fig. S2 and Movies S3–S24). None of the models could reproduce the snapping behavior of the trap, either qualitatively or quantitatively. Thus, an important additional effect essential for snap-through behavior must have been previously neglected. We have subsequently determined this effect experimentally and validated it by simulations, i.e., the mechanical state when the trap is turgescent (prestressed). As seen in the dehydration experiments, the open ready-to-snap state as predicted in the model is upheld by turgor (i.e., fully hydrated state). Here we show that when the traps lose water, the angle between the trap lobes and the central axis increases by circa 10% on average compared with open traps, accompanied by a loss of irritability (Fig. 3). This can be physically explained by a decrease of hydraulic transport rate and physiologically by the negative influences of drought on excitability (21). It remains conceivable that water-stressed traps also close more slowly (Fig. 3). However, this cannot be derived from our experiments in which one trap showed a normal closing duration (∼300 ms) (Fig. 3). This, however, might be explicable because the plant possessed the highest RWC level compared with all other dehydrated plants. The simulations in which a prestress state is included (via using a further opened geometry as the starting point, the zero-stress state) further confirm this hypothesis for both strain distributions and almost all parameter combinations. Because of both experimental difficulties and the prerequisite to test individual traps alive in different states, the quantification of turgor pressure by, for example, the pressure probe technique or indirectly by osmotic dehydration series was not possible (22).

On applying the strain distribution reported in Forterre et al. (10) as load case (interpolated load case) on models incorporating prestress, the traps are technically able to close, although in some configurations, not via snap-through (Fig. 2B and SI Appendix, Fig. S3). In addition, as can be seen from the strain–opening angle curves for any layer setup tested, additional strain is required for closure. Moreover, strong penetration of the lobes in the models often occurs (SI Appendix, Fig. S3) that does not reflect the natural situation in which the lobes of the just-closed trap do not touch and, therefore, do not exert pressure on each other. As Stuhlman (12) has established experimentally, the teeth at the lobe margins do not act as friction brakes during the fast closure. Conceivably, this aforementioned trap overacting complies with the period after the fast trap closure when the trap lobes begin to form close contact and seal the trap tightly (23). An evaluation would be interesting as to whether the tightening process (which takes some time) is attributable to the relaxation of stress and/or irreversible growth processes and modifications of cell wall mechanics (24). During fast trap closure, the use of more strain than required for snapping would be associated with high energy costs, a feature that is evolutionary unfavorable (25).

When the observations from experiments including the quantitative DIC measurements and the deformation behavior of single lobes are taken into account, the simulations with the measured strain distribution are coinciding. The models in which the middle layer (mesophyll) does not actively contribute to the actuation [contradicting (26, 27)], but results in an increase of lever between the active outer and inner epidermis, show strong accordance with the snap-trapping kinematics, trap-lobe deformation, and geometry changes of real traps and the quantitative measurements on the plant itself (Fig. 2A and SI Appendix, Fig. S3 and Movie S12). This is interesting in that it shows the importance of integrating the mesophyll into models that are more realistic to the setup of a real trap in comparison with the often used and highly simplified bilayered models (cf. ref. 13), although notably, Markin et al. (13) have previously integrated prestress in their hydrostatic elastic curvature model.

With regard to the contradictory observations described in the literature concerning the behavior of the inner epidermis during trap closure [almost no contribution (10, 18), shrinkage (13, 20)], we have exemplarily evaluated these with theoretical models (Fig. 2 D1–D3 and F1–F3). From these evaluations, we can conclude that the higher the contribution of the inner epidermis by shrinking, the less prestress strain is required for full closure incorporating snap-through. The contributions of the various layers might well be mostly plastic and dependent on trap age, dimension, and health.

Manipulation experiments with real traps might also provide tentative explanations for abnormal closing behavior of our modeled traps. Removal of one lobe or the cilia lining the lobe margins (which initiates trap closure) often leads to the leftover lobes either curling like a cigarillo or the left and right margins both folding (SI Appendix, Fig. S4) (26, 27) after a short period of time (∼5 to 10 s). We interpret this behavior as occurring because of the lack of a regulating contact (blocking force) to the opposing (missing) lobe and cilia. We saw a similar behavior of exaggerated trap bending responses in our computer models on measured strain fields where no prestress was included and the inner epidermis contracted (SI Appendix, Fig. S4). As the real traps exhibited this behavior after closure (when prestress was, at least partially, released), this indicates that water transport from the adaxial to the abaxial layers might further narrow the trap (also see refs. 14 and 15). As Forterre et al. (10) have previously mentioned, the fast closure motion of the trap is internally dampened because of the flow of interstitial water through the elastic tissue. The remaining water displacement probably leads to exaggerated lobe bending.

Further study of the relationship between the prestress state and the geometry in young traps would be of interest. Young traps close smoothly (19), which might be because of the weak curvature (10) and/or little prestress. Similarly, our models with no included prestress never exhibit true snap-through behavior (Movies S3–S24).

In this study, we have been able to show, by experiments and simulations, that the Venus flytrap closure is most likely driven by a simultaneous expansion of the outer epidermis and a lower shrinkage of the inner epidermis (cf. refs. 10 and 20). The mesophyll has no active part in the motion. Furthermore, for quick closure, it is important that the traps are in a state of ready-to-snap, resulting from internal hydraulic pressure differences between the layers, i.e., prestress. Nevertheless, because of the simplifications made in our study, some effects might be neglected. For example, water damping, i.e., the redistribution of interstitial fluid after the sudden change of geometric configuration was not considered. Furthermore, the material behavior was simplified, because of the lack of data, in order to derive reasonable assumptions for material models and parameters. The chosen isotropic model facilitates a simple interpretation of the results as no artifacts from the material are included and as the movement mechanisms and principles resulting from geometric properties are isolated. With the simplified models, we cannot therefore make any quantitative statement about stress values but can only give qualitative information such as the existence of a prestress state, as was the aim of this study. Nevertheless, we are aware that the material behavior, the geometry, and the resulting deformation are coupled and that further investigations in this respect are desirable.

Moreover, as Stuhlman (12) has observed, “the form [and speed] of the closing motion changes with the position of the trigger hair used to start the excitatory process.” The pattern of the wave of action potentials that initiates the fluid currents, leading to the initial deformation and consequent snap-buckling, could not be resolved in our DIC experiments. We are therefore particularly looking forward to visualizing and quantifying the water change dynamics during from the start of the fascinating closure of the Venus flytrap. The present study contributes to our understanding of the biology not only of this iconic plant but also of the underlying mechanical principles of snap-buckling structures in general, a topic that is also of great interest for biomimetic research and any resulting technical applications (28–30).

Materials and Methods

Plant Experiments.

Effects of hydration states on trap opening angle and trap closure time.

Healthy adult D. muscipula traps (originally purchased from Gartenbau Thomas Carow) were tested in the fully hydrated state and then left to dehydrate for 8 to 14 d (depending on the pot size) followed by a 7-d rehydration. Plants were considered to be in the hydrated states when they were growing in moist pots standing in 1 to 2 cm rainwater. The RWCs, trap opening angles, and triggering responses/closure durations were assessed in the fully hydrated, dehydrated, and rehydrated states, as described below.

Variation in RWC between D. muscipula traps of the same plant.

Analysis of the influence of various water states on trap closure duration and opening angles is not possible with single traps, as the highly invasive RWC measurements impede correct trap functioning. Therefore, we measured the RWC of a trap and analyzed closure duration and opening angle with a neighboring trap of the same plant. To test whether the RWC of a neighboring trap represents the RWC of the trap of interest (or of the whole plant), two plants with 10 traps each growing in the same large pot were analyzed with respect to their RWCs. One plant was tested before dehydration and one after dehydration. For measurement of the RWC, a circular disk was punched out of a trap lobe from each specimen by using a 4-mm metal punch. The fresh weight (FW) of each sample was obtained, then the turgescent weight (TW) (dark incubation in distilled water for 2 h), and finally, the dry weight (DW) (60 °C, >24 h). The RWC was then calculated with RWC = (FW − DW)/(TW − DW)⁻¹⋅100%. By using the software R (version 3.5.1), the RWC measurements were checked for normality by using a Shapiro–Wilk test and for variance homogeneity (Bartlett’s test), followed by an unpaired t test to determine significant differences. Among traps of the same plant, the RWC was not found to vary significantly, independent of predehydration or postdehydration. This allowed us to investigate possible effects of various water states on trap-opening angle and trap-closure time in multiple plants.

Possible effects of various hydration states on D. muscipula trap-closure time and trap-opening angle.

Because of severe water stress during the experiment, the trap death rate was ∼50%. Out of the surviving traps for which data were available throughout the trial, one trap per pot was randomly chosen for statistics, resulting in n = 9 for testing each hydration state. Traps were stimulated with a toothpick by touching the trigger hairs twice. The following closure motion was recorded with a high-speed camera (Motion Scope Y4; Redlake) at a recording speed of 1,000 fps, by using the cold light source Constellation 120 high-performance LED (Integrated Design Tools, Inc.) and the software Motion Studio ×64 (version 2.12.12.00; IDT). To determine the trap-opening angle, photographs were taken from the apex of the trap under different hydration states. For the fully hydrated state, the angle of reopened traps was measured at 4 d after initial (artificially evoked) closures. The plant pots were kept fully hydrated during this period. The opening angle was defined as the angle between the trap lobes and was analyzed using Fiji/ImageJ (1.51j) (Fig. 2C1) (31). RWCs of neighboring traps were analyzed before and after dehydration and after rehydration. All measurements were tested for normality. For opening angles and RWCs, a one-way repeated measurements ANOVA was performed using the ez package (32) in R, followed by a pairwise t test with the Bonferroni correction. For trap closure times, a one-tailed t test to determine significant differences between the different stages was performed using R. The exemplarily pot that was dehydrated upside down was treated in the same way (five surviving traps total).

Visualization of 3D deformation in closing traps (DIC).

For 3D surface deformation analyses of closing traps, two high-speed cameras with identical pixel sizes (MotionPro Y4 and NX4; Redlake Inc.) each equipped with 100-mm macro lenses (Zeiss) were synchronized via the Motion Studio software by using the Y4 camera as the master device. The cameras were placed at a stereo angle of 25° toward the specimen on a mount (custom-made by the technical workshop, Institute for Biology II/III, University of Freiburg, Germany). Calibration was performed with a calibration panel CQ20-30 ×24 (Gesellschaft für Optische Messtechnik mbH, GOM) as specified by the manufacturer. The recording speed was 1,000 fps. Different traps were used to study the inner and outer surface strains. For visualization of the inner surface, the opposing trap lobe was removed prior to the actual analysis with a razor blade, and the cut was sealed with Vaseline. The remaining lobe was allowed to reopen again (within 1 to 2 d). The software Aramis Professional (Professional 2016, GOM GmbH) was used for DIC.

As Aramis is highly sensitive to noise attributable to reflections (i.e., it is likely to lose track of reference points/surface detection because of contrast reduction), traps had to be prepared as follows: an antiglare spray (Helling 3D Laser Scanning Spray; Helling GmbH) was carefully sprayed on either the adaxial or abaxial surface of the trap lobe of interest of an open trap as a foundation to minimize glaring effects. Next, a stochastic pattern was sprayed onto the surface by using carbon black (Professional Spray Paint; Liquitex). Petiole parts covering the lobe surface were carefully removed with a razor blade. The potted plants with the prepared traps were placed into the calibrated measuring volume and illuminated with a cold light source (Techno Light 270; Karl Storz GmbH & Co. KG). In addition to surface analyses, the traps were filmed apically via a digital microscope equipped with a USB camera (Conrad Electronic SE) at 1 fps to check for any potential abnormal closing behavior. Traps were triggered with a toothpick or a thin wire. After kinematic analyses, the traps were cut transversally with a razor blade and the trap lobe thickness measured from images of the section.

DIC not only is particularly powerful and can, if correctly used, provide highly accurate measurements of deformation and strain but also is inherently complex. Important parameters, such as the stochastic pattern on the sample surface, the sizes (pixel windows) and positions of the facets, and the lens distortion, plus calibration, thermal noise, and algorithms, all influence the measurement and, hence, data accuracy. Because these factors might not only vary between the measurements of the different samples but also be dynamic within a single measurement, it is not possible to extract a definite value of the measurement error. In order to interpret data accuracy well, despite these dynamics, the signal-to-noise ratio must be considered, and various measurements should be compared. If the patterns and values obtained from an evaluation with the software are similar, the data can be considered to be robust, provided that the experiments were identically performed under optimal conditions as suggested by the manufacturer.

In our case, four inner and four outer trap-lobe surfaces were analyzed and the most informative picked for representation. The image series obtained from trap closures were analyzed by forward detection. The facet size was set to 19 × 19 pixels and the maximal distance between their midpoints to 16 pixels, for both the outer and inner surface analyses. We analyzed the major strain (being in the direction of the higher deformation) and the minor strain (being in the direction of the lower deformation) for four inner and four outer trap-lobe surfaces. The signal-to-noise ratio determined experimentally over 10 frames without trap movement is less than 0.5 pixels (i.e., <0.02 mm) for all analyzed datasets.

Simulations.

All simulations were based on the FE method, and the calculations were geometrically nonlinear static and dynamic analyses performed with the FE software ANSYS 18 (Release 18.0, ANSYS Inc.). In dynamic simulations, the effects resulting from inertia, velocity, and acceleration were considered, whereas they were neglected in (quasi-)static calculations. For static analyses, the arc length method was used to determine the static equilibrium path of the structure. Dynamic calculations were carried out by a transient analysis with 40% of the critical damping $C_{kr}=2\omega M$ (with $M$ being the mass of the trap and the first and lowest eigenfrequency $\omega$ obtained by a precedent modal analysis). A preliminary study by simulations showed that a variation on the damping ratio primarily affects the vibration behavior (swinging off attributable to a sudden stop of motion) at the end of the deformation but not the overall deformation behavior itself. To verify that the movement for trap closure had been completed at the end of the loading, one more load step was applied to hold the load level and liberate possible vibrations. Material nonlinearities were not taken into account, and an isotropic linear elastic material model was used with a Young’s modulus of E = 10 MPa (10) and a Poisson’s ratio of ν = 0.3. This simple linear elastic and isotropic material model was chosen as only little information about the material properties was available. The geometry was approximated with FE and certain mechanical assumptions (Fig. 4). Linear rod elements, as used in the system of SI Appendix, Fig. S1, can only bear loads by normal forces and are made discrete with two-node truss elements (LINK180). All surfaces in the models were thin-walled structures that were represented by a shear deformable Reissner–Mindlin shell model. For the approximation of the surfaces, we used four-node quadrilateral shell elements (SHELL181) with six degrees of freedom, three displacements, and three rotations. No contact formulation was implemented to allow penetration of the structure, namely, the two lobes.

For efficiency, only a quarter of the structure (i.e., only half of a trap lobe of D. muscipula) was modeled with FEs, and symmetry boundary conditions were applied. From the morphology of the trap tested with DIC for the outer surface deformation and depicted in Fig. 1A, the geometry was approximated and idealized. This geometry was then modified to model the further opened trap, as shown in SI Appendix, Fig. S4B. The lobe thickness interpolated linearly between 1.0 mm near the midrib and 0.5 mm at the outer edge (the thickness of the mesophyll gradually decreased toward the margins) (values as measured via cross-sections; SI Appendix, Fig. S4C). Because this specimen represented a trap of average size (33), shape, and trapping behavior, we used the resulting model for all further computer analyses. We simulated 1) three different tissue layers (defined as inner epidermis, mesophyll, and outer epidermis) representing a more detailed description of the plant section (26) or 2) a bilayer with equal proportions (sensu refs. 13, 14) (Fig. 4). Because of the fixed connection of the trap midrib to the petiole, all displacements and rotations were constrained at the connection. The volume changes attributable to turgor increase/decrease were modeled by temperature load cases (positive indicates expansion, and negative indicates contraction). Anisotropic expansion behavior was simulated by the application of different thermal expansion coefficients perpendicular and parallel to the midrib. The strain perpendicular to the midrib was visualized in all models. Preliminary simulations showed that the effect attributable to self-weight could be neglected. All displacements that are displayed or listed in the following refer to the point P (Fig. 4 A and B). For the simulation of the trap, exclusively dynamic, transient analyses were carried out to model the highly dynamic process. Such analyses also allow the depiction of the model answer to the incremental increase of the load, i.e., the thermal expansion. Furthermore, the prebuckling and postbuckling behavior patterns are similar in such analyses and quasi-static analyses. The dynamic analyses of the traps were performed with a prescribed time of 150 ms per simulation step. All units of the model were chosen to remain consistent and are summarized in Fig. 4D.

Various scenarios of turgor changes within the different tissue layers were qualitatively and quantitatively evaluated for strain distributions obtained 1) from DIC measurements and 2) for an approximated strain distribution as published by Forterre et al. (10) (summarized in Fig. 1A). The focus lay on outer epidermis expansion as indicated by ref. 10 in combination with and without contraction of the inner epidermis. Here we varied the proportion of the contribution of the inner epidermis (no contraction, contraction according to measured value, or maximal contraction 100%) in order to investigate its influence on the overall snapping movement.

Data Availability.

The data supporting the findings of this study are available within the article and SI Appendix.