Electronically driven spin-reorientation transition of the correlated polar metal Ca₃Ru₂O₇

Significance

Methods to stabilize and control magnetic ordering in solids are strongly desired both for fundamental studies and to realize new spintronic technologies. The orientation of ordered magnetic moments is typically set by details of the crystalline environment in which they reside. Here, we report the discovery of a form of magnetic anisotropy which is instead driven by a striking reconfiguration of the underlying fermiology of the system. We show for the oxide material ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ how this arises from the interplay of spin–orbit coupling, local polar distortions of the crystal structure, and pronounced electronic correlations. Our findings suggest materials design approaches for manipulating magnetic textures and open pathways to creating large magnetoelectric-type couplings in solids.

Abstract

The interplay between spin–orbit coupling and structural inversion symmetry breaking in solids has generated much interest due to the nontrivial spin and magnetic textures which can result. Such studies are typically focused on systems where large atomic number elements lead to strong spin–orbit coupling, in turn rendering electronic correlations weak. In contrast, here we investigate the temperature-dependent electronic structure of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$, a $4d$ oxide metal for which both correlations and spin–orbit coupling are pronounced and in which octahedral tilts and rotations combine to mediate both global and local inversion symmetry-breaking polar distortions. Our angle-resolved photoemission measurements reveal the destruction of a large hole-like Fermi surface upon cooling through a coupled structural and spin-reorientation transition at 48 K, accompanied by a sudden onset of quasiparticle coherence. We demonstrate how these result from band hybridization mediated by a hidden Rashba-type spin–orbit coupling. This is enabled by the bulk structural distortions and unlocked when the spin reorients perpendicular to the local symmetry-breaking potential at the Ru sites. We argue that the electronic energy gain associated with the band hybridization is actually the key driver for the phase transition, reflecting a delicate interplay between spin–orbit coupling and strong electronic correlations and revealing a route to control magnetic ordering in solids.

Polar distortions in solids give rise to the well-known functionality of switchable macroscopic polarization in ferroelectrics (1, 2) and, when combined with strong spin–orbit coupling, can mediate giant spin splittings of electronic states (3, 4). While typically found in insulators, ferroelectric-like distortions can remain robust against increasing itineracy, giving rise to so-called “polar metals” (5–10). ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ is the bilayer member of the ${\mathrm{C}\mathrm{a}}_{n+1}{\mathrm{R}\mathrm{u}}_n{\mathrm{O}}_{3n+1}$ Ruddlesden–Popper series. The small ionic size of Ca induces large coupled rotations and tilts of the ${\mathrm{R}\mathrm{u}\mathrm{O}}_6$ octahedra that make up the perovskite-like building blocks of this structure, generating a noncentrosymmetric crystal structure (space group 36: $Bb{2}_1$m; Fig. 1A) (11, 12). A symmetry-allowed trilinear coupling between the two nonpolar octahedral tilt ($X_3^{-}$) and rotation ($X_2^{+}$) modes and a polar lattice mode (${\mathrm{\Gamma }}_5^{-}$) further mediates polar distortions, just as in ${\mathrm{C}\mathrm{a}}_3{\mathrm{T}\mathrm{i}}_2{\mathrm{O}}_7$ and ${\mathrm{C}\mathrm{a}}_3{\mathrm{M}\mathrm{n}}_2{\mathrm{O}}_7$ which are part of the well-known class of improper ferroelectrics (13–15). Unlike these sister compounds, however, ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ is not an insulator. Its in-plane resistivity decreases upon cooling from room temperature, albeit with a linear temperature dependence indicative of a so-called “bad metal” state (16, 17).

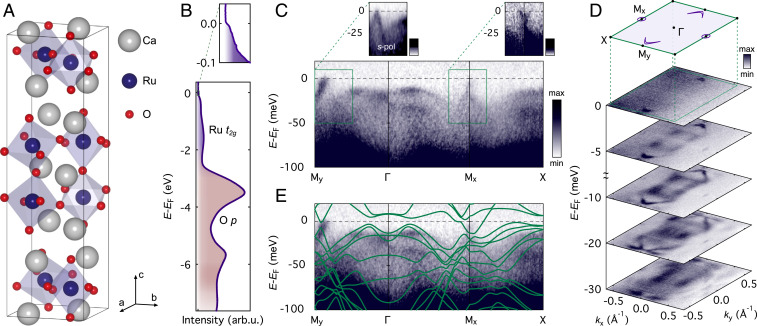
Fig. 1.

Low-energy electronic structure of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$. (A) Crystal structure of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$. (B) Overview electronic structure measured at $T=6$ K. A broad bandwidth associated with spectral weight from the Ru $t_{2g}$ states is observed, while the spectral weight becomes very small close to the Fermi level. (C) Despite this, sharp quasiparticle-like states are observed at low energy. Close to ${\mathrm{M}}_y$, a hole band just intersects the Fermi level, with both branches of the dispersion more clearly visible for measurements performed using $s$-polarized light (Left Inset; see SI Appendix, Fig. S1B for these data shown over an extended energy and momentum range). At ${\mathrm{M}}_x$, an electron-like band crosses $E_{\mathrm{F}}$, shown with enhanced contrast in Right Inset. (D) Constant energy contours measured at the Fermi level ($E_{\mathrm{F}}\pm 2$ meV) and at finite binding energy. The Fermi surface is composed of tiny electron pockets located at the high-symmetry ${\mathrm{M}}_x$ point and small boomerang-shaped hole Fermi surfaces located away from the Brillouin zone boundaries close to ${\mathrm{M}}_y$. D, Inset shows the surface projected Brillouin zone of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ with schematics of the Fermi surfaces. Due to the weak spectral weight of the electron-like Fermi pockets, they are only just visible above the noise for the ${\mathrm{M}}_x$ point at $k_x>0$, while their intensity is even further suppressed (likely by transition matrix element variations) for the pocket at $k_x<0$. Additional states with “M-shaped” dispersion are observed at slightly higher binding energy (C, starting from $E-E_{\mathrm{F}}\approx 10$ meV), which are also visible in constant energy contours below the Fermi level. (E) While the large unit cell and magnetic ordering give rise to a multitude of bands, we find that the general structure and form of the near-$E_{\mathrm{F}}$ states are well captured by ferromagnetic density-functional theory calculations (Materials and Methods) when scaling the energy by a factor of 0.15. The 2D intensity data are the same as in C.

At $T_{\mathrm{N}}=56$ K, the system undergoes a Néel ordering transition, where the spins align ferromagnetically within each bilayer, oriented along the $a$ axis, and are antiferromagnetically coupled between bilayers (18, 19). At a second phase transition at $T_{\mathrm{S}}=48$ K, the spins reorient to lie parallel to the in-plane $b$ axis (11, 18, 19). Simultaneously, an isostructural transition leads to a squashing of the unit cell along the $c$ direction (11). The resistivity exhibits a sudden jump on cooling through $T_{\mathrm{S}}$, but, although its absolute value remains relatively high (${\rho }_{ab}\left(5\hspace{0.17em}\mathrm{K}\right)\approx 50$ $\mathrm{\mu }\mathrm{\Omega }$cm), the in-plane resistivity recovers a metallic temperature dependence to low temperature (16, 17). A rich noncollinear magnetic texture has been observed under the application of magnetic fields (20), pointing to an important role of spin–orbit coupling combined with the noncentrosymmetric crystal structure, while strong electronic correlations are expected to also play an important role in shaping the electronic and magnetic properties of this system (the single-layered sister compound ${\mathrm{C}\mathrm{a}}_2{\mathrm{R}\mathrm{u}\mathrm{O}}_4$ is a Mott insulator) (21).

${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ thus stands as a particularly rich example of a correlated polar metal. Gaining a comprehensive understanding of its transport, magnetic, and electronic properties has, however, proved elusive to date. Here, we study its temperature-dependent electronic structure by angle-resolved photoemission spectroscopy (ARPES) (Materials and Methods). Our low-temperature measurements are shown in Fig. 1. Consistent with refs. 22 and 23, we find a significant spectral weight in the valence bands associated with the Ru $t_{2g}$ orbitals, but almost vanishing spectral weight at the Fermi level (Fig. 1B). Nonetheless, sharp features are still evident on low-energy scales ($\lesssim 50$ meV; Fig. 1C), indicative of well-defined Fermi liquid-like quasiparticles, albeit with very low quasiparticle residue.

Our measured electronic structure exhibits a pronounced twofold symmetry throughout the Brillouin zone. At the ${\mathrm{M}}_x$ point, an electron band intersects the Fermi level, giving rise to a small ${\mathrm{M}}_x$-centered electron pocket (just visible in Fig. 1D). This derives from a band whose occupied bandwidth is only $\lesssim 15$ meV, immediately below which another band disperses downward to higher binding energy (Fig. 1C, Right Inset). The electronic structure is markedly different along the $\mathrm{\Gamma }$–${\mathrm{M}}_y$ direction. A dispersive state is evident, intersecting the Fermi level away from the Brillouin zone boundary (Fig. 1C). An extremely weak feature is also visible with approximately the same $k_{\mathrm{F}}$ but opposite Fermi velocity (confirmed using measurements with different light polarization; Fig. 1C, Left Inset), indicating that this is the top of a $\mathrm{\Lambda }$-shaped band which barely grazes the Fermi level. Fermi surface measurements (Fig. 1D) show how this disperses along the perpendicular in-plane direction to form a very narrow boomerang-shaped hole-like Fermi surface, centered along the $\mathrm{\Gamma }$–${\mathrm{M}}_y$ line but displaced away from the Brillouin zone boundary.

We thus assign the ground state of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ to be a low carrier-density compensated semimetal, in agreement with the small Fermi pockets found previously by Shubnikov–de Haas studies (17). An additional set of sharp and rather flat states is visible in Fig. 1 C and D closer to the Brillouin zone center. These bands display a shallow local minimum at $\mathrm{\Gamma }$, disperse upward toward their band maxima which are located $\approx 10$ meV below the Fermi level (22), and then disperse back to higher binding energies, giving them a characteristic “M-shaped” appearance. They are also visible as increased spectral weight close to the Brillouin zone center in constant energy maps for energies below the Fermi level in Fig. 1D. Measurements using different light polarizations (SI Appendix, Fig. S1) indicate that there are at least three distinct states here, pointing to a rich multiband near-$E_{\mathrm{F}}$ electronic structure. To further explore this, we show in Fig. 1E density-functional theory (DFT) calculations of the low-temperature electronic structure (Materials and Methods), renormalized in energy by a factor of $\approx 7$.

The strong bandwidth renormalization needed to achieve a reasonable agreement with the measured low-energy electronic structure indicates that ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ is a highly correlated metal, consistent with its low-quasiparticle residues. In such a complex multiband system as this, momentum- and orbital-dependent self-energies may generically be expected (22), and a simple bandwidth scaling cannot be expected to capture in detail the full influence of many-body interactions on the electronic structure. Indeed, the experimental Fermi velocities of the boomerang-shaped states crossing $E_{\mathrm{F}}$ are renormalized only by a factor of $\approx 4$ compared to corresponding features in the DFT, while the flat bands appear to require significantly higher renormalizations. The results shown here thus motivate future study of interaction effects in ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ by state-of-the-art correlated electronic structure calculations, of the form that have recently proved extremely successful in describing the single-layer Sr-based sister compound (24, 25). Nonetheless, we note that a global bandwidth scaling of the calculated DFT still does a remarkably good job in reproducing the key experimental band structure features observed here, including the ${\mathrm{M}}_x$-centered electron pocket, the hole-like $\mathrm{\Lambda }$-band offset from the ${\mathrm{M}}_y$ point (located just below $E_{\mathrm{F}}$ in the calculations), and the fully occupied M-shaped states just below the Fermi level.

The marked difference in the calculated electronic structure along the $\mathrm{\Gamma }$–${\mathrm{M}}_x$ and $\mathrm{\Gamma }$–${\mathrm{M}}_y$ directions demonstrates that the large anisotropy in the measured electronic structure along these directions can be fully explained on the basis of the orthorhombic crystal structure, without invoking an electronically driven nematicity as reported in a very recent study (23). Moreover, our calculations indicate that the flattened M-shaped dispersion at the Brillouin zone center, clearly evident in the experimental electronic structure in Fig. 1C, is the result of a band hybridization between the top of a hole-like band and the bottom of an electron-like band, with a gap opening at the Fermi level. We show below that this band hybridization is in fact key to understanding much of the important physics of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$.

Fig. 2A shows the temperature-dependent evolution of the electronic structure through the two phase transitions. For temperatures below the structural and spin-reorientation transition, $T_{\mathrm{S}}$, the spectral linewidths gradually broaden with increasing sample temperature (Fig. 2B), as can generically be expected from electron–electron and electron–phonon interactions. While ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ is sometimes considered to be in an insulating state above $T\approx 30$ K, our spectroscopic measurements clearly demonstrate that well-defined quasiparticle-like states persist up to $T_{\mathrm{S}}$. In contrast, we find a sudden and dramatic loss of quasiparticle coherence when warming through $T_{\mathrm{S}}$, with extremely broad linewidths above the transition indicative of a high scattering rate. The electronic structure is also markedly altered across the transition. While the transition at $T_{\mathrm{S}}$ is known to be first order (16, 26, 27), the corresponding thermal hysteresis is small (26), and we do not observe it (or signatures of coexisting domains) within the temperature resolution of our experiments ($\sim 2$ K). While weak and broad remnants of the original Fermi crossings still persist above $T_{\mathrm{S}}$ (evident as shoulders at $k_y\approx \pm 0.55$ Å${-}^1$ in Fig. 2B), the state around the Brillouin zone center now no longer appears to bend back to form an M-shaped dispersion. Rather, it crosses directly through $E_{\mathrm{F}}$, forming a large hole-like Fermi surface centered at $\mathrm{\Gamma }$ (Fig. 2C), consistent with a known transition in the Hall coefficient from large and negative values at low temperatures to small and positive values above $T_{\mathrm{S}}$ (28, 29). We note in passing that this high-temperature Fermi surface is twofold rather than fourfold symmetric, again reflecting the large orthorhombicity of the lattice. The evident loss of quasiparticle coherence, despite the pronounced increase in carrier density, upon warming through $T_{\mathrm{S}}$ is interesting and requires further detailed study. Qualitatively it may be related to the multiband nature of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$. The creation of new Fermi pockets, and the additional density of states associated with these, will open new channels for inter- and intraband scattering. Moreover, there are a large number of bands with turning points expected in the vicinity of the Fermi level; recent work has emphasized the potential for strong scattering for all states in the Brillouin zone to be associated with the presence of hot spots localized in $k$ space (30). We note, however, that this is a complex system with both a structural and a magnetic transition occurring here, and we do not exclude that additional contributions from electron–lattice and electron–magnon coupling could contribute to the changes observed experimentally.

Fig. 2.

Fermi surface transition at $T_{\mathrm{S}}$. (A and B) Temperature-dependent ARPES dispersions (A) (measured along the $\mathrm{\Gamma }$–${\mathrm{M}}_y$ direction) and corresponding Fermi-level momentum distribution curves (MDCs) (B) ($E_{\mathrm{F}}\pm 2$ meV) indicate a gradual temperature-dependent increase in the quasiparticle linewidth with increasing temperature below the coupled structural and spin-reorientation transition at $T_{\mathrm{S}}=48$ K. Upon warming through this transition, a sudden and extreme spectral broadening is observed, pointing to a loss of quasiparticle coherence at the transition. The M-shaped states at low temperature now disperse up through the Fermi level, forming (C) a large Fermi surface, but with a very high scattering rate. No qualitative changes are observed upon warming further through the Néel transition at $T_{\mathrm{N}}=56$ K (A).

We focus below on the origin of the unusual moment orientation-dependent Fermi surface transition at $T_{\mathrm{S}}$. Our measurements indicate that once the large, zone-centered Fermi surface is established upon warming through $T_{\mathrm{S}}$, the electronic structure evolves only gradually, with no further qualitative changes as the temperature is increased to above the 56-K Néel transition (Fig. 2 A and B). Such an insensitivity to the antiferromagnetic ordering at $T_{\mathrm{N}}$ might naively suggest that it is the structural, rather than spin-reorientation, aspect of the phase transition at $T_{\mathrm{S}}$ which underpins the dramatic changes in electronic structure observed there. We show below, however, that this is in fact not the case.

Fig. 3 shows the electronic structure calculated by DFT for the experimental crystal structures above and below the structural transition at $T_{\mathrm{S}}$ and for the spin oriented along different in-plane crystallographic directions. For the spin moment oriented along the $a$ axis and for the 50-K crystal structure (Fig. 3A, found for $T_{\mathrm{S}}<T\le T_{\mathrm{N}}$), the hybridization of the electron- and hole-like bands at the Brillouin zone center is evidently suppressed. This gives rise to the large Fermi surfaces observed experimentally around the Brillouin zone center. A similar lack of band hybridization of the near-$E_{\mathrm{F}}$ states is found when considering the equivalent spin configuration but for the low-temperature crystal structure (Fig. 3B), pointing to an insensitivity of the low-energy electronic structure to the structural component of the transition at $T_{\mathrm{S}}$. In contrast, when the moment is rotated to lie along the $b$ axis (as found experimentally for $T<T_{\mathrm{S}}$), the electron and hole bands at the zone center develop a strong hybridization. The hybridization develops gradually as the moment is rotated away from the $a$ axis in both $ab$ and $ac$ planes (Fig. 3D). This demonstrates that it is the moment orientation and not the structural changes at $T_{\mathrm{S}}$ that mediates the opening of a band gap at the Fermi level observed here experimentally (Figs. 1E and 3C).

Fig. 3.

Asymmetric spin–orbit-driven band hybridization. (A) Calculated electronic structure from density-functional theory for the experimental crystal structure at $T=50$ K ($T>T_{\mathrm{S}}$) and with the spin moments aligned along the in-plane $a$ axis, as observed experimentally for $T_{\mathrm{S}}<T\le T_{\mathrm{N}}$. (B and C) Equivalent calculations for (B) the low-temperature crystal structure (for $T=8$ K) with spin moments still oriented along the $a$ axis and (C) the low-temperature crystal structure with spin moments along the $b$ axis, as observed experimentally for $T<T_{\mathrm{S}}$. The schematics in A–C show representative views of the Ru sites in a ${\mathrm{R}\mathrm{u}\mathrm{O}}_2$ bilayer, showing the tilt and resulting local polarization (purple arrows) and the spin moment orientation (green arrows). C, Inset shows the corresponding electronic structure calculated without including spin–orbit coupling, indicating that the hybridization gap which opens at the Fermi level is between spin majority-like (red) and minority-like (blue) Ru $t_{2g}$ states and opens via spin–orbit coupling. (D) The magnitude of the hybridization gap grows smoothly as the moment is rotated away from the $a$ axis within both $ab$ and (green points) and $ac$ (purple points) planes.

The relevant hybridized states at the Fermi level here derive from spin-minority–like and spin-majority–like Ru $t_{2g}$-derived bands (Fig. 3C, Inset)* . The details of the low-energy DFT band structure are sensitive to the precise degree of exchange splitting, which varies with the choice of exchange-correlation functional and is larger when using a generalized gradient approximation functional than using a local density approximation (LDA) one (see SI Appendix, Fig. S2 for a comparison). We find that the LDA calculation better describes the experimental data, with the large hole-like pocket present at $\mathrm{\Gamma }$, although the electron pocket there is not clearly seen in the dispersions measured above $T_{\mathrm{S}}$ (Fig. 2A), and the experimental situation may in fact be best reflected by an exchange splitting that is between the results of these two calculations. We stress, however, that both functionals show qualitatively the same behavior (SI Appendix, Fig. S2), namely a hybridization of zone-center electron and hole-like bands below $T_{\mathrm{S}}$. This hybridization is mediated by spin–orbit coupling (Fig. 3C), with a gap that opens throughout the Brillouin zone (Fig. 1D and cf. Fig. 2C) and develops gradually as the spin moment is rotated away from the $a$ axis (Fig. 3D), but is almost invariant when the moment is rotated between the $b$ and $c$ axes (SI Appendix, Fig. S3).

We attribute this spin moment-dependent gapping to a local breaking of inversion symmetry driven by the $X_3^{-}$ tilt mode of the ${\mathrm{R}\mathrm{u}\mathrm{O}}_6$ octahedra (14, 15). The vertically stacked octahedra of the perovskite bilayer develop hinge-like distortions about the shared apical oxygen, which reverse in direction between neighboring in-plane sites as shown schematically in Fig. 3. Each pair of outer apical oxygens is displaced in the opposite direction to the shared central apical oxygen. This leads to a local polarization oriented along the tilt direction (the $a$ axis here) with an antiferro-type ordering within the $ab$ plane. No net polarization is generated along $a$. Locally, however, an asymmetric spin–orbit coupling of the Rashba type (31–33), ${\mathcal{H}}_{\mathrm{R}}\propto \mathbf{p}\cdot \left(\mathbf{S}\times \mathbf{E}\right)$, can generically be expected, where $\mathbf{p}$ is the electron momentum, $\mathbf{E}$ is an effective internal electric field along the $a$ axis representing the local inversion asymmetry, and $\mathbf{S}$ is the electron spin of the itinerant states, which are fixed along one of the in-plane crystallographic axes by the magnetic moment orientation. This provides a natural explanation for the hybridization of intrabilayer spin-majority and -minority bands observed here. For the spin moment aligned along the $a$ axis (Fig. 3 A and B, $\mathbf{S}\times \mathbf{E}=0$), the Rashba-type term cannot act and thus no hybridization would be expected from this form of spin–orbit coupling. In contrast, at the spin reorientation transition where the moment aligns along the $b$ axis (Fig. 3C), the Rashba-like spin–orbit interaction becomes active ($\mathbf{S}\times \mathbf{E}\ne 0$), enabling the band hybridization.

When the hybridization is allowed, the large hole-like Fermi surface thus becomes gapped. The corresponding hybridization energy scale in our DFT calculations is on the order of 50 meV. In reality, however, the true hybridization gap is renormalized to significantly smaller values due to the strong electronic correlations of this system. We estimate that the true gap magnitude in the low-temperature phase is $\approx 10\text{to}15$ meV, comparable to a 13-meV gap (originally attributed to a pseudogap) which was seen to open in optical spectroscopy measurements upon cooling through $T_{\mathrm{S}}$ (34). The gap size is thus comparable to thermal energy scales at $T_{\mathrm{S}}$. We propose that at the Néel transition, the fluctuating moments of the paramagnetic state above $T_{\mathrm{N}}$ develop a long-range order, with the spin orientation fixed along the $a$ axis by conventional magnetocrystalline anisotropy effects. There is no electronic incentive for orienting the moment along $b$, as the hybridized states above $E_{\mathrm{F}}$ would be thermally populated (Fig. 4); the crystalline terms thus dominate. Upon further cooling, however, the thermal population effects are reduced. The electronic energy gain from the opening of a band gap at the Fermi level thus becomes sufficient to favor the spin reorientation such that local Rashba-type spin–orbit coupling can hybridize the relevant electronic states.

Fig. 4.

Electronically driven magnetocrystalline anisotropy. Shown is a schematic representation of the renormalized electronic structure of the zone-center states corresponding to (Left) $T>T_{\mathrm{S}}$ and (Right) $T<T_{\mathrm{S}}$. At high temperatures, the broad Fermi function leads to thermal population of the states that are pushed upward by band hybridization in the low-temperature case, removing any associated energy gain with hybridizing these states. Upon cooling, this energy gain becomes active, ultimately driving the spin reorientation to enable the band hybridization via Rashba-type spin–orbit coupling.

Our results thus suggest that a Rashba-mediated band hybridization of low-energy states ultimately leads to the first-order magnetic, and accompanying structural, phase transition in ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$. Our analysis has a number of important implications. It identifies a source of magnetic anisotropy in metals where the magnetic moment direction is set by an electronic energy gain from gapping much of the Fermi surface. In that sense it is a “magnetoelectronic” rather than a magnetocrystalline anisotropy. Materials where inversion symmetry is broken either within the host crystal structure or by heterostructuring approaches (9, 13, 35) and at surfaces and interfaces (36, 37) will provide interesting playgrounds in which to seek to stabilize such magnetoelectronic anisotropy via asymmetric spin–orbit coupling as reported here. Other crystalline symmetries could in principle also be used, with the electronic energy gain being driven by spin moment reorientations that break the symmetries which otherwise protect specific band crossings in the vicinity of the Fermi level. Conversely, external switching of the moment orientation, for example via application of magnetic fields, would provide a route to control gapping of the Fermi surface states and through this induce pronounced responses in the transport properties of multiorbital correlated magnets such as ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ studied here.

Materials and Methods

Single-Crystal Growth.

Single crystals of ${\mathrm{C}\mathrm{a}}_3{\mathrm{R}\mathrm{u}}_2{\mathrm{O}}_7$ were grown using a floating-zone method in a mirror furnace (Canon Machinery; model SCI-MDH) (38). The crystal growth was performed in an atmosphere of a mixture of Ar and ${\mathrm{O}}_2$ ($\mathrm{A}\mathrm{r}:{\mathrm{O}}_2=85:15$). In general, antiphase domains can be expected and are visible via contrast in polarized-light optical microscopy (SI Appendix, Fig. S4). We used this to select samples which are single domain over a scale of at least $500\times 500$ $\mathrm{\mu }{\mathrm{m}}^2$. The monodomain nature of our resulting samples is further evident in our measured Fermi surfaces, which show a clear twofold symmetry with no signatures of rotated features coming from different domains.

Angle-Resolved Photoemission.

ARPES measurements were performing using the Bloch beamline of the MAX IV synchrotron and the I05 beamline of Diamond Light Source. Measurements were performed using $p$-polarized 22-eV synchrotron light. Additional data measured using $s$-polarized light are shown in SI Appendix, Fig. S1. The samples were cleaved in situ and measured at temperatures between 6 and 70 K, as specified in Figs. 1 and 2. Temperature-dependent datasets were repeated on multiple samples and via both warming and recooling cycles, confirming that the changes shown in Fig. 2 are intrinsic and are not a result of sample aging upon temperature cycling.

Density-Functional Theory.

DFT calculations were performed using the local spin density approximation (LSDA) exchange-correlation functionals, as implemented in the full-potential local-orbital minimum-basis code (39–41). Additional calculations were performed with the Perdew–Burke–Ernzerhof (PBE) functional (42) and are shown and discussed in SI Appendix, Fig. S2. The experimental crystal structures were used in all cases (11), and spin–orbit coupling was included throughout. The Brillouin zone sampling employed a $k$ mesh of at least $16\times 16\times 6\hspace{0.17em}k$ points. Additional calculations were performed using WIEN2K (43) and gave consistent results. We employed ferromagnetic calculations, neglecting the antiferromagnetic coupling between neighboring bilayers. Given the ferromagnetic ordering within the bilayer and the weak coupling between bilayers, this does not affect any of the key conclusions drawn from our calculations, as confirmed by the broad agreement between our calculations and the experimentally measured electronic structure shown in Fig. 1E.

Data Availability.

The data that underpin the findings of this study are available from the University of St Andrews research portal: https://doi.org/10.17630/e8a98e0e-a6f3-4117-87c7-b1df1607dc81 (44).