Significance
Inspired by the survival war between the “spear” of mantis shrimps with Bouligand-type microstructures and the “shield” of abalone with nacreous staggered architectures, we design an architecture, a combination of Bouligand and nacreous staggered structures, which enables excellent fracture resistance with crack orientation insensitivity. The sophisticated hybrid fracture mode due to the competition of energy dissipations between crack twisting and crack bridging arising in DFB architecture is identified as the origin of maximum fracture energy at a critical pitch angle. This finding sheds light on how nature evolves materials to exceptional fracture toughness and crack orientation insensitivity. The provided design strategies with parameters selection principle enable the fabrication of formidable fracture-resistant fibrous composite systems that adapt to loads in various orientations.
Keywords: biomimetic design, fibrous composite, fracture resistance, toughening mechanism, optimization strategies
Abstract
Bioinspired architectural design for composites with much higher fracture resistance than that of individual constituent remains a major challenge for engineers and scientists. Inspired by the survival war between the mantis shrimps and abalones, we design a discontinuous fibrous Bouligand (DFB) architecture, a combination of Bouligand and nacreous staggered structures. Systematic bending experiments for 3D-printed single-edge notched specimens with such architecture indicate that total energy dissipations are insensitive to initial crack orientations and show optimized values at critical pitch angles. Fracture mechanics analyses demonstrate that the hybrid toughening mechanisms of crack twisting and crack bridging mode arising from DFB architecture enable excellent fracture resistance with crack orientation insensitivity. The compromise in competition of energy dissipations between crack twisting and crack bridging is identified as the origin of maximum fracture energy at a critical pitch angle. We further illustrate that the optimized fracture energy can be achieved by tuning fracture energy of crack bridging, pitch angles, fiber lengths, and twist angles distribution in DFB composites.
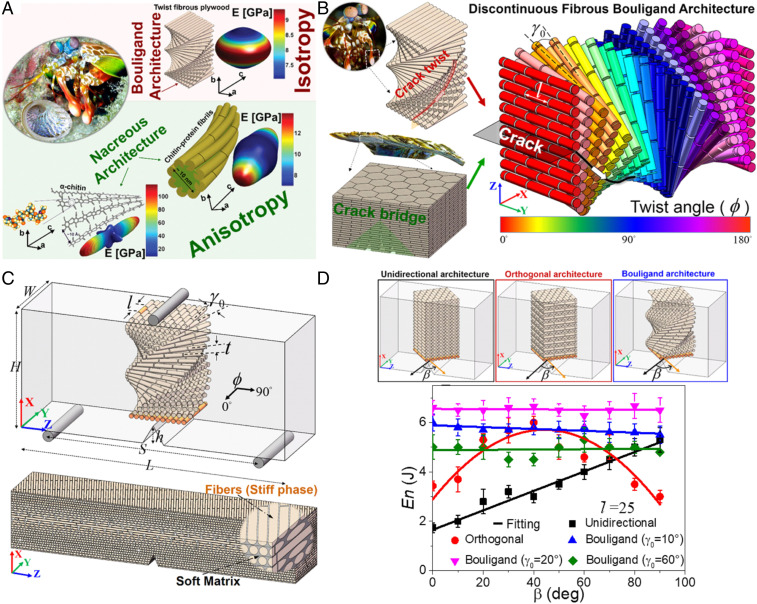
Bioinspired structural designs attract intense interest in achieving remarkable fracture resistance in synthetic fibrous composites (1–3), which provide enhanced fracture toughness well beyond their constituents by controlling crack propagation modes dictated by internal architectures (4, 5). Typically, natural fibrillar materials act as basic building reinforcements to create fracture-resistant materials through controlling fibrillar alignments and orientations in three-dimensional (3D) assembly (6). Varying the arrangements can create materials with vastly different macroscale mechanical properties (1, 2, 6, 7). One prime example is the Bouligand architecture characterized by the stacking of fibrous layers rotated by a pitch angle in chitin nanofibrils-based natural materials (8–18), such as the exoskeleton of arthropods (e.g., crab, lobster, beetles, and shrimp) and mammal bone, etc. The dactyl club of mantis shrimp composed of mineralized chitin nanofibrils lamellae organized in a twisted plywood (Bouligand) structure exhibits exceptional damage resistance (9, 11, 16, 17). In the survival war between mantis shrimps and abalones (Fig. 1A), the abalones are often the prey of mantis shrimps, and in general, the “spear” of mantis shrimps armed with powerful dactyl clubs can often shatter the “shield” of hard abalone (19). This is particularly intriguing because these abalone shells composed of mineral crystals and protein matrix with “brick-and-mortar” arrangements (i.e., nacreous architecture) are themselves considered a benchmark of supertough biocomposites (20–24). Given that both Bouligand and nacreous structures show considerable reinforcement, it is still elusive whether the Bouligand structure in its “spear” plays important role in the competition of mantis shrimp as the winner or not. Recent studies demonstrated that when the arrangements of fibrils in crustacean cuticle change from the nacreous staggered structure with an orientation along the longitudinal axis to the Bouligand pattern, the anisotropic elasticity of the structure decreases monotonously (6, 25) (Fig. 1A). This motivates us that Bouligand-type arrangements may provide efficient ways to achieve excellent mechanical performances without fiber orientation dependence, which is a severe limit in unidirectional fibrous composites (6, 26).
Fig. 1.
Structural design for DFB composites. (A) Survival wars between mantis shrimps and abalones (9), and 3D maps of Young’s modulus for different architectures in crustacean cuticle, where chitin–protein nanofibrils with a nacreous array show high anisotropy, while fibrous plywood with Bouligand architecture exhibits in-plane isotropy (25). (B) Structural characteristics in a pitch for a DFB architecture, a combination of Bouligand and nacreous structure. (C) Geometric configurations for 3D-printed single-edge notched bend specimens with DFB architecture. (D) Effects of the orientation of initial crack tip on the total energy dissipation En in the unidirectional, orthogonal, and Bouligand architectures with discontinuous fibers, respectively. Error bars represent 1 SD measured over at least three samples.
Recent investigations revealed that crack twisting mode significantly enhances fracture toughness in the Bouligand architecture where a crack plane propagates following the twisted fiber orientation (27–33). This amplifies the crack surface area and reorients fibers orientation in response to external loadings (27–29, 33), e.g., tension, bending, or impact loads. The resultant modulus oscillation in the Bouligand structure is also proposed to promote the crack twisting (30). For nacreous architectures, the crack bridging mode arising from the discontinuous platelets’ pull-out and sliding in the crack front provides enhanced toughness (23, 24, 34, 35). Both bioinspired toughening mechanisms have been successfully applied in engineering composites (22, 36–39), respectively, e.g., the impact-resistant nacreous glass and the tough Bouligand composites. Remarkably, experiments and theoretical analyses demonstrated that crack twisting and fibril bridging may coexist during the fracturing process in the natural materials with Bouligand structures, e.g., the stomatopod dactyl club and arapaima fish scale (16, 17, 40–43). In the meanwhile, experimental investigations showed that there exist critical pitch angles (the angle difference in orientation of adjacent fiber layers) corresponding to maximum fracture toughness in synthetic twisted plywood materials (37). In natural structural materials, the beetle exocuticle with Bouligand structure has a specific pitch angle about 12° to 18° and a linear twist angles distribution in a pitch (a distance for a 180° rotation) (44), and the pitch angles are about 6.2° and 22.5° in the stomatopod dactyl club (36) and the spearer telson of Lysiosquillina maculata (17), respectively. However, most previous models of twisted plywood with continuous fibers did not predict the experimentally observed hybrid toughening mechanisms of crack bridging and crack twisting. In particular, some key questions remain to be explored at present. Why a specific pitch angle and a linear twist angle distribution in a pitch are so important in such Bouligand architectures? How can we learn this to design superior fibrous composites with optimized fracture resistance by using 3D-printing technology since it provides precisely controlling for internal geometric parameters (45–48)? Here, we carried out three-point bending tests and developed a fracture mechanics model for a designed 3D-printed discontinuous fibrous Bouligand (DFB) architecture with the combination of Bouligand and nacreous staggered structures, which provides the answers to the above questions.
Results and Discussion
Experimental Investigations for a DFB Architecture.
Inspired by the structural arrangements in the exoskeleton of aggressive crustaceans (e.g., crab, lobster, or mantis shrimps), where the chitin–protein nanofibrils with finite characteristic length are arranged in a overlapped array to form lamellae and the chitin–protein fibrils lamellae are arranged in the twisted plywood pattern (9, 17, 25, 44) (Fig. 1A), although not only the structure but also the mechanical properties of the materials, size, and geometry play important roles in the competition between mantis shrimp and abalone shells in nature, we hypothesize that the structure that exhibits the combination of the toughening mechanisms of crack twisting and crack bridging endows the mantis shrimps with remarkable fracture resistance as well as crack orientation insensitivity. To prove our hypothesis, we designed a DFB architecture with the combination of Bouligand and nacreous staggered structures by 3D printing to examine how the fracture resistance depends on the controlled architectural parameters (Fig. 1B). It is worth mentioning that although the architecture of natural materials is not a standard DFB structure, the hybrid-toughening mechanism in the designed DFB structure is consistent with that in natural Bouligand materials (9, 16, 17, 43). In Fig. 1B, a rotation of 180° in DFB architectures is characterized by pitch angle , dimensionless fiber length ( is the fiber diameter) and twist angle distribution along the crack propagation direction (x axis). The orientation of fiber aligned with the y axis is defined as ϕ = 0° and the fiber layers rotate in the counterclockwise direction around x axis. The discontinuous fibers are regularly staggered with a 50% offset length in a planar nacreous array. The dimensions for 3D-printed three-point bending composites with single-edge notches were illustrated in Fig. 1C, where L, W, H, S, t, and h denote length, width, height, span length, interlayer space and notch length, respectively. The composites composed of hard fibers (VeroWhitePlus, a rigid polymer with a Young’s modulus of 0.8 GPa) and soft matrix (TangoblackPlus, a rubber-like polymer with a Young’s modulus of 0.2 MPa) with DFB arrangements were fabricated using multimaterials 3D-printing technology, and the high modulus contrast between the fibers and matrix phases promotes crack twisting along the interface. The details of the fabrication and mechanical testing of these samples are provided in Materials and Methods and SI Appendix, Supplementary Discussion 1 and Fig. S1).
We designed unidirectional, orthogonal, and Bouligand architectures with discontinuous fibers under different initial crack orientations (Fig. 1D), where the angle between the axis of initial fiber layer at notch tip and direction of the notch front (y axis) is defined as initial crack orientation , and the subsequent fiber layers are stacked in order according to pitch angle. The same three-point bending testing conditions and geometries (H = 22.5 mm, L = 5H, W = H, t = 0.9 mm, and h = H/5) are applied to all of the samples. Fig. 1D plots the total energy dissipations En in these samples as a function of given a fiber length , respectively. The values of En were obtained by integrating the force–displacement curves (SI Appendix, Fig. S2A). The En in unidirectional discontinuous fibrous composites linearly increases with . For the orthogonal discontinuous fibrous composites, En reaches maximum at β = 45°. In contrast, the values of En become insensitive to in DFB composites. In addition, the crack orientation insensitivity holds in DFB architecture under different pitch angles . Interestingly, the values of En in DFB architecture are nonmonotonically dependent on and can be higher than that in unidirectional or orthogonal architecture. The results in Fig. 1D clearly show higher energy dissipations with crack orientation insensitivity in DFB composites with an optimal pitch angle, in comparison with unidirectional discontinuous fibrous structure with nacreous staggered arrangement, which may, at least partially, explain why the stomatopod dactyl club with Bouligand structure can often shatter the hard abalone with nacreous structure in nature from a view of a structure level.
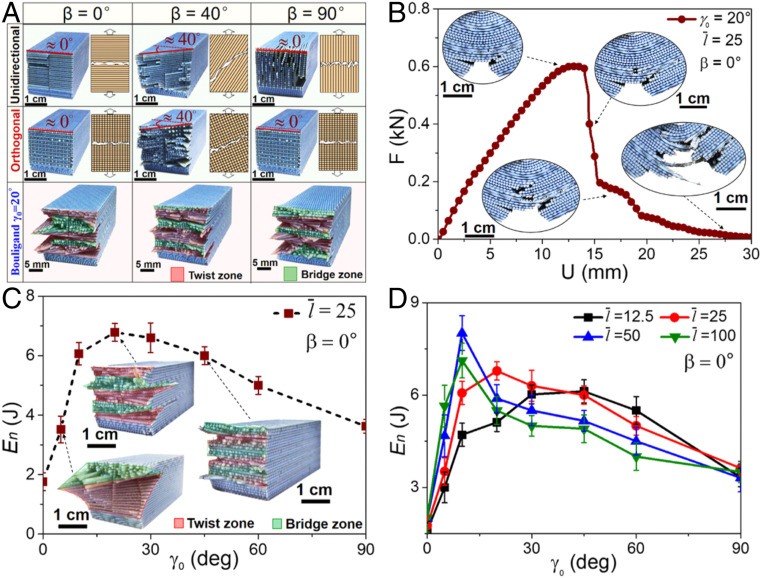
Furthermore, Fig. 2A demonstrates the postmortem fracture surface patterns of the tested specimens in Fig. 1D, respectively. In the unidirectional discontinuous fibrous architecture, the fibers can separate by opening interfibrillar gaps and the crack propagates along the soft interface between fibers when is small, while lots of fibers pull out and fracture when increases to 90°, and the tilted angle between the crack surface and the notch front is around 40° at β = 40°. Flat brittle failure surfaces with the breakage of fibers oriented along the loading axis are shown in the orthogonal discontinuous fibrous samples under β = 0° or 90°, and only half of the fibers in whole structure carry loads. However, a tilted zigzag brittle fracture surface oriented at about 40° is shown in the sample when β = 40°. Based on the curve fitting of experimental results, the area of fracture surface reaches maximum when the crack orientation is about 45°, which leads to the maximum energy dissipation in the orthogonal discontinuous fibrous structure (SI Appendix, Fig. S2B). For DFB structures with a pitch angle of 20°, the fracture surfaces morphologies clearly demonstrate the combination of crack-twisting zones and crack-bridging zones, which are consistent with multiple deformation mechanisms acting in natural Bouligand materials (9, 17, 43). In crack-twisting zones, crack plane propagates following the twisted fiber orientation. In the crack-bridging zones where the fibers are nearly parallel to the loading direction, separation of columnar stacks of fibers occurs due to discontinuous fibers’ pull-out and breakage. It is worth mentioning that the fiber fracture and the fiber pull-out are all considered as bridging toughening mechanisms and are not strictly distinguished in our work, and they all promote the fracture toughness of crack bridging. The effective area of the fracture surface in a pitch remains constant due to crack-twisting propagation in Bouligand-type architecture and is insensitive to initial crack orientations. Meanwhile, the crack-bridging toughening mechanism and the amplified fracture surface area caused by crack twisting result in much higher energy dissipation level. Therefore, the hybrid toughening mechanisms of crack twisting and bridging in DFB architecture enable excellent fracture resistance with crack orientation insensitivity.
Fig. 2.
Experimental characterizations of the 3D-printed DFB composites. (A) Fracture morphologies for the unidirectional, orthogonal, and Bouligand architectures with different initial crack orientations . (B) A force–displacement curve for the samples with , and β = 0°, and the Insets show the crack propagation paths. (C) Energy dissipation En of the structure with under different pitch angles . (D) En– curves for the DFB structure with different . Pseudocolor is applied to highlight the fracture patterns include crack-twisting zone (red) and crack-bridging zone (green) in A and C. Error bars in C and D represent 1 SD measured over at least three samples.
To examine how the fracture performances of DFB composites depend on the pitch angle , we carry out a series of three-point bending tests on 3D-printed samples with precisely designed pitch angles and fiber length at β = 0°. Some representative CAD models and force–displacement responses for the DFB composites under different pitch angles are shown in SI Appendix, Fig. S1 E and F. The snapshots and a typical force–displacement curve in Fig. 2B clearly demonstrate the fracture propagation paths included the crack twisting and the fiber bridging. It is worth mentioning that based on the experimental observation of dominating crack twisting, bridging, and insignificant crack branching, we ignored the possibility of crack branching during the crack growth in current DFB structure, which is different from the fracturing process in some fiber-reinforced composite materials. More comprehensive analyses considering more toughening mechanisms (crack branching and delamination) are of our research interest in the next step. Fig. 2C shows that the total energy dissipation En reaches maximum at a critical pitch angle (γ0 ≈ 25°), which is in good agreement with previous investigations for critical pitch angles in natural materials, e.g., the pitch angle in beetle exocuticle is about 20° and the fracture toughness reaches maximum when γ0 ≈ 15° in synthetic twisted composites (37, 44). The fracture surfaces for the samples with γ0 = 5°, 20°, and 45° clearly show the hybrid fracture mode of crack twisting and crack bridging (see Insets in Fig. 2C). As the pitch angle increases, the fracture surface morphologies change from crack-twisting–dominated pattern to crack-bridging–dominated pattern, and proportions for the crack-twisting zones and the crack-bridging zones become nearly equal at the optimized pitch angle. In contrast, the Bouligand structures with continuous fibers show an obvious catastrophic delamination, which significantly weakens structural integrity, and an optimal pitch angle at which the fracture toughness reaches maximum does not exist anymore (SI Appendix, Fig. S10). Furthermore, experimental results in Fig. 2D show that the critical pitch angle decreases as the fiber length increases. This may explain why different values of the critical pitch angle in fibrous Bouligand architectures are experimentally reported.
Fracture Mechanics Analyses.
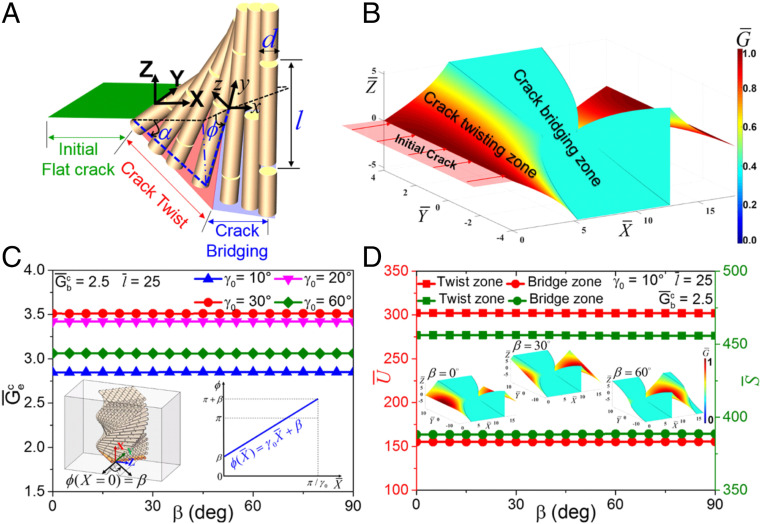
Furthermore, we developed a fracture mechanics model to elucidate the mechanism of crack orientation insensitivity and maximum energy dissipations in DFB architecture. As shown in Fig. 3A, a model that takes crack twisting and crack bridging into consideration simultaneously is developed, and details can be seen in Materials and Methods and SI Appendix, Supplementary Discussion 2–4. Based on the maximum energy release rate criterion in fracture mechanics, the fracture mode of crack bridging happens when the local energy release rate for driving crack twisting (see Eq. 3) is lower than that for crack bridging (Eq. 4). In the following calculations, we choose a representative value for the dimensionless fracture energy of crack bridging , where is the intrinsic fracture energy for steady-state crack propagation). The value is close to the values of for 3D-printed DFB composites in above experiments, the twisted chitin nanofibrils-based exoskeleton of beetles, and the synthetic twisted cellulose composites (44, 49, 50), and the detailed calculations for can found in SI Appendix, Supplementary Discussion 5. Fig. 3B shows a representative crack surface morphology and the localized energy release rate distribution in the DFB structure with γ0 = 10°, , and β = 0°. The values of the normalized local energy release rate , where is the global energy release rate) dramatically decrease as the crack propagates following the twisted fiber orientation, forming the crack-twisting zone first. Then, the crack propagates across the fibers when is too low to drive the twisting crack further propagate, forming crack-bridging zone. With the further propagation of crack plane, the increases and fracture mode returns to the crack-twisting mode. The calculated crack surface morphologies with the combination of crack-twisting zones and crack-bridging zones are in good agreement with that in experimental investigations for 3D-printed DFB composites and natural Bouligand materials (9, 17, 43).
Fig. 3.
Fracture mechanics prediction of the DFB structure. (A) Schematic of a fracture mechanics model considering crack twisting and bridging simultaneously. (B) The dimensionless local energy release rate and crack surface morphology for DFB structure with , γ0 = 10°, and . (C) The effects of initial crack orientation on the dimensionless effective fracture energy in the DFB structure under different pitch angles . (D) The values of the dimensionless released strain energy and the dimensionless crack surface area in crack-twisting zones and crack-bridging zones of the structure under different , and the Insets show the distribution of and the crack surface morphologies under different .
Fig. 3C plots the dimensionless effective fracture energy (Eq. 7) as a function of initial crack orientation in DFB architectures under different pitch angles based on the fracture mechanics model. The Insets in Fig. 3C show that the twist angle of the initial fiber layer is in the schematic configuration and the twist angle changes linearly from to in a pitch, and the detailed calculations can be seen in SI Appendix, Supplementary Discussion 3. The calculated results show that the values of in the DFB structure are really insensitive to under different (Fig. 3C), which are in good agreement with our experimental results (Fig. 1D). Fig. 3D shows that the values of released strain energy (Eq. 6) and crack surface area in crack-twisting zones and crack-bridging zones do not vary with . The Insets in Fig. 3D illustrate that, although the initial crack orientation alters the distribution of local energy release rates and the morphologies of crack surface composed of the alternation of crack-twisting zones and crack-bridging zones, the sum of crack surface area in crack-twisting zones and crack-bridging zones remains constant in a pitch under different . This insensitivity to originates from the fact that the Bouligand-type arrangements of the inner fibrous layers can adapt to different by forming twisting fracture paths and reorienting the lamellae in response to loads in different orientations. Meanwhile, both crack twisting and crack bridging significantly enhance the fracture toughness of the DFB structure. The theoretical results in Fig. 3 elucidate why the DFB architecture enables exceptional crack orientation insensitivity.
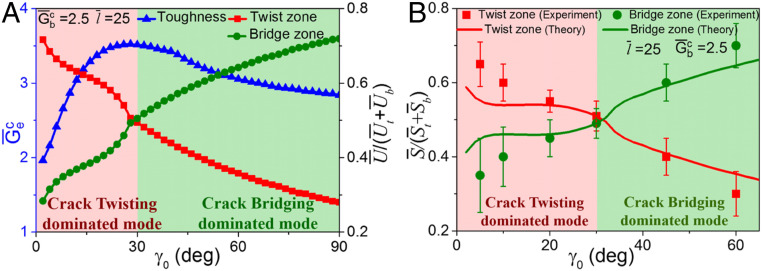
The theoretical results in Fig. 4A also show that there exists a critical pitch angle at which the effective fracture energy reaches maximum in the DFB architecture with and . In the meanwhile, the values of critical pitch angles decrease as the fiber length increases (SI Appendix, Fig. S4A). Both theoretical predictions are in good agreement with our experimental data in Fig. 2 C and D. Typically, for chitin–protein fibers of the exoskeleton of beetles (44), the fiber length is around , the optimized pitch angle for the largest fracture energy is calculated as about 16° based on our model, which agrees well with the experimental measurements. To further reveal the underlying mechanism of the existence of critical pitch angle, we analyzed the values of released strain energy contributed by crack-twisting mode and crack-bridging mode under different based on Eq. 6 in Materials and Methods, respectively (Fig. 4A and SI Appendix, Fig. S4). Fig. 4A shows that with the increase of , the proportion of released strain energy in crack-twisting zone decreases, while that in crack-bridging zone increases. At the critical pitch angle, there is a compromise in competition of strain energy release between crack twisting and crack bridging. This mechanism is further validated when we theoretically and experimentally calculated the proportion of crack area in crack-twisting zone and that in crack-bridging zone with respect to the change of the pitch angle as shown in Fig. 4B. The crack surface area of crack-twisting zone and that of crack-bridging zone become roughly equal at critical pitch angles. In contrast, there is no critical pitch angle with respect to maximum fracture energy when the fracture mode is dominated by crack twisting or by crack bridging only. For example, the values of released strain energy contributed by crack twisting are much higher than that caused by crack bridging under different in structure with and , which represents crack-twisting–dominated fracture mode (SI Appendix, Fig. S4B). Conversely, SI Appendix, Fig. S4C shows that the values of released strain energy in crack-bridging zone are much higher than that in crack-twisting zone at different in the case of crack-bridging–dominated fracture mode ( and ). In the structure with crack-twisting–dominated mode, the local energy release rates dramatically decrease as increase, so increases with the increase of the (SI Appendix, Fig. S4B). However, as the increases, the significant decrease of the area of twist crack surface results in the decrease of in the structure with crack-bridging–dominated mode (SI Appendix, Fig. S4C). Furthermore, SI Appendix, Fig. S4D shows that that there also exists an optimal fiber length at which the fracture energy reaches maximum in DFB structure, and the calculated results are consistent with the experimental results in Fig. 2D.
Fig. 4.
Optimized effective fracture energy in DFB architecture. (A) The dimensionless effective fracture energy , and the proportions of released strain energy in crack-twisting zone and crack-bridging zone under different pitch angles . (B) Experimental investigations and theoretical calculations for the proportions of crack surface area in the crack-twisting zone and crack-bridging zone under different . The background color in A and B represents the fracture modes include crack-twisting–dominated mode (red) and crack-bridging–dominated mode (green). Error bars in B represent 1 SD measured over at least three samples.
To answer why twist angle distribution in a pitch of natural Bouligand architectures [e.g., stomatopod dactyl club (9) and beetle exocuticle (44)] is linear, we designed nonlinear twist angles distribution in a pitch of the 3D-printed DFB composites to reveal the effects of the twist angle distribution on the fracture-resistance (SI Appendix, Figs. S5 and S6), and the detailed calculations and discussions can be seen in Materials and Methods and SI Appendix, Supplementary Discussion 4. Our calculated results (SI Appendix, Fig. S5) show that the effective fracture energy in the DFB structure with nonlinear twist angle distribution is lower than that in the system with linear twist angle distribution. In addition, the optimized fracture energy for the DFB composites with nonlinear twist angles distribution can also be achieved through tuning the pitch angles and fiber length (SI Appendix, Fig. S5 E and F). These trends predicted by fracture mechanics model are consistent with that in experimental measurements of 3D-printed DFB composites with nonlinear twist angles distribution (SI Appendix, Fig. S6). The above analyses demonstrate that linear twist angle distribution in a pitch in comparison to the selected nonlinear twist angle distribution may facilitate higher resistance to fracture.
Optimization Design.
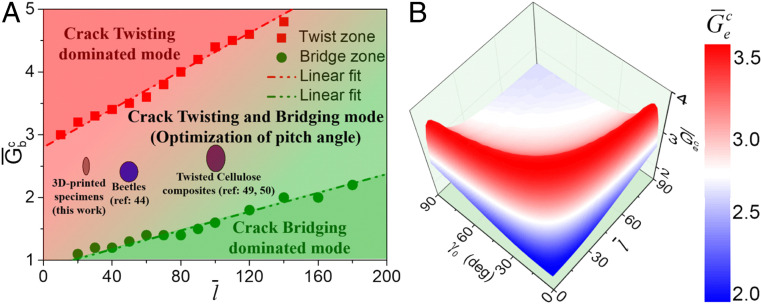
For DFB architecture with linear twist angle distribution, the pith angle , the fiber length , and the fracture energy of crack-bridging are key structural parameters for achieving formidable fracture resistance. Fig. 5A shows a phase diagram of dominated fracture modes depending on and in DFB architecture based on fracture mechanics model. The fracture mode is dominated by crack-bridging mode in the structure with larger and smaller , yet the smaller and larger leads to crack-twisting–dominated mode. There is a region for the hybrid fracture mode of crack-twisting and -bridging mode. In the region of the hybrid fracture mode, the effective fracture energy can be optimized at the critical pitch angles. Remarkably, the values of for 3D-printed DFB composites with , the beetles’ exoskeleton (44) containing chitin–protein fibers with and the synthesized twisted cellulose composites (49, 50) with are estimated around 2.5, 2.41, and 2.62, respectively (details in Supplementary Discussion 5). Fig. 5A shows that the fracture mode for these materials with Bouligand structure is really in the region of hybrid fracture mode; thereby, there exists critical pitch angles at which the effective fracture energy reaches maximum. Fig. 5B further plots as a function of and in the DFB architecture with , which provides a representative optimization scheme for the structures with the hybrid fracture mode. The above analyses explain why there exist a specific pitch angle in natural Bouligand composites and provide quantitative designing guidelines for DFB composites with multiple fracture mechanisms. Furthermore, quantitative comparisons between the DFB structure and other typical architectures, including hard-bulk structure, nacre-like structure, cross-lamellar structure, and continuous fibrous Bouligand architecture, have been presented in Supplementary Discussion 7 and SI Appendix, Figs. S8–S10, which clearly show that the DFB structure with an optimized pitch angle exhibits more superior quasistatic fracture resistance. In addition, the measured flexural strength of DFB structure increases with the decrease of the size of the fiber diameter (SI Appendix, Fig. S11), which agrees with the scaling law of the mechanical properties of fibrous composites (51). Therefore, we believe superior fibrous composites with optimized effective fracture energy by using 3D-printing technology or other composite manufacturing technologies can be designed through precisely controlling pitch angles, fiber lengths, fiber diameter, fracture energy of crack bridging, and twist angles distribution in the DFB architecture.
Fig. 5.
Optimization design for the DFB composites. (A) A phase diagram for fracture modes depending on the fracture energy of crack bridging and the fiber length, and there exists optimized effective fracture energy in the structure with the crack-twisting and -bridging mode at critical pitch angles. The fracture modes in 3D-printed DFB composites, exoskeleton of beetles, and the twisted cellulose composites (44, 49, 50) are crack-twisting and -bridging mode. (B) A representative plot for the dimensionless effective fracture energy as a function of the pitch angles and fiber length in the DFB architecture with .
Conclusion
In summary, we designed a DFB architecture, a combination of Bouligand and nacreous structures, which results in hybrid fracture modes of crack twisting and crack bridging. Three-point bending tests for 3D-printed specimens and fracture mechanics analyses reveal that the sophisticated hybrid fracture modes arising in DFB architecture leads to significantly enhanced fracture resistance and crack orientation insensitivity. The compromise in competition between the two toughening mechanisms leads to maximized effective fracture energy at a critical pitch angle in DFB structure with a linear distribution. Furthermore, we proposed structural design strategies for the optimized effective fracture energy depending on the pitch angles, fiber lengths, fracture energy of crack bridging, and twist angles distribution in DFB composites. Our findings shed light on how nature has evolved materials to exceptional fracture toughness and provide the generic design strategies for bioinspired formidable fracture-resistant fibrous composite systems that adapt to loads in various orientations.
Materials and Methods
Fracture Mechanics Model.
To understand the effects of crack orientation , the pitch angles , discontinuous fibers length , and twist angle distribution in a rotation of 180° on the fracture energy of the DFB composites, we developed a fracture mechanics model with the combination of crack twisting and crack bridging, as illustrated in Fig. 3A and SI Appendix, Fig. S3. The details of theoretical derivations can be seen in SI Appendix, Supplementary Discussions 2–4 and Fig. S3.
The configurations of Bouligand layups are described by a power function:
| [1] |
where the crack orientation is the angle between the axis of initial fiber layer at notch tip and direction of the notch front (y axis). represents linear distribution of twist angle along the crack propagation direction (x axis), i.e., the pitch angle in a pitch is constant, represents nonlinear convex function distribution of twist angle and represents nonlinear concave function distribution of twist angle (SI Appendix, Fig. S5A).
The twisted crack shape can be described by the following:
| [2] |
whereis dimensionless coordinates along the crack propagation direction, , ; is the dimensionless length of discontinuous fibers, and is the fiber diameter.
The local energy release rate of crack twisting can be calculated as follows (27, 52):
| [3] |
where , , and are the local stress intensity factors described by the twisted angle and tilted angle , is Young’s modulus, and is Poisson’s ratio. And the normalized local energy release rate for crack twisting is defined as , where is the global energy release rate and is the global applied intensity factor of mode I fracture.
Based on the crack-bridging model (34), the normalized local energy release rate and the normalized fracture energy for crack bridging are given by the following:
| [4] |
where is the toughening ratio induced by crack bridging, and is the intrinsic fracture energy for steady-state crack propagation, which is a material constant reflecting the energy dissipation by the breakage of matrix materials.
Based on the maximum energy release rate fracture criterion, the normalized energy release rate for the DFB structure can be calculated as follows:
| [5] |
The released strain energy in crack-twisting zone and crack-bridging zone can be calculated by the integration of the local energy release rate and crack area:
| [6] |
where is the dimensionless area of crack-twisting zone, and is the area of crack-bridging zone.
The dimensionless effective fracture energy with respect to the area of undeflected crack plane can be calculated by the following (52):
| [7] |
where is the angle between the normal to the twisted crack surface and normal to the undeflected crack plane.
Microstructure Design and 3D Printing-Based Fabrication.
The three-point bending specimens with different architectures were 3D printed from designed CAD models by using an Objet260 Connex 3D printer (Stratasys Ltd.). The printer is capable to print multiple materials simultaneously and has a print precision of 16 μm in the layer deposition direction and 600 dpi in the print plane. As shown in Fig. 1C, the dimensions of the 3D-printed single-edge notched bend samples consisted of 25 layers are H = 22.5 mm, L = 5H, W = H, t = 0.9 mm, h = H/5, d = 0.8 mm, and S = 80 mm, where H, L, W, t, h, d, and S denote height, length, width, interlayer space, notch length, the fiber diameter, and span length, respectively. The span length to height ratio is about 4, which ensures small end effect in the middle, and the printed crack front is further sharpened with a fresh razor blade. For the structures with different initial crack orientations, the orientation of the initial fiber layer is (Fig. 1D). The unidirectional architectures are composed of discontinuous fibers with a consistent orientation the same as the orientation of the initial fiber layer at the notch front. In the orthogonal discontinuous fibrous composites, the orientation of initial fibers layer at the notch tip is , and the subsequent orthogonally aligned fibers layers are stacked to form the structure. The DFB composites with different pitch angles are arranged with twisted plywood stacking of discontinuous fibers layers. The theoretical volume fraction of the fibers with these parameters corresponds to around 70%. The discontinuous fibers are made of a rigid polymer (VeroWhitePlus; Young’s modulus is 0.8 ± 0.2 GPa), and the matrix is made of a soft rubber-like polymer (TangoblackPlus; Young’s modulus is 0.2 ± 0.05 MPa). The details of base materials parameters are reported in SI Appendix, Supplementary Discussion 1 and Fig. S1.
Mechanical Testing.
The three-point bending tests were carried out on a Material Test System (MTS criterion 43, MTS System Company) with constant displacement mode using 5-kN load cells. All tests were performed with a support span of 80 mm at a loading rate of 0.5 mm/min. The failure morphologies of samples were recorded by a camera. The area of crack twist zones and crack bridge zones was measured by ruler based on the postfailure surface of experiment samples. The detailed characterizations of the postfailure patterns in 3D-printed samples can be seen in SI Appendix, Supplementary Discussion 6 and Fig. S7.
Data Availability.
All data are included in the manuscript and SI Appendix.
Supplementary Material
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant 11672285), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant XDB22040502), the Collaborative Innovation Center of Suzhou Nano Science and Technology, and the Fundamental Research Funds for the Central Universities (WK2090040043). This work was partially carried out at the University of Science and Technology of China Center for Micro- and Nanoscale Research and Fabrication.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2000639117/-/DCSupplemental.
References
- 1.Meyers M. A., McKittrick J., Chen P.-Y., Structural biological materials: Critical mechanics-materials connections. Science 339, 773–779 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Wegst U. G., Bai H., Saiz E., Tomsia A. P., Ritchie R. O., Bioinspired structural materials. Nat. Mater. 14, 23–36 (2015). [DOI] [PubMed] [Google Scholar]
- 3.Liu Z., Meyers M. A., Zhang Z., Ritchie R. O., Functional gradients and heterogeneities in biological materials: Design principles, functions, and bioinspired applications. Prog. Mater. Sci. 88, 467–498 (2017). [Google Scholar]
- 4.Huang W.et al., Multiscale toughening mechanisms in biological materials and bioinspired designs. Adv. Mater. 31, e1901561 (2019). [DOI] [PubMed] [Google Scholar]
- 5.Ritchie R. O., The conflicts between strength and toughness. Nat. Mater. 10, 817–822 (2011). [DOI] [PubMed] [Google Scholar]
- 6.Ling S., Kaplan D. L., Buehler M. J., Nanofibrils in nature and materials engineering. Nat. Rev. Mater. 3, 18016 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Naleway S. E., Porter M. M., McKittrick J., Meyers M. A., Structural design elements in biological materials: Application to bioinspiration. Adv. Mater. 27, 5455–5476 (2015). [DOI] [PubMed] [Google Scholar]
- 8.Bouligand Y., Twisted fibrous arrangements in biological materials and cholesteric mesophases. Tissue Cell 4, 189–217 (1972). [DOI] [PubMed] [Google Scholar]
- 9.Weaver J. C.et al., The stomatopod dactyl club: A formidable damage-tolerant biological hammer. Science 336, 1275–1280 (2012). [DOI] [PubMed] [Google Scholar]
- 10.Ritchie R. O., Natural materials: Armoured oyster shells. Nat. Mater. 13, 435–437 (2014). [DOI] [PubMed] [Google Scholar]
- 11.Grunenfelder L. K.et al., Ecologically driven ultrastructural and hydrodynamic designs in stomatopod cuticles. Adv. Mater. 30, 1705295 (2018). [DOI] [PubMed] [Google Scholar]
- 12.Kellersztein I., Cohen S. R., Bar-On B., Wagner H. D., The exoskeleton of scorpions’ pincers: Structure and micro-mechanical properties. Acta Biomater. 94, 565–573 (2019). [DOI] [PubMed] [Google Scholar]
- 13.Fabritius H. O., Sachs C., Triguero P. R., Raabe D., Influence of structural principles on the mechanics of a biological fiber-based composite material with hierarchical organization: The exoskeleton of the lobster Homarus americanus. Adv. Mater. 21, 391–400 (2009). [Google Scholar]
- 14.Wu J.et al., Natural hydrogel in American lobster: A soft armor with high toughness and strength. Acta Biomater. 88, 102–110 (2019). [DOI] [PubMed] [Google Scholar]
- 15.Quan H., Yang W., Schaible E., Ritchie R. O., Meyers M. A., Novel defense mechanisms in the armor of the scales of the “living fossil” coelacanth fish. Adv. Funct. Mater. 28, 1804237 (2018). [Google Scholar]
- 16.Yaraghi N. A.et al., A sinusoidally architected helicoidal biocomposite. Adv. Mater. 28, 6835–6844 (2016). [DOI] [PubMed] [Google Scholar]
- 17.Yaraghi N. A.et al., The stomatopod telson: Convergent evolution in the development of a biological shield. Adv. Funct. Mater. 29, 1902238 (2019). [Google Scholar]
- 18.Zimmermann E. A., Ritchie R. O., Bone as a structural material. Adv. Healthc. Mater. 4, 1287–1304 (2015). [DOI] [PubMed] [Google Scholar]
- 19.Li X.et al., Spear and shield: Survival war between Mantis shrimps and abalones. Adv. Mater. Interfaces 2, 1500250 (2015). [Google Scholar]
- 20.Mao L.-B.et al., Synthetic nacre by predesigned matrix-directed mineralization. Science 354, 107–110 (2016). [DOI] [PubMed] [Google Scholar]
- 21.Gao H.-L.et al., Mass production of bulk artificial nacre with excellent mechanical properties. Nat. Commun. 8, 287 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yin Z., Hannard F., Barthelat F., Impact-resistant nacre-like transparent materials. Science 364, 1260–1263 (2019). [DOI] [PubMed] [Google Scholar]
- 23.Gao H., Ji B., Jäger I. L., Arzt E., Fratzl P., Materials become insensitive to flaws at nanoscale: Lessons from nature. Proc. Natl. Acad. Sci. U.S.A. 100, 5597–5600 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ni Y., Song Z., Jiang H., Yu S., He L., Optimization design of strong and tough nacreous nanocomposites through tuning characteristic lengths. J. Mech. Phys. Solids 81, 41–57 (2015). [Google Scholar]
- 25.Nikolov S.et al., Revealing the design principles of high-performance biological composites using ab initio and multiscale simulations: The example of lobster cuticle. Adv. Mater. 22, 519–526 (2010). [DOI] [PubMed] [Google Scholar]
- 26.Arridge R., Fracture of fibre reinforced materials. Nature 223, 941 (1969). [Google Scholar]
- 27.Suksangpanya N., Yaraghi N. A., Kisailus D., Zavattieri P., Twisting cracks in Bouligand structures. J. Mech. Behav. Biomed. Mater. 76, 38–57 (2017). [DOI] [PubMed] [Google Scholar]
- 28.Zimmermann E. A.et al., Mechanical adaptability of the Bouligand-type structure in natural dermal armour. Nat. Commun. 4, 2634 (2013). [DOI] [PubMed] [Google Scholar]
- 29.Jia Z., Yu Y., Hou S., Wang L., Biomimetic architected materials with improved dynamic performance. J. Mech. Phys. Solids 125, 178–197 (2019). [Google Scholar]
- 30.Fischer F. D., Kolednik O., Predan J., Razi H., Fratzl P., Crack driving force in twisted plywood structures. Acta Biomater. 55, 349–359 (2017). [DOI] [PubMed] [Google Scholar]
- 31.Zaheri A.et al., Revealing the mechanics of helicoidal composites through additive manufacturing and beetle developmental stage analysis. Adv. Funct. Mater. 28, 1803073 (2018). [Google Scholar]
- 32.Gao Y., Guo Z., Song Z., Yao H., Spiral interface: A reinforcing mechanism for laminated composite materials learned from nature. J. Mech. Phys. Solids 109, 252–263 (2017). [Google Scholar]
- 33.Yin S.et al., Hyperelastic phase-field fracture mechanics modeling of the toughening induced by Bouligand structures in natural materials. J. Mech. Phys. Solids 131, 204–220 (2019). [Google Scholar]
- 34.Shao Y., Zhao H.-P., Feng X.-Q., Gao H., Discontinuous crack-bridging model for fracture toughness analysis of nacre. J. Mech. Phys. Solids 60, 1400–1419 (2012). [Google Scholar]
- 35.Pro J. W., Barthelat F., The fracture mechanics of biological and bioinspired materials. MRS Bull. 44, 46–52 (2019). [Google Scholar]
- 36.Grunenfelder L. K.et al., Bio-inspired impact-resistant composites. Acta Biomater. 10, 3997–4008 (2014). [DOI] [PubMed] [Google Scholar]
- 37.Chen S.-M.et al., Biomimetic twisted plywood structural materials. Natl. Sci. Rev. 5, 703–714 (2018). [Google Scholar]
- 38.Mencattelli L., Pinho S. T., Realising bio-inspired impact damage-tolerant thin-ply CFRP Bouligand structures via promoting diffused sub-critical helicoidal damage. Compos. Sci. Technol. 182, 107684 (2019). [Google Scholar]
- 39.Chen R.et al., Transparent impact-resistant composite films with bioinspired hierarchical structure. ACS Appl. Mater. Interfaces 11, 23616–23622 (2019). [DOI] [PubMed] [Google Scholar]
- 40.Suksangpanya N., Yaraghi N. A., Pipes R. B., Kisailus D., Zavattieri P., Crack twisting and toughening strategies in Bouligand architectures. Int. J. Solids Struct. 150, 83–106 (2018). [Google Scholar]
- 41.Song Z., Ni Y., Cai S., Fracture modes and hybrid toughening mechanisms in oscillated/twisted plywood structure. Acta Biomater. 91, 284–293 (2019). [DOI] [PubMed] [Google Scholar]
- 42.Amini S., Tadayon M., Idapalapati S., Miserez A., The role of quasi-plasticity in the extreme contact damage tolerance of the stomatopod dactyl club. Nat. Mater. 14, 943–950 (2015). [DOI] [PubMed] [Google Scholar]
- 43.Yang W., Quan H., Meyers M. A., Ritchie R. O., Arapaima fish scale: One of the toughest flexible biological materials. Matter 1, 1557–1566 (2019). [Google Scholar]
- 44.Yang R., Zaheri A., Gao W., Hayashi C., Espinosa H. D., AFM identification of beetle exocuticle: Bouligand structure and nanofiber anisotropic elastic properties. Adv. Funct. Mater. 27, 1603993 (2017). [Google Scholar]
- 45.Yang Y.et al., Biomimetic anisotropic reinforcement architectures by electrically assisted nanocomposite 3D printing. Adv. Mater. 29, 1605750 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yang Y.et al., Recent progress in biomimetic additive manufacturing technology: From materials to functional structures. Adv. Mater. 30, e1706539 (2018). [DOI] [PubMed] [Google Scholar]
- 47.Gantenbein S.et al., Three-dimensional printing of hierarchical liquid-crystal-polymer structures. Nature 561, 226–230 (2018). [DOI] [PubMed] [Google Scholar]
- 48.Gu G. X., Takaffoli M., Buehler M. J., Hierarchically enhanced impact resistance of bioinspired composites. Adv. Mater. 29, 1700060 (2017). [DOI] [PubMed] [Google Scholar]
- 49.Natarajan B.et al., Binary cellulose nanocrystal blends for bioinspired damage tolerant photonic films. Adv. Funct. Mater. 28, 1800032 (2018). [Google Scholar]
- 50.Song J.et al., Processing bulk natural wood into a high-performance structural material. Nature 554, 224–228 (2018). [DOI] [PubMed] [Google Scholar]
- 51.Zhu H.et al., Anomalous scaling law of strength and toughness of cellulose nanopaper. Proc. Natl. Acad. Sci. U.S.A. 112, 8971–8976 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Faber K. T., Evans A. G., Crack deflection processes—I. Theory. Acta Metall. 31, 565–576 (1983). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data are included in the manuscript and SI Appendix.