Abstract
Motivation
Recent advances in deep learning have offered solutions to many biomedical tasks. However, there remains a challenge in applying deep learning to survival analysis using human cancer transcriptome data. As the number of genes, the input variables of survival model, is larger than the amount of available cancer patient samples, deep-learning models are prone to overfitting. To address the issue, we introduce a new deep-learning architecture called VAECox. VAECox uses transfer learning and fine tuning.
Results
We pre-trained a variational autoencoder on all RNA-seq data in 20 TCGA datasets and transferred the trained weights to our survival prediction model. Then we fine-tuned the transferred weights during training the survival model on each dataset. Results show that our model outperformed other previous models such as Cox Proportional Hazard with LASSO and ridge penalty and Cox-nnet on the 7 of 10 TCGA datasets in terms of C-index. The results signify that the transferred information obtained from entire cancer transcriptome data helped our survival prediction model reduce overfitting and show robust performance in unseen cancer patient samples.
Availability and implementation
Our implementation of VAECox is available at https://github.com/dmis-lab/VAECox.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Cancer prognosis, including prediction of time to death of a cancer patient, remains one of the most challenging issues in the clinical domain even after decades of effort by cancer researchers (Kourou et al., 2015; Nicholson et al., 2001). One major factor for this difficulty is censored patient samples, i.e. the status of a patient may be unknown if a clinic is unable to monitor the patient. Traditional modelling approaches have difficulty in handling censored patient samples as they do not have a specific time point of death. Even the last follow-up time in the record of the censored patient sample cannot be used as its missing time of death. A model that can handle both censored and uncensored samples can be effective in time-to-death prediction. Survival analysis is a statistical method that handles censored samples (Cox, 2018). As survival analysis methods focus on whether a patient survives at a certain time point rather than when the patient dies, any patient who survives at a certain time point can be used in modelling patient survivals.
With the advent of the Human Genome Project (Venter et al., 2001), high-throughput transcriptomics data of cancer patients has become accessible and technologies for analyzing the large amount of transcriptomics data have been developed (Hanahan and Weinberg, 2011; Van’t Veer et al., 2002). Researchers have found that transcriptomics data, especially gene expression data, can be useful for cancer analysis (Lussier and Li, 2012; Valdes Mora et al., 2018). The Cox Proportional Hazard (Cox-PH) model treats predicting the survival time of patients as a regression task (Bradburn et al., 2003; Cox, 1972). The Cox-PH model predicts the probability of patient death using a hazard function. However, since the Cox-PH model is based on a linear combination of given features, it cannot learn underlying non-linear biological processes from transcriptomics data for cancer prognosis.
Deep learning has recently started to gain popularity in the bioinformatics domain due to its advancements in technology and flexibility in modelling (Chaudhary et al., 2018; Ching et al., 2018; Katzman et al., 2018). Although deep-learning approaches have been applied to most biomedical tasks, using deep learning on genomic data still remains a challenge. As the amount of cancer patient data available for deep-learning models is insufficient, using deep learning can lead to serious overfitting issues. Deep-learning models in the general domain are less likely to suffer from overfitting issues where the total number of data samples significantly exceeds the number of features. In the biomedical domain, the opposite is often the case. For example, the total number of breast cancer patient samples in the Cancer Genome Atlas, TCGA, (Tomczak et al., 2015) is approximately 1100, whereas the number of human genes for each patient is more than 20 000. From the perspective of machine learning, the lack of training samples can lead to overfitting models on the training set, and obtaining poor performance on other unseen samples.
Model simplification is one solution to overfitting issues. Cox-nnet, which was proposed in 2018, has succeeded in predicting the survival of patients with various cancer types using simple two fully connected perceptron layers (Ching et al., 2018). Huang et al. (2019b) evaluated various machine-learning models and deep-learning architectures, but found that the artificial neural network (ANN) with only one or two perceptron layers is the most effective architecture in analyzing omics data for disease classification. These results show that when all genes are considered as independent features, model simplification greatly helps avoid overfitting. However, simplifying models inevitably limit the models’ ability to learn complex non-linear relations among features.
An alternative to model simplification is transfer learning. Transfer learning is a method which involves transferring knowledge from a source task to a target task and has been used in various deep-learning models (Fernandes et al., 2017; Kandaswamy et al., 2016; Li et al., 2016). Transfer learning can be diversified depending on its learning setting (inductive, transductive and unsupervised) and transfer approach (instance-based, feature-based, parameter-based and relational knowledge-based) (Pan and Yang, 2010).
Transfer learning is a method which involves transferring knowledge from a task with an abundant number of samples to another task with an insufficient number of samples. A model can be pre-trained on a large dataset of a task and the parameters of that model are transferred to another model of a different but similar task. Subsequently, the latter model can be fine-tuned on the smaller target dataset. The number of parameters used in deep-learning models far exceeds the number of parameters used in conventional machine-learning models. Deep-learning models often use transfer learning to avoid overfitting (Fernandes et al., 2017; Kandaswamy et al., 2016; Li et al., 2016).
In this work, we introduce VAECox, a deep-learning model architecture that addresses the scarcity of data samples by exploiting transfer learning and fine-tuning. We pre-trained our variational autoencoder (VAE) on all the TCGA RNA-seq data of patients with 20 cancer types for extracting common characteristics of cancer. Then we initialized the weights of our VAECox model with the weights of our pre-trained VAE model, and fine-tuned our VAECox model on each cancer patient dataset. Our VAECox model outperformed other baseline models such as Cox-PH with LASSO and ridge penalty and Cox-nnet on the 7 of 10 different cancer-type datasets.
2 Material and methods
2.1 Dataset and pre-processing
We first downloaded the cancer patient RNA-seq gene expression data from TCGA. These data are provided by International Cancer Genome Consortium (ICGC) data portal (https://dcc.icgc.org/). For evaluating our VAECox model predicting patient survivals, we used each of the gene expression data for 10 different cancer types used for one of the baselines (Ching et al., 2018). The 10 different cancer types are bladder carcinoma (BLCA), breast carcinoma (BRCA), head and neck squamous cell carcinoma (HNSC), kidney renal cell carcinoma (KIRC), brain lower-grade glioma (LGG), liver hepatocellular carcinoma (LIHC), lung adenocarcinoma (LUAD), lung squamous cell carcinoma (LUSC), ovarian carcinoma (OV) and stomach adenocarcinoma (STAD). The 10 different cancer types were selected if they had more than 50 uncensored samples. For each of the 10 different cancer types, we compared the performance of our VAECox model to those of other baseline survival prediction models.
As our VAECox model uses transfer learning from another model trained on heterogeneous cancer sets, we used 24 TCGA cancer datasets from the ICGC data portal to train our VAE. 10 cancer types, BLCA, BRCA, HNSC, KIRC, LGG, LIHC, LUAD, LUSC, OV and STAD were first included as they are used in survival prediction models. For the remaining 14 cancer types, 3 of them which are lymphoid neoplasm diffuse large B-cell lymphoma, kidney chromophobe and sarcoma were excluded as they did not contain any RNA-seq data. In addition, we removed rectum adenocarcinoma as it has insufficient patient samples. As a result, we used 20 cancer gene expression datasets for training our VAE model.
When analyzing the dataset, we found some patient samples with a high number of missing gene expression values. We assumed that these patient samples would not be helpful in training our model. Even if we impute the missing values using the existing values, the imputed values cannot be reliable due to the high number of missing values. Therefore, we filtered samples with a high number of missing values to reduce the noise from them. If the missing value rate of the patient samples was more than 15%, the patient and the gene were excluded from the dataset. Since we extracted common traits of pan-cancers and transfer the knowledge to each cancer model, we selected 20 502 genes commonly included in cancer gene expression datasets. To regularize the scale of gene values, then we applied feature-wise Z-normalization to each gene expression dataset for the 20 cancer types. Table 1 provides the number of patient samples of each cancer type used in our study. The first 10 cancer types are used in survival prediction models. We imputed the missing values of the remaining patients using a matrix factorization-based algorithm as other straightforward methods such as mean, median or zero-value imputation are known to have limitations such as reducing the variance of the imputed variables. We used the LibFM (Rendle, 2012) package to impute the missing values and the parameters were optimized using a Monte Carlo Markov Chain algorithm.
Table 1.
Statistics of transcriptomics data for 10 cancer types on which VAECox was trained
| Cancer type | Before pre-processing |
After pre-processing |
||
|---|---|---|---|---|
| # All | # Uncensored | # All | # Uncensored | |
| BLCA | 398 | 108 | 286 | 72 |
| BRCA | 1039 | 104 | 989 | 100 |
| HNSC | 522 | 170 | 477 | 160 |
| KIRC | 528 | 162 | 512 | 159 |
| LGG | 507 | 91 | 433 | 69 |
| LIHC | 343 | 91 | 267 | 72 |
| LUAD | 480 | 122 | 440 | 113 |
| LUSC | 477 | 158 | 404 | 134 |
| OV | 578 | 301 | 260 | 147 |
| STAD | 396 | 84 | 374 | 77 |
| CESC | 288 | 60 | 251 | 53 |
| COAD | 347 | 52 | 324 | 46 |
| GBM | 592 | 446 | 158 | 106 |
| KIRP | 264 | 31 | 209 | 23 |
| LAML | 173 | 108 | 149 | 92 |
| PAAD | 181 | 66 | 138 | 45 |
| PRAD | 500 | 8 | 375 | 6 |
| SKCM | 440 | 155 | 401 | 149 |
| THCA | 501 | 14 | 495 | 14 |
| UCEC | 540 | 45 | 505 | 43 |
2.2 Dimension reduction using autoencoder and VAE
An autoencoder (AE) is a neural network model where the encoder compresses an input vector to a latent vector and the decoder decompresses the latent vector to reconstruct the input vector (Hinton and Salakhutdinov, 2006). The AE is trained to generate an output vector that is as similar as possible to its original one. During compression, the encoder learns salient features and achieves dimension reduction (Wang et al., 2016). As the number of our patient samples is much smaller than the number of features, we can achieve transfer learning using the pre-trained weights of the encoder. For input vector x, the encoded vector z and the reconstructed vector of the AE’s output are mathematically expressed as follows:
| (1) |
| (2) |
where We and be are parameters of the encoder, and Wd and bd are parameters of the decoder. denotes the tanh function which is expressed as follows:
| (3) |
For training the AE, we use a reconstruction error with root-mean-square error (RMSE) as its objective function which is mathematically expressed as follows:
| (4) |
where n is the number of samples in the training set.
A VAE is a generative model that exploits the latent distribution of input data for reconstruction (Doersch, 2016; Kingma and Welling, 2013). The VAE does not only achieve dimension reduction but also learns to model a more generalized latent prior distribution (e.g. Gaussian distribution). Before input reconstruction, the latent variables are randomly sampled from the probability distribution made by the encoder. However, these randomly sampled variables are not differentiable, which makes it difficult to calculate gradients. As the VAE’s objective is to optimize both the encoding and decoding weights, a re-parameterization trick which involves using the mean and variances of the latent distribution as deterministic parameters. Therefore, the mean and variance encoders for modelling the latent distribution’s mean and variance, respectively, are used. This allows for the optimization of both the encoding and decoding weights in the VAE model. We believe that the pre-trained encoding weights can be generally used and be effective in various tasks as they can be used to model richer and more elaborate latent features of cancer patient data.
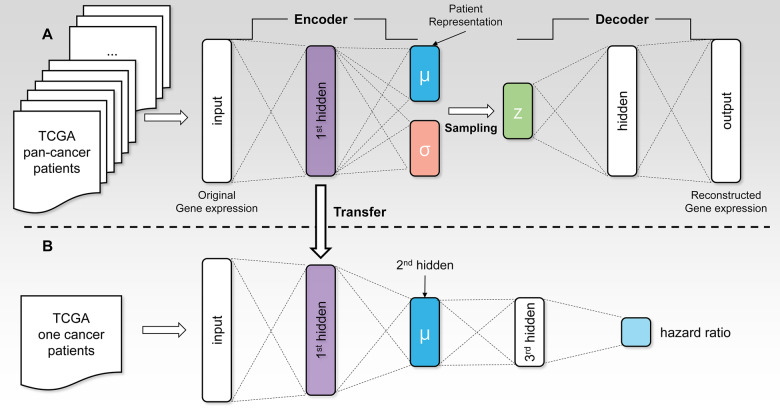
In this study, we added a hidden layer to the encoder and decoder of our VAE model architecture. The architecture of our VAE model is shown in Figure 1A.The VAE model for input vector x, the outputs of encoder μ, ν and z, and the reconstructed vector are mathematically expressed as follows:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where μ, ν and are the mean, log variance and the variance of a Gaussian distribution, respectively. ϵ is randomly sampled from the standard Gaussian distribution. W and b are trainable parameters of our VAE model.
Fig. 1.
(A) The architecture of the VAE model used in this study. A hidden layer is added to both the encoder and decoder of the original VAE. We trained this VAE model on all the TCGA RNA-seq data of patients with 20 cancer types. (B) The architecture of the VAECox model which predicts a patient’s hazard ratio. The parameters of the first two layers are transferred from the encoder part of the pre-trained VAE model
We used a reconstruction error with RMSE as an objective function for our model. We used the Kullback–Leibler divergence (Kullback and Leibler, 1951; Press et al., 2007) noted () as an additional objective function for measuring the distance between two distributions: (i) the true latent distribution of a given input; (ii) the variational latent distribution of a given input encoded by the VAE model.
| (10) |
The objective function of our VAE model is defined as follows.
| (11) |
where θVAE refers to the parameters our VAE model.
2.3 Survival analysis
The architecture of our VAECox model which can predict patient survival is shown in Figure 1B. We combined the encoder layers of the VAE model with the Cox-PH model (Cox, 1972). The Cox-PH model predicts cancer patients’ hazard ratio after taking censored patient samples into consideration. Hazard ratio is a measure of how likely a patient is to die. A lower hazard ratio means the patient is more likely to survive. The Cox-PH model is defined as follows.
| (12) |
| (13) |
where is the log hazard ratio for patient i and θ is the trainable parameters of the model. The objective function of the Cox-PH model is a negative partial log likelihood defined as follows.
| (14) |
where t is a sample’s survival time. The condition means to select samples whose survival time is longer than the ith sample’s survival time. C(i) is an indicator which has a value of 1 when the death event of ith patient sample is observed.
Our VAECox model architecture is a combination of the encoder layers of our VAE model and the Cox-PH model. Therefore, the objective function of VAECox is also the negative partial log likelihood defined at Equation 14, but the log hazard ratio of our VAECox using the pre-trained encoder defined at Equation 5 is defined as follows:
| (15) |
where W and b are the trainable parameters of the model.
2.4 Transfer learning
As explained above, transfer learning involves reusing a pre-trained model which was previously trained on a large dataset. We first trained our VAE on all TCGA RNA-seq data samples of 20 cancer types. We then transferred the pre-trained weights to the encoder layers attached to the Cox-PH layer in our VAECox model. To clarify, the weight values in the VAECox’s encoder layers were initialized with the pre-trained VAE encoder weights, whereas the remaining ones were randomly initialized. The encoder weights in VAECox were fine-tuned during training as the gradients were back-propagated.
2.5 Experimental setting
Prior to using transfer learning, we initially trained the VAE model on a combined dataset of 20 gene expression datasets of different cancer types. About 80% of this data was used for training the model, whereas the remaining 20% was used for evaluating model performance. The VAE model is trained with unsupervised learning as the model learns to copy input gene expression values to its output. Then we combined the encoder of the pre-trained VAE model with the two-layer Cox regression model and denote it as VAECox. We trained our VAECox with supervised learning. The input is a sample’s gene expression values and the output is the sample’s log hazard ratio. The model is trained to predict the log hazard ratio in the same order as the patients’ survival time based on the negative partial log-likelihood which is the objective function of VAECox.
For a fair comparison, our VAECox was evaluated in the same way as Cox-nnet (Ching et al., 2018). We compared our VAECox with baseline models on 10 TCGA gene expression datasets of different cancer types. Each cancer-specific VAECox model was trained on a different cancer dataset. We used 80% of the gene expression data as training data and evaluated the performance of the trained models on the remaining 20% of the data. The optimal hyperparameters of each model were selected based on fivefold cross validation on the training data. To avoid a sampling bias caused by the random split of training and test data, we repeated this entire evaluation process 10 times and obtained the average performance of each cancer-specific VAECox model. We used the concordance index (C-index), which is one of the most commonly used metrics to evaluate the performance of survival prediction models (Harrell Jr, 2015). C-index, which ranges from 0 to 1, measures the correlation between the ranked predicted hazard ratios of patients and the ranked survival times of patients.
We implemented all the baseline models using the PyTorch framework, and have made the implementations available in our GitHub repository. In the case of Cox-nnet, we used the same model structure including the number of layers, the number of hidden nodes and the activation function. Since Cox-LASSO and Cox-ridge are simple extensions of the Cox-PH model, they do not have model hyperparameters. By fivefold cross validation, we found the optimal learning rate and the regularization factors for all the baseline models.
The optimal hyperparameters of our VAECox model are shown in Supplementary Table S1. The third layer of VAECox has 12 hidden units. We used tanh as our activation function and optimized our model with Adam optimizer. We used PyTorch framework to implement our model. We used 80% of the gene expression data as training data, 10% of the data as validation data and the remaining 10% as test data, The hyperparameters were selected based on validation results. Training our VAECox including the VAE for a single cancer type takes around 4 h and 6 GB GPU memory. We used a NVIDIA Titan XP (12 GB) GPU to train and evaluate our VAECox.
3 Results
3.1 Survival prediction results
As shown in Figure 2, our VAECox model outperformed Cox-ridge, Cox-LASSO and Cox-nnet on most of the cancer types. Among the 10 cancer types selected for evaluation in this study, our VAECox model outperformed the other baseline models on seven cancer types (BRCA, HNSC, KIRC, LGG, LIHC, OV and STAD) in terms of average C-index. We also calculated the micro-average C-index on 10 cancer types. Micro-average considers the number of samples evaluated for each cancer type, when computing the average metric for all 10 cancer types and is mathematically expressed as,
| (16) |
where ni is the number of samples and ci is the C-index for cancer-type index i.
Fig. 2.
The box plot for the performance of the following survival prediction models on 10 cancer types: Cox-ridge, Cox-LASSO, Cox-nnet and our model VAECox. We randomly split the data into training (80%) and test sets (20%). We repeated this process 10 times and obtained 10 C-index scores. The white triangle of each box denotes the average of 10 C-index scores. The optimal hyperparameters were selected by fivefold cross validation on the training set
Our VAECox model outperformed Cox-ridge, Cox-LASSO and Cox-nnet by 0.046, 0.040 and 0.016 in terms of micro-average C-index, respectively. These results confirm that our transfer-learning method is a viable approach for improving the performance in predicting patient survival for most cancer types.
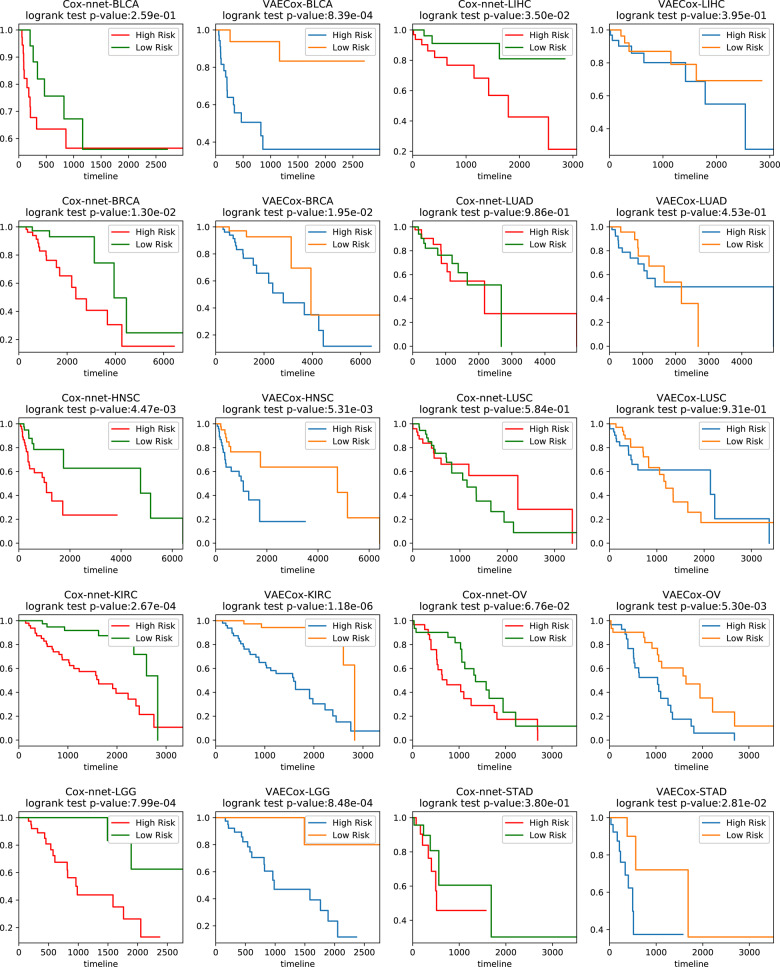
The VAECox model was also utilized to perform further survival analysis. We divided the patient samples for each of the 10 cancer types into high- and low-risk groups based on their predicted hazard ratios. A patient sample is included in high-risk group when the hazard ratio of the sample is higher than the median hazard ratios of all patient samples. We also carried out same analysis with the baseline Cox-nnet. Figure 3 shows the Kaplan–Meier plots and the log-rank test results of the high- and low-risk groups. The interesting observation is the P-value of our VAECox is lower than P-value of Cox-nnet in BLCA where our VAECox does not outperform Cox-nnet in terms of C-index. It means our VAECox shows a better performance to split samples into the high and low risk groups than the Cox-nnet.
Fig. 3.
Kaplan–Meier plots and results of the 10 cancer-types’ test patient samples from the log-rank test with VAECox and Cox-nnet. The patient samples are divided into high- and low-risk groups based on the predicted hazard ratios. A patient sample is included in high-risk group when the hazard ratio of the sample is higher than the median hazard ratios of all patient samples
3.2 Effectiveness of VAE
We performed further analysis to investigate how the transferred weights of our pre-trained VAE model affects the performance of our VAECox model in predicting patient survivals. The results obtained after transferring and fine-tuning weights in three cases are provided below:
Weight transfer from VAE without fine-tuning yielded a micro-average C-index score of 0.569.
No weight transfer from VAE yielded a micro-average C-index score of 0.629.
Weight transfer from VAE with fine-tuning yielded a micro-average C-index score of 0.649, which is our best result.
Interestingly, our pre-trained VAECox model achieved better C-index results than the randomly initialized VAECox model on the same seven cancer types where our pre-trained VAECox outperforms Cox-nnet. The results demonstrate the effectiveness of transfer learning. Both randomly initialized VAECox and Cox-nnet do not use transfer learning.
Our VAE model may have difficulty in learning survival-related characteristics of cancer types as VAE is designed for dimension reduction and reconstruction of input data. However, considering the results obtained after transferring encoder weights to VAECox and fine-tuning them during training, we can assume that the learned parameters of the VAE model based on pan-cancer expression data can be beneficial to the Cox model in learning cancer survival-related features. This is further discussed in Section 4.
We also conducted additional experiments to verify the validity of training the VAE with samples of heterogeneous cancer types. We trained the VAE with only samples of target cancer type and transferred the encoder part of the AE to our Cox regression layer. The micro-average of 10 concordance index scores of this experiment is 0.626, which is 0.023 lower than the performance of originally proposed VAECox. These results show that the VAE trained with heterogeneous cancer types are more beneficial to our VAECox model.
Finally, we did experiments on the transfer learning and Cox regression approach setting with other AEs, a simple AE and a stacked de-noising AE. We obtained 0.623 of micro-averaged concordance indices when using the simple AE, and 0.638 of micro-averaged concordance indices when using the stacked de-noising AE. The result shows the model structure of simple AE is not sufficient to capture the common characteristics of heterogeneous cancer types, and the stacked de-noising AE is better than the simple AE because of the increased model complexity but does not outperform the VAE.
3.3 Feature analysis of VAECox
We further investigated the hidden nodes of the model to find which genes were significant and which pathways were important for patient survival. We assumed that hidden nodes with high variance have a crucial role to discriminate the patient samples. At first, we extracted the top nodes with the highest variance in each of the second and third hidden layers. Then we calculated Pearson’s correlation between the values of each hidden node and the expression of each gene across all patient samples in the BRCA dataset. Figure 4 shows the correlation values of the top five genes which have the highest absolute correlation values for each hidden node of the third layer.
Fig. 4.
Pearson’s correlation values of the top five genes which have the highest absolute correlation values for each hidden node of the third layer in the BRCA dataset
To examine the association between breast cancer and the genes highly correlated with the hidden nodes of the Cox layer shown in Figure 4, we conducted a literature survey on the genes. Most of the genes are cancer-related genes, and some of them have an explicit association with breast cancer and breast cancer patients’ survival. The CDC20 gene is an essential component of cell division, and the high CDC20 expression is reported to be associated with the poor survival of breast cancer patients (Jiang et al., 2011; Karra et al., 2014). Overexpression of the C9orf86 gene, also known as RBEL1, is correlated with the survival of breast cancer patients (Li et al., 2013; Yoshimura et al., 2016). The MAMDC2 gene, whose function is unknown, is reported to be highly correlated with the disease-free survival of breast cancer patients (Mannelqvist et al., 2014; Meng et al., 2016). The high HJURP expression level of is reported to be a prognostic marker of breast cancer (de Oca et al., 2015; Hu et al., 2010). IKGKB is a type of NF-kappa B genes and reported to have a major driver in inflammatory breast cancer (Lerebours et al., 2008). The methylation of the KLHL17 gene is reported to be associated with early stage breast tumours and breast carcinogenesis (Titus et al., 2017). The DOT1L gene is reported to be highly associated with breast cancer and a new therapeutic target for aggressive breast cancer (Cho et al., 2015; Lee and Kong, 2015; Nassa et al., 2019). The BCAP31 gene is reported to activate the downstream signalling of EGFR and drive triple-negative breast cancer (Fu et al., 2019). The SCN4B gene is reported to act as a metastasis-suppressor gene and the under-expression of the SCN4B gene is correlated with tumour progression in breast cancer (Bon et al., 2016). KIAA0247, also known as DRAGO, is reported to cooperate with p53 and KIAA0247’s overexpression is reported to result in cell death in breast cancer (Huang et al., 2011; Polato et al., 2014).
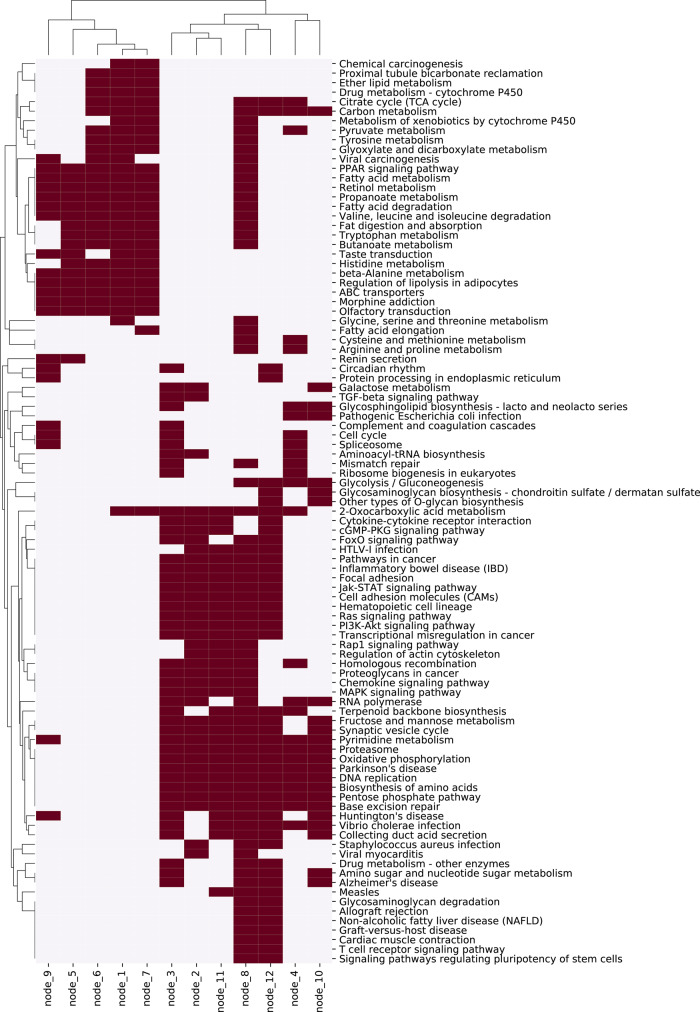
We then explored the function of hidden nodes by pathway enrichment test with the correlation values of genes. As the correlation value between a gene and a hidden node means how much the gene contributes to the value of the hidden node, we can obtain a ranked gene list for each hidden node using the correlation values. Using the ranked gene list, we found enriched pathways in KEGG pathway database. Figure 5 shows the enriched pathways for each hidden node of the third layer, and Supplementary Figure S1 shows that of the second layer.
Fig. 5.
Enriched KEGG pathways for each hidden node of the third layer in our VAECox model trained using the BRCA dataset. The pathway enrichment test is conducted using the correlation values between a vector of hidden node and a vector of gene expression value across all BRCA samples
We found an interesting difference when comparing the enriched pathways of the third layer that is the third layer of our VAECox, and the previous hidden layer that is the second layer of our VAECox. In case of the third layer, the pathways where many nodes are enriched are related to cancer, such as pathways in cancer, PI3K-Akt signalling pathway and Jak-STAT signalling pathway. But the enriched pathways in the second layer are related to only metabolism, such as fatty acid metabolism, propanoate metabolism and retinol metabolism. We can see that the third layer learns biologically basic and essential information and the second layer learns complex and disease-specific information. This observation is an interesting example in biological domain showing that a deep-learning model learns the basic signals in the front layer, and learns the high-level signals by abstracting the basic signals in the later layer.
4 Discussion
4.1 Effect of transfer learning for effective parameter initialization
To use transfer learning, we pre-trained our VAE model on a combined set of 20 gene expression datasets for different cancer types. We then transferred the encoder weights of the pre-trained VAE model to our VAECox model by initializing the weights of the VAECox model with the transferred encoder weights of the VAE model. While we did not fine-tune the transferred weights when training our VAECox model, we found that our VAECox model did not show significant improvement. Our pre-trained VAE model is designed to learn compression and reconstruction-related signals, and not survival-related latent features.
However, the encoder weights of the pre-trained VAE model contain information related to cancer, which were obtained when training our VAE model on the combined set of 20 gene expression datasets. As mentioned above, our objective is to optimize our VAECox model designed to predict the survival of cancer patients. We can use the encoder weights as the initial weights for our VAECox model and fine-tune the weights when training VAECox. The performance of our VAECox model improved more when the transferred encoder weights were fine-tuned compared to when the weights of VAECox were randomly initialized. The performance of VAECox was also higher when the transferred weights were fine-tuned than when transferring the encoder weights that were not fine-tuned. This indicates that the encoder weights of our pre-trained VAE model are effective when the transferred weights are used as the initial weights of our VAECox model and optimized to predict patient survival. The optimization of the transferred weights is required since the optimization enables the transferred weights to have survival-related information. In other words, the transfer-learning approach for customized weight initialization is effective in training our VAECox model on cancer data. Previous studies examined the importance of weight initialization (Dewa et al., 2018; Hanin and Rolnick, 2018; Li et al., 2017; Sutskever et al., 2013). The well-initialized weights can help a model learn and improve its performance as it help escape the model trapped at local optima, which is one of the main reasons for model overfitting.
4.2 VAE as a pre-trained model
The main objective of the pre-training phase is to extract common cancer knowledge on multiple heterogeneous cancer types. A simple AE is prone to overfit on some features among various cancer characteristics as it aims to perfectly reconstruct the given input data. However, as a VAE is trained using the objective function based on the reconstruction loss between a given input and a decoded output based on a randomly sampled vector, it can learn robust features among various cancer characteristics.
The main objective of the survival prediction phase is predicting deterministic patient survival, not generating probabilistic samples. The μ vector from the mean encoder in VAE can be treated as patient representation signals while the σ vector from the variance encoder in VAE can be treated as confidence signals aligned with the μ vector signals. We decided to transfer only the mean encoder weights to VAECox since the patient representation may change due to fine-tuning, depending on which type of cancer survival prediction the patient representation is used in.
4.3 Cancer types where VAEcox did not outperform the baseline model
Although our VAECox model did not outperform Cox-nnet on three cancer types (BLCA, LUAD and LUSC) in terms of C-index, our log-rank test results (Fig. 3) demonstrate that VAECox obtains higher P-value than Cox-nnet in BLCA survival prediction. We investigated why our VAECox model did not outperform Cox-nnet in LUAD and LUSC survival predictions. Both LUAD and LUSC are subtypes of non-small cell lung cancer (NSCLC). Among various types of cancer, NSCLCs are known to have distinct and heterogeneous characteristics. Therefore, we believe that common cancer characteristics extracted from samples of various cancer types affected the relatively poor survival of the heterogeneous LUAD and LUSC patients as the transferred knowledge acted as noise.
The objective of this study is to demonstrate that our VAECox model’s approach of using a VAE of multiple heterogeneous cancer types and transfer learning is effective in improving the prediction of patient survival. Even though VAECox does not outperform the baseline model on all cancer types, we believe VAECox can be used to complement other state-of-the-art survival analysis models, instead of replacing them.
5 Conclusion
In this work, we introduced VAECox which is a deep-learning-based survival prediction model. VAECox is a combination of a VAE and a Cox-PH model. We trained the VAE on transcriptomics data for 20 cancer types, and transferred the knowledge to cancer-specific survival prediction models. We showed that our VAECox model outperforms other baseline models on 7 cancer types among 10 cancer types, and extracted genes significant for patient survival based on predicted risks. In addition, we investigated the effectiveness of our VAE and discovered that the pre-trained encoder weights help train our VAECox model to learn features that can be used for patient survival prediction.
We believe that our VAECox model which can be used for cancer patient survival analysis can benefit researchers in various fields. We also believe that this study which demonstrates the effectiveness of transfer learning will aid researchers in other fields.
Despite of our efforts, overfitting still remains an obstacle. When it comes to high-dimensional transcriptomics data, the number of features still greatly exceeds the number of patient samples. One of the alternative approaches to address this issue is applying prior knowledge. Recent works have suggested taking biological interactions between different genes or proteins into consideration to develop more effective, robust models (Dimitrakopoulos et al., 2018; Huang et al., 2019a). In future works, we plan to utilize biological networks such as protein–protein interactions to better represent the omics information of cancer patients.
Supplementary Material
Acknowledgements
The authors thank Susan Kim for suggestions and editing of the manuscript.
Funding
This research was supported by the National Research Foundation of Korea (NRF-2017R1A2A1A17069645, NRF-2016M3A9A7916996 and NRF-2014M3C9A3063541).
Conflict of Interest: none declared.
References
- Bon E. et al. (2016) SCN4B acts as a metastasis-suppressor gene preventing hyperactivation of cell migration in breast cancer. Nat. Commun., 7, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradburn M.J. et al. (2003) Survival analysis part ii: multivariate data analysis —an introduction to concepts and methods. Br. J. Cancer, 89, 431–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhary K. et al. (2018) Deep learning-based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res., 24, 1248–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ching T. et al. (2018) Cox-nnet: an artificial neural network method for prognosis prediction of high-throughput omics data. PLoS Comput. Biol., 14, e1006076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho M.-H. et al. (2015) DOT1L cooperates with the c-Myc-p300 complex to epigenetically derepress CDH1 transcription factors in breast cancer progression. Nat. Commun., 6, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D.R. (1972) Regression models and life-tables. J. R. Stat. Soc. Ser. B (Methodological), 34, 187–202. [Google Scholar]
- Cox D.R. (2018) Analysis of Survival Data. Routledge, England, UK. [Google Scholar]
- de Oca R.M. et al. (2015) The histone chaperone HJURP is a new independent prognostic marker for luminal a breast carcinoma. Mol. Oncol., 9, 657–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dewa C.K. et al. (2018) Suitable CNN weight initialization and activation function for Javanese vowels classification. Proc. Comput. Sci., 144, 124–132. [Google Scholar]
- Dimitrakopoulos C. et al. (2018) Network-based integration of multi-omics data for prioritizing cancer genes. Bioinformatics, 34, 2441–2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doersch C. (2016) Tutorial on variational autoencoders. CoRR, abs/1606.05908, http://arxiv.org/abs/1606.05908.
- Fernandes K. et al. (2017) Transfer learning with partial observability applied to cervical cancer screening. In: Iberian Conference on Pattern Recognition and Image Analysis, pp. 243–250. Springer, NY, US.
- Fu W. et al. (2019) BCAP31 drives TNBC development by modulating ligand-independent EGFR trafficking and spontaneous EGFR phosphorylation. Theranostics, 9, 6468–6484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanahan D., Weinberg R.A. (2011) Hallmarks of cancer: the next generation. Cell, 144, 646–674. [DOI] [PubMed] [Google Scholar]
- Hanin B., Rolnick D. (2018) How to start training: the effect of initialization and architecture. In: Advances in Neural Information Processing Systems, Neural Information Processing Systems Foundation, La Jolla, CA, pp. 571–581. [Google Scholar]
- Harrell F.E., Jr, (2015) Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis. Springer, NY, US. [Google Scholar]
- Hinton G.E., Salakhutdinov R.R. (2006) Reducing the dimensionality of data with neural networks. Science, 313, 504–507. [DOI] [PubMed] [Google Scholar]
- Hu Z. et al. (2010) The expression level of HJURP has an independent prognostic impact and predicts the sensitivity to radiotherapy in breast cancer. Breast Cancer Res., 12, R18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C.-J. et al. (2011) A predicted protein, KIAA0247, is a cell cycle modulator in colorectal cancer cells under 5-FU treatment. J. Transl. Med., 9, 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L. et al. (2019. a) Driver network as a biomarker: systematic integration and network modeling of multi-omics data to derive driver signaling pathways for drug combination prediction. Bioinformatics, 35, 3709–3717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z. et al. (2019. b) Salmon: survival analysis learning with multi-omics neural networks on breast cancer. Front. Genet., 10, 166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang J. et al. (2011) Ganodermanontriol (GDNT) exerts its effect on growth and invasiveness of breast cancer cells through the down-regulation of CDC20 and uPA. Biochem. Biophys. Res. Commun., 415, 325–329. [DOI] [PubMed] [Google Scholar]
- Kandaswamy C. et al. (2016) High-content analysis of breast cancer using single-cell deep transfer learning. J. Biomol. Screen., 21, 252–259. [DOI] [PubMed] [Google Scholar]
- Karra H. et al. (2014) Cdc20 and securin overexpression predict short-term breast cancer survival. Br. J. Cancer, 110, 2905–2913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzman J.L. et al. (2018) DeepSurv: personalized treatment recommender system using a cox proportional hazards deep neural network. BMC Med. Res. Methodol., 18, 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma D.P., Welling M. (2013) Auto-encoding variational Bayes. CoRR, abs/1312.6114, http://arxiv.org/1312.6114.
- Kourou K. et al. (2015) Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J., 13, 8–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kullback S., Leibler R.A. (1951) On information and sufficiency. Ann. Math. Stat., 22, 79–86. [Google Scholar]
- Lee J.-Y., Kong G. (2015) Dot1l: a new therapeutic target for aggressive breast cancer. Oncotarget, 6, 30451–30452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerebours F. et al. (2008) NF-kappa B genes have a major role in inflammatory breast cancer. BMC Cancer, 8, 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y.-Y. et al. (2013) Down-regulation of C9orf86 in human breast cancer cells inhibits cell proliferation, invasion and tumor growth and correlates with survival of breast cancer patients. PLoS One, 8, e71764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y. et al. (2016) Transfer learning for survival analysis via efficient l2, 1-norm regularized cox regression. In: 2016 IEEE 16th International Conference on Data Mining (ICDM), pp. 231–240. IEEE, Piscataway, New Jersey, US.
- Li S. et al. (2017) Initializing convolutional filters with semantic features for text classification. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pp. 1884–1889.
- Lussier Y.A., Li H. (2012) Breakthroughs in genomics data integration for predicting clinical outcome. J. Biomed. Inf., 45, 1199–1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mannelqvist M. et al. (2014) An 18-gene signature for vascular invasion is associated with aggressive features and reduced survival in breast cancer. PLoS One, 9, e98787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng L. et al. (2016) Biomarker discovery to improve prediction of breast cancer survival: using gene expression profiling, meta-analysis, and tissue validation. OncoTargets Ther., 9, 6177–6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassa G. et al. (2019) Inhibition of histone methyltransferase DOT1L silences ERα gene and blocks proliferation of antiestrogen-resistant breast cancer cells. Sci. Adv., 5, eaav5590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson R. et al. (2001) EGFR and cancer prognosis. Eur. J. Cancer, 37, 9–15. [DOI] [PubMed] [Google Scholar]
- Pan S.J., Yang Q. (2010) A survey on transfer learning. IEEE Trans. Knowl. Data Eng., 22, 1345–1359. [Google Scholar]
- Polato F. et al. (2014) DRAGO (KIAA0247), a new DNA damage–responsive, p53-inducible gene that cooperates with p53 as oncosuppressor. JNCI J. Natl. Cancer Inst., 106, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press W.H. et al. (2007) Numerical Recipes 3rd Edition: The Art of Scientific Computing. Cambridge University Press, Cambridge, England. [Google Scholar]
- Rendle S. (2012) Factorization machines with libFM. ACM Trans. Intell. Syst. Technol., 3, 1–22. [Google Scholar]
- Sutskever I. et al. (2013) On the importance of initialization and momentum in deep learning. In: International Conference on Machine Learning, ACM, NY, pp. 1139–1147.
- Titus A.J. et al. (2017) Deconvolution of DNA methylation identifies differentially methylated gene regions on 1p36 across breast cancer subtypes. Sci. Rep., 7, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomczak K. et al. (2015) The cancer genome atlas (TCGA): an immeasurable source of knowledge. Contemp. Oncol., 1A, 68–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdes Mora F. et al. (2018) Single-cell transcriptomics in cancer immunobiology: the future of precision oncology. Front. Immunol., 9, 2582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van’t Veer L.J. et al. (2002) Gene expression profiling predicts clinical outcome of breast cancer. Nature, 415, 530–536. [DOI] [PubMed] [Google Scholar]
- Venter J.C. et al. (2001) The sequence of the human genome. Science, 291, 1304–1351. [DOI] [PubMed] [Google Scholar]
- Wang Y. et al. (2016) Auto-encoder based dimensionality reduction. Neurocomputing, 184, 232–242. [Google Scholar]
- Yoshimura K. et al. (2016) A novel prognostic marker of non-small cell lung cancer: chromosome 9 open reading frame 86 (C9orf86). J. Thoracic Dis., 8, 2284–2286. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.