Abstract
Phase correction (PC) is a preprocessing technique that exploits the phase of images acquired in Magnetic Resonance Imaging (MRI) to obtain real-valued images containing tissue contrast with additive Gaussian noise, as opposed to magnitude images which follow a non-Gaussian distribution, e.g. Rician. PC finds its natural application to diffusion-weighted images (DWIs) due to their inherent low signal-to-noise ratio and consequent non-Gaussianity that induces a signal overestimation bias that propagates to the calculated diffusion indices. PC effectiveness depends upon the quality of the phase estimation, which is often performed via a regularization procedure. We show that a suboptimal regularization can produce alterations of the true image contrast in the real-valued phase-corrected images. We propose adaptive phase correction (APC), a method where the phase is estimated by using MRI noise information to perform a complex-valued image regularization that accounts for the local variance of the noise. We show, on synthetic and acquired data, that APC leads to phase-corrected real-valued DWIs that present a reduced number of alterations and a reduced bias. The substantial absence of parameters for which human input is required favors a straightforward integration of APC in MRI processing pipelines.
Keywords: Phase correction, Phase estimation, Oriented laplacian, Diffusion MRI, Rician noise
Highlights
-
•
An image-by-image noise-driven methodology for phase correction is proposed.
-
•
The approach limits the occurrence of anomalies in the phase-corrected images.
-
•
Adaptive phase correction allows the unbiasing of the diffusion signal and indices.
1. Introduction
In Magnetic Resonance Imaging (MRI) the non-Gaussian distribution of the noise affecting magnitude images can be a major source of bias for estimated quantities. For instance, the bias due to Rician-like noise distributions in magnitude diffusion-weighted images (DWIs) propagates to diffusion indices (Jones and Basser, 2004; Gilbert et al., 2007; Sotiropoulos et al., 2013) such as those calculated with diffusion tensor imaging (DTI) (Basser et al., 1994a, b), diffusion kurtosis imaging (DKI) (Jensen et al., 2005; Jensen and Helpern, 2010), mean apparent propagator (MAP-MRI) (Özarslan et al., 2013), and others. In general, all of the in-voxel (local) representations of the diffusion signal are affected, so that even global techniques such as tractography and structural connectivity are biased (Jeurissen et al., 2017). Nowadays, the quest to identify the human connectome (Maier-Hein et al., 2017; Schilling et al., 2019) requires solid processing pipelines where phase correction (PC) can play a crucial role. The Rician-like noise distribution also induces a bias when averaging magnitude images acquired over multiple repetitions for the purpose of increasing the signal-to-noise ratio (SNR), therefore averaging is performed in the complex domain where the noise distribution is Gaussian with mean zero. However, if phase variations occur from one repetition to another then PC has to be used to avoid averaging complex images having incoherent pixel intensities which would lead to unwanted signal cancellation.
PC allows calculating a bias-free, real-valued version of an acquired complex DWI. The latter follows a complex Gaussian distribution (Henkelman, 1985) but its image contrast – the tissue-dependent amplitude – is split among the real and imaginary components in a way described by the DWI's true phase. If one knew the true phase, then this could be used to transpose the image contrast into the real component, where the noise distribution is Gaussian, thus avoiding the calculation of the magnitude image whose intensities are biased. However, in MRI we only have access to a noisy version of the DWI's true phase, hence this has to be estimated. The noisy phase is then corrected with the estimated one to generate a new complex image having a real component that contains the image contrast with additive Gaussian-distributed noise, and an imaginary image that mainly contains noise with the same distribution and that can be discarded following the assumption that the diffusion MRI signal is real-valued. The phase estimation method is paramount for the good outcome of PC. Bearing this in mind, our work focuses on proposing a robust methodology and methods to automatically estimate the phase by using measured properties of the noise affecting the images – the variance and its spatial variability – to perform adaptive phase correction (APC).
PC was initially proposed for MRI as a way of improving the detectability in low SNR images. The pioneering works include those by Bernstein et al. (1989), Liu and Koenig (1990), and the widespread homodyne detection by Noll et al. (1991). A strong need for it appeared in relation with DWIs due to their inherent low SNR, since the contrast is provided by a signal attenuation. Moreover, motion during acquisition can produce artifacts in the phase, especially when adopting the pulsed-gradient spin-echo (PGSE) sequence (Stejskal and Tanner, 1965), that prevent the use of complex averaging. Phase correction/estimation methods can be grouped into parametric and non-parametric. In the first case, for instance, some methods assume linear or polynomial phase with respect to the voxel location (Liu and Koenig, 1990; Hua and Hurst, 1992; McGibney et al., 1993; Chang and Xiang, 2005; Bretthorst, 2008a). Semi-parametric and non-parametric methods include Bayesian estimation (Bretthorst, 2008b; Zhao et al., 2012), various types of filtering that impose smoothness on the phase or on the complex image, such as low-pass filters (Bernstein et al., 1989; Noll et al., 1991; Prah et al., 2010), total variation (Chen et al., 2013; Eichner et al., 2015), or filters tailored according to the image reconstruction pipeline (Sprenger et al., 2016), though general denoising algorithms operating on the real and imaginary images can be used, such as those based on spectral subtraction (Ertürk et al., 2013), wavelet decomposition (Wood and Johnson, 1999; Wirestam et al., 2006; Hu et al., 2016, 2018), or PCA (Manjón et al., 2013; Veraart et al., 2016; Cordero-Grande et al., 2019). Parametric methods face limitations such as phase linearity assumptions; PCA-based methods need redundant information (generally from several gradient directions) which could prevent their image-by-image application for general MRI modalities and could be sensitive to phase variations. In this work, we focus on image-by-image phase correction and we choose to adopt an image regularization strategy in the complex domain (Eichner et al., 2015).
The major issue we tackle in this article is the choice of the amount of regularization used for phase estimation. Indeed, we show that an empirical choice leads to flawed phase correction. In fact, Sprenger et al. (2016) noticed that phase correction can produce anomalies – alterations of the true image contrast in the phase-corrected real-valued DWI – which they identify using an outliers detection method. These anomalies can have disruptive consequences for the intelligibility of the images and their processing, e.g. the calculation of diffusion indices. We show that such anomalies could be related to an excessive regularization used for estimating the phase. Moreover, in a previous simulation study (Pizzolato et al., 2016) we showed that if the regularization amount is too low, then the benefit of bias reduction on the calculated diffusion indices is suboptimal, whereas with excessively high regularization the diffusion indices can be subject to an even stronger bias compared to that induced by magnitude DWIs. To overcome these issues, we propose to adopt a noise-driven approach to automatically set the regularization amount and obtain an optimal estimation of the phase. Particularly, we first obtain a computationally efficient estimate of the regularization amount by automatically matching it with the estimated noise variance following the discrepancy criterion (Morozov, 1968; Rudin et al., 1992). This estimate is then used to initialize a more costly refining search that minimizes the Stein's Unbiased Risk Estimate (SURE) (Stein, 1981) calculated with a Monte Carlo procedure (Ramani et al., 2008). The regularization is based on an Oriented Laplacian formulation of anisotropic diffusion filters operating over each complex DWI. We propose to estimate the noise variance required for the regularization from an MRI noise map. Since parallel imaging, homogeneity correction, and the image reconstruction produce a spatially varying noise variance (Aja-Fernández and Vegas-Sánchez-Ferrero, 2016), a global regularization amount is insufficient. Hence, we propose to account for the spatial variability of the noise variance by estimating it from the noise map and including it into a spatially varying complex regularization functional to perform adaptive phase correction, in combination with the use of a spatially varying adaptation of Monte Carlo SURE (Pizzolato et al., 2019).
We organize the article as follows. Section 2 describes the theory of phase correction and the adopted regularization method. Section 3 presents the main contributions of this article, i.e. automatic (3.1) and spatially varying (3.2) PC, as well as the use of an MRI noise map. Section 4 describes the methods, the synthetic data, and the acquired datasets. Section 5 illustrates the body of experiments designed to validate the proposed adaptive phase correction. Finally, Section 6 reports our considerations on the proposed methodology based on the experimental results, and Section 7 presents our final remarks.
2. Phase correction
Given a complex image , the purpose of phase correction (PC) is to estimate a phase-corrected image, , whose real component, , contains the tissue (image) contrast with additive Gaussian noise, such that this can be used instead of the Rician magnitude . If is a good estimate of the noise-free phase of a pixel with coordinates and , then the phase-corrected intensity is obtained by complex rotation, subtracting such estimate from the noisy phase as
| (1) |
where . As a consequence, the real component of the phase-corrected complex image, , contains the signal (image contrast) plus zero-mean Gaussian-distributed noise, whereas the imaginary component, , mainly contains noise with negligible signal content. Henceforth, any classical diffusion modeling and reconstruction that takes into account additive Gaussian noise, e.g. the least squares estimation of the DT or DK models from DWIs, can be performed on where the Rician bias is mitigated, e.g. the noise floor is reduced. We calculate the phase required for the complex rotation in eq. (1) from a regularized version of the complex image, . One accepted assumption is that the phase is spatially smooth (Bammer et al., 2010). However, when attempting to estimate the phase from the regularized complex image the discontinuities caused by the image contrast have to be taken into account. For this reason, we decided to use a complex-domain regularization based on an Oriented Laplacian formulation of anisotropic diffusion filters (Sapiro and Ringach, 1996; Kornprobst et al., 1997; Tschumperlé and Deriche, 2007). For each complex image we find the regularized image as the output of an operator , where
| (2) |
which is parametrized by λ that expresses the amount of fidelity to the original image , or the reciprocal of the regularization amount, and where
| (3) |
with being a function of the image gradient norm. In the Oriented Laplacian formulation, the second term in eq. (2) is minimized through the following partial differential equation
| (4) |
where and denote the second derivatives of I along the orthogonal directions and . In the case then and and eq. (4) corresponds to the heat equation. When then and , thus the second term of eq. (2) corresponds to the total variation (Rudin et al., 1992). However, eq. (4) allows for a more general choice of α and β, decoupled from the second term of eq. (2), which can be arbitrary functions of the image's local gradient. In the article, we test the mean curvature flow (Alvarez et al., 1992).
3. Adaptive phase correction
The experimental part in our previous work (Pizzolato et al., 2016) discloses that phase correction has a great unbiasing potential provided that the estimated phase is optimal. In other words, phase correction is not effective – and can lead to more bias than that of the magnitude DWI – if the regularization is not properly performed. Indeed, leaving the choice of λ to empiricism, e.g. visual inspection, can lead to altered image content and is inefficient. Here we propose to automatically regularize based on the noise variance (3.1) and its spatial variability (3.2).
3.1. Automatic regularization
The optimal phase correction is the one allowing the estimation of a phase image, , that after performing the complex rotation in eq. (1) leads to a phase-corrected imaginary image, , with negligible image content, i.e. ideally only containing Gaussian-distributed noise. The phase image is calculated from a denoised version of the original complex DWI via eq. (2). If an estimate of the noise variance is available, , the discrepancy criterion (DC) predicts that the optimal regularization is found for that satisfies (Morozov, 1968; Rudin et al., 1992)
| (5) |
where is the total number of pixels, and being the image's dimensions, and where the factor 2 comes from considering a complex image. In order to find satisfying eq. (5), Chambolle (2004) proposed an iterative rule which we decided to practically implement by considering an average over the real and imaginary components
| (6) |
where n refers to the n-th cycle of iterations until convergence, since the regularization described by eq. (2) is performed with an iterative numerical procedure. As starting value, we set
| (7) |
as suggested by Getreuer (2012) and Duran et al. (2013). The value of λ obtained after one minimization as described by eq. (2), i.e. after one complete cycle of iterations, can be used as input for the next one. This leads to a slow monotonic convergence of for fully converged cycles. However, we note that in practice the rule in eq. (6) can be applied to iterations within one cycle, meaning that only one minimization of eq. (2) with iterative update of λ is sufficient. A similar consideration was also made by Chambolle (2004). In this case we observe that the convergence is not necessarily monotonic but leads to the same value of with approximately a hundred times less iterations. To avoid waiting for useless iterations once convergence is reached, we stop the routine when two consecutive iterations have similar norm of the residuals, particularly when their ratio almost corresponds to one according to a stop tolerance.
The discrepancy criterion is known to produce an over-regularized solution (Galatsanos and Katsaggelos, 1992), i.e. it identifies a value of λ that does not minimize the mean squared error (MSE) with respect to the ground-truth image after regularization. To overcome this limitation, it is possible to minimize an estimate of the MSE proposed by Stein (1981), named Stein's Unbiased Risk Estimate (SURE), which we decided to average over the real and imaginary components
| (8) |
where we estimate the divergence terms separately for the real and imaginary components with the Monte Carlo approach proposed by Ramani et al. (2008).
| (9) |
with being a complex image of size whose real and imaginary components are independent and have pixel intensities that are drawn from the standard normal distribution, , and where “vec” indicates vectorization. The approximation is valid for and, when dealing with images that contain a small number of pixels, the estimate can be averaged over several repetitions. The Monte Carlo SURE criterion is computationally costly since it requires at least one additional evaluation of the operator , e.g. eq. (2), for each tested λ. Moreover, the range of values for λ is unknown a priori, which could potentially lead to the need of performing many evaluations over a large space. We overcome this issue by using the solution obtained with the discrepancy criterion as reference point. Indeed, the value matching according to eq. (5) should constitute a “close enough” starting point for the λ that minimizes eq. (8), typically a lower bound considering that leads to oversmoothing. Therefore, the search space can be restricted to , where we set and . To further reduce the number of evaluations, we employed a golden section bisection method (Braun and Murdoch, 2007) to find the minimum of eq. (8) with stopping criterion specified by λ having precision corresponding to of . Experiments proving the effectiveness of the proposed solution are presented in section 5.
3.2. Spatially varying regularization
In order to consider the spatial variability of the noise variance we adapt eq. (2) inspired, for instance, by the work of Gilboa et al. (2006) as
| (10) |
where is a weighting function. We compute the weighting function from an MRI noise map and scale it such that it does not add energy to the system. To do so, we rewrite the error term of eq. (10) using its discretized form, and we match it to the sample variance, , calculated on the selected image of the noise map
| (11) |
In the case of stationary noise eq. (11) is always true for . In the case of spatially varying noise, we will find a weighting function that locally scales the error term such that the equality holds. At convergence the quantity corresponds to an estimate of the local variance, . Hence, substitution and normalization of the right hand side of eq. (11) leads to
| (12) |
that is satisfied by calculating the weighting function as
| (13) |
which corresponds to the image's sample variance divided by its local estimate. Note that whenever in the implementation of the method the standard deviation is used, then the square root of eq. (13) is considered. The solution in eq. (10) can be combined together with the automatic selection of the regularization parameter λ presented in section 3.1. Particularly, assuming prior knowledge of the sample variance in the image, , this can be used in eqs. (5)–(8) as while using the function at the same time. In order to employ the Monte Carlo SURE criterion while using the weighting function, we propose the use of a spatially varying version of it, svSURE (Pizzolato et al., 2019), where in eqs. (8), (9) is used instead of , and is replaced by its spatially varying version . By indicating with the real or imaginary component of , then the corresponding spatially varying version in is obtained as
| (14) |
which corresponds to the stationary image component multiplied by the square root of the ratio between the local variance and that averaged across the slice. We validate the approach for complex images in section 5. Both the sample and the local variance required for the calculation of the weighting function in eq. (13) can be calculated from a single realization of the noise map. We calculate the sample variance with the unbiased sample variance estimator on a selected axial slice of the MRI noise map for each component , real and imaginary, as
| (15) |
averaging the results over the real and imaginary components; here is the mean value of the noise, which should correspond to zero. The local variance is estimated with a filter that calculates the equivalent of eq. (15) in the three spatial dimensions within a spherical footprint of specified radius around each voxel. We take advantage of the complex-valued nature of the noise map to include samples from both the real and imaginary components, thus increasing the number of samples considered at each voxel location by a factor two. Experimental results related to the spatially varying regularization for phase correction are described in section 5.2.
4. Methods
Adaptive phase correction (APC) is validated experimentally in a comparative manner on synthetic and acquired data. The experiments are designed to test and validate the automatic selection of the regularization parameter, its spatially varying adaptation, the phase estimation performance, the absence of image contrast alterations, and the bias reduction achieved with APC on the signal and diffusion indices as compared to the case when magnitude DWIs are used. For APC, we implemented the Oriented Laplacian formulation of eq. (10) numerically based on an fixed point finite difference scheme. We set the maximum number of iterations to 200 and chose a stop tolerance of , although a lower value of generally leads to similar results while leading to reduced computational time. We fixed in eq. (9) (Ramani et al., 2008). The calculation of the diffusion indices is performed by fitting DTI, DKI, and MAP-MRI on DWIs. To prevent negative signal reconstructions, DTI was performed with non-negativity constraints on the signal (Koay et al., 2006). For MAP-MRI, we used radial order 4, anisotropic scaling, Laplacian regularization set to 0.05 (Fick et al., 2016), and positivity constraints on the reconstructed ensemble average propagator (Özarslan et al., 2013). We used DKI to estimate the mean kurtosis (MK) using the ordinary least squares method. This can be an issue on phase-corrected data due to possible negative signal intensities in the images. To partially mitigate this problem, we smoothed the DWIs (magnitude and real-valued phase-corrected) with at TV filter, and limited the kurtosis values in a range between 0 and 3. In all cases, the reconstruction was performed using Dipy (Garyfallidis et al., 2014).
4.1. Diffusion-weighted images
The regular PGSE sequence provided by the manufacturer was used and interface parameters were modified to allow the output of complex data. We collected two datasets from two healthy volunteers. One was used to evaluate DTI indices at different b-values (dataset 1), and the other was used for evaluating DKI and MAP-MRI indices (dataset 2). For dataset 1, the complex DWIs were acquired with maximum gradient strength , pulse separation , and duration . DWIs were acquired in two antipodal acquisitions along 7 collinear directions distributed among 4 diffusion shells, , and 7 images were included. Dataset 2 was acquired with , , and . It includes 81 DWIs distributed over 3 diffusion shells, (18,27,36) according to a multi-shell electrostatic repulsion scheme (Caruyer et al., 2013), and with 9 images collected at . The acquisitions were implemented on a Philips 3T Ingenia scanner with a 32-channel head coil, a 112x112 reconstruction matrix, 60 axial slices, 2.0 mm isotropic resolution, Partial Fourier factor of 0.7, NEX = 1, zero filling, and an antisymmetric filter during the reconstruction (Noll et al., 1991). For dataset 1, parallel imaging was based on SENSE (Pruessmann et al., 1999) with in-plane parallel imaging factor of . For dataset 2, both SENSE and Multiband-SENSE = 2 was used. Images were reconstructed using the method provided by the manufacturer. In both cases, a spatially varying Rician noise distribution is expected to affect the images. Fig. 1 illustrates a DWI of dataset 1.
Fig. 1.
The estimated spatial variability of the noise based on the real and imaginary components of a noise map (top). Below, a DWI of dataset 1 acquired at . On the right, an average non-weighted () image (top), and the estimated signal-to-noise ratio (bottom).
4.2. Noise map
The MRI noise map was acquired using an additional diffusion volume for which all radio-frequency pulses (excitation, refocusing, and fat saturation) are turned off, so that no excitation occurs. The acquisition time of such a map thus corresponds to the repetition time of the sequence, which also needs to be sufficiently long (of the order of a few seconds at least) to ensure that all transverse magnetization from the previous volume has relaxed completely. This effectively produces an image of the noise through the reconstruction pipeline. The MRI noise map is shown in Fig. 1, which also illustrates the calculated SNR map, and the averaged image for reference. Normally, the acquisition of multiple noise maps is recommended such that many noise realizations can be observed and used to obtain a voxel-by-voxel value of the noise variance with the sample estimator. However, this is often not feasible in real practice, as it would require a long acquisition time. Therefore, we propose an approximated solution based on a single acquisition of the noise map where the local variance is calculated within a spherical neighborhood of fixed radius around each voxel, as described in section 3.2. We noted that larger radii render smoother weighting functions via eq. (13) at the cost of less fidelity to the spatial variability of the noise variance. We chose a radius of 4 voxels, as we saw on synthetic data that it guarantees a mean relative error on the estimated local variance of approximately 2.5. Illustrations of the estimated sample variance, spatially varying variance, and weighting function calculated for the acquired noise map are reported in Fig. 2. In the sagittal and coronal views of the central image we notice an increasing amount of variance as the axial slice number reduces. This behavior is well captured by the standard deviation calculated using the sample estimator in eq. (15) on the image (dots in the left plot), and by averaging the local standard deviation estimates across the image (red continuous line). This trend is mainly driven by the distance to the receive coils, as locations further away from the coils show a lower SNR. Indeed, since the reconstruction includes homogeneity correction the signal is relatively spatially homogeneous, thus the noise is higher in the low SNR regions. Since the acquisition is 2D, PC is done separately for each DWI and the weighting function is calculated for each axial slice with eq. (13) by using the variance map and the slice-dependent . Consequently, the value of remains more uniform across slices compared to the local variance, as illustrated in the right side of the figure.
Fig. 2.
On the left, the standard deviation estimated, for each axial slice, by averaging the local standard deviation estimated with a variance filter across the noise map (red curve) or with a sample variance estimator (dots). In the center, the estimated noise variance from the MRI noise map and, on the right side, the calculated weighting function . Note that the average standard deviation decreases as the axial slice number increases, as observed in the variance map. This is largely driven by the distance to the receive coils: locations further away from the coils have higher noise variance.
4.3. Synthetic data
The sampling of the acquired data was replicated in the synthetic dataset, which was generated with Fiberfox (Neher et al., 2014) based on the data created for the ISMRM 2015 tractography challenge (Maier-Hein et al., 2015, 2017). An artificial phase was added independently for each DWI (Pizzolato et al., 2016). Noise was added based on that estimated from the acquired data. Particularly, complex Gaussian-distributed noise with zero mean and standard deviation σ
| (16) |
where as estimated from the SNR map of Fig. 1 within a white matter mask, being the synthetic magnitude image without diffusion weighting, and a mask defined on the pairs , e.g. a mask of the tissue-related image contrast such as the brain mask. Eventually, the standard deviation was modified locally according to the spatial variability map, also shown in Fig. 1, which corresponds to that estimated on the acquired noise map (dataset 1) using a bivariate Gaussian surface.
5. Results
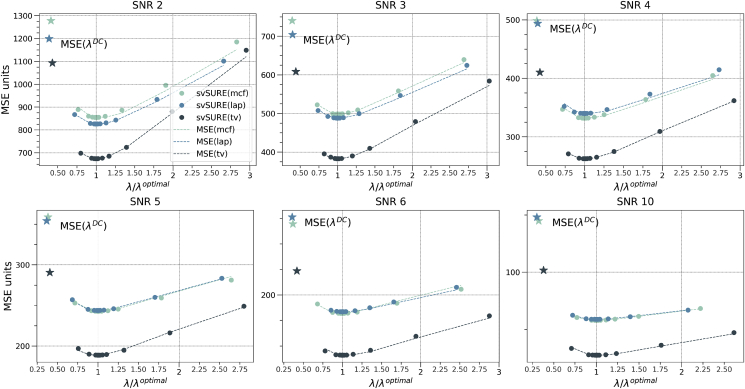
We applied the regularization described in section 3.2 in the form of TV, Laplacian, and mean curvature flow to the synthetic data for a single realization of noise with different SNRs, as reported in Fig. 3. In the plots, the dashed lines represent a trend proportional to the theoretical mean squared error (MSE), , as function of for the three different operators, whereas the dots are the svSURE estimates “visited” by the golden section bisection method. These estimates have been scaled for the sake of visualization such that their minimum corresponds to the minimum value of the corresponding MSE trend curve. The stars represent the MSE obtained with the regularization amount predicted by the discrepancy criterion, , which is used to bound the search of the bisection method. The visited estimates of svSURE well overlap with the MSE as desired. Moreover, the optimal regularization is always found at all SNRs. From these results we also conclude that TV is the best approach among those tested, as it always renders the lowest MSE. For this reason, we use TV in the other experiments and for applying APC to the acquired data, although other (possibly better) operators could be implemented based on eq. (4).
Fig. 3.
Mean squared error (MSE) for mean curvature flow (mcf), Laplacian (lap), and total variation (tv) regularizations based on the operator defined in eqs. (4), (10) (dashed lines). Dots reports the evaluation of svSURE according to the bisection search. The values of λ for each method were scaled by the inverse of the corresponding found as the one minimizing svSURE. For ease of visualization, as svSURE provides approximations to the actual MSE, the svSURE curves were shifted vertically such that their minimum corresponds to the minimum of the corresponding MSE curve.
5.1. Importance of automatic phase correction
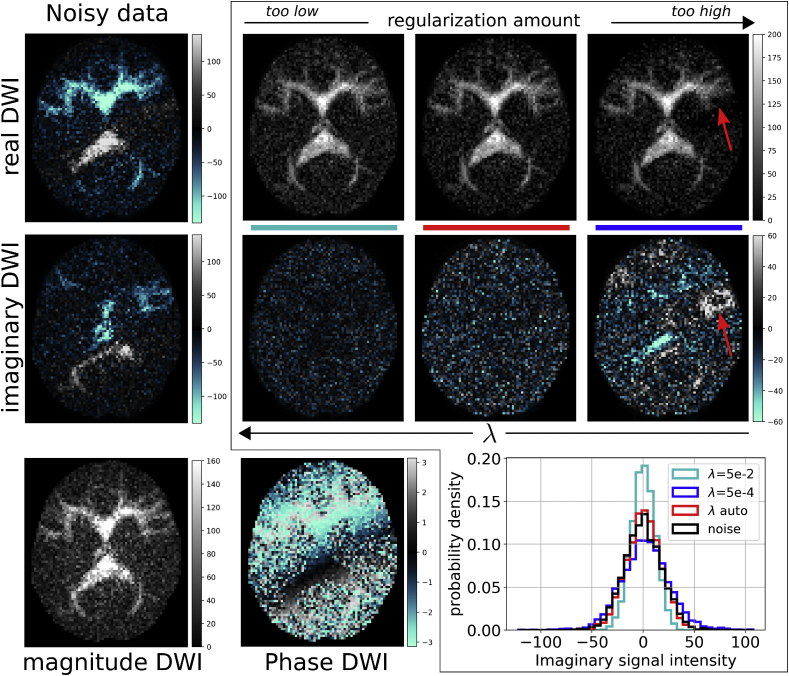
In this section, we show the influence of the regularization parameter λ on the phase correction of the DWIs when considering eq. (2), and present qualitative and quantitative results showing the benefits of using automatic regularization. Fig. 4 reports the results related to the phase correction of a synthetic DWI for different values of λ (light blue and blue) and for the automatic one (red) with the discrepancy criterion. The figure also reports the histograms of the imaginary image intensities after PC for the corresponding correction amount, together with the histogram of the added imaginary noise (black). Ideally, an optimal PC should render an imaginary DWI containing noise with the same properties (mean and variance) of the actual noise affecting the images. Indeed, the red histogram overlaps with the black one. Conversely, a higher or lower λ produces a too weak or excessive correction causing the histograms (light blue and blue) to be far from that of the noise. While in the case of weak regularization the imaginary component has very low intensities, suggesting that the corrected real component is similar to the Rician magnitude, in the case of excessive regularization the imaginary component improperly contains image contrast that should instead be part of the real-valued DWI as indicated by the red arrows. This phenomenon is disruptive for the processing and intelligibility of the images, and is limited by the automatic selection of λ. A qualitatively similar image is shown for dataset 1 in Fig. 5. There, we show the original phase of a DWI, and that estimated with different values of λ, reporting the corresponding imaginary DWIs after PC. A low amount of regularization (high λ) renders an almost zero imaginary DWI, with the consequence that the real-valued DWI practically corresponds to the Rician magnitude. On the contrary, an excessive regularization leads to an imaginary DWI that improperly contains image contrast. The imaginary DWI in the center corresponds to that obtained with automatic PC. In the figure, the imaginary images after PC report stationary noise because of the lack of adaptivity of the technique, which is the focus of the next subsection. The experimental results show that an excessive regularization leads to anomalies – due to image contrast improperly transferred from the real to the imaginary DWI – that invalidate the benefits of phase correction and prevent any further processing of the images. The use of noise properties to set the amount of regularization, on the other hand, limits the occurrence of these anomalies. Indeed, in section 5.3 we show that APC reduces the occurrence of anomalies also for the acquired data.
Fig. 4.
Outside the frame, the magnitude, phase, real, and imaginary components of a DWI of the synthetic dataset. Inside the frame, the real and imaginary components of the DWI after phase correction using different regularization amounts, values of λ, which increase along the direction indicated by the arrows, ranging between low and excessive regularization. If properly corrected, the imaginary DWI should mainly contain noise. In the plot, we report the image intensity histograms of the imaginary DWI, for different values of λ (color codes), to be compared with that of the noise (black). The red histogram corresponds to the automatic selection of λ with the discrepancy criterion as discussed in section 3.1: this well overlaps with that of the noise. A higher (light blue) or lower (blue) values of λ render histograms which are far from the black one, corresponding to low and excessive corrections. In the latter case, parts of the image tissue contrast are transferred to the imaginary image creating anomalies in the real-valued DWI; this phenomenon is indicated by the red arrows. On the other hand, when the regularization is too low the corrected real-valued DWI is very similar to the magnitude one.
Fig. 5.
The original and the estimated phase, with different values of λ, for a DWI of the acquired dataset 1 (first row), and the corresponding imaginary components of the phase-corrected DWI. Note how a too smooth estimation of the phase renders an imaginary component containing tissue contrast, thus a contrast loss in the corrected real-valued DWI. Images are here processed without considering the spatial variability of the noise variance.
5.2. Importance of spatially varying phase correction
The error committed by using stationary instead of spatially varying APC is illustrated in the plot of Fig. 6 using synthetic data. The plot reports the ratio between the mean squared error with respect to the ground truth complex DWI obtained with stationary and with spatially varying regularization. The difference is explained by the unsuited use of the regularization of eq. (2) rather than that of eq. (10). At low SNRs, where phase correction is more needed, the MSE obtained with stationary regularization can be up to 25 higher.
Fig. 6.
The mean and standard deviation of the ratio between the mean squared error (TV regularization) obtained with the stationary and the spatially varying methods, i.e. eq. (2) and eq. (10), as function of the signal-to-noise ratio (results account for 100 different realizations of the noise).
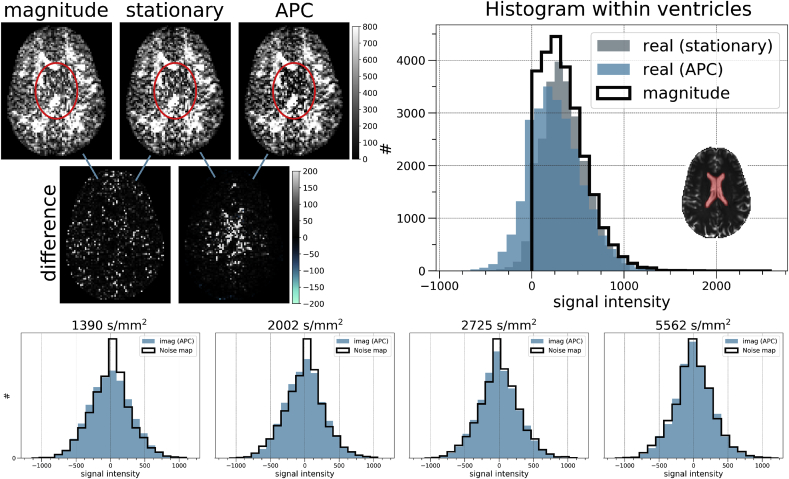
Fig. 7 shows the comparison between stationary and spatially varying phase correction (APC), and their influence with respect to magnitude data. On the left, we note that APC adapts to the higher noise intensities located in the center of the image, leading to a stronger unbiasing of the signal intensities as reported by the histograms calculated within the ventricular mask (right side). Compared to the stationary PC (gray), the spatially varying one (blue) shifts the intensities of the phase-corrected real-valued DWI towards the negative axis, indicating a stronger unbiasing that is explained by the higher noise variance in the ventricular region compared to the mean variance in the image. As expected, the magnitude signal (black) shows the typical Rician-like distribution. Using the same mask, we calculate the histograms of the imaginary DWIs corrected with APC for each b-value shell of dataset 1. These well overlap with that the corresponding histogram of the noise map intensities (black). These comparisons show the relevance of accounting for the local nature of the noise in order to perform phase correction, indicating the importance of using the formulation described in section 3.2 in combination with the noise map.
Fig. 7.
Differences between magnitude and real-valued phase-corrected versions (stationary and APC) of a DWI (). Below, the pair-wise differences. Note the signal contrasts around in the encircled ventricular region. On the right, the histograms of the corresponding signal intensities computed within a ventricular mask. Note the typical positive Rician-like distribution of the magnitude DWI (black). Compared to stationary (automatic) PC, the histogram obtained with APC (spatially varying) is shifted towards the negative axis, indicating a stronger correction due to the higher noise variance in the center as compared to the sample variance across the whole DWI. In the bottom, the histograms of the imaginary DWIs corrected with APC, each one accounting for the samples (within the ventricles) of the DWIs belonging to the same b-value shell. In black, the corresponding histogram of the noise map computed using the same bins.
5.3. Outliers detection
To better address the importance of adaptive phase correction, we implemented an outliers detection method as in the work of Sprenger et al. (2016) where phase-corrected real signal intensities are considered outliers if the difference from the original magnitude is larger than a threshold equal to twice the noise standard deviation, i.e. when . We report the results in Fig. 8 for two different regularization amounts, , tuned manually to produce a noise-like imaginary component, and for APC. The standard deviation used as threshold corresponds to that calculated from the noise map and for fairness of comparison the weighting function was used even in the case where the regularization was manually tuned (which would not normally be possible). In the figure, we illustrate DWIs acquired at four different b-values, while selecting those corresponding to the axial slice where the maximum number of outliers was detected. We count 6.7 of outliers with mean leftover beyond the threshold for , 1.6 with mean leftover for , and 0.3 with mean leftover of for APC on dataset 1 (0.27 with on dataset 2). We note that outliers percentages are likely to be higher in the case in which the manually tuned regularization amounts are not informed about the spatial variability of the noise variance. We also note that a minimal presence of outliers should be expected. The results show the importance of accounting for the noise properties when regularizing, as a wrong choice of λ could invalidate the benefits of phase correction. APC allows signal unbiasing as illustrated in Fig. 7 while minimizing the number of outliers at the same time. The performance of APC is explained by the adaptivity of the value of . In particular, as shown in the bottom of Fig. 8, the adaptive regularization leads to more smoothing (less data fidelity) at lower SNRs and less at higher SNRs. Indeed, in average decreases when the b-value increases.
Fig. 8.
Outliers detected with different regularization amounts (first two rows) and with APC (third). For a given slice, b-value, and gradient direction (the sixth is shown) voxels containing outliers are those revealing a difference between their magnitude and real-valued phase-corrected intensities that exceeds a threshold equal to twice the local noise standard deviation, thus characterizing an “anomaly”. The proximity of the two values of λ chosen after visual inspection demonstrates the difficulty in manually tuning such parameter to render a low number of outliers. The colorbar indicates the “leftover” from the threshold and is saturated at three times the image's maximum noise standard deviation. For fairness of comparison, results only account for differences in λ as in all cases the regularization was informed of the noise spatial variability. For APC, the estimated is reported in every case. In the bottom, a view of the selected data (from slice 20 to 30) averaged per-shell (left), and the mean and standard deviation of the estimated calculated for such selected data for each shell.
5.4. Phase estimation and noise correlation
We compare the adaptive phase estimation used for APC with other filtering strategies and assess the influence of the noise spatial correlation that may arise due to the use of Partial Fourier (PF) during image acquisition. In order to do this, we selected an average non-weighted () magnitude image and a phase image from one of the corresponding DWIs (dataset 1). Both images were independently smoothed with Laplacian regularization to eliminate most of the noise: in particular, the magnitude image was highly over-smoothed and the phase image was smoothed such that abrupt changes were still visible. With these two, we created an artificial complex image characterized by the anatomical resemblance of the non-weighted magnitude image and by a realistic phase typical of a DWI. These are shown in the top left side of Fig. 9. This ground truth image was corrupted with correlated and uncorrelated spatially varying noise. In the first case, 33 of the 112 lines of the k-space of the randomly generated noise were zero-filled to simulate . This produces a noise image with a noise variance reduced proportionally to the PF factor when compared to the uncorrelated case. For this reason, we generated two different versions of uncorrelated noise: the original one, which has higher variance compared to the correlated noise derived from it, and a scaled version having a sample variance that matches exactly that of the correlated noise image. The figure illustrates the mean absolute errors and the error standard deviation over 30 repetitions with different noise realizations of the phase estimation using different methods, where the noise variance was added considering mean SNRs on the image of 2.5 and 5. We implemented two low-pass filters, a boxcar filter (B3) as used by Prah et al. (2010) with kernel ,, and a Gaussian one (G3F1) as described by Sprenger et al. (2016), with kernel ,,. Inspired by the indications in the same reference, we tested a “hole mean” filter (HM) with kernel and our implementation of the decorrelated filters “G3F1H”, with kernel ,, , and “OPT3” with kernel , , . We should note that the actual kernels and the corresponding filter implementation may actually differ from the originally proposed ones; moreover, the OPT3 filter was optimized for a a specific acquisition pipeline thus it is not optimal for the experimental setup here adopted. Nevertheless, these filters are designed bearing in mind that the noise is spatially correlated (we note that other filter designs could be implemented with this regard). Indeed, the term “decorrelated” suggests that the filter attains a lower sensitivity with respect to the correlation between the noise realizations affecting adjacent pixels. In principle, a straightforward way of reducing such sensitivity consists in avoiding to process together the intensities of pixels that are adjacent one another along the direction where the correlation occurs (typically the phase-encoding direction).
Fig. 9.
Mean absolute errors and error standard deviation maps (degrees) after 30 iterations of phase estimation with different noise realizations and for different methods. At the top, the ground-truth magnitude and phase images and examples of correlated noise maps () and uncorrelated ones. The last two columns report the “reference” errors obtained by estimating the phase as the angle of the result of the image regularization based on TV when considering the ground-truth image affected by uncorrelated noise (Ref 1), eventually scaled (Ref 2). Please refer to section 5.4 for more details.
We applied the methods while considering correlated noise. As reference results, we also evaluated the TV-based regularization in the presence of uncorrelated noise without (Ref 1) and with scaling (Ref 2). In the case of the proposed adaptive method (TV), at each repetition the weighting function was estimated on a different noise realization compared to that used to create the noisy image, thus simulating a real case scenario. The results shown in Fig. 9 and summarized in Table 1 indicate that the TV-based adaptive method (APC) is the best among those tested. TV seems to render lower errors, especially in the areas corresponding to white matter, probably because of its edge-preserving characteristics and minimal footprint size. The other filters reveal a marked performance loss compared to the proposed method, with a mean absolute error up to , at mean SNR = 2.5, as opposed to the of the TV method. For these filters, the error does not seem to decrease with the increasing SNR, around the ventricles for instance, indicating the presence of a stronger bias in the presence of edges. Moreover, the error standard deviation maps clearly depict the white matter region, indicating a larger error variability in that area. Among the linear filters, the best performing one seems to be that based on the Gaussian kernel G3F1. It is possible that the level of correlation simulated is not high enough to favor the tested decorrelated filters. Finally, the performance of the proposed adaptive method in its TV formulation does not seem to be substantially influenced by the presence of noise correlation, as the results are both visually and quantitatively very similar to the reference “Ref 1” and only slightly worse compared to “Ref 2”. The experiments suggest that the TV formulation of eq. (10) provides a good regularization for performing APC, and that the simulated amount of noise correlation does not significantly affect the procedure.
Table 1.
Average values of the mean absolute error in degrees (m.a.e.) and of the error standard deviation (std) in the images accounting for 30 noise realizations. Values refer to results in the presence of spatially correlated noise. “Ref 1” and “Ref 2” refer to the error values obtained when using the TV-based adaptive method in eq. (10) on uncorrelated and on scaled uncorrelated noise respectively. Please refer to section 5.4 and Fig. 9 for more details.
| HM | G3F1H | OPT3 | G3F1 | B3 | TV | Ref 1 | Ref 2 | ||
|---|---|---|---|---|---|---|---|---|---|
| mean SNR 2.5 | m.a.e. | 11.66 | 11.32 | 11.37 | 9.64 | 9.69 | 7.75 | 7.96 | 7.33 |
| std | 13.86 | 13.56 | 13.52 | 11.05 | 11.78 | 9.48 | 9.80 | 9.07 | |
| mean SNR 5.0 | m.a.e. | 7.71 | 7.62 | 8.48 | 6.35 | 7.04 | 5.51 | 5.79 | 5.24 |
| std | 11.28 | 11.25 | 12.00 | 8.65 | 10.28 | 6.28 | 6.76 | 5.98 |
5.5. Bias reduction characterization
Phase correction's main purpose is to make complex averaging possible in order to boost the SNR of DWIs over repetitions, but also to reduce the bias of estimated quantities, such as the diffusion indices. In order to characterize the importance of unbiasing, we adopted a simulation setup to quantify the statistical bias reduction obtained with APC compared to when magnitude DWIs are used, as illustrated in Fig. 10. For each voxel we have calculated the noisy magnitude diffusion signal along different directions and for diffusion weightings, . We then calculated the corresponding phase-corrected real intensities and the reference bias-free intensities corrupted with additive Gaussian noise. For the magnitude, phase-corrected, and Gaussian signals we have calculated the diffusion indices based on DTI. The whole operation was repeated for 3000 different noise realizations thus obtaining, for each voxel, a histogram of the desired quantities, i.e. signal, axial diffusivity (AD), and fractional anisotropy (FA). In each voxel, and for each specific quantity such as AD, it was then possible to compare the magnitude-derived histogram, and the phase-corrected one, with that of the corresponding Gaussian reference. By calling , , and the voxel-specific magnitude, phase-corrected, and Gaussian normalized histograms of a specific quantity, we calculated the bias reduction as with H being the distance defined as (Hellinger, 1909)
| (17) |
where with 1 meaning maximum distance. In Fig. 10, the brightness of the images indicates the amount of statistical bias reduction – bounded between 0 and 1 – that one would obtain by performing APC instead of using magnitude DWIs. The figure reports results related to a different quantity for each column, where the contrast is restricted within a white matter mask for the sake of clarity. The first three columns from the left are related to signal intensities measured along three distinct diffusion gradient directions, with color code based on the colored FA map (Pajevic and Pierpaoli, 1999). In this way it is possible to identify the directional nature of the bias reduced using APC, which is highest in areas of the DWIs where the underlying fiber tracts are in close alignment with the considered gradient direction. For instance, in the first column the main selected color is red (see for example ), green in the second, and blue in the third. In the last two columns of Fig. 10 we report the bias reduction for FA and AD. These quantities are calculated using DWIs from the 7 different directions, therefore they do not directly show directional dependencies. However, in some regions we note values close to 1 occurring at already relatively low b-values. For instance, AD is particularly affected already at that is about the typical diffusion weighting adopted for HARDI tractography.
Fig. 10.
The amount of bias removed with APC with respect to the case in which magnitude DWIs are considered. The reduction is reported in a scale between 0 and 1, where 1 indicates the highest reduction (see section 5.5). The b-value, inverse SNR, and bias increase with the rows along the direction indicated by the arrow. The first three columns report the bias reduction on the DWI signal intensities for three different gradient directions, where the RGB color code represents the underlying tissue fiber orientation, obtained from the color FA map, and where the intensity is scaled from a minimum of 0 to a maximum of 1: note how the color intensity increases with the b-values, indicating a higher bias reduction. Moreover, different gradient directions are associated with different main colors: red for the first, green for the second, and blue for the third, since the bias is higher for voxels where the underlying tissue fibers are more aligned with the gradient direction itself. The last two columns report the bias reduction for indices calculated with DTI, such as fractional anisotropy (FA) and axial diffusivity (AD).
5.6. In vivo bias reduction on the diffusion signal and indices
We quantified the bias reduction obtained with phase correction on the diffusion signal and on diffusion indices based on the acquired DWIs of the two datasets. The phase-corrected, unbiased, real-valued image intensities are expected to be lower than the magnitude ones. Moreover, it is also expected that the amplitude of such difference increases with the decreasing SNR, i.e. with increasing b-values. To assess the validity of these considerations we calculated the difference between the phase-corrected image intensities obtained with APC and the corresponding magnitude ones. Fig. 11 illustrates such differences accounting for the average of the DWIs across the different directions of each shell of dataset 1 (left column). In the figure, these have been scaled by the local noise standard deviation as estimated from the noise map. The colorbar is therefore limited between approximately −1 and 0, where −1 indicates that the voxel-specific intensity of the phase-corrected real image is, in average, one standard deviation lower than the corresponding magnitude. We can appreciate the adaptive amount of bias correction provided by APC, where the correction is almost zero in the non-weighted image and gradually increases with the b-value. These results are in line with the trend of the estimated illustrated at the bottom of Fig. 8. Similar results are obtained also for dataset 2 (in the Supplementary Fig. 1). This does not hold true for the phase-corrected real images obtained with the G3F1 low-pass filter, which was chosen as comparing method as it scored the best results among the linear filters (Table 1). Indeed, such filter does not have an adaptive behavior since the amount of filtering performed is constant and does not depend on the underlying image. The difference in the behavior of the two strategies, APC and low-pass filtering, is illustrated in the third column of Fig. 11, where a blue color depicts a stronger signal reduction in favor of APC (as opposed to a red color) which becomes predominant at high b-values. Moreover, the use of the low-pass filter leads to a strong signal reduction in the correspondence of the boundaries between cortical and sub-cortical regions, and in regions that are likely containing image details and edges. Note that in the non-weighted image the SNR is much higher than that used for the experiments in Fig. 9 (as illustrated in Fig. 1) which can explain the different behavior of the low-pass filter in the white-matter region compared to the synthetic results.
Fig. 11.
Differences between phase-corrected real-valued image intensities (obtained with APC and with G3F1) and the magnitude ones, averaged across the different DWIs belonging to the same b-value shell, and normalized by the local standard deviation of the noise as estimated from the noise map. The third column reports the difference between the maps of the second column, obtained with the Gaussian filter (G3F1), and those in the first column (APC). Note, for APC, how the amount of signal reduction increases with the b-value, i.e. with decreasing SNR, as expected (being almost zero in the absence of diffusion weighting). On the contrary, when G3F1 is used, there is no adaptivity. The comparison in the third column clearly indicates that APC performs a higher correction at high b-values (the dominance of the blue color) whereas the Gaussian filter leads to increased correction at low b-values (red color) and in correspondence of regions with a high content of image details.
Following a similar criterion for comparison, in Fig. 12 we report the differences between diffusion indices calculated on the phase-corrected real-valued DWIs – based on APC and on the Gaussian low-pass filter – and those computed on the magnitude DWIs. For fairness of comparison, we considered the original magnitude for the non-weighted () images. In general, we believe that this is good practice as there should virtually be no bias in such images (provided that the SNR is sufficiently high), and any additional processing (such as APC) might just introduce unwanted artifacts. No further processing was applied to the DWIs such that the differences in the results only account for the use of phase correction while being affected by the same biases arising, for instance, from subject motion. In the left frame, we see that the bias reduction on axial diffusivity (AD) maps increases with the b-value: for the DTI fitting, all the DWIs of dataset 1 with b-value lower or equal than that indicated were considered. The bias reduction manifests itself with increased AD values that are mainly located in the white matter region. The fact that AD computed on magnitude DWIs is always underestimated as compared to that computed after APC suggests that APC allows Rician noise floor removal thus entailing a larger axial signal attenuation. In some cases, changes after APC accounts for values above 5. Although DTI becomes more and more invalid as the b-value increases beyond 2000, these relative difference maps well characterize the expected consequences of a reduced bias. The results for the Gaussian low-pass filtering method reveal regions where AD is lower (red) compared to that calculated from magnitude images. These regions are scattered but mainly located in the correspondence of the boundaries at the interface between gray and white matter, the interface with the ventricles, and in sub-cortical areas. Moreover, a strong relative increment of AD is found inside the ventricles, although this seems excessive since in that region the highest values of diffusivity are typically found.
Fig. 12.
Difference between phase-corrected (with APC or low-pass Gaussian filter) and magnitude quantities (relative to magnitude values where the symbol “” is indicated). In the first column, the axial diffusivity has an increased value after APC: this is more evident as the maximum b-value considered in the DTI fit increases (all the DWIs with b-value lower or equal than that indicated are considered). Mean kurtosis (MK) is generally lower after APC, suggesting that part of the kurtosis in the magnitude images might be explained by the presence of the noise floor (note that non-negativity constraints were not enforced, refer to section 4). The mean squared displacement (MSD) is higher after APC, whereas the return to origin probability (RTOP) is lower. These factors indicate the detection of a more prominent diffusion process compared to magnitude images. Similar trends are globally obtained for the indices based on the DWIs filtered with the low-pass Gaussian kernel G3F1, however there are regions where the global trend is locally inverted, which is more evident in the AD maps and in the MSD and RTOP ones.
In a similar manner, we used dataset 2 to perform multi-shell reconstruction to compute the mean kurtosis (MK) with DKI, and the mean squared displacement (MSD) and return to origin probability (RTOP) with MAP-MRI. The mean kurtosis gives an indication of the non-Gaussianity of the diffusion process in a voxel, whereas MSD and RTOP are q-space properties related, in first approximation, to the amount of detected diffusion. For instance, the MSD (Cheng, 2012) is expected to be high in the ventricles and the RTOP is expected to be low (Özarslan et al., 2013; Fick et al., 2016). In the right frame of Fig. 12 we note that MK values computed on APC data are lower than the corresponding magnitude-based ones, suggesting that non-Gaussianity in magnitude images is detected, at least in part, because of the presence of the noise floor. Differences are mainly localized at the interface between white and gray matter, and in regions containing cerebrospinal fluid such as the ventricles. After APC, the MSD has increased while the RTOP has decreased, which is particularly evident in the ventricular region. This indicates the detection of a more prominent diffusion process after APC. These results suggest that APC has an impact on multi-shell modeling and on the estimation of non-Gaussianity of the diffusion decay at high diffusion weighting regimes. In this case, the differences with the results obtained using the Gaussian low-pass filter are less evident. However, MK values are less reduced in the ventricular region compared to APC, whereas scattered regions of inverted trend are found for both MSD and RTOP maps. We note that, unlike the comparison in Fig. 11, the results of Fig. 12 likely include influences from the various models/representations and from the behaviors of the corresponding optimization methods, therefore care must be taken when drawing conclusions.
6. Discussion
The results suggest that adaptive phase correction (APC) reduces the bias on signal and diffusion indices, as illustrated in Fig. 4, Fig. 7, Fig. 10, Fig. 11, Fig. 12. As expected, the bias reduction increases with the diffusion weighting since the SNR decreases. However, some brain regions are affected already at relatively low b-values such as 1390 . In addition, some indices are more affected than others. For instance, Fig. 10 reveals that AD is more biased than FA, which is likely related to the fact that the calculation of FA involves using the diffusivities along directions that are orthogonal to that along which AD is measured, i.e. the direction along which the signal displays the highest attenuation and consequently the largest Rician bias. The reduction of the noise floor achieved by APC could also help the mitigation of other known artifacts in the calculation of the diffusion tensor, such as the shifting of the eigenvectors and the overestimation/misordering of the eigenvalues (Laun et al., 2009). Results in Fig. 12 show that the effect of APC is relevant also for multi-shell signal representations such as DKI and MAP-MRI. Similar results are expected for other signal representations tailored for high diffusion weighting regimes, such as Diffusion Spectrum Imaging (Wedeen et al., 2005). Moreover, the differences between magnitude-based and phase-corrected local indices, especially considering the orientational nature of the bias illustrated in Fig. 10, suggest that streamline propagation in tractography would also benefit from APC. This would likely have an impact on the calculation of the structural connectivity, as the effect of tractography propagates on a global scale (Jeurissen et al., 2017). With regard to signal unbiasing, we mention that there exist also methods, alternative to phase correction, that only use the information of the Rician magnitude and of the noise variance (Koay et al., 2009a; Kaden et al., 2016). However, these require in-voxel approximation/interpolation of the diffusion magnitude signal implying choices like the number of basis functions and the amount of regularization. If approximation/interpolation is not used, then the unbiased signal can present statistical suboptimalities. A phase correction approach, on the other hand, can be applied to any kind of data, for instance to multi-dimensional sequences (Westin et al., 2016), without the need of resorting to representations or modeling of the diffusion signal.
The results discussed in sections 5.1, 5.2, and illustrated in Fig. 4, Fig. 5, Fig. 6, Fig. 7, show the importance of adopting a noise-driven approach for phase correction and bias reduction. Indeed, we showed that when the phase is over-regularized – low λ – important image contrast is left on the imaginary component of the corrected DWIs (Fig. 4, Fig. 5). This contrast would be lost when working with the real-valued DWI as result of the phase correction procedure, which would lead to outliers that identify “anomalies”. Sprenger et al. (2016) proposed the outliers detection/replacement method to counteract the effects of erroneous correction. However, results in section 5.3 show that APC leads to a low number of outliers (Fig. 8), while still performing an adequate correction (Fig. 7). These results are indicative of the fact that APC is suitable also for enabling complex averaging when the phase of the image changes across repeated acquisitions.
In this work, particularly, we propose the use of a global regularizer that operates locally via a weighting function calculated from the local noise variance. This is achieved by calculating an initial amount of regularization with the discrepancy criterion that is then refined by using a spatially varying Monte Carlo SURE method. The latter was validated for complex images in Fig. 3 for very low SNRs, demonstrating that APC is suitable for high b-value and high spatial resolution diffusion-weighted images. This setup allows obtaining an adaptive amount of correction, as illustrated in Fig. 11, where the signal correction gradually increases with the decreasing SNR (increasing b-value). On the contrary, a standard low-pass filtering approach does not enable such a desired behavior. On the other hand, APC comes at the expense of the computational cost. In our implementation, it took 98 min to process the multi-shell dataset 2, composed of 4860 images, using 12 threads on an Intel® Xeon(R) CPU E5-1650v4 at 3.60 GHz (0.1 precision on λ and stop tolerance of ). The computational time largely depends on the desired precision and tolerance values, and is inherently connected to the Monte Carlo calculation of SURE that constitutes a computational bottleneck. Because of this, the present implementation of APC can only be used as an offline processing. However, some strategies could be explored in the future. One possibility consists on running APC on a subset of the data to extract the values of λ to be used for correcting the rest of it. However, this option needs a thorough feasibility assessment and is left to future work.
Although many methods could potentially be used to characterize the properties of the noise (Koay et al., 2009b; Pieciak et al., 2017; St-Jean et al., 2018), we proposed to acquire an MRI noise map, as described in section 4.2, since it offers the advantage of a straightforward estimation of the local variance. Moreover, the acquisition time of the noise map is equivalent to that necessary for the acquisition of an additional gradient direction, thus entailing a minimal time penalty of a few seconds. We note that noise statistics could be obtained by knowing some parameters of the image reconstruction (Liu et al., 2008) or through the use of the generalized pseudo-replica method (Wiens et al., 2011), however we find that the use of a noise map is more convenient for practical purposes while it allows accounting for the most relevant component for noise modeling after reconstruction. We should note, however, that the use of a single noise map leads to approximation. In our results, we estimated the local variance with a filter that accounts for a spherical neighborhood of 4 voxels radius over the complex-valued noise map. However, similarly to other local methods, the choice of a radius implements a trade-off between fidelity to the variance’ spatial variability and smoothness of the estimated variance map, which constitutes a limitation. This problem could potentially be solved by representing the spatial variability with a parametric surface such as that used in our synthetic results and shown in Fig. 1. Alternatively, the radius could be reduced by acquiring more than one noise map.
The proposed APC is designed to be used on a image-by-image basis in order to be applicable to different MRI modalities for phase correction/estimation purposes. This choice forced us to adopt an image operator approach which can suffer from the intrinsic limitations of the chosen regularization method and whose effects can propagate to the phase-corrected real-valued DWIs. Indeed, Fig. 9 shows that the TV regularization, although performing better than the other tested methods, is not free from errors in the phase estimation. Nevertheless, the proposed Oriented Laplacian formulation allows for quite some flexibility: an optimal regularization method could be chosen based on additional synthetic experiments, by visual inspection, or following an outliers minimization criterion for the specific dataset. Indeed, although results were presented for TV regularization, the proposed methodology can be generalized to other operators. We note that another possible way of improving the phase estimation consists in including information about the correlation of the phase over consecutively acquired images. We also note that although the method seems to be only marginally affected by the spatial correlation of the noise – arising, for instance, from the use of Partial Fourier – the development of decorrelation strategies and/or adaptations of eq. (10) is desirable.
Although APC improves over more conventional methods, care must be taken when processing the phase-corrected real-valued images, and visual inspection is recommended especially when dealing with clinically-relevant data. In fact, the computed maps of diffusion indices after phase-correction may contain “impurities” that may have not been present in the corresponding maps derived from the magnitude DWIs, thus the calculation of differential maps could help their identification. Perhaps, the adoption of an outliers replacement method along the line of the work by Sprenger et al. (2016) should still be employed and could be extended to the calculated diffusion indices in order to check for extreme differences and/or structural changes. Finally, as a general rule, because of the negative signal intensities that are present in the phase-corrected real-valued images, the compatibility with subsequent image and signal processing should also be verified from case to case.
7. Conclusion
In this article we proposed adaptive phase correction, a noise-driven methodology for phase correction/estimation and a method based on criteria to automatically set the amount of regularization required to estimate the phase, thus overcoming the issues related to low or excessive regularization. The local variance estimated from an MRI noise map, or potentially with other methods, is integrated within a spatially varying operator based on an Oriented Laplacian regularization in the complex domain. This is used to regularize the DWIs in order to estimate their phase, in combination with the discrepancy criterion and a spatially varying version of Monte Carlo SURE. Adaptive phase correction renders a bias reduction of the diffusion signal that fulfills the expected behavior as function of the SNR, allowing for a progressively stronger correction as the b-value increases. This in turn allows unbiasing the diffusion indices calculated from the phase-corrected real-valued DWIs, although visual inspection should always be performed to validate the results. We finally note that the proposed method is a suitable preprocessing to perform complex averaging, and that some aspects of what presented could be adopted for the processing of images acquired with other MRI modalities where there is a need for phase estimation.
Ethics statement
Data was acquired on healthy volunteers based on a protocol approved by the Centre de Recherche CHUS, Sherbrooke, Québec, Canada.
Acknowledgments
We thank Tom Dela Haije, Alexis Reymbaut, Michael Paquette, Samuel St-Jean, and Timothé Boutelier for the constructive discussions. Marco Pizzolato is supported by the Swiss National Science Foundation under Sinergia grant number CRSII5170873. Guillaume Gilbert is an employee of Philips Healthcare. Thanks to the Pr Descoteaux Institutional Research Chair in NeuroInformatics. Rachid Deriche is supported by the ERC Advanced Grant agreement No 694665:CoBCoM under the European Union's Horizon 2020 research and innovation program.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.neuroimage.2019.116274.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
figs1.
References
- Aja-Fernández S., Vegas-Sánchez-Ferrero G. Springer; 2016. Statistical Analysis of Noise in MRI. [Google Scholar]
- Alvarez L., Lions P.L., Morel J.M. Image selective smoothing and edge detection by nonlinear diffusion. ii. SIAM J. Numer. Anal. 1992;29:845–866. [Google Scholar]
- Bammer R., Holdsworth S.J., Aksoy M., Skare S. Phase errors in diffusion weighted imaging. Diffusion MRI: Theor. Methods Appl. 2010:218–249. [Google Scholar]
- Basser P.J., Mattiello J., LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J. Magn. Reson., Ser. B. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Basser P.J., Mattiello J., LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66:259. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein M.A., Thomasson D.M., Perman W.H. Improved detectability in low signal-to-noise ratio magnetic resonance images by means of a phase-corrected real reconstruction. Med. Phys. 1989;16:813–817. doi: 10.1118/1.596304. [DOI] [PubMed] [Google Scholar]
- Braun W.J., Murdoch D.J. Cambridge University Press; 2007. A First Course in Statistical Programming with R. [Google Scholar]
- Bretthorst G.L. Automatic phasing of MR images. part i: linearly varying phase. J. Magn. Reson. 2008;191:184–192. doi: 10.1016/j.jmr.2007.12.010. [DOI] [PubMed] [Google Scholar]
- Bretthorst G.L. Automatic phasing of MR images. part ii: voxel-wise phase estimation. J. Magn. Reson. 2008;191:193–201. doi: 10.1016/j.jmr.2007.12.011. [DOI] [PubMed] [Google Scholar]
- Caruyer E., Lenglet C., Sapiro G., Deriche R. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magn. Reson. Med. 2013;69:1534–1540. doi: 10.1002/mrm.24736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambolle A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004;20:89–97. [Google Scholar]
- Chang Z., Xiang Q.S. Nonlinear phase correction with an extended statistical algorithm. IEEE Trans. Med. Imaging. 2005;24:791–798. doi: 10.1109/TMI.2005.848375. [DOI] [PubMed] [Google Scholar]
- Chen N.k., Guidon A., Chang H.C., Song A.W. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE) Neuroimage. 2013;72:41–47. doi: 10.1016/j.neuroimage.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J. Université Nice Sophia Antipolis; 2012. Estimation and Processing of Ensemble Average Propagator and its Features in Diffusion MRI. Ph.D. thesis. [Google Scholar]
- Cordero-Grande L., Christiaens D., Hutter J., Price A.N., Hajnal J.V. Complex diffusion-weighted image estimation via matrix recovery under general noise models. Neuroimage. 2019;200:391–404. doi: 10.1016/j.neuroimage.2019.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duran J., Coll B., Sbert C. Chambolle's projection algorithm for total variation denoising. Image Process. Line. 2013;2013:311–331. [Google Scholar]
- Eichner C., Cauley S.F., Cohen-Adad J., Möller H.E., Turner R., Setsompop K., Wald L.L. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. Neuroimage. 2015;122:373–384. doi: 10.1016/j.neuroimage.2015.07.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ertürk M.A., Bottomley P.A., El-Sharkawy A.M.M. Denoising MRI using spectral subtraction. IEEE (Inst. Electr. Electron. Eng.) Trans. Biomed. Eng. 2013;60:1556–1562. doi: 10.1109/TBME.2013.2239293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fick R.H., Wassermann D., Caruyer E., Deriche R. MAPL: tissue microstructure estimation using laplacian-regularized MAP-MRI and its application to HCP data. Neuroimage. 2016;134:365–385. doi: 10.1016/j.neuroimage.2016.03.046. [DOI] [PubMed] [Google Scholar]
- Galatsanos N.P., Katsaggelos A.K. Methods for choosing the regularization parameter and estimating the noise variance in image restoration and their relation. IEEE Trans. Image Process. 1992;1:322–336. doi: 10.1109/83.148606. [DOI] [PubMed] [Google Scholar]
- Garyfallidis E., Brett M., Amirbekian B., Rokem A., Van Der Walt S., Descoteaux M., Nimmo-Smith I. Dipy, a library for the analysis of diffusion MRI data. Front. Neuroinf. 2014;8:8. doi: 10.3389/fninf.2014.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Getreuer P. Rudin-osher-fatemi total variation denoising using split bregman. Image Process. Line. 2012;2:74–95. [Google Scholar]
- Gilbert G., Simard D., Beaudoin G. Impact of an improved combination of signals from array coils in diffusion tensor imaging. IEEE Trans. Med. Imaging. 2007;26:1428–1436. doi: 10.1109/TMI.2007.907699. [DOI] [PubMed] [Google Scholar]
- Gilboa G., Sochen N., Zeevi Y.Y. Variational denoising of partly textured images by spatially varying constraints. IEEE Trans. Image Process. 2006;15:2281–2289. doi: 10.1109/tip.2006.875247. [DOI] [PubMed] [Google Scholar]
- Hellinger E. Neue begründung der theorie quadratischer formen von unendlichvielen veränderlichen. J. für die Reine Angewandte Math. (Crelle's J.) 1909;136:210–271. [Google Scholar]
- Henkelman R.M. Measurement of signal intensities in the presence of noise in MR images. Med. Phys. 1985;12:232–233. doi: 10.1118/1.595711. [DOI] [PubMed] [Google Scholar]
- Hu K., Cheng Q., Gao X. Wavelet-domain TI Wiener-like filtering for complex MR data denoising. Magn. Reson. Imag. 2016;34:1128–1140. doi: 10.1016/j.mri.2016.05.011. [DOI] [PubMed] [Google Scholar]
- Hu K., Cheng Q., Li B., Gao X. The complex data denoising in MR images based on the directional extension for the undecimated wavelet transform. Biomed. Signal Process. Control. 2018;39:336–350. [Google Scholar]
- Hua J., Hurst G.C. Noise and artifact comparison for Fourier and polynomial phase correction used with Fourier reconstruction of asymmetric data sets. J. Magn. Reson. Imaging. 1992;2:347–353. doi: 10.1002/jmri.1880020316. [DOI] [PubMed] [Google Scholar]
- Jensen J.H., Helpern J.A. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23:698–710. doi: 10.1002/nbm.1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen J.H., Helpern J.A., Ramani A., Lu H., Kaczynski K. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 2005;53:1432–1440. doi: 10.1002/mrm.20508. [DOI] [PubMed] [Google Scholar]
- Jeurissen B., Descoteaux M., Mori S., Leemans A. Diffusion MRI fiber tractography of the brain. NMR Biomed. 2017 doi: 10.1002/nbm.3785. [DOI] [PubMed] [Google Scholar]
- Jones D.K., Basser P.J. “Squashing peanuts and smashing pumpkins”: how noise distorts diffusion-weighted MR data. Magn. Reson. Med. 2004;52:979–993. doi: 10.1002/mrm.20283. [DOI] [PubMed] [Google Scholar]
- Kaden E., Kruggel F., Alexander D.C. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magn. Reson. Med. 2016;75:1752–1763. doi: 10.1002/mrm.25734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koay C.G., Chang L.C., Carew J.D., Pierpaoli C., Basser P.J. A unifying theoretical and algorithmic framework for least squares methods of estimation in diffusion tensor imaging. J. Magn. Reson. 2006;182:115–125. doi: 10.1016/j.jmr.2006.06.020. [DOI] [PubMed] [Google Scholar]
- Koay C.G., Özarslan E., Basser P.J. A signal transformational framework for breaking the noise floor and its applications in MRI. J. Magn. Reson. 2009;197:108–119. doi: 10.1016/j.jmr.2008.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koay C.G., Özarslan E., Pierpaoli C. Probabilistic identification and estimation of noise (PIESNO): a self-consistent approach and its applications in MRI. J. Magn. Reson. 2009;199:94–103. doi: 10.1016/j.jmr.2009.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kornprobst P., Deriche R., Aubert G. CVPR. IEEE; 1997. Non-linear operators in image restoration; p. 325. [Google Scholar]
- Laun F.B., Schad L.R., Klein J., Stieltjes B. How background noise shifts eigenvectors and increases eigenvalues in DTI. Magn. Reson. Mater. Phys. Biol. Med. 2009;22:151–158. doi: 10.1007/s10334-008-0159-6. [DOI] [PubMed] [Google Scholar]
- Liu B., Abdelsalam E., Sheng J., Ying L. Proceedings of ISMRM 16th Annual Meeting. 2008. G-factor maps of conjugate gradient SENSE reconstruction; p. 16. [Google Scholar]
- Liu J., Koenig J.L. An automatic phase correction method in nuclear magnetic resonance imaging. J. Magn. Reson. 1990;86:593–604. [Google Scholar]
- Maier-Hein K.H., Neher P.F., Houde J.C., Caruyer E., Daducci A., Dyrby T., Stieltjes B., Descoteaux M. 2015. [DOI]
- Maier-Hein K.H., Neher P.F., Houde J.C., Côté M.A., Garyfallidis E., Zhong J., Chamberland M., Yeh F.C., Lin Y.C., Ji Q. The challenge of mapping the human connectome based on diffusion tractography. Nat. Commun. 2017;8:1349. doi: 10.1038/s41467-017-01285-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manjón J.V., Coupé P., Concha L., Buades A., Collins D.L., Robles M. Diffusion weighted image denoising using overcomplete local PCA. PLoS One. 2013;8 doi: 10.1371/journal.pone.0073021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGibney G., Smith M., Nichols S., Crawley A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn. Reson. Med. 1993;30:51–59. doi: 10.1002/mrm.1910300109. [DOI] [PubMed] [Google Scholar]
- Morozov V.A. The error principle in the solution of operational equations by the regularization method. USSR Comput. Math. Math. Phys. 1968;8:63–87. [Google Scholar]
- Neher P.F., Laun F.B., Stieltjes B., Maier-Hein K.H. Fiberfox: facilitating the creation of realistic white matter software phantoms. Magn. Reson. Med. 2014;72:1460–1470. doi: 10.1002/mrm.25045. [DOI] [PubMed] [Google Scholar]
- Noll D.C., Nishimura D.G., Macovski A. Homodyne detection in magnetic resonance imaging. IEEE Trans. Med. Imaging. 1991;10:154–163. doi: 10.1109/42.79473. [DOI] [PubMed] [Google Scholar]
- Özarslan E., Koay C.G., Shepherd T.M., Komlosh M.E., İrfanoğlu M.O., Pierpaoli C., Basser P.J. Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure. Neuroimage. 2013;78:16–32. doi: 10.1016/j.neuroimage.2013.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pajevic S., Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn. Reson. Med. 1999;42:526–540. [PubMed] [Google Scholar]
- Pieciak T., Aja-Fernandez S., Vegas-Sánchez-Ferrero G. Non-stationary rician noise estimation in parallel MRI using a single image: a variance-stabilizing approach. IEEE Trans. Pattern Anal. Mach. Intell. 2017;39:2015–2029. doi: 10.1109/TPAMI.2016.2625789. [DOI] [PubMed] [Google Scholar]
- Pizzolato M., Deriche R., Canales-Rodríguez E.J., Thiran J.P. 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) IEEE; 2019. Spatially varying Monte Carlo SURE for the regularization of biomedical images; pp. 1639–1642.https://infoscience.epfl.ch/record/265384 [Google Scholar]
- Pizzolato M., Fick R., Boutelier T., Deriche R. Noise floor removal via phase correction of complex diffusion-weighted images: influence on DTI and q-space metrics. In: Fuster A., Ghosh A., Kaden E., Rathi Y., Reisert M., editors. Computational DIffusion MRI. MICCAI 2016. Mathematics and Visualization. Springer; Cham: 2016. pp. 21–34. [Google Scholar]
- Prah D.E., Paulson E.S., Nencka A.S., Schmainda K.M. A simple method for rectified noise floor suppression: phase-corrected real data reconstruction with application to diffusion-weighted imaging. Magn. Reson. Med. 2010;64:418–429. doi: 10.1002/mrm.22407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruessmann K.P., Weiger M., Scheidegger M.B., Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn. Reson. Med. 1999;42:952–962. [PubMed] [Google Scholar]
- Ramani S., Blu T., Unser M. Monte-carlo sure: a black-box optimization of regularization parameters for general denoising algorithms. IEEE Trans. Image Process. 2008;17:1540–1554. doi: 10.1109/TIP.2008.2001404. [DOI] [PubMed] [Google Scholar]
- Rudin L.I., Osher S., Fatemi E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992;60:259–268. [Google Scholar]
- Sapiro G., Ringach D.L. Anisotropic diffusion of multivalued images with applications to color filtering. IEEE Trans. Image Process. 1996;5:1582–1586. doi: 10.1109/83.541429. [DOI] [PubMed] [Google Scholar]
- Schilling K.G., Nath V., Hansen C., Parvathaneni P., Blaber J., Gao Y., Neher P., Aydogan D.B., Shi Y., Ocampo-Pineda M. Limits to anatomical accuracy of diffusion tractography using modern approaches. Neuroimage. 2019;185:1–11. doi: 10.1016/j.neuroimage.2018.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sotiropoulos S., Moeller S., Jbabdi S., Xu J., Andersson J., Auerbach E., Yacoub E., Feinberg D., Setsompop K., Wald L. Effects of image reconstruction on fiber orientation mapping from multichannel diffusion MRI: reducing the noise floor using SENSE. Magn. Reson. Med. 2013;70:1682–1689. doi: 10.1002/mrm.24623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprenger T., Sperl J.I., Fernandez B., Haase A., Menzel M.I. Real valued diffusion-weighted imaging using decorrelated phase filtering. Magn. Reson. Med. 2016 doi: 10.1002/mrm.26138. [DOI] [PubMed] [Google Scholar]
- St-Jean S., De Luca A., Viergever M.A., Leemans A. Automatic, fast and robust characterization of noise distributions for diffusion MRI. In: Frangi A.F., Schnabel J.A., Davatzikos C., Alberola-López C., Fichtinger G., editors. Medical Image Computing and Computer Assisted Intervention – MICCAI 2018. Springer International Publishing; 2018. pp. 304–312. [Google Scholar]
- Stein C.M. Estimation of the mean of a multivariate normal distribution. Ann. Stat. 1981:1135–1151. [Google Scholar]
- Stejskal E.O., Tanner J.E. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 1965;42:288–292. [Google Scholar]
- Tschumperlé D., Deriche R. Anisotropic diffusion partial differential equations for multichannel image regularization: framework and applications. Adv. Imag. Electron. Phys. 2007;145:149–209. [Google Scholar]
- Veraart J., Novikov D.S., Christiaens D., Ades-Aron B., Sijbers J., Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage. 2016;142:394–406. doi: 10.1016/j.neuroimage.2016.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedeen V.J., Hagmann P., Tseng W.Y.I., Reese T.G., Weisskoff R.M. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn. Reson. Med. 2005;54:1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- Westin C.F., Knutsson H., Pasternak O., Szczepankiewicz F., Özarslan E., van Westen D., Mattisson C., Bogren M., O’donnell L.J., Kubicki M., Topgaard D., Nilsson M. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage. 2016;135:345–362. doi: 10.1016/j.neuroimage.2016.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiens C.N., Kisch S.J., Willig-Onwuachi J.D., McKenzie C.A. Computationally rapid method of estimating signal-to-noise ratio for phased array image reconstructions. Magn. Reson. Med. 2011;66:1192–1197. doi: 10.1002/mrm.22893. [DOI] [PubMed] [Google Scholar]
- Wirestam R., Bibic A., Lätt J., Brockstedt S., Ståhlberg F. Denoising of complex MRI data by wavelet-domain filtering: application to high-b-value diffusion-weighted imaging. Magn. Reson. Med. 2006;56:1114–1120. doi: 10.1002/mrm.21036. [DOI] [PubMed] [Google Scholar]
- Wood J.C., Johnson K.M. Wavelet packet denoising of magnetic resonance images: importance of Rician noise at low SNR. Magn. Reson. Med. 1999;41:631–635. doi: 10.1002/(sici)1522-2594(199903)41:3<631::aid-mrm29>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- Zhao F., Noll D.C., Nielsen J.F., Fessler J.A. Separate magnitude and phase regularization via compressed sensing. IEEE Trans. Med. Imaging. 2012;31:1713–1723. doi: 10.1109/TMI.2012.2196707. [DOI] [PMC free article] [PubMed] [Google Scholar]