Abstract
Motivation
The human body hosts more microbial organisms than human cells. Analysis of this microbial diversity provides key insight into the role played by these microorganisms on human health. Metagenomics is the collective DNA sequencing of coexisting microbial organisms in an environmental sample or a host. This has several applications in precision medicine, agriculture, environmental science and forensics. State-of-the-art predictive models for phenotype predictions from metagenomic data rely on alignments, assembly, extensive pruning, taxonomic profiling and reference sequence databases. These processes are time consuming and they do not consider novel microbial sequences when aligned with the reference genome, limiting the potential of whole metagenomics. We formulate the problem of predicting human disease from whole-metagenomic data using Multiple Instance Learning (MIL), a popular supervised learning paradigm. Our proposed alignment-free approach provides higher accuracy in prediction by harnessing the capability of deep convolutional neural network (CNN) within a MIL framework and provides interpretability via neural attention mechanism.
Results
The MIL formulation combined with the hierarchical feature extraction capability of deep-CNN provides significantly better predictive performance compared to popular existing approaches. The attention mechanism allows for the identification of groups of sequences that are likely to be correlated to diseases providing the much-needed interpretation. Our proposed approach does not rely on alignment, assembly and reference sequence databases; making it fast and scalable for large-scale metagenomic data. We evaluate our method on well-known large-scale metagenomic studies and show that our proposed approach outperforms comparative state-of-the-art methods for disease prediction.
Availability and implementation
1 Introduction and background
The human body hosts one of the densest and diverse microbial environments in the world. Trillions of microbial cells in the human body are collectively referred to as the human microbiome (Backhed, 2005; Turnbaugh et al., 2007). Metagenomics is the sequencing of the collective DNA of microbial organisms coexisting as communities in an environmental sample or a host (Hugenholtz and Tyson, 2008). Metagenomics has enabled the investigation of the human microbiome and provided key insights into the roles played by microbes in a host. Typical Metagenome Wide Association Study (MWAS) produces millions of DNA sequence fragments from healthy and unhealthy cohorts. This genomic information can be utilized to estimate microbial diversity and predict diseases leading to the design of novel therapeutics and diagnostics (Chiu et al., 2019). However, sequencing technologies do not deliver the complete genome of an organism (millions in length), but a large number of short contiguous subsequences called reads in random order. Sequence reads from different microbes are mixed with a high amount of repetitions (Hugenholtz and Tyson, 2008) resulting in large datasets that range from gigabytes (GB) to terabytes (TB). These factors impose serious challenges when developing machine learning algorithms to predict disease from whole-metagenomic data.
This article focuses on predicting clinical phenotypes, i.e. diseases from whole-metagenomic data. Existing approaches for disease prediction utilize microbial profiling (McIntyre et al., 2017) combined with conventional supervised learning methods for predictive analysis. Microbial profiling involves searching of the input metagenomic sequences against the known microbial genome using computationally expensive alignments. The current knowledge about microbes is largely achieved in the unnatural conditions of growing them in artificial media in pure culture without ecological context (Quince et al., 2017). Moreover, it is estimated that less than 2% of the bacteria can be cultured in the laboratory (Handelsman, 2004; Wade, 2002). When microbial profiling is used before disease prediction, the sequences that match with known microbial genome contribute to the feature creation process. The sequences without sufficient match which may represent partial genome of potentially novel microbes, are ignored and do not partake in feature creation. A metagenomic sample with millions of sequence reads is represented with a single vector which is then used to train classification models. The predictive models also include errors and biases from prior alignments and microbial profiling processes.
In our proposed approach, we aim to avoid the use of sequence assembly and microbial profiling before classifying diseases from metagenomic samples. To scale with millions of repetitive sequence reads and achieve efficiency, we embed the DNA sequences in a fixed-length vector representation and perform clustering on these embeddings avoiding the computationally expensive alignment-based clustering. For the prediction, we leverage the Multiple Instance Learning (MIL) framework, where a single sample (known as a bag) may include many data instances. MIL imposes two restrictions on the generic classifiers: (i) the data will be represented with the bag-instance relations and (ii) instances need to be labeled along with the bags. Each of the instances in the bag has its features, collectively representing the bag. As a result, the classifier is exposed to more variations among the samples which help to classify accurately. The second restriction allows for easy interpretations. These utilities make MIL a good candidate for various predictive analyses in metagenomics. We represent the metagenomic sample of a person as a bag and the cluster prototypes within the sample as instances. Besides bag-level classification, the MIL approach allows for inferring which instances, i.e. groups of DNA sequences are likely to be associated with the phenotypic labels.
Once formulated, the classification in MIL can be performed in different ways, i.e. modification of the maximum margin formulation of support vector machine (SVM), deep learning, etc. We utilize deep learning to solve the MIL formulation because: (i) it extracts relevant latent features from the earlier layers in a step-by-step manner—a unique capability of deep learning compared to other machine learning approaches and (ii) deep-learning approaches are highly nonlinear making them suitable for learning complex relations among the latent features. Specifically, we use a novel attention-based deep convolutional neural network (CNN). Deep CNN models (Krizhevsky et al., 2012; Simonyan and Zisserman, 2004) extract latent features from input in a step-by-step manner using multiple layers of convolution operations. The neural attention (Vaswani et al., 2017) learns which features to focus on as part of the deep-learning model. We use the positional attention values to infer which groups of sequences in the unhealthy cohort may correlate to a disease. We refer to our approach as Interpretable Deep Multiple Instance Learning (IDMIL). We apply IDMIL on five large-scale metagenomic datasets. We show that IDMIL outperforms existing state-of-the-art approaches in predictive performance. Via qualitative case studies, we show the interpretation capability provided by IDMIL.
1.1 Metagenomics and disease prediction
Qin et al. (2012) performed statistical analysis on microbial diversity among the samples from type-2 diabetes (T2D) patients and healthy controls for marker identification. Saulnier et al. (2011) identified significant differences between the gut microbiomes of healthy people and people who suffer from irritable bowel syndrome. Other studies discovered the correlations among colorectal cancer (Zeller et al., 2014), inflammatory bowel disease (IBD) (Qin et al., 2010) and obesity (Le Chatelier et al., 2013); and the variations in microbial abundance. These approaches require extensive preprocessing of samples and microbial profiling.
MetAML (Pasolli et al., 2016) uses machine-learning methods for disease classification. It first identifies marker genes and species-level abundance using the MetaPhlAn2 (Truong et al., 2015) method. MetaPhlAn2 (Truong et al., 2015) is used for the quantitative taxonomic profiling of the microbial communities in metagenomic samples. MetAML uses these features to train a random forest or SVM classifier to predict clinical phenotypes. Rahman et al. (2017) used clustering to identify cluster centroids and then used the minimum distance from a sample to the centroids as features for classifiers.
1.2 Deep learning and metagenomics
Deep learning has achieved unprecedented success in wide-ranging domains (Gu et al., 2018). Deep learning has been used in metagenomic studies for different prediction tasks. Fioravanti et al. (2018) proposed Ph-CNN which takes as input the operational taxonomic unit (OTU) abundance distribution and the OTU distance matrix, and outputs the class of each sample using deep CNN. DeepARG (Arango-Argoty et al., 2018) uses a deep neural network on the dissimilarity matrix created using all known categories of antibiotic resistance genes to predict their presence in metagenomic samples. RegMIL (Rahman and Rangwala, 2018) uses Canopy-based sequence clustering (Rahman et al., 2017) to score the reads based on the cluster memberships. It then uses a deep neural network-based regression to score sequences in test samples and classify samples based on sequence score distributions.
Dna2vec (Ng, 2017) uses similar technique as word-embedding (Le and Mikolov, 2014) in natural language processing to embed DNA sequences. This approach uses random lengths for DNA sub-sequences (kmers) which increases entropy and directly affects the reproducibility of the sequence representations. PLG–ABD (Nguyen et al., 2017) uses MetaPhlAn2 (Truong et al., 2015) method to estimate microbial abundance and then sorts species-level abundances based on biological taxonomy to represent the metagenomic samples as images. It then uses deep CNN to classify healthy and patient samples. It suffers from the same limitations as MetAML that discards a large number of DNA sequences during the profiling process. Moreover, the possibility of interpretation is lost in the latent space after convolution.
1.3 Multiple Instance Learning
In the original formation of MIL (Dietterich et al., 1997), a bag is classified as positive if one or more instances within it are positive, whereas a negative bag contains only negative instances. Different formulations of the MIL problem have been developed over the years (Amores, 2013). MISVM (Andrews et al., 2003) and sbMIL (Bunescu and Mooney, 2007) are two of the popular MIL algorithms which follow the standard assumption. These methods use local information-based comparisons between individual instances and treat bag labels as aggregations of instance labels. Kotzias et al. (2015) proposed a MIL formulation titled group-instance cost function (GICF) where negative bags contain some positive instances and developed a general cost function for determining individual instance labels from group labels. In contrast with the standard assumption, this is referred to as the collective assumption.
Neural attention has been used to create bag-level representation from instances (Ilse, 2018) and then classify the bags. This approach uses a deep CNN for latent feature extraction and applies neural attention to the fully connected layer when all latent features are already extracted. As a result, mapping with the original feature space is lost, and the attention values are not interpretable, especially for nonimage input data, i.e. DNA sequences. We refer to this approach as attention-based deep MIL (AttMIL) and use it as one of the state-of-the-art models for comparative analysis. LaPierre et al. (2016) proposed a phenotype prediction from metagenomic data that utilizes instance space. This approach used the distances in instance space to represent bags which were then classified by the SVM classifier.
2 Problem formulation
Given a metagenomic sample of a person consisting of sequence reads, our objective is to classify the person as either healthy or unhealthy. We represent groups of similar DNA sequences in a metagenomic sample as instances and use the instances to represent a sample as a bag in MIL. Formally, the jth sample is represented as a bag with a set of c instances . Here, an instance represents a cluster of similar DNA sequences in the sample j. We associate with each bag with a class label to indicate if the jth person is healthy () or unhealthy (). For a total of m samples, the problem of predicting disease from metagenomic data now can be formulated as learning a function where are the collections of bags representing the samples taken from the healthy and unhealthy cohorts and are the bag labels such that a bag has the label . We also want to learn the contributions of the DNA sequences to the disease state within a bag.
3 Materials and methods
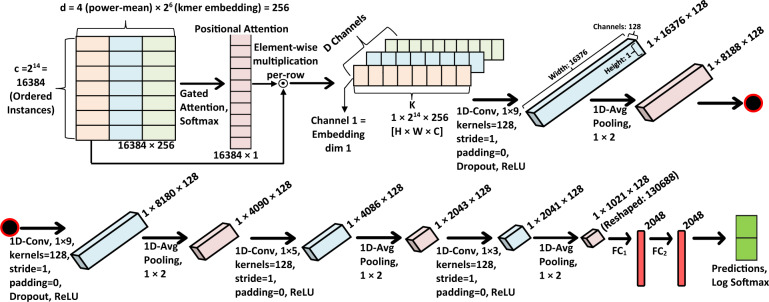
Figure 1 shows an overview of our proposed IDMIL. We first embed the DNA subsequences (kmers) into a fixed dimension and then use power-mean statistics to represent a sequence as a vector from its corresponding kmers. These sequence representations are clustered to create instances. We then represent the metagenomic samples as bags composed of these instances and classify the bags.
Fig. 1.
Overview of our proposed IDMIL. We first embed the kmers in a fixed dimension. The kmer embeddings are used to represent the sequence reads. Clustering is performed to create instances of MIL which form the bags in MIL, as healthy or unhealthy
3.1 DNA subsequence (kmer) embedding
We first embed the k-length contiguous DNA subsequences (known as kmer) in a fixed-length vector space. For this purpose, we use an approach similar to continuous bag-of-word-based representation (Mikolov et al., 2013). For a read S with a sequence of t kmers, , we define as the set of kmers immediately preceding kmeri in S and as the set of kmers immediately following kmeri in S where is a randomly chosen context window such that and . We define as the context set of kmeri w.r.t. Skmers such that . We learn a d-dimensional embedding vector for each kmeri by maximizing its probability of appearing in a DNA sequence given its context. Hence, the probability of kmeri given its context set Qi:
| (1) |
where and are the output vector and the context-based input vector of kmeri, respectively. Vi is computed as the average of all the input embedding vectors of kmers in the context set Qi. We use a shallow two-layer neural network to train the kmer embeddings that maximize the probability of kmers given the suffix and prefix. The error in kmer predictions from their context is used to update the network parameters via a backpropagation algorithm using the Adaptive Moment Estimation (Adam) optimizer (Ba et al., 2016). This context-based kmer embedding helps to reduce noise inherent in the metagenomic data. Two kmers with similar suffix and prefix will be closer to each other in the embedding space. Subtle noise within similar kmers with similar suffix and prefix will not affect the kmer embeddings drastically. Inspired by the natural language processing, we perform term frequency–inverse document frequency (TF–IDF) (Rajaraman and Ullman, 2011) based kmer pruning before starting the kmer embedding process for better efficiency. The TF–IDF score of kmeri for any sequence Sj is represented as:
| (2) |
where is the score of kmeri in a sequence Sj, is the frequency of kmeri in sequence Sj, D is the total number of sequences in the sample and dfi is the total number of sequences in the sample containing kmeri. Based on this score, we take the top 70% of the kmers from each sequence and prune the rest. The set of the remaining kmers from all DNA sequences creates our kmer vocabulary. The TF-term ensures that infrequent kmers which are likely to be inherent noise, receive low scores. The IDF-term ensures highly frequent kmers appearing in most of the sequences, receive low scores. Such kmers are also likely to be system-generated noise and do not provide any discriminatory information. This way TF–IDF effectively reduces the total number of kmers and noise. We also utilize binary tree-based hierarchical softmax with Huffman encoding to estimate the final softmax (Eq. 1) (Mikolov et al., 2013). This reduces the complexity of softmax computations from O(N) to O(logN) where N is the size of the pruned kmer vocabulary.
3.2 DNA sequence representation
We use the kmer embeddings (Section 3.1) to represent the raw sequence reads in the whole-metagenomic sample. In natural language processing, sentences and documents are often embedded in fixed-dimensional vector space using Sentence2vec and Doc2vec, respectively (Le and Mikolov, 2014). If we consider each DNA sequence as a sentence and kmers as words then Sentence2vec requires learning the weights for millions of DNA sequence making the process computationally infeasible. We can consider the metagenomic samples as documents and embed the whole sample using the kmer embeddings with an approach similar to doc2vec (Le and Mikolov, 2014). But this approach will not help to interpret the predictions. State-of-the-art encoder–decoder-based sentence embedding approaches, for example recurrent neural network (Mikolov et al., 2010), gated recurrent unit (Chung et al., 2014) and long–short-term memory networks (Palangi et al., 2016) are capable of encoding sequence ordering. But they operate on a few hundreds of time-steps and suitable for text data with only a few thousands of sentences, unlike the whole-metagenomic data with millions of sequences per sample.
We use an approach similar to concatenated power-mean of word-embeddings (Ruckle et al., 2018) to represent sequence reads using kmer embeddings. Power-mean does not require learning additional weights, making it a suitable choice for whole-metagenomic data. The power-mean (Hardy et al., 1952) is a generalization of the averaging. For a sequence S with total t kmers, where are embedded using d-dimensional vectors , respectively (Section 3.1); the element-wise power-mean is defined as:
| (3) |
Different values of power-mean (p) provide interesting statistics, for example minimum (p=−∞), harmonic mean (p=−1), geometric mean (p = 0), arithmetic mean (p = 1), maximum (p=+∞) and others. We make a matrix from all the kmer embeddings in a sequence S with t kmers where each and . Let be the vector whose d components are the element-wise power-means of and p is the power-mean value. To get a summary statistics from the kmer embeddings, we calculate total n power-means and represent S as a vector:
| (4) |
where ⊕ stands for concatenation and are total n different power-mean values. Concatenation is effective here because it produces a more precise summary and reduces the uncertainty of representations compared to averaging the kmer embeddings which may result in similar representations of different DNA sequences due to their similarities in averages. Among the choices of power-mean values minimum, maximum and positive odd numbers are found to be effective in text processing (Ruckle et al., 2018). The minimum and maximum considers the range of kmer embedding values. The rationale for positive numbers is that, negative power-mean are discontinuous and undefined when input is zero. Odd power-mean values are preferable because they preserve the input sign. A higher positive value of p tends to and can significantly increase the data dimension. Hence, we have used all and concatenate them for sequence representations.
3.3 Instance representation
After representing the DNA sequences with a fixed dimension, we perform clustering with the Mini-batch KMeans algorithm (Sculley, 2010) within each metagenomic sample. Metagenomics produces repetitive DNA sequence fragments from different parts of the microbial whole-genome. By clustering the embedded sequences and using the cluster prototypes, we remove redundancies. The Mini-batch KMeans is a variant of the KMeans algorithm which uses mini-batches to reduce the computation time, while still attempting to optimize the same objective function of KMeans. Say the jth metagenomic sample is represented by a set of sequence representations Bj (Section 3.2). The objective function of the Mini-batch KMeans:
| (5) |
where, is a set of c cluster centers in the jth sample, each is a sequence representation (Section 3.2) in the jth sample and returns the nearest cluster center of x using Euclidean distance. Each mini-batch updates the clusters using a convex combination of the values of the cluster centers and the data by applying a learning rate that decreases with the number of iterations. As a result, Mini-batch KMeans converges faster than naive KMeans and does not suffer increased computational cost for large-scale metagenomic data. The resultant cluster representatives become the instances in our proposed MIL approach.
3.4 Bag representation
We order the instances in a bag based on their Euclidean distances from a reference data point. We define the reference data point href as the average of all the cluster centers (instances) in the training set. Instances in a bag are sorted in ascending order based on their corresponding distances from href. For the jth sample with total c ordered instances , this implies:
| (6) |
where returns the Euclidean distance between two vectors. Finally, we represent the jth bag with ordered instances as a matrix where is the instance dimension (Section 3.3). Here, for kmer-embedding size of d and total n power-mean values. The ordering serves two purposes: (i) it combines similar instances within a locality which is required by the CNN during the prediction phase and (ii) the positional information of instances can be used for interpreting prediction results via the attention mechanism.
3.5 Classification model
Figure 2 shows an overview of our proposed prediction model. We use a deep CNN on the bag representation. Our motivation for using a deep CNN model: (i) CNNs are extremely effective in extracting the latent features hierarchically from the input, (ii) they learn complex, nonlinear relationship among these latent features which can be leveraged for a complex classification task such as ours where we differentiate samples at molecular level, (iii) CNNs provide an advantage over feed-forward networks by considering locality of features, i.e. our proposed instance ordering within the bags and (iv) a carefully designed CNN model can provide interpretation of the predictions in addition to the high accuracy. Our model is similar to AlexNet (Krizhevsky et al., 2012), a popular deep CNN-based model while keeping the number of layers and learning weights minimal to make the model scalable for whole-metagenomic data and avoid overfitting. We use multiple hidden layers with rectified linear unit (ReLU) as the nonlinear activation function. We use the negative log-likelihood (NLL) as the loss function for our binary classification tasks (healthy versus unhealthy):
| (7) |
where is the true class label of any bag and is the model’s predicted probability of the class being . Because we use the NLL-loss, the last layer is equipped with the log-softmax activation function which produces the log probability vector (Goodfellow et al., 2016). We adopt the dropout regularization at hidden layers (Srivastava, 2014) which helps the model to avoid overfitting by ignoring randomly selected hidden units during the training. The objective of the classification model is to minimize the loss. The error in prediction is used to update the network parameters via a backpropagation algorithm using the Adaptive Moment Estimation (Adam) optimizer (Ba et al., 2016). We start our model with only one hidden layer. The number of hidden layers is then increased by one until the increment does not result in achieving a higher area under curve of the receiver operating characteristic (AUC-ROC) value on a validation set.
Fig. 2.
Overview of the deep CNN-based classification model. The figure shows operations and shapes of transformed data. The operations follow from the top-left to the bottom-right. After applying attention, the bags are reshaped into a 3D tensor where each embedding dimension becomes a channel. A series of convolution layers is applied before classification. represents the ith fully connected layer
3.6 Attention mechanism
Attention in deep learning involves learning a vector of importance-weights of elements in the data, i.e. group of pixels in an image, word or sentence in a text corpus (Vaswani et al., 2017). In the attention mechanism, we estimate how strongly an element is correlated with (attends to) other elements for the classification. Attentions weights are usually learned as part of the deep-learning model of the actual classification task. The same back-propagation algorithm that trains the classification model also trains the attention values. Softmax is used for the final calculation of the attention weights. As a result, these weights are within the range and sum to 1. The attention values reduce noise by dampening or highlighting data instances such that it reduces classification errors. It also helps to interpret the prediction results. We start with the bag representation of dimension where c is the number of instances and is the instance dimension. Here, for d-dimensional kmer embedding and n power-mean values. We apply attention to instance positions as follows:
| (8) |
where is the attention value for the jth row of a bag, is the jth instance of a bag, and are the learning weights of the hidden layers for the attention vector with l units, is the element-wise hyperbolic tangent function, is the element-wise sigmoid function and is the element-wise multiplication. For attention calculations, we use the tangent hyperbolic nonlinearity which includes both negative and positive values and ensures proper gradient flow. However, tanh(x) becomes linear for limiting the effectiveness the deep learning model. To solve this issue, we use the gating mechanism (Dauphin et al., 2017) which combines hyperbolic tangent and sigmoid nonlinearity for effective gradient propagations. This way we achieve an attention values for each of the c rows (instances) of the bag matrix.
We label the disease and healthy states with class labels 1 and 0, respectively. Higher attention value for an instance position infers that the instances at that position in the unhealthy samples can be associated with the disease. This allows us to map the original sequences to the clusters representing these highly attended instances. This way we can interpret the result of the prediction by inferring association between groups of similar sequences and a disease. Alignments and microbial profiling can be performed only on these selected sets of sequences reducing much of the computational overhead. Applying attention to hidden layers will not help to interpret because mapping between the latent features and the original feature space is not straightforward (blackbox), especially for nonimage data where hidden layers are unlikely to be human-understandable when visualized. We first multiply the bags with positional attention values before proceeding with the rest of the proposed model.
3.7 Convolutional neural network configuration
Color image data are represented in a CNN model using 3D tensors with shape where w, h and c represent the width, height and the color channels (one for gray-scale and three for color), respectively. Following this notation, we reshape a bag into a 3D tensor where , the instance-dimension becomes the number of channels. The convolution operation involves calculating weighted averages of the locales in the matrix by sliding a convolutional kernel over the matrix. The weights are learned by the neural network using the back-propagation algorithm. When applying convolution on multichannel data, each convolutional filter is composed of the same number of kernels as the number of input channels. Each kernel performs convolution on their respective channels. These channel-wise convolution outputs are then combined by an element-wise addition. After adding a bias term, the filter outputs a single channel from all the input channels.
We apply one-dimensional convolutions with filters of size 9. In IDMIL, the instances within a bag are ordered based on their corresponding distances from a reference point which is the average of all instances in the training set (Section 3.4). The effectiveness of this ordering is subjected to the choice of reference point. When we apply a one-dimensional convolutional filter of size 9, the convolution will take total nine instances for each of the weighted average calculations. The filters will see a similar set of instances when slid on the tensor which reduces the effect of variations in the instance ordering. We start with only 24 convolutional filters per hidden layer and increase this number as a power of two until the increase does not provide higher AUC-ROC values on a validation set. We apply a one-dimensional average pooling of size and stride of two for sampling the learned features. The last two layers apply convolution with smaller filter sizes (5 and 3) which allows the model to focus more within the smaller locality of more relevant features than earlier layers. Finally, fully connected layers perform the predictions upon collapsing the hidden units.
3.8 Data augmentation
Data augmentations are used to introduce variations to the prediction model which helps the model to avoid overfitting and generalize. In image classification, data augmentations involve duplicating the images with a combination of affine transformations. Additional neural networks have been utilized to learn the augmentation process (Perez and Wang, 2017) which involves learning more weights and additional computations. Most of the MWASs contain a few hundred samples each with millions of DNA sequences. In our proposed approach, we utilize data augmentation without introducing any additional learning weights to make the prediction model generalized. Once the bag is formed with ordered instances, we randomly shuffle the positions of the instances within a small window of size . This introduces perturbation within a small locality of the bag when z > 1. The label of this new bag remains the same as the original one.
4 Experimental setup
4.1 Datasets
Table 1 shows the key statistics regarding the metagenomic datasets used in this article with the number of unhealthy and healthy samples and the average number of DNA sequences (in millions) in each sample. These datasets are the metagenomic studies of liver cirrhosis (Qin et al., 2014), colorectal cancer (Zeller et al., 2014), IBD (Qin et al., 2010), obesity (Le Chatelier et al., 2013) and T2D (Qin et al., 2012). The minimum number of average DNA sequences in a sample is 40.2 million in the T2D dataset. This shows how large these datasets can be. We removed class imbalances by combining random oversampling and our proposed data augmentations (Section 3.8) within the training set of each 10-fold cross-validation experiment.
Table 1.
Dataset statistics
| Datasets | Total samples | Unhealthy cases | Healthy controls | Avg. sequences per-sample (std) (in millions) |
|---|---|---|---|---|
| Liver cirrhosis | 232 | 118 | 114 | 51.6M (30.9M) |
| Colorectal cancer | 121 | 48 | 73 | 60.0M (25.5M) |
| Inflammatory bowel disease (IBD) | 110 | 25 | 85 | 45.2M (18.4M) |
| Obesity | 253 | 164 | 89 | 68.2M (23.2M) |
| Type-2 diabetes (T2D) | 344 | 170 | 174 | 40.2M (11.8M) |
4.2 Data preprocessing
We preprocessed the FASTQ files using fastp (https://github.com/OpenGene/fastp) an efficient, opensource FASTQ processing tool. The adapter sequences are removed using the fastp tool. Quality scores are checked from both 5′ to 3′ and 3′ to 5′ ends. fastp then checks how many of the total bases from both ends have a quality score lower than a predefined quality-threshold (20 in our case). If 30% (threshold parameter) of the bases are low quality, then the read is removed. fastp then merges paired-end reads based on the overlapping information. It tries to find an overlap between the forward-read to the reverse complement of the reverse-read. This is performed for each pair in parallel. If the length of the overlapping region is lower than 30 (threshold parameter) and the number of mismatches within the overlap is higher than 20% (threshold parameter) of the overlapping length, then fastp removes the read. Otherwise, a merged sequence is created from each paired-end read. This process creates a single FASTA file with the merged sequences.
4.3 Evaluation metrics
We evaluate the success of our MIL-based approach in several ways. The simplest measure is accuracy which measures the percentage of samples that are classified correctly. We also use the AUC-ROC, which is the plot of false-positive rate versus true-positive rate. We repeated each experiment 10 times and calculated the margin of error for the mean with 95% confidence interval. The margin of error can be calculated as:
| (9) |
where is the significance level, is critical value of the t distribution with n – 1 degrees of freedom for an area of for the upper tail, σs is the sample standard deviation and n is the sample size.
4.4 Software and hardware
We implemented the kmer embedding and the deep CNN model using PyTorch (https://pytorch.org/) a popular Python-based open-source deep-learning framework. For the Mini-batch KMeans, we used Scikit-learn (Pedregosa et al., 2011). We used the ARGO computing cluster configured with dual Intel Xeon 28 core CPUs, 1.5 TB RAM and four Nvidia v100 GPUs each with 32GB VRAM available at George Mason University (http://wiki.orc.gmu.edu/index.php/About_ARGO).
5 Discussion
5.1 Comparative analysis
Table 2 shows the comparison of mean accuracies and mean AUC-ROC values with margin of errors from different approaches for 10-fold cross validations on the metagenomic datasets used in this article. We compare our proposed approach, IDMIL with non-MIL-based approaches such as MetAML (Pasolli et al., 2016) and PLG–ABD (Nguyen et al., 2017). We also compare IDMIL with some of the popular MIL approaches such as miSVM (Andrews et al., 2003), MISVM (Andrews et al., 2003), sbMIL (Bunescu and Mooney, 2007), GICF (Kotzias et al., 2015) and AttMIL (Ilse, 2018). All of these approaches are briefly discussed in Section 1. Among these approaches miSVM, MISVM, sbMIL and GICF were developed to handle numeric data and most of them rely on costly kernel computation in the instance space. We used the publicly available open-source (https://github.com/garydoranjr/misvm) implementations of these models. For the AttMIL, we used the author provided source code (https://github.com/AMLab-Amsterdam/AttentionDeepMIL). To run these MIL algorithms in our problem setup, we used our proposed instance and bag representations (Section 3.4) as input to these MIL approaches. We observe that our proposed, IDMIL significantly outperforms all the baseline approaches used in this article.
Table 2.
Comparison of mean performances (10-fold cross validation) on different datasets with the margin of errors for 10 repeated trials.
| Methods | Cirrhosis |
Colorectal |
IBD |
Obesity |
T2D |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | AUC-ROC | Accuracy | AUC-ROC | Accuracy | AUC-ROC | Accuracy | AUC-ROC | Accuracy | AUC-ROC | |
| MetAML (Pasolli et al., 2016) | 0.877 | 0.945 | 0.805 | 0.873 | 0.809 | 0.809 | 0.644 | 0.655 | 0.664 | 0.744 |
| (0.042) | (0.029) | (0.061) | (0.053) | (0.042) | (0.044) | (0.036) | (0.071) | (0.054) | (0.048) | |
| PLG–ABD (Nguyen et al., 2017) | 0.891 | 0.914 | 0.742 | 0.815 | 0.836 | 0.847 | 0.660 | 0.675 | 0.626 | 0.691 |
| (0.031) | (0.026) | (0.049) | (0.042) | (0.030) | (0.016) | (0.032) | (0.042) | (0.048) | (0.039) | |
| miSVM (Andrews et al., 2003) | 0.772 | 0.815 | 0.692 | 0.743 | 0.742 | 0.759 | 0.594 | 0.617 | 0.584 | 0.611 |
| (0.038) | (0.041) | (0.036) | (0.042) | (0.029) | (0.044) | (0.027) | (0.041) | (0.042) | (0.041) | |
| MISVM (Andrews et al., 2003) | 0.796 | 0.826 | 0.664 | 0.728 | 0.739 | 0.748 | 0.576 | 0.592 | 0.592 | 0.628 |
| (0.022) | (0.019) | (0.038) | (0.051) | (0.036) | (0.051) | (0.026) | (0.037) | (0.035) | (0.038) | |
| sbMIL (Bunescu and Mooney, 2007) | 0.782 | 0.818 | 0.714 | 0.753 | 0.752 | 0.763 | 0.602 | 0.618 | 0.597 | 0.612 |
| (0.042) | (0.029) | (0.035) | (0.048) | (0.021) | (0.032) | (0.038) | (0.026) | (0.016) | (0.017) | |
| GICF (Kotzias et al., 2015) | 0.812 | 0.847 | 0.738 | 0.785 | 0.772 | 0.792 | 0.624 | 0.648 | 0.622 | 0.684 |
| (0.029) | (0.032) | (0.029) | (0.037) | (0.028) | (0.035) | (0.038) | (0.024) | (0.021) | (0.033) | |
| AttMIL (Ilse, 2018) | 0.864 | 0.881 | 0.792 | 0.826 | 0.813 | 0.847 | 0.688 | 0.724 | 0.724 | 0.759 |
| (0.018) | (0.024) | (0.021) | (0.033) | (0.025) | (0.031) | (0.026) | (0.019) | (0.029) | (0.037) | |
| IDMIL | 0.917 | 0.951 | 0.845 | 0.895 | 0.867 | 0.882 | 0.767 | 0.793 | 0.782 | 0.816 |
| (0.027) | (0.021) | (0.042) | (0.035) | (0.024) | (0.024) | (0.047) | (0.028) | (041) | (0.036) | |
Note: Bold texts indicate comparatively better performances.
Note: Bold texts indicate comparatively better performances.
When predicting liver cirrhosis disease IDMIL has achieved 91.7% accuracy and 95.1% AUC-ROC which is better than the non-MIL-based approaches, i.e. MetAML (87.7% accuracy, 94.5% AUC-ROC), PLG–ABD (89.1% accuracy, 91.4% AUC-ROC) and other nondeep-learning-based MIL approaches such as GICF (81.2% accuracy, 84.7% AUC-ROC) as well as deep-learning-based MIL approach AttMIL (86.4% accuracy, 88.1% AUC-ROC). We see that other MIL-based approaches provide competitive predictive performance compared to the non-MIL approaches. This shows the effectiveness of our proposed instance and bag generation mechanism as well as the effectiveness of the MIL paradigm in predicting disease from large-scale DNA sequence data.
In this article, we only focus on the DNA sequence data for disease predictions. IDMIL performs well with only the DNA sequence data compared to other approaches. However, factors other than the microbial composition can affect health conditions. For obesity and T2D datasets, all approaches showed lower predictive performances compared to the other datasets. Possible reasons may include more subtle shifts in microbial diversity from a healthy state to obesity or T2D compared to other diseases. External factors such as medication, living style and diet (Pasolli et al., 2016) may play key role in identifying these diseases. Therefore, the type of disease is an important factor impacting the predictive performance. IDMIL’s better performance can be attributed to:
Noise reduction: The TF–IDF-based pruning removes kmers that are likely to be noise. The kmer-embedding considers the suffix and prefix reducing the effects of few nucleotide changes among the kmers. Instances are represented as cluster centroids which reduces dependency on a single sequence. The initial attention mechanism only prioritizes instances that help to classify the sample accurately. As a result, the effects of nondiscriminative instances are reduced.
Data utilization: IDMIL takes the raw sequences as the input. It does not restrict itself by using reference genome sequences or any knowledge as a priori. Therefore, IDMIL can generalize over different datasets as well as various sequencing technologies. Unlike MetAML (Pasolli et al., 2016) and PLG–ABD (Nguyen et al., 2017), IDMIL avoids microbial profiling prior to prediction and takes full advantage of the vast amount of genomic information inherent in the whole-metagenomic data.
Hierarchical feature extraction: The CNN models are proven to be effective for hierarchically generating the latent features. Unlike other approaches, deep CNN-based IDMIL learns complex nonlinear relations among these latent features.
Data augmentation: The data augmentation process and a minimal number of learning weights ensure that the model avoids overfitting and generalizes easily.
5.2 Parameters and sensitivity analysis
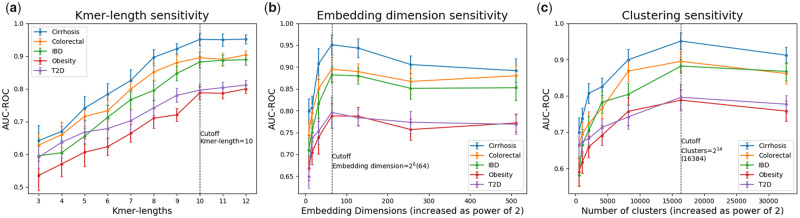
We used a grid search on a validation set for model selection. We train the model with 0.0001 as the learning rate, 500 as the maximum number of iterations and 5 as the batch size. The size of kmer vocabulary increases exponentially with the length of the kmers ( for k-length kmers) which directly affects the runtime of the kmer-embedding process (Section 3.1). Figure 3a shows the effect of various kmer-lengths on average AUC-ROC values with the margin-of-errors from ten repeated trials. We observe that when k’s value is in the range , we get the steepest ascent in the average AUC-ROC values. We also observe that the margin-of-error reduces with increasing value of k. This is because the model better approximates the sequence reads with long subsequences. The value of k = 10 is suggestive from our empirical evaluation for high accuracy and scalability.
Fig. 3.
Sensitivity of AUC-ROC with respect to (a) kmer-lengths, (b) kmer embedding dimensions and (c) number of clusters in Mini-batch KMeans. Each experiment is performed a total 10 times and the average AUC-ROC values are reported with the margin of errors. Cutoff values used in this article are shown using vertical dashed lines with the corresponding values
Figure 3b shows the effect of various kmer embedding dimensions (increased as the power of 2) on AUC-ROC values. We notice a sharp increase in AUC-ROC values as we increase the embedding size from 8 to 64. Further increase in the embedding dimension does not provide any dramatic improvement in predictive performance but increases the computational overhead. We observe lower values of AUC-ROC (Fig. 3c) when the number of clusters is small. This is because the clustering algorithm forcefully combines dissimilar sequences in the same cluster when the number of clusters is small and the bags contain inadequate numbers of instances. However, selecting a large number of clusters result in near-empty clusters and higher computational runtime. Overall, an embedding dimension of and a total of clusters per sample provided the best results for all the datasets used in this article.
5.3 Interpreting instance attentions
The attention mechanism enables us to assign a weight to each instance position i in the bags. A higher value of ai implies that the instances in position i of the bags contribute more to the class label (unhealthy) than the class label (healthy), whereas lower ai implies the opposite. Our experiments show that highly attended sequence groups come from some of the well-known pathogens. After training the model, we take the instances from the unhealthy bags of the training set where the instance position receives attention higher than 0.5. Each instance maps to a group of similar DNA sequences. We use the basic local alignment search tool (Altschul et al., 1990) to identify the species represented by those clusters. An identified species receives the attention of the cluster it belongs to. If a species is identified in multiple clusters then we take the average of the attention weights.
We show two use cases using the instance-level interpretation for liver cirrhosis and colorectal cancer disease. Figure 4a shows some of the identified species with high attention weights for liver cirrhosis diseases. Veillonella dispar, Klebsiella pneumoniae and Streptococcus anginosus are some of the known pathogens for liver cirrhosis (Pasolli et al., 2016; Qin et al., 2014). Fusobacterium nucleatum, Peptostreptococcus stomatis, Gemella morbillorum and others (Fig. 4b) are found to be associated with colorectal cancer disease (Kwong et al., 2018; Zeller et al., 2014). IDMIL’s user can utilize the attention-based ranking by pruning the lowly attended sequences and use any assembler and profiling tool on the remaining highly attended sequences. The pruning reduces much of the computational burden from subsequent analysis. Our proposed approach does not restrict how microbes will be quantified in a cohort. It uses the disease classifications to infer which of the sequences can be ignored before proceeding to the microbial quantification. This allows for the discovery of novel microbes, better data utilization and easy generalization. This shows that IDMIL is also interpretable, and it has clinical significance.
Fig. 4.
Association between species and (a) liver cirrhosis disease and (b) colorectal cancer disease. Sequences from the unhealthy cohort with high attention values were used
6 Conclusion
We demonstrate a MIL-based disease prediction method from large-scale metagenomic data harnessing the hierarchical latent feature extraction capability of deep CNN. For this purpose, we propose an efficient, scalable and unsupervised bag-instance representation of the whole-metagenomic data. Our proposed approach does not require sequence assembly and microbial profiling before the disease classification. The data representations are parallel, and the prediction phase involves a minimal number of learning weights which helps this approach scale with metagenomic data. IDMIL is capable of fully utilizing the enormous amount of sequence reads in the whole-metagenomic data while providing high accuracy and efficiency. IDMIL can infer associations between DNA sequences and diseases using the attention mechanism which can lead to efficient microbial profiling and finding associations between microbes and diseases. Our proposed model is highly parallel in nature and easy to replicate in any distributed system. More generally, we have shown the effectiveness of MIL methods within metagenomics. The proposed approach has shown both strong results and significant potential for further improvements.
Funding
This work was supported by National Science Foundation (NSF) Career Award 1252318 to Huzefa Rangwala.
Conflict of Interest: none declared.
References
- Altschul S.F. et al. (1990) Basic local alignment search tool. J. Mol. Biol., 215, 403–410. [DOI] [PubMed] [Google Scholar]
- Amores J. (2013) Multiple instance classification: review, taxonomy and comparative study. Artif. Intell., 201, 81–105. [Google Scholar]
- Andrews S. et al. (2003) Support vector machines for multiple-instance learning. In: Advances in Neural Information Processing Systems, pp. 577–584. MIT Press. Cambridge, MA.
- Arango-Argoty G. et al. (2018) DeepARG: a deep learning approach for predicting antibiotic resistance genes from metagenomic data. Microbiome, 6, 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ba J.L. et al. (2016) Layer normalization. arXiv preprint arXiv:1607.06450. Cornell University. Ithaca, New York, US.
- Backhed F. (2005) Host-bacterial mutualism in the human intestine. Science, 307, 1915–1920. [DOI] [PubMed] [Google Scholar]
- Bunescu R.C., Mooney R.J. (2007) Multiple instance learning for sparse positive bags. In: Proceedings of the 24th International Conference on Machine Learning, pp. 105–112. Association for Computing Machinery (ACM). New York, US.
- Chiu C.Y. et al. (2019) Clinical metagenomics. Nat. Rev. Genet., 20, 341–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung J. et al. (2014) Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555. Cornell University. Ithaca, New York, US.
- Dauphin Y.N. et al. (2017) Language modeling with gated convolutional networks. In Proceedings of the 34th International Conference on Machine Learning, Vol. 70, pp. 933–941. JMLR.org. Sydney, Australia. [Google Scholar]
- Dietterich T.G. et al. (1997) Solving the multiple instance problem with axis-parallel rectangles. Artif. Intell., 89, 31–71. [Google Scholar]
- Fioravanti D. et al. (2018) Phylogenetic convolutional neural networks in metagenomics. BMC Bioinformatics, 19, 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodfellow I. et al. (2016) Deep learning. MIT Press. Cambridge, MA, US. [Google Scholar]
- Gu J. et al. (2018) Recent advances in convolutional neural networks. Pattern Recogn., 77, 354–377. [Google Scholar]
- Handelsman J. (2004) Metagenomics: application of genomics to uncultured microorganisms. Microbiol. Mol. Biol. Rev., 68, 669–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy G.H. et al. (1952) Inequalities. Cambridge University Press. Cambridge, United Kingdom. [Google Scholar]
- Hugenholtz P., Tyson G.W. (2008) Microbiology: metagenomics. Nature, 455, 481–483. [DOI] [PubMed] [Google Scholar]
- Ilse M. (2018) Attention-based deep multiple instance learning. arXiv preprint arXiv:1802.04712. Cornell University. Ithaca, New York, US.
- Kotzias D. et al. (2015) From group to individual labels using deep features. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 597–606. Association for Computing Machinery (ACM). New York, US.
- Krizhevsky A. et al. (2012) Imagenet classification with deep convolutional neural networks. In: Advances in Neural Information Processing Systems, pp. 1097–1105. Curran Associates, Inc. NY.
- Kwong T.N. et al. (2018) Association between bacteremia from specific microbes and subsequent diagnosis of colorectal cancer. Gastroenterology, 155, 383–390. [DOI] [PubMed] [Google Scholar]
- LaPierre N. et al. (2016) CAMIL: Clustering and Assembly with Multiple Instance Learning for phenotype prediction. In 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), pp. 33–40. IEEE.
- Le Q., Mikolov T. (2014) Distributed representations of sentences and documents. In: International Conference on Machine Learning, pp. 1188–1196. JMLR Workshop and Conference Proceedings. Volume 32.
- Le Chatelier E. et al. (2013) Richness of human gut microbiome correlates with metabolic markers. Nature, 500, 541–546. [DOI] [PubMed] [Google Scholar]
- McIntyre A.B. et al. (2017) Comprehensive benchmarking and ensemble approaches for metagenomic classifiers. Genome Biol., 18.1, 182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikolov T. et al. (2010) Recurrent neural network based language model. In: Eleventh Annual Conference of the International Speech Communication Association. International Speech Communication Association (ISCA).
- Mikolov T. et al. (2013) Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781. Cornell University. Ithaca, New York, US.
- Ng P. (2017) dna2vec: Consistent vector representations of variable-length k-mers. arXiv preprint arXiv:1701.06279. Cornell University. Ithaca, New York, US.
- Nguyen T.H. et al. (2017) Deep learning for metagenomic data: using 2d embeddings and convolutional neural networks. arXiv preprint arXiv:1712.00244. Cornell University. Ithaca, New York, US.
- Palangi H. et al. (2016) Deep sentence embedding using long short-term memory networks: analysis and application to information retrieval. IEEE/ACM Trans. Audio Speech Lang. Process. (TASLP), 24, 694–707. [Google Scholar]
- Pasolli E. et al. (2016) Machine learning meta-analysis of large metagenomic datasets: tools and biological insights. PLoS Comput. Biol., 12, e1004977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F. et al. (2011) Scikit-learn: machine learning in Python. J. Mach. Learn. Res., 12, 2825–2830. [Google Scholar]
- Perez L., Wang J. (2017) The effectiveness of data augmentation in image classification using deep learning. arXiv preprint arXiv:1712.04621. Cornell University. Ithaca, New York, US.
- Qin J. et al. (2010) A human gut microbial gene catalogue established by metagenomic sequencing. Nature, 464, 59–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin J. et al. (2012) A metagenome-wide association study of gut microbiota in type 2 diabetes. Nature, 490, 55–60. [DOI] [PubMed] [Google Scholar]
- Qin N. et al. (2014) Alterations of the human gut microbiome in liver cirrhosis. Nature, 513, 59–64. [DOI] [PubMed] [Google Scholar]
- Quince C. et al. (2017) Shotgun metagenomics, from sampling to analysis. Nat. Biotechnol., 35, 833–844. [DOI] [PubMed] [Google Scholar]
- Rajaraman A., Ullman J.D. (2011) Mining of massive datasets. Cambridge University Press. Cambridge, United Kingdom. [Google Scholar]
- Rahman M.A., Rangwala H. (2018) RegMIL: Phenotype classification from metagenomic data. In Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics, pp. 145–154. Association for Computing Machinery (ACM). New York, US.
- Rahman M.A. et al. (2017) Phenotype prediction from metagenomic data using Clustering and Assembly with Multiple Instance Learning (CAMIL). In: IEEE/ACM Transactions on Computational Biology and Bioinformatics. Institute of Electrical and Electronics Engineers (IEEE). New Jersey, US. [DOI] [PubMed]
- Rahman M.A. et al. (2017) Metagenome sequence clustering with hash-based canopies. J. Bioinf. Comput. Biol., 15, 1740006. World Scientific. [DOI] [PubMed] [Google Scholar]
- Ruckle A. et al. (2018) Concatenated power mean word embeddings as universal cross-lingual sentence representations. arXiv preprint arXiv:1803.01400. Cornell University. Ithaca, New York, US.
- Saulnier D.M. et al. (2011) Gastrointestinal microbiome signatures of pediatric patients with irritable bowel syndrome. Gastroenterology, 141, 1782–1791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sculley D. (2010) Web-scale k-means clustering. In Proceedings of the 19th International Conference on World Wide Web ACM, pp. 1177–1178. Association for Computing Machinery (ACM). New York, US.
- Simonyan K., Zisserman A. (2014) Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556. Cornell University. Ithaca, New York, US.
- Srivastava N. et al. (2014) Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res., 15, 1929–1958. [Google Scholar]
- Truong D.T. et al. (2015) MetaPhlAn2 for enhanced metagenomic taxonomic profiling. Nat. Methods, 12, 902–903. [DOI] [PubMed] [Google Scholar]
- Turnbaugh P.J. et al. (2007) The human microbiome project. Nature, 449, 804–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaswani A. et al. (2017) Attention is all you need. In: Advances in Neural Information Processing Systems, pp. 5998–6008. Curran Associates, Inc.
- Wade W. (2002) Unculturable bacteria—the uncharacterized organisms that cause oral infections. J. R. Soc. Med., 95, 81–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeller G. et al. (2014) Potential of fecal microbiota for early-stage detection of colorectal cancer. Mol. Syst. Biol., 10, 766. [DOI] [PMC free article] [PubMed] [Google Scholar]