Phylogenetic double placement of mixed samples

Abstract

Motivation

Consider a simple computational problem. The inputs are (i) the set of mixed reads generated from a sample that combines two organisms and (ii) separate sets of reads for several reference genomes of known origins. The goal is to find the two organisms that constitute the mixed sample. When constituents are absent from the reference set, we seek to phylogenetically position them with respect to the underlying tree of the reference species. This simple yet fundamental problem (which we call phylogenetic double-placement) has enjoyed surprisingly little attention in the literature. As genome skimming (low-pass sequencing of genomes at low coverage, precluding assembly) becomes more prevalent, this problem finds wide-ranging applications in areas as varied as biodiversity research, food production and provenance, and evolutionary reconstruction.

Results

We introduce a model that relates distances between a mixed sample and reference species to the distances between constituents and reference species. Our model is based on Jaccard indices computed between each sample represented as k-mer sets. The model, built on several assumptions and approximations, allows us to formalize the phylogenetic double-placement problem as a non-convex optimization problem that decomposes mixture distances and performs phylogenetic placement simultaneously. Using a variety of techniques, we are able to solve this optimization problem numerically. We test the resulting method, called MIxed Sample Analysis tool (MISA), on a varied set of simulated and biological datasets. Despite all the assumptions used, the method performs remarkably well in practice.

Availability and implementation

The software and data are available at https://github.com/balabanmetin/misa and https://github.com/balabanmetin/misa-data.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Comparing a set of unassembled reads sequenced from a query biological sample against a reference library of assembled genomes or unassembled reads can reveal much about the query sample. For example mapping reads to a closely related assembled genome and variant calling enables population genetic analyses. For more diverse collections of species, genomic distances can be estimated, and distances can allow phylogenetic placement (Balaban et al., 2020). Sample identification at the population level or higher taxonomic/phylogenetic levels is crucial in many applications, such as characterizing biodiversity, studying food provenance and detecting toxic contamination. When both the reference and the query are unassembled, as is the case for low-pass sequenced genome skims that do not avail themselves to assembly, we can still compute genomic distances (Fan et al., 2015; Ondov et al., 2016) even when the coverage is low (Sarmashghi et al., 2019; Tang et al., 2019). These scalable assembly-free methods have the potential to enable large-scale yet cost-effective genome-wide sample identification because they do not require the genome in the reference library to be assembled. Several tools for assembly-free genome comparison have pursued this ambition (e.g. Dai et al., 2008; Fan et al., 2015; Roychowdhury et al., 2013; Ulitsky et al., 2006; Yang and Zhang, 2008; Yi and Jin, 2013). However, this methodology has to contend with challenges such the presence of contamination (Rachtman et al., 2020) and the potential for mixed samples.

Mixed sample identification is the problem of identifying what species are present in a mixed biological sample of unknown origin. While the metagenomics literature has grappled with a similar conceptual challenge, here, we are specifically focusing on eukaryotic genomes and mixtures of a small number of species with large genomes (only two in this article). The two problems are quite different. Here, in contrast to metagenomics, our samples are not a mixture of a large number of species with small genomes. Instead, we have a mixture of a handful of large genomes (two in this work). Also, unlike microbes, eukaryotic genomes do not present certain difficulties, such as an unclear definition of species and rampant horizontal gene transfer.

The ability to identify the constituents of a mixed sample has obvious applications in food provenance where the goal is to detect adulteration. For example given a herbal food supplement, can we pinpoint the exact ingredients used, as opposed to those advertised? It also is important for many analyses of ecology and biodiversity where cells of multiple species are intertwined in ways that make physical separation difficult or impossible. For example, bee-breads are mixtures of pollen and fungi; understanding the makeup of these mixes can reveal the pollen composition (indicative of floral diversity), which has been linked to local land used for farming (Donkersley et al., 2017). Finally, even when biologists aim to obtain pure single-species samples, technical issues can lead to the sequencing of what is, in reality, a mixed sample. Missing these cases can lead to invalid downstream analyses and false conclusions.

A related concept is recent hybridization. Hybrid speciation is abundant, both in the wide and in agricultural and industrial use (Mallet, 2007). The genome of a recent hybrid, especially for alloploids, can be modeled similarly to a mixed sample with two constituents. Such recent hybrids are both abundant and consequential. For example recent hybridization in yeast species has been hypothesized to contribute to the development of lager beer (Dunn and Sherlock, 2008), among other food products.

Little is known about the optimal way to identify the constituents of a mixed sample in the scenario we described. When the genomes of constituents are available in a reference library, pipelines based on read mapping can seek to find the signature of the mixture (e.g. Langdon et al., 2018). However, as an exact match to constituents is not always present in the reference set, read mapping is not a general solution. Alignment-based methods have been developed to place a single sequence (e.g. a read) on a phylogeny of assembled references (e.g. Barbera et al., 2019; Matsen et al., 2010; Mirarab et al., 2012; Stark et al., 2010). More broadly, many methods have been developed for analyzing metagenomic samples (see McIntyre et al., 2017; Meyer et al., 2019; Sczyrba et al., 2017; Ye et al., 2019, for benchmarking of these tools). By treating reads as independent, these methods can potentially be applied to mixed samples, and are routinely used for analyzing metagenomic samples. However, they often require assembled references and do not work under the assumption that most reads would belong to one or two species. Also, many of these tools come with pre-trained libraries of microbial references. Thus, they are not designed for solving the eukaryotic mixture problem.

In this article, we formulate the mixture analysis without exact matches in the reference library as the solution to a ‘deconvolution’ optimization combined with a phylogenetic placement problem. Sample identification for single-species samples without an exact match is possible through phylogenetic placement (Balaban et al., 2020), a methodology that can handle unassembled genome skims for both the reference and the query. To extend phylogenetic placement to mixed samples, we develop a model for decomposing distances between a mixed sample and reference species into distances of its constituent parts to reference species. We present several theoretical results under the model, including results showing that a mixed sample has its minimum possible distance to both of its constituents. Using this model and a non-convex optimization problem, we develop a method for simultaneous deconvolution and phylogenetic placement of samples. Our method, called MIxed Sample Analysis tool (MISA), is the first to try this kind of analysis and shows promising results on extensive simulation analyses on mixed samples and a real hybridization dataset.

2 Approach

2.1 Model

2.1.1. Assumptions and definitions

Our model makes several assumptions. (i) Each genome (skim) consists of n unique k-mers. We represent a genome A with the set S_A of its fixed-length k-mers. (ii) For two constituent genomes A and B, the mixture M includes all k-mers of both genomes: $S_M=S_A\cup S_B$. (iii) Evolution is modeled using the time-reversible Jukes and Cantor (1969) model, where each position mutates to other positions independently and identically. Evolution occurs along a phylogenetic tree T with genomes as leaves and branch lengths measured in the unit of the expected number of substitutions per position. Let $d_{ij}^T$ be the path length between two nodes i and j in T. Then, according to the Jukes and Cantor (1969) model, the probability of observing a change along the branch is ${\delta }_{ij}=h(d_{ij}^T)=\frac{3}{4}(1-e^{-4/3d_{ij}^T})$. We use the h function and its inverse $h^{-1}$ to translate between phylogenetic distance and probability of observed substitution (i.e. expected hamming distance). (iv) We compare the mixture versus a reference genome, referred to by R. For three genomes A, B and R, let $L(A,B,R)$ (shorthanded to L when clear) be the only node with degree three in T when restricted to these three genomes (Fig. 1). We define $d_1=d_{AR}^T,\hspace{0.17em}{d}_2=d_{BR}^T$ and $d_3=d_{AB}^T$, and let ${\delta }_i=h(d_i)$. Note that by additivity of tree distances, $d_{LA}^T=(d_1+d_3-d_2)/2$ ($d_{LB}^T$ and $d_{LR}^T$ can be written similarly). Also, tree distances ($d_1,d_2,d_3$) conform to the triangle inequality. (v) We assume $d_1+d_2+d_3<2$, which will enable further approximations. Note that, a total branch length of two is very high, corresponding to an expectation of two substitutions per site. Thus, the assumption is reasonable. (vi) $S_A\cap S_B\cap S_R\subset S_L$. Under these assumption, it is exceedingly unlikely for a k-mer to be present in A, B and R but not in L (see Supplementary Fig. S1).

Fig. 1.

(a) Venn diagram showing the intersection of k-mers of mixture M and R. (b) Distances between mixture constituents A and B and a third genome R. The distance between ancestral genome L and extant genome A is $(d_1+d_3-d_2)/2$

Recall that the Jaccard index J is a similarity measure between two sets defined as the ratio of their intersection to their union. Fan et al. (2015) used the Jaccard index J_AR of sets S_A and S_R to estimate

$${\widehat{\delta }}_{AR}=1-{\left(\frac{2J_{AR}}{1+J_{AR}}\right)}^{\frac{1}{k}}$$ (1)

and Sarmashghi et al. (2019) later extended this equation to account for low coverage and sequencing error. Their tool, Skmer, computes the Jaccard index and k-mer frequencies and uses these values to estimate δ directly from reads, accounting for coverage (as low as $1/8\times$) and error.

2.1.2. Formulation

The Jaccard-based methodology does not easily translate to mixed samples. Let $J_{M R}$ be the Jaccard index of a mixed sample M and a reference genome R. We can easily compute $J_{M R}$ but cannot translate it to a distance (akin to Eq. 1) in an obvious way. A more complex formulation is needed. Note that (Fig. 1a)

$$\begin{array}{c}{J}_{M R}=\frac{|S_A\cap S_R|+|S_B\cap S_R|-|S_A\cap S_B\cap S_R|}{|S_A\cup S_B\cup S_R|}\hfill \\ =\frac{|S_A\cap S_R|+|S_B\cap S_R|-|S_A\cap S_B\cap S_R|}{3n-|S_A\cap S_R|-|S_B\cap S_R|-|S_A\cap S_B|+|S_A\cap S_B\cap S_R|}\hspace{0.17em}.\hfill \end{array}$$ (2)

A k-mer is shared between A and B only if no change is observed in any position on the k-mer. In expectation, $|S_A\cap S_R|=n{(1-{\delta }_1)}^k,\hspace{0.17em}|S_B\cap S_R|=n{(1-{\delta }_2)}^k$ and $|S_A\cap S_B|=n{(1-{\delta }_3)}^k$. Moreover, due to our assumptions in Section 2.1.1, a k-mer is shared between all three genomes A, B and R only if that k-mer is present in L. Therefore, in expectation:

$$\begin{array}{cc}\hfill & |S_A\cap S_B\cap S_R|=n{(1-{\delta }_{LA})}^k{(1-{\delta }_{LB})}^k{(1-{\delta }_{LR})}^k\hfill \\ \hfill & =n{((1-h\left(\frac{d_1+d_3-d_2}{2}\right))(1-h\left(\frac{d_2+d_3-d_1}{2}\right))(1-h\left(\frac{d_1+d_2-d_3}{2}\right)))}^k\hfill \end{array}$$ (3)

We define ${\widehat{\delta }}_{M R}=1-{(2J_{M R}/(1+J_{M R}))}^{1/k}$ [for skims, instead of plugging J into Equation 1, we can use the more complex coverage-aware equations of Sarmashghi et al. (2019)]. Note that ${\widehat{\delta }}_{M R}$ is just a mathematical construct without a clear biological meaning. By re-writing $J_{M R}$ in terms of d₁, d₂, d₃ and k, plugging it in this definition, and further simplifications, we derive the following model.

$$\begin{array}{c}{\widehat{\delta }}_{M R}=1-(\frac{2}{3-{(1-h(d_3))}^k}({(1-h(d_1))}^k+{(1-h(d_2))}^k\\ -{((1-h\left(\frac{d_1+d_3-d_2}{2}\right)\left)\right(1-h\left(\frac{d_2+d_3-d_1}{2}\right)\left)\right(1-h\left(\frac{d_1+d_2-d_3}{2}\right)\left)\right)}^k{)}^{\frac{1}{k}}\end{array}$$

Furthermore, under assumptions in Section 2.1.1, $n(1-{\left(h\right(\frac{d_1+d_2+d_3}{2}\left)\right)}^k)$ approximates Equation 3 well, falling within 5% of its value in much of the relevant space (Fig. 2a). Thus, we further simplify the model to:

$${\widehat{\delta }}_{M R}=1-{\left(2\frac{{(1-h(d_1))}^k+{(1-h(d_2))}^k-{(1-h(\frac{d_1+d_2+d_3}{2}\left)\right)}^k}{3-{(1-h(d_3))}^k}\right)}^{\frac{1}{k}}$$ (4)

Fig. 2.

Demonstration of model properties. (a) We show $(1-h(\frac{d_1+d_2-d_3}{2}))(1-h(\frac{d_2+d_3-d_1}{2}))(1-h(\frac{d_3+d_1-d_2}{2}))$ divided by $=1-h\left(\frac{d_1+d_2+d_3}{2}\right)$ and for a set of d₁ and d₂ values (red: no approximation error). We set d₃ to its median value according to triangle inequality ($\max (d_1,d_2)$) but see Supplementary Figure S2 for other choices. (b) y-axis shows the distance between A and R relative to distance between M and R, assuming R is more similar to A than B. We show the bounds of Proposition 1. (c) The fast convergence of ${\widehat{\delta }}_{M R}=1-{\left(\frac{3-{(1-{\delta }_3)}^k}{2}\right)}^{-1/k}$ to its upper-bound for k = 31. (d) The value of ${\widehat{\delta }}_{M R}$ shown as contours versus distance of constituents (x: δ₁ and y: δ₂) with ${\delta }_3=\max ({\delta }_1,{\delta }_2)$ according to our model (Eq. 4) is shown in the rightmost plot. The other three plots compare this model to three simpler models: arithmetic mean, harmonic mean and minimum. Note that ${\widehat{\delta }}_{M R}$ is close to the minimum value and to a lesser extent to the harmonic mean, but not to the arithmetic mean

All our subsequent results are based on this model.

As expected, in this model, ${\widehat{\delta }}_{M R}$ is a function of d₁, d₂ and d₃. Plotting Equation 4 shows (Fig. 2d) that ${\widehat{\delta }}_{M R}$ resembles the harmonic mean of δ₁ (i.e. $h(d_1)$) and δ₂ much better than their arithmetic mean; moreover, ${\widehat{\delta }}_{M R}$ is quite close to the minimum of δ₁ and δ₂. This observation can be further formalized as a bound.

Proposition 1. (Proof in Appendix 1) Let ${\delta }_{AR}\le {\delta }_{BR}$. For a fixed value $z={\widehat{\delta }}_{M R}$, the lower-bound for δ_AR is $1-{\left(\frac{3}{2}\right)}^{\frac{1}{k}}(1-z)$and its upper-bound u is given by $\frac{4{(1-u)}^k-2{(1-2u)}^k}{3-{(1-2u)}^k}={(1-z)}^k$.

Thus, the distance between the reference genome and the closer of constituent samples bounds the distance to the mix (Fig. 2b). We utilize this lower bound in our algorithm (described later).

2.1.3. Reference-guided deconvolution

Given the Skmer distance ${\widehat{\delta }}_{M R}$, our aim is to estimate the distance between R and constituents A and B of M; i.e. to estimate d₁ and d₂ (and less crucially, also d₃). Given these estimates, we can place the mix on two branches of the phylogeny using distance-based phylogenetic placement (e.g. Balaban et al., 2020). The challenge is that d₁, d₂ and d₃ are not observed directly from the data, and all three impact our single observation ${\widehat{\delta }}_{M R}$. Thus, we have to deconvolute ${\widehat{\delta }}_{M R}$ to constituent parts. However, the problem has infinitely many solutions, including trivial ones like $h(d_1)=h(d_2)={\widehat{\delta }}_{M R},\hspace{0.17em}{d}_3=0$.

Our main insight is that although the problem is underdetermined when only one reference point (R) exists, given multiple ${\widehat{\delta }}_{M{R}_i}$ values and a phylogenetic tree, we can impose constraints on the values of these ${\widehat{\delta }}_{M{R}_i}$ variables. The simplest example of such implicit constraints is the triangle inequality (e.g. given ${\delta }_{R_1{R}_2}=0.1$, two inequalities must hold: $0.1\ge |{\delta }_{A{R}_1}-{\delta }_{A{R}_2}|$ and ${\delta }_{A{R}_1}+{\delta }_{A{R}_2}\ge 0.1$). Moreover, the correctly deconvoluted values should be close to additive (i.e. should fit a tree). Our approach is to define a set of constraints on deconvoluted distances based on the model and to seek a combined deconvolution and placement solution that minimizes deviations from additivity. We then define an optimization problem to find the optimal value for all the variables.

2.2 Phylogenetic double-placement

We extend the distance-based phylogenetic placement problem of Balaban et al. (2020) to introduce the distance-based phylogenetic double-placement problem. Let an unrooted tree T be a weighted connected acyclic undirected graph with leaves denoted by $\mathcal{R}=\{R_1\cdots R_m\}$. Placement of a query sequence can be represented by the placement edge as well as distal and pendant edge lengths of the added taxon (Supplementary Fig. S3). Given the phylogenetic tree T, a mixture M of A and B, and Jaccard-driven estimates of ${\widehat{\delta }}_{M{R}_i}$, we aim to find the optimal position of A and B on T. We represent the solution as two placement trees P and Q, each obtained by adding a new leaf (A or B) to a specific position on a branch in T with a pendant edge length.

2.2.1. Mixture of known species

We start with cases where the mixture is of two genomes present in the reference phylogeny. In this case, luckily, the smallest ${\widehat{\delta }}_{M{R}_i}$ values readily identify the constituents.

Proposition 2. (Proof in Appendix 1) When $A\in \mathcal{R}$and $B\notin \mathcal{R},\hspace{0.17em}\underset{R_i}{\inf }{\widehat{\delta }}_{M{R}_i}=A$. Also, ${\widehat{\delta }}_{M A}=1-{\left(\frac{2}{3-{(1-{\delta }_3)}^k}\right)}^{1/k}$

Corollary 3. Without loss of generality, Let $\inf \left\{{\widehat{\delta }}_{M{R}_i}\right|R_i\in \mathcal{R}\}=R_1$and $\inf \left\{{\widehat{\delta }}_{M{R}_i}\right|R_i\in \mathcal{R}\setminus \left\{R_1\right\}\}=R_2$. If $A\in \mathcal{R}$and $B\in \mathcal{R},\hspace{0.17em}A,B\in \{R_1,R_2\}$and ${\widehat{\delta }}_{M{R}_1}={\widehat{\delta }}_{M{R}_2}=1-{\left(\frac{2}{3-{(1-{\delta }_3)}^k}\right)}^{\frac{1}{k}}$.

Thus, ${\widehat{\delta }}_{M A}$ and ${\widehat{\delta }}_{M B}$ values are expected to be identical to a function of k and δ₃ (unknown). Luckily, regardless of δ₃, this value has a constant upper-bound with a small value $1-{(3/2-1/2{(1-3/4)}^k)}^{-1/k}$. Moreover, as δ₃ increases, ${\widehat{\delta }}_{M R}$ quickly approaches this upper bound (Fig. 2d). Therefore, when the reference library includes both constituents, one can simply find the smallest two among all ${\widehat{\delta }}_{M{R}_i}$ and the identification problem is solved. Moreover, in this scenario, ${\widehat{\delta }}_{M{R}_i}$ should not exceed a small constant (e.g. 0.013 for k = 31).

2.2.2. Mixture of unknown species

The most interesting case, which necessitates phylogenetic placement, is when the mixture is of two species absent from the reference set. For distance-based phylogenetic placement, we use the ordinary least squares (OLSs) criterion (Cavalli-Sforza and Edwards, 1967). Following the standard formulation, we seek the solution that minimizes:

$$\sum _{i=1}^n(h^{-1}({\delta }_{Ai})-d_{Ai}^P{)}^2+\sum _{i=1}^n(h^{-1}({\delta }_{Bi})-d_{Bi}^Q{)}^2\hspace{0.17em}.$$

If ${\delta }_{Ai},{\delta }_{Bi}$ were known, due to the independence of the two placements in this formulation, the problem could be considered as two single-species placement problems. However, for a mixed sample, we do not have ${\delta }_{Ai},{\delta }_{Bi}$. Instead, we consider ${\delta }_{Ai},{\delta }_{Bi}$ as variables and approach the determination of these variables and placement of mixtures constituents as a simultaneous solution of the deconvolution problem and the placement problem.Least squares phylogenetic double-placement:

Input: A backbone tree T on $\mathcal{R}$ and a vector with elements ${\widehat{\delta }}_{M i}$, each giving the Jaccard-based distance between M and a species $i\in \mathcal{R}$;

Output: Vectors $x_{*}^A,x_{*}^B$, variable x₃, and two placement trees P and Q that add A and B on T respectively, such that:

$$\hspace{1em}\sum _{i=1}^n{(x_i^A-d_{Ai}^P)}^2+\sum _{i=1}^n{(x_i^B-d_{Bi}^Q)}^2$$ (5)

is minimized, subject to:

$${\widehat{\delta }}_{M i}=1-{\left(2\frac{{(1-h(x_i^A))}^k+{(1-h(x_i^B))}^k-{(1-h(\frac{x_i^A+x_i^B+x_3}{2}\left)\right)}^k}{3-{(1-h(x_3))}^k}\right)}^{\frac{1}{k}}$$ (6)

This problem formulation can be extended to multiple query sequences to define a phylogenetic multi-placement problem. In this article, we only focus on the special case of double placement. We are faced with a non-convex optimization problem with many variables.

2.3 Solving the non-convex optimization problem

For each constituent, the number of possible placement edges is $2n-3$, and for each placement edge, one distal and one pendant edge length characterize a placement tree (Supplementary Fig. S3). We encode these two lengths as two more variables. To solve the optimization problem, we iterate over all pairs of edges (in parallel), and for each pair, find $2n+1$ distance variables and four distal and pendant edge length variables that minimize the optimization score. At the end, we return the placement with the minimum least square error across all $\left(\begin{array}{c}2n-2\\ 2\end{array}\right)$ placements. All the $d_{ij}^T$ values are pre-computed using a simple dynamic programming.

For a fixed pair of edges, our optimization problem has a quadratic objective function and non-linear constraints. We solve the problem numerically, using the trust region method of Conn et al. (2000), as implemented in the SciPy optimize module (Virtanen et al., 2020). For this numerical optimization solutions to converge, several difficulties need to be addressed.

Jacobian and Hessian. Providing the Jacobian and Hessian of the optimization score (Eq. 5) and non-linear constraints (Eq. 6) to the numerical solver is crucial in achieving convergence. To be able to compute derivatives of Equation 6 analytically and to help achieve convergence, we had to adopt two further approximations. First, having $h()$ on the right-hand side (RHS) is a challenge. To deal with this difficulty, on the left-hand side (LHS), we replace ${\widehat{\delta }}_{M i}$ with $h^{-1}({\widehat{\delta }}_{M i})$, and on RHS, we replace all $h(x_i^A)$ terms with $h^{-1}(h(x_i^A))=x_i^A$ (ditto for $x_i^B$). This approximation is akin to making an infinite sites assumption and is negligible when distances are relatively small [i.e. h(x) is close to identity for x close to 0]. Second, having a variable x₃, which represents $h(d_3)$, that is shared between all n constraints makes derivations of Jacobian and Hessian difficult and complicate the optimization since constraints cannot be handled independently. We therefore approximate x₃ with $\max \{d_{uv}^T,d_{u\prime v\prime }^T,d_{uv\prime }^T,d_{u\prime v}^T\}$ where $(u,u\prime )$ and $(v,v\prime )$ denote the placement edges being tested. These approximations make it relatively easy to derive the Jacobian and Hessian (Supplementary Appendix S1).

Inequality constraints. We further impose lower bounds on values of $x_{*}^A$ and $x_{*}^B$ according to the upper and lower bounds obtained in Proposition 1. These constraints dramatically reduce the feasible solution space and help with faster convergence.

Initialization and termination. Trust region method requires a valid initial point (i.e. one that satisfies the constraints). We always initialize pendant and distal edge lengths to 0. Let ${\widehat{x}}_3$ be the constant approximated value of x₃ described previously. For each reference sequence R_i, we initialize one of $x_i^A$ and $x_i^B$ to a value $x^0$ and set the other to $x^0+{\widehat{x}}_3$ such that when we plug $x_i^A$ and $x_i^B$ in Eq. 6, the constraint is satisfied. This is achieved by $x^0=1-(1-h^{-1}({\widehat{\delta }}_{M i})){((3-{(1-{\widehat{x}}_3)}^k)/2)}^{1/k}$. To decide whether $x_i^A$ or $x_i^B$ are set to $x^0$, we compare $d_{iA}^T$ and $d_{iB}^T$ and choose the smaller.

We use the default termination conditions for the trust region algorithm but limit the maximum number of iterations to 5000. In our preliminary tests, we observed that, in most cases, low residual errors and convergence are obtained in much fewer iterations (e.g. see Supplementary Fig. S4).

2.3.1. MISA

We implement our algorithm in a tool called MISA. The input to MISA is the vector ${\widehat{\delta }}_{M{R}_i}$ of distances between the query sample and target species (e.g. computed using Skmer or Mash), the value of k and the backbone tree. It uses the Jukes and Cantor (1969) model to correct phylogenetic distances, uses Treeswift (Moshiri, 2018) for tree operations, and generates the output in the jplace format (Matsen et al., 2012).

Automatic choice of k. MISA can suggest a k for a given backbone dataset. To do so, it computes the LSE of the backbone tree with regards to the reference genomes for a set of k values (here, all odd values of $21\le k\le 31$) and picks the k that leads to the minimum LSE error (indicative of additivity).

3 Experimental setup

3.1 Datasets

Drosophila dataset (simulated mixture). We use a set of 14 Drosophila assemblies published by Miller et al. (2018) (Supplementary Table S1) to evaluate the accuracy of our approach in an ideal setting where the mixed sample consists of the concatenation of the assemblies. We test 20 simulated mixtures of randomly chosen species in three scenarios where none, one, or both of the constituents are present in the reference library.

Columbicola (Lice) dataset (simulated mixture). To evaluate the accuracy of our method on genome skimming data, we use a set of 61 genome skims by Boyd et al. (2017) (PRJNA296666), including 45 known Lice species (some represented multiple times) and seven undescribed species. We use randomly subsampled genome-skims of 4 Gb. We use BBTools (Bushnell, 2014) to filter subsampled reads for adapters and contaminants and remove duplicated reads. Then, we create five replicates each containing 20 organisms sampled from the full dataset at random. For each replicate, we simulate five mixtures with A and B chosen uniformly at random. We simulate mixtures by simply combining preprocessed genome skims of the two constituents. The exact coverage of the genome skims is unknown but is estimated to range between 4× and 15× by Skmer.

Yeast dataset (real hybridization). In addition to simulated mixtures, we create a dataset of real hybrid yeast species. We select representative genomes for eight non-hybrid Saccharomyces species with assemblies available on NCBI. We also create a second extended dataset where we include seven more species from Genera Naumovozyma, Nakaseomyces and Candida (see Supplementary Table S2 for accession numbers). We curate four assembled and two unassembled strains of hybrid yeast species, some of which were previously analyzed by Langdon et al. (2018). Unassembled hybrid strains muri (Krogerus et al., 2018) and YMD3265 are subsampled from NCBI SRA to 100 Mb and filtered for contaminants in the same fashion as the previous dataset. We do not include strains such as Saccharomyces bayanus that are conjectured to be hybrid of three species (Libkind et al., 2011). For each hybrid species, the hypothesized ancestors are known from the literature (Krogerus et al., 2018; Langdon et al., 2018, 2019) and NCBI Taxonomy annotation, and we use these postulated ancestors as the ground truth.

3.2 Distance calculation and backbone trees

On all datasets, we compute reference-to-reference and reference-to-query sequence distances using Skmer. To select k, we use the automatic procedure described earlier (i.e. the k with the minimum LSE on the backbone). This procedure chooses k = 21 for the two assembly-based datasets (Drosophila and yeast) and k = 31 for the skim-based dataset (Columbicola) (Table 1). The backbone tree topologies are set to those of previously published phylogenies for yeast (Shen et al., 2016; Sulo et al., 2017), Drosophila (Miller et al., 2018) and Columbicola (Boyd et al., 2017). For all datasets, the backbone tree branch lengths are re-estimated (Supplementary Fig. S5) by running FastME2.0 (Lefort et al., 2015) on sequence distances according to the Jukes and Cantor (1969) model. This branch re-estimation method can produce negative branch lengths. In the case of the yeast dataset, the tree includes one branch with a negative length. In the Lice data, four branches have negative estimated length. In three out of our 25 total replicates in the Lice dataset, the placement distal edge length is negative. These likely reflect errors (like contamination) in the data, and our approach does not model negative length. To remedy this, we set length of negative branches on backbone tree to zero. In addition, one species (called 931 here) contributes disproportionately to the LSE error of the backbone tree compared to other species (Supplementary Fig. S6). While this species is suspect (e.g. may be contaminated), we keep it in the analyses.

Table 1.

Impact of k on the additivity of the backbone trees

	(a) Columbicola		(b) Drosophila		(c) Yeast
	LSE	FME	LSE	FME	LSE	FME
k=21	0.053	4.768	0.0003	0.014	0.0094	0.106
k=23	0.0385	6.4778	0.0005	0.0158	0.0094	0.1133
k=25	0.0275	4.4182	0.0005	0.0193	0.0097	0.1254
k=27	0.0208	3.1422	0.0006	0.0235	0.01	0.1385
k=29	0.0167	2.272	0.0007	0.0278	0.01	0.1508
k=31	0.013	1.5779	0.0008	0.0348	0.0102	0.1641

Note: Error is measured using the unweighted least square error (LSE) and Fitch and Margoliash (1967) weighted least square error (FME). In FME, each squared error term is weighted by the inverse of observed distance squared, reducing the contribution of longer distances. Error for the backbone tree including all 61 species in the dataset is shown for Columbicola. Error for extended backbone tree is shown for yeast. The lowest error values for each dataset are shown with underline.

To create test cases with the query constituents missing from the reference set, we simply remove the constituents from the full backbone tree, but we do not recompute the backbone or its branch lengths.

3.3 Evaluation

Evaluation metric. We quantify the error in each placement by counting the number of branches between the placement found by each method and the correct placement. We report the error for the two placements separately. We simply define the placement with the lower error to be the primary placement and the other placement to be the secondary placement. Note that the primary/secondary distinction is not made by the tool and is solely used to facilitate the analysis of error in an interpretable way. When constituents are in the reference tree, we also compute the tree distance between the constituent and the placement tree; ideally, this distance should be zero for simulated mixes.

Methods compared. No existing method can solve the mixture problem as defined here (input: reads from a mixed sample, a tree and reads from each leaf of the tree; output: two placements on the tree). Thus, we are forced to compare MISA to two control methods.

The simplest alternative method is TOP2: compute the distance of the mixed sample to all reference species and place the query as sister to the species with smallest two distances. By Corollary 3, this method should work well when the constituents are in the reference. Note that we do not use Corollary 3 in the design of the MISA method. The second alternative to MISA is to pretend the mix is a single-species sample and to perform phylogenetic placement using APPLES (Balaban et al., 2020); in this scenario, we set both placements to be equal. By definition, APPLES is not trying to get both placements correct; however, we can hope it can place at least one of the two constituents correctly.

4 Results

4.1 Simulated mixture datasets

4.1.1 Constituents sampled in the reference set

When both constituents are in the reference library, the MISA method perfectly identifies both constituent species both for the assembly-based Drosophila data and assembly-free Lice data (Fig. 3). In agreement with Corollary 3, TOP2 detects the correct placement in 89 out of 90 placements across the two datasets. In one case on the Columbicola dataset, the secondary placement of TOP2 is wrong by six edges. APPLES is able to correctly place one of the two constituents everywhere except one case (out of 20) for Drosophila and five cases (out of 25) for Lice. APPLES, by design, fails to identify the second species unless the constituents happen to form a cherry.

Fig. 3.

Placement error for each method when constituents of simulated mixtures are both present, one present and one absent, or both absent in the reference set. Distributions are over 20 replicates for Drosophila (a), and 25 replicates for Columbicola/Lice (b) datasets. We show the number of branches between each placement and the correct placement (i.e. 0 means perfect accuracy). Because there are two placements, we show the error for both placements, designating the one with lower error as primary and the second one as secondary

MISA also produces branch lengths that can be examined. When mixed species are in the library, ideally, the total branch length between output placements and constituents should be zero. For both datasets, the distance between the MISA placement and the correct placement is in all but one case below 0.013 for both primary and secondary placements and is 0.018 in the remaining case (Fig. 4a).

Fig. 4.

(a) For each placement found by MISA, we show the tree distance between the placement and the correct constituent (which, here, is present in the reference set) on Columbicola, Drosophila and yeast (Saccharomyces) datasets. For yeast, we show results both for small and extended backbone tree. (b) Observed distances between mixtures to constituents (e.g. ${\widehat{\delta }}_{M A}$ and ${\widehat{\delta }}_{M B}$) in Drosophila and Lice datasets. Horizontal red line indicates the value predicted by our model (with k = 31 and k = 21, respectively). The outliers are labeled

Examining ${\widehat{\delta }}_{M R}$ values on the Drosophila dataset, as predicted by the theory, ${\widehat{\delta }}_{M A}$ and ${\widehat{\delta }}_{M B}$ are close to the theoretical bound 0.019 for k = 21 (always between 0.015 and 0.025; see Fig. 4b). On the Lice dataset, both ${\widehat{\delta }}_{M A}$ and ${\widehat{\delta }}_{M B}$ are close to 0.013 (theoretical bound for k = 31) in all but three cases. In one case, the mixture has close to zero distance to both constituents, one of which is 931; as mentioned before, this species contribute abnormally high levels to the error of the backbone phylogeny (Supplementary Fig. S6) and should be treated as suspect. The other outlier is a species, which we call 932, where the distance to mixture is 0.03. This species has the longest terminal branch length in the tree (Supplementary Fig. S5). Interestingly, despite not agreeing with the numerical predictions of the model, the 932 species is placed correctly by MISA, whereas it is not placed correctly using TOP2 (the only case where TOP2 has an error).

4.1.2 Constituents fully or partially missing in the reference set

When one of the constituents is in the reference library, TOP2 finds that species with perfect accuracy (Fig. 3). However, it cannot accurately find the second constituent; the median error is two edges for both Lice and Drosophila datasets, and it can be as high as eight edges for the Lice dataset. Thus, TOP2 is only partially successful. APPLES similarly performs well for one of the constituents but cannot find the second species. MISA, in contrast, has high accuracy in this scenario. Its primary placements are always correct in both datasets. The secondary placements are correct in 19 of 20 cases in Drosophila dataset. In one replicate, the secondary placement is off by one edge. On Lice dataset, its secondary placements have a median error of zero edges. The error is two edges or less in all but three cases (Fig. 3b). One of these outlier cases is the only example in the Lice dataset where the two constituents happen to form a cherry (i.e. are sister taxa). Thus, they must be both placed on the same branch, but MISA only places one of them on the correct branch. Nevertheless, for partially complete reference sets, MISA greatly outperforms the alternatives.

When both constituents are missing from the set, TOP2 remains surprisingly accurate in finding one of the two species (Fig. 3); its primary placements are correct in all cases except for one replicates of the Drosophila and three replicate of the Lice datasets. However, for the second placement, TOP2 has high error levels (median: two edges for Drosophila and three edges for Lice). APPLES has higher error than TOP2.

MISA has much better accuracy than the alternatives. It remains fully accurate on the primary placement and has a median error of zero for the secondary placement on both datasets. On Drosophila data, MISA finds the correct secondary placement in 75% of cases, and its error does not exceed three branches in any replicate. On the more challenging Lice dataset, it is within three edges for the secondary placement in all but four outlier cases where its second placement is five or six branches away from the correct placement. One of the outlier cases is again the cherry, and another outlier is a replicate where the true placement is on a zero-length branch. A third outlier is a replicate where species 932, which was the outlier in terms of distance to the mixture (Fig. 4b), is one of the two constituents.

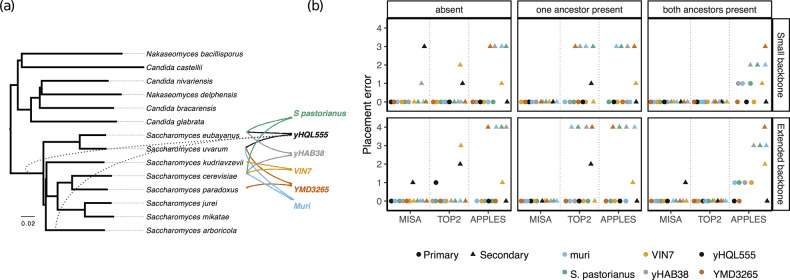
4.2 Fungal hybridization

In the fungal dataset, overall, MISA has the best ability to identify the ancestral species (Fig. 5). When both ancestors are present in the database, MISA is able to identify both ancestors correctly in all six cases with the small backbone and all but one ancestor with the larger backbone. The exception is yHQL555, which is a mix of two sister species (i.e. a cherry). MISA puts the hybrid at relatively low phylogenetic distances (0.018 or lower in all but three cases) to both constituent (Fig. 4a). However, distances are generally larger than Drosophila and Lice datasets, which were true mixes. These larger distances on the hybrid yeast data may indicate some amount of evolution after the hybridization event. With ancestors present, TOP2 has perfect accuracy. APPLES is rarely correct and often finds both ancestors incorrectly.

Fig. 5.

Results on the yeast (Saccharomyces) hybrid dataset. (a) The phylogeny of 14 ‘pure’ species and the origins for each of the six hybrid species and strains as postulated in the literature (solid lines). The dotted lines show the placement of yHQL555 when the ancestors are removed from the database. All other species are correctly placed by MISA when given this extended backbone tree. (b) Placement error for each yeast hybrid species when hybrid ancestors are both present, one present and one absent, or both absent in the reference set. The error is shown for both a backbone phylogeny of 8 Saccharomyces species and an extended phylogeny of 14 yeast species sampling various genera. Errors are shown separately for the two placements (circle: the placement with the minimum error; triangle: the placement with a maximum error)

The advantage of MISA compared to TOP2 becomes clear when one of the ancestors are missing. When one ancestor is present, TOP2 finds it correctly in every case. However, except for VIN7, it finds the second ancestor incorrectly, and it can be up to four branches off. In contrast, MISA finds both placements correctly in all cases. Similar patterns are observed when both ancestors are absent. TOP2 finds one of the two placements correctly everywhere except for yHQL555 (with the large backbone) but fails to find the correct placement for the second ancestor for VIN7 and yHQL555. Here, MISA has similar performance but manages to find both ancestors correctly for VIN7 and one of the ancestors for yHQL555.

5 Discussion

We introduced MISA, a method for inserting a mixed sample onto two positions in a reference phylogeny. MISA is a traditional distance-based phylogenetic method with a novel twist: it seeks to decompose the measured distances between the mix and reference species into their constituent parts. To enable this ‘deconvolution’, we introduced a simplified model that, despite its various assumptions and approximations, is useful in making sense of mixture distance (Eq. 4). Our results showed that not only MISA has high accuracy in identifying constituents of a mixed sample, it can also identify ancestors of a recently hybridized species. Moreover, MISA can accomplish this difficult task using the simplest possible form of input—sets of unassembled reads both for the mixed query sample and the reference set.

Our model also allowed us to prove an interesting result: a mixed sample is expected to have a lower measured distance to its constituents than to any other reference. More surprisingly, this minimum distance is expected to be lower than a small constant value. Thus, in addition to MISA, we were able to describe a simple method called TOP2 that simply picks the two smallest distances as constituents. Our theoretical and empirical results showed that this fast and simple method works well when the constituents are part of the reference set but can have reduced accuracy in other scenarios. Therefore, the power of MISA, driven from its reliance on phylogenetic placement, is needed when we suspect a mixture may include novel or unsampled species.

Our model predicts that ${\widehat{\delta }}_{M{R}_i}$ is close to the minimum of ${\widehat{\delta }}_{M A}$ and ${\widehat{\delta }}_{M B}$ (Fig. 2d) for k = 31. The gap between our model and this minimum value, however small, is crucial for the successful deconvolution of distances (with the minimum model, both constituent distances cannot be recovered). Importantly, this gap vanishes as k goes to infinity and becomes larger for smaller k. Our experiments show that a reasonable way to choose k is to examine the additivity of distances obtained from different values. On Drosophila and yeast data, increasing k from 21 to 31 results in an increase in error in double-placement (Supplementary Fig. S7) as well as the lack of additivity as measured by the LSE error (Table 1). We therefore choose k that yields the most additive distances for the backbone tree.

MISA was relatively fast on our datasets. On the largest dataset (Lice) with 20 backbone species, the average execution time of an analysis on a mixture was approximately 30 s using 36 cores Intel(R) Xeon(R) Gold 6240 CPU 2.60 GHz with 384GB of DDR4. Solving the optimization problem for a pair of branches took $\approx$1 s on average, and MISA runs in an embarrassingly parallel fashion across all branch pairs. To be able to extend this approach to much larger backbone trees, we will need to design heuristic methods that avoid examining all pairs of placement branches.

5.1 Relevant literature

Our approach to mixture analysis is quite different from the literature. Methods developed for metagenomics focus on matching reads to marker genes (e.g. Liu et al., 2011; Segata et al., 2012; Sunagawa et al., 2013) or reference genomes (e.g. Wood and Salzberg, 2014), placing reads on a phylogenetic tree (e.g. Barbera et al., 2019; Nguyen et al., 2014) and finding signatures of composition (e.g. Brady and Salzberg, 2009; Rosen et al., 2011). Here, we take a distance-based approach and seek to decompose observed distances into their individual parts. A somewhat similar philosophy was used by Koslicki et al. (2013, 2014), who used spectral methods to factorize a matrix of k-mer frequencies into an abundance vector and observed k-mer frequency matrices. This approach is different from ours because it (i) assumes constituents are in the library, (ii) operates on k-mer frequencies (for small k) rather than k-mer presence or absence (for large k) and (iii) formulates the problem as matrix factorization. While these metagenomics methods are not presently available in forms that avail themselves to application in our setting (placement of eukaryote mixtures), future work should explore whether they can be adapted to our setting.

Another relevant literature is phylogenetic network reconstruction in the face of hybridization (see Nakhleh, 2013). The problem addressed in network phylogeny is more challenging than our problem because networks could have hybridization at ancestral nodes. In our case, hybridization (or mixture) happens only between leaves of the tree, and little or no evolution occurs after hybridization (as time passes, the hybrid eventually ceases to resemble the combination of its constituents). Because of their more ambitious goal, explicit network methods do not operate on distances and are not based on alignment-free methods. Instead, they operate on aligned homologous loci and seek to find a network that best explains the distribution of observed gene trees. In contract, some of the popular implicit network methods, such as SplitsTree (Huson, 1998), use distances. However, these methods do not seek to find the correct placement under any model; they simply provide means of visualizing discordance (i.e. lack of additivity) among observed distances. Because the problem we address is simpler than explicit network reconstruction, we can approach it using assembly-free distance-based methods. At the same time, unlike implicit methods, we use a model that generates interpretable output (as opposed to simple visualizations of discordance). Finally, we note that our model, as presently constructed, can handle alloploidy but not homoploidy (where the hybrid is not the union of both ancestors).

5.2 Shortcomings and future work

While generally accurate, MISA had a clear loss of accuracy under a special case. When the constituents of the hybrid form a cherry (e.g. are sister species), both placements should be on the same branch. The only incorrect identification by MISA on the real fungal dataset (yHQL555) was a cherry, and some of the four outlier cases with high error on the Lice dataset were cherries. While the current formulation of MISA as two separate placements precludes finding a cherry as the output, one can still hope that it puts the two placements on the same branch. However, MISA is often able to place one but not both of the constituents on the correct branch. This limitation is not a fundamental shortcoming of our model or methodology and can be ameliorated in the future by allowing cherries as the solution to the optimization problem. Achieving this improvement requires a second round of cherry placements on the phylogeny and a change in the approximations used for x₃.

Incorrect placements of MISA can be due to either an imperfect distance deconvolution or inaccurate of distance-based placement using OLSs. In other words, even if distances are deconvoluted perfectly, we can still observe erroneous placements. In fact, on both simulated datasets, where we know the true deconvolution, we observe this pattern (Supplementary Fig. S8). In particular, on the Drosophila dataset, distance deconvolution seems to contribute very little to the final error.

On the optimization side, we can enforce more constraints such as triangle inequality, but these extra constraints may challenge convergence. Also, we did not fully explore optimizer settings (e.g. the number of iterations and multiple initial points), leaving such exploration to future work. Finally, some of the approximations (e.g. the use of $h^{-1}$ for the derivation of Jacobian or the approximation of x₃) could perhaps be improved in the future.

The optimization formulation can also be further improved. Here, we enforce the model (Eq. 4) as hard constraints and optimize the OLS error between phylogenetic distances and sequence distances. Thus, MISA tries to find the double-placement that is closest to additivity while enforcing expectations under our model. However, our model involves stochastic uncertainty (which we ignored; see below), and thus, the constraints may be too rigid. Future work can explore alternative formulations where the model of ${\widehat{\delta }}_{M{R}_i}$ is treated as uncertain. For example, we can incorporate the difference between LHS and RHS of Equation 6 as part of the optimization score; such a formulation would require a principled way to combine this penalty with the penalty for deviations from additivity (i.e. the current objective function). Furthermore, we assigned equal weight to every term in Equation 5. Previous results on distance-based placement of single-species samples show that employing a weighting scheme (e.g. Fitch and Margoliash, 1967) improves accuracy by downscaling the error contribution of long distances. At the cost of increasing the complexity of the objective function, using FM weighting may improve the accuracy of MISA.

Our model leaves several questions unanswered. We do not know whether under our model constituent distances are unique given observed distances to a set of references (we know they are not for one or two references). Moreover, in deriving the model, we freely replaced random quantities with their expectations without care for careful statistical modeling. These derivations, therefore, have another level of approximation built into them. Our model also assumes a limit on the evolutionary divergence among reference and query species. We have no reason to believe that MISA has high accuracy on mixtures of highly divergent species (e.g. from different phyla). Nevertheless, we find it remarkable that despite all the simplifying assumptions and approximation, the method still works with high accuracy on data that violate many of those assumptions. Note that our simulated datasets were far from fully complying with our assumptions. For example the genomic contribution of the constituents to the mixture varies from 40 to 60% in Drosophila and 36 to 62% in Lice datasets (Supplementary Fig. S9).

Our analyses of hybrid yeast dataset only focused on mixes of two species. There are known cases of mixes of three species, such as S.bayanus, which is hybrid of S.uvarum, S.cerevisiae and S.eubayanus (Libkind et al., 2011). Applied on S.bayanus, MISA identifies one of the ancestors, S.uvarum and places the second ancestor on the root of the (extended) backbone tree. Performing a second deconvolution of the uncertain placement may help identify the remaining two ancestors. In general, how this model can be extended to mixtures of three or more species remains a topic of future research.

Financial Support: This work was supported by the National Science Foundation (NSF) grants [NSF-1815485 to M.B. and S.M.] and [NSF-1845967 to S.M.]; Computations were performed on the San Diego Supercomputer Center (SDSC) through XSEDE allocations, which is supported by the NSF [ACI-1053575].

Conflict of Interest: none declared.