TopicNet: a framework for measuring transcriptional regulatory network change

Abstract

Motivation

Recently, many chromatin immunoprecipitation sequencing experiments have been carried out for a diverse group of transcription factors (TFs) in many different types of human cells. These experiments manifest large-scale and dynamic changes in regulatory network connectivity (i.e. network ‘rewiring’), highlighting the different regulatory programs operating in disparate cellular states. However, due to the dense and noisy nature of current regulatory networks, directly comparing the gains and losses of targets of key TFs across cell states is often not informative. Thus, here, we seek an abstracted, low-dimensional representation to understand the main features of network change.

Results

We propose a method called TopicNet that applies latent Dirichlet allocation to extract functional topics for a collection of genes regulated by a given TF. We then define a rewiring score to quantify regulatory-network changes in terms of the topic changes for this TF. Using this framework, we can pinpoint particular TFs that change greatly in network connectivity between different cellular states (such as observed in oncogenesis). Also, incorporating gene expression data, we define a topic activity score that measures the degree to which a given topic is active in a particular cellular state. And we show how activity differences can indicate differential survival in various cancers.

Availability and Implementation

The TopicNet framework and related analysis were implemented using R and all codes are available at https://github.com/gersteinlab/topicnet.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

In recent years, large-scale data on the interaction between proteins and DNA has enabled the construction of complex transcriptional regulatory networks (Liu et al., 2015; Zhang et al., 2014). These networks model the molecular program for gene transcription by representing genes and regulatory elements as nodes, and regulatory relationships as edges. Transcription factors (TFs), a major class of protein regulators in gene expression (Thompson et al., 2015), are pivotal regulatory factors in these networks. Under different cellular conditions, TFs may undergo dramatic functional changes (or ‘network rewiring’) according to the gains and losses of their regulatory target genes. These rewiring events provide insight into differential cellular responses across conditions in the form of altered regulatory programs. Studies have revealed that network rewiring events and the altered regulatory programs they generate have strong phenotypic impacts (Assi et al., 2019; Bhardwaj et al., 2010).

However, quantification of network rewiring is challenging due to the condensed and complex nature of regulatory networks (Gerstein et al., 2012). Genes from various functional modules, pathways and molecular complexes can play varying roles depending on their local associations with other genes. As a result, gains or losses of some gene connections may impact network alterations in a functionally significant way, while others may not. This indicates that identifying the gene functional subgroups and estimating the network rewiring at the subgroup level should be more robust and informative as compared to investigating changes of each individual gene.

These low-dimensional representations of the functional subgroups that underlie network data resemble semantic topics in documents. Based on this consideration, the low-dimensional representation can be constructed using topic modeling techniques, including latent Dirichlet allocation (LDA). LDA was proposed by Pritchard et al. (2000) for population genotype inference, and was ‘rediscovered’ by Blei et al. (2003) with applications in natural language processing as a simple and efficient means to extract latent topics from high-dimensional data. This approach has been successfully implemented in several biological scenarios that require decomposition and dimensionality reduction of data (Pinoli et al., 2014; Wang et al., 2011).

Here, we propose a method called TopicNet that makes use of various features of the LDA model to measure the regulatory potential, perturbation tolerance and intranetwork dynamics of TFs in terms of their target gene ‘topics’. To apply LDA, we represent the targets of a TF under a specific condition (cell line or tissue) as a ‘document’, with the TFs’ target genes as ‘words’ and latent functional subgroups as gene ‘topics’ comprised these words. We applied the procedure to a corpus including all of the regulatory networks inferred from 863 chromatin immunoprecipitation-sequencing (ChIP-seq) assays of the ENCODE dataset.

We first applied the LDA model to the regulatory network to characterize gene topics in an unsupervised fashion. From the trained model, the topic composition represents the distribution of words for each topic, and the topic weights, in turn, are the distribution over topics in a given document. The topic compositions can be further annotated for biological significance in terms of their relevance to various biological pathways and processes. The change in topic weights between documents can be used to quantify the network rewiring between two cellular conditions (i.e. between different cell types or different time points). Lastly, we defined a topic activity score by combining the cell-specific expression of target genes with the various topic compositions to characterize the overall activity of each topic, and demonstrated that this quantity is useful for predicting cancer survival.

In summary, our framework provides a straightforward quantitative representation of a TF regulatory network with biological significance, which could be further applied to many downstream analyses.

2 Materials and methods

2.1 Data preprocessing and construction of the regulatory network

We used 863 ChIP-seq experimental results for 387 TFs from the ENCODE portal for model training due to their high-quality control and consensus peak calling. In addition, we included ChIP-Atlas data collections with more than 6000 ChIP-seq experimental results to test the model. The number of target genes included in this dataset ranges from hundreds to thousands (Supplementary Fig. S11), and the TFs with the greatest availability among different cell lines include CTCF, EP300, MYC and REST (Supplementary Fig. S12).

From each ChIP-seq experiment, the regulatory target genes of specific TFs are defined as those with ChIP-seq peaks in proximal regions (±2500 bp) of their transcription start site. The cell type-specific TRN is then defined based on these results.

2.2 TopicNet—topic modeling

Each regulatory network for a TF in a specific cell line is regarded as an independent input document. We treat target genes that exist in these documents as ‘words’, which collectively constitutes the ‘vocabulary’ of the model. Based on existence of all genes as a regulatory target of the TF in the given condition, a document–gene matrix is then constructed. This matrix is used as the input for the LDA model. We use R package topicmodels for LDA learning and inference.

Let $M,\mathrm{ }K,\mathrm{ }V$ be the number of documents, the number of topics and the vocabulary size, respectively. In this scenario, each document is modeled as a mixture of topics, and each topic is a probabilistic distribution over genes. Each document $i$ is represented as a $N_i$-dimensional vector $W_i$, where $N_i$ is the number of genes in the document, and each element takes the value $1\dots V$. The probability of observing a gene $w_{ij}$ in a document $W_i$ is determined by the mixture of topic compositions within the document and the probabilistic distribution of those topics. The existence of a word in a document is modeled as follows (Fig. 1c):

Fig. 1.

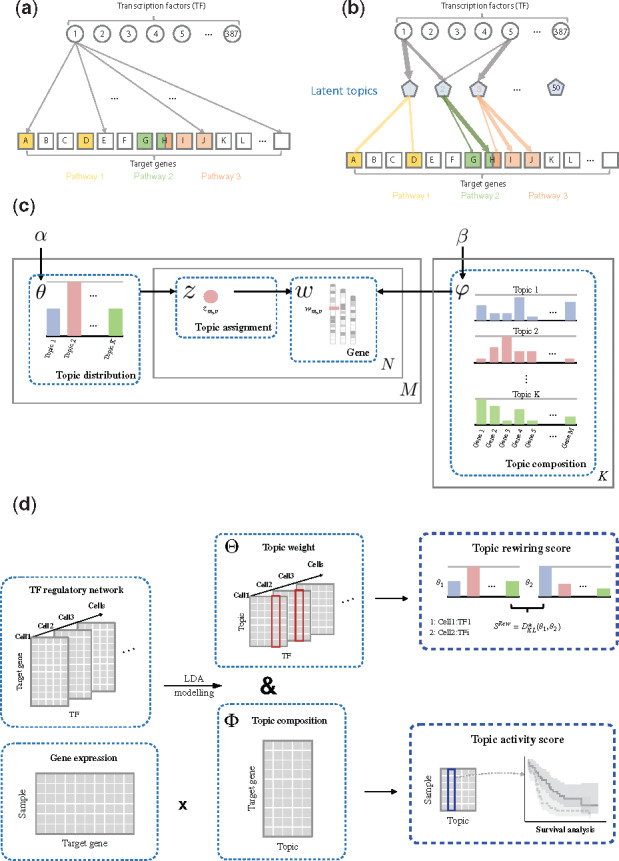
Overview of method and data. (a) An example of a TF–gene regulatory network. (b) The high-dimensional regulatory network is decomposed into latent topics related to certain biological pathways. (c) Diagram explaining the meanings and biological relevance of the parameters in the LDA model. (d) General workflow of our analytical framework

Given two priors ($\alpha$ as the prior for document-topic distribution, and $\beta$ as the prior topic-gene distribution) we can sample

$${\theta }_i\sim \mathrm{\hspace{0.17em}}\mathrm{Dirichlet}(\alpha )$$

as the probability of all topics appearing in a document $i$, which constitutes the $M\times K$ matrix for document-topic distribution; and

$${\phi }_k\sim \mathrm{\hspace{0.17em}}\mathrm{Dirichlet}(\beta )$$

as the probability of all genes appearing in a topic $k$, which constitutes the $K\times V$ matrix for topic-gene distribution.

We can then sample latent topic assignment of each word $j$ in document $i$ as

$$z_{i,j}\sim \mathrm{\hspace{0.17em}}\mathrm{Multinomial}\left({\theta }_i\right)$$

which is the topic that generates this gene. Each $z_{i,j}$ can take the value $1\dots K$.

Given the membership of latent topics, the existence of genes in a document can be drawn as

$$w_{i,j}\mathrm{\hspace{0.17em}}\sim \mathrm{\hspace{0.17em}}\mathrm{Multinomial}\left({\phi }_{z_{i,j}}\right)$$

which constitutes the observed document-word matrix, where ${\phi }_{z_{i,j}}\mathrm{ }$is the topic-word distribution for the sampled topic $z_{i,j}$.

2.3 Model inference

Let $W$ and $Z$ be the collection of all aforementioned $w_{i,j}$’s and $z_{i,j}$’s indexed by document and gene position pair. Gibbs sampling can be performed on the Markov chain $\left\{W,Z\right\}$ to obtain the estimation of $\phi$ and $\theta$. See Supplementary Methods for details.

For a stable and robust topic-gene composition matrix, we averaged the results of 100 runs. As the topics learned by the LDA model for each run were represented in randomized order, topics across different samplings were first mapped against each other based on the correlations of their composition. For any pair of outputs, each topic from the first run was assigned with the same ID as the topic it most strongly correlated with in the other run. We then produced the ensemble model by taking the median of the probability distribution over the composition for all topics that were mapped to the same ID.

Once we obtained the model, we could apply it to unseen documents with the same vocabulary and determine their posterior distribution over topics given the generative processes above.

2.4 Selection of topic numbers

The number of topics $K$ used was selected using three criteria implemented by the R package ldatuning’s FindTopicsNumber method:

1. The posterior likelihood of the data given the LDA model of different number choices (Griffiths and Steyvers, 2004) (blue). A higher value was preferred;

2. The Kullback–Leibler (KL) divergence of the document–gene matrix (Arun et al., 2010b) (red). A lower value was preferred;

3. The average cosine distance r within topics (Cao et al., 2009) (green). A lower value was preferred.

All three metrics reached optimal performance at around 50 topics (Supplementary Fig. S1). Based on these results, we used 50 as the number of topics for downstream analysis.

2.5 Reconstructed correlations

We performed LDA, non-negative matrix factorization (NMF) and K-means with 50 topics on each sample to obtain one 50-dimensional embedding vector of each sample for all three models. We represent the raw data for document $i$ as a vector $v_i=[v_{i,1},\mathrm{ }{v}_{i,2},\dots ,v_{i,N}]$ with binary values, where $N$ is the number of all genes in the vocabulary. The embedding procedure for each method is as follows:

For LDA, we obtained the document-topic weight matrix $\mathrm{\Theta }$ as described above. For each document $i$, the embedding vector is the weight of the 50 topics, which is the $i$th column of matrix $\mathrm{\Theta }$:

$$v_i^{\mathrm{LDA}}={\theta }_i.$$

NMF decomposes the input matrix into two non-negative matrices: the feature matrix $W$, and the coefficient matrix $H$. For a document $i$, we use its weights as the embedding vector, which is the $i$th column of matrix $W$:

$$v_i^{\mathrm{NMF}}=w_i.$$

K-means identifies k = 50 clusters from the dataset, and each cluster is represented as its cluster centroid ${\overline{v}}_1,\mathrm{ }{\overline{v}}_2,\mathrm{ }\dots ,\mathrm{ }{\overline{v}}_{50}$, which is the average of all samples assigned to the respective cluster. Each document $i$ is represented as the Euclidean distances between the raw vector and the 50 cluster centroids:

$$v_i^{\mathrm{KM}}=[d\left(v_i,{\overline{v}}_1\right),\mathrm{ }d\left(v_i,{\overline{v}}_2\right),\dots ,d\left(v_i,{\overline{v}}_{50}\right)].$$

For each document pair in the dataset, we could calculate the Pearson correlation using the raw vectors and the 50-dimensional embedded vectors of the three methods. To evaluate whether the embedding retains correlations in the original data, the ‘reconstructed’ correlation calculated from the embedding vectors was then plotted against the ‘original’ correlation using the raw vectors. Linear regression was also performed between the reconstructed and original correlation for the three methods.

2.6 Evaluation of topic importance

The importance of the ensemble topics was evaluated by calculating the KL divergence between the topic weights of all of the documents and a background uniform distribution. Given the document-topic weight vector for all documents $\theta =\left[{\theta }_1,\mathrm{ }{\theta }_2,\mathrm{ }\dots ,\mathrm{ }{\theta }_M\right]\mathrm{ }$(where M is the number of documents), the noise distribution is defined as$:$

$${\theta }_{\mathrm{background}}=[1/M,1/M,\dots ,1/M].$$

The distance between the ensemble distribution and the null distribution is defined as the KL divergence:

$$D_{\mathrm{KL}}(\theta |\left|{\theta }_{\mathrm{background}}\right)={\sum }_i\left({\theta }_i\right)\log \left(\frac{{\theta }_i}{{\theta }_{\mathrm{backgroun}{\mathrm{d}}_i}}\right).$$

2.7 Gene set enrichment analysis

We used topic composition as the statistic for gene set enrichment analysis (GSEA). Gene sets in the C2, C5 and C6 categories from Molecular Signatures Database (MSigDB) (Subramanian et al., 2005) were used in the analysis. GSEA was performed with the R package fgsea. The affinity between gene sets is defined by their overlapping of gene sets.

2.8 Quantification of network rewiring: topic rewiring score

For a pair of documents in a rewiring event of a given TF $(X_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}},\mathrm{ }{X}_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}})$, we can calculate the KL divergence between their topic weight vectors ${\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}}$ and ${\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}}$, here using the latter as reference:

$$D_{\mathrm{KL}}\left({\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}}\mathrm{ }\right|\left|\mathrm{ }{\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}}\right)={\sum }_i\left({\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\},i}\right)\mathrm{l}\mathrm{og}\left(\mathrm{ }\frac{{\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\},i}}{{\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\},i}}\mathrm{ }\right).$$

Since KL divergence is asymmetric depending on which distribution is used as reference, we consider the symmetrized KL divergence of the two directions to be a better metric for rewiring, which is:

$$D_{\mathrm{KL}\mathrm{ }}^{\mathrm{*}}\left({\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}},\mathrm{ }{\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}}\right)=\frac{1}{2}\left(D_{\mathrm{KL}}\left({\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}}\mathrm{ }\left|\right|{\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}}\right)+\mathrm{ }{D}_{\mathrm{KL}}\left({\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}}\mathrm{ }\left|\right|{\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}}\right)\right).$$

The rewiring score based on KL divergence identifies distinct clusters for closely related cell types like GM cell lines and fibroblasts in hierarchical clustering among CTCF-related documents as shown in Supplementary Fig. S13. This indicates that KL divergence is more robust and interpretable than Jaccard distance on raw vectors.

2.9 Topic activity score

Gene expression data for BRCA, LAML, LIHC and GBM patient samples from TCGA were obtained from GDC data portal (https://portal.gdc.cancer.gov/). The gene expression levels of every sample for each cancer type were formulated into an expression matrix $E$, where rows represent genes and columns represent samples. For each cancer type, the expression data was first quantile normalized. Only genes that appeared in the topic-gene matrix were retained. We then obtained the expression matrix $E$ by first ranking the expression of the genes for each sample, and then transformed the value for gene $i$ in the matrix of column $j$ (corresponding to patient sample $j$) to $E_{i,j}=1/\mathrm{ran}{\mathrm{k}}_{i,j}$, where $\mathrm{ran}{\mathrm{k}}_{i,j}$ is the rank of gene $i$ in sample $j$.

For a sample $t$ with expression vector $E_t$, the topic activity score is calculated as $S_t^{\mathrm{Act}}={\mathrm{\Phi }}^{\mathrm{T}}{E}_t$, where each element in the vector is the activity score of the corresponding target.

2.10 Definition of gain or loss genes

Given two TF regulatory networks under two conditions, we arbitrarily assigned one as an ‘altered condition’ and the other as the reference condition. We define ‘gain’ genes as those that are only regulated by the TF in the altered condition but not the reference condition (formally called ‘gain genes in the altered condition’) and the loss genes vice versa (called ‘loss genes in the altered condition’). For annotation of selected topics, we were particularly interested in the gain or loss genes that are among the top-ranked genes of the topic (i.e. those that have high values in the topic composition). We took the intersection between these two sets and named the resulting set of genes as ‘top-ranked gain/loss genes in the altered condition for topic k’.

2.11 PPI network analysis of topic-related target genes

The genes in the corpus were first sorted according to their contributions to the topic. Among the top 500 genes, those that were directly regulated by the given TF (i.e. bound by the TF in the corresponding ChIP-seq experiment) were selected and provided to STRING (Franceschini et al., 2012). The resulting interaction graph contained the selected genes along with their first-layer neighbors.

2.12 Survival analysis

Clinical information for each patient regarding vital status, days to last follow-up and days to death were downloaded from the GDC data portal (https://portal.gdc.cancer.gov/). Records with missing information were discarded. Patients that were still alive in the record were right censored. The values of all 50 topics were used as variables to perform Cox proportional hazards (coxph) regression and implemented with the coxph function from R package survival, with days to death (or days to last follow-up for censored living patients) as the response.

We then selected the topics whose activity score achieved P-value <0.05 in the coxph analysis, for further analysis. For each of these candidate topics, the patients were then separated into two groups by the median activity score. The survival curve was then estimated using the Kaplan–Meier (KM) estimator. The topics that achieved the lowest P-value were selected and shown.

3 Results

3.1 TopicNet framework

We used an LDA model to decompose the high-dimensional regulatory network into a selected number of latent topics related to certain biological pathways (Fig. 1a and b). Based on the results, we constructed the TopicNet framework to include two parts: topic rewiring score and topic activity score (Fig. 1c and d).

3.2 LDA model

In our study, we treated the regulatory targets of a TF under a specific cellular condition as a ‘document’, denoted as $W_{\left\{\mathrm{TF},\mathrm{cell}\right\}}$. The target genes act as ‘words’ and constitute the general ‘vocabulary’ of the corpus. The LDA then identified functional topics from the genes in these documents (see Fig. 1c). The analogy between topic modeling terms and biological terms is elaborated in Supplementary Table S1.

We used published metrics to choose the number of topics K; in particular, we used K = 50 as the optimal number for our model (Supplementary Fig. S1; see Section 2). Two important matrices can be inferred from the trained model:

1. The document-topic weight matrix $\mathrm{\Theta }$, which is cellular condition dependent, represents the weight of topics for all documents. Each column ${\mathrm{\theta }}_{\left\{\mathrm{TF},\mathrm{cell}\right\}}$ is a vector of the distribution over topics for the corresponding document (note here {TF, cell} represents a single index), and the element ${\theta }_{\left\{\mathrm{TF},\mathrm{cell}\right\},k}$ represents the weight of topic $k$ in document $W_{\left\{\mathrm{TF},\mathrm{cell}\right\}}$.

2. The topic-gene composition matrix $\mathrm{\Phi }$, which is cell independent, indicates the distribution over the target genes within the topics. Each column ${\phi }_k$ represents the composition of a topic (i.e. the distribution of target genes or the contribution of genes to the topic). ${\phi }_{k,j}$ represents the contribution of gene $j$ to topic $k$.

We further developed the topic rewiring score and topic activity score based on these two matrices.

3.3 Topic rewiring score

Raw network rewiring can be described as the differences between documents of the same TF in two cell types, ${\mathrm{ }W}_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}}$ and $W_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}}$. For comparisons between two documents in terms of topics, we defined the network rewiring score as $S^{\mathrm{Rew}}\left({\theta }_{\left\{\mathrm{T}{\mathrm{F}}_1,\mathrm{cel}{\mathrm{l}}_1\right\}},\mathrm{ }{\theta }_{\left\{\mathrm{T}{\mathrm{F}}_2,\mathrm{cel}{\mathrm{l}}_2\right\}}\right)$ as a symmetrized KL divergence between the topic weights

$${\theta }_{\left\{\mathrm{T}{\mathrm{F}}_1,\mathrm{cel}{\mathrm{l}}_1\right\}} \mathrm{and} {\theta }_{\left\{\mathrm{T}{\mathrm{F}}_2,\mathrm{cel}{\mathrm{l}}_2\right\}}. S^{\mathrm{Rew}}\left({\theta }_{\left\{\mathrm{T}{\mathrm{F}}_1,\mathrm{cel}{\mathrm{l}}_1\right\}},\mathrm{ }{\theta }_{\left\{\mathrm{T}{\mathrm{F}}_2,\mathrm{cel}{\mathrm{l}}_2\right\}}\right)=D_{\mathrm{KL}\mathrm{ }}^{\mathrm{*}}({\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_1\right\}},\mathrm{ }{\theta }_{\left\{\mathrm{TF},\mathrm{cel}{\mathrm{l}}_2\right\}}).$$

3.4 Topic activity score

Note that $\mathrm{\Theta }$ gives an effective weighting to topics in a given condition. However, often the cell type-specific regulatory network is lacking but gene expression is available. In these cases, we can define an effective topic activity score. Given a sample $t$ with gene expression vector $E_t$, we compute the vector of activity score for all topics by multiplying the gene expression vector by the composition matrix $\mathrm{\Phi }$ (i.e. $S_t^{\mathrm{Act}}={\mathrm{\Phi }}^{\mathrm{T}}{E}_t$).

3.5 Validation of the LDA model

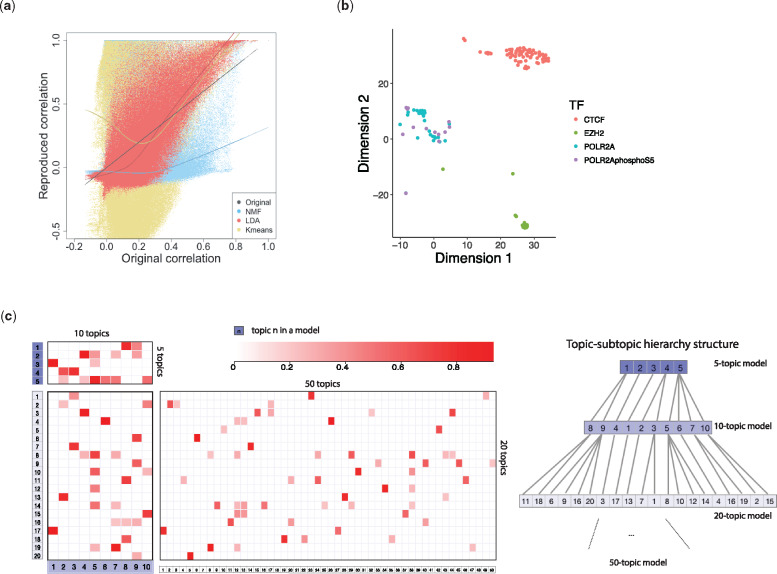
We determined K = 50 as an optimal number of topics using several metrics (Arun et al., 2010a; Cao et al., 2009; Griffiths and Steyvers, 2004). We then tested how similarities in the original data can be preserved compared with two other algorithms, NMF and K-means, using methods presented by Guo and Gifford (2017). Each method gives a 50-dimensional representation of the samples. For every pair of samples, we computed their correlation in terms of both the raw data (‘raw’ correlation) and the 50-dimensional representation (‘reconstructed’ correlation) from each method. Among the three algorithms, LDA could reconstruct the raw correlations better than the other two (Fig. 2a and Table 1). T-distributed stochastic neighbor embedding (T-SNE) of the 50-dimensional representation also demonstrates LDA’s ability to preserve similarities because samples about the same TF tend to form distinct clusters in the embedding space (Fig. 2b).

Fig. 2.

Tuning and performance evaluation of the LDA model. (a) Reproduced pairwise correlations after applying three-dimensionality reduction methods plotted against original correlations. (b) T-SNE embedding of topic weights (50 topic model) for data samples on CTCF, EZH2, POL2A and POL2AphosphoS5. (c) Left: Correlation between topic compositions identified by LDA models with different topic numbers (5, 10, 20, 50). Right: Hierarchical structure of topics inferred from topic correlations (topic correlation is ignored if it has value <0.4 and is not the maximum in its column)

Table 1.

Linear regression of the reconstructed correlation against the raw correlation

Method	Correlation	Linear regression slope	Linear regression $R^2$
K means	0.1047	0.3828	0.0110
NMF	0.4047	0.4365	0.1638
LDA	0.7886	1.3519	0.6219

We also investigated the connection of models that were inferred by the varying topic number K. We associated topics from models with topic number $K=5,\mathrm{ }10,\mathrm{ }20,\mathrm{ }50\mathrm{ }$based on the correlation of their topic-gene composition matrix, and observed a topic–subtopic hierarchical structure among these models (Fig. 2c). This demonstrates that topics may be further split into multiple subtopics when increasing the total number of topics in the model.

The topics can be associated with protein complexes and functional modules. We performed hierarchical clustering on all TF documents in HeLa cells using their topic weights. We observed distinct clusters, indicating coactivation and collaborative binding (Supplementary Fig. S2). Among them, we observed clustering of nuclear transcription factor (NFY) subunits (NFYA and NFYB) and FOS, which have been previously shown to colocalize extensively (Fleming et al., 2013). We observed similar groupings for CTCF and cohesin subunits SMC3 and RAD21, the latter of which frequently cobinds with CTCF (Parelho et al., 2008; Rubio et al., 2008).

3.6 Functional annotation of identified gene topics

We calculated the importance of each topic by measuring the KL divergence between the topic weights across all documents against a background uniform distribution. Important topics should be more specific and, therefore, only highly represented in some documents. In contrast, the topics that show close to a uniform distribution would have almost equal weights in most documents and would be less interesting. The rank of all 50 topics’ importance is shown in Figure 3a. Of particular interest are Topics 3 and 14: from the top genes of these two topics, we identified several functional groups such as transcription regulation, cell proliferation, metabolism and mitosis (Fig. 3b).

Fig. 3.

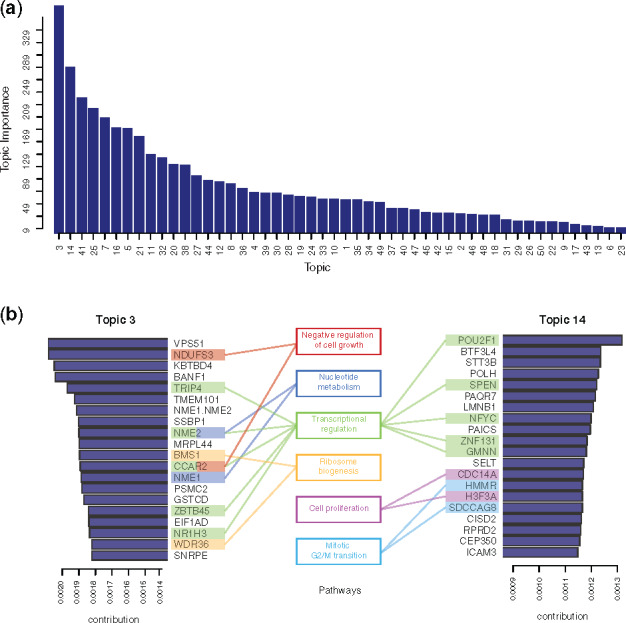
Annotation of the identified topics. (a) All 50 topics ranked by their importance measure (average KL divergence of topic weights against uniform distribution across all samples). (b) Genes with the highest contributions to the top-ranked topics (Topics 3 and 14) along with their related functional roles

To investigate the biological significance of each topic, we annotated their functions using GSEA. For each topic, the probability distribution over target genes can be used directly as the statistics for GSEA. Using C2 and C5 gene sets from the MsigDB (Subramanian et al., 2005), Topic 3, which showed the highest importance, was enriched with gene sets related to breast cancer and glioblastoma tumors (Supplementary Fig. S3).

3.7 Quantification of TF regulation rewiring using topic weights

For each TF, we calculated the pairwise topic rewiring score for all available cell types. The average rewiring score for a TF reflects its cell type specificity, as higher values correspond to greater difference between cell lines (i.e. higher specificity) (Fig. 4a and Supplementary Fig. S4). We observed that many TFs with higher cell specificity were related to biological processes displaying highly variable regulatory activity across conditions, such as pluripotency, cell cycle regulation, tumor suppression or tumorigenesis, including EP300 (Kim et al., 2013), BCL11A (Dong et al., 2017; Khaled et al., 2015), ZBTB33 (Pozner et al., 2016) and JUND (Caffarel et al., 2008; Millena et al., 2016). On the contrary, TFs with more constant roles such as NR2C2 (O’Geen et al., 2010) showed very little difference between cell types. Interestingly, ZNF274 and SIX5, which have been shown to relate to CTCF binding sites (Hong and Kim, 2017), also showed low specificity, similar to CTCF. Supplementary Figure S5 lists the individual rewiring events with top values. Many of these events involve TFs with high cell-type specificity, such as EP300, SUZ12, ZBTB33 and FOS.

Fig. 4.

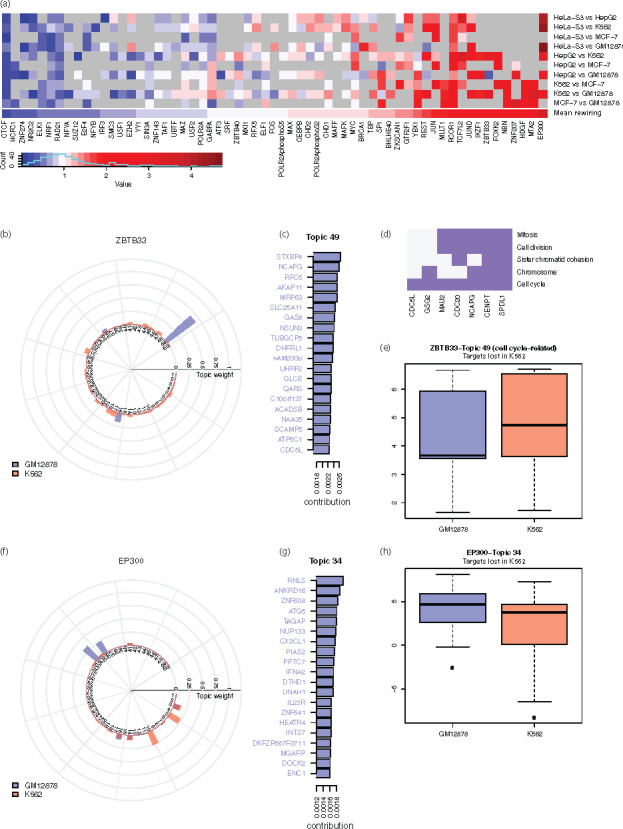
Quantified rewiring analysis using the identified topics. (a) Heatmap of rewiring of TFs in selected cell lines against GM12878 (gray grids correspond to unavailable data). (b) Topic weight for the rewiring event of ZBTB33 in GM12878 and K562. (c) Top-weighted genes of the two topics with greatest difference in the rewiring event of ZBTB33 in GM12878 and K562. Colored gene names indicate true regulatory targets in the ChIP-seq experiment. (d) Functional clustering of top-ranked genes of Topic 49 that are related to cell cycle and cell division. (e) Expression of the top-ranked genes of Topic 49 that are lost in K562. (f) Topic weight for the rewiring event of EP300 in GM12878 and K562. (g) Top-ranked genes of the two topics with the greatest difference in the rewiring event of EP300 in GM12878 and K562. Colored gene names indicate true targets in the ChIP-seq experiment. (h) Expression of the top-ranked genes of Topic 34 that are lost in K562

We pinpointed two cell lines, GM12878 and K562, and studied specific rewiring events for several TFs. Among the 69 TFs shared in both cell lines, ZBTB33 and EP300 showed the highest rewiring values. Specifically, Topic 49 and 16 showed the greatest difference in the rewiring of ZBTB33 (Fig. 4b), and Topic 34 and 10 in that of EP300 (Fig. 4f). For these topics, the majority of the top-ranked genes are true targets in the respective cell line (Fig. 4c and g, Supplementary Fig. S6).

Given a specific TF, we defined ‘gain’ target genes in K562 compared to GM12878 as those that are exclusively present in the former, and ‘loss’ target genes as those exclusively present in the latter. In this scenario, we were particularly interested in the gain or loss genes among those with high contribution to the topic (i.e. the top-ranked genes) that showed a major difference.

For ZBTB33, Topic 49 showed a very high weight in GM12878. We found that the top-ranked loss genes in K562 for Topic 49 were enriched in the gene set related to cell cycle and cell division function (Fig. 4d). The loss of ZBTB33 regulation resulted in higher expression of its target genes in K562, corresponding to known deacylation and transcriptional suppressive roles of ZBTB33 (Pozner et al., 2016; Fig. 4e). Another highly rewired TF, EP300 (a known transcriptional activator), regulates a wide range of genes from different functional groups. In concordance with EP300’s function, Topics 5 and 10 were deficient in K562 and the top-ranked loss genes from these topics were significantly downregulated in K562. For topics of EP300 that were highly represented in K562 (34, 36), we observed an adverse trend (Fig. 4h and Supplementary Fig. S6). To summarize, topics showing major differences in the rewiring of these TFs were related to the TFs’ molecular functions. Comparatively, TFs with low rewiring scores, like CTCF and ZNF274, had almost identical topic distributions (Supplementary Fig. S7).

These results further demonstrate the potential of using a rewiring score derived from LDA as a quantitative measure of change. The rewiring events with high scores could be associated with previously reported biological significance of corresponding TFs.

3.8 Network rewiring shows dynamic topic changes in a time-course study

Temporal changes of topic weights could be used to represent dynamic responses in the cellular regulatory system. To demonstrate this, we further applied our methods to the time series regulatory networks for estrogen receptor (ESR1) in MCF-7 cell lines at 2, 5, 10, 40 and 160 min after estradiol treatment (Guertin et al., 2014). The rewiring score between these time points showed a transition of the topic weights across time points. The first few minutes after estradiol treatment showed dramatic topic changes, followed by a gradual trend to stability (Fig. 5a).

Fig. 5.

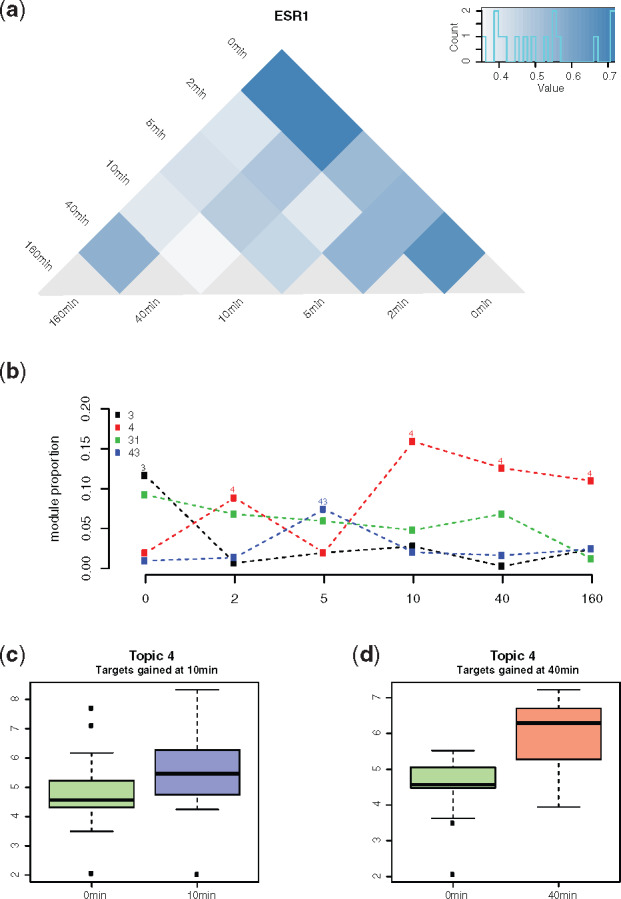
ESR1 regulation dynamics represented by topic weights. (a) Pairwise KL divergence between the topic weights of ESR1 in all time points. (b) Time-course change of the topics with the highest weights across the time points. (c) and (d) Expression of the genes gained in 10 (c) and 40 min (d), as compared to 0 min, that are among the top-ranked genes of Topic 4

The time-course pattern of the topic membership demonstrated that Topic 3 had the highest weight prior to treatment. Later, Topic 4 became the most prominent topic after a short fluctuation, which experienced a sharp increase at the 10 min time point and then underwent a gradual decrease while remaining dominant until completion (160 min) (Fig. 5b). We then studied the roles of ESR1 target genes that are related to these highly represented topics. At 0 min, true ESR1 target genes that were top-ranked in Topic 3 included genes that are most related to cell proliferation functions: ribosomal functions, protein folding and mRNA splicing (Supplementary Fig. S8). At the 10 min time point for Topic 4, top-ranked target genes included genes related to signal transduction and apoptosis, with some interacting directly with EP300. This result is consistent with a study demonstrating the redistribution of EP300 target genes after the treatment of estradiol (Guertin et al., 2014; Supplementary Fig. S8).

The treatment of estradiol turned the MCF-7 cell line’s topic from Topics 3 to 4, which indicates the top-weighted genes in Topic 4, especially for the gained genes, may play a crucial role in the treatment. We compared the nascent gene expression of 10 and 40 min with 0 min for the gained top-ranked genes in Topic 4. These gained top-ranked genes showed significant (P-value <${10}^{-5}$) upregulation in 10 and 40 min (Fig. 5c and d).

3.9 Topic activity score and its relationship to tumor survival

The topic activity score incorporates cell type-independent topic composition with cell type-specific gene expression and can be associated with clinical significance. We used patient samples of three cancer types with clinical information from The Cancer Genome Atlas (TCGA) data portal for breast cancer (BRCA), acute myeloid leukemia (LAML) and liver hepatocellular carcinoma (LIHC). We evaluated the topic activity scores for each cancer type and used them for survival analysis. We found that the activity scores of several topics were associated with patient survival (Fig. 6). For each cancer type, we characterized the biological relevance of the most predictive topic:

Fig. 6.

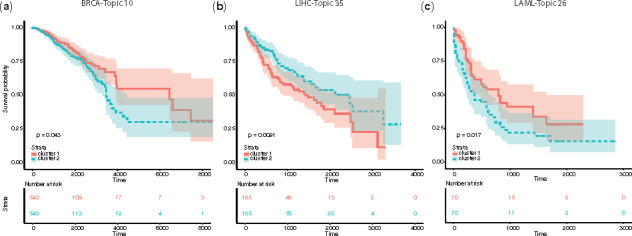
Topic activity level related to cancer survival. (a)–(c) KM survival curve of thee cancer types using their related topic activity levels: BRCA with Topic 10 (a), LIHC with Topic 35 (b) and LAML with Topic 25 (c)

1. The activity score of Topic 10 was predictive for the survival of BRCA patients (Fig. 6a). Correspondingly, Topic 10 was highly represented in the document of {GATA3, MCF-7} (Zhang et al., 2017), and its composition was enriched with the CtIP-associated gene set (Supplementary Fig. S9a). GATA3 and CtIP are known to interact with each other and functionally correlate with breast cancer: GATA3 can regulate BRCA1 (Zhang et al., 2017) and CtIP forms a repressor complex with BRCA1 whose removal accelerates tumor growth (Furuta et al., 2006) (Supplementary Fig. S10a).

2. The activity score of Topic 26 was predictive of LAML patient survival. For Topic 26, which was highly represented in the document {NR2C2, K562} (Fig. 6b and Supplementary Fig. S9b), its compositions were also enriched with genes upregulated in response to activation of the cAMP signaling pathway (van Staveren et al., 2006) (Supplementary Fig. S10b). NR2C2 can be induced by cAMP (Liu et al., 2009) and has been found to be significantly activated in almost all the cancer types (Falco et al., 2016).

3. The activity score of Topic 35 predicted survival outcome of LIHC patients with high accuracy. Topic 35 was highly represented in documents {ATF3, HepG2} and {JUN, HepG2} (Fig. 6c and Supplementary Fig. S9c), and its composition was enriched with gene sets that were upregulated in response to overexpression of the proto-oncogene MYC (Bild et al., 2006) (Supplementary Fig. S10c). Among these factors, ATF3 is a cAMP-responsive element and acts as a tumor suppressor in LIHC (Chen et al., 2018). JUN is a known oncogene and promotes liver cancer (Maeda and Karin, 2003). MYC is also a highly expressed oncogene and correlates with high proliferative activity (Zheng et al., 2017).

In summary, we found associations between the survival-related topics and their biological significance via the activity and function of the TFs that regulate these topics. These results further validate the biological relevance of the identified topics, indicating their potential as prognostic markers and sources for biomarker discovery.

4 Discussion

Rewiring analysis of the regulatory network could provide critical information about the alteration of molecular programs across conditions. Several attempts have been made to derive an effective procedure for identifying network rewiring (Assi et al., 2019; Han and Goetz, 2019; Shou et al., 2011; Xu et al., 2018). In this study, we successfully developed the TopicNet framework. Our framework extracts a low-dimensional representation of a network in the form of functional topics and defines a network rewiring score and topic-weighted activity score. We then demonstrated the application of our framework and showed that the network rewiring score can aid in the identification of the functional rewiring of TFs between cellular conditions. Moreover, the topic-weighted activity score can be applied to sample-specific cohort data for the prediction of patient survival.

To evaluate our framework, we also investigated the biological meaning of the identified topics. We interpreted the learned topics by utilizing two important matrices inferred from the model: document-topic weight and topic-gene composition matrices. The former demonstrates the activity of the topic as a distinctive functional module, and the latter indicates possible biological functions or pathways that the topic represents. Rewiring analysis using topic weights is both efficient and highly interpretable with gene topics serving as bridges between TFs and genes.

Our framework facilitates comparison between regulatory networks under different conditions from multiple sources. Thus, the analysis can be extended to various studies where network changes are of major interest. For example, time-course network changes, such as those after treatment or during the cell cycle, could help pinpoint TFs, genes and pathways that play critical roles in these processes. Having demonstrated the potential application of our method on time- course data, we expect our method to offer valuable insights into network dynamics studies in the future.

Similar to the conclusion from our comparison, LDA has been shown to be advantageous over some other common dimensional reduction techniques (e.g. NMF, SVD and pLSI) in terms of performance and interpretability (Liu et al., 2011; Stevens et al., 2012). The most advantageous feature of LDA is the control of sparsity of low-dimensional representations, which gives a robust representation for the noise reduction.

Furthermore, several extensions could be introduced for future studies. In our framework, we treated all TF–cell line pairs as independent regardless of possible relationships between cell lines and TFs. In addition, the low-dimensional gene topic defined by TopicNet is a simplified representation, which does not take into account the complex and hierarchical gene–gene interactions. These relations can be modeled by reorganizing the data into a cell–TF-target 3D tensor and training on all three dimensions simultaneously. For example, a recent study integrated the incomplete epigenome data as a cell-assay-position 3D tensor and used an artificial neural network to impute the missing data and find latent representations of the epigenome (Schreiber et al., 2019). We are aware that recent advances in topic modeling and other machine learning methods have enabled modeling of more complex dependencies and structures (Blei and Lafferty, 2006; Momeni et al., 2018; Zhou et al., 2017). Though LDA could capture some of these dependencies in an unsupervised fashion, we expect incorporation of such information would help identify even more meaningful patterns from the regulatory network.