Identifying diagnosis-specific genotype–phenotype associations via joint multitask sparse canonical correlation analysis and classification

Abstract

Motivation

Brain imaging genetics studies the complex associations between genotypic data such as single nucleotide polymorphisms (SNPs) and imaging quantitative traits (QTs). The neurodegenerative disorders usually exhibit the diversity and heterogeneity, originating from which different diagnostic groups might carry distinct imaging QTs, SNPs and their interactions. Sparse canonical correlation analysis (SCCA) is widely used to identify bi-multivariate genotype–phenotype associations. However, most existing SCCA methods are unsupervised, leading to an inability to identify diagnosis-specific genotype–phenotype associations.

Results

In this article, we propose a new joint multitask learning method, named MT–SCCALR, which absorbs the merits of both SCCA and logistic regression. MT–SCCALR learns genotype–phenotype associations of multiple tasks jointly, with each task focusing on identifying one diagnosis-specific genotype–phenotype pattern. Meanwhile, MT–SCCALR cannot only select relevant SNPs and imaging QTs for each diagnostic group alone, but also allows the selection of those shared by multiple diagnostic groups. We derive an efficient optimization algorithm whose convergence to a local optimum is guaranteed. Compared with two state-of-the-art methods, MT–SCCALR yields better or similar canonical correlation coefficients and classification performances. In addition, it owns much better discriminative canonical weight patterns of great interest than competitors. This demonstrates the power and capability of MTSCCAR in identifying diagnostically heterogeneous genotype–phenotype patterns, which would be helpful to understand the pathophysiology of brain disorders.

Availability and implementation

The software is publicly available at https://github.com/dulei323/MTSCCALR.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Alzheimer’s disease (AD) is a severe neurodegenerative disorder incurring heavy economic and emotional costs to patients and their families (Alzheimer's Association, 2013). Generally, AD, as well as other neurodegenerative and neuropsychiatric disorders, exhibits the heterogeneity and diversity (Lam et al., 2013; Wang et al., 2015), supported by mounting evidence that the sporadic AD could be multiple diseases instead of a single disease (Au et al., 2015). Therefore, uncovering the diagnosis-specific, including subgroup-specific and normal ageing-specific, genetic factors, imaging phenotypes and their interactions is an important and meaningful research topic. This could underpin AD subgroup identification, thereby help with mechanistic understanding of this neurodegenerative disorder.

Brain imaging genetics provides us a powerful opportunity to gain new in-depth insights into the genetic basis of the phenotypic characteristics of the brain (Shen and Thompson, 2020). Within this area, the genetic variations such as single nucleotide polymorphisms (SNPs) and brain imaging quantitative traits (QTs) are jointly analyzed with expectation to understand the normal and disordered brain function and behavior (Saykin et al., 2015; Shen et al., 2014).

Given a large number of SNPs and imaging QTs, the univariate methods and the regression based methods have limited capability. The univariate methods treat each marker (SNP or QT) independently and thus they inevitably overlook the relationship within SNPs and imaging QTs (Shen et al., 2010). The regression-based methods alleviate this issue by looking into multiple SNPs’ (QTs’) impact on a single imaging QT (SNP) or a few candidate imaging QTs (SNPs). Obviously, they cannot select features of interest for SNPs and imaging QTs simultaneously, which, however, is a critical issue in imaging genetics.

The above drawback can be addressed by bi-multivariate learning methods, such as sparse canonical correlation analysis (SCCA), partial least squares regression (Beaton et al., 2014) and reduced rank regression (Vounou et al., 2010). Among which SCCA and its variants become more and more popular due to its simplicity but powerful detection capability (Chen et al., 2013; Du et al., 2016, 2018, 2019a; Witten and Tibshirani, 2009). However, SCCA is unsupervised and thus the diagnosis information is usually overlooked. This might lead to discovering disease irrelevant SNP–QT associations even though the discriminative information among distinct diagnostic groups has been implied in imaging QTs. Many efforts have been made in this direction to enable supervised SCCA. For example, Yan et al. (2017) proposed discriminative SCCA (DSCCA) which considers the relationship within the same diagnostic group and that between groups. They later designed another outcome-relevant SCCA (Yan et al., 2018) to make use of the diagnosis information through regularization with the similarity matrix among subjects. Zille et al. (2018) proposed a fused method in which the diagnosis information is considered by the regression objective while the SNP–QT association is captured by the SCCA objective simultaneously. A common critical issue holding by methods above is that they find out only one feature subset in terms of SNP–QT associations for all diagnostic groups. According to the feature selection taxonomy in the machine learning community (Baggenstoss, 1999; Pineda-Bautista et al., 2011), these SCCAs fall into the traditional feature selection category, in contrast to the class-specific [or diagnosis-specific (The diagnosis-specific and class-specific are alternatively used throughout this article without distinction.)] feature selection (Pineda-Bautista et al., 2011), as they only select a single feature subset to discriminate all classes. Obviously, the identified SNP–QT associations are not diagnosis-specific. Nevertheless, identifying diagnosis-specific imaging genetic patterns could be of great interest and meaning, to which the targeted in-depth investigation, subgroup identification and personalized medication could be applied (Mukherjee et al., 2018).

On this account, the diagnosis-specific feature selection methods which select a feature subset (possibly different) for each diagnostic group (Pineda-Bautista et al., 2011) is more desirable and essential. This topic is in agreement with class-specific feature selection. For example, Wang et al. (2015) used the multitask support vector machine (SVM) to learn multiple heterogeneous classification tasks together. This method is somewhat difficult to interpret due to its nonobvious modeling strategy, and it only identifies imaging markers which is insufficient to subtype identification. The joint SCCA (JSCCA) (Fang et al., 2016) studied the imaging genetic associations within each diagnostic group via a modified multiview SCCA (mSCCA). However, its shortcoming is conspicuous as many undesirable associations could dominate the association of interest when conducting SCCA within a single diagnostic group (Lorena et al., 2008). Strictly speaking, both methods are beyond the diagnosis-specific feature selection due to their nonstandard modeling paradigm (Pineda-Bautista et al., 2011; Wang et al., 2016; Zhang and Wu, 2015). Thus, both of them are inadequate for diagnosis-specific identification. It is straightforward to employ well-studied diagnosis-specific algorithms for imaging genetics (Pineda-Bautista et al., 2011). Unfortunately, they are classification-based methods indicating that they can only identify label-relevant features. As a result, the primary mission of brain imaging genetics, i.e. identifying meaningful SNP–QT associations, is overlooked.

To address the issues above, we propose a novel multitask bi-multivariate learning method with feature selection to identify diagnosis-specific genotype–phenotype patterns for each patient group as well as normal controls. The proposed method, named MT–SCCALR, integrates multitask SCCA and multitask logistic regression (LR) in a unified model. The advantages of MT–SCCALR are fourfold. First, different to existing unsupervised and supervised SCCAs, MT–SCCALR can identify diagnosis-specific SNP–QT associations by jointly learning multiple SCCA tasks and LR tasks. The identified diagnosis-specific feature set, including SNPs and imaging QTs, is exclusively held by a specific diagnostic group. Second, better than JSCCA which incurs undesirable diagnosis-irrelevant features, MT–SCCALR follows sophisticated class-specific modeling strategy, and thus could avoid the diagnosis-irrelevant QTs, SNPs and their associations. Third, using regularization techniques, MT–SCCALR not only selects features such as SNPs and QTs for each diagnostic group, but also those that are commonly carried by all subjects, enabling a hierarchical strategy for feature selection. Fourth, an efficient iteration optimization algorithm is derived, which is demonstrated to converge to a local optimum.

To evaluate the performance of MT–SCCALR, we use four synthetic datasets with distinct characters and a real neuroimaging genetic dataset downloaded from the Alzheimer’s disease neuroimaging initiative (ADNI) database (Mueller et al., 2005). There are 755 non-Hispanic Caucasian participants with their 18-Fr florbetapir PET scans and genotyping data contained. We aim to detect the diagnosis-specific associations between these imaging QTs and SNPs. Compared with two state-of-the-art methods (Fang et al., 2016; Yan et al., 2017), the experimental results show that MT–SCCALR performs better than or similarly to benchmarks in terms of correlation coefficients and classification accuracies. Interestingly, the canonical weights reveal that our method successfully identifies QTs, SNPs and their associations being specific for each diagnostic group while those competitors cannot. In a word, the proposed integrated multitask SCCA and multitask LR offers a very promising new strategy for brain imaging genetics.

2 Materials and methods

In this article, lowercase letters denote vectors, and uppercase ones denote matrices. ${\mathbf{x}}^i$ and ${\mathbf{x}}_j$ denote the ith row and jth column of matrix $\mathbf{X}=(x_{ij})$. ${\Vert \mathbf{x}\Vert }_2$ denotes the Euclidean norm, ${\Vert \mathbf{X}\Vert }_{1,1}=\sum _i\sum _j\left|x_{ij}\right|$ denotes the element-wise ${\ell }_1$-norm, ${\Vert \mathbf{X}\Vert }_{2,1}=\sum _i{\Vert {\mathbf{x}}^i\Vert }_2$ denotes the ${\ell }_{2,1}$-norm, and ${\Vert \mathbf{X}\Vert }_{\mathrm{F}}=\sqrt{\sum _i\sum _j{x}_{ij}^2}$ denotes the Frobenius norm.

2.1 Overview

To identify diagnosis-specific features in imaging genetics, it is straightforward to train multiple classifiers independently with respect to different tasks. For example, we can build a classifier to discriminate HC from AD, and build another classifier to discriminate between MCI and AD. However, this strategy treats these tasks as independent and isolated models, hence the underlying interacting relationships among tasks might be overlooked. Another critical issue is that it is somewhat difficult to interpret the identified features as it is not a rigorous model for class-specific feature selection (Pineda-Bautista et al., 2011).

In this article, we formally define the diagnosis-specific feature selection model for imaging genetics following the strategy in traditional feature selection community (Pineda-Bautista et al., 2011; Zhang and Wu, 2015). Figure 1 presents the framework of the diagnosis-specific feature selection workflow. First, the whole target population is divided into different groups such as healthy control (HC), mild cognitive impairment (MCI) and AD. If possible, the AD patients can be further split into AD subgroups, e.g. the typical, limbic-predominant, or hippocampal-sparing groups (Ferreira et al., 2017). Second, the class binarization is applied to construct multiple classification tasks via the one-versus-all [OVA, or one-against-all (OAA)] decomposition strategy. The OVA has shown, in general, good performance for all datasets (Lorena et al., 2008). In particular, each task in our method is to classify a specific diagnostic group out of those subjects not in this group, e.g. HC versus non-HC or MCI versus non-MCI. This is of great importance and meaning as doing this is helpful to understand the in-depth and unique characters for the diagnostic group of interest, making personalized clinical diagnosis and treatment possible. Besides, if necessary, the class balancing techniques such as oversampling will be used to overcome the class imbalance issue (Pineda-Bautista et al., 2011). Third, the novel heterogeneous multitask method, i.e. the joint multitask SCCA and multitask LR, is proposed to simultaneously and systematically considering the different diagnostic groups’ relatedness. The SCCA objective is used to learn the association between QTs and SNPs, and the LR objective is used to learn discriminating features. In addition, the class-specific as well as class-consistent characteristics of both imaging QTs and SNPs are also considered by newly designed penalties. Finally, we obtain the dementia-related, including both MCI and AD, and the normal ageing-related imaging QTs and SNPs. These diagnosis-specific feature sets would be of more interest than a single set for all diagnosis groups.

Fig. 1.

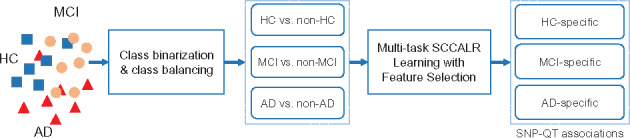
Framework of diagnosis-specific imaging genetic pattern identification with three diagnostic groups: HC, MCI and AD. There certainly can be more than three diagnostic groups

The class binarization and class balancing are easy to implement (Pineda-Bautista et al., 2011). Thus we focus on discussing the MT–SCCALR algorithm which is also the major contribution of this study.

2.2 The diagnosis-specific feature selection model for imaging genetics

MT–SCCALR is a heterogeneous multitask method with class-specific feature selection which fuses the bi-multivariate (SCCA) associations identification and classification (multiclass LR). Suppose we are given n participants with p SNPs and q imaging QTs from C diagnostic groups, we then use ${\mathbf{X}}_c\in {\mathbb{R}}^{n\times p}$ to load the genetic data, ${\mathbf{Y}}_c\in {\mathbb{R}}^{n\times q}$ to collect the imaging QT data and ${\mathbf{z}}^l\in {\mathbb{R}}^{1\times C}$ to collect the diagnostic label vector of subject l. Generally, in ${\mathbf{z}}^l$, only one element is one and others are zeros. Then we directly learn two canonical weight matrices as $\mathbf{U}=\left[\begin{array}{ccc}{u}_{11}& \cdots & u_{1C}\\ \cdots & \cdots & \cdots \\ u_{p1}& \cdots & u_{pC}\end{array}\right]\in {\mathbb{R}}^{p\times C}$, and $\mathbf{V}=\left[\begin{array}{ccc}{v}_{11}& \cdots & v_{1C}\\ \cdots & \cdots & \cdots \\ v_{q1}& \cdots & v_{qC}\end{array}\right]\in {\mathbb{R}}^{q\times C}$, where u_ic is the weight of the ith SNP for the cth task, and v_jc is the weight of the jth imaging QT for the cth task. Obviously, these two canonical weight matrices can capture the local feature importance for both SNPs and imaging QTs with respect to each class, indicating their class-specific influence. In contrast, the traditional SCCA learns a canonical weight vector for SNPs and QTs, resulting in inability to select diagnosis-specific features. To identify the class-specific features and account for their interrelationships, we fuse the LR objective and the SCCA objective, i.e.

$$\underset{\mathbf{U},\mathbf{V}}{\min }{\mathcal{L}}_{\text{LR}}(\mathbf{V})+{\mathcal{L}}_{\text{SCCA}}(\mathbf{U},\mathbf{V}).$$ (1)

In this model, ${\mathcal{L}}_{\text{LR}}$ identifies the discriminating imaging QTs by conducting multitask classification for C tasks. After that, ${\mathcal{L}}_{\text{SCCA}}$ jointly learns the bi-multivariate associations between imaging QTs and SNPs for multiple tasks. It is worth mentioning that we do not include the logistic term between SNPs and the class label as associations between QTs and SNPs will finally encourage the identified SNPs being discriminating. This is reasonable and will make our model concise.

The model above encounters severe overfitting problem as generally the number of SNPs or imaging QTs is much larger than the sample size. Therefore, the sparsity regularization technique is utilized. On this account, our MT–SCCALR model becomes

$$\underset{\mathbf{U},\mathbf{V}}{\min }{\mathcal{L}}_{\text{LR}}(\mathbf{V})+{\mathcal{L}}_{\text{SCCA}}(\mathbf{U},\mathbf{V})+\Omega (\mathbf{U})+\Omega (\mathbf{V}).$$ (2)

The $\Omega (\mathbf{U})$ is the sparsity-inducing penalty to identify those SNPs of interest, and $\Omega (\mathbf{V})$ is to identify relevant imaging QTs. In this class-specific multitask model, $\Omega (\mathbf{U})$ and $\Omega (\mathbf{V})$ are designed to incorporate three types of regularization methods for feature selection, i.e. the class-consistent sparsity, the class-specific sparsity in terms of selecting features jointly and individually for SNPs and imaging QTs.

To sum up, the multitask SCCA term captures the SNP–QT associations. The LR term captures the QT–diagnosis relationship. The sparsity-inducing terms help select relevant QTs and SNPs holding by a specific diagnosis group while accounting for those shared by multiple groups. Therefore, this novel fusion model is endowed with a diverse feature selection, especially the interesting class-specific feature selection. Next, we will present each term of MT–SCCALR in details.

2.3 The OVA multiclass classification via the LR

The LR is a popular classification method due to its simplicity but efficiency. In the proposed model, we regress the class label on imaging QTs by the LR objective to learn their associations. In the multiclass setting, we train multiple binary classifiers by the multitask modeling, i.e.

$${\mathcal{L}}_{\text{LR}}(\mathbf{V})=\sum _{c=1}^C\frac{1}{n_c}\sum _{l=1}^{n_c}\hspace{0.17em}[\text{log}(1+e^{{\mathbf{y}}_c^l{\mathbf{v}}_c})-z_{lc}{\mathbf{y}}_c^l{\mathbf{v}}_c],$$ (3)

where n_c is the sample size for each classification task. n_c’s could be equal without class balancing or unequal after class balancing. z_lc is the corresponding class label of the lth subject for the cth task, and ${\mathbf{y}}_c^l$ is the data vector of the lth subject for the cth task. This objective is usually called the negative log-likelihood and is convex (Zaidi and Webb, 2017).

2.4 The bi-multivariate association identification via the multitask SCCA

Conventional SCCA cannot identify class-specific SNP–QT associations as it only learns a single feature subset for all classes. The multitask SCCA (Du et al., 2019b) systematically considers the relatedness among multiple SCCA tasks and thus can be applied to handle class-specific SNP–QT associations identification. Denoting data matrices with respect to the cth SCCA task as ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$, the multitask SCCA is defined as

$$\begin{array}{c}\underset{{\mathbf{u}}_c,{\mathbf{v}}_c}{\min }\sum _{c=1}^C-{\mathbf{u}}_c^{\top }{\mathbf{X}}_c^{\top }{\mathbf{Y}}_c{\mathbf{v}}_c\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \mathrm{s}.\mathrm{t}. {\Vert {\mathbf{X}}_c{\mathbf{u}}_c\Vert }_2^{\mathrm{2}}=1,{\Vert {\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}=1, \forall c.\end{array}$$ (4)

According to (Du et al., 2019b), this equation can be equivalently rewritten as

$$\begin{array}{c}\underset{{\mathbf{u}}_c,{\mathbf{v}}_c}{\min }\sum _{c=1}^C{\Vert {\mathbf{X}}_c{\mathbf{u}}_c-{\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\\ \mathrm{s}.\mathrm{t}. {\Vert {\mathbf{X}}_c{\mathbf{u}}_c\Vert }_2^{\mathrm{2}}=1,{\Vert {\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}=1, \forall c.\end{array}$$ (5)

based on $\forall c,\hspace{0.17em}{\Vert {\mathbf{X}}_c{\mathbf{u}}_c\Vert }_2^{\mathrm{2}}=1$ and ${\Vert {\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}=1$.

This objective jointly learns bi-multivariate associations and thus, in general, outperforms conventional SCCAs (Du et al., 2019b). It is worth noting that in this model, ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$ correspond to the whole population but not only subjects in the cth class. For example, suppose the cth task is MCI versus non-MCI as shown in Figure 1, ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$ contain all subjects other than only MCI subjects. On the contrary, in JSCCA model, both ${\mathbf{X}}_c$ and ${\mathbf{Y}}_c$ come from only the MCI group (Fang et al., 2016). As we analyzed earlier, features identified by our model possess stronger discriminating ability than that of JSCCA whose might be out of interest.

2.4.1. Regularization for imaging QTs via class-consistent and class-specific sparsity

The brain disorder such as AD usually exhibits the heterogeneity for multiple diagnostic groups (Lam et al., 2013; Wang et al., 2015). This diversity and complexity raise three critical questions. First, an imaging QT could present similar degenerative pattern among all diagnostic groups, because that both dementia brain and normal ageing brain suffer from functional and structural degeneration. Second, more commonly, an imaging QT probably exhibits diverse and different degenerative patterns across multiple diagnostic groups. The hippocampal-sparing AD patients show similar atrophy to normal aging in hippocampus (Murray and Dickson, 2008), while typical AD patients suffer from pronouncedly severer hippocampus atrophy compared to normal ageing subjects. The last but not the least, the network or graph structure has been clearly observed by autopsy or noninvasive imaging techniques (Bullmore and Sporns, 2009). Thus, a damage to the network structure might be a sign of dementia. On the contrary, this implies that an intact network might only exist in normal ageing subjects but not AD patients.

Therefore, to consider the complexity of brain disorders, we defined $\Omega (\mathbf{V})$ as follows

$$\Omega \left(\mathbf{V}\right)={\lambda }_{v1}{\Vert \mathbf{V}\Vert }_{2,1}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{1,1}+{\lambda }_{v3}\sum _{c=1}^C{\Vert {\mathbf{v}}_c\Vert }_{\mathit{GGL}},$$ (6)

where ${\lambda }_{v1},\hspace{0.17em}{\lambda }_{v2}$ and ${\lambda }_{v3}$ are nonnegative parameters and can be obtained by cross-validation or holdout.

The first term is the ${\ell }_{2,1}$-norm which is defined as follows

$${\Vert \mathbf{V}\Vert }_{2,1}=\sum _{j=1}^q{\Vert {\mathbf{v}}^j\Vert }_2=\sum _{j=1}^q\sqrt{\sum _{c=1}^C{v}_{jc}^2}.$$ (7)

This penalty encourages the task-consistent sparsity, indicating that elements of vector ${\mathbf{v}}^j(j=1,\dots ,q)$ will be zeros or nonzeros simultaneously. As a result, an imaging QT presenting similar degenerative pattern for all groups will be selected or discarded jointly. Using this penalty is more practical since by finding out QTs shared among multiple diagnostic groups, the identified class-specific QTs could be more helpful.

The second regularizer is the ${\ell }_{1,1}$-norm (${\ell }_1$-norm for matrices) which is defined as

$${\Vert \mathbf{V}\Vert }_{1,1}=\sum _{j=1}^q{\Vert {\mathbf{v}}^j\Vert }_1=\sum _{j=1}^q\sum _{c=1}^C \left|v_{jc}\right|$$ (8)

This ${\ell }_{1,1}$-norm penalty first prompts the individual sparsity for an imaging QT across all classes, and then prompts the sparsity for all imaging QTs. This is important and meaningful as it cannot only select relevant imaging QTs, but also determinate whether an imaging QT is relevant for a specific class. Similar to ${\ell }_1$-norm, although ${\ell }_{1,1}$-norm is nonsmooth, it is convex and thus is easy to optimize.

The third term is the graph-guided pairwise group Lasso (GGL) (Du et al., 2017, 2020) whose definition is

$${\Vert {\mathbf{v}}_c\Vert }_{\mathit{GGL}}=\sum _{(j,k)\in E}\sqrt{v_{jc}^2+v_{kc}^2},$$ (9)

where E is the edge set of the graph in which those highly correlated nodes are connected. Given the network structure of the brain (knowledge-guided), or considering the brain as a completed graph (data-driven), this penalty captures the high-level structure information among imaging QTs. As shown in Du et al. (2017, 2020), it holds the capability to assign similar weights for highly correlated imaging QTs, and thus can help identify the network structure. Moreover, using this penalty within each diagnostic group, we could capture the network holding by a specific group alone. Finally, the GGL penalty is convex, indicating that it can be easily solved.

In summary, combining these three regularizers together can well address three questions raised at the beginning of this subsection. On this account, plugging $\Omega (\mathbf{V})$ into MT–SCCALR will make it a more reasonable model, and thus yield class-consistent and class-specific feature subsets of interest.

2.4.2. Regularization for SNPs via class-consistent and class-specific sparsity

Once those relevant imaging QTs, including both class-consistent and class-specific ones, are correctly identified, they could guide us to identify those class-consistent and class-specific SNPs as well. It is well known that SNPs usually affect the brain structure and function at both group level [linkage disequilibrium (LD) structure (Reich et al., 2001)] and individual level. In particular, at the individual level, a SNP could affect normal ageing brain and dementia brain at the same time, while another SNP might only influence the dementia one. This requires both class-consistent and class-specific feature selection for an individual SNP. In addition, at the group level, SNPs within the same LD or gene might jointly affect the brain structure and function (Wang et al., 2012b). An important thing is that, the genetic variation might happen to patients but not HCs, resulting in that an LD structure could only exist in healthy subjects. For this reason, we define the $\Omega \left(\mathbf{U}\right)$ as

$$\Omega \left(\mathbf{U}\right)={\lambda }_{u1}{\Vert \mathbf{U}\Vert }_{2,1}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{1,1}+{\lambda }_{u3}\sum _{c=1}^C{\Vert {\mathbf{u}}_c\Vert }_{\mathit{FGL}},$$ (10)

with ${\lambda }_{u1},\hspace{0.17em}{\lambda }_{u2}$ and ${\lambda }_{u3}$ being nonnegative tuning parameters. Both ${\ell }_{2,1}$-norm and ${\ell }_{1,1}$-norm are the same to that in Eqs. (7–8). They encourage class-consistent and class-specific feature selection for a single SNP.

In addition, the third term in Eq. (10) is the fused pairwise group Lasso (FGL) imposed on each ${\mathbf{u}}_c$ (Du et al., 2020), i.e.

$${\Vert {\mathbf{u}}_c\Vert }_{\mathit{FGL}}=\sum _{i=1}^{p-1}\sqrt{u_{ic}^2+u_{(i+1)c}^2},$$ (11)

This penalty endows the model with a chain of smoothness across all elements of ${\mathbf{u}}_c$, encouraging the selection of two adjacent and strongly correlated variables (Du et al., 2020). This penalty shows clearly grouping effects and thus could be used to automatically identify group structures. This plays a key role in our model as it considers the feature selection at a higher level. In this article, we use this penalty within each diagnostic group via the data-driven setup with expectation to identify the group structure that only exists in a specific group.

2.5 The optimization and convergence

Now we explicitly write both objectives and penalties with respect to imaging phenotypes and genotypes,

$$\begin{array}{c}\underset{\mathbf{U},\mathbf{V}}{\min }\sum _{c=1}^C\frac{1}{n_c}\sum _{l=1}^{n_c}\hspace{0.17em}[\text{log}(1+e^{{\mathbf{y}}_c^l{\mathbf{v}}_c})-z_{lc}{\mathbf{y}}_c^l{\mathbf{v}}_c]+\sum _{c=1}^C{\Vert {\mathbf{X}}_c{\mathbf{u}}_c-{\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}\\ +{\lambda }_{v1}{\Vert \mathbf{V}\Vert }_{2,1}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{1,1}+{\lambda }_{v3}\sum _{c=1}^C{\Vert \mathbf{v}}_c\Vert {}_{\mathit{GGL}}\\ +{\lambda }_{u1}{\Vert \mathbf{U}\Vert }_{2,1}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{1,1}+{\lambda }_{u3}\sum _{c=1}^C{\Vert \mathbf{u}}_c\Vert {}_{\mathit{FGL}}\\ \mathrm{s}.\mathrm{t}. {\Vert {\mathbf{X}}_c{\mathbf{u}}_c\Vert }_2^{\mathrm{2}}=1, {\Vert {\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}=1, \forall c.\end{array}$$ (12)

Mathematically, Eq. (12) is neither convex nor smooth. To handle this issue, by replacing ${\Vert {\mathbf{X}}_c{\mathbf{u}}_c\Vert }_2^{\mathrm{2}}=1$ with ${\Vert {\mathbf{X}}_c{\mathbf{u}}_c\Vert }_2^{\mathrm{2}}\le 1$ and ${\Vert {\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}=1$ with ${\Vert {\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}\le 1$, we analyze that Eq. (12) is convex if we consider V as a constant, and vice versa. Fortunately, this biconvexity has been well studied previously (Gorski et al., 2007), based on which we can solve U and V alternatively after smoothing those nonsmooth penalties such as $\Omega (\mathbf{U})$ and $\Omega (\mathbf{V})$.

2.5.1. The solution to V

First, we fix U to solve V. The Lagrangian of Eq. (12) with respect to V can be simplified as

$$\begin{array}{c}\sum _{c=1}^C\frac{1}{n_c}\sum _{l=1}^{n_c}\hspace{0.17em}[\text{log}(1+e^{{\mathbf{y}}_c^l{\mathbf{v}}_c})-z_{lc}{\mathbf{y}}_c^l{\mathbf{v}}_c]+\sum _{c=1}^C{\Vert {\mathbf{X}}_c{\mathbf{u}}_c-{\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}\\ +{\lambda }_{v1}{\Vert \mathbf{V}\Vert }_{2,1}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{1,1}+{\lambda }_{v3}\sum _{c=1}^C{\Vert \mathbf{v}}_c\Vert {}_{\mathit{GGL}}+{\gamma }_v\sum _{c=1}^C{\Vert {\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}\end{array}$$ (13)

by discarding those constants.

Using the subgradient of these penalties, we can obtain the derivative of Eq. (13) with respect to each ${\mathbf{v}}_c$. Letting it be zero yields [When ${\Vert {\mathbf{v}}^j\Vert }_2=0$, we regularize the jth diagonal element of ${\tilde{\mathbf{D}}}_1$ as $\frac{1}{2{\Vert {\mathbf{v}}^j+\xi \Vert }_2}$, where ξ is a very small positive value. ${\overline{\mathbf{D}}}_1$ and ${\mathbf{D}}_1$ can be regularized similarly. It is easy to prove that when $\xi \to 0$, the regularized problem is equivalent to problem Eq. (13).]

$$\begin{array}{c}\frac{\partial {\mathcal{L}}_{LR}(\mathbf{V})}{\partial {\mathbf{v}}_c}-2{\mathbf{Y}}_c^{\top }{\mathbf{X}}_c{\mathbf{u}}_c+2{\lambda }_{v1}{\tilde{\mathbf{D}}}_1{\mathbf{v}}_c+2{\lambda }_{v2}{\overline{\mathbf{D}}}_1{\mathbf{v}}_c+2{\lambda }_{v3}{\mathbf{D}}_1{\mathbf{v}}_c\\ +2({\gamma }_v+1){\mathbf{Y}}_c^{\top }{\mathbf{Y}}_c{\mathbf{v}}_c=0,\end{array}$$ (14)

where ${\tilde{\mathbf{D}}}_1$ is a diagonal matrix with the jth element being $\frac{1}{2{\Vert {\mathbf{v}}^j\Vert }_2}(j=1,\dots ,q)$, and ${\overline{\mathbf{D}}}_1$ is a diagonal matrix where the jth element is $\frac{1}{2{\Vert v_{jc}\Vert }_2}$$(j=1,\dots ,q; \text{and} \mathrm{c}=1,\dots ,\mathrm{C})$. ${\mathbf{D}}_1$ is also a diagonal matrix with its jth element being $\sum _{j,(j,k)\in E}\frac{1}{2\sqrt{v_{jc}^2+v_{kc}^2}}$$(j=1,\dots ,q;k=1,\dots ,q; \text{and} \mathrm{c}=1,\dots ,\mathrm{C})$ (Du et al., 2017). Obviously, ${\tilde{\mathbf{D}}}_1,\hspace{0.17em}{\overline{\mathbf{D}}}_1$ and ${\mathbf{D}}_1$ depend on the independent variable V, and thus they are unknown. On this account, the iterative algorithm can be a solver which first guesses an initial value of V, and then calculates these diagonal matrices.

Once ${\tilde{\mathbf{D}}}_1,\hspace{0.17em}{\overline{\mathbf{D}}}_1$ and ${\mathbf{D}}_1$ are available, we can solve Eq. (14) correspondingly. However, we cannot find a closed-form solution due to the nontrivial derivative of the logistic term. Thus we address this using the Newton’s method which depends on the Hessian matrix. Based on this, solving Eq. (14) is equivalent to solve

$$\begin{array}{c}\underset{\mathbf{V}}{\min }{\mathcal{L}}_{LR}(\mathbf{V})+\sum _{c=1}^C{\Vert {\mathbf{X}}_c{\mathbf{u}}_c-{\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}+{\lambda }_{v1}Tr({\mathbf{V}}^{\top }{\tilde{\mathbf{D}}}_1\mathbf{V})\\ +{\lambda }_{v2}Tr({\mathbf{V}}^{\top }{\overline{\mathbf{D}}}_1\mathbf{V})+{\lambda }_{v3}Tr({\mathbf{V}}^{\top }{\mathbf{D}}_1\mathbf{V})+{\gamma }_v\sum _{c=1}^C{\mathbf{v}}_c^{\top }{\mathbf{Y}}_c^{\top }{\mathbf{Y}}_c{\mathbf{v}}_c.\end{array}$$ (15)

According to Krishnapuram et al. (2005) and Lee et al. (2006), we first obtain the first-order derivative of the logistic objective with respect to each v_jc

$$\frac{\partial {\mathcal{L}}_{LR}(\mathbf{V})}{\partial v_{jc}}=\frac{1}{n_c}\sum _{l=1}^{n_c}(P(z_{lc}=1|{\mathbf{y}}_c^l)-z_{lc})y_{lj,c},$$ (16)

where $P(z_{lc}=1|{\mathbf{y}}_c^l)$ is the class posterior probability (Zaidi and Webb, 2017). Here we use $y_{lj,c}$ denote the lth row and jth column element of matrix ${\mathbf{Y}}_c$.

Then we can calculate the second-order derivative based on Eq. (16),

$$\frac{\partial {\mathcal{L}}_{LR}(\mathbf{V})}{\partial v_{jc}\partial v_{kc}}=\frac{1}{n_c}\sum _{l=1}^{n_c}(1-P(z_{lc}=1|{\mathbf{y}}_c^l))P(z_{lc}=1|{\mathbf{y}}_c^l)y_{lj,c}{y}_{lk,c}.$$ (17)

After both the first-order and second-order derivatives have been obtained, we can easily calculate the gradient (or subgradient) vector $\mathbf{g}({\mathbf{v}}_c)$ and the Hessian matrix $\mathbf{H}({\mathbf{v}}_c)$ of Eq. (15) regarding ${\mathbf{v}}_c$. Therefore, the solution to each ${\mathbf{v}}_c$ can be finally attained via

$${\mathbf{v}}_c={\mathbf{v}}_c-{\mathbf{H}}^{-1}({\mathbf{v}}_c)\mathbf{g}({\mathbf{v}}_c).$$ (18)

2.5.2. The solution to U

Given V, the solution to U can be attained as well. First, we write the Lagrangian of Eq. (12) with U being unknown variable,

$$\begin{array}{c}\sum _{c=1}^C{\Vert {\mathbf{X}}_c{\mathbf{u}}_c-{\mathbf{Y}}_c{\mathbf{v}}_c\Vert }_2^{\mathrm{2}}\\ +{\lambda }_{u1}{\Vert \mathbf{U}\Vert }_{2,1}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{1,1}+{\lambda }_{u3}\sum _{c=1}^C{\Vert {\mathbf{u}}_c\Vert }_{\mathit{FGL}}+{\gamma }_u{\Vert {\mathbf{X}}_c{\mathbf{u}}_c\Vert }_2^{\mathrm{2}}\end{array}$$ (19)

where those constants are discarded. If we treat $\mathbb{Y}=[{\mathbf{Y}}_1{\mathbf{v}}_1,\dots ,{\mathbf{Y}}_c{\mathbf{v}}_c]$ as dependent variables and ${\mathbf{X}}_c$’s as independent variables, this equation becomes a multiregression task learning method with class-consistent and class-specific feature selection. To solve this multitask problem, we take its derivative with respect to ${\mathbf{u}}_c$ and set it to zero, i.e.

$$-{\mathbf{X}}_c^{\top }{\mathbf{Y}}_c{\mathbf{v}}_c+{\lambda }_{u1}{\tilde{\mathbf{D}}}_2{\mathbf{u}}_c+{\lambda }_{u2}{\overline{\mathbf{D}}}_2{\mathbf{u}}_c+{\lambda }_{u3}{\mathbf{D}}_2{\mathbf{u}}_c+({\gamma }_u+1){\mathbf{X}}_c^{\top }{\mathbf{X}}_c{\mathbf{u}}_c=0.$$ (20)

Similarly to solving V, ${\tilde{\mathbf{D}}}_2$ here is a diagonal matrix whose ith element is $\frac{1}{2\Vert {\mathbf{u}}^i{�}_2}(i=1\cdots ,p)$, and ${\overline{\mathbf{D}}}_2$ is a diagonal matrix with the ith element being $\frac{1}{2{\Vert u_{ic}\Vert }_2}$$(i=1,\dots ,p; \text{and} \mathrm{c}=1,\dots ,\mathrm{C})$. Finally, ${\mathbf{D}}_2$ is a diagonal matrix whose ith diagonal entry is $\frac{1}{2\sqrt{u_{(i-1)c}^2+u_{ic}^2}}+\frac{1}{2\sqrt{u_{ic}^2+u_{(i+1)c}^2}}$$(i=1,\dots ,p; \text{and} \mathrm{c}=1,\dots ,\mathrm{C})$ [The first element of ${\mathbf{D}}_2$ is $\frac{1}{2\sqrt{u_{1c}^2+u_{2c}^2}}$, and the pth element is $\frac{1}{2\sqrt{u_{(p-1)c}^2+u_{pc}^2}}$. See Du et al. (2020) for details.].

Using the iteration algorithm, we can obtain the closed-form equation regarding each ${\mathbf{u}}_c$, i.e.

$${\mathbf{u}}_c={({\lambda }_{u1}{\tilde{\mathbf{D}}}_2+{\lambda }_{u2}{\overline{\mathbf{D}}}_2+{\lambda }_{u3}{\mathbf{D}}_2+({\gamma }_u+1){\mathbf{X}}_c^{\top }{\mathbf{X}}_c)}^{-1}{\mathbf{X}}_c^{\top }{\mathbf{Y}}_c{\mathbf{v}}_c.$$ (21)

Now we have the building blocks for optimizing Eq. (12). The final solution can be attained via iteratively and alternatively optimizing V and U. The pseudocode is presented in Algorithm 1 which is guaranteed to converge to a local optimum. In this algorithm, Steps 1 and 5 are easily and very fast to calculate. Step 3 involves computing the Hessian matrix which can be obtained efficiently based on (Lin et al., 2007). At last, Steps 4 and 6 can be attained by efficiently solving a system of linear equations (Wang et al., 2012a,b).

Algorithm 1.

The MT-SCCALR algorithm

Require:

 The genotype data $\mathbf{X}\in {\mathbb{R}}^{n\times p}$ and imaging phenotype data $\mathbf{Y}\in {\mathbb{R}}^{n\times q}$ of C diagnostic groups. The pre-tuned ${\lambda }_{v1},\hspace{0.17em}{\lambda }_{v2},\hspace{0.17em}{\lambda }_{v3}$, γ_v, ${\lambda }_{u1},\hspace{0.17em}{\lambda }_{u2},\hspace{0.17em}{\lambda }_{u3}$, and γ_u.

Ensure:

 Canonical weights V and U.

1: Class binarization and class balancing, initialize $\mathbf{U}\in {\mathbb{R}}^{p\times C}$ and $\mathbf{V}\in {\mathbb{R}}^{q\times C}$;

2: while not convergence do

3:  Calculate the first-order and second-order derivatives of Eq. (15);

4:  Solve ${\mathbf{v}}_c$ according to Eq. (18), and scale ${\mathbf{v}}_c$ so that $\Vert {\mathbf{Y}}_c{\mathbf{v}}_c{\Vert }_2^{\mathrm{2}}=1$;

5:  Update ${\tilde{\mathbf{D}}}_2,\hspace{0.17em}{\overline{\mathbf{D}}}_2$ and ${\mathbf{D}}_2$;

6:  Solve ${\mathbf{u}}_c$ according to Eq. (21), and scale ${\mathbf{u}}_c$ as that $\Vert {\mathbf{X}}_c{\mathbf{u}}_c{\Vert }_2^{\mathrm{2}}=1$;

7: end while

8: Sorting each ${\mathbf{u}}_c$ and ${\mathbf{v}}_c$ in descending order based on their absolute value respectively.

2.5.3. Convergence analysis

We have the following theorem for the MT–SCCALR Algorithm.

Theorem 1. The Algorithm 1 decreases the objective in each iteration.

The proof is contained in Supplementary Material due to space limitation. We have known that MT–SCCALR is biconvex, and obviously, Eq. (12) has the lower bound of zero, hence a local optimum can be attained finally by running Algorithm 1. To ensure efficiency, we stop our algorithm when both ${\max }_i{\max }_c\left|\widehat{\mathbf{U}}-\mathbf{U}\right|\le ϵ$ and ${\max }_j{\max }_c\left|\widehat{\mathbf{V}}-\mathbf{V}\right|\le ϵ$ hold. In addition, we empirically set the tolerance error $ϵ={10}^{-5}$ in this article for all experiments, and certainly, ϵ can be obtained based on experiments.

3 Experimental results and discussions

3.1 Experimental design

We compared our method with two most related SCCA method, i.e. the discriminate SCCA (DSCCA) (Yan et al., 2017) and the JSCCA (Fang et al., 2016), which directly identify imaging QTs and SNPs with discriminating ability. DSCCA extended the traditional SCCA by the locality preserving projection penalty. Its identified imaging QTs and proteomic markers can successfully discriminate between every two diagnostic groups such as HC versus AD. JSCCA was a type of mSCCA (Witten and Tibshirani, 2009) which learns the association between QTs and SNPs within the same diagnostic group. Therefore, using DSCCA and JSCCA as benchmarks, our approach was compared with the state-of-the-art discriminating SCCA method, assuring a practical and meaningful performance evaluation. Of note, our primary aim in this study was to identify meaningful diagnosis-specific features other than just classification. Thus we did not compare to methods which use one versus one classification or a nonobvious modeling strategy (Wang et al., 2015).

To find out suitable parameters, we used the fivefold cross-validation strategy to fine-tune them. Generally, we set parameters to those which generate the highest testing canonical correlation coefficients (CCC) and classification accuracy. There were in total eight parameters in the original model which was time intensive. To alleviate this issue for both MT–SCCALR and benchmarks, we fixed ${\gamma }_v=1$ and ${\gamma }_u=1$ because that they mainly affect the amplitude of U and V (Chen and Liu, 2012). In addition, we also used several heuristic rules to further reduce the time effort. Specifically, if we prefer the class-specific feature selection as in this study, we could use large parameters for ${\ell }_{1,1}$-norm, FGL-norm and GGL-norm. On the contrary, we might sometimes desire for the class-consistent feature selection, and then we could set large parameters for the ${\ell }_{2,1}$-norm. This could yield reasonable results as only focusing on the CCC might lead to undesirable features. Besides, we used a two-stage tuning procedure which first tuned parameters from ${10}^i$ ($i=-2,-1,0,1,2$) with a large interval, and then further tuned them from a relative smaller interval $\Gamma \pm [0.1,0.2,\dots ,\dots ,1]$, where Γ was the optimal parameters obtained from the first stage. Usually, this two-stage parameter tuning could yield better performance, compared to blindly grid search, for both correlation coefficients and feature selection. In experiments, we only tuned parameters in the first loop where the first fold was used for testing and the remaining folds were used for training, and these tuned parameters were used for all experiments to generate final results. According to experiments, this setup will not affect the performance significantly and could reduce the time consumption significantly. All methods used the same experimental setup to assure a fair comparison.

3.2 Simulation study

We generated four simulation datasets based on different ground truths to make a thorough comparison. We assumed three groups of imaging data Y and genotype data X. The first two datasets (n = 100, p = 120 and q = 150) contained the same true signal but different noise levels. The third dataset (n = 100, p = 120 and q = 150) mainly simulated a task-specific situation while the fourth one (n = 200, p = 400 and q = 300) primarily simulated a task-consistent situation. Specifically, in the fourth dataset, there was a successive relationship among classes to simulate the relationship between HC and MCI, and that between MCI and AD. All four datasets are generated as follows. First, we created two sparse matrices $\mathbf{U}\in {\mathcal{R}}^{p\times C}$ and $\mathbf{V}\in {\mathcal{R}}^{q\times C}$. Within both U and V, there are features shared by all tasks and specifically hold by a single task. We then generated a latent vector $\mathbf{z}\in {\mathcal{R}}^{n\times 1}$, based on which we generated three pairs of ${\mathbf{X}}_c\sim N(z_i{\mathbf{u}}_c,{\mathbf{I}}_{p\times p})$ and ${\mathbf{Y}}_c\sim N(z_i{\mathbf{v}}_c,{\mathbf{I}}_{q\times q})$ to form three diagnostic groups. We showed the ground truth in Figure 2 (top row).

Fig. 2.

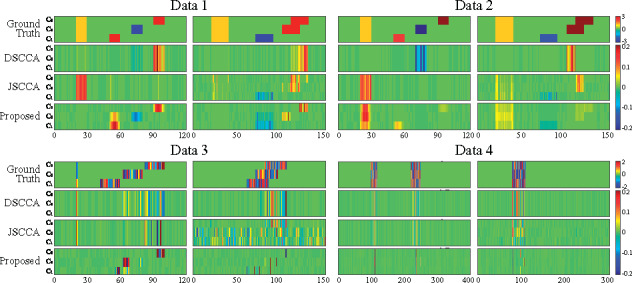
Canonical weights on synthetic data. Row 1–4: Ground truth, DSCCA, JSCCA and MT–SCCALR respectively. For each data, canonical weights U is shown on the left, and V is shown on the right. In each panel, there are three rows (each row contains fivefold canonical weights) corresponding to three tasks

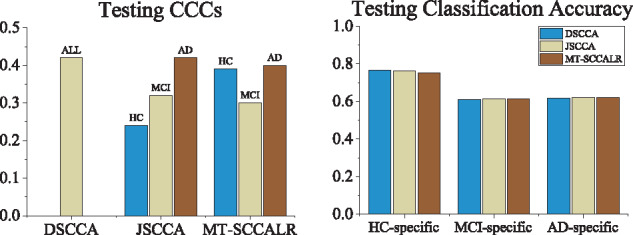
As we mainly focus on the identified class-specific features, in Figure 2, we first showed the heatmaps of canonical weights which indicate the importance of features. DSCCA identified one canonical weight vector for all classes, and then we stacked it for C times to make its heatmap available. JSCCA generated one canonical weight vector for u and C canonical weight vectors for V, and thus we only stacked u for C times. In this figure, the features identified by MT–SCCALR were consistent to the ground truth, while DSCCA cannot. JSCCA performed slightly better than DSCCA, and they both had little capability in identifying class-specific features. From Data 4, we observed that if there were no class-specific features, all three methods could find out these class-consistent features. These results demonstrated that MT–SCCALR had more diverse feature selection ability than DSCCA and JSCCA. In Figure 3, we showed the testing CCCs and testing classification accuracies which were obtained by SVM based on LIBSVM (https://www.csie.ntu.edu.tw/∼cjlin/libsvm/) software package. The CCCs and classification performance showed no significant difference between MT–SCCALR and DSCCA, and they both performed better than JSCCA, especially on the CCCs. This demonstrated that MT–SCCALR had similar CCCs and classification performance to benchmarks, but identified much better class-specific features while those benchmarks cannot.

Fig. 3.

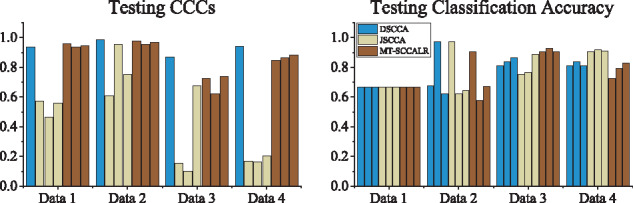
Comparison of the mean CCCs and classification accuracy obtained from fivefold testing trials on synthetic data

3.3 Real neuroimaging genetic study

The real brain imaging and genotyping data were obtained from the ADNI (adni.loni.usc.edu) database. The primary goal of the initiative is to test whether serial magnetic resonance imaging (MRI), or other biological markers, and clinical and neuropsychological assessments can be combined to measure the progression of MCI and early AD. For up-to-date information, see www.adni-info.org.

There are 755 non-Hispanic Caucasian participants, including 182 HC, 292 MCI and 281 AD, whose baseline 18-Fr florbetapir PET scans were collected. We used the pipeline to preprocess these PET scans such as average, alignment, resample, smoothness and normalization to obtain the standardized uptake value ratio (SUVR) images (Jagust et al., 2010). To reduce the time consumption and boost the statistical power, we extracted the region of interest level amyloid measurements instead of the voxel level measurements. We finally generated 116 mean amyloid measurements spanning the whole brain according to the MarsBaR AAL atlas (Tzourio-Mazoyer et al., 2002), and used them as imaging QTs. Moreover, these imaging QTs were preadjusted to remove the effects of the baseline age, gender, handedness and years of education (Table 1).

Table 1.

Participant characteristics

	HC	MCI	AD
Number	182	292	281
Gender (M/F, %)	48.90/51.10	48.63/51.37	53.38/46.62
Handedness (R/L, %)	89.56/10.44	88.70/11.30	90.39/9.61
Age (mean±SD)	73.93±5.51	70.90±6.84	72.61±8.15
Education (mean±SD)	16.43±2.68	16.18±2.68	15.95±2.82

The genotyping data were genotyped by the Human 610-Quad or OmniExpress Array platform (Illumina, Inc., San Diego, CA, USA), and preprocessed following standard quality control and imputation procedures. There were 1692 SNPs included which were collected from the neighbor of AD risk gene APOE according to the ANNOVAR annotation. In this study, we intend to study bi-multivariate associations between regional imaging amyloid depositions and SNPs, and with focus on identifying diagnosis-specific amyloid depositions and SNPs, as well as their interactions.

3.3.1. Identification and interpretation of imaging QTs

We applied all three methods to this real neuroimaging genetic data. The selected imaging QTs are highlighted in Figure 4, in which there are three columns for both MT–SCCALR and JSCCA. We stacked the canonical weight vector of DSCCA for three times. We observed that DSCCA did not hold the diagnosis-specific feature selection capability due to the nature of its modeling method. JSCCA identified multiple weights corresponding to multiple diagnostic groups, showing a somewhat diverse feature selection. Our method performed the best among three methods as we could observe a much clear diagnosis-specific feature selection profiles. Besides, MT-SCCALR showed a clearly group feature selection patterns due to the structure identification penalties such as FGL and GGL.

Fig. 4.

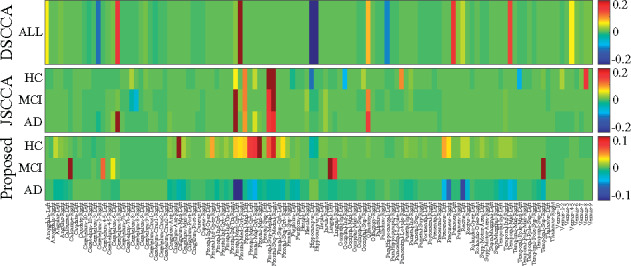
Canonical weights (mean) of imaging QTs from fivefold cross-validation trials. Each row corresponds to an SCCA method: (1) DSCCA; (2) JSCCA and (3) MT–SCCALR

We further investigated the meaning of the selected imaging QTs. MT–SCCALR identified three canonical weight vectors in accordance to three diagnostic groups, i.e. HC, MCI and AD. Most of the HC-specific signals were from the frontal areas, indicating that a subject’s health condition could be determined based on the amyloid burden of these areas. Besides, the cingulum and the precuneus were also highlighted by MT–SCCALR. Interestingly, most of the AD-specific signals were from the frontal area too but with oppositive signs, which matches our intuition. It is obvious that oppositive weights of these areas for HCs and ADs tell us that there are an oppositive amyloid deposition pattern for these two groups. In contrast, both DSCCA and JSCCA cannot draw this in-depth conclusion. For MCI-specific imaging QTs, our method reported signals from the bilateral calcarine, lingual, fusiform and temporal. It seems strange as the frontal areas were not identified, but the truth is not. In general, MCIs have intermediate amyloid burden and thus using the deposition measurement from the frontal might not discriminate MCI subjects from those non-MCI subjects. Moreover, these brain areas had been shown to be related to MCI (Pan et al., 2017), confirming the detection power of our method. Of note, both DSCCA and JSCCA could not identify heterogeneous imaging QTs. The results together demonstrated that the diagnosis-specific feature selection is of great interest and meaning.

3.3.2. Identification and interpretation of SNPs

We presented the identified SNPs in Figure 5. In this figure, both DSCCA and JSCCA only identified one canonical weight vector for all tasks, and we stacked them for three times. We observed that all three methods identified rs429358 (APOE), i.e. the well-known AD-risk loci. Taking the top five selected SNPs as examples, DSCCA identified two additional AD associated locus rs7412 (APOE) (Yi et al., 2014) and rs10119 (TOMM40), with further investigation being warranted for rs4803792 and rs203711. JSCCA also identified SNPs from AD-associated genes such as APOC1 (rs7247707, rs10414043 and rs7256200) and APOE (rs1081105), indicating its better identification than DSCCA. MT-SCCALR exhibited distinct patterns as it assigned different weight values (importance) for each SNP for different groups. At first glance, the SNPs for HC, MCI and AD were similar. However, similar to that for imaging QTs, our method yielded oppositive feature signs for HC versus non-HC, and AD versus non-AD tasks. This is interesting as it reveals that HCs and ADs hold different genotypes which provide us a more in-depth clue. Compared to benchmarks which only tell us that a SNP is relevant or irrelevant, our method not only reveals whether a SNP is relevant, but also implies the directionality of the genetic effect. One may argue that we can swap both signs for imaging QTs and SNPs simultaneously, but the directionality of the imaging genetic correlation stays the same. Therefore, based on the heterogeneous multitasking, our method could successfully identify a diverse diagnosis-specific SNPs. These results suggest that MT-SCCALR is quite promising and might possess enhanced feature selection ability in imaging genetics.

Fig. 5.

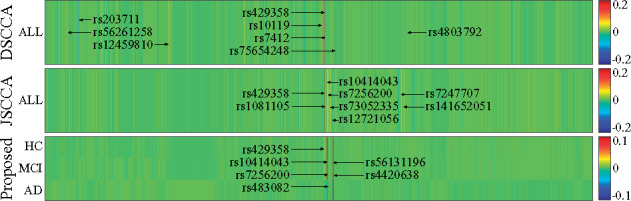
Canonical weights (mean) of SNPs from fivefold cross-validation trials. Each row corresponds to an SCCA method: (1) DSCCA; (2) JSCCA and (3) MT–SCCALR

3.3.3. Bi-multivariate association and classification

Finally, the testing CCC and classification accuracy are shown in Figure 6, in which a higher value indicated a stronger association or more accurate prediction. It is clear that DSCCA estimated the highest CCCs as it used all sample size to yield the CCC. Our method obtained better CCCs than JSCCA due to the OAA class binarization. Using the top ten selected features, including both imaging QTs and SNPs, of each method, we used LIBSVM (https://www.csie.ntu.edu.tw/∼cjlin/libsvm/) software package to implement SVM using the linear kernel with default setting. The classification results showed that all three methods performed similarly, implying that it is difficult to separate this real imaging genetic data (Wang et al., 2012a). On the contrary, this confirms the necessity and meaning of the diagnosis-specific feature selection, which could be helpful to subgroups identification. As a result, following the multitask modeling, MT–SCCALR showed a promising performance in multiclass imaging genetics.

Fig. 6.

Comparison of the mean CCCs and classification accuracy obtained from fivefold testing trials on ADNI

4 Conclusion

Identifying diagnosis-specific genetic markers and brain imaging measurements is an important task in precision medicine. AD is a severe neurodegenerative disorder presenting significant heterogeneity and diversity (Lam et al., 2013; Wang et al., 2015). Most existing bi-multivariate learning methods were unsupervised. Although a few studies made progress on supervised bi-multivariate learning, they could not identify diagnosis-specific biomarkers. We formally defined the framework of diagnosis-specific feature selection for imaging genetics, and proposed a computational method to identify diagnosis-specific, as well as diagnosis-consistent, feature subsets. Different to existing supervised SCCA, MT–SCCALR learned canonical weight matrices with each column corresponding to a diagnostic group. Using fused LR and SCCA, as well as the regularization, our model could identify meaningful and distinct imaging QTs and SNPs for each group. The algorithm was proved to converge to a local optimum.

Experiments on both synthetic data and real neuroimaging genetic data were conducted. Compared with two state-of-the-art methods [DSCCA (Yan et al., 2017) and JSCCA (Fang et al., 2016)], MT–SCCALR obtained similar correlation coefficients and classification accuracies to DSCCA and JSCCA. But it outperformed both benchmarks on revealing canonical weights on both synthetic and real data. In particular, our method successfully identified diagnosis-specific features including QTs and SNPs, while those benchmarks cannot. We also demonstrated that within each diagnostic group, the identified imaging QTs and SNPs were inconsistent, indicating that different diagnostic groups could carry different feature subsets. This is more reasonable and practical than existing methods as mounting evidences suggest that the sporadic AD might not be a single disease (Au et al., 2015). These results reveal that MT-SCCALR gains a promising success in diverse feature selection for multiple diagnostic groups in imaging genetics as well as multiple omics analysis. However, as the calculation of Hessian matrix and gradient of GGL penalty is time-intensive, we suggest using brain region-based imaging measurements other than voxel-based ones. An interesting future direction could be to make our method able to stratify different AD patients instead of only identifying diagnosis-specific features.