Abstract
Motivation
Species tree estimation is a basic part of biological research but can be challenging because of gene duplication and loss (GDL), which results in genes that can appear more than once in a given genome. All common approaches in phylogenomic studies either reduce available data or are error-prone, and thus, scalable methods that do not discard data and have high accuracy on large heterogeneous datasets are needed.
Results
We present FastMulRFS, a polynomial-time method for estimating species trees without knowledge of orthology. We prove that FastMulRFS is statistically consistent under a generic model of GDL when adversarial GDL does not occur. Our extensive simulation study shows that FastMulRFS matches the accuracy of MulRF (which tries to solve the same optimization problem) and has better accuracy than prior methods, including ASTRAL-multi (the only method to date that has been proven statistically consistent under GDL), while being much faster than both methods.
Availability and impementation
FastMulRFS is available on Github (https://github.com/ekmolloy/fastmulrfs).
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Species trees are important models that can be used to address many biological questions, for example how is biodiversity created/maintained and how do species adapt to their environments (Cracraft et al., 2004). There is also a vast literature regarding gene tree reconciliation, where gene trees are compared to an established species tree in order to understand how genes evolved (for some of the recent literature on this question, see Delabre et al., 2020; Dondi et al., 2019; El-Mabrouk and Noutahi, 2019; Hasić and Tannier, 2019; Jacox et al., 2016; Kundu and Bansal, 2018; Lai et al., 2017; Muhammad et al., 2018). However, in most cases, species trees are not known in advance and instead must be estimated.
Most species tree estimation methods are designed for orthologous genes, which are genes related through speciation events only and not through duplication events (Fitch, 2000; Moreira and Philippe, 2000). Because orthology prediction is still difficult to do correctly (Altenhoff et al., 2019; Lafond et al., 2018; Sousa da Silva et al., 2014) and mistakes in orthology prediction can result in incorrect species trees, multi-copy genes are often excluded from species tree estimation (e.g. Leebens-Mack et al., 2019; Wickett et al., 2014). Methods that can estimate species trees from gene families are of increasing interest, as this would enable phylogenetic signal to be extracted from multi-copy genes while avoiding the challenges of orthology prediction.
Several methods have been proposed to infer species trees from multi-copy genes. PHYLDOG (Boussau et al., 2013), perhaps the most well-known method explicitly based on a parametric model of gene duplication and loss (GDL), uses likelihood to co-estimate the species tree and gene family trees (which may contain multiple copies from some species). This is very computationally intensive, so PHYLDOG is limited to very small datasets with 10 or so species. Recently, De Oliveira Martins et al. (2016) proposed the Bayesian supertree method, guenomu, which requires the posterior distribution to be estimated for each gene family tree, for example using MrBayes (Ronquist and Huelsenbeck, 2003). Thus, guenomu is also not fast enough to use on genome-scale datasets with 100 or more species.
Non-parametric methods are more commonly used alternatives. For example, gene tree parsimony (GTP) methods take a set of (estimated) gene family trees as input, and then seek a species tree that implies the minimum number of evolutionary events, such as gene duplications and gene losses. Examples of GTP methods include DupTree (Wehe et al., 2008), iGTP (Chaudhary et al., 2010) and DynaDup (Bayzid and Warnow, 2018). Since GTP is NP hard, most of these methods operate by using hill climbing. DynaDup, in contrast, uses dynamic programming to find an optimal solution within a constrained search space; this type of approach, to the best of our knowledge, was first proposed in Hallett and Lagergren (2000) and has since been utilized for other problems, including the maximum quartet support supertree problem (Bryant and Steel, 2001; Mirarab et al., 2014) and the Robinson-Foulds Supertree (RFS) problem (Vachaspati and Warnow, 2016). Although GTP methods can be computationally intensive, they are more scalable than other approaches (e.g. PHYLDOG), and several phylogenomic studies have used GTP methods (Burleigh et al., 2011; Sanderson and McMahon, 2007).
Other fast approaches include supertree methods that have been adapted to work with gene family trees, referred to as multrees, as they can have multiple copies from each species. The most well-known supertree method for multrees is perhaps MulRF (Chaudhary et al., 2014b), which attempts to find a solution to the NP-hard Robinson-Foulds Supertree problem for multrees (RFS-multree). Although MulRF does not explicitly account for GDL, it has been shown to produce more accurate species trees than DupTree and iGTP on datasets simulated under challenging model conditions with GDL, incomplete lineage sorting (ILS), horizontal gene transfer and gene tree estimation error (GTEE) (Chaudhary et al., 2014a).
In a very recent advance, Legried et al. (2020) proved that ASTRAL-multi (Rabiee et al., 2019), an extension of ASTRAL (Mirarab et al., 2014) to address multi-allele inputs, is statistically consistent under the standard stochastic model of GDL proposed by Arvestad et al. (2009) in which all the genes evolve independently and identically distributed (i.i.d.) within a species tree, with duplication and loss rates fixed across the edges of the species tree. In fact, ASTRAL-multi is the only method that has been proven statistically consistent under any GDL model. Yet, a comparison reported by Legried et al. (2020) between ASTRAL-multi and three earlier species tree estimation methods, including DupTree, STAG (Emms and Kelly, 2018), and MulRF, showed that ASTRAL-multi had good but not exceptional accuracy; specifically, when the duplication and loss rates were both high, ASTRAL-multi was more accurate than DupTree (except when GTEE was low) and STAG (which often failed to complete), but was less accurate than MulRF.
The high accuracy of MulRF in comparison to ASTRAL-multi encouraged us to explore the optimization problem that MulRF attempts to solve (RFS-multree), and led to the following advances.
We prove (Theorem 5) that the true species tree is an optimal solution to the NP-hard RFS-multree problem, provided there is no adversarial GDL (which occurs when the pattern of duplication and loss events produces bipartitions that are incompatible with the species tree). This model is less restrictive than the standard GDL model in that it does not assume genes evolve i.i.d. (similar to the No Common Mechanism model of Tuffley and Steel, 1997), but is more restrictive in that it prohibits adversarial GDL. However, we conjecture (Conjecture 7) that adversarial GDL will occur with sufficiently low probability so that an exact solution to the RFS-multree problem will be statistically consistent for reasonable duplication and loss probabilities.
We present FastMulRFS, a polynomial-time algorithm that uses dynamic programing to solve the RFS-multree problem exactly within a constrained search space (computed from the input gene family trees), and prove (Theorem 6) that FastMulRFS is statistically consistent under a generic GDL model when no adversarial GDL occurs.
We prove (Theorem 2) that when solving the RFS-multree problem, any input set of multrees can be replaced by a set of smaller trees (with each species labeling at most one leaf), thus reducing memory and running time for methods that attempt to solve the RFS-multree problem.
We evaluate FastMulRFS in comparison to ASTRAL-multi, DupTree and MulRF on 1200 different datasets with 100 species and up to 500 genes, generated under 120 model conditions with varying levels of GDL, ILS and GTEE. We find that FastMulRFS is generally more accurate than DupTree and ASTRAL-multi, and ties for most accurate with MulRF. We also find that FastMulRFS is much faster than MulRF and ASTRAL-multi, and ties for fastest with DupTree. The improvement in performance over ASTRAL-multi is the most important result, as ASTRAL-multi is the only other method to date that has been proven statistically consistent under a stochastic GDL model.
In summary, FastMulRFS is a new and very fast method for species tree estimation that does not require reliable orthology detection and outperforms the leading alternative methods (even under conditions for which FastMulRFS is not yet established to be statistically consistent).
2 The RFS-multree problem and FastMulRFS
We define the RFS-multree and present FastMulRFS, an algorithm that solves this problem exactly within a constrained search space. Later, we prove that FastMulRFS is statistically consistent under a generic model of GDL when no adversarial GDL occurs. We begin with terminology and definitions.
2.1 Terminology
A phylogenetic tree T is defined by the triplet , where t is its unrooted tree topology, S is the label set and is the assignment of labels to the leaves of t. If each label is assigned to at most one leaf, then we say that T is singly labeled, whereas if any label is assigned to two or more leaves, then we say that T is multi-labeled (equivalently, T is a multree). The edges that are incident with leaves are referred to as terminal (or trivial) edges, and the remaining edges are referred to as internal (or non-trivial) edges.
Deleting an edge e but not its endpoints from T produces two subtrees tA and tB that define two label sets: and . If no label appears on both sides of e, then A and B are disjoint sets, and the edge e induces a bipartition πe on the label set of T (i.e. the edge e splits the leaf labels into two disjoint sets). However, if some label appears on both sides of e then A and B are not disjoint, and so by definition, the edge e does not induce a bipartition. We let C(T) denote the set of bipartitions induced by edges in tree T, noting that not all edges of T will necessarily contribute bipartitions to C(T), unlike the case of singly-labeled trees.
A key concept in FastMulRFS is compatibility, originally described by Estabrook et al. (1975), which we now define (see also Warnow, 2017). Let be the true (fully resolved) species tree on S, and let be a bipartition on . Then π is compatible with if and only if there is a bipartition so that and . Equivalently, bipartition π on label set is compatible with if there exists such that is identical to π when restricted to label set S0. Similarly, a tree T on label set S0 is compatible with the species tree if every bipartition in T is compatible with .
2.2 Robinson-Foulds supertree problem for multrees
The RF distance (Robinson and Foulds, 1981) between two singly-labeled trees on the same label set has a simple definition as the bipartition distance (i.e. number of bipartitions in one but not in both trees). Now suppose T and are singly-labeled trees on label sets S and , respectively. Then the RF distance between T and can be computed as
| (1) |
| (2) |
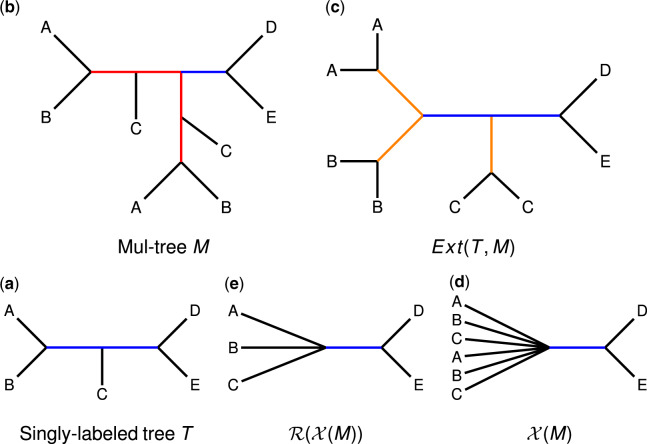
where denotes T restricted to leaves with labels in set R (after suppressing internal nodes with degree 2). When one or both trees is a multree, then the RF distance has an alternative definition (which is equal to the standard definition when both trees are singly labeled and on the same label set): the edit distance under contraction-and-refinement operations, where a contraction is collapsing a single edge, and a refinement is inserting a single edge to decrease the degree of a polytomy (i.e. node of degree four or more). When both trees are multrees, computing the RF distance is NP-complete (Chaudhary et al., 2013). However, Chaudhary et al. (2013) proved that the RF distance between a multree and a singly-labeled tree can be computed in polynomial time as follows: (i) extend T with respect to M, denoted Ext(T, M) (Fig. 1), (ii) relabel the leaves of M and Ext(T, M) in a mutually consistent fashion so that both trees are singly labeled and (iii) compute the RF distance using Equation (1) between the relabeled versions of Ext(T, M) and M, denoted and , respectively; see Appendix for additional details.
Fig. 1.
Reduction of the RFS-multree problem to the Robinson-Foulds Supertree (RFS) problem. To compute the RF distance between a singly-labeled tree T (a; bottom left) and a multree M (b; top left), we replace M by a smaller singly-labeled tree (e; bottom center). We then compute the RF distance between T and using Equation (1). Here we explain why this works. Suppose that T (a) is a candidate singly-labeled, binary supertree for a set of multrees and that M (b) is one of the multrees in . To compute the RF distance between T and M, we extend T with respect to M, producing Ext(T, M) (c). Note that Ext(T, M) has the same non-trivial edges (shown in blue) and the same trivial edges (shown in orange) as T, and for every leaf label (species), it has the same number of leaves with that label as multree M. The trivial edges in Ext(T, M) exist in any possible singly-labeled, binary tree on S; thus, these edges do not impact the solution to the RFS-multree problem. Similarly, multree M has edges (shown in red) that will be incompatible with an extended version of any possible singly labeled, binary tree on S; thus, these edges do not impact the solution to the RFS-multree problem. An edge is incompatible with every possible singly-labeled supertree if and only if it fails to induce a bipartition (i.e. deleting an edge e splits the leaf labels into two non-disjoint sets). Thus, we collapse all internal edges in M that fail to induce a bipartition, producing (d). Furthermore, because all leaves with the same label are now on the same side of every bipartition in , we can delete all but one leaf with each label, producing (e). The resulting tree is a non-binary, singly-labeled tree on S, so we can compute the RF distance between T and using Equation (1) when searching for the solution to the RFS-multree problem. These observations are formalized in Lemma 13 (Appendix), and it follows that an RFS-multree supertree for is an RF supertree for , as summarized in Theorem 2
Chaudhary et al. (2013) then proposed the RFS-multree. The input is a set of multrees with leaves labeled by elements of the set S, and the output is a binary (i.e. fully resolved) tree T bijectively labeled by S that minimizes
| (3) |
Any tree that minimizes this score is called an RFS-multree supertree for . Finally, when is a profile of singly-labeled trees, then the RFS-multree problem is the well-known RFS problem (Bansal et al., 2010; Vachaspati and Warnow, 2016).
2.3 Reducing from multrees to singly-labeled trees
We simplify the RFS-multree problem by providing an alternative proof that the RF distance between a singly-labeled tree T and a multree M and can be computed in polynomial time (Lemma 13 in Appendix). We summarize the intuition behind this lemma in Figure 1, which leads easily to Theorem 2.
Definition 1.
Given a multree , we collapse internal edges with some species labeling leaves on both sides of the edge, denoting the result . We then delete all but one leaf with each species label, denoting the result . We define .
Theorem 2.
Let T be a singly-labeled, binary tree on label set S, and let be a set of multrees. Then, T is an RFS-multree supertree for if and only if T is a RF supertree for . Equivalently, T is an RFS-multree supertree for (with multree Mi on label set ) if and only if T is a binary tree that maximizes .
2.4 FastMulRFS
A consequence of Theorem 2 is that any heuristic for the RFS problem can be used for the RFS-multree problem simply by computing (i.e. by transforming the input multrees into singly-labeled trees) and then running the heuristic on . In this study, we explore the impact of using FastRFS (Vachaspati and Warnow, 2016), an effective heuristic for the RFS problem, and we refer to this two-phase approach as FastMulRFS.
The input to FastRFS is a profile of singly-labeled trees, each on a (possibly proper) subset of S and a set Σ of allowed bipartitions on S; FastRFS provably returns a (binary) supertree T that minimizes the total RF distance to the trees in subject to . FastRFS uses dynamic programing to solve the constrained optimization problem in time, where and . As we will show, Σ can be defined from the input multrees so that FastMulRFS runs in polynomial time and is statistically consistent under a generic GDL model when no adversarial GDL occurs.
We now describe FastMulRFS, which takes a profile of multrees, each on a (possibly proper) subset of the species set S.
Step 1: We construct from by collapsing all internal edges that have species labeling leaves on both sides of the edge and then deleting all but one of the multiple copies of any species. Thus, is a set of potentially unresolved single-copy gene trees. In the Supplementary Material (Algorithm 1), we show how to compute the set from in O(mnk) time, where , and m is the largest number of leaves in any multree in .
Step 2: We run ASTRAL given the set of single-copy gene trees to produce the set Σ of allowed bipartitions. The default technique for constructing Σ uses every bipartition in every single-copy gene tree on the complete label set S. In this case, it is easy to see that . Additional bipartitions may be included to guarantee that at least one fully resolved tree T satisfies and to improve accuracy (by expanding the space of allowed solutions); however, ASTRAL-III (Zhang et al., 2018) enforces . While the total running time of ASTRAL-III is , we run ASTRAL-III to construct Σ and then exit.
Step 3: We run FastRFS on the pair .
In summary, FastMulRFS runs in time, where n is the number of species, k is the number of multrees and m is the largest number of leaves in any of the multrees. The default technique for constructing the set Σ of allowed bipartitions enforces and, as we will show in the next section, suffices for proofs of statistical consistency under some generic GDL models.
3 Species tree estimation using FastMulRFS
Generic GDL models. Our generic GDL models are similar to the No Common Mechanism models described in Tuffley and Steel (1997), in that there is a common rooted binary model species tree, but each gene evolves down the tree with its own duplication and loss parameters. We make natural assumptions that every gene has duplication probability and loss probability strictly <1 on every edge, and note these probabilities can depend on the gene and on the edge. Thus, our generic models contain the GDL models of Arvestad et al. (2009) as sub-models.
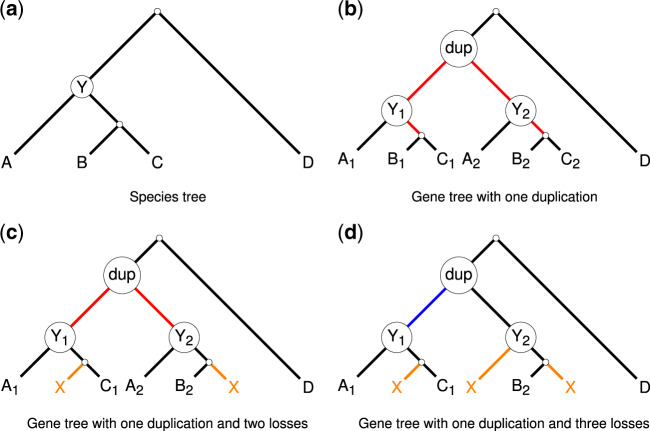
Adversarial GDL. We define adversarial GDL to be when the gene evolution process produces a gene family tree with a bipartition π that is not compatible with the true species tree (see Section 2.1 for the definition of compatibility). Adversarial GDL requires a sequence of events (a duplication followed by a carefully selected set of losses) that coordinate to produce such a bipartition. Figure 2d illustrates a scenario that produces adversarial GDL: the gene duplicates on the edge above Y in the species tree (shown in Fig. 2a), so that Y has two copies of the gene. Then the first copy of the gene is lost on the edge above B, whereas the second copy of the gene is lost on the edge above A and the edge above C. As a result, the gene family tree shown in Figure 2d is singly labeled, but the gene family tree induces a bipartition () that is incompatible with the species tree; by definition, this is adversarial GDL. Alternatively, suppose the first copy of the gene had been lost on the edge above A and on the edge above (B, C), then not only is there no adversarial GDL, but also the gene family tree induces a bipartition () that is compatible with the species tree.
Fig. 2.
Impact of gene duplications and losses (GDL) on species tree estimation using RFS-multree methods. (a) Shows a species tree and (b) through (d) show three gene family trees that evolved within the species tree. (b) Shows gene family tree with a duplication event in species Y (i.e. the most recent common ancestor of species A, B and C). All edges below the duplication (shown in red) fail to induce bipartitions and so will be contracted, and will therefore not impact the solution space for the RFS-multree criterion. (c) Shows gene tree with a duplication event in species Y followed by the first copy of the gene being lost from species B and the second copy of the gene being lost from species C. Because one of the species that evolved from Y retains both copies of the gene, the non-trivial edges below the duplication node fail to induce bipartitions, and so these edges also do not impact the solution space for RFS-multree. (d) Shows gene family tree with a duplication event in species Y followed by the first copy of the gene being lost from species B and the second copy of the gene being lost from both species A and C. None of the species that evolved from Y retain both copies of the gene, so all edges below the duplication node induce bipartitions and hence will not be contracted; we refer to this situation as ‘adversarial GDL, because it produces bipartitions in the singly-labeled trees in that conflict with the species tree (shown in blue). Such a scenario leads to the possibility that the true species tree may not be an optimal solution to the RFS-multree problem
Another interesting case to consider is when the gene duplicates on the edge above Y, and then the first copy is lost on the edge above B and the second copy is lost on the edge above C. As a result, the gene family tree shown in Figure 2c does not induce any bipartitions. Now suppose A, B and C were clades (rather than leaves), then every edge in the two A clades (and the edges connecting the two A clades) would fail to induce a bipartition (assuming no other loss events). In contrast, every edge in the B clade and the C clade would induce a bipartition compatible with the species tree (assuming no other duplication events). In some sense, duplication events hide bipartitions, while losses (following a duplication event) can reveal bipartitions. A carefully selected pattern of losses (after the duplication) can result in adversarial GDL (i.e. a particular bipartition π that is not in the species tree), but small changes to that pattern may well produce bipartitions that are in the true species tree or are incompatible with π. Thus, overall, while adversarial GDL may occur, it may not have high impact on tree estimation based on the RFS-multree criterion.
In this section, we will discuss model conditions under which adversarial GDL cannot occur: the duplication-only case, where all genes evolve with duplication but no loss, and the loss-only case, where all genes evolve with loss but no duplication. To prove that a model condition prohibits adversarial GDL, we need to establish that any bipartition that appears in a gene family tree is compatible with the species tree; equivalently, if it appears in full in any gene family tree then it must also appear in the species tree, while any incomplete bipartition that appears in any gene family tree can be extended (by adding the missing species) to become a bipartition that is in the species tree. It is trivial to see that if a gene evolves only with losses, then there is no adversarial GDL for that gene (Lemma 3), but the proof for duplication-only evolution is more interesting (Lemma 4).
Lemma 3.
Let be a set of true gene trees that evolved within the rooted species tree under a stochastic loss-only model of gene evolution. Then for , π is compatible with . Hence, loss-only models have no adversarial GDL.
Lemma 4.
Let be the set of true gene trees that evolved within the rooted species tree under a stochastic duplication-only model of gene evolution. Then for every multree . Equivalently, for any , every edge e in MX (Definition 1) defines a bipartition πe in . Hence, duplication-only models have no adversarial GDL.
Proof.
Let M be an unrooted gene family tree, and let e be an internal edge in E(M). We will show that an internal edge e is collapsed in producing if and only if e lies below at least one duplication node in the rooted version of M. Hence, the singly-labeled tree will only retain the edges in M that have no duplication nodes above them in the rooted version of M. To see why, consider any edge e that has no duplication node above it in the rooted gene family tree: no species appears on both sides of e and hence e will not be collapsed. Conversely, if internal edge e is collapsed, then there must be at least one species on both sides of e, and so e must be below at least one duplication node in the true rooted gene family tree. Finally, consider a bipartition defined by an edge that is not collapsed, and hence has no duplication nodes above it. This bipartition appears in the true species tree , since the only events that cause the gene family tree to differ from the true species tree are duplications. □
We now prove that FastMulRFS is statistically consistent under generic GDL models if no adversarial GDL occurs.
Theorem 5.
The true species tree is an RFS-multree supertree for any input for which no adversarial GDL occurred.
Proof.
The optimization problem seeks a binary tree T that minimizes the sum of the RF distances to the input multrees; this is equivalent to maximizing the sum of the number of compatible bipartitions in the input multrees. If no adversarial GDL occurs, then by definition, every bipartition in the input multrees is compatible with the true species tree , and so is an optimal solution to the RFS-multree problem. □
Theorem 6.
FastMulRFS is statistically consistent under any GDL model for which adversarial GDL is prohibited.
Proof.
Let be the true species tree. By Theorem 5, is an optimal solution to the RFS-multree problem for any input for which no adversarial GDL occurred. Since our generic GDL models assume that the probability of no duplication or loss occurring on an edge is always strictly positive for every gene, the true species tree has strictly positive probability of appearing in the set of gene family trees. Therefore, as the number of genes increases, Σ (as constructed by the default setting within FastMulRFS) will converge to with probability converging to 1, and will be the unique tree that is optimal under the RFS-multree problem for input . FastMulRFS finds an optimal solution to RFS-multree problem subject to the tree T it returns satisfying , by Theorems 2 and 3 in Vachaspati and Warnow (2016). Since Σ converges to as the number of genes increases, the probability that FastMulRFS will return converges to 1. □
We finish this section with a conjecture.
Conjecture 7. FastMulRFS is statistically consistent under a generic model of GDL for probabilities of GDL, so that adversarial GDL has sufficiently low probability.
4 Experimental study
4.1 Materials and Methods
We evaluated FastMulRFS in comparison to ASTRAL-multi, DupTree and MulRF on biological and simulated datasets, considering species tree topological accuracy and running time. All simulated datasets are available on the Illinois Data Bank (https://doi.org/10.13012/B2IDB-5721322_V1), and the commands necessary to reproduce this study are provided in the Supplementary Material.
Biological dataset. We analyzed a fungal dataset with 16 species and 5351 genes from Rasmussen and Kellis (2012), who provided gene family trees estimated from their nucleotide alignments. In a prior study, Butler et al. (2009) estimated species trees from this same dataset (specifically the concatenated amino acid alignment of putatively orthologous sequences) using MrBayes (Ronquist and Huelsenbeck, 2003), constrained to enforce the out-grouping of S. castellii with respect to S. cerevisiae and C. glabrata. The other reported trees differed with respect to this group (i.e. not all analyses returned this as a clade) and differed in the placement of K. waltii. According to their study, none of these resolutions are clearly correct.
Simulation study. We generated a collection of 100-species datasets (each with 1000 model gene trees) under the DLCoal model (Rasmussen and Kellis, 2012), which is a unified model of GDL and ILS. The easiest model condition was based on parameters estimated from the 16-species fungal dataset (Du et al., 2019; Rasmussen and Kellis, 2012), and then we increased the GDL rates and ILS levels (by increasing population size) to make more challenging model conditions. We used RAxML (Stamatakis, 2014) to estimate gene trees under the GTR + Γ model from the simulated alignments, with sequence lengths varied to produce four different levels of GTEE. Finally, we estimated species tree giving methods the first 25, 50, 100 and 500 gene family trees, either true or estimated, as input. This created 120 model conditions (3 GDL rates, 2 levels of ILS, 5 levels of GTEE and 4 numbers of genes), each with 10 replicates, for a total of 1200 datasets. Importantly, none of the model conditions prohibits adversarial GDL, allowing us to explore method performance when adversarial GDL may occur.
Evaluation criteria. On the fungal biological dataset, we evaluated accuracy with respect to established evolutionary relationships, and on the simulated datasets, we quantified error using the RF error rate, with respect to the true (model) species tree. We also recorded empirical running time; however, it should be noted that all experiments were performed on the Campus Cluster at the University of Illinois at Urbana-Champaign, which is a heterogeneous system (i.e. compute nodes do not have the same specifications; see here: https://campuscluster.illinois.edu/resources/docs/nodes/).
4.2 Results
Results on biological dataset. We analyzed the fungal dataset using ASTRAL-multi, FastMulRFS, DupTree and MulRF. All produced trees that are very similar to the MrBayes concatenation tree (Supplementary Fig. S1), and the differences are minor given (i) the variability in the trees found by Butler et al. (2009), (ii) the use of a topological constraint in their MrBayes analysis and (iii) the uncertainty about the placement of specific taxa in the tree. For further information on these analyses, see Section 5 in the Supplementary Information from Butler et al. (2009).
Given that the topological differences are minor, we report the running time differences. FastMulRFS and DupTree completed in under a minute each, ASTRAL-multi completed in 18 min, and MulRF completed in 40 min. Hence, FastMulRFS is much faster than MulRF and ASTRAL-multi. While all four of these methods are relatively fast on 16 taxa, we expect the difference between methods to increase on datasets with larger numbers of species and higher rates of gene duplication. The improvement in running time over MulRF and ASTRAL-multi is due in part to the fact that both MulRF and ASTRAL-multi use the original gene family trees, while FastMulRFS uses the reduced singly-labeled trees; hence, as the number of leaves or the duplication rate increase, the advantage in running time for FastMulRFS should also increase.
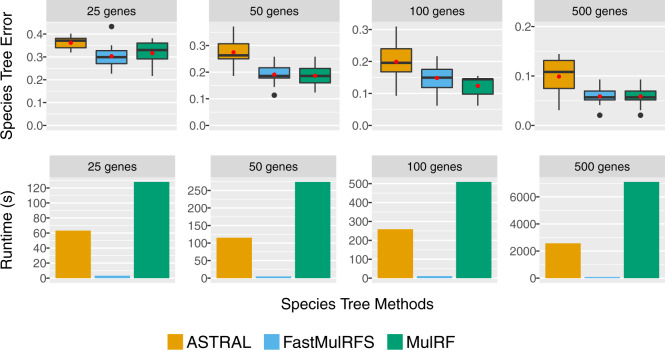
Results on the simulated datasets. DupTree had poorer accuracy than the other tested methods (Section 4.1 in Supplementary Material). Hence, we focus on comparing MulRF, FastMulRFS and ASTRAL-multi. The fastest method was FastMulRFS, MulRF was the slowest and ASTRAL-multi was intermediate. All methods improved in accuracy with larger numbers of genes and degraded in accuracy with higher GTEE levels, ILS levels and/or GDL rates. The relative accuracy between methods was consistent across all model conditions, although the degree of difference depended on the model conditions, with bigger differences for smaller numbers of genes and higher GTEE levels, ILS levels and GDL rates. When given 500 gene trees, error levels were low and differences between methods were (usually) small, so that the main difference was running time. We present results in Figure 3 for MulRF, FastMulRFS and ASTRAL-multi under the highest GDL rate, the highest level of ILS and the second highest level of GTEE (about 53%). We note that high GTEE (such as in this setting) is consistent with the generally low bootstrap branch support values reported for several phylogenomic datasets (e.g. about 25% for exon and 45% for intron datasets from Jarvis et al., 2014; also see Table 1 in Molloy and Warnow, 2018). See Supplementary Material for additional results.
Fig. 3.
Species tree error rate (i.e. RF error rate) and running time (s) are shown for FastMulRFS, MulRF and ASTRAL-multi under the most challenging model conditions with 100 species. All datasets have the second highest GTEE level (moderate GTEE: 52%), the highest ILS level (low/moderate ILS: 12%) and the highest GDL rate (D/L rate: ). Red dots (first row) and bars (second row) are means for 10 replicate datasets
FastMulRFS versus MulRF. Both try to solve the RFS-multree problem but use different approaches; they were essentially tied for accuracy across all tested conditions, but FastMulRFS was dramatically faster (Fig. 3; Supplementary Tables S3 and S4). In addition, FastMulRFS nearly always returned trees with better RFS-multree scores than MulRF (Section 4.2 in Supplementary Material).
FastMulRFS versus ASTRAL-multi. Figure 3 shows results for the second highest GTEE level, where FastMulRFS was much more accurate than ASTRAL-multi for all numbers of genes. FastMulRFS was always at least as accurate as ASTRAL-multi (often more accurate) across the other model conditions (Supplementary Table S3), with larger differences between methods for the higher GTEE condition and smaller differences for the lower GTEE conditions. The running times for ASTRAL-multi and FastMulRFS increased with the number of genes, but FastMulRFS was always much faster (Fig. 3, Supplementary Table S4). For example, on the 500-gene model conditions, FastMulRFS typically completed in 1–2 min (and always in under 5 min), but ASTRAL-multi used between 10 min and 1.2 h.
5 Discussion
To date, only two methods have been proven statistically consistent under any GDL model—ASTRAL-multi and FastMulRFS—but the conditions under which these two methods have been proven statistically consistent are different. ASTRAL-multi is established consistent under a gene evolution model that allows both gene duplication and loss to occur for each gene, but requires that all the genes evolve i.i.d. In contrast, FastMulRFS has been proven consistent under a generic model that does not require the genes to evolve i.i.d. (and indeed allows for a very broad no-common-mechanism model); this is a relative strength for the theoretical result for FastMulRFS, as genes do not evolve i.i.d. down a species tree, as discussed in Dondi et al. (2019). On the other hand, FastMulRFS has only been proven consistent when no adversarial GDL occurs; this is a relative weakness of the theoretical result for FastMulRFS (although see Conjecture 7). Thus, from a theoretical perspective, there are advantages and disadvantages for both methods.
We now consider the empirical performance of the methods evaluated in this study, focusing on the simulated datasets (since differences on the biological dataset were minor, except for running time). Under most of the model conditions we examined, FastMulRFS was more accurate and more robust to GTEE than ASTRAL-multi. Furthermore, the only conditions in which the two methods achieved similar accuracy were characterized by low GTEE and large numbers of genes, where both methods achieved very high accuracy. In addition, FastMulRFS was much faster than ASTRAL-multi, with large improvements in speed, especially for large numbers of genes and high GTEE. Thus, FastMulRFS had superior performance compared to ASTRAL-multi, the only previous method to date established statistically consistent under a stochastic GDL model.
A comparison between FastMulRFS and MulRF is also interesting. Both methods attempt to solve the same NP-hard optimization problem, and neither is guaranteed to find an optimal solution. However, FastMulRFS is guaranteed to find an optimal solution within a constrained search space within polynomial time, whereas MulRF uses a local search strategy that is not guaranteed to find optimal solutions and is not guaranteed to complete in polynomial time. Furthermore, the way that FastMulRFS constrains its search space is sufficient to ensure that it is statistically consistent, but this statement is not guaranteed for MulRF. From a theoretical perspective, therefore, FastMulRFS is superior to MulRF. In terms of empirical performance in our study, the two methods were very close in accuracy, but FastMulRFS was dramatically faster. Therefore, overall, FastMulRFS was superior to MulRF.
We note that FastMulRFS matched or improved on the other methods under all conditions we explored, where gene trees evolved under a unified model of ILS and GDL (which did not prohibit adversarial GDL). Hence, our study suggests that FastMulRFS may have good robustness and high accuracy, even under conditions where it has not (yet) been proven statistically consistent. However, future work is clearly needed to evaluate FastMulRFS and other methods under a wider range of model conditions, including explicit conditions where adversarial GDL occurs.
6 Summary and conclusions
FastMulRFS is a new method that can estimate species tree from unrooted gene family trees, without needing to have any information about orthology. FastMulRFS is provably statistically consistent under a GDL model that allows genes to evolve under a no-common-mechanism model [a more general model than the Arvestad et al. (2009)i.i.d. model assumed in the proof of statistical consistency for ASTRAL-multi], provided that adversarial GDL does not occur. Prior to this study, ASTRAL-multi was the only method proven to be statistically consistent for estimating species trees in the presence of GDL.
FastMulRFS always matched or improved on the accuracy of ASTRAL-multi (often substantially) in our simulation study, which included three GDL, two ILS levels and five GTEE levels, and it was also faster than ASTRAL-multi. Furthermore, these model conditions do not prohibit adversarial GDL. This improvement in accuracy over ASTRAL-multi is significant, since our proof only establishes statistical consistency under models where no adversarial GDL, ILS or GTEE is present. Although accuracy is difficult to evaluate on biological datasets, FastMulRFS produced trees that were similar to those produced by other methods and did not violate known relationships.
This study suggests several directions for future work. In particular, we should explore additional simulation conditions to evaluate the impact of higher GDL rates (including conditions that explicitly have adversarial GDL) and larger numbers of genes, where the relative performance of species tree estimation methods might be different. Simulations should also be performed to evaluate other scenarios that produce multi-copy genes, for example whole genome duplication events, which impact species tree estimation for many major clades, including fungi (Butler et al., 2009) and plants (Leebens-Mack et al., 2019). More complex simulations should also be considered, including ILS, introgression, gene conversion, etc., in order to better understand the conditions in which each method performs well. Furthermore, it would be helpful to characterize biological datasets in understand realistic levels of ILS and GDL (including the frequency of adversarial GDL).
A limitation of this study is that we only examined a few methods, and future studies should also evaluate other methods, including guenomu (discussed earlier) and MixTreEM (Ullah et al., 2015), to discover the places in the parameter space of model species trees where each method outperforms the others. Furthermore, methods that operate by making predictions of orthology could be used in a three-phase approach: given inputs with sequence alignments and multrees, predict orthology, reduce to datasets with just orthologous genes (and hence singly-labeled gene trees) and then run a preferred species tree estimation method. For example, in a recent preprint, Zhang et al. (2019) presented another modification of ASTRAL, A-PRO and proved it statistically consistent under a GDL model if given correctly rooted and ‘tagged’ gene trees (i.e. each node in each gene tree is correctly identified as either a duplication or a speciation); however, this assumption means that orthology can be inferred without error (an assumption that is not made for ASTRAL-multi). Future studies should evaluate A-PRO as well in estimating a species tree from multrees. Such studies would enable biologists to select methods with the best expected accuracy for their datasets.
An important direction for future work is to evaluate the theoretical properties (such as statistical consistency) of FastMulRFS under parametric GDL models, where adversarial GDL is possible. The statistical consistency of DupTree and other methods (e.g. MixTrEm, guenomu and even modifications to concatenation to enable such analyses on multi-copy gene family datasets) should also be evaluated.
Overall, the recent advances in development of statistically consistent methods for species tree estimation under GDL models is exciting, and the good performance of many of these methods under a range of model conditions suggests that novel combinations and ideas may lead to even better methods that provide improved accuracy and scalability.
Supplementary Material
Acknowledgements
The authors thank the anonymous reviewers as well as Siavash Mirarab and the members of the Warnow Lab for feedback that improved this article.
Funding
This study was supported in part by the U.S. National Science Foundation (NSF) through Grant Nos. 1535977 and 1513629 (to T.W.) and by the Ira and Debra Cohen Graduate Fellowship in Computer Science (to E.K.M.). This study was performed on the Illinois Campus Cluster and the Blue Waters supercomputer, resources operated and financially supported by UIUC in conjunction with the National Center for Supercomputing Applications. Blue Waters is supported by the state of Illinois and the NSF through Grant Nos. 0725070 and 1238993.
Conflict of Interest: none declared.
Appendix
We begin with the following two additional definitions from Ganapathy et al. (2006) and Chaudhary et al. (2013).
Definition 8 (Full Differentiation). We say that is a full differentiation of multree if is a bijection. In other words, is a singly labeled version of M.
Definition 9 (Mutually Consistent Full Differentiations). Let and be full differentiations of multrees and , respectively. For i = 1, 2, we define to be the set of labels given to the leaves in that are labeled s in Mi. We say that and are mutually consistent full differentiations (MCFDs) of M1 and M2 if .
Ganapathy et al. (2006) showed that if M1 and M2 are both multrees, then their RF distance can be computed as
which implies an exponential-time algorithm for computing the RF distance between two multrees (Ganapathy et al., 2006), Later, Chaudhary et al. (2013) showed this problem is NP-complete and introduced a special case, where one of the two multrees has the property: every leaf with the same label is grouped together into polytomy that is separated by an edge from the rest of the tree. A multree with this property can be viewed as an extended version of a singly-labeled tree.
Definition 10 (Extended Version). Let be a singly-labeled tree, and let be a multree. Let ks be the number of leaves with label s in M. The extended version of T with respect to M, denoted Ext(T, M), is created by attaching ks new leaves to the leaf labeled s in T, assigning label s to each of these new leaves, and repeating this process for all .
Chaudhary et al. (2013) showed that the RF distance between a multree M and (the extended version of) a singly-labeled tree T, both on label set S, can be computed in polynomial time. Here, we provide an alternative proof that further simplifies this problem. First, we present two transformations that can be applied to a multree or to its full differentiation by using the function with property that for all .
Definition 11 (Contracted Version). The contracted version of M, denoted , is created by contracting every edge e that fails to induce a bipartition, because some species label appears on both sides of e. Similarly, the contracted version of , denoted , is created by contracting every edge e with such that .
Definition 12 (Reduced Version). If all leaves with species label s are on the same side of every edge in E(m), then they can be represented by a single leaf labeled s. The reduced version of M or , denoted or , respectively, is created as follows. For every with the aforementioned property, delete all but one of the leaves in the set (suppressing internal vertices of degree 2) and relabel the remaining leaf s.
It is easy to see that is a singly-labeled tree that is isomorphic to , because after applying the function to either or M, all the leaves with species label s will be on the same side of every edge and thus can be replaced by a single leaf with species label s by applying the function . This observation holds for all .
Lemma 13. Let T be a singly-labeled, fully resolved tree on label set S, let be a multree, and let and be MCFDs of Ext(T, M) and M, respectively. Then,
| (4) |
where and K is a constant that does not depend on the topology of the singly-labeled tree T on S.
Proof. Let be a function with property that for all , and define and . Thus, X contains bipartitions that cannot exist in for any singly-labeled tree T on S, and R contains bipartitions that must exist in for any singly-labeled tree T on S. Let denote . Then,
Let c be the number of species in M that have multiple copies. Then,
where S, c, E(m), , R and L(m) are independent of T. □
References
- Altenhoff A.M. et al. (2019) Inferring orthology and paralogy In: Anisimova M. (ed.) Evolutionary Genomics: Statistical and Computational Methods. Vol. 1 Springer, : New York, NY, USA, pp. 149–175. [Google Scholar]
- Arvestad L. et al. (2009) The gene evolution model and computing its associated probabilities. J. ACM, 56, 1–44. [Google Scholar]
- Bansal M.S. et al. (2010) Robinson-Foulds supertrees. Algorithms Mol. Biol., 5, 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayzid M.S., Warnow T. (2018) Gene tree parsimony for incomplete gene trees: addressing true biological loss. Algorithms Mol. Biol., 13, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boussau B. et al. (2013) Genome-scale coestimation of species and gene trees. Genome Res., 23, 323–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryant D., Steel M. (2001) Constructing optimal trees from quartets. J. Algorithms, 38, 237–259. [Google Scholar]
- Burleigh J.G. et al. (2011) Genome-scale phylogenetics: inferring the plant tree of life from 18,896 gene trees. Syst. Biol., 60, 117–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler G. et al. (2009) Evolution of pathogenicity and sexual reproduction in eight Candida genomes. Nature, 459, 657–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhary R. et al. (2010) iGTP: a software package for large-scale gene tree parsimony analysis. BMC Bioinformatics, 11, 574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhary R. et al. (2013) Inferring species trees from incongruent multi-copy gene trees using the Robinson-Foulds distance. Algorithms Mol. Biol., 8, 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhary R. et al. (2014. a) Assessing approaches for inferring species trees from multi-copy genes. Syst. Biol., 64, 325–339. [DOI] [PubMed] [Google Scholar]
- Chaudhary R. et al. (2014. b) MulRF: a software package for phylogenetic analysis using multi-copy gene trees. Bioinformatics, 31, 432–433. [DOI] [PubMed] [Google Scholar]
- Cracraft J. et al. , eds. (2004) Assembling the Tree of Life. Joel, C. and Michael,J.D. (eds) Oxford University Press, Oxford, UK. See here: https://www.amazon.com/Assembling-Tree-Life-Joel-Cracraft/dp/0195172345. [Google Scholar]
- De Oliveira Martins L. et al. (2016) A Bayesian supertree model for genome-wide species tree reconstruction. Syst. Biol., 65, 397–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delabre M. et al. (2020) Evolution through segmental duplications and losses: a Super-Reconciliation approach Algorithms Mol. Biol, 15, 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dondi R. et al. (2019) Reconciling multiple genes trees via segmental duplications and losses. Algorithms Mol. Biol., 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du P. et al. (2019) Species tree inference under the multispecies coalescent on data with paralogs is accurate. bioRxiv, doi:10.1101/498378.
- El-Mabrouk N., Noutahi E. (2019) Gene family evolution—an algorithmic framework In: Warnow T. (ed.) Bioinformatics and Phylogenetics. Computational Biology, vol 29, pp. 87–119. Springer, Cham. 10.1007/978-3-030-10837-3_5. [Google Scholar]
- Emms D., Kelly S. (2018) STAG: species tree inference from all genes. bioRxiv, doi:10.1101/267914.
- Estabrook G. et al. (1975) An idealized concept of the true cladistic character. Math. Biosci., 23, 263–272. [Google Scholar]
- Fitch W.M. (2000) Homology: a personal view on some of the problems. Trends Genet., 16, 227–231. [DOI] [PubMed] [Google Scholar]
- Ganapathy G. et al. (2006) Pattern identification in biogeography. IEEE/ACM Trans. Comput. Biol. Bioinform., 3, 334–346. [DOI] [PubMed] [Google Scholar]
- Hallett M.T., Lagergren J. (2000) New algorithms for the duplication-loss model. In: Proceedings of the Fourth Annual International Conference on Computational Molecular Biology, RECOMB ‘00, New York, NY, pp. 138–146. ACM.
- Hasić D., Tannier E. (2019) Gene tree species tree reconciliation with gene conversion. J. Math. Biol., 78, 1981–2014. [DOI] [PubMed] [Google Scholar]
- Jacox E. et al. (2016) ecceTERA: comprehensive gene tree-species tree reconciliation using parsimony. Bioinformatics, 32, 2056–2058. [DOI] [PubMed] [Google Scholar]
- Jarvis E.D. et al. (2014) Whole-genome analyses resolve early branches in the tree of life of modern birds. Science, 346, 1320–1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu S., Bansal M.S. (2018) On the impact of uncertain gene tree rooting on duplication-transfer-loss reconciliation. BMC Bioinform., 19, 21–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lafond M. et al. (2018) Accurate prediction of orthologs in the presence of divergence after duplication. Bioinformatics, 34, i366–i375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai H. et al. (2017) Fast heuristics for resolving weakly supported branches using duplication, transfers, and losses In: RECOMB International Workshop on Comparative Genomics, pp. 298–320. Springer, Cham. [Google Scholar]
- Leebens-Mack J.H. et al. (2019) One thousand plant transcriptomes and the phylogenomics of green plants. Nature, 574, 679–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legried B. et al. (2020) Polynomial-time statistical estimation of species trees under gene duplication and loss. In: Schwartz,R. (ed) Research in Computational Molecular Biology (RECOMB). Lecture Notes in Computer Science, vol 12074. pp. 120-135. Springer, Cham. doi: 10.1007/978-3-030-45257-5_8. [DOI] [PubMed]
- Mirarab S. et al. (2014) ASTRAL: genome-scale coalescent-based species tree estimation. Bioinformatics, 30, i541–i548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molloy E.K., Warnow T. (2018) To include or not to include: the impact of gene filtering on species tree estimation methods. Syst. Biol., 67, 285–303. [DOI] [PubMed] [Google Scholar]
- Moreira D., Philippe H. (2000) Molecular phylogeny: pitfalls and progress. Int. Microbiol., 3, 9–16. [PubMed] [Google Scholar]
- Muhammad S.A. et al. (2018) Species tree-aware simultaneous reconstruction of gene and domain evolution. bioRxiv, doi:10.1101/336453.
- Rabiee M. et al. (2019) Multi-allele species reconstruction using ASTRAL. Mol. Phylogenet. Evol., 130, 286–296. [DOI] [PubMed] [Google Scholar]
- Rasmussen M.D., Kellis M. (2012) Unified modeling of gene duplication, loss, and coalescence using a locus tree. Genome Res., 22, 755–765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson D.F., Foulds L.R. (1981) Comparison of phylogenetic trees. Math. Biosci., 53, 131–147. [Google Scholar]
- Ronquist F., Huelsenbeck J.P. (2003) MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics, 19, 1572–1574. [DOI] [PubMed] [Google Scholar]
- Sanderson M.J., McMahon M.M. (2007) Inferring angiosperm phylogeny from EST data with widespread gene duplication. BMC Evol. Biol., 7, S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stamatakis A. (2014) RAxML Version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics, 30, 1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sousa da Silva A.W. et al. (2014) Big data and other challenges in the quest for orthologs. Bioinformatics, 30, 2993–2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuffley C., Steel M. (1997) Links between maximum likelihood and maximum parsimony under a simple model of site substitution. Bull. Math. Biol., 59, 581–607. [DOI] [PubMed] [Google Scholar]
- Ullah I. et al. (2015) Species tree inference using a mixture model. Mol. Biol. Evol., 32, 2469–2482. [DOI] [PubMed] [Google Scholar]
- Vachaspati P., Warnow T. (2016) FastRFS: fast and accurate Robinson-Foulds Supertrees using constrained exact optimization. Bioinformatics, 33, 631–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warnow T. (2017) Computational Phylogenetics: An Introduction to Designing Methods for Phylogeny Estimation. Cambridge University Press, Cambridge UK. [Google Scholar]
- Wehe A. et al. (2008) DupTree: a program for large-scale phylogenetic analyses using gene tree parsimony. Bioinformatics, 24, 1540–1541. [DOI] [PubMed] [Google Scholar]
- Wickett N.J. et al. (2014) Phylotranscriptomic analysis of the origin and early diversification of land plants. Proc. Natl. Acad. Sci. USA, 111, E4859–E4868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C. et al. (2018) ASTRAL-III: polynomial time species tree reconstruction from partially resolved gene trees. BMC Bioinform., 19, 153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C. et al. (2019) ASTRAL-Pro: quartet-based species tree inference despite paralogy. bioRxiv, doi:10.1101/2019.12.12.874727. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.