Robust and accurate deconvolution of tumor populations uncovers evolutionary mechanisms of breast cancer metastasis

Abstract

Motivation

Cancer develops and progresses through a clonal evolutionary process. Understanding progression to metastasis is of particular clinical importance, but is not easily analyzed by recent methods because it generally requires studying samples gathered years apart, for which modern single-cell sequencing is rarely an option. Revealing the clonal evolution mechanisms in the metastatic transition thus still depends on unmixing tumor subpopulations from bulk genomic data.

Methods

We develop a novel toolkit called robust and accurate deconvolution (RAD) to deconvolve biologically meaningful tumor populations from multiple transcriptomic samples spanning the two progression states. RAD uses gene module compression to mitigate considerable noise in RNA, and a hybrid optimizer to achieve a robust and accurate solution. Finally, we apply a phylogenetic algorithm to infer how associated cell populations adapt across the metastatic transition via changes in expression programs and cell-type composition.

Results

We validated the superior robustness and accuracy of RAD over alternative algorithms on a real dataset, and validated the effectiveness of gene module compression on both simulated and real bulk RNA data. We further applied the methods to a breast cancer metastasis dataset, and discovered common early events that promote tumor progression and migration to different metastatic sites, such as dysregulation of ECM-receptor, focal adhesion and PI3k-Akt pathways.

Availability and implementation

The source code of the RAD package, models, experiments and technical details such as parameters, is available at https://github.com/CMUSchwartzLab/RAD.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Breast cancer is the second most common cause of death in women (Lin et al., 2004), with metastasis the dominant mechanism by which breast cancer results in mortality (Riihimäki et al., 2018). Although the overall survival of breast cancer patients has improved substantially in recent decades, there are usually limited treatment options once metastasis has occurred (Guan, 2015). Understanding how tumors evolve, and especially how they evolve across the metastatic transition, is thus crucial in further understanding and preventing cancer mortality.

Cancers develop through a process of clonal evolution, in which populations of genetically distinct tumor cells evolve and adapt functionally coordinate with interaction with various non-cancerous stromal cell populations (Beerenwinkel et al., 2016). Metastasis occurs when a population of tumor cells escape normal controls on cell growth, migrate to a distant site and successfully establish themselves in that site and continue to develop (Riihimäki et al., 2018). Because of its medical importance, the metastatic transition has been the focus of intensive prior study (Nguyen et al., 2009). It is particularly important to understand this process at a clonal level if we wish to identify those tumors at particular risk for metastasis and find markers and potential therapeutic targets specific to their metastatic clones (Tao et al., 2019a).

Previous research has revealed multiple recurrent features common to breast cancer metastasis, such as dramatic perturbations in the PI3K-Akt, RET and ErbB pathways based on the paired transcriptome of breast primary and brain metastatic sites (Priedigkeit et al., 2017b; Vareslija et al., 2018). Methods for tumor phylogenetics (Schwartz and Schäffer, 2017), i.e. inference of evolutionary trees on tumor cell populations, have proven powerful for characterizing genomics of progression processes, including in metastatic progression. Past research has shown that deconvolution and phylogenetic methods allow one to infer evolutionary trajectories in breast cancer brain metastases from either bulk genomic or transcriptomic alterations (Brastianos et al., 2015; Körber et al., 2019; Tao et al., 2019b). However, much remains unknown, including whether one can reliably identify those clones most susceptible to metastasis and whether the premetastatic genomics of these clones or their subsequent evolutionary trajectories influence their eventual metastatic sites (brain, ovary, bone and gastrointestinal tract).

Much of the current advances in tumor phylogenetics are coming from single-cell sequencing technologies, such as single-cell RNA-Seq (scRNA) and single-cell DNA-Seq (scDNA), which allow one to characterize clonal heterogeneity with precision (Navin, 2015). In practice, though, these kinds of data are rarely available for matched primary and metastatic samples. Such studies depend on analyzing paired samples generally gathered years apart, where primary tumors are generally archived and no longer amenable to single-cell analysis. While rapid autopsy studies (Alsop et al., 2016) are beginning to recruit cohorts in which data can be gathered promptly at both initial diagnosis and mortality, the difficulty of recruiting subjects and cost of gathering comprehensive single-cell data makes it still prohibitive to gather paired single-cell data for reasonable sizes of study cohort. In contrast, matched bulk data, e.g. RNA-Seq of both breast primary and metastatic samples, are easier to acquire when one or both samples have been archived (Zhu et al., 2019). Inferring clonal evolution from paired archived samples is thus still dependent on an older class of method that sought to study cancer at the clonal level through deconvolution (unmixing) of genomic data from bulk samples (Beerenwinkel et al., 2005).

Here we build on our past work in developing deconvolution methods for understanding the metastatic transition (Tao et al., 2019b). Our contributions in this work are twofold. Methodologically, we proposed and developed a tool kit called robust and accurate deconvolution (RAD), the core algorithm of which takes bulk RNA as input, and infers the expressions and proportions of groups of associated tumor cells, which we denote cell communities. We refer readers to Section 2.2 and Section 3.3 for the major novelty and advancement of RAD, and the differences between RAD and previous deconvolution algorithms such as NMF (Lee and Seung, 2000), Geometric Unmixing (Schwartz and Shackney, 2010), LinSeed (Zaitsev et al., 2019) and NND (Tao et al., 2019b). We show that RAD can automatically identify correct numbers of cell populations and identify perturbed biomarkers, such as cancer pathways. We validated its superiority over alternative deconvolution algorithms through comprehensive validations on both simulated and real datasets. Biologically, we applied the RAD algorithm to transcriptomic data from matched breast cancer primary and metastatic samples (Basudan et al., 2019; Priedigkeit et al., 2017a,b; Zhu et al., 2019), extending our prior analysis of brain metastasis specifically (Tao et al., 2019b) to consider variations across multiple metastatic sites. We further applied a refined phylogeny inference algorithm to trace the evolutionary trajectories from the primary tumor to different metastatic sites (Tao et al., 2019b). Our analysis showed that although the breast tumors of different metastatic types encompass heterogeneous and distinct cell populations, there exist common patterns of perturbed pathways detected at the early stage of primary breast cancer, suggesting that our framework might shed light on early diagnostic and treatment options.

2 Materials and methods

2.1 Overview

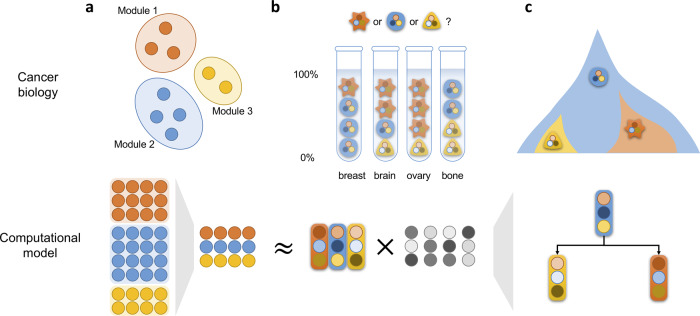
Figure 1 illustrates the general approach for unmixing bulk RNA from paired breast cancer metastatic samples and inferring underlying tumor evolutionary processes. To reduce the noise of bulk RNA, we first compress the expression levels of individual genes into the modules using external knowledge bases (Fig. 1a; Section 2.2.2). We then apply a novel RAD algorithm to unmix the compressed expression data into expression profiles and fractions of individual cell communities (Fig. 1b; Section 2.2). Finally, we infer the evolutionary trajectories of the unmixed tumor communities. We then analyze perturbed biomarkers, such as activity of cancer-related regulatory pathways, during tumor metastasis (Fig. 1c; Section 2.3).

Fig. 1.

Illustration of discovering underlying cancer evolutionary mechanisms of metastatic progression using the proposed computational models. (a) Gene module compression. Genes from the same modules have similar coexpression patterns. By mapping the individual genes into modules, we can get a cleaner representation of bulk RNA data. (b) Deconvolution of bulk RNA. Using the RAD algorithm, we unmixed the bulk data into two matrices: expression matrix and fraction matrix, which represent the expression profile and fractions of individual cell populations. (c) Phylogeny inference of cell communities. The inferred phylogeny represents the most likely evolutionary trajectories of cell populations

Note that our overall goal is to deconvolve tumor cell communities (Tao et al., 2019b), as opposed to necessarily single cells, and describe their evolution across the metastatic transition. A cell community is defined as one or more cell types with potentially distinct expression profiles that share common mixture proportions across samples, indicative of their possible interaction or coassociation in the tumor. For example a set of immunogenic tumor clones and the immune cell types infiltrating them may form a community exhibiting an overall expression pattern that is a mixture of those of its constituent cell types. Although our deconvolution algorithm can identify correct numbers of distinct clones when they are mixed in distinct proportions in different samples (Section 3.2), it is more proper to interpret results as describing cell communities when the sample size is small or when tumor cells may associate or coevolve with their stroma (Beerenwinkel et al., 2016).

2.2 RAD: toolkit for robust and accurate deconvolution

We proposed and developed the toolkit called RAD. RAD is a set of tools that solves the problem of (i) estimating the number of cell communities from bulk RNA, (ii) unmixing the cell communities from bulk data and (iii) inferring other biomarkers such as pathways from the deconvolved communities. Table 1 shows an example of applying RAD to a common RNA deconvolution problem.

Table 1.

Functions in the RAD package

Function	Demo code
compress_module	B_M = compress_module(B, module)
estimate_number	k = estimate_number(B_M)
estimate_clones	C_M, F = estimate_clones(B_M, k)
estimate_marker	C_P = estimate_marker(B_P, F)
	C = estimate_marker(B, F)

Note: The five-line demo shows a typical application of RAD package, which takes as input the bulk RNA data $\mathbf{B}$, bulk marker data ${\mathbf{B}}_{\mathrm{P}}$ and gene module knowledge, and outputs deconvolved RNA $\mathbf{C}$, biomarker ${\mathbf{C}}_{\mathrm{P}}$, and fractions $\mathbf{F}$.

RAD is different from the traditional non-negative matrix factorization (NMF; Lee and Seung, 2000) widely used in this problem domain. First, RAD considers a biologically meaningful unmixing problem (Section 2.2.1), which has additional constraints that make it much harder to solve than the general NMF problem. Although there exist many NMF variants that consider different regularizations, such as NMF with ${\ell }_1$-norm (Shen et al., 2014) and sparseness (Hoyer, 2004), these NMF algorithms mainly consider the prior of data distribution instead of the biological feasibility. As far as we know, the only algorithm that solves this specific deconvolution problem is our gradient descent-based NND method (Tao et al., 2019b). Algorithms derived from the widely used multiplicative update (MU) rules do not necessarily guarantee the convergence or accuracy in this new scenario (Lei et al., 2020a,b), a problem that RAD tackles by using a hybrid solver. Second, NMF is fragile since the unmixed matrices may be distinct given a different initialization seed. In contrast, RAD uses both the prior knowledge of gene modules and the minimum similarity criteria to generate robust and reliable output. Finally, RAD is a toolkit that aims to resolve a series of problems in the deconvolution of bulk RNA, whereas NMF mainly focuses on optimizing the objective function efficiently.

2.2.1 Deconvolution problem formulation

Given a non-negative bulk RNA-Seq expression matrix $\mathbf{B}\in {\mathbb{R}}_{+}^{m\times n}$, where each row i is a gene, each column j is a tumor sample, our goal is to infer an expression profile matrix $\mathbf{C}\in {\mathbb{R}}_{+}^{m\times k}$, where each column l is a cell community, and a fraction matrix $\mathbf{F}\in {\mathbb{R}}_{+}^{k\times n}$, such that: $\mathbf{B}\approx \mathbf{C}\mathbf{F}$. To be more concrete, we formulated the problem, as in our prior work (Tao et al., 2019b), as follows:

$$\underset{\mathbf{C},\mathbf{F}}{\min }\hspace{1em}{\Vert \mathbf{B}-\mathbf{C}\mathbf{F}\Vert }_{\text{Fr}}^2,$$ (1)

$$\mathrm{s}.\mathrm{t}.\hspace{1em}{C}_{il}\ge 0, \hspace{1em}\hspace{0.17em}i=1,\dots ,m,\hspace{0.17em}l=1,\dots ,k,$$ (2)

$${\mathbf{F}}_{lj}\ge 0, \hspace{0.17em}l=1,\dots ,k,\hspace{0.17em}j=1,\dots ,n,$$ (3)

$$\sum _{l=1}^k{\mathbf{F}}_{lj}=1, \hspace{0.17em}j=1,\dots ,n,$$ (4)

where $\left|\right|\mathbf{X}|{|}_{\text{Fr}}$ is the Frobenius norm. The column-wise normalization of Equation (4) ensures that the total fractions of all cell communities in the same sample sum up to one. This optimization problem is non-convex and non-trivial to resolve. In addition, the bulk data $\mathbf{B}$ is noisy, so even an optimal solution does not necessarily fit the ground truth $\mathbf{C}$ and $\mathbf{F}$. Our overall approach to solve for this problem consists of three phases—a randomized warm-start procedure to develop an initial guess as to a solution, coordinate descent optimization to improve fit to the objective, and a minimum similarity selection procedure to identify the most informative partitioning among a set of random restarts—as described in more detail below.

2.2.2 Knowledge-driven gene module compression

By default, RAD unmixes the raw expression matrix $\mathbf{C}$ directly. However, gene module compression (compress_module) is a suggested option if we have prior information on what genes belong to the same gene modules. Gene expressions within the same gene modules are highly correlated, which can be explained by their shared genomic context, similar biological functions, or participation in the same interaction network (Tao et al., 2020). Intuitively, we can compress the noisy expressions of individual genes into cleaner ‘gene modules’ (Desmedt et al., 2008; Park et al., 2009), to reduce the signal-to-noise ratio (SNR).

Here we utilize the functional annotation clustering tool in DAVID to group the top 3000 most varied genes into around 100–200 modules (Huang et al., 2009), where multiple external knowledge databases are used to facilitate the clustering. The gene expressions within the same module are averaged to get the module expression value. The resulting bulk compressed module matrix is ${\mathbf{B}}_{\mathrm{M}}\in {\mathbb{R}}_{+}^{m_1\times n}$, where m₁ is the total number of modules.

The gene module compression in our work is knowledge-driven, which is reliable even when only limited tumor samples are available, in contrast to prior work using data-driven clustering of coexpressed genes (Zaitsev et al., 2019), which is more dependent on large sample sizes. We validate the superiority of knowledge-driven compression over data-driven compression on a real dataset (Fig. 4b and e), and the effect of such knowledge-driven compression (Fig. 4d and e) in Section 3.3.

Fig. 4.

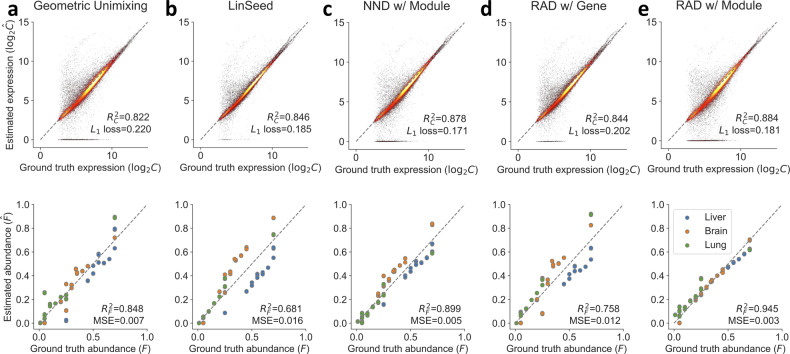
Performance of different deconvolution algorithms on GSE19830 dataset. We compared the accuracy of both estimated $\mathbf{C}$ and $\mathbf{F}$ across four different deconvolution algorithms. RAD with the module achieves best the performance among all the deconvolution algorithms evaluated in $R_{\mathrm{C}}^2,\hspace{0.17em}{R}_{\mathrm{F}}^2$, and MSE. The module information facilitates the RAD to achieve better performance. (a) Geometric Unmixing. (b) LinSeed. (c) NND (with module). (d) RAD (with gene). (e) RAD (with module)

2.2.3 Core algorithm of RAD

The core algorithm of RAD (estimate_clones) unmixes the compressed bulk RNA data ${\mathbf{B}}_{\mathrm{M}}$ into expression profiles ${\mathbf{C}}_{\mathrm{M}}$ and fractions $\mathbf{F}$ of individual communities. The method works in three phases—warm-start, coordinate descent and minimum similarity selection—to achieve accuracy and robustness. RAD can directly unmix the original bulk RNA data $\mathbf{B}$ as well, and we will remove the subscript _M in this section for simplicity.

Warm-start The warm-start phase borrows its idea from the MU rules for the general NMF problem (Lee and Seung, 2000). It first randomly initializes $\mathbf{C}$ and $\mathbf{F}$ from the uniform distribution U(0, 1) then iterates the following loop until the objective function converges:

$$\mathbf{C}\leftarrow \mathbf{C}\odot \left(\mathbf{B}{\mathbf{F}}^{⊺}\right)\oslash \left(\mathbf{C}\mathbf{F}{\mathbf{F}}^{⊺}\right),$$ (5)

$$\mathbf{F}\leftarrow \mathbf{F}\odot \left({\mathbf{C}}^{⊺}\mathbf{B}\right)\oslash \left({\mathbf{C}}^{⊺}\mathbf{C}\mathbf{F}\right),$$ (6)

$${\mathbf{F}}_{lj}\leftarrow {\mathbf{F}}_{lj} /\sum _{l\prime =1}^k{\mathbf{F}}_{l\prime j}, \hspace{1em}\hspace{0.17em}l=1,\dots ,k,\hspace{0.17em}j=1,\dots ,n,$$ (7)

where $\odot$ and $\oslash$ are element-wise product and element-wise division operators. We add an additional MU step, Equation (7), to the original two MU steps, Equations (5) and (6), to satisfy the constraint Equation (4). This deteriorates the convergence guarantee of the original MU rules. Therefore, we have to stop the update once the objective stops decreasing. However, the revised MU rules in the warm-start phase still have the advantage of fast convergence even when the initial values of $\mathbf{C}$ and $\mathbf{F}$ are far from optimal solution, and can provide a reasonable starting point for the second phase.

Coordinate descent After the warm-start phase, the coordinate descent phase optimizes over the two coordinates $\mathbf{C}$ and $\mathbf{F}$ iteratively until the objective function converges:

$$\mathbf{C}\leftarrow \arg \underset{\mathbf{C}}{\min }\hspace{1em}{\Vert \mathbf{B}-\mathbf{C}\mathbf{F}\Vert }_{\text{Fr}}^2,$$ (8)

$$\mathrm{s}.\mathrm{t}.\hspace{1em}{\mathbf{C}}_{\text{il}}\ge 0, \hspace{1em}\hspace{0.17em}\mathrm{i}=1,\dots ,\mathrm{m},\hspace{0.17em}\mathrm{l}=1,\dots ,\mathrm{k},$$ (9)

and

$$\mathbf{F}\leftarrow \arg \underset{\mathbf{F}}{\min }\hspace{1em}{\Vert \mathbf{B}-\mathbf{C}\mathbf{F}\Vert }_{\text{Fr}}^2,$$ (10)

$$\mathrm{s}.\mathrm{t}.\hspace{1em}{\mathbf{F}}_{lj}\ge 0, \hspace{1em}\hspace{0.17em}l=1,\dots ,k,\hspace{0.17em}j=1,\dots ,n,$$ (11)

$${\sum }_{l=1}^k{\mathbf{F}}_{lj}=1, \hspace{0.17em}j=1,\dots ,n,$$ (12)

Although the original optimization problem, Equations (1–4), is non-convex, the two subproblems of the coordinate descent are convex and can be solved using general quadratic programming. We used the Python package cvxopt (Andersen et al., 2011). The coordinate descent phase can usually further reduce the loss function by around 5–30% after the warm-start phase, as evaluated on a real dataset GSE19830 (Section 2.5.2; Shen-Orr et al., 2010).

Minimum similarity selection Since the deconvolution problem, Equations (1–4), is non-convex, different initialization values of $\mathbf{C}$ and $\mathbf{F}$ may converge to distinct solutions. We reran the initialization, warm-start and coordinate descent for multiple times (10 in our experiments) and selected the solution with minimum similarity of expression profiles. We defined the unnormalized cosine similarity of a specific solution $\mathbf{C}$ as:

$$\text{cosim}(\mathbf{C})=\sum _{l=1}^{k-1}\sum _{l\prime =l+1}^k{\mathbf{C}}_{·l}^{⊺}{\mathbf{C}}_{·l\prime }.$$ (13)

Biologically, the use of minimum similarity is motivated by the assumption that individual cell communities should be distinct from each other. Minimum similarity performs slightly better than minimum loss on GSE19830 dataset, although the two criteria often overlap empirically.

2.2.4 Estimating number of communities

The core algorithm of RAD infers the $\mathbf{C}$ and $\mathbf{F}$ from $\mathbf{B}$ given a specific number of communities k, which in practice is unknown to us in advance. RAD estimates the number of cell components (estimate_ number) through cross-validation (CV). The estimated/optimal k reflects the trade-off between model bias and the variance.

We take a 20-fold CV as an example: In each fold, 5% of the elements in $\mathbf{B}$ are unseen at the time of training/optimization. At the time of test, the loss is calculated only on these unseen 5% elements. Technically, we realized it by utilizing the mask matrices with the same shape of $\mathbf{B}$: $\mathbf{M},{\mathbf{M}}_{\text{test}}\in {\{0,1\}}^{m\times n}$ ($\mathbf{M}$ is ${\mathbf{M}}_{\text{train}}$. We omit the subscript ${}_{\text{train}}$ for simplicity.), and $\mathbf{M}+{\mathbf{M}}_{\text{test}}=1^{m\times n}$. ${\mathbf{B}}_{ij}$ is blocked when the corresponding position of ${\mathbf{M}}_{ij}=0$. In each fold, 5% of the ${\mathbf{M}}_{\text{test}}$ are 1’s, and 95% of the $\mathbf{M}$ are 1’s. Note that the positions of the 1’s and 0’s are randomly distributed across the whole matrices $\mathbf{M}$ and ${\mathbf{M}}_{\text{test}}$, rather than column-wise or row-wise.

At the time of validation, we can calculate the ‘normalized MSE’ as the CV error on validation set:

$${\Vert M_{\text{test}}\odot \left(B-\widehat{C}\widehat{F}\right)\Vert }_2^2/{\Vert M_{\text{test}}\odot B\Vert }_2^2$$ (14)

At the time of training, we want to optimize the following objective function with the same constraints to Equations (2–4):

$$\underset{\mathbf{C},\mathbf{F}}{\min }\hspace{1em}{\Vert \mathbf{M}\odot \left(\mathbf{B}-\mathbf{C}\mathbf{F}\right)\Vert }_{\text{Fr}}^2.$$ (15)

There exist corresponding algorithms for MU warm-start and coordinate descent phases when a mask $\mathbf{M}$ exists. The MU rules to optimize the masked objective, Equation (15), is similar to Equations (5–7). However, Equations (5) and (6) are revised to the following rules:

$$\mathbf{C}\leftarrow \mathbf{C}\odot \left(\left(\mathbf{M}\odot \mathbf{B}\right){\mathbf{F}}^{⊺}\right)\oslash \left(\left(\mathbf{M}\odot (\mathbf{C}\mathbf{F})\right){\mathbf{F}}^{⊺}\right),$$ (16)

$$\mathbf{F}\leftarrow \mathbf{F}\odot \left({\mathbf{C}}^{⊺}\left(\mathbf{M}\odot \mathbf{B}\right)\right)\oslash \left({\mathbf{C}}^{⊺}\left(\mathbf{M}\odot (\mathbf{C}\mathbf{F})\right)\right).$$ (17)

The coordinate descent iterations of the masked version are the same to the unmasked version, Equations (8–12), except that $\left(\mathbf{B}-\mathbf{C}\mathbf{F}\right)$ in Equations (8) and (10) are replaced with $\mathbf{M}\odot \left(\mathbf{B}-\mathbf{C}\mathbf{F}\right)$. The subproblems of the two masked coordinate descent steps are still quadratic programming problems.

2.2.5 Cancer-related pathway annotation

We further processed the bulk data to derive aggregate biomarkers profiling activity of cancer-related pathways. Although this is not part of the RAD toolkit, we make use of bulk biomarkers and estimates of their activity in individual cell components (Section 2.2.6) to interpret the results of the RAD. We extracted 24 cancer-related pathways and the corresponding genes from the pathways in cancer (hsa05200), breast cancer (hsa05224) and glioma (hsa05214) of the KEGG database (Kanehisa and Goto, 2000). The value of each pathway is the average expression of all genes within it. We mapped the original bulk gene matrix $\mathbf{B}$ into the cancer pathway probes matrix ${\mathbf{B}}_P\in {\mathbb{R}}_{+}^{24\times n}$. Readers can find the list of pathways in Figure 5.

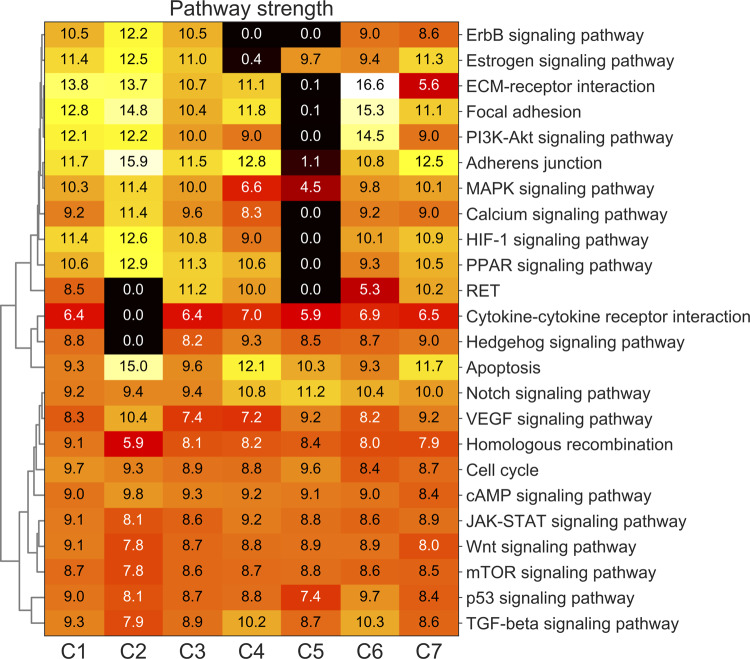
Fig. 5.

Cancer-related pathway strengths of each cell component from BrM dataset. The strengths are shown in log-scale ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2({\mathbf{C}}_{\mathrm{P}}+1)$

Cancer pathways are distinct from gene modules, which capture the major variance across samples and the coexpression patterns using prior knowledge to facilitate more reliable deconvolution. However, coexpression modules are often weakly linked to biological functions and not informative for downstream analysis. In contrast, biomarkers such as cancer-related pathways facilitate functional interpretation of results. We did not use cancer-related pathways or other biomarkers for deconvolution, since they are not representative of the expression profiles.

2.2.6 Pathway estimation of cell communities

Given the bulk cancer pathway data ${\mathbf{B}}_P$, RAD utilizes the deconvolved $\mathbf{F}$ to infer the pathway values of cell populations ${\mathbf{C}}_{\mathrm{P}}$ (estimate_marker), similar to the paradigm of the Digital Sorting Algorithm (DSA; Zhong et al., 2013), by replacing $\mathbf{B}$ and $\mathbf{C}$ with ${\mathbf{B}}_{\mathrm{P}}$ and ${\mathbf{C}}_{\mathrm{P}}$ in Equations (8) and (9). The unmixed $\mathbf{C}$ or ${\mathbf{C}}_{\mathrm{M}}$ may not be easy to interpret. However, other biomarkers, such as cancer pathways, provide a possible way to explain the biological process of each cell community, and can be used as input to infer the phylogeny and perturbed pathways during progression (Section 2.3).

2.3 Phylogeny inference through minimum elastic potential

Given the deconvolved cell clone profiles $\mathbf{C}\in {\mathbb{R}}_{+}^{n\times k}$ of k cell components, we inferred trees describing the observed extant and unobserved ancestral Steiner communities. We use the term ‘phylogeny’ to refer to these trees to highlight their connection to tumor phylogenetics methods often used for similar purposes and on similar data (Schwartz and Schäffer, 2017), although we recognize that these trees describe changes in mean transcriptomic states of groups of associated cells rather than strictly clonal evolution and thus are not proper phylogenies.

RAD works in the original non-log linear space, which recovers underlying components with higher accuracy and lower bias (Zhong and Liu, 2012). In the phylogeny inference algorithm, however, we instead used the log space to focus on the fold change of expressions $\mathbf{C}\leftarrow {\hspace{0.17em}\text{log}\hspace{0.17em}}_2\left(\mathbf{C}+1\right)$. We also normalize the expression to make them have zero mean value for each gene.

We used a variant of the minimum elastic potential (MEP) method to infer the phylogeny structure and expression values of Steiner nodes (Tao et al., 2019b). Taking $\mathbf{C}$ as input, the MEP first builds the phylogeny tree that includes k extant nodes and $(k-2)$ ancestral Steiner nodes using the neighbor-joining algorithm (Nei and Saitou, 1987). To identify the perturbed biological processes and gene expression during tumor evolution, MEP infers expression values of the unknown Steiner nodes by minimizing an ‘elastic potential energy’. For a specific pathway or gene, this is equivalent to a quadratic programming problem:

$$\underset{\mathbf{x}}{\min }\hspace{1em}\frac{1}{2}{\mathbf{x}}^{⊺}\mathbf{P}(\mathcal{W})\mathbf{x}+\mathbf{q}{(\mathcal{W},\mathbf{y})}^{⊺}\mathbf{x},$$ (18)

where $\mathbf{x}\in {\mathbb{R}}^{k-2},\hspace{0.17em}\mathbf{y}\in {\mathbb{R}}^k$ are the expression values of Steiner and extant nodes; $\mathbf{P}(\mathcal{W})$ is a function that takes as input the tree edge weights $\mathcal{W}$ and outputs a matrix $\mathbf{P}\in {\mathbb{R}}^{(k-2)\times (k-2)}$; $\mathbf{q}(\mathcal{W},\mathbf{y})$ is a function that takes as input edge weights $\mathcal{W}$ and vector $\mathbf{y}$ and outputs a vector $\mathbf{q}\in {\mathbb{R}}^{k-2}$. We further added an ${\ell }_2$-regularization $\lambda {\mathbf{I}}^{(k-2)\times (k-2)}$ to the $\mathbf{P}(\mathcal{W})$. In practice we use $\lambda =0.001$, which helps more stable inference when the total number of nodes is large. Interested readers can find detailed problem formulation, derivatives and proofs of MEP in the previous work (Tao et al., 2019b).

Although we used the notation $\mathbf{C}$ for the explanation in this section, in our application, we used the pathway probes ${\mathbf{C}}_P$ to infer the cancer pathway values of each Steiner nodes for downstream interpretation.

2.4 Evaluation

The deconvolution algorithm outputs both the estimated expression profiles $\widehat{\mathbf{C}}$ and the fractions $\widehat{\mathbf{F}}$ of each cell communities. We utilized four different metrics to measure the accuracy and error of the two estimators with the ground truth $\mathbf{C}$ and $\mathbf{F}$ following previous research (Newman et al., 2015; Zaitsev et al., 2019; Zhu et al., 2018): $R_{\mathrm{C}}^2$ (Pearson coefficient of $\widehat{\mathbf{C}}$ and $\mathbf{C}$), L₁ loss (${\Vert \widehat{\mathbf{C}}-\mathbf{C}\Vert }_1/{\Vert \mathbf{C}\Vert }_1$), $R_F^2$ (Pearson coefficient of $\widehat{\mathbf{F}}$ and $\mathbf{F}$), MSE (Mean square error of $\widehat{\mathbf{F}}$ and $\mathbf{F}$).

2.5 Datasets and preprocessing

We utilized three datasets throughout this work: one real dataset of breast cancer metastasis (BrM; Zhu et al., 2019); one real dataset of both pure and mixed transcriptome of liver, brain and lung (GSE19830; Shen-Orr et al., 2010); and one simulated dataset. All three datasets contain bulk transcriptome $\mathbf{B}$, which is the input of RAD and downstream analysis. Ground truths $\mathbf{C},\hspace{0.17em}\mathbf{F}$ are only available in simulated and GSE19830 datasets, and unknown in BrM dataset. Ground truth module knowledge of genes are only available in simulated dataset, GSE19830 and BrM datasets instead used DAVID to infer gene module.

2.5.1 Simulated dataset

We simulated a series of datasets with different parameters of module size (1, 2, 4,…, 512) and noise level $\sigma \in [0,5]$ to validate the effectiveness of RAD and module compression. We selected most of the parameters following Zaitsev et al. (2019), with selected parameters consistent with the distribution of the real dataset GSE19830.

We considered the expression of 2048 interested genes and assumed three pure cell clones $\mathbf{C}\in {\mathbb{R}}_{+}^{2048\times 3}$. In the case where each module consists of just one gene, $\mathbf{C}$ was drawn from a log-normal distribution independently (Bengtsson, 2005):

$${\mathbf{C}}_{il}\sim 2^{\mathcal{N}\left(6,{2.5}^2\right)},\hspace{1em}\hspace{0.17em}i=1,2,\dots ,2048,\hspace{0.17em}l=1,2,3.$$ (19)

We assumed that genes from the same module are highly correlated and prone to coexpress. When module size is greater than one, e.g. there are four genes in a module, for each gene module ${\mathbf{C}}_S\in {\mathbb{R}}_{+}^{4\times 3}$ (a subblock of $\mathbf{C}$), we draw each gene module as follows:

$${\left({\mathbf{C}}_S\right)}_{·l}\sim 2^{\mathcal{N}\left({[6,6,6,6]}^{⊺},{2.5}^2\Sigma \right)},\hspace{1em}\hspace{0.17em}l=1,2,3,$$ (20)

where Σ is the covariance matrix of four genes in the module:

$$\Sigma =\left[\begin{array}{cccc}1& 0.95& 0.95& 0.95\\ 0.95& 1& 0.95& 0.95\\ 0.95& 0.95& 1& 0.95\\ 0.95& 0.95& 0.95& 1\end{array}\right].$$ (21)

We assumed 100 mixture samples of bulk RNA, and drew the fractions of mixture samples uniformly from a unit simplex:

$${\mathbf{F}}_{·j}\sim U[{\Delta }^3],\hspace{1em}\hspace{0.17em}j=1,2,\dots ,100,$$ (22)

Finally, we added the noise of magnitude σ to get the final bulk data:

$${\mathbf{B}}_{ij}\sim {\left(\mathbf{C}\mathbf{F}\right)}_{ij}+2^{\mathcal{N}\left(0,{\sigma }^2\right)},\hspace{0.17em}i=1,2,\dots ,2048,\hspace{0.17em}j=1,2,\dots ,100.$$ (23)

2.5.2 GSE19830 dataset

GSE19830 contains RMA-normalized Affymetrix expressions of cells from rat brain, liver and lung biospecimens (Shen-Orr et al., 2010). It mixed the three pure tissues in different predefined proportions, leading to 33 mixture samples. Expression profiles of each pure and mixed sample were measured three times.

We removed the non-protein coding genes, conducted quantile normalization and took the average of three replicates. This yielded three matrices for the GSE19830 data: expression profiles of the three pure clones $\mathbf{C}\in {\mathbb{R}}_{+}^{13741\times 3}$, fractions of three clones in all mixture data $\mathbf{F}\in {\mathbb{R}}_{+}^{3\times 33}$ and bulk data $\mathbf{B}\in {\mathbb{R}}_{+}^{13741\times 33}$.

2.5.3 BrM dataset

The BrM dataset contains matched transcriptome data of breast cancer metastasis patients (Zhu et al., 2019). There are 102 samples from 51 patients in total. There are four possible different metastatic sites for each breast cancer patient in the dataset: brain (BR; 22 patients), ovary (OV; 13 patients), bone (BO; 11 patients) and gastrointestinal tract (GI; 5 patients). A sample from the primary breast site has a matched sample from the metastatic site of the same patients. RNA-Seq of around 60 000 genes are available. We will denote the sample from the metastatic site and the corresponding primary site as MBR/PBR, MOV/POV, MBO/PBO, MGI/PGI. We removed the non-protein coding genes and conducted quantile normalization to get the final bulk data: $\mathbf{B}\in {\mathbb{R}}_{+}^{19689\times 102}$.

3 Results

3.1 Gene modules facilitate robust deconvolution

RAD can act directly on the bulk gene expression $\mathbf{B}$ or on the knowledge-based compressed bulk gene module expression ${\mathbf{B}}_{\mathrm{M}}$ (Section 2.2.2). We validated that the gene module compression is beneficial to RAD through both simulated data and real datasets.

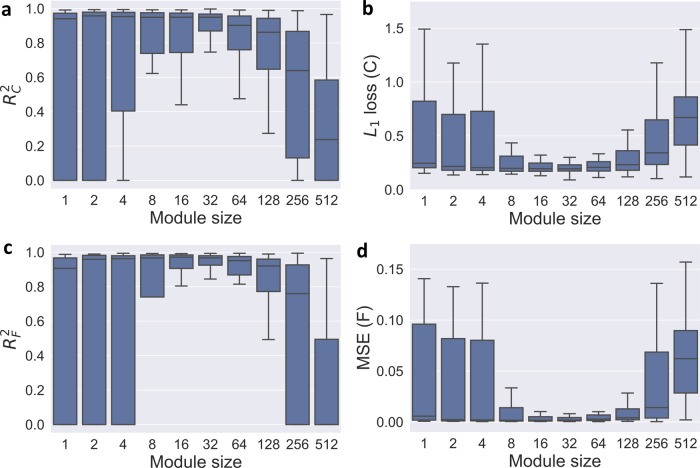
As a proof of concept, we first assume the knowledge of gene modules is correct and known to us. We generated simulated bulk data with a noise level σ = 4 and various module sizes from 1 to 512 (Section 2.5.1). We calculated four metrics to evaluate the accuracy of RAD estimation on these data, and repeated all experiments 100 times (Fig. 2). A moderate module size of 32 makes RAD the most accurate (highest median accuracy) and robust (smallest variance), which is helpful to deconvolution. RAD is less robust (high variance) on the original uncompressed bulk gene data (module size of one). However, when module size is too large, RAD has both inaccurate and unstable performance. We refer interested readers to Supplementary Figure S1 for a more comprehensive result on the effects of both module size and noise level on RAD performance.

Fig. 2.

Effectiveness of gene module representation. Compressing the expression of individual genes into gene modules can promote more robust deconvolution with proper module size. We tested on the simulated bulk data with the noise level of σ = 4, and repeated all the experiments for 100 times to get the boxplot. We evaluated four metrics that measure the accuracy of deconvolution with different gene module sizes. Note that ‘module size’ of one is equivalent to the original gene expression without module compression. (a) Accuracy of expression matrix estimation: $R_{\mathrm{C}}^2$. (b) Error of expression matrix estimation: L₁ loss. (c) Accuracy of fraction matrix estimation: $R_{\mathrm{F}}^2$. (d) Error of fraction matrix estimation: MSE

We further examined whether the module knowledge from DAVID generates a reasonable module size and facilitates robust RAD deconvolution. We applied RAD to both the uncompressed and compressed GSE19830 dataset. As shown in Figure 4d, e, module compression based on DAVID improve the RAD estimation of both $\mathbf{C}$ and $\mathbf{F}$.

We could not directly validate the effectiveness of DAVID compression on unmixing the BrM dataset, but we found the gene module representation informative for separating primary and metastatic samples (Supplementary Fig. S2).

3.2 RAD detects the correct number of cell components

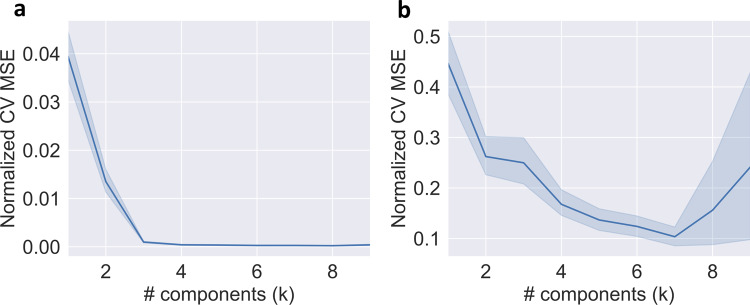
RAD utilizes CV to identify the number of underlying cell populations (Section 2.2.4). To validate its correctness, we applied a 20-fold CV to the GSE19830 data. As shown in Figure 3a, the CV error, Equation (14), drops quickly when the number of cell components k increases from one to three, and flattens after k goes over three. In this case, we identify the correct number of cell clones to be three (Although k =8 gives minimum CV error, it is due to the small noise or artifacts in the samples.).

Fig. 3.

Cross-validation to automatically select the number of cell communities. We conducted a 20-fold cross-validation to infer the optimal number of cell component k as the input of RAD algorithm. (a) Cross-validation on GSE19830 dataset. The actual number of cell clones is three. (b) Cross-validation on BrM dataset. The inferred number of cell components is seven, which is used as the input parameter for Figures 5–7

For the BrM dataset, we applied a 20-fold CV as well and found the CV error drops when k is smaller than seven, and increases with substantial variance because of overfitting when k is higher than seven. We therefore used k = 7 as the number of communities in the BrM data. Previous research using a subset of the BrM dataset (only breast cancer brain metastasis samples) identified only five cell populations (Tao et al., 2019b). With a larger sample size, and more heterogeneous data, we can identify more fine-grained unmixed cell communities.

3.3 RAD estimates cell populations robustly and accurately

We then evaluated the accuracy and error of RAD relative to alternative deconvolution algorithms. There are many algorithms to solve the ‘partial deconvolution’ problem, where the expression profiles of clones $\mathbf{C}$ are available at the time of deconvolution, e.g. DSA (Zhong et al., 2013). For tumor samples, however, the underlying cell types are often unknown, and partial deconvolution can be unstable. We consider the ‘complete deconvolution’ problem here (Zaitsev et al., 2019), where the expression profiles of populations $\mathbf{C}$ are not available and must be inferred.

There are a few existing algorithms that seem to be suitable for the complete deconvolution problem, e.g. principal components analysis (PCA), independent components analysis (ICA) and NMF. However, none of these algorithms account for the fraction normalization constraints, Equation (4), and PCA and ICA do not guarantee the non-negativity of expression profiles, Equation (2). A few more well-designed algorithms have been developed for the specific complete deconvolution problem, including Geometric Unmixing (Schwartz and Shackney, 2010), LinSeed (Zaitsev et al., 2019) and NND (Tao et al., 2019b):

• Geometric Unmixing: It poses unmixing as a problem from computational geometry by assuming all the bulk samples are located in a simplex, where the corners of the simplex represent the expression profiles of pure clones.

• LinSeed: Based on the observation that genes in the same module are highly correlated to each other. It first identifies these anchor genes through linear correlation. Then it uses a partial deconvolution algorithm DSA to infer the fractions $\mathbf{F}$ and expressions of non-anchor genes $\mathbf{C}$ (Zhong et al., 2013).

• NND: It converts the complete deconvolution problem equivalently into an optimization problem, which can be implemented as a neural network. It uses backpropagation (gradient descent) to optimize.

For RAD, we can directly take as input the bulk gene expression matrix $\mathbf{B}$ (Fig. 4d), or use the more noise-free bulk module expression matrix ${\mathbf{B}}_{\mathrm{M}}$ (Fig. 4e). Although the NND can also take $\mathbf{B}$ or ${\mathbf{B}}_{\mathrm{M}}$ in principle, we only included results of ‘NND w/Module’ (Fig. 4c), due to the intractable training time of ‘NND w/Gene’.

Figure 4 compares the performance of the five deconvolution algorithms and module-compressed variants on the GSE19830 dataset. The gene module compression improves the accuracy of RAD significantly (Fig. 4d and e), consistent with the observations in Figure 2. The RAD on the compressed module data outperforms the other three algorithms in metrics $R_{\mathrm{C}}^2,\hspace{0.17em}{R}_{\mathrm{F}}^2$ and MSE (Fig. 4a–c and e). It also has comparable L₁ loss with the ‘NND w/Module’ algorithm (Fig. 4c and e). These results reveal the superiority and accuracy of the RAD algorithm and module compression.

The elevated accuracy and robustness of RAD over competing algorithms is crucial for downstream analyses such as phylogeny inference. For example RAD reveals a more detailed portrait of perturbed pathways (Section 3.5) during metastasis than our previous NND algorithm (Tao et al., 2019b).

3.4 Landscape of tumor cell communities

We derived the fractions of cell communities in each sample $\mathbf{F}$ using RAD, and further inferred the pathway values of each cell community from ${\mathbf{B}}_{\mathrm{P}}$ and $\mathbf{F}$ (Section 2.2.6). Although there exists inter-tumor heterogeneity across cancer samples, RAD aims to separate the shared features of cell populations across these tumors from sample-specific features as in prior cross-cohort deconvolutional phylogeny studies (Roman et al., 2015; Schwartz and Shackney, 2010) and prior oncogenetic tree methods that do not include a deconvolution step (Desper et al., 2004; Riester et al., 2010).

Expression profiles of cell communities Figure 5 shows the pathway values of each cell population in log scale ${\hspace{0.17em}\text{log}\hspace{0.17em}}_2\left({\mathbf{C}}_{\mathrm{P}}+1\right)$ after applying RAD to the BrM dataset. C5 is the most abnormal community, having lost half of the pathways completely (almost zero expression), including PI3K-Akt, ECM-receptor and Calcium. Another unusual cell community is C2, which is specifically enriched in neurotransmitter and calcium homeostasis functions (Calcium and cAMP; Hofer and Lefkimmiatis, 2007). We hypothesize that C2 might reflect a cell community combining both neural cells and metastatic tumor cells. In contrast, C6, which we infer to approximate the primary breast tumor community, has a relatively high expression of PI3K-Akt (Brastianos et al., 2015) and immune function (Cytokine-cytokine receptor; Zhu et al., 2019).

Distribution of cell communities Figure 6 shows the distribution of cell components across different metastatic sites. We classified the tumor sites into eight categories: MBR/PBR, MOV/POV, MBO/PBO and MGI/PGI (Section 2.5.3). We observe that C6 is always decreased in the metastatic samples, from which we infer it may approximate the primary clones and capture features that distinguish primary clones from metastatic ones in general. Other components are increased in specific metastasis types. For example C1 in OV and BO; C2 in BR, OV and GI; C3 in BR, OV and GI; C4 in BO; C5 in BR, OV and BO; and C7 in BR. This indicates that there exist different cell population mixtures in different metastatic sites, likely in part reflecting site-specific stroma but also revealing commonalities across metastatic sites. We further note that the distribution of cell clones across primary sites is related to their eventual sites of metastasis. This result is suggestive that there may be a signal in the primary clonal composition of whether a primary tumor is likely to metastasize to a particular site, although that suggestion requires further evaluation and validation.

Fig. 6.

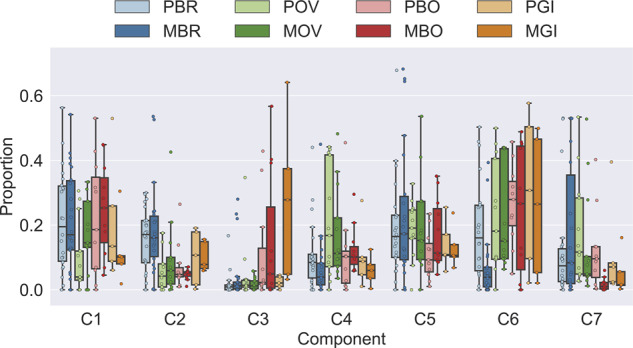
Fractions of communities in both primary and metastatic sites of four different metastasis types from BrM dataset. The differences of cell distribution exist both between primary (lighter) and metastatic (darker) sites, and across four metastatic cases (different colors)

We do not know the ground truth cell populations in the BrM dataset. Given that the component C3 mainly exists in the GI samples (Fig. 6), though, we would predict that removing the GI samples would decrease the optimal number of components from 7 (Fig. 3b) to 6, which is indeed the case (Supplementary Fig. S3).

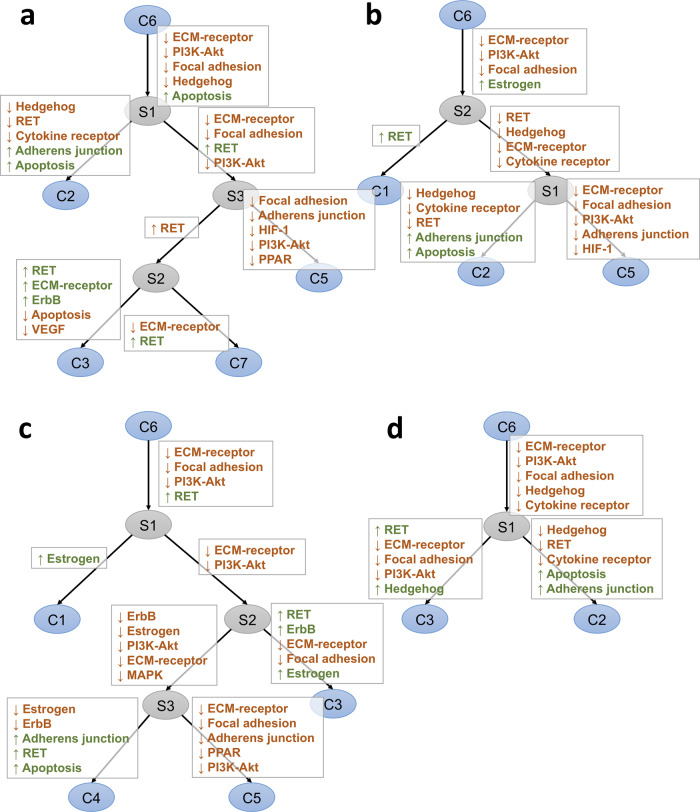
3.5 Common evolutionary mechanisms of breast cancer metastasis

Using the unmixed cell clones ${\mathbf{C}}_{\mathrm{P}}$, we built a phylogeny and inferred the pathway values of Steiner nodes using the MEP algorithm (Section 2.3). Since there are vast differences across the four metastasis types (Fig. 6), we inferred a phylogeny tree for each metastasis type (Fig. 7a–d; Supplementary Tables S1–S4). We presented C6 as the common root node, as it consistently decreases in all four metastasis types, and identified the communities whose average fractions increase in the metastatic communities of specific metastasis types. Figure 7 shows the top five most differentially expressed pathways for more than onefold along each edge.

Fig. 7.

Phylogenies of four different metastatic cases. Although there are large differences in tumor communities across the four metastasis sites, there exists common mechanisms, such as the early events of perturbed PI3K-Akt, ECM-receptor and focal adhesion pathways. (a) Breast cancer brain metastasis. (b) Breast cancer ovary metastasis. (c) Breast cancer bone metastasis. (d) Breast cancer GI metastasis

As shown, there are common patterns at the early stage of metastasis, e.g. the decrease of PI3K-Akt, ECM-receptor interaction and focal adhesion. The loss of PI3K/Akt/mTOR in metastatic tumors has already been identified in brain metastasis research based on both genomic and transcriptomic data (Brastianos et al., 2015; Tao et al., 2019b). Our result indicates the loss of PI3K-Akt pathway is a common event among the general metastasis types as well, not limited to brain metastasis. Loss of ECM-receptor interaction and focal adhesion also plays a critical role in tumor cell migration generically (Nagano et al., 2012). Tumor cells adhere to the extracellular matrix (ECM), forming the structures called focal adhesions and loss of these interactions is a key step in enabling metastatic migration.

There are also substantial differences across metastatic sites that may suggest potential markers of incipient site-specific metastasis. The dysregulation of some perturbed pathways have already been shown to be closely related to tumor progression (Hedgehog, Apoptosis; Gupta et al., 2010). RET and ErbB have been shown recurrently perturbed in metastasis (Priedigkeit et al., 2017b). The reduction of Cytokine-cytokine receptor may reflect the reduced immune cell recruitment in metastatic samples (Zhu et al., 2019).

4 Discussion

We developed a tool called RAD for deconvolution of multi-stage transcriptomic data corresponding to primary and metastatic tumor samples. We have shown that RAD can robustly and accurately estimate the number of cell populations, unmix the cell populations and infer biomarkers from bulk RNA-Seq of tumor samples, while showing improved reliability and accuracy over other deconvolution algorithms on both simulated and real RNA datasets. We applied RAD with gene module compression and a phylogeny inference algorithm to bulk transcriptome data collected from matched breast primary and four different metastatic sites to characterize similarities and variations in tumor clonal populations by eventual site of metastasis. Significant perturbations of cancer-related pathways, such as PI3K-Akt, ECM-receptor and focal adhesion emerge as common early events across sites of breast cancer metastasis, showing the potential of the method to reveal recurrent evolution mechanisms of breast cancer metastasis.

It has been observed that the noise of RNA expression grows with its amplitude, suggesting that a more principled probabilistic model instead of Frobenius norm could potentially further improve the deconvolution accuracy (Zhu et al., 2018). Furthermore, we applied RAD by considering a limited two-stage progression process, without use of the time-series information. One future direction might be extending RAD into a temporal model to take advantage of more precise information on time to metastasis when available or more extensive time-series data on multiple time points such as might be produced by ‘liquid biopsy’ technologies. We mainly focused on transcriptome data in this work, but we expect the RAD algorithm to be versatile and potentially applicable to other types of continuous biological data, such as epigenome and proteome. With moderate adaptations, it is also possible to apply RAD to genome data, which is one major focus of cancer phylogenetics, such as copy number variations (Eaton et al., 2018). While much of the motivation for this work is the difficulty of acquiring scRNA for primary tumor samples when examining metastases years later, we do anticipate that this problem will lessen over time. It is thus worth considering for the future whether our methods might be adapted for working on limited and noisy scRNA with matched bulk data (Elyanow et al., 2020).