Geometric potentials from deep learning improve prediction of CDR H3 loop structures

Abstract

Motivation

Antibody structure is largely conserved, except for a complementarity-determining region featuring six variable loops. Five of these loops adopt canonical folds which can typically be predicted with existing methods, while the remaining loop (CDR H3) remains a challenge due to its highly diverse set of observed conformations. In recent years, deep neural networks have proven to be effective at capturing the complex patterns of protein structure. This work proposes DeepH3, a deep residual neural network that learns to predict inter-residue distances and orientations from antibody heavy and light chain sequence. The output of DeepH3 is a set of probability distributions over distances and orientation angles between pairs of residues. These distributions are converted to geometric potentials and used to discriminate between decoy structures produced by RosettaAntibody and predict new CDR H3 loop structures de novo.

Results

When evaluated on the Rosetta antibody benchmark dataset of 49 targets, DeepH3-predicted potentials identified better, same and worse structures [measured by root-mean-squared distance (RMSD) from the experimental CDR H3 loop structure] than the standard Rosetta energy function for 33, 6 and 10 targets, respectively, and improved the average RMSD of predictions by 32.1% (1.4 Å). Analysis of individual geometric potentials revealed that inter-residue orientations were more effective than inter-residue distances for discriminating near-native CDR H3 loops. When applied to de novo prediction of CDR H3 loop structures, DeepH3 achieves an average RMSD of 2.2 ± 1.1 Å on the Rosetta antibody benchmark.

Availability and Implementation

DeepH3 source code and pre-trained model parameters are freely available at https://github.com/Graylab/deepH3-distances-orientations.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The adaptive immune system of vertebrates is responsible for coordinating highly specific responses to pathogens. In such a response, B cells of the adaptive immune system secrete antibodies to bind and neutralize some antigen. The central role of antibodies in adaptive immunity makes them attractive for the development of new therapeutics. However, rational design of antibodies is hindered by the difficulty of experimental determination of macromolecular structures in a high-throughput manner. Advances in computational modeling of antibody structures provides an alternative to experiments, but computations are not yet sufficiently accurate and reliable.

Antibody structure consists of two sets of heavy and light chains that form a highly conserved framework region (F_c) and two variable regions responsible for antigen binding (F_v). The structural conservation of the F_c is functionally significant, enabling the recognition of different antibody isotypes by their receptors and the F_c lends well to homology modeling. The F_v contains several segments of sequence hypervariability that provide the structural diversity necessary to bind a variety of antigens. This diversity is largely focused in six β-strand loops known as the complementarity determining regions (CDRs). Five of these loops (L1–L3, H1 and H2) typically fold into one of several canonical conformations (Chothia et al., 1989) that are predicted well by existing methods (North et al., 2011). However, the third CDR loop of the heavy chain (H3) is observed in a diverse set of conformations and remains a challenge to model (Almagro et al., 2014; Berrondo et al., 2014; Fasnacht et al., 2014; Maier and Labute, 2014; Shirai et al., 2014; Weitzner et al., 2014; Zhu et al., 2014). Although the CDR loops are sometimes flexible and context-dependent, the change is typically small (<1 Å) between bound and unbound forms (Sela-Culang et al., 2012). Because each antibody CDR H3 sequence evolves in an individual organism, evolutionary sequence history is not generally available [although there are exceptions (Eshleman et al., 2019; Wu et al., 2011)].

Application of deep learning techniques has yielded significant advances in the prediction of protein structure in recent years. At CASP13, AlphaFold (Senior et al., 2020) and RaptorX (Xu, 2019) demonstrated that inter-residue distances could be accurately learned from sequence and coevolutionary features. Both approaches used deep residual network architectures with dilated convolutions to predict inter-residue distances, which provide a more complete structural description than contacts alone. trRosetta built on this progress by expanding beyond distances to predict a set of inter-residue orientations (Yang et al., 2020). This rich set of inter-residue geometries allows trRosetta to outperform leading approaches on the CASP13 dataset, even with a shallower network (Yang et al., 2020).

The effectiveness of inter-residue orientations for discriminating protein structures has also recently been demonstrated by methods such as SBROD and KORP (Karasikov et al., 2019; López-Blanco and Chacón, 2019). SBROD is a single-model quality assessment function that considers inter-residue interactions, backbone atom interactions, hydrogen bonding and solvent-solute interactions. Those features are extracted from a set of decoys from various CASP experiments and the SBROD scoring function is trained via ridge regression (Karasikov et al., 2019). KORP is a knowledge-based potential constructed from a set of six inter-residue geometric descriptors similar to those of trRosetta (López-Blanco and Chacón, 2019). Structures are scored according to a 6D joint probability distribution extracted from a database of non-redundant protein structures.

Our work expands on the progress in general protein structure prediction by applying similar techniques to a challenging problem in antibody structure prediction. Specifically, we propose DeepH3, a deep residual network that learns to predict inter-residue distances and orientations from antibody heavy and light chain sequence alone. When compared to state-of-the-art scoring methods, DeepH3 can identify near-native CDR H3 loops more accurately. When used for de novo prediction of CDR H3 loop structures, DeepH3 produces lower-root-mean-squared distance (RMSD) structures than existing methods.

2 Materials and methods

2.1 Overview

DeepH3 is a deep residual network (He et al. 2016) that learns to predict inter-residue distances and orientations from antibody heavy and light chain sequences. The architecture of DeepH3 draws inspiration from RaptorX (Wang et al., 2017; Xu, 2019), which performed well on general protein structure prediction at CASP13. The relative scarcity of structural data for antibodies compared to general proteins presents challenges (as in any subproblems of structure prediction). We alleviate this limitation by reducing the depth of our network compared to previous methods, and we verify the generalization by examining performance on a highly diverse benchmark dataset. The outputs of DeepH3 are converted into geometric potentials in order to better discriminate between CDR H3 loop structures (decoys) generated using a standard homology modeling approach (Marze et al., 2016) and to predict new CDR H3 loop structures de novo.

2.2 Antibody structure datasets

2.2.1 Benchmark dataset

The Rosetta antibody benchmark dataset consists of 49 F_v structures with CDR H3 loop lengths ranging from 9 to 20 residues (Marze et al., 2016; Weitzner and Gray, 2017). These structures were selected from the PyIgClassify database (Adolf-Bryfogle et al., 2014) based on their quality, with each having resolution of 2.5 Å or better, a maximum R value of 0.2 and a maximum B factor of 80.0 Ų for every atom (Marze et al., 2016; Weitzner and Gray, 2017). The diversity of the set is enhanced by ensuring that no two structures share a common CDR H3 loop sequence, but the set is limited by the restriction to structures from humans and mice.

2.2.2. Training dataset

The training dataset for this work was extracted from SAbDab, a curated database of all antibody structures in the Protein Data Bank (Dunbar et al., 2014). We enforced thresholds of 99% sequence identity and 3.0 Å resolution to produce a balanced, high-quality dataset. This high sequence identity cutoff was chosen due to the high conservation of sequence characteristic of antibodies. In cases where multiple chains existed for the same structure, only the first chain in the PDB file was used. Finally, any structures present in the Rosetta antibody benchmark dataset were removed. These steps resulted in 1433 structures, of which a random 95% were used for model training and 5% were used for validation. This small validation set was found to be sufficient to control for overfitting. Note that testing is carried out on an independent benchmark sharing no structures with the training/validation sets.

2.3 Learning inter-residue geometries from antibody sequence

2.3.1. Input features

Unlike most comparable networks, DeepH3 relies only on amino acid sequence as input. For general protein structure prediction, current methods typically utilize some combination of multiple sequence alignments (MSAs), sequence profiles, coevolutionary data, secondary structures, etc. (Senior et al., 2020; Wang et al., 2017, 2018; Xu, 2019; Yang et al., 2020). While these additional input features provide rich information for general protein structure predictions, each antibody evolves independently in one single organism, and we rarely have relevant evolutionary histories for CDR H3 loop sequences. Thus, we omit sequence alignment data like MSAs. DeepH3 takes as input a one-hot encoded sequence formed by concatenating the target heavy and light chains (F_v) sequences. A chain delimiter is added to the last position in the heavy chain, resulting in an input of dimension L × 21, where L is the cumulative length of the heavy and light chain sequences.

2.3.2. Inter-residue geometries

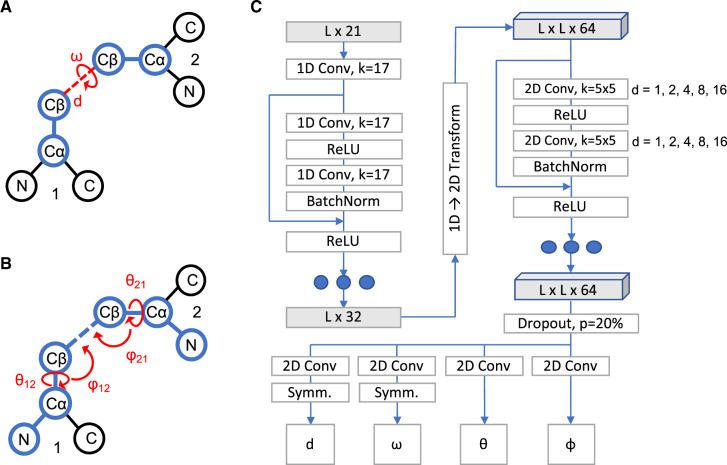
In addition to inter-residue distances, DeepH3 is also trained to predict the set of dihedral and planar angles previously proposed for trRosetta (Yang et al., 2020). For two residues i and j, the relative orientation is defined by six parameters [d, ω, θ_ij, θ_ji, φ_ij and φ_ji, Figure 1A and B, adapted from (Yang et al., 2020)]. The distance (d) is defined using C_β atoms or for glycine residues, C_α. Distances were discretized into 26 bins, with 24 in the range of [4, 16 Å] and two additional bins for all distances below 4 Å or above 16 Å. The dihedral angle ω is formed by atoms C_αi, C_βi, C_βj and C_αj, and the dihedral angle θ_ij is formed by atoms N_i, C_αi, C_βi and C_βj. Both dihedral angles were discretized into 26 equal-sized bins in the range of [–180, 180°]. The planar angle φ_ij is formed by atoms C_αi, C_βi and C_βj. Planar angles were discretized into 26 equal-sized bins in the range of [0, 180°]. Orientation angles were not calculated for glycine residues, due to the absence of the C_β atom.

Fig. 1.

Architecture of DeepH3 deep residual neural network. (A) Illustration of the distance d and dihedral ω for two residues. (B) Illustration of the dihedrals θ₁₂ and θ₂₁ and planar angles θ₁₂ and φ₂₁ for two residues. (C) Architecture diagram of residual neural network to learn inter-residue geometries from concatenated antibody F_v chain sequences

2.3.3. Network architecture

DeepH3 applies a series of 1D and 2D convolutions to the aforementioned sequence input feature to predict four inter-residue geometries, as diagrammed in Figure 1C. The first 1D convolution (kernel size of 17) projects the L × 21 input features up to an L × 32 tensor. Next, the L × 32 tensor passes through a set of three 1D residual blocks (two 1D convolutions with kernel size of 17), which maintain dimensionality. Following the 1D residual blocks, the sequential channels are transformed to pairwise by redundantly expanding the L × 32 tensor to dimension L × L × 32 and concatenating with the transpose, resulting in a L × L × 64 tensor. This tensor passes through 25 2D residual blocks (two 2D convolutions with kernel size of 5 × 5) that maintain dimensionality. Dilation of the 2D convolutions cycles through values of 1, 2, 4, 8 and 16 every five blocks (five cycles in total). Each of the preceding convolutions is followed by a batch normalization. Next, the network branches into four paths, which each apply a 2D convolution (kernel size of 5 × 5) to project down to dimension L × L × 26 (for 26 output bins). Symmetry is enforced for the d and ω branches after the final convolution by summing the resulting tensor with its transpose. The four resulting L × L × 26 tensors are converted to pairwise probability distributions for each output using the softmax function. DeepH3 was implemented using PyTorch (Paszke et al., 2019) and is freely available at https://github.com/Graylab/deepH3-distances-orientations.

2.3.4. Training

Categorical cross-entropy loss was calculated for each output tensor and the resulting losses were summed with equal weight before back propagation. The Adam optimizer was used with an initial learning rate of 0.01 and reduction of learning rate upon plateauing of total loss. Dropout was used after the last 2D residual block, with entire channels being zeroed out at 20% probability. The network was trained using 95% of antibody dataset described above (1388 structures) for 30 epochs. Each epoch utilized the entire training dataset, with a batch size of 4. Training lasted about 35 h using one NVIDIA Tesla K80 GPU on the Maryland Advanced Research Computing Center (MARCC).

2.4 Network predictions as geometric potentials

2.4.1. Implementation

We applied DeepH3 to each sequence in the Rosetta antibody benchmark dataset to produce pairwise probability distributions for the four output geometries. Distributions for pairs of residues that did not include a member of the CDR H3 (according to Chothia number) loop were discarded. Additionally, pairs of residues for which the maximum probability bin of the distance output was greater than 12 Å were discarded to focus on local interactions that are likely to carry biophysical meaning. We also disregarded those predicted distributions that were not informative enough, chosen as those with a maximum probability below 10%. The remaining distributions were converted to potentials by taking the negative natural log of each output bin probability. Continuous, differentiable Rosetta constraints (AtomPair for d, Dihedral for ω and θ and Angle for φ) were created for each potential using the built-in spline function. Within Rosetta, a histogram corresponding to each pairwise potential is fit to a cubic spline. These constraint functions are used calculate the DeepH3 energy term for each structure.

2.4.2. CDR H3 loop discrimination

To test the effectiveness of predicted geometric potentials for discriminating between near-native CDR H3 loops, we collected a set of 2800 decoy structures generated by RosettaAntibody for each of the 49 Rosetta antibody benchmark targets (Marze et al., 2016). These structures were generated by homology modeling, with decoys for each target assuming various heavy/light-chain orientations and non-H3 CDR loop conformations (Marze et al., 2016; Weitzner et al., 2017). After scoring each structure with DeepH3, we compared the discrimination performance to three other state-of-the-art scoring methods: SBROD (Karasikov et al., 2019), KORP (López-Blanco and Chacón, 2019) and the ref2015 full-atom energy function (referred to as Rosetta energy) (Alford et al., 2017).

2.4.3. Discrimination score

The discrimination score is a common metric for measuring the success of structure prediction calculations by assessing whether the minimum energy structures are near-native, with a lower value being indicative of a more successful prediction (Weitzner and Gray, 2017). In order to compare between different energy schemes, we first scale the scores for all decoy structures such that the 95th percentile energy has a value of 0.0 and the 5th percentile energy has a value of 1.0. The discrimination score is then calculated as (Conway et al., 2014):

$$D=\sum _{rϵ\{\mathrm{1,1.5,2},\mathrm{2.5,3},\mathrm{4,6}\}}\underset{i,\mathrm{RMSD}\left(i\right)ϵ[0,r]}{\min }{E}_i-\underset{i,\mathrm{RMSD}\left(i\right)ϵ[r,\mathrm{\infty }]}{\min }{E}_i$$ (1)

where r is the RMSD cutoff in Å, E_i is the scaled energy for the i-th decoy structure, and the discrimination score, D, is the sum of the energy differences for the best scoring decoys above and below each RMSD cutoff.

2.5 De novo prediction of CDR H3 loop structures

2.5.1. DeepH3 prediction on crystal F_v framework

We applied the Rosetta LoopModeler protocol (Mandell et al., 2009; Stein and Kortemme, 2013) to each target in the Rosetta antibody benchmark to build the CDR H3 loop onto the F_v crystal structure (script provided as Supplementary Material). Prior to modeling, the crystallographic loop was extended by setting ϕ and ψ angles to 180° to emulate a blind prediction. Throughout the modeling process, the KIC algorithm was guided only by DeepH3 energy, with all Rosetta energy function terms disabled. For each target, 500 decoys were generated. We elected to use a relatively low number of decoys after observing faster convergence with DeepH3 energy than is typical for Rosetta energy.

2.5.2. TrRosetta heavy chain prediction

The most similar approach to DeepH3 is trRosetta for general protein structure prediction. To better understand the impacts of designing a network specifically for antibody structures, we tested the performance of trRosetta on the Rosetta antibody benchmark using the public trRosetta server (Yang et al., 2020). Because trRosetta was designed to predict the structure of single-chain proteins, we submitted only heavy chain sequences (i.e. omitting the light chain). The five resulting structures were aligned to the heavy chain in the crystal structure to measure the RMSDs of the CDR H3 loop heavy atoms.

3 Results

3.1 DeepH3 accurately predicts inter-residue geometries

To evaluate the accuracy of DeepH3’s predictions, we applied our model to the entire Rosetta antibody benchmark dataset (not seen during training or validation). For residue pairs involving a CDR H3 loop residue, the predicted values for each geometry are plotted against experimental structure values in Figure 2. We limit our analysis to pairs including an H3 loop residue to ensure that DeepH3 is effectively learning the most variable regions of the antibody structure, rather than just the conserved framework. DeepH3 displays effective learning across all outputs; the Pearson correlation coefficients (r) for d and φ were 0.87 and 0.79, respectively, and the circular correlation coefficients (r_c) for dihedrals ω and θ were 0.52 and 0.88, respectively.

Fig. 2.

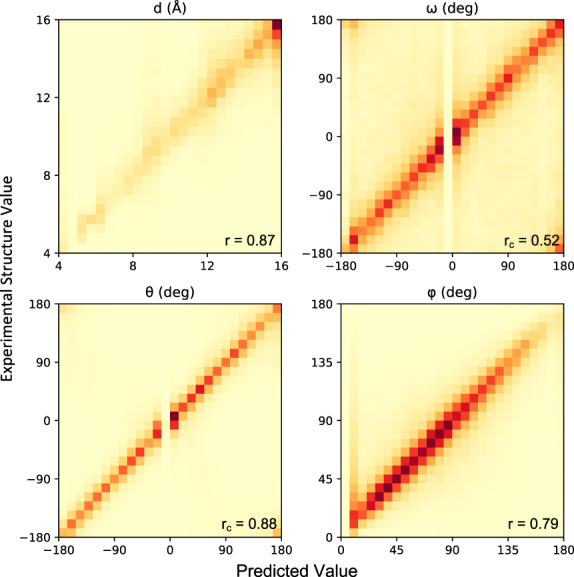
Accuracy of predicted inter-residue geometries. Pearson correlation coefficients (for d and φ) and circular correlation coefficients (for ω and θ) are calculated between DeepH3 predictions and experimental values

3.2 Geometric potentials discriminate near-native CDR H3 loop structures

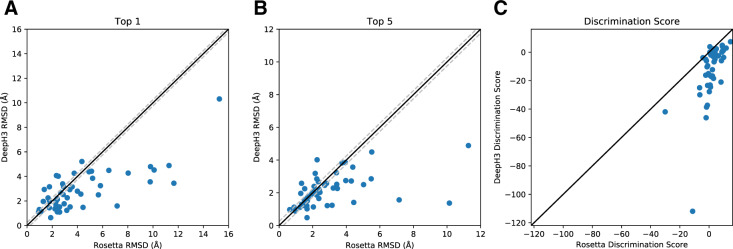
To evaluate the effectiveness of DeepH3 energy for identifying near-native structures, predicted DeepH3 geometric histograms were converted to potentials (Section 2) that were then evaluated on RosettaAntibody generated structure decoys. Reported RMSD values are measured between the heavy atoms of CDR H3 loops after aligning the F_v backbone heavy atoms. When the best-scoring structures (top 1) by Rosetta energy and DeepH3 energy were compared, DeepH3 selected better-, same- and worse-RMSD structures for 33, 6 and 10 out of 49 targets, respectively, with an average RMSD improvement of 1.4 Å (Fig. 3A). When the set of five best-scoring structures (top 5) by Rosetta energy and DeepH3 energy were considered, DeepH3 energy identified a better-, same- and worse-RMSD structures for 24, 16 and 9 out of 49 targets, respectively, with an average RMSD improvement of 0.8 Å (Fig. 3B). We also compared the ability of Rosetta energy and DeepH3 energy to discriminate between decoys for each benchmark target (Fig. 3C, Table 2). The mean discrimination scores for Rosetta energy and DeepH3 energy across the benchmark were 1.7 and –12.2, respectively, indicating that DeepH3 was much more successful in general. When individual targets are considered, DeepH3 energy was successful in discriminating between decoys for 36 out of 49 targets, while Rosetta energy was successful for only 15 out of 49 targets.

Fig. 3.

Effectiveness of predicted inter-residue geometries for decoy discrimination. (A, B) Comparison of the quality of structures selected by Rosetta energy and DeepH3 energy (using all geometric potentials). The quality of structures is considered the same if the difference in RMSD is within ±0.25 Å, indicated with dashed lines. (A) DeepH3 energy selected better-, same- and worse-RMSD structures for 33, 6 and 10 out of 49 targets, respectively, when the best-scoring structures were compared (top 1). (B) When the set of five best-scoring structures were considered (top 5), DeepH3 energy identified better-, same- and worse-RMSD structures for 24, 16 and 9 out of 49 targets, respectively. (C) Comparison of the discrimination scores for Rosetta energy and DeepH3 energy

Table 2.

Discrimination score metrics for DeepH3 energy and several state-of-the-art energy functions

Energy terms	Successful	Unsuccessful	Mean D
SBROD	8	41	3.7
KORP	21	28	0.2
Rosetta	15	34	1.7
DeepH3	36	13	–12.2
d	32	17	–7.4
ω	32	17	–7.8
θ	38	11	–15.6
φ	36	13	–9.6

Notes: DeepH3 energy is further divided into individual inter-residue geometries. Negative discrimination scores, D, are considered successful and positive are considered unsuccessful.

Table 3.

Performance of geometric potentials versus Rosetta energy function for selecting low-RMSD antibody decoys

Energy terms	Top 1				Top 5
	Better	Same	Worse	ΔRMSD	Better	Same	Worse	ΔRMSD
d	27	9	13	–1.1	22	14	13	–0.5
ω	30	8	11	–1.3	26	14	9	–0.4
θ	31	7	11	–1.5	23	13	13	–0.7
φ	29	7	13	–1.4	26	14	9	–0.8

Notes: Top-1 metrics compare the RMSD of the best-scoring structure by Rosetta energy against that of a given DeepH3 potential. Top-5 metrics compare the lowest-RMSD structure among the five best-scoring structures selected by Rosetta energy and that of a given DeepH3 potential. The average difference in RMSD between the structures selected by a given DeepH3 potential and Rosetta energy is reported as ΔRMSD (Å).

To compare against alternative state-of-the-art methods, we also scored the RosettaAntibody decoy using SBROD (Karasikov et al., 2019) and KORP (López-Blanco and Chacón, 2019) (Tables 1 and 2). In a comparison of the top-rated structures from the decoy set, DeepH3 demonstrated improvements over SBROD (38 targets were better, 6 same and 5 worse; average ΔRMSD of –1.8 Å). The comparison of the five top-scoring structures was similar (35 better, 11 same and 3 worse; ΔRMSD = –1.1 Å). In general, SBROD was unsuccessful in discriminating near-native decoys, with only 8 out of 49 benchmark targets having a negative discrimination score and an average D of 3.7. DeepH3 also outperformed KORP among best-scoring structures (32 better, 10 same and 7 worse; ΔRMSD = –0.9 Å) and when comparing the lowest-RMSD structure among the five best-scoring decoys for each target (25 better, 18 same and 6 worse; ΔRMSD = –0.6 Å). KORP was generally unsuccessful in discriminating near-native CDR H3 loop decoys, with only 21 out of 49 targets having negative discrimination scores and an average D = 0.2.

Table 1.

Performance of DeepH3 energy versus alternative methods for selecting low-RMSD antibody decoys

Energy function	Top 1				Top 5
	Better	Same	Worse	ΔRMSD	Better	Same	Worse	ΔRMSD
SBROD	38	6	5	–1.8	35	11	3	–1.1
KORP	32	10	7	–0.9	25	18	6	–0.6
Rosetta	33	6	10	–1.4	24	16	9	–0.8

Notes: Top-1 metrics compare the RMSD of the best-scoring structure by DeepH3 energy against that of a given energy function. Top-5 metrics compare the lowest-RMSD structure among the five best-scoring structures selected by DeepH3 energy and that of a given energy function. The average difference in RMSD between the structures selected by DeepH3 energy and a given energy function is reported as ΔRMSD (Å). ‘Better,’ ‘Same’ and ‘Worse’ indicate the number of targets that achieve a lower, same, or higher RMSD, respectively, when scored by DeepH3.

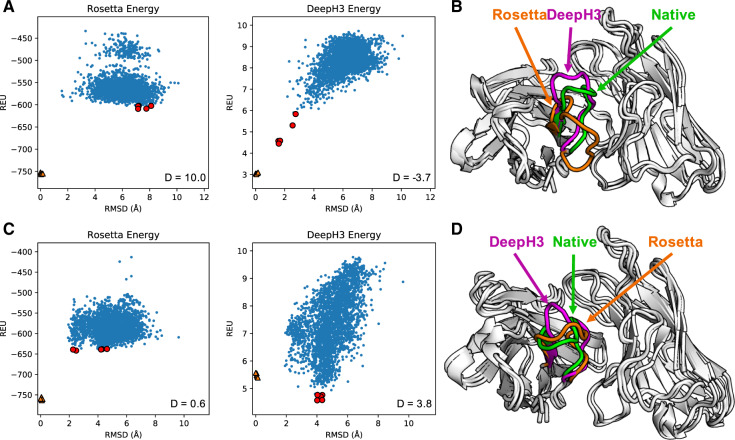
To provide a better understanding of how predicted geometric potentials improve discrimination between CDR H3 structures, we detail two case studies: anti-ALOX12 scF_v (scF_v of mouse antibody with a 12-residue CDR H3 loop, PDB ID: 4H0H) and anti-dansyl mAb (humanized mouse antibody with a 12-residue CDR H3 loop, PDB ID: 1DLF) (Weitzner and Gray, 2017). Figure 4A–C shows energy funnels for anti-ALOX12 and anti-dansyl, respectively, with the discrimination score calculated for each. For anti-ALOX12, Rosetta energy displays little ability to discriminate with structures ranging from 2 to 8 Å RMSD (D = 10.0). DeepH3 energy, however, earns a negative discrimination score (D = –3.7), indicating an ability to easily distinguish the near-native structures. The best scoring anti-ALOX12 decoy structures as selected by Rosetta energy (orange, 7.2 Å RMSD) and DeepH3 energy (violet, 1.6 Å RMSD) are shown in Figure 4B.

Fig. 4.

Results for two Rosetta antibody benchmark targets. (A) Plots of Rosetta energy and DeepH3 energy versus RMSD from the experimental structure for 2800 decoy structures for anti-ALOX12 scF_v. The five best-scoring structures in each funnel plot are indicated in red. Five relaxed native structures are plotted as orange triangles. (B) Experimental structure of anti-ALOX12 scF_v (green) with best-scoring structures by Rosetta energy (orange, 7.2 Å RMSD) and DeepH3 energy (violet, 1.6 Å RMSD). (C) Plots of energy versus RMSD from the experimental structure for anti-dansyl mAb. (D) Experimental structure of anti-dansyl mAb (green) with best-scoring structures by Rosetta energy (orange, 2.5 Å RMSD) and DeepH3 energy (violet, 4.0 Å RMSD)

For anti-dansyl, Rosetta energy is generally unsuccessful in discriminating between decoys (D = 0.6), again with minor energetic differences across a wide range of RMSD values. DeepH3 energy appears to converge to an alternative loop conformation around 4 Å RMSD, resulting in a poor discrimination score (D = 3.8). Figure 4D shows the best-scoring anti-dansyl decoy structures as selected by Rosetta energy (orange, 2.5 Å RMSD) and DeepH3 energy (violet, 4.0 Å RMSD).

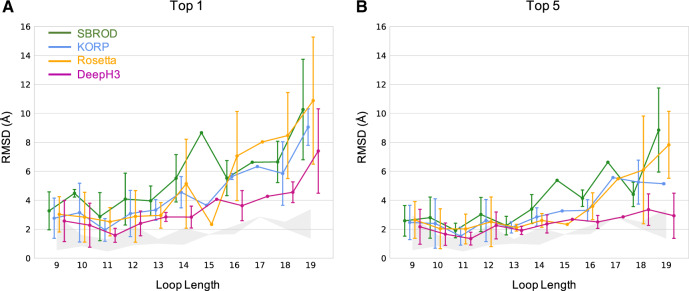
3.3 Longer loops remain a challenge

The Rosetta antibody benchmark dataset encompasses a diverse set of CDR H3 loop lengths. Longer loops introduce greater degrees of freedom (two DOFs per residue), and thus present additional challenges to effective sampling and discrimination. To investigate the performance of DeepH3 across loop lengths, we sub-divided the benchmark targets by length and compared to three alternative scoring methods: SBROD, KORP and the Rosetta energy function (Fig. 5). For nearly every loop length considered, DeepH3 identified the lowest RMSD structures according to the top-1 and top-5 criteria (see above). For several loop lengths, DeepH3 identified decoys near the lowest-RMSD for particular targets in the dataset, as indicated by the shaded region. In general, the average RMSD increased with loop length across all four methods, though DeepH3 displayed notable consistency across loop lengths according to the top-5 criteria.

Fig. 5.

Performance of DeepH3 and alternative methods across various loop lengths. (A and B) Comparison across loop lengths of the error in structures selected by SBROD (green), KORP (blue), Rosetta energy (orange) and DeepH3 score (violet). The shaded areas show the range of lowest RMSD values sampled for targets across loop lengths. (A) Average RMSD of the best-scoring structure (top 1). (B) Average of the lowest-RMSD present within the five best-scoring structures (top 5)

3.4 Orientation potentials are more effective than distance potentials

We also evaluated the utility of individual geometric potentials for selecting low-RMSD decoys (Table 3). Notably, when DeepH3 distance potentials alone were used, performance was only moderately better than Rosetta energy. When the best-scoring structures by Rosetta energy and distance potentials were compared, distance potentials selected better-, same- and worse-RMSD structures for 27, 9 and 13 out of 49 targets, respectively, with an average RMSD improvement of 1.1 Å. When the set of five best-scoring structures by Rosetta energy and distance potentials were considered, DeepH3 energy identified better-, same- and worse -RMSD structures for 22, 14 and 13 out of 49 targets, respectively, with an average RMSD improvement of 0.5 Å. Individual orientation potentials were more effective at selecting low-RMSD decoys than distance, even matching or outperforming the total DeepH3 energy by some metrics. We also calculated discrimination scores for each geometric potential (Table 2). Distance and ω orientation potentials displayed the weakest performance among geometric potentials but still showed significant improvement over Rosetta energy, with 32 out of 49 simulations being successful for both. The other orientation potentials produced more successful simulations and lower mean discrimination scores.

3.5 DeepH3 effectively predicts new CDR H3 loop structures de novo

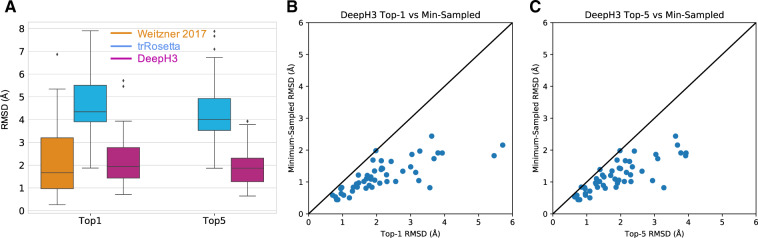
The ultimate goal of DeepH3 was to improve the de novo prediction of CDR H3 loops. Towards this end, we used DeepH3 to create potentials that we then used in Rosetta for de novo structure prediction of the CDR H3 loops (Section 2). The average (± SD) RMSD of the best-scoring structures generated with DeepH3 potentials for each target (top 1) was 2.2 ± 1.1 Å. When the set of five best-scoring structures for each target were considered (top 5), the average RMSD fell to 1.9 ± 0.9 Å. We compare the best-scoring structures generated with DeepH3 potentials to those published by Weitzner et al. (Weitzner and Gray, 2017) (Fig. 6A) and find effectively equivalent performance (ΔRMSD < 0.1 Å) (Top-5 metrics were not reported by Weitzner et al.). The recently published trRosetta provides another deep learning prediction method to compare. trRosetta is trained broadly on diverse protein structures, and DeepH3 has fewer input features (just sequence). trRosetta is designed for single-chain proteins, so we omitted the light chain and predicted structures for the heavy chain alone. On the same benchmark, trRosetta achieves average accuracies of 4.7 ± 1.4 Å (top 1) and 4.3 ± 1.3 Å (top 5, Fig. 6A). Compared to trRosetta, DeepH3’s top-1 and top-5 metrics are 2.5 Å and 2.4 Å RMSD better, respectively.

Fig. 6.

Performance of DeepH3 for de novo CDR H3 loop structure prediction. (A) DeepH3 achieves lower average RMSD (2.2 ± 1.1 Å) than trRosetta (4.7 ± 1.4 Å) and ties Weitzner et al. (2.2 ± 1.5 Å) (Weitzner et al., 2017) when the best scoring structures for each target were compared (top 1). When the lowest-RMSD structure among the five best-scoring structures were considered (top 5), DeepH3 (1.9 ± 0.9 Å) outperformed trRosetta (4.3 ± 1.3 Å). Top-5 metrics were not available for Weitzner et al. (B) Comparison of the minimum RMSD sampled by DeepH3 to the RMSD of the best-scoring structure (top 1) for each target. (C) Comparison of the minimum RMSD sampled by DeepH3 to the lowest RMSD within the set of five best-scoring structures (top 5) for each target.

To better understand the sampling performance of DeepH3, we compared the lowest-RMSD decoy sampled to the best-scoring (top 1, Fig. 6B) and the lowest-RMSD among the five best-scoring (top 5, Fig. 6C). DeepH3 samples structures with sub-angstrom RMSD for 38.8% of the targets and 95.9% for <2 Å. On the other hand, DeepH3 is able to identify a sub-angstrom decoy as the best-scoring structure (top 1) for 14.3% of targets and 55.1% for <2 Å. When considering the set of five best-scoring decoys (top 5), DeepH3 identifies a sub-angstrom decoy for 18.4% of targets and 63.2% for <2 Å. These results are promising and point to possibility of further refining the DeepH3 geometric potentials for de novo prediction.

4 Discussion

The results here suggest that the significant advances by deep learning approaches in general protein structure can also be realized in subproblems in structural modeling. Specifically, we demonstrate that a deep residual network can effectively capture the local inter-residue interactions that define antibody CDR H3 loop structure. DeepH3 achieves these results without MSAs and coevolutionary data, while using significantly fewer residual blocks (3 1D + 25 2D blocks) than similar networks, such as AlphaFold (220 2D blocks) (Senior et al., 2020), RaptorX (6 1D + 60 2D blocks) (Wang et al., 2017; Xu, 2019) and trRosetta (61 2D blocks) (Yang et al., 2020). Fewer blocks may suffice because we limited our focus to antibodies, which are highly conserved, rather than the entire universe of protein structures. By omitting MSAs and coevolutionary, we demonstrate that these features, which have seemed essential to the advances in general protein structure prediction, may not be necessary for some subproblems. In the future, similar specialized networks could achieve enhanced performance in other challenging domains of protein structure prediction, but further research is required.

Breakdown of DeepH3 energy into individual geometric potentials revealed that inter-residue orientations were significantly more effective for scoring CDR H3 loop structures than distances. This finding was surprising, given the improvements that distances alone have enabled in general protein structure prediction. This observation could also underlie the improved performance of trRosetta compared to methods that do not use orientations. Or possibly distance restraints are effective at placing residues globally, but local interactions in loops are captured by inter-residue orientations.

Application of DeepH3 to de novo prediction of CDR H3 loop structures highlights the promise of deep learning in this challenging area. Comparison with the results from Weitzner et al., which leveraged an explicit H3-kink geometric constraint (Weitzner and Gray, 2017), demonstrates that DeepH3 effectively learned challenging features of H3 loop structure. While this work focused only on the CDR H3 loop, we anticipate that applying DeepH3 to other aspects of antibody structure prediction may yield further advances. Because DeepH3 learns from full F_v heavy and light chain sequences, the current network may already capture other critical aspects of antibody structure prediction [V_L–V_H orientations (Marze et al., 2016), non-H3 CDR loop conformations (North et al., 2011) etc.], though future work will be necessary to explore these areas.

Funding

This work was supported by National Institutes of Health grants R01-GM078221 and T32-GM008403 and National Science Foundation Research Experience for Undergraduates grant DBI-1659649. Computational power was provided by the Maryland Advanced Research Computing Cluster (MARCC).

Conflict of Interest: none declared.