Abstract
Study Objectives
Polysomnography is the gold standard for diagnosis of obstructive sleep apnea (OSA) but it is costly and access is often limited. The aim of this study is to develop a clinically useful support vector machine (SVM)-based prediction model to identify patients with high probability of OSA for nonsleep specialist physician in clinical practice.
Methods
The SVM model was developed using the features routinely collected at the clinical evaluation from 6,875 Chinese patients referred to sleep clinics for suspected OSA. Three apnea-hypopnea index (AHI) cutoffs, ≥5/h, ≥15/h, and ≥30/h were used to define the severity of OSA. The continuous and categorized features were selected separately and were further selected through stepwise forward feature selection. The modeling was achieved through fivefold cross-validation. The model discriminative ability was evaluated for the whole data set and four subgroups categorized with gender and age (<65 versus ≥65 years old [y/o]).
Results
Two features were selected to predict AHI cutoff ≥5/h with six features selected for ≥15/h, and six features selected for ≥30/h, respectively, to reach Area under the Receiver Operating Characteristic (AUROC) 0.82, 0.80, and 0.78, respectively. The sensitivity was 74.14%, 75.18%, and 70.26%, while the specificity was 74.71%, 68.73%, and 70.30%, respectively. Compared to logistic regression, Berlin questionnaire, NoSAS Score, and Supersparse Linear Integer Model (SLIM) scoring system, the SVM model performs better with a more balanced sensitivity and specificity. The discriminative ability was best for male <65 y/o and modest for female ≥65 y/o.
Conclusion
Our model provides a simple and accurate modality for early identification of patients with OSA and may potentially help prioritize them for sleep study.
Keywords: machine learning, modeling, polysomnography, prediction, sleep apnea, obstructive
Statement of Significance.
The prediction models for identifying patients with high probability of obstructive sleep apnea (OSA) reported in previous studies tend to have high sensitivity but low specificity which may lead to overprescription of polysomnography. Moreover, physiological signals or physical examination findings are required in some models which may limit their clinical application. This data mining-driven study proposed a support vector machine (SVM)-based prediction model built with 2, 6, and 6 features commonly collected at clinic visits to identify patients with apnea-hypopnea index (AHI) ≥5/h, ≥15/h, and ≥30/h, respectively. The model was fivefold cross-validated and had a balanced sensitivity (74.14%, 75.18%, and 70.26%) and specificity (74.71%, 68.73%, and 70.30%) which performed better than Berlin questionnaire, NoSAS Score, and Supersparse Linear Integer Model (SLIM) scoring system, particularly for man <65 years old.
Introduction
Obstructive sleep apnea (OSA) is characterized by repeated episodes of upper airway obstruction that results in cessation of airflow during sleep [1]. OSA is a common disease with a prevalence of 9%–38% in the general population [2]. Risk factors for OSA included age, male, obesity, smoking, anomalies of craniofacial features, and menopause in women [3]. Symptoms suggestive of OSA included habitual snore, witnessed apnea, choking or gasping at sleep, frequent awakening, nocturia, unrefreshed sleep, and daytime sleepiness [3]. Early diagnosis of OSA is essential because untreated OSA may increase the probability of developing cardiovascular diseases, metabolic disorders, and neurocognitive dysfunctions [4]. The overnight polysomnography (PSG) is the gold standard for the diagnosis of OSA, and the OSA severity is commonly determined by apnea-hypopnea index (AHI) with cutoff ≥5/h for the presence of OSA, ≥15/h for the presence of moderate–severe OSA, and ≥30/h for the presence of severe OSA [2]. However, PSG is costly and the access is often limited. As a result, prioritizing patients with high risk for moderate–severe OSA for PSG can be crucial for many sleep labs.
A recent meta-analysis showed that care of patients with OSA by nonsleep specialist physician (NSSP) and sleep specialist physician brought similar outcomes in terms of mortality, quality of life, adherence, and symptom score. Since most NSSPs in the included studies had extensive training in sleep medicine, the results may be inferior in the NSSP who were less seasoned or inadequately trained [5]. Hence, the development of a screening model based on clinical features commonly collected at clinic visits to predict the likelihood of OSA would be extremely practical for NSSP. Such a model can also help NSSP to prioritize patients with high pretest probability of OSA for PSG [6].
Prediction models reported in the literature were mostly built using clinical features including demographics (age, gender, smoking, alcohol consumption), comorbidities, anthropometrics, OSA symptoms, physical findings [7], and physiologic measurements (e.g. blood pressure, overnight pulse oximetry, and pulmonary function) [8] collected from either sleep lab- or community-based population. Among prediction models proposed so far, the sensitivity to predict AHI ≥5/h ranged from 66% to 100% while specificity ranged from 30.8% to 76.2%, and the sensitivity to predict AHI ≥15/h ranged from 60.3% to 92.7% while specificity ranged from 33.3% to 90.7% (Supplementary Table S1). The wide-range discriminative ability of models could be attributed to the model complexity, number of participants, prevalence of OSA, and imbalance between different OSA severity proportion. Moreover, most prediction models for OSA tend to have a higher sensitivity with a lower specificity to promote early diagnosis (Supplementary Table S1). These models can potentially cause a high false-positive rate and lead to overprescription of PSG. Nevertheless, some models were established based on the data of which patients with comorbidities were excluded [9], where the generalizability of clinical implication would be constrained.
It is also crucial to validate the model efficacy in subgroups categorized with different features. For example, male patients often have fat distributed to the upper body and a higher percentage of snoring than female patients [10, 11]. Elder patients with OSA may be less susceptible to adverse effects of OSA like sleepiness, impaired quality of life, and mortality compared to middle-aged patients [12, 13]. It is also known that the Asian patients have higher AHI compared to body mass index (BMI)-matched Caucasians due to narrower craniofacial features [14].
Machine learning has been found to be a potential means in addressing these problems by its massive parallelism, self-organization, adaptive learning capability, and robustness. support vector machine (SVM) has been increasingly applied in medical healthcare during the past few years since it can provide systematized architecture for analyzing and extracting important information from complex data [15]. Hence, SVM-based machine learning model may be promising for the prediction of OSA.
The present study aimed to propose an easy-to-use and accurate model to identify patients with OSA at three AHI cutoffs (≥5/h, ≥15/h, ≥30/h). We developed a data mining-driven SVM prediction model using a large-scale sleep lab database with features routinely collected at clinic visits. The model discriminative ability was also tested in the subgroups categorized with gender (men versus women) and age (<65 versus ≥ 65 years old (y/o)). The model discriminative ability was also compared with that of logistic regression, Berlin questionnaire (BQ), NoSAS Score, and Supersparse Linear Integer Model (SLIM) scoring system.
Methods
Data set
The data set developed from information prospectively collected from 7,830 adult patients who underwent initial overnight PSG for the first time in the Center of Sleep Disorder of National Taiwan University Hospital between January 2009 and December 2016. For data mining, only patients who had any following conditions were excluded: non-Chinese (n = 11), total recording time <240 min (n = 7), and missing data (n = 936). A total of 6,875 patients, with 5,223 men and 1,652 women (5,985 < 65 y/o and 890 ≥ 65 y/o), were included (Table 1; Supplementary Table S2).
Table 1.
Comparison of clinical features between patients with and without OSA at three AHI cutoffs
| Feature name | Overall (N = 6,875) | AHI < 5 (N = 1,206) | AHI ≥ 5 (N = 5,669) | AHI < 15 (N = 2,664) | AHI ≥ 15 (N = 4,211) | AHI < 30 (N = 4,084) | AHI ≥ 30 (N = 2,791) |
|---|---|---|---|---|---|---|---|
| Age (y/o) | 47.8 ± 14.5 | 40.6 ± 15.1 | 49.4 ± 13.9 | 44.1 ± 15.0 | 50.2 ± 13.7 | 46 ± 14.8 | 50.47 ± 13.8 |
| Man, n (%) | 5,223 (76.0) | 660 (54.8) | 4,563 (80.5) | 1,673 (62.8) | 3,550 (84.3) | 2,798 (68.5) | 2,425 (86.9) |
| BMI (kg/m2) | 27.0 ± 5.0 | 23.5 ± 3.5 | 27.7 ± 4.9 | 24.6 ± 3.9 | 28.4 ± 5.0 | 25.3 ± 4 | 29.3 ± 5.3 |
| Neck circumference (cm) | 37.7 ± 4.1 | 34.6 ± 3.4 | 38.3 ± 4.0 | 35.6 ± 3.7 | 39.0 ± 3.9 | 36.3 ± 3.8 | 39.7 ± 3.8 |
| Waist circumference (cm) | 91.4 ± 13.0 | 80.9 ± 10.2 | 93.6 ± 12.5 | 84.4 ± 10.9 | 95.8 ± 12.3 | 86.8 ± 11.2 | 98 ± 12.7 |
| Current smoker, n (%) | 1,104 (16.1) | 135 (11.2) | 969 (17.1) | 334 (12.5) | 770 (18.3) | 520 (12.7) | 584 (20.9) |
| Alcohol consumption, n (%) | 688 (10.0) | 80 (6.6) | 608 (10.7) | 182 (6.8) | 506 (12.0) | 328 (8) | 360 (12.9) |
| Hypnotic, n (%) | 634 (9.2) | 151 (12.5) | 483 (8.5) | 314 (11.8) | 320 (7.6) | 435 (10.7) | 199 (7.1) |
| Comorbidity | |||||||
| Hypertension, n (%) | 2,021 (29.4) | 126 (10.4) | 1,895 (33.4) | 435 (16.3) | 1,586 (37.7) | 835 (20.4) | 1,186 (42.5) |
| Diabetes, n (%) | 580 (8.4) | 31 (2.6) | 549 (9.7) | 117 (4.4) | 463 (11) | 231 (5.7) | 349 (12.5) |
| CAD, n (%) | 248 (3.6) | 16 (1.3) | 232 (4.1) | 62 (2.3) | 186 (4.4) | 119 (2.9) | 129 (4.6) |
| CHF, n (%) | 101 (1.5) | 6 (0.5) | 95 (1.7)† | 22 (0.8) | 79 (1.9) | 37 (0.9) | 64 (2.3) |
| CVA, n (%) | 124 (1.8) | 5 (0.4) | 119 (2.1) | 31 (1.2) | 93 (2.2)† | 54 (1.3) | 70 (2.5) |
| CKD, n (%) | 62 (0.9) | 7 (0.6) | 55 (1.0)& | 13 (0.5) | 49 (1.2)† | 18 (0.4) | 44 (1.6) |
| COPD, n (%) | 67 (1.0) | 14 (1.2) | 53 (0.9)& | 22 (0.8) | 45 (1.1)& | 37 (0.9) | 30 (1.1)& |
| Asthma, n (%) | 490 (7.1) | 105 (8.7) | 385 (6.8)† | 210 (7.9) | 280 (6.6)& | 321 (7.9) | 169 (6.1)† |
| Hypothyroidism, n (%) | 156 (2.3) | 25 (2.1) | 131 (2.3)& | 63 (2.4) | 93 (2.2)& | 103 (2.5) | 53 (1.9)& |
| Habitual sleep pattern | |||||||
| Habitual SOL (min) | 20.9 ± 22.5 | 25 ± 29.9 | 20 ± 20.5 | 23.7 ± 26.7 | 19.1 ± 19.3 | 22.6 ± 24.2 | 18.4 ± 19.6 |
| Habitual SOL < 30 min, n (%) | 4,794 (69.7) | 770 (63.8) | 4,024 (71.0) | 1,744 (65.5) | 3,050 (72.4) | 2,752 (67.4) | 2,042 (73.2) |
| Habitual sleep duration (h) | 6.6 ± 3.3 | 6.6 ± 2.7 | 6.5 ± 3.5 | 6.5 ± 2.6 | 6.6 ± 3.7† | 6.5 ± 2.8 | 6.6 ± 4& |
| Unrefreshed sleep, n (%) | 3,685 (53.6) | 770 (63.8) | 2,915 (51.4) | 1,613 (60.5) | 2,072 (49.2) | 2,325 (56.9) | 1,360 (48.7) |
| Frequency of awakening in sleep (time/night) | 0.5 ± 1.5 | 0.5 ± 1.5 | 0.6 ± 1.5& | 0.5 ± 1.5 | 0.6 ± 1.5& | 0.5 ± 1.5 | 0.6 ± 1.5 |
| Awakening at sleep ≥3 times/ night | 1,504 (21.9) | 237 (19.7) | 1,267 (22.3)† | 526 (19.7) | 978 (23.2)† | 802 (19.6) | 702 (25.2) |
| ESS | 10.3 ± 4.9 | 10.0 ± 4.9 | 10.4 ± 4.9† | 9.8 ± 4.8 | 10.6 ± 4.9 | 9.9 ± 4.7 | 11 ± 5 |
| EDS, n (%) | 3,764 (54.7) | 628 (52.1) | 3,136 (55.3)† | 1,355 (50.9) | 2,409 (57.2) | 2,098 (51.4) | 1,666 (59.7) |
| Symptom suggestive of OSA | |||||||
| Snoring, n (%) | 5,480 (79.7) | 753 (62.4) | 4,727 (83.4) | 1,912 (71.8) | 3,568 (84.7) | 3,099 (75.9) | 2,381 (85.3) |
| Witnessed apnea, n (%) | 1,066 (15.5) | 79 (6.6) | 987 (17.4) | 221 (8.3) | 845 (20.1) | 417 (10.2) | 649 (23.3) |
| Frequency of nocturia (times/ night) | 1.1 ± 1.2 | 0.9 ± 1.1 | 1.2 ± 1.2 | 1 ± 1.1 | 1.3 ± 1.2 | 1 ± 1.1 | 1.3 ± 1.3 |
| Nocturia ≥2 times/night, n (%) | 2,352 (34.2) | 308 (25.5) | 2,044 (36.1) | 746 (28.0) | 1,606 (38.1) | 1,203 (29.5) | 1,149 (41.2) |
| Witnessed leg jerks in sleep, n (%) | 3,278 (47.7) | 603 (50) | 2,675 (47.2)& | 1,303 (48.9) | 1,975 (46.9)& | 1,974 (48.3) | 1,304 (46.7)& |
| Morning headache, n (%) | 799 (11.6) | 192 (15.9) | 607 (10.7) | 351 (13.1) | 448 (10.6)† | 513 (12.6) | 286 (10.2)† |
| Dry throat at waking up, n (%) | 3,856 (56.1) | 577 (47.8) | 3,279 (57.8) | 1,324 (49.7) | 2,532 (60.1) | 2,132 (52.2) | 1,724 (61.8) |
| AHI (/h) | 29.6 ± 26.0 | 1.9 ± 1.5 | 35.5 ± 24.9 | 6.1 ± 4.5 | 44.5 ± 22.8 | 11.6 ± 8.7 | 56 ± 19.5 |
The data were presented as mean ± standard deviation or number (percentage). CAD, coronary artery disease; CHF, congestive heart failure; CVA, cerebrovascular accident; COPD, chronic obstructive pulmonary disease; CKD, chronic kidney disease. The comparisons between non-OSA and OSA participants were analyzed with the independent t-test and chi-square test. All p-values were <0.001, except for variable marked with & and †, of which the p-values were >0.05 and <0.05, respectively.
Thirty-two clinical features including demographics, anthropometrics, comorbidities, self-reported habitual sleep patterns, and OSA symptoms were collected through self-administered questionnaires and medical records (Table 2). The demographics included age, gender, smoking, alcohol consumption, and hypnotic use defined as taking hypnotics ≥1 time/week over the past month. Anthropometrics included BMI, neck circumference, and waist circumference. Sleep history and OSA symptoms were collected with a self-administered questionnaire (description and definition listed in Supplementary Table S3). Sleep history included unrefreshed sleep, subjective sleepiness, frequency of awakening, awakening ≥3 times/night during sleep, minutes of sleep onset latency (SOL), and hours of sleep duration over the past month. In addition, the SOL < 30 min and the sleep duration categorized as <6 h/day, 6–8 h/day, and ≥8 h/day were added. Subjective sleepiness was assessed by the Sleepiness Scale (ESS) with excessive daytime sleepiness (EDS) defined as ESS ≥ 10 [16]. The OSA symptoms included snore, witnessed apnea, frequency of nocturia, witnessed leg jerks at sleep, morning headache, nocturia ≥2 times/night, and dry throat at wake up.
Table 2.
Thirty-two features input in both SVM model and logistic regression
| Demographics | Anthropometric | Comorbidities | Sleep history | Symptoms suggestive of OSA |
|---|---|---|---|---|
| Age | BMI | Hypertension | SOL (min) | Snore |
| Gender | Neck circumference | Diabetes | SOL < 30 min | Witnessed apnea |
| Alcohol consumption | Waist circumference | CAD | Sleep duration, <6, 6–8, and ≥8 h | Frequency of nocturia (time/night) |
| Current smoking | CHF | Unrefreshed sleep | Nocturia ≥2 times/night | |
| Hypnotics | CVA | Frequency of awakenings at sleep (time/night) | Witnessed leg jerks in sleep | |
| CKD | Awakenings in sleep ≥3 times/night | Morning headache | ||
| COPD | ESS | Dry throat at waking up | ||
| Asthma | EDS | |||
| Hypothyroidism |
CAD, coronary artery disease; CHF, congestive heart failure; CVA, cerebrovascular accident; CKD, chronic kidney disease; COPD, chronic obstructive pulmonary disease.
The BQ consists of three categories including snore, fatigue, and hypertension, with each category including 2–5 questions with a total of 11 questions. Presence of positive responses to two or more categories indicates high risk for OSA [17]. The NoSAS Score is a 5-item questionnaire which includes neck circumference, BMI, snore, age, and gender. With a range of 0–17, NoSAS Score 4 for neck circumference ≥ 40 cm, scores 3 for BMI 25–30 kg/m2, scores 5 for BMI ≥ 30 kg/m2, scores 2 for snoring, scores 4 for >55 y/o, and scores 2 for male gender. The total score ≥ 8 is considered as high risk for OSA [18]. The SLIM scoring system (size 10) is a 10-feature machine learning model which include age, BMI, diabetes, hypertension, smoking, and female gender. The total points >29 is considered as high risk for OSA [19].
All methods were carried out in accordance with relevant guidelines and regulations. The study protocol was approved by the Research Ethics Committee of NTUH (protocol number 201603113RIND) and the need for consent from participants was waived by the Research Ethics Committee.
Polysomnography
Overnight PSG (Embla N7000, Medcare Flaga, Reykjavik, Iceland) was performed as previously reported [20]. Sleep stages and respiratory events were scored according to the 2007 AASM scoring rule [21]. Apnea was defined as ≥90% decrease in airflow for ≥10 s while hypopnea was ≥30% decrease in airflow ≥10 s associated with ≥4% reduction in arterial oxygen saturation. The PSG parameters collected included sleep efficiency, percentage of slow-wave sleep (% SWS) and % rapid eye movement, AHI, oxygen desaturation index (ODI), percentage of total sleep time with SpO2 < 90% (%TST-SpO2 < 90%), and arousal index (AI).
Feature selection and prediction model design
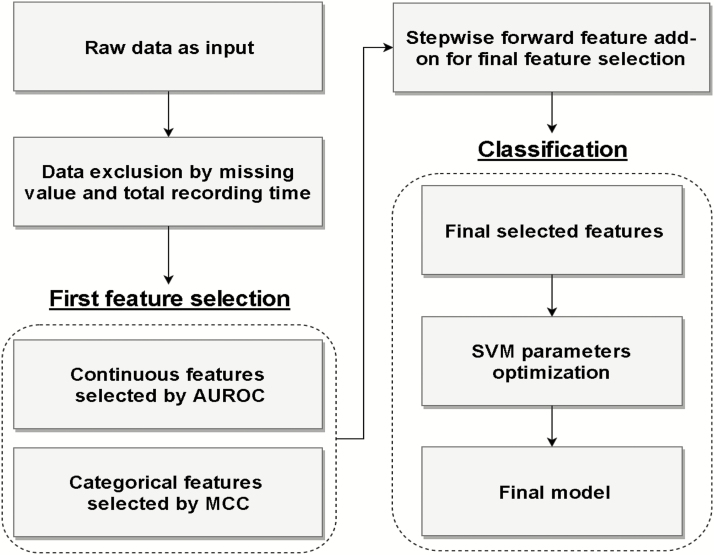
Figure 1 illustrates the flowchart of SVM prediction model development (Supplementary Table S4 shows the detail of model development). The training procedure of the proposed prediction model includes data input, data exclusion, feature selection, and OSA classification. The training procedure conducted in this study was based only on the training data set to prevent overfitting (i.e. a model that just repeats the samples that it has just seen would have a perfect score but would fail to predict unseen data). Subsequently, a comprehensive blind validation using the testing data set was conducted during the testing stage. In the proposed method, we applied the cross-validation (CV) approach in this study to test the effectiveness of the selected features and the machine learning model. CV is a resampling procedure used to hold out part of the available data as a testing set for model evaluation when data are limited. To perform CV, we put aside a portion of the data not used in model training for testing/validation (Supplementary Figure S1).
Figure 1.
The flow chart of developing SVM-based prediction model. Non-Chinese (n = 11), total recording time <240 min (n = 7), and any missing data (n = 936) were excluded. In the first feature selection stage, we observed that the top half of AUROC and MCC feature ranks were similar in all three different AHI cutoffs suggesting the robustness of these features. Therefore, only features with AUROC or MCC higher than median remained in the model. During the last feature selection, the fewest features were selected to keep AUROC ≥ 0.80.
To optimize the discriminative ability using the fewest features, continuous and categorical features were selected by single-feature SVM Area under the Receiver Operating Characteristic (AUROC) and Matthews Correlation Coefficient (MCC), respectively, during the feature selection [22]. Due to different mathematical characteristics between continuous and categorical features, this study developed a two-stage feature selection procedure to prevent the selection relying on a single type of feature set in the proposed model. In the first stage, only the continuous and categorical features with the top half of AUROC (Table 3) and MCC (Figure 2), respectively, were reserved to reduce the interference from the redundant features, in which these features may be robustly related to different AHI cutoffs. Subsequently, forward stepwise feature selection (FSFS) was exploited in the second half of feature selection. The feature set selected by FSFS was increased stepwise based on the greedy approach [23]. Specifically, the features with the maximum AUROC or MCC in the first stage were regarded as the feature candidates in the second stage. Afterward, each feature from the feature candidates was randomly integrated then used to train a new SVM for evaluating classification performance. During each iteration in the second stage, the add-on feature with the superior SVM performance was reserved for updating the selected feature. Accordingly, the updated selected set was used to evaluate the next incoming feature candidate (Supplementary Table S5). The whole training procedure of FSFS was iterated until the stopping criteria (AUROC ≥ 0.8). To achieve significant clinical application, the selected feature set based on FSFS was aimed to achieve target criteria in AUROC in three AHI cutoffs during the selection procedure. Eventually, the selected feature set after the two-stage feature selection was used to establish the prediction model for OSA recognition based on SVM [24]. The posterior probability of the SVM was used to determine the class of the incoming datum [25], either OSA or non-OSA. To further optimize the classification result, the Youden’s index was employed to find the optimal threshold of SVM posterior probability to determine categories. In addition, the fivefold CV was randomly repeated five times to verify the model reliability. The average AUROC of the fivefold CV for each of the three AHI cutoffs was calculated. The prediction model was trained by sleep lab-based data set with three AHI cutoff 5/h, 15/h, and 30/h, respectively, which means the models based on three AHI cutoffs were fairly trained and validated. To further evaluate the model robustness, the learning curves of three AHI cutoffs were depicted (Supplementary Figure S2).
Table 3.
AUROC of single continuous feature at SVM model for three AHI cutoffs
| Order | AHI ≥ 5/h | AHI ≥ 15/h | AHI ≥ 30/h | |||
|---|---|---|---|---|---|---|
| Feature | AUROC | Feature | AUROC | Feature | AUROC | |
| 1 | Waist | 0.794 | Waist | 0.763 | Waist | 0.754 |
| 2 | BMI | 0.772 | Neck | 0.747 | Neck | 0.742 |
| 3 | Neck | 0.769 | BMI | 0.739 | BMI | 0.736 |
| 4 | Age | 0.665 | Age | 0.561 | Age | 0.584 |
| Features not selected | ||||||
| 5 | SOL | 0.525 | Frequency of nocturia | 0.520 | Frequency of nocturia | 0.510 |
| 6 | Frequency of nocturia | 0.513 | ESS | 0.516 | ESS | 0.518 |
| 7 | Frequency of awakening in sleep | 0.513 | Frequency of awakening in sleep | 0.494 | Frequency of awakening in sleep | 0.503 |
| 8 | ESS | 0.495 | SOL | 0.488 | SOL | 0.493 |
The features were in order according to the AUROC value. In the first stage of feature selection, features with AUROC higher than median were selected.
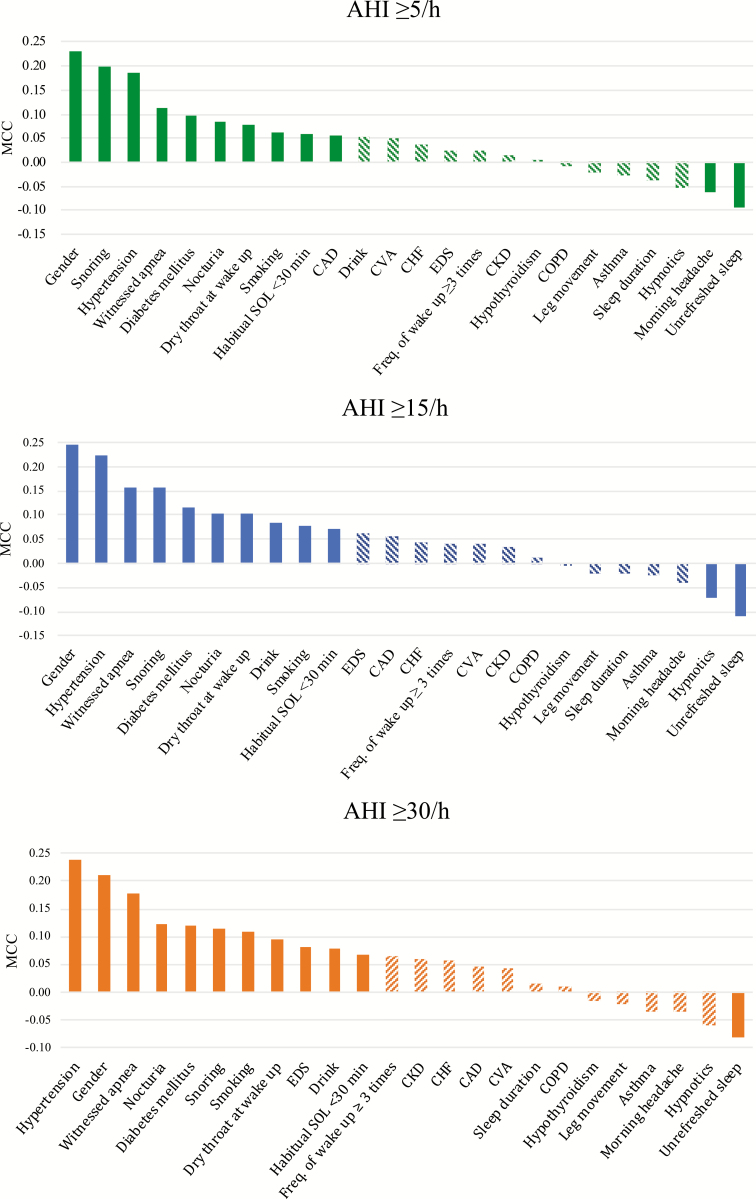
Figure 2.
MCC values of categorical features correlated with AHI ≥ 5/h, AHI ≥ 15/h, and AHI ≥ 30/h. The feature order was sorted by absolute MCC. The solid bars indicated features with MCC higher than median while the bars with stripe indicate features with MCC lower than median. CKD, chronic kidney disease; CAD, coronary artery disease; CHF, congestive heart failure; CVA, cerebrovascular accident; COPD, chronic obstructive pulmonary disease.
Data analysis
The discriminative ability of the proposed SVM model was evaluated using average of fivefold CV of AUROC, F1 score, accuracy, sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and positive likelihood ratio (LR+), and negative likelihood ratio (LR−) for each of the three AHI cutoffs. The performance was expressed as mean (95% confidence interval [CI]). The cutoff of AUROC value was identified using the Youden’s index. The SVM model was tested in subgroups categorized by gender (men versus woman) and age (<65 y/o versus ≥65 y/o) to identify subgroups for which the model worked best. The performance of the SVM model was compared to logistic regression, BQ, NoSAS Score, and SLIM scoring system.
For logistic regression, 67% of participants were randomly selected as training set, while the remaining 33% of the participants were selected as testing set. Logistic models with forward selection were used to identify suitable factors to establish the prediction model for AHI ≥5/h, ≥15/h, and ≥30/h in the training test. Each parameter has to be significant at the 0.0001 level to remain in the model. All the remaining variables were listed with odds ratio (OR) and 95% CI. The predictability of AHI ≥5/h, ≥15/h, and ≥30/h was assessed by the AUROC. In addition, sensitivity, specificity, PPV, and NPV were calculated by using the cutoff of Youden’s index.
The clinical features were compared between patients with and without OSA and among four subgroups at three AHI cutoffs. Continuous variables were expressed as mean ± standard deviation (SD) and categorical variables were expressed as percentage. Independent samples t-test and chi-square test were applied as appropriate in comparison of OSA data sets and non-OSA data sets as well as in the subgroups. A two-tailed p-value <0.05 was considered statistically significant. All statistical analyses were conducted by Python (Python Software Foundation. Python Language Reference, version 3.6.1. Available at http://www.python.org), and SAS Version 9.3 (SAS Institute, Cary, NC).
Results
The clinical features of patients are listed in Table 1 and Supplementary Table S2. The mean age was 47.8 y/o and 76% were men. The mean AHI was 29.6/h with a prevalence of 82.5%, 61.3%, and 40.6% at AHI ≥5/h, ≥15/h, and ≥30/h cutoffs, respectively. Compared to patients without OSA, those with OSA were older, more obese, sleepier, and had higher percentage of men, history of smoking and alcohol consumption, comorbidities, and OSA symptoms as well as shorter SOL. The patients without OSA had longer SOL, higher percentage of witnessed leg jerks in sleep, and morning headache than those with OSA. The habitual SOL is weakly correlated with SOL recorded by PSG (Pearson correlation, γ = 0.202, p < 0.001).
Feature selection
The MCCs of categorical features for different AHI cutoffs are listed in Figure 2. Twelve categorical features with top half of MCC value were selected for each AHI cutoff. The results of AUROC evaluation with SVMs trained by each single continuous feature are listed in Table 3. Four continuous features with top half of AUROC in predicting OSA were waist, neck circumference, BMI, and age. In total, 16 features were selected.
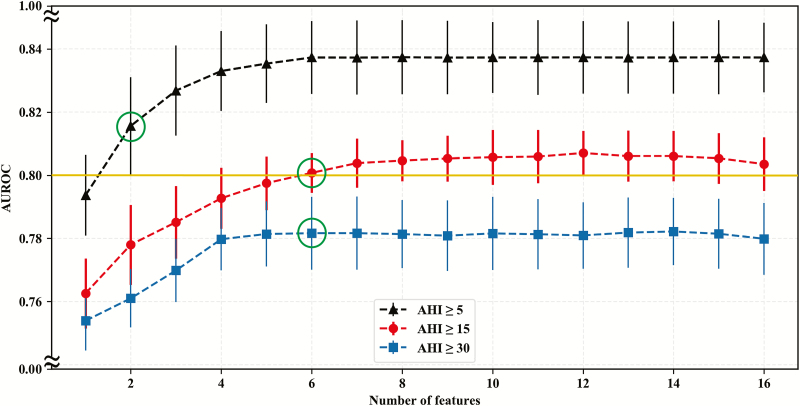
In the final feature selection, 2, 6, and 6 features were selected with FSFS for AHI ≥5/h, ≥15/h, and ≥30/h, respectively (Table 4; Figure 3) where the detailed iterations are listed in Supplementary Table S5. The learning curve showed no evidence of overfitting (Supplementary Figure S2). In addition to waist circumference and age, snoring, neck circumference, witnessed apnea, and SOL < 30 min were selected for AHI ≥ 15/h and AHI ≥ 30/h (Table 4). For logistic regression, 7, 10, and 10 features were selected for AHI ≥5/h, ≥15/h, and ≥30/h, respectively (Table 4; Supplementary Table S6). Five features selected in the SVM model including waist circumference, age, neck circumference, snoring, and witnessed apnea were also selected in the LR. The SOL was selected instead of SOL < 30 min. Additional selected features in LR includes BMI, dry throat, gender, hypnotic, and hypertension (Table 4).
Table 4.
The features selected with forward stepwise feature selection of SVM model and logistic regression for three AHI cutoffs
| Method | Order | AHI ≥ 5/h | AHI ≥ 15/h | AHI ≥ 30/h |
|---|---|---|---|---|
| SVM | 1 | Waist circumference | Waist circumference | Waist circumference |
| 2 | Age | Age | Witnessed apnea | |
| 3 | Neck circumference | Age | ||
| 4 | Snoring | Neck circumference | ||
| 5 | Witnessed apnea | Snoring | ||
| 6 | SOL < 30 min | SOL < 30 min | ||
| Logistic regression | N/A | Snoring | Snoring | Witnessed apnea |
| Gender | Witnessed apnea | Gender | ||
| Age | Dry throat | Snoring | ||
| Neck circumference | Gender | Hypertension | ||
| SOL | Hypnotic | Dry throat | ||
| BMI | Age | Waist circumference | ||
| Waist circumference | Waist circumference | Age | ||
| Neck circumference | Neck circumference | |||
| SOL | BMI | |||
| BMI | SOL |
In SVM model, the minimal feature set was selected to achieve the target criteria in the AUROC. When AHI cutoffs were 5/h and 15/h, the target AUROC was set as 0.8. While AHI cutoff was 30/h, the experiment showed that the maximum AUROC was 0.78, so we selected minimum features to achieve the performance. N/A, not applicable.
Figure 3.
This figure illustrates the relationship between AUROC of prediction model and corresponding numbers of features in the stepwise forward feature selection. The results show that fewest numbers of features to achieve AUROC ≥ 0.80 were 2, 6, and 6 for AHI ≥ 5/h, 15/h, and 30/h, respectively. The solid dot and bar indicated mean and standard deviation, respectively. The green circles indicated selected feature numbers with specific AHI cutoff.
Model discriminative ability
The discriminative ability of the SVM model and logistic regression, BQ, NoSAS Score, and SLIM scoring system for three AHI cutoffs are shown in Table 5. The performance of SVM model remains good consistently across three AHI criteria. The AUROC was 0.82, 0.80, and 0.78 for AHI ≥5/h, ≥15/h, and ≥30/h, respectively, while the accuracy was 74.24%, 72.68%, and 70.28%, respectively. The sensitivity was 74.14%, 75.18%, and 70.26%, for AHI ≥5/h, ≥15/h, and ≥30/h, respectively, while the specificity was 74.71%, 68.73%, and 70.30% respectively. Compared to logistic regression, SVM model had similar AUROC and accuracy across three AHI cutoffs. Moreover, at higher AHI cutoffs, the SVM model upheld good sensitivity and NPV without losing specificity and PPV. Compared to BQ, the SVM model had higher AUROC, accuracy, specificity, PPV, and NPV across three AHI criteria while it had higher AUROC, accuracy, sensitivity, and NPV compared to NoSAS Score. Compared to SLIM scoring system, the SVM model had higher AUROC, accuracy, and sensitivity across three AHI criteria.
Table 5.
The performance of SVM, logistic regression, BQ, NoSAS Score, and SLIM scoring system at three AHI cutoffs
| Model | AHI cutoff (/h) | Feature no. | AUROC | F1 factor | Accuracy (%) | Sensitivity (%) | Specificity (%) | PPV (%) | NPV (%) | LR+ | LR− |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | ≥5 | 2 | 0.82 (0.79–0.85) | 0.83 (0.81–0.85) | 74.24 (71.59– 76.89) | 74.14 (71.33– 76.95) | 74.71 (70.88– 78.54) | 93.23 (92.17– 94.29) | 38.15 (34.79– 41.52) | 2.96 (2.52– 3.41) | 0.35 (0.30– 0.40) |
| ≥15 | 6 | 0.80 (0.79–0.81) | 0.77 (0.74–0.80) | 72.68 (70.52– 74.84) | 75.18 (67.61– 82.76) | 68.73 (61.72– 75.75) | 79.32 (76.84– 81.80) | 64.03 (59.75– 68.31) | 2.45 (2.04– 2.87) | 0.36 (0.29– 0.43) | |
| ≥30 | 6 | 0.78 (0.77–0.80) | 0.66 (0.61–0.70) | 70.28 (68.68– 71.88) | 70.26 (60.21– 80.31) | 70.30 (64.18– 76.43) | 61.93 (59.21– 64.35) | 77.86 (73.68– 82.03) | 2.39 (2.14– 2.64) | 0.42 (0.32– 0.52) | |
| LR | ≥5 | 7 | 0.84 (0.83–0.86) | — | 73.77 | 94.41 | 37.87 | 72.55 | 79.56 | 1.52 | 0.15 |
| ≥15 | 10 | 0.81 (0.80–0.82) | — | 72.14 | 79.94 | 62.69 | 72.21 | 72.03 | 2.14 | 0.32 | |
| ≥30 | 10 | 0.79 (0.78–0.81) | — | 72.83 | 65.01 | 78.77 | 69.94 | 74.77 | 3.06 | 0.44 | |
| BQ | ≥5 | — | 0.54 (0.52–0.56) | — | 67.58 | 74.95 | 32.91 | 84.01 | 21.89 | 1.11 | 0.76 |
| ≥15 | — | 0.53 (0.52–0.55) | — | 58.39 | 76.09 | 30.41 | 63.34 | 44.58 | 1.09 | 0.79 | |
| ≥30 | — | 0.53 (0.51–0.54) | — | 48.09 | 76.68 | 28.55 | 42.31 | 64.17 | 1.07 | 0.81 | |
| NoSAS Score | ≥5 | 4 | 0.70 (0.68–0.71) | — | 57.25 | 50.62 | 88.39 | 95.31 | 27.58 | 4.36 | 0.56 |
| ≥15 | 4 | 0.68 (0.67–0.70) | — | 66.01 | 57.99 | 78.67 | 81.13 | 54.23 | 2.72 | 0.53 | |
| ≥30 | 4 | 0.68 (0.67–0.69) | — | 68.30 | 64.88 | 70.64 | 60.16 | 74.64 | 2.20 | 0.50 | |
| SLIM (10 size) | ≥5 | 10 | 0.69 (0.67–0.70) | 0.63 | 54.68 | 47.10 | 90.30 | 95.80 | 26.64 | 4.86 | 0.59 |
| ≥15 | 10 | 0.68 (0.67–0.69) | 0.65 | 64.77 | 54.33 | 81.27 | 82.10 | 52.96 | 2.90 | 0.56 | |
| ≥30 | 10 | 0.68 (0.67–0.70) | 0.62 | 69.40 | 62.24 | 74.29 | 62.33 | 74.22 | 2.42 | 0.51 |
The data were presented as mean (95% confidence interval). LR, logistic regression.
The discriminative ability of SVM model in four subgroups are shown in Table 6. The AUROC and accuracy were similar between male and female while AUROC, accuracy, specificity, PPV, and NPV were higher in <65 y/o than ≥65 y/o subgroup. Moreover, the discriminative ability was best for male <65 y/o and modest for female ≥65 y/o. To make this proposed prediction model available to researchers and clinicians, we have built an easy-to-use website (http://howareyou.csie.ntu.edu.tw), which provides OSA probability prediction based on our machine learning model.
Table 6.
The performance of SVM model in subgroups including men, women, <65 y/o, and ≥65 y/o
| AHI cutoff | No. of ≥AHI cutoff | AUROC | F1 score | Accuracy (%) | Sensitivity (%) | Specificity (%) | PPV (%) | NPV (%) | LR+ | LR− | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Male | ≥5 | 4,653 | 0.80 (0.77–0.83) | 0.82 (0.80–0.83) | 71.82 (69.59–74.04) | 71.21 (69.04–73.37) | 76.06 (73.04–79.08) | 95.35 (94.67–96.04) | 27.69 (25.55–29.84) | 3.00 (2.59–3.42) | 0.38 (0.34–0.42) |
| ≥15 | 3,550 | 0.77 (0.77–0.78) | 0.76 (0.70–0.81) | 69.86 (65.74–73.98) | 69.30 (59.97–78.63) | 71.08 (63.99–78.16) | 83.70 (81.83–85.58) | 52.62 (48.17–57.07) | 2.44 (2.07–2.82) | 0.43 (0.35–0.51) | |
| ≥30 | 2,425 | 0.76 (0.74–0.78) | 0.66 (0.59–0.73) | 69.65 (67.17–72.13) | 64.58 (52.25–76.91) | 74.06 (67.47–80.64) | 68.50 (66.53–70.48) | 71.09 (66.21–75.98) | 2.52 (2.29–2.74) | 0.47 (0.36–0.59) | |
| Female | ≥5 | 1,106 | 0.78 (0.73–0.83) | 0.79 (0.74–0.84) | 72.76 (67.28–78.24) | 77.75 (70.55–84.96) | 62.64 (56.94–68.35) | 80.79 (77.74–83.85) | 58.64 (50.32–66.96) | 2.11 (1.65–2.58) | 0.36 (0.23–0.48) |
| ≥15 | 661 | 0.79 (0.75–0.83) | 0.67 (0.65–0.69) | 67.92 (63.79–72.06) | 81.84 (79.15–84.53) | 58.64 (50.16–67.12) | 57.13 (52.74–61.53) | 82.87 (81.88–83.86) | 2.02 (1.65–2.39) | 0.31 (0.29–0.33) | |
| ≥30 | 366 | 0.79 (0.75–0.82) | 0.52 (0.47–0.57) | 68.17 (61.43–74.91) | 77.04 (74.41–79.67) | 65.64 (56.66–74.62) | 39.47 (33.20–45.75) | 90.91 (89.86–91.96) | 2.33 (1.68–2.98) | 0.35 (0.31–0.40) | |
| <65 y/o | ≥5 | 4,870 | 0.82 (0.79–0.85) | 0.83 (0.80–0.85) | 74.52 (71.62–77.41) | 74.68 (71.42–77.93) | 73.81 (69.80–77.82) | 92.56 (91.41–93.71) | 40.14 (36.42–43.86) | 2.88 (2.46–3.31) | 0.34 (0.29–0.40) |
| ≥15 | 3,577 | 0.81 (0.80–0.82) | 0.77 (0.74–0.81) | 73.43 (71.47–75.39) | 76.46 (68.81–84.10) | 68.94 (62.42–75.46) | 78.66 (76.51–80.82) | 66.74 (62.27–71.22) | 2.50 (2.15–2.85) | 0.34 (0.27–0.41) | |
| ≥30 | 2,347 | 0.79 (0.78–0.81) | 0.66 (0.62–0.70) | 70.96 (69.22–72.70) | 71.83 (62.05–81.61) | 70.40 (63.93–76.87) | 61.22 (58.19–64.25) | 79.75 (75.68–83.82) | 2.46 (2.13–2.79) | 0.40 (0.29–0.50) | |
| ≥65 y/o | ≥5 | 799 | 0.70 (0.64–0.76) | 0.78 (0.76–0.79) | 65.84 (63.68–68.00) | 65.83 (63.37–68.30) | 65.73 (52.01–79.45) | 94.47 (92.42–96.52) | 17.94 (14.85–21.04) | 2.19 (0.88–3.50) | 0.53 (0.43–0.63) |
| ≥15 | 634 | 0.69 (0.67–0.72) | 0.72 (0.66–0.79) | 64.94 (59.99–69.88) | 65.75 (54.68–76.82) | 62.92 (50.00–75.84) | 81.77 (77.98–85.57) | 42.92 (39.06–46.79) | 1.87 (1.33–2.40) | 0.54 (0.46–0.63) | |
| ≥30 | 444 | 0.70 (0.68–0.72) | 0.62 (0.54–0.69) | 64.16 (61.20–67.12) | 58.52 (45.19–71.85) | 69.74 (60.90–78.58) | 66.07 (63.15–68.99) | 63.23 (58.75–67.71) | 1.97 (1.71–2.23) | 0.59 (0.47–0.71) | |
| Male < 65 y/o | ≥5 | 3,972 | 0.81 (0.78–0.84) | 0.82 (0.80–0.84) | 72.47 (70.56–74.37) | 71.80 (69.64–73.97) | 76.81 (72.96–80.67) | 95.29 (94.52–96.06) | 29.46 (27.70–31.22) | 3.14 (2.63–3.65) | 0.37 (0.33–0.40) |
| ≥15 | 3,075 | 0.78 (0.77–0.79) | 0.76 (0.72–0.81) | 70.74 (67.41–74.07) | 70.18 (61.74–78.62) | 71.89 (64.65–79.14) | 83.77 (81.54–86.01) | 54.50 (50.56–58.44) | 2.56 (2.08–3.05) | 0.41 (0.34–0.48) | |
| ≥30 | 2,077 | 0.77 (0.75–0.79) | 0.66 (0.61–0.72) | 70.15 (68.40–71.91) | 65.96 (54.65–77.26) | 73.64 (67.30–79.97) | 67.68 (65.67–69.69) | 72.62 (68.15–77.10) | 2.53 (2.29–2.78) | 0.46 (0.35–0.56) | |
| Male ≥ 65 y/o | ≥5 | 591 | 0.66 (0.50–0.82) | 0.77 (0.71–0.84) | 64.99 (56.26–73.71) | 65.65 (58.02–73.28) | 57.09 (30.16–84.02) | 94.53 (90.98–98.08) | 13.31 (5.67–20.95) | 1.82 (0.85–2.79) | 0.81 (-0.07–1.70) |
| ≥15 | 475 | 0.69 (0.64–0.75) | 0.72 (0.59–0.85) | 64.67 (52.79–76.55) | 64.21 (46.97–81.45) | 66.08 (57.94–74.23) | 84.07 (81.07–87.07) | 40.99 (30.06–51.92) | 1.91 (1.45–2.37) | 0.54 (0.31–0.76) | |
| ≥30 | 348 | 0.68 (0.65–0.72) | 0.60 (0.51–0.70) | 61.58 (57.45–65.71) | 54.82 (40.88–68.77) | 69.49 (61.48–77.50) | 67.95 (66.43–69.47) | 57.03 (52.80–61.27) | 1.80 (1.68–1.92) | 0.64 (0.52–0.77) | |
| Female < 65 y/o | ≥5 | 898 | 0.78 (0.72–0.84) | 0.78 (0.74–0.83) | 72.32 (67.63–77.01) | 78.52 (72.21–84.82) | 61.35 (55.96–66.73) | 78.23 (75.33–81.13) | 62.05 (54.74–69.35) | 2.06 (1.67–2.45) | 0.35 (0.24–0.46) |
| ≥15 | 502 | 0.79 (0.76–0.83) | 0.66 (0.62–0.70) | 67.70 (62.00–73.39) | 85.67 (81.39–89.94) | 57.70 (48.59–66.82) | 53.22 (48.26–58.19) | 87.83 (84.22–91.43) | 2.07 (1.68–2.45) | 0.25 (0.17–0.33) | |
| ≥30 | 270 | 0.79 (0.76–0.83) | 0.49 (0.43–0.55) | 66.83 (59.86–73.80) | 81.11 (76.69–85.54) | 63.44 (55.04–71.83) | 35.01 (28.68–41.34) | 93.33 (91.53–95.14) | 2.30 (1.61–2.99) | 0.30 (0.21–0.39) | |
| Female ≥ 65 y/o | ≥5 | 208 | 0.71 (0.57–0.85) | 0.78 (0.72–0.85) | 68.88 (62.49–75.26) | 68.31 (56.76–79.85) | 71.07 (47.64–94.50) | 93.19 (89.36–97.02) | 29.79 (28.03–31.56) | 3.14 (1.14–5.13) | 0.44 (0.39–0.49) |
| ≥15 | 159 | 0.68 (0.61–0.74) | 0.66 (0.59–0.73) | 60.30 (54.38–66.22) | 60.32 (50.11–70.54) | 60.39 (50.49–70.30) | 73.41 (68.65–78.17) | 46.04 (39.42–52.66) | 1.56 (1.25–1.86) | 0.66 (0.49–0.84) | |
| ≥30 | 96 | 0.70 (0.65–0.76) | 0.59 (0.49–0.69) | 66.88 (56.89–76.87) | 60.47 (47.36–73.59) | 70.95 (55.26–86.63) | 58.64 (42.90–74.38) | 73.92 (65.99–81.84) | 2.66 (0.42–4.91) | 0.57 (0.34–0.79) |
The data were presented as mean (95% confidence interval).
Discussion
In this study, we proposed a data mining-driven SVM model using a large-scale sleep lab-based data set to predict OSA with three different AHI cutoffs. The features selected in the model were as few as 2, 6, and 6 for AHI ≥5/h, ≥15/h, and ≥30/h, respectively, and all were collected at the clinics. Compared to logistic regression, the SVM model had noninferior discriminative ability, balanced sensitivity and specificity, and with fewer features. The discriminative ability of SVM model was better than BQ, NoSAS Score, and SLIM scoring system. The SVM model worked best for male <65 y/o.
A major strength of our model is that our SVM prediction is built using a large-scale data set from sleep clinics with very few exclusions which enhance the representativeness of the data set and minimize the selection bias of small samples (Supplementary Table S1) [9, 18, 19, 26–36]. Moreover, all 32 features are information routinely collected at the clinic visits and are not physiological parameters derived from overnight pulse oximetry or pulmonary function test. Unlike certain model [7] that includes physical findings of oral cavity which may be difficult to measure precisely [27], we did not include such features for the model development. Similarly, we were concerned that single office blood pressure may not be representative so we did not include it as an input feature.
Another strength of this study is that we designed a two-stage feature selection process with three AHI cutoffs. First-stage feature selection allowed categorical features and continuous features to be selected separately and thus the inclusion of categorical features like witnessed apnea and SOL < 30 min. Furthermore, the FSFS allowed priorities of features to change with different AHI cutoff. Using three AHI cutoffs for OSA would be more stringent than single cutoff. Models that predict AHI ≥ 5/h tend to have high sensitivity but low specificity [27] and could increase the risk of over prescriptions of PSG for those without OSA. Our model achieved a balance in sensitivity and specificity compared to the discriminative ability of the previous studies. When compared to the Duarte’s model [36], which has a high sensitivity and low specificity with two features (Supplementary Table S1), our model has a higher AUROC, sensitivity, and specificity across three AHI cutoffs. The balanced discriminative ability of our model could allow early identification of the patients with high probability of OSA without overprescribing sleep study.
The six features, with the exception of SOL < 30 min, were often selected in the prediction models reported in the literature while SOL < 30 min has never been described to predict AHI ≥ 15/h or AHI ≥ 30/h (Supplementary Table S1). The selection of SOL < 30 min as a feature in the SVM model was a surprise but was echoed by the selection of SOL in logistic regression. Despite that SOL was an input feature in the Boosting model proposed by Caffo et al., it was not selected for their modeling [30]. The difference may be due to the fact that the participants in the Caffo study were from a community population and were older with more females.
Similar to the findings of other studies, neither ESS nor EDS was selected as a model feature, which reflects that there is a high prevalence of EDS in OSA patients regardless of AHI. It may be related to the clinical practice that patients with EDS are more prone to be referred for sleep study and sleepiness is not necessarily concordant with OSA severity [27].
Our results are comparable to another model validated in the Chinese population. Liu et al. [33] developed an SVM-based model to predict OSA with three anthropometric features, i.e. waist size, neck size, and BMI. That study included age, BQ, and anthropometrics as features. The predictability for AHI ≥ 15/h and AHI ≥ 30/h in Liu’s model is highest in females ≤50 y/o. Compared to the discriminative ability for AHI ≥ 15/h in the model reported by Liu et al., our model has higher AUROC and accuracy in elderly males while lower in elderly females. The difference in performance is likely due to the inclusion of OSA symptoms such as snoring and witnessed apnea. Moreover, the age cutoff in our study for subgroup analysis is 65 y/o as opposed to 50 y/o in the study by Liu. We arbitrarily chose 65 y/o as cutoff for subgroup analysis. Elderly OSA patients often have poorer association between AHI and body habitus variables (neck size, BMI, and waist-to-hip ratio), a lower percentage of habitual snoring, and a longer SOL compared to younger patients [5], which may contribute to the poorer performance of our model in the elderly as our model was built with anthropometrics and OSA symptoms.
There are a few limitations in the present study. First, several features highly associated with OSA such as hyperlipidemia and atrial fibrillation were not included in the database and thus not employed for model development. Second, the data set was built form the information collected from the patients referred to our sleep lab for sleep study in whom the prevalence of OSA is high. The result may not be applicable to the general population where the prevalence of OSA is much lower. Third, the participants are all Chinese and the accuracy of this model in other ethnic groups remains unclear. The validity of this model needs to be confirmed in community populations of multiple ethnicity to address the significance and implication. Fourth, using AHI cutoff as the sole target of prediction is one of the limitations of our study. AHI has been known for its loose association with OSA-related outcomes [37] while factors like EDS may have a better prediction of cardiovascular outcome than AHI [38]. In the future, other parameters such as morbidity should be considered as targets of prediction. Fifth, we did not compare our model with STOP-Bang [39] as STOP-Bang was not included as part of our sleep lab routine questionnaires until January 2017. Further study comparing our SVM model with STOP-Bang may be warranted.
In conclusion, our SVM model provides a simple and accurate modality for early identification of patients with OSA. Future studies and machine learning model algorithm development should focus on validation in the sleep lab- and community-based populations with multiethnicity for greater clinical application.
Supplementary Material
Acknowledgments
The authors also thank the Taiwan Clinical Trial Bioinformatics and Statistical Center, Training Center, and Pharmacogenomics Laboratory, founded by the National Research Program for Biopharmaceuticals (NRPB) at the National Science Council (NSC) of Taiwan; the Ministry of Science and Technology (MOST); and the Department of Medical Research of NTUH, for the statistical assistance.
Funding
This research was funded by grants from the National Science Council of Taiwan (NSC102-2314-B002-099); Ministry of Science and Technology, Taiwan (project number MOST 103-2314-B-002-139-MY3); National Taiwan University (project number NTU-ERP-104R8951-1, 105R8951-1, 106R880301); National Taiwan University Hospital (NTUH 107-19, 108-S4331); “Center for electronics technology integration (NTU-107L900502, 108L900502)” from the Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan; and NTU-NTUH-MediaTek Innovative Medical Electronics Research Center. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Conflict of interest statement. None declared.
References
- 1. Patil SP, et al. Adult obstructive sleep apnea: pathophysiology and diagnosis. Chest. 2007;132(1):325–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Senaratna CV, et al. Prevalence of obstructive sleep apnea in the general population: a systematic review. Sleep Med Rev. 2017;34:70–81. [DOI] [PubMed] [Google Scholar]
- 3. Bradley TD, et al. Obstructive sleep apnoea and its cardiovascular consequences. Lancet. 2009;373(9657):82–93. [DOI] [PubMed] [Google Scholar]
- 4. Somers VK, et al. Sleep apnea and cardiovascular disease: an American Heart Association/American College of Cardiology Foundation Scientific Statement from the American Heart Association Council for High Blood Pressure Research Professional Education Committee, Council on Clinical Cardiology, Stroke Council, and Council on Cardiovascular Nursing. J Am Coll Cardiol. 2008;52(8):686–717. [DOI] [PubMed] [Google Scholar]
- 5. Kunisaki KM, et al. Provider types and outcomes in obstructive sleep apnea case finding and treatment: a systematic review. Ann Intern Med. 2018;168(3):195–202. [DOI] [PubMed] [Google Scholar]
- 6. Harding SM. Prediction formulae for sleep-disordered breathing. Curr Opin Pulm Med. 2001;7(6):381–385. [DOI] [PubMed] [Google Scholar]
- 7. Kirby SD, et al. Neural network prediction of obstructive sleep apnea from clinical criteria. Chest. 1999;116(2):409–415. [DOI] [PubMed] [Google Scholar]
- 8. Zerah-Lancner F, et al. Predictive value of pulmonary function parameters for sleep apnea syndrome. Am J Respir Crit Care Med. 2000;162(6):2208–2212. [DOI] [PubMed] [Google Scholar]
- 9. Zou J, et al. An effective model for screening obstructive sleep apnea: a large-scale diagnostic study. PLoS One. 2013;8(12):e80704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Appleton S, et al. Influence of gender on associations of obstructive sleep apnea symptoms with chronic conditions and quality of life. Int J Environ Res Public Health. 2018;15(5):930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Lin CM, et al. Gender differences in obstructive sleep apnea and treatment implications. Sleep Med Rev. 2008;12(6):481–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Launois SH, et al. Sleep apnea in the elderly: a specific entity? Sleep Med Rev. 2007;11(2):87–97. [DOI] [PubMed] [Google Scholar]
- 13. Martínez-García MA, et al. Obstructive sleep apnea has little impact on quality of life in the elderly. Sleep Med. 2009;10(1):104–111. [DOI] [PubMed] [Google Scholar]
- 14. Yamagishi K, et al. Cross-cultural comparison of the sleep-disordered breathing prevalence among Americans and Japanese. Eur Respir J. 2010;36(2):379–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Tomar D, et al. A survey on data mining approaches for healthcare. International Journal of Bio-Science and Bio-Technology. 2013;5(5):241–266.
- 16. Chen NH, et al. Validation of a Chinese version of the Epworth sleepiness scale. Qual Life Res. 2002;11(8):817–821. [DOI] [PubMed] [Google Scholar]
- 17. Luo J, et al. STOP-Bang questionnaire is superior to Epworth sleepiness scales, Berlin questionnaire, and STOP questionnaire in screening obstructive sleep apnea hypopnea syndrome patients. Chin Med J (Engl). 2014;127(17):3065–3070. [PubMed] [Google Scholar]
- 18. Marti-Soler H, et al. The NoSAS score for screening of sleep-disordered breathing: a derivation and validation study. Lancet Respir Med. 2016;4(9):742–748. [DOI] [PubMed] [Google Scholar]
- 19. Ustun B, et al. Clinical prediction models for sleep apnea: the importance of medical history over symptoms. J Clin Sleep Med. 2016;12(2):161–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Liu HW, et al. Combining MAD and CPAP as an effective strategy for treating patients with severe sleep apnea intolerant to high-pressure PAP and unresponsive to MAD. PLoS One. 2017;12(10):e0187032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Iber C, et al. for the American Academy of Sleep Medicine The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology and Technical Specifications. 1st ed. Westchester, IL: American Academy of Sleep Medicine; 2007. [Google Scholar]
- 22. Boughorbel S, et al. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS One. 2017;12(6):e0177678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Alvarez D, et al. Assessment of feature selection and classification approaches to enhance information from overnight oximetry in the context of apnea diagnosis. Int J Neural Syst. 2013;23(5):1350020. [DOI] [PubMed] [Google Scholar]
- 24. Yuanyuan S, et al. The comparison of optimizing SVM by GA and grid search. In: proceedings from the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI); October 20–22, 2017.
- 25. Karatzoglou A, et al. Support vector machines in R. J Stat Softw. 2006;15(9):1–28. [Google Scholar]
- 26. Rowley JA, et al. The use of clinical prediction formulas in the evaluation of obstructive sleep apnea. Sleep. 2000;23(7):929–938. [DOI] [PubMed] [Google Scholar]
- 27. Rodsutti J, et al. A clinical decision rule to prioritize polysomnography in patients with suspected sleep apnea. Sleep. 2004;27(4):694–699. [DOI] [PubMed] [Google Scholar]
- 28. Sharma SK, et al. Prediction of obstructive sleep apnea in patients presenting to a tertiary care center. Sleep Breath. 2006;10(3):147–154. [DOI] [PubMed] [Google Scholar]
- 29. Takegami M, et al. Simple four-variable screening tool for identification of patients with sleep-disordered breathing. Sleep. 2009;32(7):939–948. [PMC free article] [PubMed] [Google Scholar]
- 30. Caffo B, et al. A novel approach to prediction of mild obstructive sleep disordered breathing in a population-based sample: the Sleep Heart Health Study. Sleep. 2010;33(12):1641–1648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Bouloukaki I, et al. Prediction of obstructive sleep apnea syndrome in a large Greek population. Sleep Breath. 2011;15(4):657–664. [DOI] [PubMed] [Google Scholar]
- 32. Ting H, et al. Decision tree based diagnostic system for moderate to severe obstructive sleep apnea. J Med Syst. 2014;38(9):94. [DOI] [PubMed] [Google Scholar]
- 33. Liu WT, et al. Prediction of the severity of obstructive sleep apnea by anthropometric features via support vector machine. PLoS One. 2017;12(5):e0176991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Tan A, et al. Validation of NoSAS score for screening of sleep-disordered breathing in a multiethnic Asian population. Sleep Breath. 2017;21(4):1033–1038. [DOI] [PubMed] [Google Scholar]
- 35. Traxdorf M, et al. The Erlangen Questionnaire: a new 5-item screening tool for obstructive sleep apnea in a sleep clinic population - a prospective, double blinded study. Eur Rev Med Pharmacol Sci. 2017;21(16):3690–3698. [PubMed] [Google Scholar]
- 36. Duarte RLM, et al. Simplifying the screening of obstructive sleep apnea with a 2-item model, no-apnea: a cross-sectional study. J Clin Sleep Med. 2018;14(7):1097–1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Zinchuk A, et al. Sleep apnea heterogeneity, phenotypes, and cardiovascular risk. Implications for trial design and precision sleep medicine. Am J Respir Crit Care Med. 2019;200(4):412–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Mazzotti DR, et al. Symptom subtypes of obstructive sleep apnea predict incidence of cardiovascular outcomes. Am J Respir Crit Care Med. 2019;200(4):493–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Chung F, et al. Alternative scoring models of STOP-Bang questionnaire improve specificity to detect undiagnosed obstructive sleep apnea. J Clin Sleep Med. 2014;10(9):951–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.